Local Directional Fractal Signature Method for Surface Texture Analysis

Abstract

The detection of changes in surface texture characteristics is an important issue in manufacturing, contact mechanics, control of interactions between surfaces, machine failure analysis, and others. These changes can be detected early on when surface texture is quantified locally at each point. To this end, a new method called local directional fractal signature has recently been developed that calculates local fractal dimensions (FD = 3 − slope) at individual scales and directions. In this method, texture parameters are derived from the slopes of lines fitted to log–log plots of local surface profiles against scales, and FDs to measure local surface roughness and directionality. First, the method is tested on computer-generated isotropic fractal surfaces with the objective to evaluate its ability to differentiate between surfaces exhibiting an increasing local roughness. This follows the method application to detect the anisotropy changes in computer-generated surfaces with increasing roughness in two directions. Finally, the method’s detection ability in finding differences between surfaces is evaluated. Microscopic range-images of sandblasted and abraded titanium alloy plates are used in the evaluation. This work is a further contribution to the advancement in the characterization of surface textures, the numerical tools development for the design of tribological components and the diagnosis of worn and damaged surfaces. Practical applications of the method (e.g., classification of wear images, characterization of coated and uncoated surfaces) would be reported later in the future.

1 Introduction

Fractal geometry is a foundation of the numerical methods used to characterize surface textures. Two fractal-based methods currently included in ASME [1] and ISO [2, 3] standards are: a patchwork and a morphological structuring element method. These two methods measure a surface roughness by calculating a fractal dimension (FD). A higher value of the dimension means a rougher surface. Successful applications of these standard methods have been reported. For example, the former has been used effectively to measure a skin roughness [4] and to study the effects of a food surface roughness on an oil absorption [5]. The latter has been useful in the roughness measurement of human cornea membrane [6], polymer films [7] and aluminum nitride epilayers [8]. The range of applications of these methods is, however, limited. This arises from the fact that the methods provide a single value of FD for the entire surface area, while currently produced surfaces exhibit topographical features of various sizes and orientations recurring at different locations.

Previous studies have shown that the directionality, size and spatial location of surface topographical features affect interactions between surfaces. For example, the local surface roughness has been shown to influence the frictional shear stress and the flash temperature in fretting contacts [9], the quality of sheet metal forming products [10] and others. In other study, the stimulation to growth of trabecular bone on implant surfaces has been attributed to the roughness and directionality of local micro-texture patterns [11]. The strong link has been reported between the emissivity of a material surface and the local roughness factors [12]. Therefore, it seems necessary to develop methods that calculate FDs for local surface features/patterns at individual scales and in different directions.

Our earlier unified approach proposed for directional fractal signatures (DFSs) addresses the problem of calculating local FDs to some extent [13]. It quantifies the surface roughness, curvature and slope over a range of scales in different directions. However, the limitation is that the surface topographical features are quantified without providing the information about where these features are located on the surface.

Several fractal methods are able to quantify changes of surface roughness at single locations. For example, the method developed by Pentland [14] divides the surface image data into non-overlapping windows and then, applies a Fractal Brownian function to each window to calculate a local FD. The method by Novianto et al. calculates FDs at each pixel location by applying a blanket covering algorithm to moving windows [15]. Wenxue et al. proposed a triangular-prism method that calculates local FDs using a divisor step sampling algorithm [16]. The shortcoming of these methods is that they do not calculate FDs at individual scales and directions.

In the present work, we propose a new method, called local directional fractal signatures (LDFS) method, that calculates FSs in all possible directions at each location point, i.e., at each pixel on a surface image. The directions are automatically selected using a special algorithm called automated circumferential direction selection (ACDS). The algorithm uses a small circular search region that is centered at pixel. Based on the border and diameters of the region, local surface profiles comprising image gray-scale level values are selected in different directions. DFSs are then calculated for each local profile. The calculation is carried out at each pixel location and then, the whole process is repeated for larger size circular regions. The performance of this method was evaluated on computer-generated isotropic fractal surfaces with increasing FD and anisotropic surfaces with two dominating directions and on confocal microscopy images of sandblasted and ground surfaces.

2 Materials and Methods

2.1 Texture Representation

Surface texture is represented as an image with $N_{x}$ by $N_{y}$ pixels and $N_{z}$ (= 255) grey-scale levels in the horizontal and vertical directions, respectively. The image can be defined as a function $z_{ij} = I\left( {x_{i} ,y_{j} } \right)$ which assigns a grey-scale level value $z_{ij} \in L_{z}$ to a pixel located at $\left( {x_{i} ,y_{j} } \right) \in L_{x} \times L_{y}$, where $L_{x} = \left\{ {1,2, \ldots ,N_{x} } \right\}$, $L_{y} = \left\{ {1,2, \ldots ,N_{y} } \right\}$ and $L_{z} = \left\{ {0,1, \ldots ,N_{z} } \right\}$ are spatial and grey-scale level domains.

2.2 LDFS Method

The method calculates FSs in all possible directions and at each pixel location of the surface image. Directions are automatically selected using an ACDS algorithm. The algorithm generates circular search regions with radii ranging from 1 to N_r in steps of one pixel, i.e., r = 1,2, …, N_r where N_r = floor(min(N_y, N_x)/10) is the maximum radius. The value of 1/10 is chosen in accordance with the Rank Taylor Hobson criterion that the surface sampling length should include about 10 roughness marks [17, 18]. The following steps are taken to select the directions:

• 1. Let r = 1.

• 2. Centre a circular search region $L_{xy}$ of radius r at pixel (x,y) (Fig. 1a).

• 3. Select border pixels of the region (Fig. 1b).

• 4. For each pixel selected generate a diameter line (Fig. 1c) and then, rasterize the line using the Bresenham’s line algorithm (Fig. 1d).

• 5. Store pixels of the rasterized lines into sets $P_{{\theta_{n} r}}$, $n = 1,2, \ldots ,N_{l}$ where $N_{l }$ is the total number of lines. The set $P_{{\theta_{n} r}}$ represents a local surface profile with the direction of $\theta_{n}$ and the length of 2r + 1. The direction $\theta_{n}$ is measured with respect to the image horizontal axis.

• 6. If $r < N_{r}$ then r $= r + 1$ and go to step 2.

• 7. For each direction $\theta_{n}$ calculate the number of radii using the sets $P_{{\theta_{n} r}}$ and then, discard directions with less than three radii. The number of directions obtained is equal to $N_{\theta }$$.$

Fig. 1

Schematic illustration of the ACDS algorithm

The LDFS method calculates local FSs in the following steps (Fig. 2):

• 1. Let $j = 1$.

• 2. Let $i = 1$.

  • 2.1 For pixel (x_i, y_j) construct sets $P_{{\theta_{n} r}}$ using the ACDS algorithm.

  • 2.2 Let n = 1.

  • 2.3 If $n < N_{\theta }$ then n $= n + 1$ and go to step A.

    A. Let r = 1.

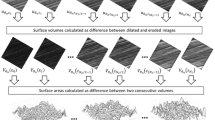
    B. Within set $P_{{\theta_{n} r}}$ calculate a difference between the maximum and minimum values of gray-scale levels, i.e., $A_{{\theta_{n} r}}$ = max($P_{{\theta_{n} r}}$)-min($P_{{\theta_{n} r}}$). The difference is called a local profile area.

    C. If $r < N_{r}$ then r $= r + 1$ and go to step B.

  • 2.4 Let n = 1.

    A. Plot $A_{{\theta_{n} r}}$ against radii r in log–log coordinates.

    B. Divide the log–log plot of data points into overlapping subsets of three points shifted by one data point and fit a line to each subset. The radius associated with the middle point of each subset represents an individual scale s, and the slope of the line fitted is calculated.

    C. Calculate FD = 3 − slope and store FD at individual scales ($s_{1} , s_{2} , \ldots ,s_{{N_{\theta } }} )$ in the direction $\theta_{n}$.

  • 2.5 If $n < N_{\theta }$ then n $= n + 1$ and go to step A.

• 3. If $i < N_{x}$ then $i = i + 1$ and go to step 2.1.

• 4. If $j < N_{y}$ then $j = j + 1$ and go to step 2.

Fig. 2

Flow chart of the LDFS method

At each pixel location, the slopes calculated can be presented in the following table

$${\text{Slope}}_{i,j} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{Slope}}_{{s_{1} \theta_{1} }} } & {{\text{Slope}}_{{s_{2} \theta_{1} }} } \\ {{\text{Slope}}_{{s_{1} \theta_{2} }} } & {{\text{Slope}}_{{s_{2} \theta_{2} }} } \\ \end{array} } & \cdots & {\begin{array}{*{20}c} {{\text{Slope}}_{{s_{{N_{1} }} \theta_{1} }} } \\ {{\text{Slope}}_{{s_{{N_{2} }} \theta_{2} }} } \\ \end{array} } \\ \vdots & \ddots & \vdots \\ {\begin{array}{*{20}c} {{\text{Slope}}_{{s_{1} \theta_{{N_{\theta } }} }} } & {{\text{Slope}}_{{s_{2} \theta_{{N_{\theta } }} }} } \\ \end{array} } & \cdots & {{\text{Slope}}_{{s_{{N_{\theta } }} \theta_{{N_{\theta } }} }} } \\ \end{array} } \right]_{i,j}$$

A similar table can be constructed for the local FDs, called a local directional fractal signature (LDFS), i.e.,

$${\text{LDFS}}_{i,j} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\text{FD}}_{{r_{1} \theta_{1} }} } & {{\text{FD}}_{{r_{2} \theta_{1} }} } \\ {{\text{FD}}_{{r_{1} \theta_{2} }} } & {{\text{FD}}_{{r_{2} \theta_{2} }} } \\ \end{array} } & \cdots & {\begin{array}{*{20}c} {{\text{FD}}_{{r_{{N_{1} }} \theta_{1} }} } \\ {{\text{FD}}_{{r_{{N_{2} }} \theta_{2} }} } \\ \end{array} } \\ \vdots & \ddots & \vdots \\ {\begin{array}{*{20}c} {{\text{FD}}_{{r_{1} \theta_{{N_{\theta } }} }} } & {{\text{FD}}_{{r_{2} \theta_{{N_{\theta } }} }} } \\ \end{array} } & \cdots & {{\text{FD}}_{{r_{{N_{\theta } }} \theta_{{N_{\theta } }} }} } \\ \end{array} } \right]_{i,j}$$

2.3 Texture Parameters

Texture parameters can be derived from the local slopes of lines fitted to log–log plots of local surface profiles against scales, and FDs at individual scales, directions, and location points. In this study, we calculate the following three texture parameters:

• 1. Global mean fractal dimension (GFD_MEAN): The parameter is defined as a mean value of all local FDs calculated. It is a measure of the global surface roughness across all scales, directions and locations.

• 2. Global mean fractal signature (GFS_MEAN): It represents a set of the mean values obtained by averaging all local FDs separately at each scale. GFS_MEAN measures the global surface roughness at individual scales.

• 3. Local mean fractal signature (LFS_MEAN): The signature is a set of the mean values obtained by averaging local FDs calculated at a single location at individual scales. LFS_MEAN measures the surface roughness at individual scales at a single location, i.e., the local surface roughness at each scale.

For each location and scale, the absolute values of slopes ${\text{abs}}\left( {{\text{Slope}}_{i,j} } \right)$ are plotted in polar coordinates as a function of direction and then, an ellipse is fitted to each plot. From each ellipse, the following two texture parameters are calculated:

• 1. Global mean surface texture aspect ratio signature (GStrS_MEAN): The signature is defined as a set of mean values obtained by averaging all Str ratios separately at each scale. The Str ratio is obtained by dividing the minor axis by the major axis of the ellipse fitted. It takes the value of zero for the ideal isotropic surface (i.e., surface with the same roughness in all directions) and less than one for other surfaces. GStrS_MEAN measures a degree of the surface anisotropy at individual scales.

• 2. Local surface texture aspect ratio signature (LStrS): The signature differs from GStrS_MEAN in using Str ratios from a single location instead of all locations. It measures a degree of the surface anisotropy at individual scales at a single location.

2.4 Image Databases

Three databases of surface images were used in this study. Two databases comprised computer-generated images of isotropic and anisotropic fractal surfaces. The isotropic surfaces exhibited increasing roughness while the anisotropic surfaces had two dominating directions. The directions are the angles defined with respect to the image horizontal axis. These two databases were used to evaluate the LDFS method’s ability to differentiate between surfaces with increasing roughness and to detect changes in surface anisotropy, respectively. The third database comprised 3D range-images of real surfaces was used to evaluate the method’s ability to differentiate between engineering surfaces. The number of gray-scale level values was set to 256.

2.4.1 Isotropic Fractal Surfaces

Isotropic surfaces with the theoretical FD (FD_t) ranging from 2.1 to 2.9 in steps of 0.1 were generated in three image sizes, i.e., 64 × 64, 128 × 128 and 200 × 200 pixels, using Stein method [19]. For each image size 450 images were generated, i.e., 9 × (50 images per FD_t). Example surfaces are shown in Fig. 3.

Fig. 3

Examples of isotropic fractal images with a, d, g FDt = 2.1, b, e, h 2.5 and c, f, i 2.9 in sizes of 64 × 64, 128 × 128 and 200 × 200 pixels, respectively

2.4.2 Anisotropic Fractal Surfaces

Two sets of anisotropic fractal surface images were generated using an inverse Fourier transform method [20]. The first set (Set 1) comprised 100 images with FD_t equals to 2.2 and 2.6 in the direction 120° and 30°, respectively. In the other set (Set 2) the surfaces have the direction of 0° and 90°, respectively. The image size was 200 × 200 pixels (Fig. 4).

Fig. 4

Images of anisotropic fractal surfaces with FD_t values equal to 2.2 and 2.6 in the direction of a 120° and 30° and b 0° and 90°, respectively. The image size is 200 × 200 pixels

2.4.3 Real Engineering Surfaces

One isotropic and three anisotropic surface samples taken from our previous work were analyzed [13]. The isotropic surface, denoted as SI, was obtained by sandblasting a titanium alloy (Ti–6Al–4 V) plate, while three anisotropic surfaces (SA1, SA2 and SA3) were produced by abrading the SI in different directions. Details of the experimental procedure are given in [13]. Briefly, SA1 was obtained by rubbing lightly SI in the vertical direction using an emery paper (SiC P2000 grade) under dry conditions. SA2 was generated by rubbing moderately SA1 with the P1200 grade emery paper in the 45° direction. The third sample (SA3) was produced by abrading severely SA2 with the P800 grade paper in the horizontal direction.

3D topography of these surfaces was acquired using a chromatic confocal profilometer (AltiSurf 530, Altimet, France). The scanned area was 3.75 × 3.75 mm and the lateral sampling intervals were set to 5 µm. The arithmetical mean height (S_a) and the texture aspect ratio (Str_ISO) were calculated. Values of these two standard parameters were 2.39 µm and 0.756 for SI, 2.40 µm and 0.766 for SA1, 2.12 µm and 0.764 for SA2 and 2.18 µm and 0.757 for SA3, respectively.

For each surface the elevation points were encoded into a range image of 750 × 750 pixels. The brightest and darkest pixels were assigned to the highest and lowest surface elevation points, respectively. Each image was then divided into 36 non-overlapping sub-images of 125 × 125 pixels. The total number of sub-images produced was 144. Example range images are shown in Fig. 5.

Fig. 5

Examples of range-images of a SI isotropic, b SA1, c SA2 and d SA3 anisotropic engineering surfaces. The image size is 0.625 × 0.625 mm

2.5 Statistical Analysis

Normality of the data was assessed with Shapiro–Wilk tests, while homogeneity of variances was checked with Levene’s tests. P < 0.01 was considered as statistically significant. Differences in texture parameters calculated for the isotropic fractal surfaces were evaluated using one-way ANOVA test. To analyze differences between isotropic and anisotropic fractal surfaces unpaired t-tests were used. The same tests were used to check the differences between texture parameters for pairs of engineering surfaces: SI-SA1, SI-SA2 and SI-SA3. The statistical analyses were performed using SPSS Statistics 21 (IBM, Corporation, Somers, NY). P < 0.05 was considered as statistically significant.

3 Results

3.1 Measurement of Surface Roughness

The mean ± standard deviation (SD) values of GFD_MEAN are listed in Table 1. A monotonic increase of GFD_MEAN with FD_t was observed for all image sizes. Example values are 2.161 ± 0.031 (FD_t = 2.1), 2.349 ± 0.019 (FD_t = 2.5) and 2.545 ± 0.006 (FD_t = 2.9) for 64 × 64; 2.144 ± 0.027 (FD_t = 2.1), 2.384 ± 0.020 (FD_t = 2.5) and 2.624 ± 0.006 (FD_t = 2.9) for 128 × 128; 2.168 ± 0.032 (FD_t = 2.1), 2.427 ± 0.018 (FD_t = 2.5) and 2.678 ± 0.005 (FD_t = 2.9) for 200 × 200 pixel images. ANOVA tests showed that the differences between GFD_MEAN values were statistically significant (p < 0.05). The tests were also conducted for LFS_MEAN. At almost all location points (99.74%), the differences in LFS_MEAN between the isotropic fractal surfaces were statistically significant.

Table 1 Mean ± SD values of GFD_MEAN calculated for isotropic fractal surface images with increasing FD_t and in different image sizes [pixel × pixel]

3.2 Measurement of Anisotropy

The mean ± SD values of GStrS_MEAN are listed in Table 2. For the isotropic surfaces GStrS_MEAN was statistically significantly higher at all scales as compared to the anisotropic surfaces.

Table 2 Mean ± SD values of GStrS_MEAN calculated for isotropic and anisotropic fractal surface images

A large amount of data was obtained from the comparison of LStrS since the signature was calculated at each pixel location. To present the data, maps of p values were constructed. The red color was chosen to show locations where the differences between isotropic and anisotropic surfaces were statistically significant (p < 0.05). Otherwise, the blue color was used. Maps obtained for the scales of 3, 6, 9, 13, 16 and 19 pixels for anisotropic surfaces (Set 1) are shown in Fig. 6. Maps obtained for Set 2 are similar (not shown). It was found that the number of non-statistically significant differences varies with scale, ranging from 0.44 (scale 13) to 89.34% (scale 19).

Fig. 6

Maps of p values of statistically significant (red) and non-significant (blue) differences in the LStrS parameter calculated between isotropic and anisotropic (Set 1) fractal surfaces at scales of 3, 6, 9, 13, 16 and 19 pixels (Color figure online)

3.3 Detection of Differences Between Engineering Surfaces

Higher values of GFS_MEAN were found for the anisotropic surfaces SA1, SA2, SA3 as compared to the isotropic surface SI (Table 3). The differences were statistically significant at one scale for SI-SA1 and six and seven scales for SI-SA2 and SI-SA3 as shown in Table 4. For example, at the scale of 55 µm the values obtained were 2.578 ± 0.014 (SI), 2.587 ± 0.012 (SA1), 2.590 ± 0.015 (SA2) and 2.594 ± 0.014 (SA3), respectively. Maps of p values obtained for the parameter GFS_MEAN are shown in Fig. 7 at the scales of 15, 35 and 55 µm. It can be seen from this figure that the majority of surface locations (about 94%) does not show significant differences.

Table 3 Mean ± SD values of GFS_MEAN and GStrS_MEAN calculated for the engineering surfaces SI, A1, SA2 and SA3

Table 4 p values of the differences (scales in μm) in the GFS_MEAN and GStrS_MEAN parameters calculated for the isotropic and anisotropic surfaces SI, SA1, SA2 and SA3

Fig. 7

Maps of p values of statistically significant (red) and non-significant (blue) differences in the LFS_MEAN parameter calculated between isotropic and anisotropic engineering surfaces: a–c SI-SA1, d–f SI-SA2 and g–i SI-SA3 at scales of 15, 35 and 55 µm (Color figure online)

Values of GStrS_MEAN were higher for SA1 at the scales ranged from 35 to 45 µm and SA2 at all scales, except 15 and 40 µm as compared to those obtained for SI, while they were lower for SA3 at all scales (Table 3). For example, the values of StrS_MEAN were 0.212 ± 0.003 (SI), 0.215 ± 0.004 (SA1), 0.214 ± 0.004 (SA2) and 0.200 ± 0.005 (SA3) at the scale of 45 µm. LStrS was also calculated for the real surfaces. The maps of p values obtained for the parameter show that about 93% of the locations are not statistically significant (Fig. 8).

Fig. 8

Maps of p values of local statistically significant (red) and non-significant (blue) differences in the LStrS parameter calculated between isotropic and anisotropic engineering surfaces: a–c SI-SA1, d–f SI-SA2 and g–i SI-SA3 at scales of 15, 35 and 55 µm (Color figure online)

Real surfaces were also analyzed using ISO roughness standard parameters, i.e., S_a and Str_ISO. Results of this analysis are summarized in Table 5.

Table 5 Mean ± SD values of the standard parameters S_a and Str_ISO calculated for the engineering surfaces SI, SA1, SA2 and SA3

3.4 Computational Time

The number of slopes or local FDs calculated for a single surface image is high and increases quadratically with image size. The LDFS method produced 40,960 FDs after applying to the 64 × 64 pixel surface image shown in Fig. 3a–c. There were 4 directions and the scales ranged from 1 to 4 pixels per direction. For the larger surface images shown in Fig. 3d–f (128 × 128) and Fig. 3g–i (200 × 200) the number of FDs increased to 786,432 and 5,360,000, and the directions and the range of scales increased to 16, 40 and 1–10, 1–18, respectively. Processing the images took 0.5, 5 and 29 min using a Linux Workstation with an eight-core 2.5 GHz CPU. The method was implemented in MATLAB and a single CPU core was utilized. Possible ways for reduction of the computational time are discussed below.

4 Discussion

A new method, called LDFS, was developed for the characterization of surface texture images. Unlike other multiscale methods, it measures the roughness and directionality of surface texture at individual location points. At each image pixel location, the method calculates FDs in all possible directions and over a wide range of scales. The scales range from the instrument resolution to 1/10 of the image shortest size and there are at least three scales per direction. This is a major advancement from the directional signature methods developed earlier [13]. Analyses of fractal and real surface images show that the LDFS method is able to measure and detect minute local changes in surface roughness and directionality.

4.1 Artificially Generated Fractal Surfaces

The ability in measuring local surface roughness was evaluated using isotropic fractal surfaces with increasing FD_t at three different image sizes. It was found that the values of GFS_MEAN calculated were statistically significantly different at all scales and image sizes, increasing monotonically with FD_t. This indicates that the LDFS method can be applied in comparisons of local surface roughness. Differences observed between the values of calculated and theoretical FDs can be explained by the fact that the fractal surface images are digital approximations of continuous fractals with a limited resolution. The lack of exact agreement with FD_t, however, is not of concern as long as the method is able to differentiate between surfaces with different local roughness.

The LDFS method was evaluated in the detection of differences in directionality between isotropic and anisotropic surfaces. Statistically significantly higher values of GStrS_MEAN were obtained for the anisotropic surfaces at all scales (Table 2). This indicates that the method can detect changes in surface roughness with the direction.

4.2 Real Engineering Surfaces

The performance of the LDFS method in the analysis of real engineering surfaces was also evaluated. One isotropic and three anisotropic surfaces were used for the tests. The anisotropic surfaces SA1 and SA2 were rougher (higher GFS_MEAN) than the isotropic surface SI, while SA3 was smoother (lower GFS_MEAN). The number of differences found increases with the anisotropy of surfaces analyzed, i.e., four differences for S1-SA1, fourteen for S1-SA2 and sixteen for S1-SA3. This agrees with the successive abrasion of S1 used in the production of anisotropic surfaces.

Differences between the real engineering surfaces were also analyzed using the standard ISO parameters S_a and Str_ISO. It was found that SI is rougher than SA2 and SA3 and no differences were detected in surface direction. This poor performance can be attributed to the smoothing out of local details and the lack of ability to quantify at individual scales and directions. It is noteworthy that some of the standard parameters used are calculated at point topographic features and therefore they are able to quantify locally surface texture. These parameters are the maximum peak height (S_p) and the maximum valley depth (S_v). Although useful, they are limited in application as focusing on specific surface features.

4.3 Reduction of Computational Time

Computational time required to process a single image varied between 30 s and 30 min. From a practical view point the process takes rather a long time. Possible way to reduce the time is to perform calculations at locations of interest (LOIs), e.g., at peaks, valleys or edges. Self-avoiding walker algorithms [21] could be applied in the selection of LOIs. For example, the algorithms can generate adjustable “crawlers” that follow regions of increasing intensity [22]. Other way is to accelerate computations by means of graphics processing units. Future work will focus on these two and other possible solutions to address this challenging computational problem.

Results obtained suggest that the LDFS method is able to quantify locally surface images at individual scales and directions. This ability would be useful in the development of automated systems; for example, in the detection and classification of machine wear where images of surfaces with local damage are analyzed [23,24,25]. The method will be also useful in the evaluation of wear and friction properties of coated surfaces [26,27,28], the studies of evolution of two-phase titanium alloys surfaces [29], damage and deformation of metal matrix composite (MMC) surfaces [30] and others. In medicine, the method could be applied to radiographic images of knees and hands, producing local bone texture parameters for the prediction and early detection of osteoarthritis [31, 32].

However, further studies would still be required before the method can be widely used. Most importantly, studies are needed which would include effects of pixel size, spatial sampling intervals, scan speed, image blur and noise on values of local FDs [33,34,35]. We plan to do that but we will evaluate the performance of LFDS method under different imaging conditions and practical applications first.

5 Conclusions

The following conclusions can be drawn from this study:

• The new method, called LDFS, that calculates FDs at each pixel location of surface image was developed. Unlike other methods it measures the local surface roughness and directionality at individual scales and directions. The method produces the fractal signatures and the aspect ratio (directionality) signatures at the scales ranging from the instrument resolution to 1/10 of the image shortest size.

• The method is accurate in measuring the local surface texture at individual scales and directions. It detects an increase of local surface roughness in isotropic fractal surfaces and the differences in local directionality in anisotropic fractal surfaces.

• It detects changes in surface roughness between isotropic (sandblasted) and anisotropic (abraded) real engineering surfaces. The methods accuracy and sensitivity is much higher than the currently used standard parameters.