1 Introduction

Modeling of almost any phenomenon in geological formations requires three essential ingredients: (i) the correct governing equations describing the phenomenon; (ii) a model of the formation that represents faithfully the most important features that affect the outcome of the phenomenon, and (iii) efficient and large-scale computations, not only for generating the model, but also for solving the governing equations. The governing equations are usually known, as they are based on the fundamental conservation laws. It is the second and third ingredient that necessitate large-scale and intensive computations.

Geological formations are heterogeneous over many distinct and disparate length scales, from pore, to core, field, and regional scales. At small length scales, the heterogeneities manifest themselves in the morphology of the pore space—the size and shape of the pores, the structure of their rough surface, and their pore connectivity. At much larger length scales the heterogeneities are represented by the spatial distributions of the porosity, flow and transport properties, and the elastic moduli, as well as the distributions of fractures and faults. Given that the length scales over which such heterogeneities are widely separated and differ by many orders of magnitude, developing a model that incorporates the effect of all of them is very difficult, if not impossible. Thus, the best strategy may perhaps be a multiscale approach in which the results of simulations at one scale can be used as the input to those at a larger and distinct length scale. Even within such a framework, the computations are still very intensive, particularly those for the largest scales—field and regional.

Aside from the complexity associated with geological formations, one must also consider the effect of various factors that are contributed by phenomena with distinct physics, without which an accurate model of such systems might not be developed. For example, coupling the variables due to chemical, thermal, mechanical, and hydromechanical effects has been shown to represent the complex physics of fluid–solid interactions in geomedia, but such a coupling is computationally very expensive. Furthermore, one must also decide the level of complexity and resolution for each of such factors that should be used. Clearly, the higher the resolution, the more expensive are the computations.

Significant advances have, of course, been made in the computer technology, hence helping to increase the speed of computations very significantly. In addition to the developments in computer languages that allow one to program computations more efficiently, such as new versions of Fortran and C++, as well as Python (Guttag 2016), such technologies as graphics processing units (GPU) (Matthews 2018) and optical computing that uses photons (Cohen et al. 2016) and new materials (Bretscher et al. 2021) can increase the speed of computations even further and are still being developed.

But the most promising route to computations with speeds that can even be hardly imagined is, perhaps, through use of quantum computers (QCs), the subject of this perspective.

2 Quantum Computers

In a seminal paper, physicist Paul Benioff (1980) proposed a microscopic quantum mechanical model of computers. The computer was represented by a Turing machine. More specifically, Benioff showed that for every number n and Turing machine \(\mathcal{T}\) one has a quantum mechanical Hamiltonian (total energy) \(\mathcal{H}_n^\mathcal{T}\) and a class of appropriate initial states, such that if \(\Psi _n^\mathcal{T}(0)\) is the initial state, then \(\Psi _n^\mathcal{T} (t)=\exp (-i\mathcal{H}_n^\mathcal{T}t)\Psi _n^\mathcal{T}(0)\) will describe correctly the states that correspond to the completion of the first, second, \(\cdots \), nth computation step of \(\mathcal{T}\) at times \(t_3,\;t_6,\;\cdots ,\;t_{3n}\). Benioff also showed that, at all times after completion of a step and before the beginning of the next, or after 3n steps, the energy of the systems is the same as it was at the beginning. In other words, there is no net transfer of energy to the computer as the computations move forward. Thus, he suggested that such computers would dissipate no energy and, therefore, produce no heat, which have always been a problem in large computers. Benioof’s paper is now considered as the initial foundation for the QCs. Shortly thereafter, Nobel Laureate Richard Feynman suggested (Feynmann, 1985) that QCs could potentially perform computations that classical computers can not.

But, how do QCs work?

2.1 Quantum Logic Gates

In classical computers that we have been using, logical operations are carried out using the definite position of a physical state for anything that is to be computed. Such states are binary, implying that the operations are based on one of two positions, with a single state, such as 1 or 0, being called the familiar bit. But as the word quantum suggests, the QCs carry out computations based on probabilities. Their operations utilize the quantum state of an object in order to produce what is called a qubit, which are states that are undefined properties of an object before they are detected. Thus, as in quantum mechanics, instead of having a well-defined position, unmeasured or unoccurred quantum states exist in a mixed superposition of both 1 and 0, somewhat similar to a coin that is spinning through the air, and whose state is unknown to us, until it lands on the ground, or on a table. Quantum computing also takes advantage of such properties as entanglement, a phenomenon in which any change in the state of one qubit results in changes in the state of another qubit, even if it is “far away.”

It is due to such properties that QCs can, in principle, solve many classes of problems much faster than classical computers. For example, using 53 qubits, Arute et al. (2019) reported that their QC carried out a specific calculation that is beyond the realm of current practical capabilities of a classical computer. They estimated that the same calculation with even the best classical supercomputer will take 10,000 years to complete.

We use the bra-ket notation to denote a quantum state. A ket is of the form \(|v\rangle \) and denotes a vector v that, physically, represents a state of a quantum system. A bra is of the form \(\langle \mathbf{f}|\) and represents a linear map that maps each vector in a vector space onto a complex number in the complex plane. Then, consider n bits of information. A memory that consists of such information has \(2^n\) possible states, forming a probability vector in which each entry represents one of the \(2^n\) states. In other words, the memory is represented by the probability vector. In the limit \(n=1\) a memory is either in the 1 or 0 state. Thus, we have

$$\begin{aligned} |1\rangle := \left( \begin{array}{c} 0\\ 1 \end{array}\right) \;,\;\;\;|0\rangle :=\left( \begin{array}{c} 1\\ 0 \end{array}\right) \end{aligned}$$
(1)

On the other hand, a quantum memory is expressed in terms of a quantum superposition \(|\psi \rangle \) of the two states \(|1\rangle \) and \(|0\rangle \):

$$\begin{aligned} |\psi \rangle := a|0\rangle +b|1\rangle \;, \end{aligned}$$
(2)

where a and b are called quantum amplitudes and are, in principle, complex numbers. One must also have \(|a|^2+|b|^2=1\), implying that when the quantum memory \(|\psi \rangle \) is measured or realized, the states \(|0\rangle \) and \(|1\rangle \) will occur with probabilities, respectively, of \(|a|^2\) and \(|b|^2\), as their sum adds up to one (conservation of probabilities).

Given the representation (1), one sets up a quantum logic gate \(G_n\) for n bits of information. The simplest of such gates is what is referred to as the NOT gate, represented by a matrix \(\mathbf{G}_1\) given by \(\mathbf{G}_1=(|1 \rangle \;\;|0\rangle )\), which is also referred to as the X gate. Thus,

$$\begin{aligned} \mathbf{G}_1=\text{ X } \text{ gate }=\text{ NOT } \text{ gate }=\left( \begin{array}{cc} 0 &{} 1\\ 1 &{} 0 \end{array}\right) , \end{aligned}$$
(3)

so that, \(\mathbf{G}_1|0\rangle =|1\rangle \) and \(\mathbf{G}_1|1\rangle =|0\rangle \), i.e., the operations are simple matrix multiplications. Other gates can also be constructed. For example, with \(a=1/\sqrt{2}\) and \(b=-1/\sqrt{2}\) one obtains the Hadamard- or H-gate:

$$\begin{aligned} \text{ H-gate }=\frac{1}{\sqrt{2}}\left( \begin{array}{cc} 1 &{} 1\\ 1 &{} -1 \end{array}\right) \;. \end{aligned}$$
(4)

Similarly, in the limit \(n=2\), the two-qubit quantum memory can be in one of four states:

$$\begin{aligned} |11\rangle :=\left( \begin{array}{c} 0\\ 0\\ 0\\ 1 \end{array}\right) ,\;|10\rangle :=\left( \begin{array}{c} 0\\ 0\\ 1\\ 0 \end{array}\right) ,\;|01\rangle :=\left( \begin{array}{c} 0\\ 1\\ 0\\ 0 \end{array}\right) ,\;|00\rangle := \left( \begin{array}{c} 1\\ 0\\ 0\\ 0 \end{array}\right) \end{aligned}$$
(5)

Associated with the four states is the so-called cNOT quantum logic gate \(\mathbf{G}_2\), also called XOR gate, and is given by, \(\mathbf{G_2}:=(|00\rangle \;|01 \rangle \;|11\rangle \;|10\rangle )\), or

$$\begin{aligned} \mathbf{G}_2=\text{ XOR } \text{ gate }=\left( \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ 0 &{} 0 &{} 1 &{} 0 \end{array}\right) \;. \end{aligned}$$
(6)

\(\mathbf{G}_2\) has some interesting properties, since \(\mathbf{G}_2|00\rangle =|00 \rangle \) and \(\mathbf{G}_2|01\rangle =|01\rangle \), whereas \(\mathbf{G}_2|11\rangle = |10\rangle \) and \(\mathbf{G}_2|10\rangle =|11\rangle \). This implies that if the first qubit is \(|0\rangle \), \(\mathbf{G}_2\) does nothing to either qubit, but if and only if the first qubit is \(|1\rangle \), \(\mathbf{G}_2\) operates the NOT gate \(\mathbf{G}_1\) on the second qubit. One also has a two-qubit gate, referred to as the SWAP-gate, which, as its name suggests, exchanges the state of two qubits with each other:

$$\begin{aligned} \text{ SWAP-gate }=\left( \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 \end{array}\right) . \end{aligned}$$
(7)

Clearly, one can define quantum logic gates \(\mathbf{G}_3,\;\mathbf{G}_4,\cdots ,\; \mathbf{G}_n\) for n qubits of information, which are, however, interrelated. Thus, quantum computation is represented by a network of such quantum logic gates and is executed as a sequence of single-qubit gates \(\mathbf{G}_1\) and the cNOT gate \(\mathbf{G}_2\). Although it may seem that such a set of gates is infinitely long, American mathematician Robert M. Solovay and, independently, Russian-American physics professor Alexei Kitaev (Kitaev (1997)) proved that it can be done by a finite set of gates, which is now known as the Solovay-Kitaev theorem.

3 Potential Applications to Geoscience

Although we are still away from large-scale complex computations with the QCs, we can envision the potential use of such computers for several important classes of problems in geoscience.

3.1 Reconstruction of Porous Media as an Optimization Problem: Quantum Annealer

Developing models of porous media, at both small and large cales, has always been a problem of great interest to chemical and petroleum engineers, geoscientists, materials scientists, and applied physicists. The model depends, of course, on the amount of data that is available, and there are many approaches to modeling of porous media (Sahimi 2011; Blunt 2017). One approach to the problem is by reconstruction: Given a certain amount of data for a porous medium, one tries to construct a model, or a plausible realization of the medium, which not only honors the data, but also provides accurate predictions for those properties of the medium for which no data were used in the reconstruction, or they were not available. Sahimi and Tahmasebi (2021) provide a comprehensive description of the current reconstruction methods.

Several approaches to reconstruction have been proposed, including generative adversarial neural networks (Mosser et al. 2020 and references therein), simulation based on a cross-correlation function (Tahmasebi and Sahimi 2013, 2016a, b), and other methods (see Sahimi and Tahmasebi (2021) for a review). An important approach is based on optimization: One defines a cost or an energy function \(\mathcal{C}\) as the sum of the squares of the differences between the data and the corresponding predictions by the reconstructed model and determines its global minimum, which would represent the “best” matching model for the given data. Determining the global minimum of \(\mathcal{C}\) is, of course, an optimization problem.

A popular optimization method used extensively is simulated annealing (SA), first proposed by Kirkpatrick et al. (1983) for statistical mechanical problems, which was then developed for modeling of complex porous media, first by Long et al. (1991) and then by Yeong and Torquato (1998). The cost or total energy \(\mathcal{C}\) of the system is defined by

$$\begin{aligned} \mathcal{C}=\sum _j |f(\mathbf{O}_j)-f(\mathbf{S}_j)|^\gamma \;, \end{aligned}$$
(8)

where \(\mathbf{O}_j\) and \(\mathbf{S}_j\) are vectors of the observations or data, and simulated (or reconstructed) predictions of the system, respectively, \(\gamma \) is a constant, and \(f(\mathbf{x})\) is a real monotonic function. The data could be of any type, depending on the nature of the system whose global minimum energy (GME) is to be determined. The SA method may be used if one has, (i) a set of possible configurations of the system; (ii) a method for systematically changing the configuration; (iii) the cost or energy function to be minimized, and (iv) an annealing schedule of changing a temperature-like variable, so that the system can be driven toward its true GME.

Consider, as an example, the development of a model for an oil reservoir or an aquifer. A configuration means a given spatial distribution of the permeabilities and porosities. A set of configurations means many of such models, or realizations, in which the permeability and porosity of any given block of the computational grid representing the medium vary from realization to realization. To systematically change the configurations, one defines the neighboring states (see below). The energy function is defined by Eq. (5) where the observed response can, for example, be the oil production of the reservoir at a particular point (well) and time, or the tracer concentration at a well. The annealing schedule is defined shortly.

Suppose that \(\{C\}\) denotes the set of all the possible configurations of the system under study. Requirement (iii) is a method by which a given configuration is varied. We assign a probability function for randomly selecting a configuration, and then decide probabilistically whether to move the system to a new configuration, or keep it in the current one. One may also define the neighborhood \(N_C\) of C as the set of all the configurations that are very “close” to C. Annealing the system means selecting a configuration from the set \(N_C\) and comparing it with C. In order to make the comparison precise, one defines the energy or cost function \(\mathcal{C}\), the third ingredient of the SA method. The probability distribution of the configurations is then assumed to be expressable as the Gibbs’ distribution

$$\begin{aligned} p(C)=a\exp [\mathcal{C}(C)/T]\;, \end{aligned}$$
(9)

where a is a renormalization constant, and T a temperature-like variable.

Because p(C) is a Gibbs’ distribution, C, the current configuration of the system may be modeled as a Markov random field, implying that the transition probability for moving from C to \(C'\) depends only on the two, and not on the previous configurations farther away from the set \(\{C\}\). Thus, the transition probability can change from configuration to configuration, but it does not depend on the previous configurations that were examined. Given C and \(N_C\), the transition probability for moving from C to \(C'\) is equal to the probability that one selects \(C'\) times the probability that the system would make the transition to configuration \(C'\). Therefore,

$$\begin{aligned} p\{C\rightarrow C'|C\}=\left\{ \begin{array}{ll} 0 &{} C' \notin N_C\;,\\ p(C'|C) \times 1 &{} C' \in N_C\;,\\ &{} \mathcal{C}(C')-\mathcal{C}(C)\le 0\;,\\ p(C'|C)\exp \{[\mathcal{C}(C)-\mathcal{C}(C')]/T\} &{} C' \in N_C\;,\\ &{} \mathcal{C}(C')-\mathcal{C}(C)> 0\;, \end{array}\right. \end{aligned}$$
(10)

where for the last equation we must have, \(C\ne C'\). The final ingredient of the model is a schedule for lowering the temperature as the annealing proceeds. This means that as the annealing continues, one is less likely to keep those configurations of the system that increase the energy. Many annealing schedules have been proposed; for discussions and comparison of the schedules see Capek (2018).

The quantum version of the SA is quantum annealing (QA). Whereas the classical SA takes advantage of the thermal, or thermal-like, fluctuations in order to determine the GME, in the QA the GME is computed by a process based on quantum fluctuations. It is, therefore, a procedure for identifying a process that computes the absolute minimum from within a very large but finite set of possible solutions. Given the earlier discussions, it should be clear that evaluating the cost or energy function in the QA must be done probabilistically, due to the large extent of the space of configurations of size \(2^n\) for large n qubits of data.

Quantum annealing was originally proposed by Finnila et al. (1994), and in its present form by Kadowaki and Nishimori (1998) for the transverse Ising model (TIM). The TIM is the quantum version of the classical Ising model, a model of thermal phase transition. Similar to its classical version, the TIM consists of a lattice of spins with nearest-neighbor interactions that are set by the alignment or anti-alignment of spin projections along the z axis (perpendicular to the plane of the lattice), and an external magnetic field perpendicular to the z axis. The QA procedure for the TIM is as follows (see Heim et al. (2015) for a careful analysis). (i) The computations begin from a quantum-mechanical superposition of the all possible states—the candidate states—to which equal weights are attributed. (ii) The system then evolves according to the time-dependent Schrödinger equation. The candidate states’ amplitudes change continuously, generating a quantum parallelism according to the time-dependent strength of the transverse field, and causing quantum tunneling between states. The system remains close to the ground state of the instantaneous Hamiltonian (total energy) of the TIM, if the rate of change of the transverse field is slow enough. But if the rate is increased, the system might temporarily come out of the ground state and produce a higher probability of ending up in the ground state of the final Hamiltonian. When the transverse field is finally removed, the system reaches, or should reach, the ground state of the classical Ising model that corresponds to the solution of the original optimization problem. The success of the QA for random magnets was demonstrated experimentally by Brooke et al. (1999).

O’Malley (2018) has proposed the use of the QA to hydrologic inverse problems, which in essence is the reconstruction problem that was described above. To apply the QA to problems other than the TIM, such as the problem of reconstruction of porous media, as well as fluid flow problems (see below), the variables in the problem are viewed as the classical degrees of freedom, and the energy or cost functions to be the classical Hamiltonian. A suitable term that consists of non-commuting variable(s)—those with nonzero commutator with the variables in the original problem—must be introduced artificially (“by hand”) in the Hamiltonian, which play the role of the tunneling field in the TIM, i.e., the kinetic part. The process is controlled by the strength of tunneling field \(\mathcal{F}\), which is the analogue of temperature in the SA (hence the name QA). The quantum Hamiltonian, constructed by summing the original function and the non-commuting term, is then used in the computations, and the simulation with the Hamiltonian proceeds in the same manner as for the TIM. At the beginning, the strength of the tunneling field is high, so that the neighborhood consists of the entire space, but the strength is gradually shrunk and reduced to a few configurations. The efficiency of the annealing depends on the choice of the non-commuting term. Das and Chakrabarti (2008) provide a good review of the QA.

It has been demonstrated that, in certain cases, particularly when the potential energy landscape consists of very high but thin energy barriers surrounding shallow local minima, the QA can outperform the SA. As discussed earlier, the transition probabilities in the SA are proportional to the Boltzmann’s factor \(\exp [-\Delta \mathcal{C}/(k_BT)]\), which depends only on the height \(\Delta \mathcal{C}\) of the barriers. If the barrier is very high, it is extremely difficult for thermal fluctuations in the SA to push the system out of such local minima. But, as argued by Ray et al. (1989), the quantum tunneling probability through the same barrier depends not only on the height \(\Delta \mathcal{C}\), but also on its width w and is approximately given by, \(\exp (-\sqrt{\Delta \mathcal{C}}w/\mathcal{F})\). In the presence of quantum tunneling the additional factor w can be of great help in speeding up the computations, because if the barriers are thin enough, i.e., if \(w\ll \sqrt{\Delta \mathcal{C}}\), then quantum fluctuations can surely take the system out of the shallow local minima.

The DWave machines (see https://www.dwavesys.com/software) were the first commercially available annealing-based quantum computers (one of which is at the University of Southern California). It uses quantum mechanical phenomena of superposition, entanglement,Footnote 1 and tunneling to explore a given energy landscape and returns the distribution of possible energy states with the global minimum, ideally as the state with the highest probability, hence solving an optimization problem. We will return to this point later.

3.2 Simulating Fluid Flow

Let us first point out that quantum algorithms have been developed for solving partial differential equations (Heinrich 2006; Childs et al. 2021), which can be exploited in the numerical simulation of fluid flow problems. The solution of the governing equations for fluid flow, either the Navier-Stokes (NS) equation when inertial is important, or the Stokes’ equation in the limit of slow flow, is the most important aspect of simulating any flow phenomenon in a pore space. There are two approaches for implementing a computational approach on a QC, which are as follows.

3.2.1 Direct Quantum-Computation Algorithms

An important point must first be mentioned: The macroscale behavior of a system in which the NS equation is solved by a QC is classical (deterministic), but the microscale dynamics is quantum mechanical. The algorithms for solving the governing equations of fluid flow may be divided into two groups, namely the lattice gas (LG) and lattice Boltzmann (LB) models, and those that solve the NS equations.

Quantum LG and LB Models. To our knowledge, the first direct route for quantum computing of problems in hydrodynamics was proposed by Yepez (1998), (Yepez 2001) who considered a LG or LB model. As is well known, the LG model was first proposed by pioneered Hardy et al. (1976) and Frisch et al. (1986) for numerical simulation of fluid flow problems, and represents the precursor to the LB methods that are now used routinely in many studies of hydrodynamic phenomena. The sites on a lattice can take on a certain number of various states, with the various states being particles with certain velocities. The system evolves in discrete time steps, and after each time step, the state at a given site is determined by the state of the site itself and its neighbors. The state at each site is purely Boolean, namely there either is or is not a particle moving in each direction emanating from that site, and at each time step two processes are carried out, namely propagation (particle movement between sites) and collision. In order to recover the NS equation in the continuum limit, the lattice must have high symmetry, such as the hexagonal lattice in two dimensions.

The way the system evolves in a quantum algorithm is as follow. If one has n qubits, the quantum state \(|\Psi (t)\rangle \) (the wave function of the system) resides in a large Hilbert space with \(2^n\times 2^n\) dimensions.Footnote 2 For a short period of time \(\tau \), a new quantum state \(|\Psi (t+\tau )\rangle \) is generated by application of a unitary operator (i.e., a bounded linear operator \(U:\;H\rightarrow H\) on a Hilbert space H that satisfies \(U^*U=UU^*=I\), where \(U^*\) is the adjoint of U, and I is the identity operator) represented by a unitary matrix of size \(2^n\times 2^n\):

$$\begin{aligned} |\Psi (t+\tau )\rangle =\exp (iH\tau /\hbar )|\Psi (t)\rangle \;. \end{aligned}$$
(11)

If applying \(\exp (iH\tau /\hbar )\) is continued, one obtains an ordered sequence of states, with each given a unique time label. For example, if the first state is labeled by t, then the next one is labeled by \(t+\tau \), and the next by \(t+2\tau \), and so on. Thus, one may view the computational time as advancing incrementally in unit steps of duration \(\tau \).

Then, given Eq. (11), Yepez’s formulation of quantum mechaical LG model is as follows. A group of qubits resides at each site of the lattice that are acted upon by a sequence of quantum gates (see above) whose action is mediated by external control. The evolution of the quantum LG is described by a special limit of Eq. (11) in which one sets, \(\exp (iH\tau /\hbar )\equiv \mathbf{SC}\), so that

$$\begin{aligned} |\Psi (\mathbf{x}_1,\mathbf{x}_2,\cdots ,\mathbf{x}_N;t+\tau )\rangle =\mathbf{SC} |\Psi (\mathbf{x}_1,\mathbf{x}_2,\cdots ,\mathbf{x}_N;t)\rangle \end{aligned}$$
(12)

where N is the number of lattice nodes, \(\mathbf{x}_i\) is the spatial position of node i, and S and C are, respectively, the streaming and collision operators, which have classical versions in the standard (“classical”) LG and LB methods. S is a square orthogonal permutation matrix, i.e., one that has only one entry of 1 in each row and each column and 0 elsewhere, such that if it is multiplied by another matrix A, it permutes the rows in A if SA is formed, or columns in A if AS is formed. S is the same as in the classical LG streaming operator, which causes particles to move from one site to the next by exchanging qubit states between nearest neighboring sites. C, on the other hand, is a unitary collision operator, i.e., one whose conjugate is the same as its inverse, which has complex entries, such that the quantum LG reduces to the classical one when C is a permutation matrix. If C is stochastically switched between various permutation matrices during the dynamical evolution of the lattice, then the quantum LG reduces to the classical LG.

As is well known, in the classical LG and LB models one has a particle distribution function \(f_i(\mathbf{x},t)\) for the ith local state, which is defined at the mesoscopic scale whose numerical estimates are obtained by either ensemble averaging over many independent microscopic realizations, or by coarse-grain averaging over space-time blocks with a single microscopic system. In the quantum version, \(f_i(\mathbf{x},t)\) is expressed in terms of the quantum mechanical density matrix, \(\varrho (\mathbf{x},t)=|\Psi (\mathbf{x},t)\rangle \langle \Psi (\mathbf{x},t)|\), such that

$$\begin{aligned} f_i(\mathbf{x},t)=\mathrm{Tr}[\varrho (\mathbf{x},t)\mathbf{n}_i]\;, \end{aligned}$$
(13)

where Tr denotes the trace operation, and \(\mathbf{n}_i\) is the number operator for the ith local state. As soon as the particle distribution function is defined in terms of \(\varrho (\mathbf{x},t)\), i.e., in terms of \(|\Psi (\mathbf{x},t) \rangle \) and \(\langle \Psi (\mathbf{x},t)|\), one has the usual formulation of the LG and LB models, namely expressing the particle density \(\rho (\mathbf{x},t)\) and momentum \(\rho (\mathbf{x},t)\mathbf{v}(\mathbf{x},t)\) in terms of \(f_i(\mathbf{x},t)\) and, hence the quantum formulation of the LG and LB models with which quantum computations can be carried out.

Mezzacapo et al. (2015) further developed the quantum algorithm for the LB model. They utilized the similarities between the Dirac and LB equations in order to develop a quantum simulator, which is suitable for encoding fluid dynamics phenomena within a lattice kinetic formalism. They showed that both the streaming and collision processes of the LB dynamics (see above) can be implemented with controlled quantum operations, using a heralded quantum protocol to encode non-unitary scattering processes.

Solution of NS Equation. Steijl and Barakos (2018), Steijl (2019), and Gaitan (2020) proposed algorithms for solving the NS equation with a QC (see also Gaitan (2021), for a brief review of the methods). In the work of Steijl, and Steijl and Barakos, quantum Fourier transform (QFT) is used in order to develop the numerical algorithm. Recall that in the classic discrete Fourier transform, one expresses a vector, \(\mathbf{x}=(x_0,x_1,\cdots , x_{N-1})^\mathrm{T}\) in terms of another vector y,

$$\begin{aligned} \mathbf{y}=\frac{1}{\sqrt{N}}\sum _{n=0}^{N-1}x_n\exp (-2\pi kni/N)\;,\;\;\;k=1,2, \cdots , N-1\;. \end{aligned}$$
(14)

Similarly, the QFT expresses a quantum state \(|\Psi \rangle =\sum _{i=0}^{N-1} \Psi _i|i\rangle \) in terms of a quantum state \(\sum _{i=0}^{N-1}y_i|i\rangle \), given by

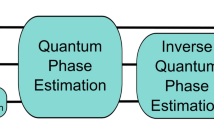
$$\begin{aligned} \mathbf{y}=\frac{1}{\sqrt{N}}\sum _{n=0}^{N-1}\Psi _n\exp (2\pi kni/N)\;,\;\;\;k=1,2, \cdots , N-1\;. \end{aligned}$$
(15)

It has been shown (Nielsen and Chuang 2000) that the QFT can be computed highly efficiently on a QC with a decomposition into a product of simpler unitary matrices. Using a simple decomposition, the discrete FT on \(2^n\) amplitudes can be implemented as a quantum circuit consisting of only \(\mathcal{O} (n^2)\) Hadamard and controlled phase shift gates (see above), with n being the number of qubits, which should be compared with the classical discrete FT that takes \(\mathcal{O}(n2^n)\) gates, with n being the number of bits, which is exponentially larger than the former. In addition, the QFT is now a part of many quantum algorithms, such as Shor’s algorithm (1997) for factorization that is used in the solution of systems of linear equations, as well as computing the discrete logarithm. Thus, using the QFT, one can take the governing equations to the QFT space, and compute the numerical solution with a QFT. Post-processing of the results will yield the solution in real space.

Gaitan (2020) used a more direct approach for solving the NS equation using a QC. He discretized the spatial derivatives by finite difference, hence reducing them to algebraic equations. When the resulting equation is rearranged, one obtains the following equation for the velocity field v of the fluid,

$$\begin{aligned} \frac{d\mathbf{v}}{dt}=F(\mathbf{v})\;, \end{aligned}$$
(16)

which constitutes a set of ordinary differential equations (ODEs). This is the crucial point, because there is already an (almost) optimal quantum algorithm for computing the numerical solution of a set of nonlinear ODEs (Kacewicz (2006)). Therefore, Gaitan (2020) showed that by combining spatial discretization and the quantum algorithm for solving ODEs, one obtains a quantum algorithm for solving the NS equation.

The quantum algorithm for solving ODEs utilizes the quantum amplitude estimation algorithm (QAEA), developed by Brassard et al. (2000), to obtain an approximate solution of ODEs. The QAEA is a generalization of a search algorithm developed by Grover (1996), who developed a quantum algorithm for an unstructured search that, with high probability, identifies the unique input to “a black box” function that produces a particular output value. It is a nearly optimal algorithm since it utilizes only \(\mathcal{O}(\sqrt{M})\) evaluations of the function, where M is the size of the function’s domain. The analogous problem in classical computation cannot be solved in fewer than \(\mathcal{O}(M)\) evaluations.

3.2.2 Solution as an Optimization Problem

When the governing equations for flow, transport, deformation, or wave propagation are to be solved in a given geomedium, they are first discretized by, for example, the finite-difference or finite-element method. If the equations are linear, one naturally obtains a large set of linear equations. If they are nonlinear, then they are linearized so that they can be solved by an iterative method, such as Newton’s iteration. In both cases, one must solve a large set of linear equations.

Solving such a set of equations by a quantum algorithm has distinct advantage over the classical methods. Quantum computing is based on matrices acting on vectors in high-dimensional space and, therefore, it can be perfectly adopted for solving the set of equations much faster than any classical method. Indeed, it has been demonstrated that, by constructing matrix transformations, quantum computers perform common linear algebraic operations exponentially faster than their best efficient classical counterparts ((Harrow et al., 2009; see also the next section).

But there is another way of formulating the problem by a quantum algorithm. Vaez Allaei and Sahimi (2005) demonstrated how the solution of a set of linear equations can be obtained more efficiently, if formulated as an optimization problem. Thus, just as the reconstruction problem described earlier can be formulated as an optimization problem, to which quantum optimization, and in particular quantum annealing, can be applied, one can also take the same approach in the present problem.

Since the quantum processor unit (QPU) of the DWave QC is based on annealing, it may be used for the problem of minimizing an unconstrained binary objective or cost function (see above), which is also known as the quadratic unconstrained binary optimization (QUBO) problem. Ray et al. (2019) used the second-order central finite-difference scheme to discretize the spatial derivatives in the NS equation, and backward/implicit Euler scheme for the time derivative that describes the dynamic evolution of the flow field. Then, they mapped the resulting set of equations onto a QUBO form and solved the resulting problem with the DWave quantum annealer. To do so, they used a two-step approach. First, they converted real variables (the discretized fluid velocity at the grid points) to binary variables by using a fixed-point approximation, and then utilized a linear least-squares formulation to transform the problem to one of optimization with binary variables.

Fixed-point representation is a discrete representation for real data that have a fixed number of digits after a radix/fixed point and, therefore, it represents a real number by scaling an integer value with an implicit scaling factor that remains fixed throughout the computations (O’Malley et al. 2016). Therefore, the solution \(v_i\) at grid point i is represented by

$$\begin{aligned} v_i=\sum _{j=1}^m 2^{j_0-1}q_j\;, \end{aligned}$$
(17)

where m represents the precision of the representation, \(j_0\) is the position of the fixed point, and \(q_j\) is the jth binary variable. Thus, if we fix the precision and vary \(j_0\), we obtain various ranges of decimal values. For example (Ray et al. (2019)), for \(n=1,2,\cdots ,6\) the maximum bound for real values with fixed point after position 1 are, respectively, 1, 1.5, 1.75, 1.875, 1.9375, and 1.96875, with the leftmost position being the starting bit. Note that increasing the precision n by one increases the range by an amount \(2^{n+1}\), whereas moving the fixed point position by one would lead to doubling the maximum value.

3.3 Burgers’ Equation

Burgers’ equation, first introduced by Bateman (1915), but studied extensively by Burgers (1948), is a simplified, 1D version of the Navier-Stokes equation,

$$\begin{aligned} \frac{\partial v}{\partial t}+v\frac{\partial v}{\partial x}= \nu \frac{\partial ^2v}{\partial x^2}\;, \end{aligned}$$
(18)

and has been used for studying turbulence. If the spatial derivatives are discretized over a discrete space \(x_i\) with \(i=0,\;1,\;2,\cdots ,m\) with \(x_0\) and \(x_m\) representing the boundaries of the system, one reduces the Burgers’ equation to \(m-2\) ODEs in the time domain. Thus, as discussed above, one can employ the quantum algorithm developed by Kacewicz (2006) for solving the nonlinear ODEs to compute the numerical solution of the Burgers’ equation, an approach suggested by Oz et al. (2022). Their analysis indicated that the quantum solver for ODEs provides very significant speed-up over the classical solvers. Clearly, that is also true of the full NS equation. Note that Burgers’ equation has found many applications other than those in hydrodynamics.

3.4 Mass Transport and Groundwater Contamination

Dispersion in flow through a porous medium is a highly important problem that appears in a wide variety of phenomena, ranging from spreading of contamination in groundwater, to miscible displacement and enhanced oil recovery, and operation of packed-bed reactors. As is well known (Sahimi (2011); Blunt (2017)), dispersion is modeled by the convective-diffusion equation (CDE), also referred to as the advection-diffusion equation (ADE). Budinski (2021) proposed a quantum algorithm for solving the CDE by the LB method (see above), the classical version of which was developed by many; see, for example, Shi and Guo (2009) and Chai and Zhao (2013). His algorithm is composed of two major steps. In the first step, equilibrium distribution function \(f_i(\mathbf{x},t)\), presented in the form of a non-unitary diagonal matrix, is quantum circuit implemented by using a standard-form encoding approach. In the second step, the quantum walk (QW) procedure is used in order to implement the propagation step of the LB approach. Budinski (2021) developed his algorithm as a series of single- and two-qubit gates, as well as multiple-input controlled-NOT gates (see above).

The QWs are quantum analogues of classical random walks. As one may expect, unlike the classical random walk in which the walker occupies definite states and the randomness arises due to stochastic transitions between states, in the QWs randomness is due to quantum superposition of the states; non-random, reversible unitary evolution (see above), and collapse of the wave function \(|\Psi (\mathbf{x},t)\rangle \) due to measuring the the state. Childs (2009) showed that a QW can be a tool for universal quantum computations, while Shakeel 2020 presented an efficient algorithm for implementing a QW.

3.5 Machine Learning

Machine learning (ML) algorithms have begun to play a leading role in breakthroughs in science. It is, therefore, becoming increasingly clear that it is imperative to adopt advanced ML methods for problems in geoscience, because they may enable researchers to solve many problems that would otherwise be very difficult, if not impossible, to address. At the same time, one can use the already existing extensive knowledge of geomedia to endow the ML algorithms in order to develop novel physics-guided approaches and models, especially modeling of fluid flow, transport, deformation, geochemical reactions, and wave propagation in such media. Indeed, there has been an explosion of papers reporting on various applications of the ML algorithms to problems in geoscience; for a compreghensive recent review, see Tahmasebi et al. (2020).

But, similar to every major computational problem, application of the ML methods to geoscience hits the ultimate wall of speed and duration of the calculations. A way out of the problem may perhaps be through quantum machine learning (QML) algorithms (Sasaki and Carlini 2002; Almuer et al. 2013; Schuld et al. 2014; Biamonte et al. 2018), because a wide variety of methods of data analysis, as well as ML algorithms are based on carrying out matrix operations acting on vectors in a high-dimensional vector space, which is the essence of quantum mechanics and quantum computations.

Recall, as described above, that the quantum state of n qubits is a vector in complex vector space whose dimension is \(2^n\), and that quantum logic operations or measurements performed on qubits simply multiply the corresponding state vector by \(2^n\times 2^n\) matrices. It has been demonstrated that, by constructing such matrix transformations, quantum computers perform common linear algebraic operations exponentially faster than their best efficient classical counterparts (Harrow et al., 2009). Examples include Fourier transformation (Shor 1997) that was already described, determining eigenvectors and eigenvalues of a large matrix (Nielsen and Chuang (2000)), and solving linear sets of equations over \(2^n\)-dimensional vector spaces in time polynomial in n. Note that the original variant assumed that one has a sparse well-conditioned matrix, which is what one typically has in solving the discretized equations of flow, transport, deformation, and wave propagation (see above). In applying the ML algorithms, the matrix may not necessarily turn out to be sparse. But that assumption has been relaxed in several newer quantum computing algorithms (Wossnig et al. (2018)). Several quantum algorithms, which can be used as subroutines when linear algebra techniques, are employed in quantum machine learning are described by Biamonte et al. (2018).

As the review by Tahmasebi et al. (2020) discussed, classical deep neural networks (DNN) have been shown to be highly accurate ML tools. Thus, they have inspired the development of deep quantum learning algoroithms. In particular, quantum annealers described earlier are well-suited for constructing deep quantum learning networks (see, for example, Adachi and Henderson (2015)). The starting point is the Boltzmann machine, which is the simplest DNN that can be quantized. Its classical version consists of bits with tunable interactions that are adjusted so that the machine can be trained, and the thermal statistics of the bits, which are described by the Boltzmann–Gibbs distribution, reproduce the statistics of the data. To quantize the Boltzmann machine, one takes an approach similar to quantum annealing, namely, one remodels the neural network as a set of interacting quantum spins, corresponding to a tunable Ising model, described earlier. The input neurons are then initialized in the Boltzmann machine and are kept as a fixed state. The system is then thermalized, and the output qubits represent the solution to the problem in hand.

A great advantage of deep quantum learning is that it does not need a large QC. In particular, quantum annealers, described earlier, are well suited for the application of quantum deep learning, and are much easier to construct and scale up than a general-purpose QC, which may explain why they have been commercialized, a well-known example of which is the aforementioned DWave quantum annealer.

Training of fully connected Boltzmann machine is highly intensive computationally, but because thermalization of a system by quantum algorithms is quadratically faster than their classical counterpart (Temme et al. 2011; Yung and Aspuru-Guzik 2012) Chowdhury and Somma (2017), it has become completely practical. Given that the neuron activation pattern in the Boltzmann machine is stochastic, one bottleneck of training the Boltzmann machine by the classical algorithms is the need for sampling the data repeatedly in order to find success probabilities, which is time consuming. But quantum algorithms sample the data very efficiently, since quantum coherence reduces quadratically the number of the samples needed.Footnote 3 Moreover, quantum algorithms require quadratically fewer accesses to the training data than classical methods, implying that they train a DNN using a large data set, but reading only a very small fraction of all the training vectors.

3.6 Pattern Recognition and Analysis of Big Data

Over the past decade significant breakthroughs have been achieved in exploring the so-called big data in geoscience, recognition of complex patterns, and predicting intricate variables. In particular, big scientific datasets are providing new solutions to many problems as the paradigm shifts from being model-driven to data-driven approaches using ML algorithms. One may define big data based on two distinct perspectives: (i) datasets that cannot be acquired, managed, or processed on common computers within an acceptable time (Mayer-Schonberger and Cukier 2013), and (ii) datasets that are characterized based on the so-called 4V, namely volume, variety, veracity, and velocity (Douglas 2012), an example of which is Digital Earth (De Longueville et al. 2010)

The question of how to exploit big data in geoscience is gaining increasing attention and importance. For example, in addition to the fact that, at least over the next two decades we should still be modeling oil, gas and shale reservoirs to which quantom computing algorithms are completely relevant, as we move away from fossil energy and turning to batteries, we need more cobalt. Therefore, the question is, how can we use big data to discover the next major mineral deposits of cobalt? As the environment, both soil and the atmosphere, become more polluted, can we use big data from geochemical analysis to discover the polluting factors of groundwater aquifers? As addressing the problem of climate change becomes extremely urgent, can we use past big data from landslides or fires to identify a climate change signal. If we can, can they be used to predict future events?

It should be clear that quantum computing algorithms can contribute much to the processing of big data in various ways: (i) If the data are to be analyzed by the traditional statistical methods, then, since such analyses involve considerable matrix and vector operations, such algorithms will speed up the computations (see above). (ii) More recently, however, the ML algorithms have been used for analyzing big data, pattern recognition, etc., which involve dimensionality reduction, clustering, and classification. In particular, several ML algorithms have been used that include deep learning approaches that create and sift through data-driven features; incremental learning algorithms in associative memory architectures that adapt seamlessly to future datasets and sources; faceted learning that learns the hierarchical structure of a data set, and multitask learning that learns a number of predictive functions in parallel.

Given the discussions in the last section regarding quantum computing approaches that accelerate the ML algorithms, it is clear that if the analysis of big data is to be carried out by a ML algorithm, then quantum computing will accelerate the computations very significantly.

3.7 Image Processing

Accounting for the morphology of geomedia that are highly heterogeneous over multiple length scale is a difficult problem. Although two- or three-dimensional images of porous formations may be obtained and analyzed, they either may not capture the smallest features of the geomedia, or they may be too small to provide an accurate representation of the system, or both. There may also be artifacts in the images that distort them and must be removed before the images are analyzed. Thus, digital image processing that increases the resolution of the images, and addresses other problems that distort their contents is often necessary. The development of the science of image processing began in the 1960s and continues to date.

Vlasov (1997) was perhaps the first who used a quantum computational algorithm for recognizing orthogonal images. Later on, Venegas-Andraca and Bose (2003) developed what they called the qubit lattice, which was the first general quantum algorithm for storing, processing and retrieving images. Latorre (2005) developed quantum algorithms for image compressions and entanglement, while Venegas-Andraca and Ball (2010) demonstrated that maximally entangled qubits can be used to reconstruct images without using any additional information (see also above regarding reconstruction). Thus, the science of quantum image processing (QIMP) has undergone considerable developments (see Yan et al. (2016), for a review) to the extent that the QIMP algorithms have been developed for feature extraction (Zhang et al. 2015), segmentation (Caraiman and Manta 2014), image comparison (Yan et al. 2013), filtering (Caraiman and Manta 2013), classification (Ruan et al. 2016), and stabilization (Yan et al. 2016) of images.

Clearly, all such advances can be used for processing and, therefore, analyzing images of geomedia, which are computationally very intensive when done by the classical methods. There is also another approach to enhancing images of geomedia that can benefit from quantum algorithms. Kamrava et al. (2019) proposed a novel hybrid algorithm by which a stochastic reconstruction method (see Sect. 3.1) is used to generate a large number of plausible images of a porous formation, using very few input images at very low cost, and then train a deep learning convolutional network by the stochastic realizations. Therefore, it is clear that the application of quantum algorithms to the ML and DNN computations that were already described may be combined with the method proposed by Kamrava et al. (2019) in order to speed up the image processing considerably.

4 Hurdles to Practical Use of Quantum Computing in Geoscience

While development of many quantum computation algorithms for solving problems that have direct applications to geoscience is truly exciting, there are still significant hurdles to their practical implementations, some of which are as follows.

4.1 Quantum Decoherence and Noiseless Computations

As is well known and understood, quantum mechanics describes particles by wave function in order to represent their quantum state. If there is a definite phase relation between different states, then the system is coherent, which is also necessary for carrying out quantum computing. Although the laws of quantum mechanics preserve coherence, the condition for it is that the system should remain isolated. But, a system in complete isolation is impractical since, for example, one would like to carry out some measurements. Thus, if a QC is not in total isolation, its coherence is shared with the surrounding environment, which interacts with the qbits and, as a result, cohence may be lost over time, a process referred to as quantum decoherence, which is manifested by the presence of noise.

The practical implication of quantum decoherence for quantum computing is enormous, since a key question is whether in practice QCs can carry out long computations without noise rendering the results useless. According to the quantum threshold theorem, or quantum fault-tolerance theorem, a QC with a physical error rate less than a certain threshold can, through the application of quantum error correction schemes, suppress the logical error rate to arbitrarily small levels. Thus, at least theoretically, QCs can be made fault-tolerant.

But, although a fault-tolerant QC is still far into the future, noisy intermediate-scale quantum (NISQ) devices are available whose capabilities have been demonstrated for various problems, such as electronic structure calculations (O’Malley et al. 2016; Kandala et al. 2017), simulations of spectral functions (Chiesa et al. 2019; Francis et al. 2020), and out-of-equilibrium dynamical systems (Lamm and Lawrence (2018); Smith et al. (2019)). Richter and Pal (2021) demonstrated that NISQ devices can be simulated problems in hydrodynamics, the most important problem in geoscience when simulating fluid flow and transport processes.

(ii) Another difficulty is constructing a QC with a very large number of qubits, which are necessary for certain types of problems dealing with complex processes in complex media. The largest number of qubits in a QC that the authors are aware of has 256 qubits in a special QC, dubbed QuEra (see https://www.quera.com/), designed for solving certain problems, and announced in November 2021. The designers expect to build another QC with 1000 qubits within the next two years. This is still far from what is needed to address the type of complex problems considered in this perspective. But progress is being made steadily.

(iii) Solving different problems by QCs may require the atoms that made the qubits to be placed in different configurations. The implication is that certain classes of problems require their own specific design of certain types of QCs. Of course, if such QCs are designed, the speed-up in the computations will also be very large. This has also been the case with classical computers. For example, special-purpose computers were built for the aforementioned Ising model (Taiji et al. 1988; Talapov et al. 1993) and for computing conductivity of heterogeneous materials (Normand and Herrmann 1995) with considerable speed-ups.

5 Summary

Characterization and modeling of geomedia, computing their effective flow, transport, elastic, and other properties, and simulating various phenomena that occur there constitute some of the most intensive calculations in science and engineering. Although the speed of the classical computers has increased tremendously, and many efficient computational algorithms have also helped increassing the speed of large-scale calculations, there are still many problems in geoscience that are difficult to simulate with the classical computers, as they take very long times. On the other hand, over the past twenty-five years, development of quantum computers has made great progress, and powerful quantum computations algorithms have been proposed for simulating many important and computationally difficult problems, with potentially large speed-ups over the most efficient classical algorithms, if implemented in a QC.

This perspective described such algorithms and discussed their potential applications to problems to geomedia. Figure 1 summarizes such potential applications, which range anywhere from reconstruction and modeling of such media, to simulating fluid flow by the Navier-Stokes equations or by lattice Boltzmann method, numerical solution of the advection-diffusion equation, pattern recognition in big data and their analysis, machine learning methods, and image processing.

Fig. 1
figure 1

Summary of potential applications of quantum computational algorithms to problems in geoscience

Full size image

Although a fault-tolerant QC is still far into the future, noisy intermediate-scale QCs are already available whose capabilities have been demonstrated for various problems. They include the aforementioned DWave, with the University of Southern California being the first academic institution operating one since 2016 (see, for example, Liu et al. 2020), Honeywell’s QC, and IBM’s Big Blue machine with one hundred qubits.

It may turn out that, even if QCs become fully practical for complex problems, not all the problems associated with geomedia and geoscience can benefit from such computers. But, given that many quantum computational algorithms have already been developed, it might be the time for geoscientists, including those who work in the areas of characterization and modeling of porous media and fluid flow and transport therein, to begin thinking, planning, and eventually executing research problems using quantum computers over the next 5–10 years.