1 Introduction

Equipped sandwich structures address at least three-layered structures including a central layer integrated with top and bottom equipped face sheets. Highly progressive demands of different industries for the low weight to strength ratio structures utilization inspired scientists to survey the structures with the capability to satisfy the needs of low weight and high strength requests (Akbaş et al. 2021; Amir et al. 2019a; Civalek et al. 2021; Ge et al. 2021; Le et al. 2021). Therefore, in the passages of years, equipped porous types of sandwich structures’ analysis became an interesting field of scholars' research. Moreover, such structures' crucial role in various aspects of manufacturing (costs, stability, durability, etc.) placed them in the central point of scholars' attention more than before. One of the pioneering studies in this context is done by Khatua and Cheung (1973). Their study was about the mechanical behavior of multilayered sandwich beams and plates. Afterward, Maheri and Adams (1994) went further in this context and conducted a study regarding a special type of vibration of the sandwich beams including the honeycomb layer. What's more, considering a porous plate that was saturated, as a model, its lateral vibrational behavior is analyzed by Leclaire et al. (2001). Takahashi and Tanaka (2002) had an investigation about the vibration of imperfect plates. Moreover, Duc et al. (2017) hired first-order shear deformation plate theory (FSDT) von Karman's assumption, Airy stress functions, Galerkin method, and fourth-order Runge–Kutta method, to study the vibration of sandwich composite cylindrical shells with honeycomb core layer. Then, Amir et al. (2020c) examined the buckling behaviors of sandwich plates. For adding more accuracy, the flexoelectric effect is assumed to exist on both face sheets by them. As another attempt, they captured the flexoelectric impact on the vibrational analysis of sandwich plates (Amir et al. 2020c). Furthermore, Babaei et al. (2019) examined thermal buckling and post-buckling responses of geometrically imperfect functionally graded (FG) porous beams based on the physical neutral plane. Fu et al. (2021a) studied the dynamic instability of porous FG conical shells. Their model was exposed to parametric excitation in a thermal environment. Furthermore, they succeed to capture the boundary condition effect on the stability of FG sandwich conical shells (2021b). Soleymani-Javid et al. (2021) conducted a study regarding the vibrational characteristics of sandwich plates. In their honeycomb-based model, various boundary conditions and flexoelectricity effect are taken into account. In another study, Fu et al. (2021c) examined the dynamic instability of laminated FG carbon nanotubes (CNTs) reinforced conical shells. They considered their model rested on the elastic foundations. Also, Kumar and Renji (2019) had a study on the sandwich panels which were composed of honeycomb and composite layers. Their model was subjected to a diffuse acoustic field in a reverberation chamber. Earlier, Sobhy (2020) utilized the differential quadrature method (DQM) for bending analysis of the FG curved sandwich beam. What's more, in addition to the aforementioned attempts regarding sandwich structures, much hardworking is done exclusively, to introduce different types of composite beams, plates, and shells as an unavoidable part of sandwich structures that carry the massive volume fraction of whole sandwich structures' stiffness. As an instance, Amir et al. (2019a) conducted an analytical study on the vibrational behavior of a sandwich FG porous plate. They used quasi-3D tangential deformation plate hypothesis as displacement field, and also, to integrity, they assumed their model in a hygrothermal surrounding and under the force of Lorentz. Also, Fu et al. (2021d) proposed a theoretical model for the eccentrically stiffened composite sandwich cylindrical shell under external mean fluid. Furthermore, Arshid et al. (2020a) handled a study regarding the dynamic and static behavior of annular FG graphene nanoplatelets (FG-GNPs) reinforced nanocomposite including pores. They considered modified strain gradient theory (MSGT) to take small dimension impacts into account. As another work, Foroutan et al. (2021) examined nonlinear buckling and vibrations of imperfect FG carbon nanofillers (FG-CNFs) reinforced composite cylindrical shells in a hygrothermal environment. In another work, Arshid et al. (2021a) prepared a thermal buckling investigation on the annular/circular microplates. Their model was made of FG graphene nanoplatelets (GNPs) reinforced porous nanocomposite. Further studies are conducted by other scholars in such a broad context (Amir et al. 2020a; Mousavi et al. 2021). Putting such aforementioned simple type of composites aside, nowadays, advanced composite structures are more under evaluation due to their refined mechanical properties. As an example, Moradi-Dastjerdi et al. (2020a) analyzed the buckling behavior of a sandwich plate made of CNTs reinforced porous core patched to two piezoelectric face sheets. They took advantage of the third-order shear deformation plate theory (TSDPT) and Eshelby–Mori–Tanaka's (EMT)'s approach to handle the motion equations. The most important novelty in their work backs to their CNT agglomeration effects consideration. In addition, Dabbagh et al. (2020a) had an attempt to capture the impacts of CNTs agglomeration on the stability of the nanocomposite beams using refined higher-order beam theories. As another instance, Kamarian et al. (2015) by evaluating CNFs agglomeration impact on the vibrations of a sandwich beam proved that in the most agglomeration states of nanocomposite sandwich beams, the mechanical characteristics become improved due to the presence of agglomerations. Besides strength, another important characteristic of sandwich structures that leads such structures toward popularity is their low weight. So, many scholars move their investigations toward porous layers composed of high-strength materials as functionally graded materials (FGMs). Among them, Fu et al. (2020) investigated thermoacoustic variations of a FG cylindrical shell containing pores. Moreover, Van et al. (2020) investigated nonlinear transient behavior of porous FGM plates. Their model was under hygrothermal and mechanical loads affection. Some other applications of nano- and macro-scaled beams can be found in the literature (Avcar 2019; Zenkour and Radwan 2021, 2020; Lazreg and Avcar 2021a, 2021b; Daikh and Zenkour 2019; Jalaei and Civalek 2019; Zenkour 2008, 2018, 2020; Demir and Civalek2017; Barati and Zenkour 2017).

Keeping mentioned papers in mind, the authors decided to examine the vibrational responses of an equipped sandwich beam (ESB) including FG porous core (FGPC) patched to the two same agglomerated CNFs reinforced composites (ACNFRCs) at the top and bottom. So, in the present study, the vibrational behavior of a novel equipped sandwich beams is evaluated. The sandwich structure is placed on the Vlasov's substrate and also, under the thermal environment affection. By Hamilton’s principle, Navier's solution technique, and CNFs' agglomeration effect consideration, governing equations are gained and solved analytically. Finally, response variations against various parameters' changes are depicted in the results portion. Based on the present study results, designing and producing different equipments become possible, and also, a higher ratio of stiffness to weight is accessible more than before. Furthermore, considering CNFs' agglomeration effect on the vibrational behavior of such a model is one of the novelties of this study.

Furthermore, our two-parameter Vlasov’s foundation model included the advantages of the Winkler foundation model and the Pasternak foundation model, and two independent elastic constants are used to represent the characteristics of the given elastic substrate.

2 ESB Analytical Modeling

2.1 Geometrical Information

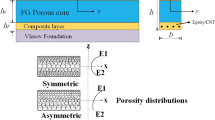
An ESB with length a and total thickness h is considered as a model to evaluate its vibrational responses due to the different variables' variations. As it is displayed in Fig. 1, the ESB is composed of three layers; FGPC and two identical ACNFRC face sheets. The thickness of the FGPC, top ACNFRC, and bottom ACNFRC is demonstrated by the signs hc, ht, and hb, respectively, and their summation denotes ESB total elevation (h). The Cartesian coordinate system (x, y, z) is attached to the imaginary mid-plane of ESB where x and z axes are along with the model's length and thickness directions, one after another. Furthermore, the whole structure is placed on the Vlasov's substrate as an elastic foundation, and also, it is under thermal environment affection.

Fig. 1
figure 1

Configuration of the ESB model

Full size image

2.2 General Equations

For the sake of integrity, various displacement field theories are used in this work. So, the ESB's general displacement field can be defined as (Arshid and Amir 2021; Khorasani et al. 2021):

$$\begin{aligned} U\left( {x,z,t} \right) = & u\left( {x,t} \right) - zw_{,x} \left( {x,t} \right) + f(z)u_{1} \left( {x,t} \right), \\ V\left( {x,z,t} \right) = & 0, \\ W\left( {x,z,t} \right) = & w\left( {x,t} \right) \\ \end{aligned}$$
(1)

where u and w denote longitudinal and transverse movement components of mid-surface. The term u1 is the beam rotation representative. Furthermore, subscript comma (,) is the derivative sign, and f(z) is the considered shape function which denotes the transverse shear stress distribution along the z-direction (Sayyad and Ghugal 2019). By the means of shape function, sufficient flexibility becomes available to switch among different types of displacement fields as is mentioned in Table 1 (Şimşek and Reddy 2013).

Table 1 The various shape functions corresponding to the different displacement fields (Şimşek and Reddy 2013)
Full size table

Where SSDT, HSDT, and ESDT refer to the sinusoidal, hyperbolic, and exponential shear deformation theories. Also, to address the Timoshenko beam model, the displacement component along x-direction should be considered as \(\left( {x,z,t} \right) = u\left( {x,t} \right) + zu_{1} \left( {x,t} \right)\). In the case of Timoshenko beam model utilization, a shear correction factor equals to 5/6 is considered.

The strain tensor of under evaluation model can be obtained as (Arshid et al. 2021b):

$$\left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\gamma_{xz} } \\ \end{array} } \right]^{c,t,b} = \left[ {\begin{array}{*{20}c} {U_{,\,x} } \\ {U_{,\,z} + W_{,\,x} } \\ \end{array} } \right]$$
(2)

In which, superscript c, t, and b address the words core, top, and bottom layer.

Stress–strain equations for each of the three layers are identical, whereas the properties vary layer to layer. Stress field can be presented as (Arshid et al. 2020b; Khorasani et al. 2020):

$$\left[ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\tau_{xz} } \\ \end{array} } \right]^{c,t,b} = \left[ {\begin{array}{*{20}c} {S_{11} } & 0 \\ 0 & {S_{55} } \\ \end{array} } \right]^{c,t,b} \left[ {\begin{array}{*{20}c} {\varepsilon_{xx} - \theta \,\,\Delta T} \\ {\gamma_{xz} } \\ \end{array} } \right]^{c,t,b} ,$$
(3)

where S and θ serve as an elastic constant and thermal expansion coefficient, respectively.

Besides this, ΔT is the temperature difference and can be specified as \(\Delta T = T\left( z \right) - T_{ref}\).

In which Tref denotes the reference temperature which is equal to ambient temperature (293) and T(z) represents temperature variation across the ESB's height and, in the linear format, it can be addressed as (Tang and Ding 2019):

$$T(z) = T_{b} + \Delta T_{tb} \left( {0.5 + \frac{z}{h}} \right)$$
(4)

In which, Tb is the ESB's bottom surface temperature, and also, it is considered as the reference temperature in the current study. Moreover, ΔTtb stands for the temperature difference between ESB's top and bottom surfaces (i.e., ΔTtb = Tt—Tb).

2.3 ACNFRC Face Sheets' Properties.

Generally, the philosophy of CNFs' utilization in a polymeric matrix is to improve the mechanical properties of the structure. As the elasticity modulus of the reinforcing phase is much more than the matrix, a polymeric matrix that is reinforced by CNFs has improved mechanical properties in comparison with the pure matrix.

Despite the mentioned high stiffness, CNFs' high level of aspect ratio results in their low level of bending strength. As a consequence, CNFs pose a great tendency to be bundled together and form some CNFs concentrated spherical inclusions named clusters. The mentioned effect serves as an agglomeration effect which plays a constructive role in the composite layers' mechanical properties refinement. On the other hands, CNFs can also be distributed in the matrix without being concentrated in clusters. Therefore, there are two different types of CNFs' in the polymeric matrix. By definition, μ and η specify the CNFs concentrated region volume fraction and the sprinkled CNFs inside the clusters volume fraction as (Dabbagh et al. 2020a):

$$\begin{aligned} \mu = & {{V^{{{\text{Cluster}}}} } \mathord{\left/ {\vphantom {{V^{{{\text{Cluster}}}} } V}} \right. \kern-\nulldelimiterspace} V} \\ \eta = & {{V_{r}^{{{\text{Cluster}}}} } \mathord{\left/ {\vphantom {{V_{r}^{{{\text{Cluster}}}} } {V_{r} }}} \right. \kern-\nulldelimiterspace} {V_{r} }} \\ \end{aligned}$$
(5)

In which, V is a sign to illustrate the representative volume element (RVE), VCluster addresses the net volume of CNFs concentrated regions inside the borders of RVE, VrCluster denotes the total volume of CNFs inside the clusters, and the term Vr implies the net volume of CNFs inside the RVE. It should be noticed that the magnitude of μ in the maximum case is equal to η. To provide a clear physical imagination for the abovementioned parameters, it is worthwhile mentioning that:

  • μ equal to zero specifies non-agglomerated layer which means there is no concentration of CNFs in the CNFRCs. On the other hands, when its value is equal to one, the whole composite layer serves as a big agglomerated region.

  • Considering the abovementioned methodology limitation (\(\eta \ge \mu\)), η equal to zero implies there is no CNF inside the clusters, so basically there is no cluster. While η equal to one denotes all CNFs are accumulated inside the clusters and ACNFRCs contain no CNF out of the clusters.

  • In a specific case, when μ = η = 1, there is fully CNFs agglomerated composite.

For the sake of ACNFRCs' mechanical properties capturing, the Eshelby–Mori–Tanaka technique (EMTT) is hired (Shi et al. 2004). Based on the EMTT, the bulk modulus (K) and the shear modulus (G) inside and outside of the clusters can be defined as (Moradi-Dastjerdi et al. 2020b; Shi et al. 2004):

$$K_{in}^{t,b} = K_{p} + \left( {{\raise0.7ex\hbox{${(\delta_{r} - 3K_{p} \alpha_{r} )f_{r}^{t,b} \eta }$} \!\mathord{\left/ {\vphantom {{(\delta_{r} - 3K_{p} \alpha_{r} )f_{r}^{t,b} \eta } {3(\mu - f_{r}^{t,b} \eta + f_{r}^{t,b} \eta \alpha_{r} )}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3(\mu - f_{r}^{t,b} \eta + f_{r}^{t,b} \eta \alpha_{r} )}$}}} \right),$$
(6)
$$G_{in}^{t,b} = G_{p} + \left( {{\raise0.7ex\hbox{${(\eta_{r} - 2G_{p} \beta_{r} )f_{r}^{t,b} \eta }$} \!\mathord{\left/ {\vphantom {{(\eta_{r} - 2G_{p} \beta_{r} )f_{r}^{t,b} \eta } {2(\mu - f_{r}^{t,b} \eta + f_{r}^{t,b} \eta \beta_{r} )}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${2(\mu - f_{r}^{t,b} \eta + f_{r}^{t,b} \eta \beta_{r} )}$}}} \right),$$
(7)
$$K_{out}^{t,b} = K_{p} + \left( {{\raise0.7ex\hbox{${(\delta_{r} - 3K_{p} \alpha_{r} )f_{r}^{t,b} (1 - \eta )}$} \!\mathord{\left/ {\vphantom {{(\delta_{r} - 3K_{p} \alpha_{r} )f_{r}^{t,b} (1 - \eta )} {3((1 - \mu ) - f_{r}^{t,b} (1 - \eta ) + f_{r}^{t,b} (1 - \eta )\alpha_{r} )}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3((1 - \mu ) - f_{r}^{t,b} (1 - \eta ) + f_{r}^{t,b} (1 - \eta )\alpha_{r} )}$}}} \right),$$
(8)
$$G_{out}^{t,b} = G_{p} + \left( {{\raise0.7ex\hbox{${(\eta_{r} - 2G_{p} \beta_{r} )f_{r}^{t,b} (1 - \eta )}$} \!\mathord{\left/ {\vphantom {{(\eta_{r} - 2G_{p} \beta_{r} )f_{r}^{t,b} (1 - \eta )} {2((1 - \mu ) - f_{r}^{t,b} (1 - \eta ) + f_{r}^{t,b} (1 - \eta )\beta_{r} )}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${2((1 - \mu ) - f_{r}^{t,b} (1 - \eta ) + f_{r}^{t,b} (1 - \eta )\beta_{r} )}$}}} \right)$$
(9)

where subscripts p, r, and the term fr address the polymeric matrix, CNFs reinforcing phase, and the total volume fraction of CNFs inside the composite. The evaluation of the vibrational response of the current ESB due to the various types of CNFs distribution through the polymeric matrix is accessible by the means of following CNFs volume fraction equations as (Amir et al. 2019b):

$$f_{r}^{t,b} = \left\{ {\begin{array}{*{20}l} {f^{*} } \hfill & U \hfill \\ {\frac{4}{{h_{t,\,\,b} }}\left| {z \mp \frac{{h_{c} + h_{t,\,\,b} }}{2}} \right|\,\,f^{*} } \hfill & {FG - X} \hfill \\ {2(1 - \frac{2}{{h_{t,\,\,b} }})\left| {z \mp \frac{{h_{c} + h_{t,\,\,b} }}{2}} \right|\,\,f^{*} } \hfill & {FG - O} \hfill \\ {(1 - \frac{2}{{h_{t,\,\,b} }})(z \mp \frac{{h_{c} + h_{t,\,\,b} }}{2})\,\,f^{*} } \hfill & {FG - A} \hfill \\ {(1 + \frac{2}{{h_{t,\,\,b} }})(z \mp \frac{{h_{c} + h_{t,\,\,b} }}{2})\,\,f^{*} } \hfill & {FG - V} \hfill \\ \end{array} } \right.$$
(10)

In Fig. 2, the variation of CNFs volume fraction versus composite layer thickness is displayed for different types of CNFs distribution.

Fig. 2
figure 2

The variation of CNFs volume fraction versus thickness of composite face sheets for different types of CNFs distribution

Full size image

What's more, the terms αr, βr, ηr, and δr can be written as follows (Moradi-Dastjerdi et al. 2020a):

$$\alpha_{r} = {\raise0.7ex\hbox{${(3(K_{p} + G_{p} ) + k_{r} - l_{r} )}$} \!\mathord{\left/ {\vphantom {{(3(K_{p} + G_{p} ) + k_{r} - l_{r} )} {3(G_{p} + k_{r} )}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3(G_{p} + k_{r} )}$}},$$
(11)
$$\beta_{r} = 0.2\left[ {\frac{{4G_{p} + 2k_{r} + l_{r} }}{{3(G_{p} + k_{r} )}} + \frac{{4G_{p} }}{{G_{p} + p_{r} }} + \frac{{2\left\{ {G_{p} (3K_{p} + G_{p} ) + G_{p} (3K_{p} + 7G_{p} )} \right\}}}{{G_{p} (3K_{p} + G_{p} ) + m_{r} (3K_{p} + 7G_{p} )}}} \right],$$
(12)
$$\eta_{r} = 0.2\left[ \begin{gathered} 0.66(n_{r} - l_{r} ) + \frac{{8G_{p} p_{r} }}{{G_{p} + p_{r} }} + \frac{{8G_{p} m_{r} (3K_{p} + 4G_{p} )}}{{3K_{p} (G_{p} + m_{r} ) + G_{p} (G_{p} + 7m_{r} )}} \hfill \\ + \frac{{2(k_{r} - l_{r} )(2G_{p} + l_{r} )}}{{3(G_{p} + k_{r} )}} \hfill \\ \end{gathered} \right],$$
(13)
$$\delta_{r} = 0.33\left[ {n_{r} + 2l_{r} + \frac{{(2k_{r} + l_{r} )(3K_{p} + 2G_{p} - l_{r} )}}{{G_{p} + k_{r} }}} \right]$$
(14)

At the current equations kr, lr, mr, pr, and nr address the CNFs' elastic Hill’s constants which are varied for various types of CNFs concerning their chiral index magnitude. In the current study mentioned constants related to single-walled carbon nanofillers (SWCNFs) with a chirality index equal to 10 are used (Fantuzzi et al. 2017).

So, the thickness-dependent bulk modulus and the shear modulus of the ACNFRCs are obtained by the means of EMTT as (Dabbagh et al. 2020b):

$$K_{n}^{t,b} (z) = K_{out}^{t,b} \left\{ {1 + {\raise0.7ex\hbox{${\mu \,\left( {\frac{{K_{in}^{t,b} }}{{K_{out}^{t,b} }} - 1} \right)}$} \!\mathord{\left/ {\vphantom {{\mu \,\left( {\frac{{K_{in}^{t,b} }}{{K_{out}^{t,b} }} - 1} \right)} {\left( {1 + \alpha^{t,b} \left( {1 - \mu } \right)\left( {\frac{{K_{in}^{t,b} }}{{K_{out}^{t,b} }} - 1} \right)} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {1 + \alpha^{t,b} \left( {1 - \mu } \right)\left( {\frac{{K_{in}^{t,b} }}{{K_{out}^{t,b} }} - 1} \right)} \right)}$}}} \right\},$$
(15)
$$G_{n}^{t,b} (z) = G_{out}^{t,b} \left\{ {1 + {\raise0.7ex\hbox{${\mu \left( {\frac{{G_{in}^{t,b} }}{{G_{out}^{t,b} }} - 1} \right)}$} \!\mathord{\left/ {\vphantom {{\mu \left( {\frac{{G_{in}^{t,b} }}{{G_{out}^{t,b} }} - 1} \right)} {\left( {1 + \beta^{\,t,b} \left( {1 - \mu } \right)\left( {\frac{{G_{in}^{t,b} }}{{G_{out}^{t,b} }} - 1} \right)} \right)}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left( {1 + \beta^{\,t,b} \left( {1 - \mu } \right)\left( {\frac{{G_{in}^{t,b} }}{{G_{out}^{t,b} }} - 1} \right)} \right)}$}}} \right\}$$
(16)

In which subscript n denotes nano ACNFRCs and:

$$\alpha^{\,t,b} = {\raise0.7ex\hbox{${(1 + \nu_{out}^{t,b} )}$} \!\mathord{\left/ {\vphantom {{(1 + \nu_{out}^{t,b} )} {3(1 - \nu_{out}^{t,b} )}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${3(1 - \nu_{out}^{t,b} )}$}}$$
(17)
$$\beta^{\,t,b} = {\raise0.7ex\hbox{${2(4 - 5\nu_{out}^{t,b} )}$} \!\mathord{\left/ {\vphantom {{2(4 - 5\nu_{out}^{t,b} )} {15(1 - \nu_{out}^{t,b} )}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${15(1 - \nu_{out}^{t,b} )}$}}$$

And

$$\nu_{out}^{t,b} = {\raise0.7ex\hbox{${(3K_{out}^{t,b} - 2G_{out}^{t,b} )}$} \!\mathord{\left/ {\vphantom {{(3K_{out}^{t,b} - 2G_{out}^{t,b} )} {(6K_{out}^{t,b} + 2G_{out}^{t,b} )}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${(6K_{out}^{t,b} + 2G_{out}^{t,b} )}$}}$$
(18)

Finally, the elastic modulus (E), Poisson's ratio (ν) density (ρ) and thermal expansion coefficient (θ) of the nano ACNFRCs can be simulated as (Kamarian et al. 2016; Moradi-Dastjerdi et al. 2020a):

$$E^{t,b} (z) = {\raise0.7ex\hbox{${9K_{n}^{t,b} G_{n}^{t,b} }$} \!\mathord{\left/ {\vphantom {{9K_{n}^{t,b} G_{n}^{t,b} } {(3K_{n}^{t,b} + G_{n}^{t,b} )}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${(3K_{n}^{t,b} + G_{n}^{t,b} )}$}},$$
(19)
$$\nu^{\,t,b} (z) = {\raise0.7ex\hbox{${(3K_{n}^{t,b} - 2G_{n}^{t,b} )}$} \!\mathord{\left/ {\vphantom {{(3K_{n}^{t,b} - 2G_{n}^{t,b} )} {(6K_{n}^{t,b} + 2G_{n}^{t,b} )}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${(6K_{n}^{t,b} + 2G_{n}^{t,b} )}$}},$$
(20)
$$\rho^{t,b} (z) = (\rho_{r}^{t,b} - \rho_{p}^{t,b} )\,f_{r}^{t,b} + \rho_{p}^{t,b} ,$$
(21)
$$\theta^{\,t,b} (z) = \left( {\frac{{E + 4\nu K_{n} (1 + \nu )}}{{E + 4K_{n} (1 + \nu )^{2} }}} \right)^{\,\,t,b} \left( {\frac{{f_{r}^{t,b} E_{11}^{CNF} \theta_{11}^{CNF} + (1 - f_{r}^{t,b} )E_{p} \theta_{p} }}{{f_{r}^{t,b} E_{11}^{CNF} + (1 - f_{r}^{t,b} )E_{p} }}} \right)$$
(22)

The elastic constants for top and bottom face sheets are identical in the formulation as (Zhang et al. 2021):

$$\left[ {\begin{array}{*{20}c} {S_{11} (z)} \\ {S_{55} (z)} \\ \end{array} } \right]^{\,\,t,b} = \left[ {\begin{array}{*{20}c} {E(z)(1 - \nu^{2} (z))^{ - 1} } \\ {0.5E(z)(1 + \nu (z))^{ - 1} } \\ \end{array} } \right]^{\,\,t,\,\,b}$$
(23)

2.4 FGPC Properties

As mentioned before, the ESB's core is an imperfect layer that is made of FGMs. So, the top and bottom surfaces of the FGPC are assumed to be pure ceramic and pure metal. To add more elaboration in this context, three different types of imperfection dispersions are taken into account and their impact on the mechanical behavior of the whole sandwich model is compared to each other. Based on the rule of the mixture in its imperfection-dependent format, the FGPC's mechanical properties in the case of uniform porosity dispersion can be defined by the following formulation (Kumar et al. 2021):

$$R^{c} (z) = (R_{c} - R_{m} )\,\,V_{c} + R_{m} - (R_{c} + R_{m} )\frac{e}{2}$$
(24)

where R is the sign to address different mechanical properties as E, ν, ρ, and θ. Also, subscripts c and m are used to distinguish ceramic properties and metallic properties. Furthermore, e denotes porosity index, and Vc stands for ceramic volume fraction which can be presented as (Dastjerdi et al. 2020):

$$V_{c} (z) = \left( {0.5 + \frac{z}{{h_{c} }}} \right)^{n} ,\;V_{c} = 1 - V_{m}$$
(25)

In which, n is the power-law index, gradient index, or material property exponent. Based on the aforementioned equation, the ceramic and metal volume fractions variation versus core thickness is plotted in Fig. 3 for various material property exponents.

Fig. 3
figure 3

The variation of ceramic and metal volume fractions versus core thickness for different power-law indexes

Full size image

As it is visible in Fig. 3, the power-law index enhancement results in ceramic volume fraction increasing at a lower rate across the first half-thickness of the core (Akgöz and Civalek 2014).

The core mechanical properties in the case of X type dispersion of porosities can be presented as (Fan et al. 2021):

$$R^{c} (z) = (R_{c} - R_{m} )\,\,V_{c} + R_{m} - (R_{c} + R_{m} )\left| {\frac{2z}{{h_{c} }}} \right|\frac{e}{2},$$
(26)

And finally, dispersing porosities within the FGPC based on the O pattern result in the following model for FGPC's mechanical properties capturing as (Thanh et al. 2019):

$$R^{c} (z) = (R_{c} - R_{m} )\,\,V_{c} + R_{m} - (R_{c} + R_{m} )\left\{ {1 - \left| {\frac{2z}{{h_{c} }}} \right|} \right\}\frac{e}{2},$$
(27)

Also, it seems to be mandatory to mention that setting e equal to zero in each type of pores dispersion causes having perfect FGC instead of the FGPC.

To provide a more comprehensive physical mental background about FGPC and based on Eqs. (24, 26 and 27), the FGPC's elastic moduli variation against its thickness is plotted as it is visible in Fig. 4. As curves say, passing from the core bottom surface to the top surface, the FGPC's elastic modulus for all types of porosity dispersion increases, by and large. Such behavior is due to the high elastic modulus of ceramic over metal. Another noticeable point is that in this figure, there are three important points; i.e., \(z=0, \frac{h}{2}\mathrm{ and }h\). As it is obvious, at the top and bottom surface of FGPC, the elastic modulus related to the curves perfect FGC and O-FGPC has the same values. Also, there is a similar attitude regarding U-FGPC and X-FGPC. On the other hands, within the specific region of the core thickness, the value of the X-FGPC's elastic moduli becomes higher than that of O-FGPC's which is due to the type of pores dispersion in this region. Using the abovementioned properties, the elastic modulus of the FGPC can be formulated as:

$$\left[ {\begin{array}{*{20}c} {S_{11} (z)} \\ {S_{55} (z)} \\ \end{array} } \right]^{\,\,c} = \left[ {\begin{array}{*{20}c} {E(z)(1 - \nu^{2} (z))^{ - 1} } \\ {0.5E(z)(1 + \nu (z))^{ - 1} } \\ \end{array} } \right]^{\,\,c}$$
(28)
Fig. 4
figure 4

The FGPC's elastic moduli variation against its thickness for different types of pores dispersion

Full size image

3 Governing Equations

Hamilton's principle that serves as an energy-based technique is implemented to extract the governing equations of motion as (Arshid et al. 2020c):

$$\delta \int_{{t_{1} }}^{{t_{2} }} {\left\{ {\Psi + \Xi - \Gamma } \right\}dt} = 0$$
(29)

where Ψ, Ξ, and Γ give a hint to the kinetic energy, externally applied work, and the strain energy, correspondingly.

The kinetic energy of the whole ESB can be derived as (Arshid and Khorshidvand 2018):

$$\Psi = 0.5\int\limits_{x} {\int\limits_{ - h/2}^{ + h/2} {\rho^{\,c,t,b} (z)\left[ {\left( {U_{,\,t} } \right)^{2} + {\mkern 1mu} {\mkern 1mu} \left( {W_{,\,t} } \right)^{2} } \right]} \,dzdx}$$
(30)

The second term of Hamilton's principle is the external work that is originated from the externally applied force due to the thermal environment affection. The thermal force in response to the addressed thermal surrounding is simulated as (Arshid et al. 2021c):

$$F_{x}^{T} = \int\limits_{ - h/2}^{ + h/2} {S_{11}^{\,c,t,b} \theta^{c,t,b} \Delta Tdz} ,$$
(31)

The thermal external work can be simulated as (Arshid et al. 2019b):

$$\Xi = 0.5\int_{x} {F_{x}^{T} (w_{,x} )^{2} } dx$$
(32)

Passing from the kinetic energy and the external work, the third part of Hamilton's principle equation addresses the strain energy of the ESB that becomes divided into two branches; classic strain energy of the beam and strain energy of the Vlasov's substrate.

The classical strain energy of the ESB will be derived using the following equation as (Amir et al. 2020b):

$$\Gamma_{1} = 0.5\int\limits_{x} {\int\limits_{ - h/2}^{ + h/2} {\left[ {\sigma_{xx} \varepsilon_{x} + \tau_{xz} \gamma_{xz} } \right]^{\,c,t,b} } dzdx}$$
(33)

About foundation, it is better to mention a short background regarding Vlasov's foundation model and its properties, firstly. At the first time, Vlasov, to consider the vertical shearing parameter, based on the variational approach and also continuum principles progressed a bi-parameter novel foundation model that becomes famous as Vlasov's foundation. His model is assumed to be elastic, homogeneous, and isotropic. Furthermore, silica aerogel is assumed to play the role of constituting substrate material for under examination ESB. Based on Vlasov's foundation model and by considering a Cartesian coordinate system attached to the top surface of the substrate, the strain energy of substrate can be addressed as (Ghorbanpour Arani and Zamani 2019):

$$\Gamma_{2} = 0.5\int_{ - \infty }^{ + \infty } {\int_{ - H}^{0} {\left[ {\sigma_{xx} \varepsilon_{xx} + \sigma_{zz} \varepsilon_{zz} + \tau_{xz} \gamma_{xz} } \right]^{f} } \,} dzdx,$$
(34)

In which H implies the foundation thickness and superscript f addresses Vlasov's foundation. Moreover, the related stress and strains can be defined by defining a new displacement field for the substrate as (Navarro et al. 2013):

$$\begin{aligned} \overline{U} \left( {x,z,t} \right) = & 0, \\ \overline{W} \left( {x,z,t} \right) = & w\left( {x,t} \right)\lambda (z) \\ \end{aligned}$$
(35)

It should be noticed that the displacement in the x-direction is considered zero based on this assumption that its value is relatively negligible in comparison with vertical displacement. Also, λ is correlated with the shape function of the substrate with boundary conditions as:

$$\lambda (0) = 1,\;\lambda ( - H) = 0$$
(36)

Accordingly, the foundation's stress and strain fields are presented as (Ghorbanpour Arani and Zamani 2018):

$$\left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{zz} } \\ {\gamma_{xz} } \\ \end{array} } \right]^{\,\,f} = \left[ {\begin{array}{*{20}c} {\overline{U}_{,\,x} } \\ {\overline{W}_{,\,z} } \\ {\overline{U}_{,\,z} + \overline{W}_{,\,x} } \\ \end{array} } \right],\;\left[ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\tau_{xz} } \\ {\sigma_{zz} } \\ \end{array} } \right]^{\,\,f} = \left[ {\begin{array}{*{20}c} {S_{11} } & 0 & {S_{13} } \\ 0 & {S_{22} } & 0 \\ {S_{31} } & 0 & {S_{33} } \\ \end{array} } \right]^{\,\,f} \left[ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\gamma_{xz} } \\ {\varepsilon_{zz} } \\ \end{array} } \right]^{\,\,f}$$
(37)

In which S serves as the foundation elastic coefficient and can be defined as:

$$\begin{aligned} S_{11}^{f} = & S_{33}^{f} = \frac{{(1 - \nu^{f} )E^{f} }}{{(1 + \nu^{f} )(1 - 2\nu^{f} )}}, \\ S_{13}^{f} = & S_{31}^{f} = \frac{{E^{f} \nu^{f} }}{{(1 + \nu^{f} )(1 - 2\nu^{f} )}}, \\ S_{22}^{f} = & \frac{{E^{f} }}{{2(1 + \nu^{f} )}} \\ \end{aligned}$$
(38)

Inserting Eq. (37) into Eq. (34) and its rewriting led the foundation strain energy formulation to the final format as:

$$\Gamma_{2} = 0.5\int_{ - \infty }^{ + \infty } {\int_{ - H}^{0} {\left[ {S_{33}^{f} (w\lambda_{,z} )^{2} + S_{22}^{f} (\lambda w_{,x} )^{2} } \right]} \,} dzdx$$
(39)

This equation, by minimizing respect to w, is capable to transform to the differential type equation through mathematical considerations as (Navarro et al. 2013):

$$- L_{1} \frac{{\partial^{2} w}}{{\partial x^{2} }} + L_{2} w = 0$$
(40)

In which, L1 and L2 are the foundation parameters and address, respectively, the shear parameter of foundation and the compression parameter of foundation.

$$\begin{aligned} L_{1} = & S_{22}^{f} \int_{ - H}^{0} {\lambda^{2} dz,} \\ L_{2} = & S_{33}^{f} \int_{ - H}^{0} {(\lambda_{,z} )^{2} dz} \\ \end{aligned}$$
(41)

In which the shape function is presented as follows (Vallabhan et al. 1991):

$$\lambda (z) = \frac{{\sinh \left[ {\Sigma \left( {1 - \frac{z}{H}} \right)} \right]}}{\sinh \left[ \Sigma \right]},\;\left( {\frac{\Sigma }{H}} \right)^{2} = \frac{{S_{22}^{f} }}{{S_{33}^{f} }}\frac{{\int_{ - \infty }^{ + \infty } {(w_{,x} )^{2} dx} }}{{\int_{ - \infty }^{ + \infty } {w^{2} dx} }}$$
(42)

where Σ is the parameter correlated with the deformation of the core.

Finally, the net ESB's strain energy is catchable using the summation principle as:

$$\Gamma = \Gamma_{1} + \Gamma_{2}$$
(43)

Substituting Eqs. (30, 32, 43) into Eq. (29) and applying some mathematical manipulations as, districting integrals with respect to z and integrating by part, equations of motion can be obtained in the stress resultants terms as:

$$\delta u:$$
$$- \frac{\partial }{\partial x}N_{xx0} - J_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - J_{1} \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}} - J_{4} \frac{{\partial^{2} u_{1} }}{{\partial t^{2} }} = 0,$$
(44)
$$\delta u_{1} :$$
$$- \frac{\partial }{\partial x}N_{xx4} + N_{xz5} - J_{4} \frac{{\partial^{2} u}}{{\partial t^{2} }} + J_{14} \frac{{\partial^{3} w}}{{\partial t^{2} \partial x}} - J_{44} \frac{{\partial^{2} u_{1} }}{{\partial t^{2} }} = 0,$$
(45)
$$\delta w:$$
$$- \frac{{\partial^{2} }}{{\partial x^{2} }}N_{xx1} - J_{1} \frac{{\partial^{3} u}}{{\partial t^{2} \partial x}} + J_{2} \frac{{\partial^{4} w}}{{\partial t^{2} \partial x^{2} }} - J_{14} \frac{{\partial^{3} u_{1} }}{{\partial t^{2} \partial x}} - J_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} - L_{1} \frac{{\partial^{2} w}}{{\partial x^{2} }} + L_{2} w - F_{x}^{T} \frac{{\partial^{2} w}}{{\partial x^{2} }} = 0$$
(46)

In which:

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {N_{xx0} ,} & {N_{xx1} ,} & {N_{xx4} } \\ \end{array} } \right] = & \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} \,\,\sigma_{xx} \left[ {\begin{array}{*{20}c} {1,} & {z,} & {f(z)} \\ \end{array} } \right]dz, \\ \left[ {N_{xz5} } \right] = & \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} \,\,\sigma_{xz} \frac{\partial }{\partial z}f(z)dz \\ \end{aligned}$$
(47)

By inserting some mathematical manipulation, the stress resultants can be defined as:

$$\begin{aligned} N_{xx0} = & S_{110} \frac{\partial u}{{\partial x}} - S_{111} \frac{{\partial^{2} w}}{{\partial x^{2} }} + S_{114} \frac{{\partial u_{1} }}{\partial x}, \\ N_{xx1} = & S_{111} \frac{\partial u}{{\partial x}} - S_{112} \frac{{\partial^{2} w}}{{\partial x^{2} }} + S_{1114} \frac{{\partial u_{1} }}{\partial x}, \\ N_{xx4} = & S_{114} \frac{\partial u}{{\partial x}} - S_{1114} \frac{{\partial^{2} w}}{{\partial x^{2} }} + S_{1144} \frac{{\partial u_{1} }}{\partial x}, \\ N_{xz5} = & S_{5555} u_{1} \\ \end{aligned}$$
(48)

In which:

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {S_{110} ,} & {S_{111} ,} & {S_{112} ,} & {S_{114} } \\ \end{array} } \right] = & \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} \,\,S_{11} \left[ {\begin{array}{*{20}c} {1,} & {z,} & {z^{2} ,} & {f(z)} \\ \end{array} } \right]dz, \\ \left[ {\begin{array}{*{20}c} {S_{1114} ,} & {S_{1144} } \\ \end{array} } \right] = & \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} \,\,S_{11} \left[ {\begin{array}{*{20}c} {zf(z),} & {f(z)^{2} } \\ \end{array} } \right]dz, \\ \left[ {S_{5555} } \right] = & \int_{{ - \frac{h}{2}}}^{\frac{h}{2}} \,\,S_{55} \left[ {\frac{\partial f(z)}{{\partial z}}} \right]^{2} dz \\ \end{aligned}$$
(49)

Also, coefficients related to the kinematic terms can be defined as:

$$\begin{aligned} J_{0} = & \int\limits_{{ - 0.5h_{c} - h_{b} }}^{{ - 0.5h_{c} }} {\rho^{\,b} (z)} dz + \int\limits_{{ - 0.5h_{c} }}^{{ + 0.5h_{c} }} {\rho^{\,c} (z)dz} + \int\limits_{{ + 0.5h_{c} }}^{{ + 0.5h_{c} + h_{t} }} {\rho^{\,t} (z)dz,} \\ J_{1} = & \int\limits_{{ - 0.5h_{c} - h_{b} }}^{{ - 0.5h_{c} }} {z\rho^{\,b} (z)} dz + \int\limits_{{ - 0.5h_{c} }}^{{ + 0.5h_{c} }} {z\rho^{\,c} (z)dz} + \int\limits_{{ + 0.5h_{c} }}^{{ + 0.5h_{c} + h_{t} }} {z\rho^{\,t} (z)dz,} \\ J_{2} = & \int\limits_{{ - 0.5h_{c} - h_{b} }}^{{ - 0.5h_{c} }} {z^{2} \rho^{\,b} (z)} dz + \int\limits_{{ - 0.5h_{c} }}^{{ + 0.5h_{c} }} {z^{2} \rho^{\,c} (z)dz} + \int\limits_{{ + 0.5h_{c} }}^{{ + 0.5h_{c} + h_{t} }} {z^{2} \rho^{\,t} (z)dz,} \\ J_{4} = & \int\limits_{{ - 0.5h_{c} - h_{b} }}^{{ - 0.5h_{c} }} {f(z)\rho^{\,b} (z)} dz + \int\limits_{{ - 0.5h_{c} }}^{{ + 0.5h_{c} }} {f(z)\rho^{\,c} (z)dz} + \int\limits_{{ + 0.5h_{c} }}^{{ + 0.5h_{c} + h_{t} }} {f(z)\rho^{\,t} (z)dz,} \\ J_{14} = & \int\limits_{{ - 0.5h_{c} - h_{b} }}^{{ - 0.5h_{c} }} {zf(z)\rho^{\,b} (z)} dz + \int\limits_{{ - 0.5h_{c} }}^{{ + 0.5h_{c} }} {zf(z)\rho^{\,c} (z)dz} + \int\limits_{{ + 0.5h_{c} }}^{{ + 0.5h_{c} + h_{t} }} {zf(z)\rho^{\,t} (z)dz,} \\ J_{44} = & \int\limits_{{ - 0.5h_{c} - h_{b} }}^{{ - 0.5h_{c} }} {f(z)^{2} \rho^{\,b} (z)} dz + \int\limits_{{ - 0.5h_{c} }}^{{ + 0.5h_{c} }} {f(z)^{2} \rho^{\,c} (z)dz} + \int\limits_{{ + 0.5h_{c} }}^{{ + 0.5h_{c} + h_{t} }} {f(z)^{2} \rho^{\,t} (z)dz} \\ \end{aligned}$$
(50)

4 Analytical Solution Procedure

Based on Navier's solution technique, the governing equations are solved analytically. Regarding this technique, the geometrical boundary conditions for the simply supported type of beam become satisfied using the following expressions for displacement components as (Arshid et al. 2019c):

$$\left[ {\begin{array}{*{20}c} {u(x,t)} \\ {u_{1} (x,t)} \\ {w(x,t)} \\ \end{array} } \right] = \sum\limits_{m = 1}^{\infty } {\left[ {\begin{array}{*{20}c} {U{\mkern 1mu} \cos \left( {\chi {\mkern 1mu} x} \right)} \\ {U_{1} {\mkern 1mu} \cos \left( {\chi x} \right)} \\ {W{\mkern 1mu} \sin \left( {\chi {\mkern 1mu} x} \right)} \\ \end{array} } \right]} \,e^{{i\omega {\kern 1pt} t}}$$
(51)

where U, U1, and W serve as unknown coefficients. Also, \(\chi = \frac{m\pi }{a}\) and m denotes the mode number along ESB's length. For the sake of simplicity, the final formulation is capable to have a compact and matrixial expression as (Thai et al. 2015):

$$\left[ {A - B\omega^{2} } \right]_{3*3} \left[ \Lambda \right]_{3*1} = 0$$
(52)

In the final formulation, A, B, and Λ address stiffness matrix, mass matrix, and displacement vector, correspondingly. The matrix A and B can be presented in detail as:

$$A = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & {A_{13} } \\ {A_{21} } & {A_{22} } & {A_{23} } \\ {A_{31} } & {A_{32} } & {A_{33} } \\ \end{array} } \right],\;B = \left[ {\begin{array}{*{20}c} {B_{11} } & {B_{12} } & {B_{13} } \\ {B_{21} } & {B_{22} } & {B_{23} } \\ {B_{31} } & {B_{32} } & {B_{33} } \\ \end{array} } \right]$$
(53)

where

$$\begin{aligned} \left[ {\begin{array}{*{20}c} {A_{11} ,} & {A_{12} ,} & {A_{13} } \\ \end{array} } \right] = & \chi^{2} \left[ {\begin{array}{*{20}c} {S_{110} ,} & {S_{114} ,} & { - \chi S_{111} } \\ \end{array} } \right], \\ \left[ {\begin{array}{*{20}c} {A_{21} ,} & {A_{22} ,} & {A_{23} } \\ \end{array} } \right] = & \left[ {\begin{array}{*{20}c} {\chi^{2} S_{114} ,} & {\chi^{2} S_{1144} + S_{5555} ,} & { - \chi^{3} S_{1114} } \\ \end{array} } \right], \\ \left[ {\begin{array}{*{20}c} {A_{31} ,} & {A_{32} ,} & {A_{33} } \\ \end{array} } \right] = & \left[ {\begin{array}{*{20}c} { - \chi^{3} S_{111} ,} & { - \chi^{3} S_{1114} ,} & {\chi^{4} S_{112} + \chi^{2} L_{1} + L_{2} + \chi^{2} F_{x}^{T} } \\ \end{array} } \right], \\ \left[ {\begin{array}{*{20}c} {B_{11} ,} & {B_{12} ,} & {B_{13} } \\ \end{array} } \right] = & \left[ {\begin{array}{*{20}c} { - J_{0} ,} & { - J_{4} ,} & {\chi J_{1} } \\ \end{array} } \right], \\ \left[ {\begin{array}{*{20}c} {B_{21} ,} & {B_{22} ,} & {B_{23} } \\ \end{array} } \right] = & \left[ {\begin{array}{*{20}c} { - J_{4} ,} & { - J_{44} ,} & {\chi J_{14} } \\ \end{array} } \right], \\ \left[ {\begin{array}{*{20}c} {B_{31} ,} & {B_{32} ,} & {B_{33} } \\ \end{array} } \right] = & \left[ {\begin{array}{*{20}c} {\chi J_{1} ,} & {\chi J_{14} ,} & { - \chi^{2} J_{2} - J_{0} } \\ \end{array} } \right] \\ \end{aligned}$$
(54)

5 Numerical Results and Discussion

Passing from the abovementioned sections and formulations, in the current section, the vibrational responses of the ESB to the different variables' variations are presented to accounts for their impacts on the current model's vibrational behaviors. As mentioned previously, ESB is constituted from an FGPC and two ACNFRCs as face sheets. The thickness of the core, the thickness of each one of the face sheets, and the length of the model assumed to be 5 mm, 0.5 mm, and 20 mm, respectively. What's more and for the sake of integrity, the effect of FGPC's different materials' utilization is considered in the current study. The properties of all used materials are collected and displayed in Table 2 (Sharma et al. 2018) and Table 3 (Moradi-Dastjerdi et al. 2020a).

Table 2 ESB's core constituents' properties (Sharma et al. 2018)
Full size table
Table 3 ESB's face sheets constituents' properties (Moradi-Dastjerdi et al. 2020a)
Full size table

Moreover, about Vlasov's foundation, getting a glimpse of Eqs. (40–42), it can be concluded that deformation (w), through foundation's parameters, depends on the Σ. Also, the magnitude of Σ is dependent on the w. So, as presented graphically by Fig. 5, an iterative technique is required to find the exact value of Σ.

Fig. 5
figure 5

The iterative technique procedure to determine the exact value of γ

Full size image

Base on Fig. 5, at the first stage, Σ assumed to be equal to 2. Then, using Eqs. (40–41), foundation's parameters become determined. Then, governing equations are solved, and w is evaluated mathematically. Using obtained w, the new magnitude of Σ becomes extracted. There are two possibilities in this stage;

  • \(\left| {\Sigma_{i} - \Sigma_{i - 1} } \right| < \varepsilon\). So, the new magnitude of Σ is reliable and based on this value substrate's parameter becomes obtained and used in the solution of the governing equations.

  • \(\left| {\Sigma_{i} - \Sigma_{i - 1} } \right| > \varepsilon\). So, using the new magnitude of Σ the closed-loop circuit continues till the first condition become satisfied.

Furthermore, other mechanical and geometrical properties of the used Vlasov's model are specified in Table 4 (Lei et al. 2013).

Table 4 Mechanical and geometrical properties of Vlasov's foundation (Lei et al. 2013)
Full size table

For the sake of the results' reliability demonstration, Tables 5 and 6 are presented to compare the non-dimensional frequencies of the current model with their counterparts at the previously published works by Pagani et al. (2013) and Ghorbanpour Arani et al. (2018) according to various beam theories and mode numbers. For this reason, a beam with thickness h = 0.2 m, length a = 2 m, elastic modulus E = 75GPa, density ρ = 2700 kg/m3 and Poisson’s ratio v = 0.33 is considered.

Table 5 Validating the non-dimensional frequencies (\(\varpi = \frac{{\omega a^{2} }}{h}\sqrt {\rho /{\rm E}}\)) of the current model with Pagani et al. (2013) based on the classic theory (CT) and FSDT for different mode numbers
Full size table
Table 6 Non-dimensional natural frequency (\(\varpi = \frac{{\omega a^{2} }}{h}\sqrt {\rho /{\rm E}}\)) comparison between the current model results and those of Ghorbanpour Arani et al. (2018) based on the SSDT and different mode numbers
Full size table

As it is visible in the valid table, a good and close agreement among results elicited from the current formulation and those in the literature, guarantees the reliability of presented study exclusive results, truly. Also, the tiny differences among results can be due to the different software utilizations for the results obtaining. Furthermore, the way of code writing can be addressed as another reason for such a difference. From now on, the main topic of discussion is about exclusive results of the under examination ESB which are obtained by considering presented assumptions in Table 7 as:

Table 7 The basic assumptions for the current paper exclusive results obtaining
Full size table

Table 8 illustrates the impacts of the power-law index and used materials in the FGPC on the vibrational behavior of ESB. This table states that the power-law index enhancement results in normalized frequency reduction which leads to a lower level of rigidity as an important physical and mechanical property. Furthermore, having a constant power-law index, each ceramic cooperation with Al for FGPC formation addresses ESB more stiffness in comparison with that ceramic cooperation with other metals.

Table 8 ESB's vibrational responses due to the various FGPC materials and different power-law exponents
Full size table

Figure 6 contains curvatures correlated with the vibrational responses to the various mode numbers and length to thickness ratio of the ESB. The curvatures imply a tremendous effect of the mode number enhancement which results in normalized frequency pushing up. As another output of this figure and from a physical point of view, it should be noted that by keeping ESB's total thickness constant and increasing its length continuously, the stiffness of the whole sandwich model decreases dramatically which causes the normalized frequency to fall as well. In accordance with provide a more touchable physical mindset, a ruler with different lengths can be assumed; it is obvious that the taller ruler is less stiff.

Fig. 6
figure 6

Normalized frequency of the ESB versus length to thickness ratio at different mode numbers

Full size image

As mentioned before, Vlasov's foundation assumed as the elastic substrate in this paper. The effects of the foundation thickness and its elasticity moduli on the vibrational behavior of the current model are investigated in Fig. 7. As curvatures show, elasticity moduli and thickness of the Vlasov's substrate have an inverse impact on the normalized frequency and stiffness of the model; where the elasticity moduli enhancement and thickness reduction lead the whole structure to the more rigid and stiffer condition. Also, it is noticeable to mention that such a mentioned impact is more significant at the lower magnitudes of young modulus.

Fig. 7
figure 7

The effects of the foundation thickness and its elasticity moduli on the vibrational behavior of the ESB

Full size image

The influence and importance of the ACNFRC face sheets' agglomeration degree on the frequential responses of the ESB are put under evaluation in Fig. 8. By the means of this figure, it is evident that the clusters' volume fraction (μ) elevation causes higher magnitudes of the normalized frequency and stiffness as follows. This result stresses the constructive effect of the agglomeration presence within the ACNFRC top and bottom face sheet. On the other hands, it is proved that as the CNFs' volume fraction inside the clusters (η) becomes increased, the rigidity and stiffness of the model tend to decrease.

Fig. 8
figure 8

The influence of the ACNFRC face sheets' agglomeration degree on the frequential responses of the ESB

Full size image

The current model is subjected to the thermal environment affection in which, the temperature varies linearly across the model's thickness. The bottom surface's temperature and ambient temperature are assumed to be equal to 300 K and 293 K, and also, the temperature variation across the z-direction is assumed to be linear. On the mentioned basis, Fig. 9 is concentrated on the vibrational behavior of the ESB model under variations of the temperature difference between the top and bottom surfaces and also, different face sheets' thickness. Using Fig. 9, it is demonstrated that as the top and bottom surfaces' temperature difference increases, the internal energy of the system enhances which, at the nano-scale, leads to the atomic bonding breakage. Furthermore, CNFs in nano-scale reinforce the material by the means of different mechanisms as bridging. By this mechanism, CNF forms a bridge between two granular materials. Increasing the temperature causes such a hardening mechanism to weaken and finally results in rigidity and stiffness loss. However, face sheets' thickness enhancement leads to the whole structure's thickness growth and finally, normalized frequency and stiffness growth as well. To originate an appropriate physical point of view, rulers with different thicknesses can be imagined. Which one is harder to bend?

Fig. 9
figure 9

Thermal environment effect on the normalized frequency of the sandwich model against ACNFRC face sheets' thickness variations

Full size image

Considering the uniform distribution of CNFs within the ACNFRCs, Fig. 10 stands to discuss the probability of ESB's mechanical behavior improvement by the means of appropriate.

Fig. 10
figure 10

Normalized frequency of the current ESB model versus CNFs volume fraction for different FGPC's materials

Full size image

FGPC's material and CNFs volume fraction (f *) of the ACNFRCs. As it is displayed in this figure, higher values of f * cause normalized frequency enhancement and, consequently, a higher level of rigidity of the sandwich model. In fact, by increasing the reinforcement phase the ability of the structure for carrying higher values of load enhances due to the high young modulus of CNFs. Secondly, based on Fig. 10, it is revealed that in an identical situation, the composition of Al, Ti-6Al-4 V, and SUS304 with Al2O3 as the FGPC's ingredients provides stiffer ESB, respectively.

Figure 11 is responsible to demonstrate ESB's vibrational behavior due to the material property exponent variations for the different displacement fields at the fourth mode. From a technical and analytical point of view, material property exponent increasing causes ceramic volume fraction reduction. As the ceramic young modulus is more than metal's young modulus considerably, it is rational that a stiffness reduction occurs by the ceramic volume fraction falling. Furthermore, as another result, it is proved that FSDT, HSDT, SSDT, and ESDT estimate the highest normalized frequency and rigidity for the sandwich prototype, one after another (Mohammadimehr et al. 2019). The difference between the results based on the FSDT and the results based on the other theories backs to the different types of shear deformation consideration in different theories. Therefore, by the means of FSDT, the effect of shear deformation is considered as a first-order/linear function of z. On the other hands, by the means of higher-order theories, shear deformation impact is based on the nonlinear function of z. Such a nonlinearity results in more complex equations and finally, a higher level of results’ accuracy (Arshid et al. 2019a).

Fig. 11
figure 11

The fourth mode normalized frequency against power-law exponent considering different displacement fields

Full size image

The influence of the different types of CNFs distribution within the ACNFRCs on the ESB's stiffness at the fourth mode is investigated in Fig. 12. It is also important to mention that for CNFs distribution within the top and bottom ACNFRC, the symmetry principle is respected. (i.e., whole under evaluation model is symmetrical to the mid-plane, even in CNFs distribution). According to the curvatures in this figure, the CNFs V-A pattern application provides the highest rigidity and consequently normalized frequency for the sandwich model. As the composite layers become thicker, the effect of CNF's distribution types on the normalized frequency becomes more considerable. That is why the difference among gained curves is more touchable in higher values of face sheets' thickness.

Fig. 12
figure 12

The effect of the various CNFs distribution pattern within the ACNFRC face sheets on the vibrational behavior of the sandwich beam

Full size image

Figure 13 at the m = 4 displays normalized frequency versus porosity-dependent parameters to survey their effects on the ESB's stiffness. Regarding Fig. 13, it can be observed that porosity index elevation results in density, normalized frequency, and stiffness reduction. Such an impact seems to be rational by imagining Cheetos or other porous materials in our surroundings. Furthermore, as curves say, the O type of pores dispersion addresses a higher level of rigidity in comparison with X type and uniform type of pores dispersions. Such behavior is due to the impact of different types of porosity dispersion on the mechanical properties of the model. The frequency magnitude is proportional to the second root of the stiffness (Young’s modulus (E)) to density ratio. The mentioned ratio for O, X, and uniform type of pores dispersion captures the highest value, respectively. Also, by increasing the porosity index value, mentioned ratio’s variation rate is more for uniform dispersion of pores, and consequently, the rate of the normalized frequency decreasing for the mentioned case is higher than two other types of pores’ dispersion.

Fig. 13
figure 13

Normalized frequency versus porosity-dependent parameters at the fourth mode

Full size image

A three-dimensional diagram is presented by Fig. 14 to examine agglomerating and CNFs volume fraction effects on the normalized frequency of the ESB, simultaneously. To address the values more easily, Fig. 14 is presented as a bulk figure, but it should be noticed that the normalized frequency values are the surface values of the presented bulk figure. As it is obvious, both parameters' elevations have a constructive influence on the sandwich structures and lead it to a more rigid configuration.

Fig. 14
figure 14

The 3D diagram of the normalized frequency versus the CNFs volume fraction and agglomeration degree

Full size image

6 Conclusion

In this paper, the authors proposed a challenge regarding the vibrational behavior of an equipped sandwich beam including two ACNFRC face sheets and an FGPC on Vlasov's model substrate and also, under a thermal environment. The most considerable novelty of this work is the agglomeration impact application in the composite face sheets in such structures. In a conclusion, the clusters' presence in the composite face sheets plays a crucial constructive role in such sandwich structures' stiffness and rigidity. Furthermore, it is proved that the CNFs V-A pattern application and porosities O pattern application provide the highest stiffness and consequently normalized frequency for the sandwich model over other types of CNFs’ distribution and porosities dispersion. Also, it is concluded the Vlasov's substrate elasticity moduli and thickness enhancement have constructive and destructive impacts on the stiffness and normalized frequency of the aforementioned model, respectively. As another conclusion, it is worthwhile mentioning that Al & Si3N4 as the core material constituting and Timoshenko model of the beam predict higher stiffness of the whole structure in comparison with other materials and beam's theories. Furthermore, it is concluded that the sandwich model thickness and CNFs volume fraction have an identical impact on the normalized frequency and stiffness of the model (i.e., their enhancement in value results in stiffness enhancement and vice versa). To put it all in a nutshell, this paper seems to be helpful for future investigations in such a broad context.