1 Introduction

Convection in porous media is a subject of extensive investigation not only due to its numerous applications in natural and engineering sciences, but also has a fundamental interest in the context of pattern formation in nonequilibrium systems. First investigations were mostly focused on thermal convection in porous media (Bories and Combarnous 1973; Elder 1967). Later, convection in porous media has received a new interest within investigations of different particle suspension and mixture seepage, for example, in filtration systems (which are widely used in deep-bed filtration in oil recovery, groundwater treatment, catalysis) or geological carbon storage, etc (see, for example, Liang et al. 2018).

The most simple and well-established approach describing solutal convection is the Darcy–Boussinesq model, according to which the density variation can be ignored everywhere except the gravity term. To describe evolution of solute concentration, the Fick’s law is usually applied. However, the porous medium has a rather complex spatial structure, and many experiments (for example, Kay and Elrick 1967; Gouze et al. 2008) demonstrate that the diffusion process is often slower than predicted by the Fick’s law. One of the common alternative approaches, which is used in the present study, is the MIM approach (Deans 1963; Van Genuchten and Wierenga 1976), according to which the presence of two solute phases (mobile and immobile) can be considered.

The mobile phase is associated with particles moving with a fluid flow, while the immobile one linked to the particles, which are stuck to the solid matrix or stagnation of some particles ( Lindstrom et al. 1967; Van Genuchten and Wierenga 1976; Selim and Amacher 1997). Within the MIM model, the transport of the mobile phase is described by the classical diffusion equation with the additional influx to the immobile phase. The dependence of this influx on the mobile and immobile solute concentrations describes the kinetics of “phase transition”. The detailed description of the different MIM model can be found in Maryshev (2016).

The present paper is devoted to the study of solutal convection in a horizontal layer of a porous medium with imposed horizontal seepage. Since the solutal and thermal convections are described by identical equations Nield and Bejan (2017), the problem under consideration is similar to the classical Horton–Rogers–Lapwood (HRL) problem (Horton and Rogers 1945; Lapwood 1948). It is known that for the HRL problem convection regimes arise as a set of convective cells, with a width equal to the layer thickness. The influence of an external horizontal flux on such a regime was made in Prats (1966). It was shown that the steady external flux leads to excitation of an oscillatory mode; however, the wavelength of critical perturbations and convection threshold (the critical value of the Rayleigh–Darcy number) do not change. Later on, the problem was complicated by the account of solute particle immobilization (Maryshev 2015; Klimenko and Maryshev 2017) using the MIM approach (Deans 1963; Van Genuchten and Wierenga 1976). The investigation was carried out numerically in the framework of the linear MIM model (Maryshev 2015) and the fractal one (Klimenko and Maryshev 2017). It was demonstrated that the particle immobilization leads to the dependence of the critical parameters on the external flux intensity.

In the present study, we focus on a solute mixture with a moderate and even high concentration. We took into account the effect of saturation of the immobile phase (the concentration of immobile solute should not exceed some value). As it was shown in Selim and Amacher (1997), the second-order kinetic model, in which the adsorption rate linearly depends on the difference between the limiting saturation concentration of porous medium and the concentration of immobile solute, is a fruitful approach. Moreover, occupation by immobile solute particles of some part of the pore space leads to an essential decrease in the media porosity. To describe such an effect, we use the simplest and most universal Carman–Kozeny equation, which links the permeability and porosity of the media (Carman 1937). The described problem, first of all, is interesting from the fundamental point of view; however, the same situation can be realized in the natural system when permeable layer bounded by the soluble rock (for example salt) or in the industrial application as a thin layer between two reservoirs with different solute concentrations.

The paper contains six sections. Section 1 is an introduction where the previous study and motivation are discussed. Section 2 is devoted to the problem statement and derivation of governing equations. In Sect. 3, the base solution as a regime of the homogeneous horizontal equation is obtained. Section 4 contains the derivation of equations for small perturbations and its reduction to ODE for normal perturbations. Section 5 is devoted to the discussion of the stability maps which are obtained from the numerical solution of equations for normal perturbations. Section 6 provides a conclusion.

2 Problem Statement

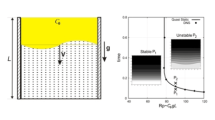
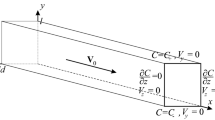
We consider a flow of a mixture through a horizontal layer, which is filled with a porous medium. Configuration of the problem is sketched in Fig. 1. A mixture consists of solid nanoparticles and incompressible fluid; the solid nanoparticles are considered as a solute within continuous approach. The flow is generated by the external filtration flux with given velocity \({\mathbf {V}}=\left( V(y),0\right)\).

The solute flow can be described within the Darcy–Boussinesq approximation (Nield and Bejan 2017) with the pore velocity \({\mathbf {V}}\), which obeys the Darcy law and incompressibility condition;

$$\begin{aligned} -\nabla p&= \frac{\eta \phi _0}{\kappa (\phi )}{\mathbf {V}}-\rho \beta _c c g {\mathbf {j}},\nonumber \\ \nabla \cdot {\mathbf {V}}&=0, \quad p=p'+\rho g y, \end{aligned}$$
(1)

where \(\kappa\) is the permeability of the porous medium, \(\eta\) is the dynamic fluid viscosity, \(\rho\) is the fluid density, \(\beta _c\) is the coefficient of concentration expansion, p is the deviation of pressure from the hydrostatic one, g is the gravity acceleration, \({\mathbf {j}}\) is the unit vertical vector and \(\phi _0\) is the porosity of the clean medium. The porous medium is assumed to be ideal (nondeformable, inert, uniform, homogeneous, and isotropic).

The solute concentration c can be obtained within the mobile-immobile media (MIM) model (or two-region solute transport model). According to this model, the solute can be partitioned into distinct mobile (or flowing, with volume concentration c) and immobile (stagnant, with volume concentration q) phases. These phases are coupled by kinetic equation, which described the solute influx (\(\partial _{t} q\)) into both phases, or it also can be interpreted as phase transition kinetics. The general form of equations for solute concentrations is

$$\begin{aligned} \partial _{t} c+\partial _{t} q&= D\nabla ^2 c-{\mathbf {V}} \cdot \nabla c,\nonumber \\ \partial _{t}q&= R(q,c), \end{aligned}$$
(2)

where D is the effective diffusivity and the coupling function R(q, c) is defined from the specific type of the MIM model. The formulation of the boundary value problem is completed by prescribing this function.

In order to investigate solute transport of moderate and high concentration, which is the aim of present paper, we used nonlinear kinetic function with Langmure saturation of porous matrix (\(q_0\)) in the form Selim and Amacher (1997)

$$\begin{aligned} \partial _{t}q=\alpha (c(q_0-q)-K_{d}q), \end{aligned}$$
(3)

where \(\alpha\) is the mass transport coefficient and \(K_{d}\) is the solute distribution coefficient. The main mechanism of adsorption [described by Eq. (3)] is van der Waals interaction between solute particle and pore wall. This interaction for fine particles (with size \(r<1\mu m\)) is much greater than the hydrodynamic viscous force induced by the flow (see Elimelech et al. 2013; Klimenko and Maryshev 2020) because of that the mass transport coefficient is determined by the frequency of particle-wall impact as ordinary diffusion. The parameter \(K_d\) is determined by the competition of van der Waals interaction between the solute particle and pore wall and thermal fluctuations (see for example Elimelech et al. 2013). Using the estimations which presented in Klimenko and Maryshev (2020), we can conclude that the \(K_d\) increases as the square root of particle size because van der Waals interaction intensity is proportional to \(1/r^3\), while the intensity of random force, which is induced by thermal fluctuation, is proportional to \(1/\sqrt{r^5}\). The parameter q0 is determined by the Van der Waals interaction between particles. The estimation for two spheres gives (see Elimelech et al. 2013) the decreasing of interaction intensity with size as 1/r.

Accounting of dynamic of the immobile concentration, q leads to the decrease in the volume of pore space (due to process of solute sorption onto the pore walls), which means that the porosity of the medium reduces as well, specifically, as \(\phi =\phi _0-q\). To describe such effect of porosity decreases, we use the Carman–Kozeny equation for the permeability of porous medium \(\kappa\);

$$\begin{aligned} \kappa (\phi )=\gamma \phi ^3/(1+\phi )^2, \end{aligned}$$

with \(\gamma\) is the Carman–Kozeny constant. The Carman-Kozeny model is applicable for flow through natural porous media with porosity variation, but the Carman-Kozeny constant in the form of original work \(\gamma =D_p/150\) (\(D_p\) is mean diameter of spherical granules) should be applied only for the porous matrix which consists of spherical granules. In the present paper, we applied the general approach where the Carman–Kozeny constant is assumed as a parameter of the model and in a described case can be measured from the permeability of clean media \(\phi =\phi _0\) (see, for example, Roth et al. 2015; Parvan et al. 2020).

Fig. 1
figure 1

Sketch of the problem

Full size image

Thus, the governing equation system for solute convection with immobilization and clogging yields

$$\begin{aligned} \frac{\partial }{\partial t}\left( c+q\right)&= -{\mathbf {V}}\cdot \nabla c +D\nabla ^2 c, \nonumber \\ -\nabla p&= \frac{\eta \phi _0}{\kappa (\phi )}{\mathbf {V}}-\rho \beta _c c g {\mathbf {j}},\nonumber \\ \nabla \cdot \mathbf{V }&=0, \nonumber \\ \frac{\partial q}{\partial t}&=\alpha \left( c(q_0-q)-K_d q\right) ,\nonumber \\ \kappa (\phi )&=\gamma \phi ^3/(1+\phi )^2, \quad \phi =\phi _0-q . \end{aligned}$$
(4)

Let us describe boundary conditions. We assume that the boundaries of a layer are impermeable for the fluid, and solute concentrations are kept constant: \(C_{+}\) is at the upper boundary and \(C_{-}\) is at the lower one. The pressure gradient along the layer boundaries is constant as well

$$\begin{aligned} \left. {\mathbf {V}}\cdot {\mathbf {j}} \right| _{y=0,1}&=0,\nonumber \\ \left. c \right| _{y=1}&=C_{+}, \quad \left. c \right| _{y=0}=C_{-},\nonumber \\ \left. \frac{\partial p}{\partial x} \right| _{y=0,1}&=-A. \end{aligned}$$
(5)

We now formulate the dimensionless governing equations and boundary conditions by measuring distance, time, velocity, pressure and concentration as h, \(h^2/D\), \(\left( 1-\phi _0\right) ^2/\phi _0^3 D/h\), Ah, \(C_0=C_{+}-C_{-}\), respectively.

In the dimensionless form the problem (4)–(5) is

$$\begin{aligned} \frac{\partial }{\partial t}\left( c+q\right)&= -\frac{1}{\kappa _0}{\mathbf {V}}\cdot \nabla c + \nabla ^2 c, \nonumber \\ {\mathbf {V}}&=\kappa \left( -\mathrm{Pe}\nabla p+\mathrm{Rp}\; c {\mathbf {j}}\right) ,\nonumber \\ \frac{\partial q}{\partial t}&=ac\left( q_{C0}-q\right) -bq,\nonumber \\ \nabla \cdot \mathbf{V }&=0, \nonumber \\ \kappa (\phi )&=\phi ^3/(1+\phi )^2, \quad \phi =\phi _0-C_0q , \nonumber \\ \left. {\mathbf {V}}\right| _{y=0,1}&=0, \nonumber \\ \left. c \right| _{y=0}&=1, \quad \left. c \right| _{y=1}=0. \end{aligned}$$
(6)

Here, \({\kappa _0}=\kappa (\phi _0)/\gamma\) is the dimensionless permeability of the clean medium.

The boundary value problem (6) is characterized by governing parameters: the solutal Rayleigh–Darcy number, the Péclet number, the dimensionless adsorption and desorption rates and the dimensionless concentration for the Langmure saturation;

$$\begin{aligned} \mathrm{Rp} =\frac{C_0 g \kappa (\phi _0) \rho \beta _c h }{D\eta \phi _0 },\quad \mathrm{Pe} =\frac{A\kappa (\phi _0) h}{D\eta \phi _0},\quad a=\frac{\alpha C_0 h^2}{ D},\quad b=\frac{\alpha K_d h^2}{D},\quad q_{C0}=\frac{q_0}{C_0}. \end{aligned}$$

Further, we investigated numerically how convective threshold (in terms of the critical Rayleigh–Darcy number) depends on the rest governing parameters.

3 Homogeneous Horizontal Filtration: Base State

We note that the steady solution of boundary values problem (6) yields x-independent components of velocity, concentration and pressure fields; \(c=c^0(y)\), \(q=q^0(y)\), \(\mathbf (V)=\mathbf (V)^0=\left( u^0(y),0\right)\), \(p=p^0(y)\). Indeed, for such solution, equations (6) can be simplified as

$$\begin{aligned} \partial ^2_y c^0&= 0, \nonumber \\ 0&= ac^0\left( q_{C0}-q^0\right) -bq^0,\nonumber \\ \mathbf {V^0}&= \kappa \left( -\mathrm{Pe}\nabla p^0+\mathrm{Rp}\, c^0 {\mathbf {j}}\right) , \end{aligned}$$
(7)

where symbol \(\partial ^2_y\) denotes the second derivative with respect to vertical coordinate y.

Taking into account, the boundary conditions (5), solution of Eq. (7) can be written in the form

$$\begin{aligned} p^0&= -x-\frac{\mathrm{Rp}}{2\mathrm{Pe}}y^2, \nonumber \\ u^0&= \kappa (\phi ^0)\mathrm{Pe}=\frac{\left( \phi _0-C_0 q^0\right) ^3}{\left( 1-\phi _0+C_0q^0\right) ^2}\mathrm{Pe},\nonumber \\ q^0&= \frac{aq_{C0}}{ay+b}y,\nonumber \\ c^0&= y,\nonumber \\ \phi ^0&= \phi _0+C_0q^0. \end{aligned}$$
(8)

In order to justify this steady solution, we consider two limiting cases: (1) \(\phi _0-C_0q_{C0}\ll 1\) together with \(b\ll 1\), and (2) \(C_0\ll \phi _0,q_0\). The first one corresponds to the saturated porous media, while the second case describes the convection with small initial concentration.

Indeed, for the first case from Eq. 7, the second equation one can find that \(q^0=q_{C0}\), \(\phi =\phi _0-C_0q_{C0}\ll 1\) and \(\kappa (\phi )\ll 1\). Thus, the solution has the form

$$\begin{aligned} p^0&=-x-\frac{\mathrm{Rp}}{2\mathrm{Pe}}y^2, \nonumber \\ u^0&=\kappa (\phi ^0)\mathrm{Pe}\ll 1,\nonumber \\ q^0&=q_{C0},\nonumber \\ c^0&=y, \end{aligned}$$
(9)

which coincide with slow seepage through fully clogged porous media with very slow kinetics of solute phase transition.

While for the second case (Eq. 7), the second equation can be linearised as \(0 =ac^0q_{C0}-bq^0\), which leads, in turn, to the following solution

$$\begin{aligned} p^0&=-x-\frac{\mathrm{Rp}}{2\mathrm{Pe}}y^2, \nonumber \\ u^0&=\kappa (\phi _0)\mathrm{Pe}=\frac{\phi _0^3}{\left( 1-\phi _0\right) ^2}\mathrm{Pe},\nonumber \\ q^0&=\frac{aq_{C0}}{b}y,\nonumber \\ c^0&=y, \end{aligned}$$
(10)

which coincide with linear MIM model without clogging (Maryshev 2015).

As it can be seen, the stationary solution of the problem (6) depends on the sorption parameters as well as on filtration rate (the Peclet number). The linear stability analysis of this regime with respect to the small perturbations is performed in the next Section.

4 Small Perturbation Equations

We are interested in the evolution of perturbations to the base state (8) given by \(q=q^0+Q\), \(c=c^0+C\), \({\mathbf {V}}={\mathbf {V}}^0+{\mathbf {W}}\), \(p=p^0+P\), \({\mathbf {W}}=(U,V)\).

We focused on two-dimensional perturbations which are corresponded to transversal rolls with axes perpendicular to the main imposed throughflow. Any other perturbations can be constructed by the superposition of described rolls with the rolls co-directed to imposed throughflow. The threshold of last rolls does not depend on immobilisation process as it is shown in Maryshev and Klimenko (2019). Because of that, the most interesting perturbations have a form of rolls normal to throughflow.

Substituting of latter expression in Eq. (6) and keeping only linear terms one can gain the following system for small perturbations

$$\begin{aligned} \frac{\partial }{\partial t}\left( C+Q\right)&=-\frac{1}{\kappa _0}u^0\frac{\partial }{\partial x} C -\frac{1}{\kappa _0}V+ \nabla ^2 C, \nonumber \\ {\mathbf {W}}&={\kappa ^0}\left( -\mathrm{Pe}\nabla P+\mathrm{Rp}\; C{\mathbf {j}}\right) +{\kappa }\left( -\mathrm{Pe}\nabla p^0+\mathrm{Rp}\,c^0{\mathbf {j}}\right) ,\nonumber \\ \frac{\partial Q}{\partial t}&=aC\left( q_0-q^0\right) -\left( b+ac^0\right) Q,\nonumber \\ \nabla \cdot \mathbf{W }&=0, \nonumber \\ \kappa ^0=\kappa (\phi ^0)&=\frac{\left( \phi _0-C_0 q^0\right) ^3}{\left( 1-\phi _0+C_0q^0\right) ^2}, \nonumber \\ \left. {\mathbf {W}}\cdot {\mathbf {j}}\right| _{y=0,1}&=0, \nonumber \\ \left. C,Q \right| _{y=0,1}&=0,\nonumber \\ \left. \partial _x P \right| _{y=0,1}&=0. \end{aligned}$$
(11)

It is convenient to rewrite this equation system in terms of the stream function \(\varPsi\) related to the velocity components as \(U=-\partial _y \varPsi\), \(V=\partial _x \varPsi\);

$$\begin{aligned} \partial _t\left( C+Q\right)&= \partial _x^2 C + \partial _y^2 C -\frac{1}{\kappa _0}u^0\partial _x C-\frac{1}{\kappa _0}\partial _x\varPsi ,\nonumber \\ \partial _x^2 \varPsi + \partial _y^2 \varPsi&= - \mathrm{Rp}\kappa ^0\partial _x C-C_0\frac{\kappa '}{\kappa ^0}\partial _yq^0\partial _y \varPsi \nonumber \\&\quad + {C_0}^2PeQ\left( \frac{\kappa '^2}{\kappa ^0}-\kappa ''\right) \partial _yq^0+C_0\kappa '\mathrm{Pe}\partial _yQ,\nonumber \\ {\partial _t}Q&=aC\left( q_0-q^0\right) -\left( b+ac^0\right) Q,\nonumber \\ \kappa '&=\frac{\partial \kappa }{\partial \phi }(\phi ^0)=\frac{\left( \phi ^0\right) ^2\left( 3-\phi ^0\right) }{\left( 1-\phi ^0\right) ^3},\quad \kappa ''=\frac{\partial ^2\kappa }{\partial \phi ^2}(\phi ^0)=\frac{6\phi ^0}{\left( 1-\phi ^0\right) ^4},\nonumber \\ \varPsi \mid _{y=0,1}&=0, \quad C,Q \mid _{y=0,1}=0. \end{aligned}$$
(12)

Here, symbols \(\partial _t\), \(\partial _x\) and \(\partial _y\) denote the derivatives with respect to t, x and y.

A solution of the problem (12) can be performed in the form of normal perturbations: \(Q,C,\varPsi \sim \exp \left( kx-\omega t\right)\), where k is horizontal wave number and \(\omega\) is the frequency of neutral perturbations. In the terms of normal neutral perturbations, the problem (12) becomes

$$\begin{aligned} -i\omega \left( C+Q\right)&= (\partial _y^2-k^2-ik\frac{\kappa ^0}{\kappa _0} \mathrm{Pe})C-\frac{ik}{\kappa _0}\varPsi ,\nonumber \\ (\partial _y^2-k^2) \varPsi&= -ik \mathrm{Rp}\kappa ^0 C -C_0\frac{\kappa '}{\kappa ^0}\partial _yq^0 \partial _y \varPsi \nonumber \\&\quad +{C_0}^2PeQ\left( \frac{\kappa '^2}{\kappa ^0} -\kappa ''\right) \partial _yq^0+C_0\kappa '\mathrm{Pe}\partial _yQ,\nonumber \\ -i\omega Q&=aC\left( q_0-q^0\right) -\left( b+ac^0\right) Q,\nonumber \\ \varPsi \mid _{y=0,1}&=0, \quad C,Q \mid _{y=0,1}=0. \end{aligned}$$
(13)

In case of constant \(\kappa ^0\), this system coincide with obtained in Maryshev (2015) for small concentration, which is described in “Appendix A”.

Problem (13) is an eigenvalue problem. It was solved numerically by the differential sweep method (Goldshtik and Stern 1977). As a result, the neutral curves (\(\mathrm{Rp}(k)\) and \(\omega (k)\)) and the critical values of parameters \(\mathrm{Rp}\), \(\omega\), k are described in the next Section.

5 Results

The solution of Eq. (12) is neutral curves similar to the classical Horton–Rogers–Lapwood problem (Horton and Rogers 1945). The example of neutral curves in terms of the dependences \(\mathrm{Rp}(k)\) and \(\omega (k)\) is plotted in Fig. 2.

As it is shown in Fig. 2, the increase in the concentration difference between the boundaries (\(C_0\)) leads to the stabilization of horizontal seepage and slowing down of the oscillation dynamics. This effect can be explained by the clogging of porous media with a high concentration of solute, which leads to the solute accumulation in the immobile phase. A flow through porous media slows down which is the reason for stabilization and oscillations frequency decreasing.

The neutral curves contain information about all perturbations, but the information about critical perturbation is the most useful. The critical perturbation corresponds to the minimal value of the Rayleigh–Darcy number and further we focus on the critical values of problem parameters for obtaining the stability maps.

Fig. 2
figure 2

The neutral curves into the parameter plane \(\mathrm{Rp}\), k (left panel) and \(\omega\), k (right panel). The curves are obtained for the fixed values of problem parameters: \(a=8\), \(b=4\), \(\mathrm{Pe}=7\), \(q_{C0}=0.4\), \(\phi _0=0.4\) and various values of the solute concentration difference between the boundaries \(C_0\), which are indicated on the legend

Full size image
Fig. 3
figure 3

Dependences of the critical values of the Rayleigh–Darcy number (\(\mathrm{Rp}_{\min }\)) (left panel), the wave number (\(k_{\min }\)) (central panel) and the oscillation frequency (\(\omega _{\min }\)) (right panel) on the Peclet number (\(\mathrm{Pe}\)). The curves are obtained for the fixed values of problem parameters: \(a=8\), \(b=8\), \(C_0=0.5\), \(q_{C0}=0.4\), \(\phi _0=0.4\)

Full size image

The stability map in the plane \(\mathrm{Rp}\), \(\mathrm{Pe}\) is plotted in Fig. 3. It is seen that a more intensive regime of horizontal seepage is more stable because the intensive flow made perturbations of solute concentration more homogeneous. The homogeneity of the solute also leads to an intensification of solute transition between phases, which, in turn, increases the frequency of oscillations. The wave number of critical perturbations is not monotonous but its variation is tiny.

The dependences of critical parameters on the adsorption rate are presented in Fig. 4. The adsorption intensification leads to the clogging of media which stabilizes the horizontal filtration and slowing down of the oscillatory dynamics. The effect of the clogging also leads to an increase in the size of critical convective cells (the critical wavelength (\(k_{\min }\)) decreases). Analytical investigation of the case without adsorption (\(a=0\)) is in a good agreement with the numerical data (see “Appendix B, C”).

Fig. 4
figure 4

Dependences of the critical values of the Rayleigh–Darcy number (\(\mathrm{Rp}_{\min }\)) (left panel), the wave number (\(k_{\min }\)) (central panel) and the oscillation frequency (\(\omega _{\min }\)) (right panel) on adsorption rate (a). The curves are obtained for the fixed values of problem parameters: \(\mathrm{Pe}=7\), \(b=8\), \(C_0=0.5\), \(q_{C0}=0.4\), \(\phi _0=0.4\)

Full size image

The effect of the desorption rate variation to critical parameters is presented in Fig. 5. This effect is reversed to the effect of the adsorption rate variation.

Fig. 5
figure 5

Dependences of the critical values of the Rayleigh–Darcy number (\(\mathrm{Rp}_{\min }\)) (left panel), the wave number (\(k_{\min }\)) (central panel) and the oscillation frequency (\(\omega _{\min }\)) (right panel) on desorption rate (b). The curves are obtained for the fixed values of problem parameters: \(\mathrm{Pe}=7\), \(a=8\), \(C_0=0.5\), \(q_{C0}=0.4\), \(\phi _0=0.4\)

Full size image
Fig. 6
figure 6

Dependences of the critical values of the Rayleigh–Darcy number (\(\mathrm{Rp}_{\min }\)) (left panel), the wave number (\(k_{\min }\)) (central panel) and the oscillation frequency (\(\omega _{\min }\)) (right panel) on porosity of clean media (\(\phi _0\)). The curves are obtained for fixed values of problem parameters: \(\mathrm{Pe}=7\), \(a=8\), \(b=8\), \(C_0=0.5\), \(q_{C0}=0.4\)

Full size image
Fig. 7
figure 7

Dependences of the critical values of the Rayleigh–Darcy number (\(\mathrm{Rp}_{\min }\)) (left panel), the wave number (\(k_{\min }\)) (central panel) and the oscillation frequency (\(\omega _{\min }\)) (right panel) on concentration of solid matrix saturation (\(q_{C0}\)). The curves are obtained for the fixed values of problem parameters: \(\mathrm{Pe}=7\), \(a=8\), \(b=8\), \(C_0=0.5\), \(\phi _0=0.4\)

Full size image

The effect of concentration of a solid matrix saturation variation (\(q_{C0}\)) is presented in Fig. 6. It is seen that enlargement of \(q_{C0}\) value leads to stabilization and slowing down of the oscillatory dynamics. This effect is conditioned by an increase in the ability of media to accumulate the solute and, as a sequence, the media become less permeable. The influence of a clean media porosity variation (\(\phi _0\)) on the critical parameters is shown in Fig. 7. For the range \(\phi _0 \in [0..0.4]\), this effect is opposite to the effect of \(q_{C0}\) variation because an increase in \(q_{C0}\) decreases porosity and permeability of media, but the growth of \(\phi _0\) increases these both parameters of the media.

However, the curves in Fig. 7 contain an extremal point between values \(\phi _0=0.5\) and \(\phi _0=0.6\). In this point, the regime of horizontal seepage is the most unstable. We denote the values of critical parameters in the extremal point as \(\phi {*}\), \(\mathrm{Rp}{*}_{\min }\), \(k{*}_{\min }\) and \(\omega {*}_{\min }\). We can propose plenty of explanations of this effect, but the most plausible is that \(\phi {*}\) is the extremal point of a relative permeability variation \(\kappa '/\kappa\). If we describe the clean media \(\phi =\phi _0\) than in the point \(\phi _0=3-\sqrt{6}\approx 0.55\) the effect of \(\phi _0\) variation to permeability \(\kappa\) variation is minimal and the effect of porosity change due to the immobilization as weakest as possible. The additional argument to this explanation is the dependence of all for the parameters \(\phi {*}\), \(\mathrm{Rp}{*}_{\min }\), \(k{*}_{\min }\) on \(q_{C0}\). If the main effect is in the optimal porosity of media then for the clean media without the immobilization (\(q_{C0}=0\)) we should obtain \(\phi {*}=0.55\) and the dependence of \(\phi {*}\) on \(q_{C0}\) should be linear due to (6). All these suggestions are proved by Fig. 8.

Fig. 8
figure 8

Dependences of the extremal critical parameter values on \(q_{C)}\): the extremal value of clean media porosity (\(\phi _0=\phi {*}\)) [panel (a)], the extremal value of the Rayleigh–Darcy number (\(\mathrm{Rp}_{\min }={\mathrm{Rp}{*}}_{\min }\)) [panel (b)], the extremal value of oscillation frequency (\(\omega _{\min }={\omega{{*}}}_{\min }\)) [panel (c)] and the extremal value of wave number (\(k_{\min }={k{*}}_{\min }\)) [panel (d)]. The curves are obtained for the fixed values of problem parameters: \(\mathrm{Pe}=7\), \(a=8\), \(b=8\), \(C_0=0.5\)

Full size image

6 Conclusion

Summarizing, we have considered the problem of exciting of convective motion inside the horizontal porous layer under horizontal seepage of a mixture taking into account immobilization and clogging processes. We focus on the case of high solute concentrations, in which the immobilization is described by the nonlinear MIM (mobile/immobile media) model. The presence of immobile solute decreases the porosity of the media; hence, the porous media become less permeable. The variation of porosity is modelled by a linear function of solute concentration in the immobile phase, while the dependence of the permeability of the media on porosity is modelled within the Carman–Kozeny equation. The solution of the problem in the regime of the homogeneous horizontal filtration is obtained analytically. The equations for small perturbations of the obtained regime are derived. The stability problem is presented as a system of ODE and solved by the standard differential sweep method. As a result, neutral curves in the parameter space are plotted. It is shown that the immobilization leads to stabilization of the considered regime and to slowing down of the perturbation dynamics. The stability maps were plotted in a wide range of system parameters.

The presented results correspond to the dimensionless parameters which are varied in the range \(0< \mathrm{Pe}<20\), \(0<a<40\), \(0<b<40\) and \(40<\mathrm{Rp}<140\). If we imagine the convection in the layer between two large reservoirs of solute with different concentrations than it may be safely suggested that at such values of the parameters the instability near the threshold can occur in the layer of thickness \(h\sim 1\,\mathrm{m}\). For NaCl in water \(\beta _c=1.16\) , \(\alpha \sim 10^{-6}\) (usual value for natural systems see Van Genuchten and Wierenga 1976; De Smedt and Wierenga 1979), \(K_d\sim 0.1\) and \(q_0\sim 0.6\) (see Martinez-Vertel et al. 2019). The layer should be prepared from porous material with porosity \(0.1<\phi _0<0.5\) and permeability \(\kappa_0 =1..100\,\mathrm{Da}\) (the pore size \(d=1.10\,\upmu \mathrm{m}\)), the effective diffusivity of salt in such media is \(D\sim 10^{-7}\) (see, for example, Maryshev et al. 2017). The concentration difference between the layer boundaries and its value should be \(C_0 =0.2..0.5\). The values of the actual external pressure gradient are \(A= 0..10\,\mathrm{kPa/m}\).