1 Introduction

In the paper, the convective transport of nanoparticles in a horizontal porous layer saturated with fluid is studied. It is usually assumed that the transport in porous media obeys Fick’s law similar to the Fourier law for heat conduction. Consequently, the solutal and thermal convection are described by identical equations (see, e.g., Nield and Bejan 2006). In this sense, the problem under consideration is similar to the well-known Horton–Rogers–Lapwood (HRL) problem (Horton and Rogers 1945; Lapwood 1948). The flow regime within the framework of this problem is governed by two dimensionless parameters: the dimensionless horizontal wave number and the Rayleigh–Darcy number. The latter number characterizes the effect of buoyancy forces, which results in the appearance of convective flow and pattern formation. The analysis of possible pattern formation within the HRL problem is presented in work (Joseph 1976).

The stability of a homogeneous fluid seepage along the horizontal layer of a porous medium with the net mass flow (or imposed external flux) was studied in Prats (1966) and Nield and Barletta (2009). In this case, the speed of the external flow is described by an additional dimensionless parameter, which is called the Péclet number. It has been shown in Prats (1966) that the introduction of horizontal net mass flow along the layer leads to a replacement of the monotonic mode of instability by the oscillatory mode. However, the critical values of the wave number and Rayleigh–Darcy number do not change, and the oscillation frequency is proportional to the Péclet number. Moreover, later in work (Lyubimov and Teplov 1998), it is demonstrated that the external flux modulated in time affects the vibrational flow regime, but the threshold remain invariable.

It is obvious that the transfer of the results obtained for the HRL problem to its solutal analog is possible only within Fick’s law approximation. However, the porous medium has a rather complex spatial structure, and many experiments performed on porous medium evidence that solute spreading sometimes deviates from Fick’s law. The mobile/immobile media (MIM) approach is often used for studying the transport phenomena. It is assumed that the total solute concentration is separated into two phases. The first is the concentration of the mobile solute linked to the particles moving with flow. The second is the immobile concentration linked to the particles, which are stuck to the solid matrix or related to the trapped fluid (Lindstrom et al. 1967; Van Genuchten and Wierenga 1976; Selim and Amacher 1997), which is confirmed by experiments (Bromly and Hinz 2004; Gouze et al. 2008).

Within the MIM model the transport of the mobile phase is described by the classical diffusion equation with the additional term that describes the influx of solute to the immobile phase. The dependence of this influx on the mobile and immobile solute concentrations describes the kinetics of “phase transition”.

The model of this type was first proposed in Shamir and Harleman (1967), and a few months later in Lindstrom et al. (1967). In these articles, the kinetics law is taken as a linear relationship (\(C=\xi Q\)) between the concentrations of immobile (Q) and mobile (C) solutes. This approach allows one to slow down the diffusion process but is hardly correct, because it simply reduces the diffusivity by a factor of \(1+\xi \). The proposed relationship gives a poor fit to the experimental data. This fact has been mentioned in work (Van Genuchten and Wierenga 1976), in which the first-order kinetics model of solute transition between the phases has been introduced for the first time. The developed model adequately evaluates the diffusion of solutes at low concentrations. The low concentration means that it is smaller than the concentration of saturation of solid porous matrix (the maximum possible amount of solute that can be adsorbed per unit volume of the porous medium). In the opposite case it is recommended to use a model of second-order kinetics, which is proposed in Selim and Amacher (1997).

In the present work we consider the two-dimensional linear stability problem of a horizontal mixture seepage in the porous medium with the immobilization of solutes. The fluid flow equation is modeled by the Oberbeck–Boussinesq approximation under the assumption of small fluid acceleration (Nield and Bejan 2006). The solute transport is described by a linear mobile/immobile media (MIM) model (Van Genuchten and Wierenga 1976).

The paper consists of five parts. The first part is devoted to the problem statement. The second part deals with the stability of a horizontal mixture seepage imposed by the uniform external flux. The third part examines the influence of unsteady net mass flow. The linear differential equation that describes the onset of convection is obtained and is investigated in a number of important limiting cases. In the fourth part, the equation is investigated numerically in order to obtain the conditions for generation of various convection flow modes. The final part is the conclusion where we discuss the main results of this study.

2 Problem Statement

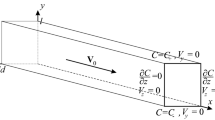
We consider a mixture flow through a horizontal layer of a porous medium initiated by a horizontal filtration flow. The mixture consists of solid nanoparticles and carrier fluid. The solid nanoparticles are treated as a solute within the continuous approach. The sorption of nanoparticles is described as immobilization of the solute in the framework of the MIM model (Van Genuchten and Wierenga 1976). Therefore, the solute is distributed between two phases. The volume concentration of the solute in the mobile and immobile phases are denoted as C and Q, respectively. Solute concentrations at the upper and lower boundaries of the layer are kept constant and denoted by \(C_{+}\) and \(C_{-}\) (\(C_{+}>C_{-}\)), respectively. It is assumed that the solute is heavier than the carrier fluid. The difference between the solute and solvent densities leads to a solutal convection. The sketch of the problem is shown in Fig. 1.

Fig. 1
figure 1

Sketch of the problem. The layer of thickness (l) is infinite in the x-direction. The flow through the layer with constant velocity V is imposed. The unit vector \(\mathbf {\gamma }\) shows the direction of gravity field

Full size image

The equations for the solutal convection can be written as

$$\begin{aligned} \frac{\eta }{\kappa }\phi \mathbf {V}= & {} -\nabla p'+\rho g\varvec{\gamma },\nonumber \\ \nabla \cdot \mathbf {V}= & {} 0,\nonumber \\ \partial _{t}C+\partial _{t}Q= & {} D\nabla ^2 C-\mathbf {V}\cdot \nabla C,\nonumber \\ \partial _{t}Q= & {} \alpha \left( C-K_{d}Q\right) , \end{aligned}$$
(1)

where \(\partial _{t}\) denotes the time derivative, \(\mathbf {V}\) is the two-dimensional vector of the flow velocity, \(p'\) is pressure, \(\varvec{\gamma }\) is the unit vertical vector, and \(\rho \) is the mixture density. The symbols \(D, \kappa , \eta , and g\) denote the effective diffusivity, permeability of porous media, dynamic viscosity and gravity acceleration, respectively. The kinetics of immobilization is described by the following parameters: \(\alpha \) is the mass transport coefficient and \(K_\mathrm{d}\) is the solute distribution coefficient (Harter and Baker 1977). The first of Eq. (1) represents the Darcy law with account for the buoyancy force (Nield and Bejan 2006), the second is the incompressibility condition, the third is the advection–diffusion equation with additional term, which describes an influx into the immobile phase (\(\partial _{t}Q\)) (Shamir and Harleman 1967), and the last equation represents linear kinetics of the phase transition (Van Genuchten and Wierenga 1976). Within the framework of the Bousinesq approximation, it is assumed that \(\rho =\rho _{f}\left( 1+\beta _{c}C\right) \) (Nield and Bejan 2006), here \(\rho _{f}\) is the density of the carrier fluid and \(\beta _{c}\) is the coefficient of concentration expansion. Let \(p=p'-\rho _{f}gy\) is the deviation of pressure from the hydrostatic one. In order to obtain the dimensionless form of Eq. (1), the following scales for pressure, time, length, concentration, and velocity are chosen: \(D\eta \phi /\kappa ,\quad l^{2}/D,\quad l,\quad C_{0},\quad D/l\), where l is the layer thickness and \(C_{0}=C_{+}-C_{-}\) is the concentration difference between the layer boundaries. Equation (1) in dimensionless form read

$$\begin{aligned} \mathbf {V}= & {} -\nabla p+RpC\varvec{\gamma },\nonumber \\ \nabla \cdot \mathbf {V}= & {} 0,\nonumber \\ \partial _{t}\left( C+Q\right)= & {} D\nabla ^2 C-\mathbf {V}\cdot \nabla C,\nonumber \\ \partial _{t}Q= & {} aC-bQ. \end{aligned}$$
(2)

The boundary conditions for Eq. (2) are

$$\begin{aligned} C\mid _{y=1}=1,\; C\mid _{y=0}=0,\;\mathbf {V}_{y}\mid _{y=1}=0,\;\mathbf {V}_{y}\mid _{y=0}=0,\; \mathbf {V}_{x}\mid _{x=\pm \infty }=Pe\cdot f\left( t\right) , \end{aligned}$$
(3)

where \(Pe\cdot f(t)\) is the time-dependent velocity of the imposed external flow, and \(\mathbf {V}_{x}\) and \(\mathbf {V}_{y}\) denote the x and y components of the flow velocity, respectively.

Problem (2), (3) involves the following dimensionless parameters

$$\begin{aligned} Rp=\frac{\beta _{c}C_{0}gl\kappa \rho _{f}}{\phi D\eta },\quad Pe=\frac{Vl}{D},\quad a=\frac{\alpha l^{2}}{D},\quad b=\frac{\alpha K_{d}l^{2}}{D}. \end{aligned}$$
(4)

Here Rp is the Rayleigh–Darcy number, Pe is the Péclet number, \(a>0\) is the dimensionless adsorption coefficient and \(b>0\) is the dimensionless desorption coefficient.

The uniform seepage solution to the problem (2), (3) is

$$\begin{aligned} C_{h}=y,\;\mathbf {V}_{h}=\left( Pe\cdot f(t),0\right) ,\; Q_{h}=ay/b. \end{aligned}$$
(5)

Let the perturbations of the base solution (5) are \(c=C-y,\;\mathbf {v}=\left( u,w\right) =\left( \mathbf {V}_{x}-Pe\cdot f(t),\mathbf {V}_{y}\right) ,\; q=Q-ay/b\). The equations for perturbations of the concentration and filtration velocity \(c,\; q,\; u,\; w\) read

(6)

where \(\partial _{x}\) and \(\partial _{y}\) denote x- and y-derivatives, respectively, \(\nabla ^2=\partial _{x}^{2}+\partial _{y}^{2}\) is the Laplace operator. Let \(u=-\partial _{y}\psi \) and \(w=\partial _{x}\psi \) where \(\psi \) is the stream function. As a result, Eq. (6) can be written in a more convenient form as follows:

(7)

For the linearized problem (7) we assume that \(\left| \partial _{x}\psi \partial _{y}c-\partial _{y}\psi \partial _{x}c\right| \ll 1\) and \(c,\;\psi ,\;q\sim \exp \left[ ikx-i\omega t\right] \), where k is the horizontal wave number and \(\omega \) is the frequency of neutral perturbations. Under these assumptions the final linear form of Eq. (7) is

$$\begin{aligned} -i\omega \left( c+q\right) +ik\psi +ikPef(t)c= & {} \partial _{y}^{2}c-k^{2}c,\nonumber \\ \partial _{y}^{2}\psi -k^{2}\psi= & {} -ikRpc,\nonumber \\ -i\omega q= & {} ac-bq, \end{aligned}$$
(8)

where i is the imaginary unit. Equation (7) should be supplemented by the following boundary conditions

$$\begin{aligned} c,\psi ,q\mid _{y=0,1}=0. \end{aligned}$$
(9)

The obtained problem (8)–(9) is the linear stability problem. The sections that follows are devoted to its solution.

3 Stability Problem: Steady External Flux

In this section, we describe the problem with time-independent external flux. It means that \(f(t)=1\). Due to boundary conditions (9) the solution can be sought as \(c,\;\psi ,\; q\sim \sin \left[ \pi ny\right] \). In this case Eq. (8) become

$$\begin{aligned} i\omega \left( 1+\frac{a}{b-i\omega }\right) + ik\frac{ikRp}{\left[ \pi ^{2}n^{2}+k^{2}\right] }+ ikPe=-\left[ \pi ^{2}n^{2}+k^{2}\right] . \end{aligned}$$
(10)

The complex Eq. (10) is equivalent to the following pair of real-valued equations, which define the frequency of critical perturbations and the critical value of the Rayleigh–Darcy number

$$\begin{aligned}&\omega ^{3}-\omega ^{2}kPe+\omega b\left( a+b\right) -b^{2}kPe = 0,\nonumber \\&Rp = \frac{\left[ \pi ^{2}n^{2}+k^{2}\right] ^{2}}{k^{2}}+\frac{\pi ^{2}n^{2}+ k^{2}}{k^{2}}\frac{\omega ^{2}a}{b^{2}+\omega ^{2}}. \end{aligned}$$
(11)

Some consequences can be deduced from the obtained formula (11). First, the convection threshold increases because of taking into account both the imposed seepage and immobilization. This effect can be explained by a transition of the solute to the immobile phase. Because of depletion of the mobile phase, a greater concentration gradient across the layer is required for the onset of convective flow. Second, if the immobilization effect is excluded from the consideration (\(a=0\)), the solution of Eq. (11) is

$$\begin{aligned} \omega= & {} kPe,\nonumber \\ Rp= & {} \frac{\left[ \pi ^{2}n^{2}+k^{2}\right] ^{2}}{k^{2}}. \end{aligned}$$
(12)

It is a well-known solution, which has been first obtained in work Prats (1966) in the case when the external flux has no effect on the threshold of convection. Third, in the case when desorption is absent (\(b=0\)), expressions (11) become

$$\begin{aligned} \displaystyle&\omega =kPe,\nonumber \\ \displaystyle&Rp=\frac{\left[ \pi ^{2}n^{2}+k^{2}\right] ^{2}}{k^{2}}+\left[ \pi ^{2}n^{2}+ k^{2}\right] \frac{a}{k^{2}}, \end{aligned}$$
(13)

The threshold now increases because of the solute transition to the immobile phase, but the inverse process is blocked and thereby the solute redistribution between phases is blocked also. As a result, the external flux again has no effect on the threshold of convection. Finally, it is reasonable to obtain the solution to (11) for some limiting cases. The subsections that follows are devoted to an extended discussion of these cases.

3.1 The Case Without External Flux

Let us start with formula (11) using the assumption \(Pe=0\). The critical values of Rp and \(\omega \) in the explicit form are

$$\begin{aligned} \omega= & {} 0,\nonumber \\ Rp= & {} \frac{\left[ \pi ^{2}n^{2}+k^{2}\right] ^{2}}{k^{2}}, \end{aligned}$$
(14)

and the critical perturbations (for \(n=1\)) correspond to

$$\begin{aligned} k_\mathrm{min}= & {} \pi ,\nonumber \\ Rp_\mathrm{min}= & {} 4\pi ^{2}. \end{aligned}$$
(15)

The obtained values of the critical parameters (14) and (15) are similar to the results of work (Horton and Rogers 1945), which is explained by the fact that the immobilization has no effect for the monotonous perturbations (\(\omega =0\)). This is a common results of any MIM-type model (Van Genuchten and Wierenga 1976; Selim and Amacher 1997).

3.2 Weak External Flux

Let \(kPe\ll a+b\). Under this assumption Eq. (11) are

$$\begin{aligned} \displaystyle&\omega =\frac{bkPe}{a+b},\nonumber \\ \displaystyle&Rp=\frac{\left[ \pi ^{2}n^{2}+k^{2}\right] ^{2}}{k^{2}}+ \left[ \pi ^{2}n^{2}+k^{2}\right] \frac{Pe^{2}a}{\left( a+b\right) ^{2}}, \end{aligned}$$
(16)

and the critical perturbations (\(n=1\)) correspond to

$$\begin{aligned} k_\mathrm{min}= & {} \frac{4\left( a+b\right) ^{2}}{4\left( a+b\right) ^{2}+aPe^{2}}\pi ,\nonumber \\ Rp_\mathrm{min}= & {} 2\pi ^{2}\left( 2+\frac{Pe^{2}a}{\left( a+b\right) ^{2}}\right) . \end{aligned}$$
(17)

The frequency of critical perturbation is proportional to the Péclet number, as in the case when immobilization is absent. However, it is because of immobilization that the threshold value of the Rayleigh–Darcy number increases and the wave number decreases in compliance with (12). More detailed analysis of the solution to Eq. (11) is presented in “Weak external flux” of Appendix.

3.2.1 High Desorption Rate

If we additionally assume that \(b\gg a\), then the solution (16) becomes

$$\begin{aligned} \displaystyle&\omega =kPe,\nonumber \\ \displaystyle&Rp=\frac{\left[ \pi ^{2}n^{2}+k^{2}\right] ^{2}}{k^{2}}+ \left[ \pi ^{2}n^{2}+k^{2}\right] \frac{Pe^{2}a}{b^{2}}, \end{aligned}$$
(18)

and the critical perturbations correspond to

$$\begin{aligned} k_\mathrm{min}= & {} \frac{4b^{2}}{4b^{2}+aPe^{2}}\pi ,\nonumber \\ Rp_\mathrm{min}= & {} 2\pi ^{2}\left( 2+\frac{Pe^{2}a}{b^{2}}\right) . \end{aligned}$$
(19)

In this case, the expression for frequency is similar to the case without immobilization. Because of high desorption rate, the concentration of the immobilized solute is negligible.

3.2.2 High Adsorption Rate

In the opposite case of \(a\gg b\) the solution (16) can be written as follows:

$$\begin{aligned} \omega= & {} \frac{bkPe}{a},\nonumber \\ Rp= & {} \frac{\left[ \pi ^{2}n^{2}+k^{2}\right] ^{2}}{k^{2}}+ \left[ \pi ^{2}n^{2}+k^{2}\right] \frac{Pe^{2}}{a}, \end{aligned}$$
(20)

and the parameter values for the critical perturbations are

$$\begin{aligned} k_\mathrm{min}= & {} \frac{4a}{4a+Pe^{2}}\pi ,\nonumber \\ Rp_\mathrm{min}= & {} 2\pi ^{2}\left( 2+\frac{Pe^{2}}{a}\right) . \end{aligned}$$
(21)

The high rate of adsorption leads to the removal of solute from the mobile phase provoking severe slowing down of the system dynamics. The migration of the solute to the immobile phase occurs quickly, which favors the establishment of the dynamic equilibrium between the two phases. As a result, the critical values of the wavelength and Rayleigh–Darcy number tend to take on the values obtained for the system without external flow.

3.3 Strong External Flux

For \(kPe\gg a+b\) the balance of the first and second terms in the first of Eq. (11) leads to the expression \(\omega =kPe\). More detailed analysis of the solution to Eq. (11) with the assumption of strong external flux is presented in “Strong external flux” of Appendix. Equation (11) becomes

(22)

and for critical perturbations one can obtain the following expressions

$$\begin{aligned} \begin{array}{l} k_\mathrm{min}=\pi \sqrt{B},\\ Rp_\mathrm{min}=\pi ^{2}\frac{\left( 1+a+B\right) \left( 1+B\right) }{B}\\ B=\sqrt{1+\frac{a^{2}}{\pi ^{2}}}. \end{array}, \end{aligned}$$
(23)

The high velocity of the external flow leads to the solution which is identical to that obtained for \(b=0\) (see expressions 13). Here the threshold increases because of solute immobilization, but the perturbation frequency is very high and the dynamic effects of the concentration redistribution have no time to change it.

3.4 General Solution

In this section we discuss the results of solving Eq. (11) for a wide range of parameters.

It is seen from Fig. 2 that the dependence of the critical wavelength on the Péclet number is generally nonmonotonic. The variation of the critical wavenumber with Pe is within 10%. This allows one to control the distribution of the solute by adjusting the velocity of the external flow.

Fig. 2
figure 2

Dependences of the critical values of the Rayleigh–Darcy number (a), the oscillation frequency (b) and wave number (c) on the Péclet number. The solid lines show the numerical result within (11). The dotted lines indicate the asymptotic solution (23) obtained for the high rate of the external flow. The dash-dotted lines correspond to the low rate of the external flow (17). The values of the sorption coefficients are \(a=4,\; b=4\)

Full size image

Figure 3 shows that at small adsorption rates the critical Rayleigh–Darcy number increases almost linearly. This increase can be explained by the solute withdrawal from the mobile phase. As a result, a larger concentration gradient is required to generate the convective flow. The oscillation frequency diminishes with increasing adsorption rate. As soon as the characteristic time for reaching the dynamic equilibrium between the phases (\(\sim 1/a\)) becomes smaller than the characteristic time of the concentration field pulsation (\(\sim 1/\omega \)), the critical value of the Rayleigh–Darcy number starts decreasing (the extremum point Fig. 3a). With a further growth of the adsorption coefficient the system tends to a steady state, whereas the external flux serves as a small correction only (21).

Fig. 3
figure 3

Dependences of the critical values of the Rayleigh–Darcy number (a), oscillation frequency (b) and wave number (c) on the adsorption coefficient. The solid lines show the numerical result within (11). The dotted lines indicate the asymptotic solution (21) obtained for high adsorption rate. The values of the Péclet number and the desorption coefficient are \(Pe=2,\; b=4\)

Full size image

It is evident from Fig. 4 that the dependence of the critical wavelength and oscillation frequency on the desorption coefficient is nonmonotonic. The asymptotic solution obtained for high desorption rate is in good agreement with the results of numerical analysis. The starting points of curves at \(b=0\) correspond to expressions (13).

Fig. 4
figure 4

Dependences of the critical values of the Rayleigh–Darcy number (a), oscillation frequency (b) and wave number (c) on the desorption coefficient. The solid lines show the numerical result within (11). The dotted lines indicate the asymptotic solution (19) obtained for the high desorption rate. The values of the Péclet number and the adsorption coefficient are \(Pe=2,\; a=4\)

Full size image

Figures 2, 3 and 4 show that the most interesting effects are observed at moderate values of the parameters, namely at \(1<Pe<10, 1<a<10, 1<b<10\) and \(40<Rp<50\). It may be safely suggested that at such values of the parameters the instability near the threshold can occur in the layer of thickness l = 1–10 cm. The layer should be prepared from porous material (ceramic or natural (soils)) with porosity \(0.1<\phi <0.5\) and permeability \(\kappa \) = 1–100 Da (the pore size d = 1–10 \(\upmu \)m). The solute should contain solid particles of size \(\ell \sim \)50–100 nm, for example, metallic, ceramic or semiconducting particles. The concentration difference between the layer boundaries depends on the particle density and its value should be \(C_{0}\) = 1–5 %. The values of the actual external flow velocity are V = 2–20 cm/h.

4 Stability Problem: Modulated in Time External Flux

The time-modulated seepage flow is taken into account by the substitution of \(f\left( t\right) =\left( S+A\cos {\varOmega }t\right) \) in Eq. (7). Here, S is the strength of the average flow and A is the relative amplitude of modulation. Since the external flow is time dependent, the perturbations should be written as \(c,\;\psi ,\; q\sim \exp \left( ikx\right) \sin \left( \pi ny\right) \) and the Eq. (7) are rearranged to give

$$\begin{aligned} \partial _{t}\left( c+q\right) +ik\psi +ikPe\left( S+A\cos {\varOmega }t\right) c= & {} -\pi ^{2}n^{2}c-k^{2}c,\nonumber \\ -\pi ^{2}n^{2}\psi -k^{2}\psi= & {} -ikRpc,\nonumber \\ \partial _{t}q= & {} ac-bq, \end{aligned}$$
(24)

or in the explicit form for \(\psi \) and c they can be written as

$$\begin{aligned} \partial _{t}\left( c+q\right) +ikPe\left( S+A\cos {\varOmega }t\right) c= & {} -\left( \pi ^{2}n^{2}+k^{2}\right) c-ik\psi , \nonumber \\ \psi= & {} \frac{ikRp}{\pi ^{2}n^{2}+k^{2}}c,\nonumber \\ c= & {} \frac{1}{a}\left[ \partial _{t}q+bq\right] , \end{aligned}$$
(25)

and finally the governing equation for q is

$$\begin{aligned} \begin{array}{l} \partial _{tt}q+\partial _{t}q\left[ b+a-\gamma +ikPe\left( S+A\cos {\varOmega }t\right) \right] +b\left[ ikPe\left( S+A\cos {\varOmega }t\right) -\gamma \right] q=0 \end{array}, \nonumber \\ \end{aligned}$$
(26)

where symbol \(\partial _{tt}\) denotes the second time derivative and

$$\begin{aligned} \gamma =\frac{k^{2}Rp}{\pi ^{2}n^{2}+k^{2}}-\pi ^{2}n^{2}-k^{2}. \end{aligned}$$
(27)

Equation (26) is the second-order ordinary differential equation, which describes the time evolution of the system. Note that Eq. (26) does not describe the case \(a=0\), which will be studied separately. The next section of the paper is devoted to the analysis of Eq. (26). First, we consider important limiting cases, which can be treated analytically.

4.1 The Case Without Immobilization

In order to study this case (\(a=0\)), we return to (25) and set \(q=0\); this yields

$$\begin{aligned} \partial _{t}c=\left[ \gamma -ikPe\left( S+A\cos {\varOmega }t\right) \right] c. \end{aligned}$$
(28)

The solution c to Eq. (28) is given by the formula

$$\begin{aligned} c=\exp \left[ \gamma t-ikPe\left( St+\frac{A}{{\varOmega }}\sin {\varOmega }t\right) \right] . \end{aligned}$$
(29)

To ensure the stability of the base state, the solution (29) should decay with time. This is the case of \(Re(\gamma )<0\) (where Re denotes the real part of expression). One can obtain the stability threshold from (27), which is expressed by the second equation from (14). The condition (14) is obtained in the absence of external flux. Here the external flux affects only the temporal evolution of perturbations, but not the stability threshold. This characteristic feature of the impact of time-modulated external flux on the HRL problem was obtained in Lyubimov and Teplov (1998).

4.2 Weak External Flux

A solution to (26) is found as a series in small parameter \(\varepsilon =kPe\ll \left( a+b\right) \)

$$\begin{aligned} q= & {} q_{0}+\varepsilon q_{1}+\ldots \;,\nonumber \\ \gamma= & {} \varepsilon \gamma _{1}+\varepsilon ^{2}\gamma _{2}+\ldots \;. \end{aligned}$$
(30)

A series for \(\gamma \) begins with the first order because in the case of \(Pe=0\) (\(\varepsilon =0\) the zeroth order) the critical value of the \(\gamma \) is zero (see Eq. 14). In the case when \(\gamma _{0}=0\), solution to (26) is given by \(q_{0}={\text {const}}\).

Equation (26) in the first order in \(\varepsilon \) is

$$\begin{aligned} \partial _{tt}q_{1}+\partial _{t}q_{1}\left[ b+a\right] =b\left[ \gamma _{1}- i\left( S+A\cos {\varOmega }t\right) \right] q_{0}. \end{aligned}$$
(31)

The no-secular term condition (Nayfeh 2004) allows one to obtain the expression \(\gamma _{1}=ikS\). This relation does not change the threshold condition (\(Re(\gamma _1)=0\)). Because of this it is necessary to find the solution to (31) and consider the next order in \(\varepsilon \). The solution in the first order is

$$\begin{aligned} q_{1}=q_{0}\left[ \frac{ibA}{{\varOmega }^{2}+\left( b+a\right) ^{2}}\cos {\varOmega }t-\frac{ib\left( b+a\right) }{{\varOmega }^{2}+\left( b+a\right) ^{2}}\sin {\varOmega }t\right] . \end{aligned}$$
(32)

Equation (26) in the second order in \(\varepsilon \) reads

$$\begin{aligned} \partial _{tt}q_{2}+\partial _{t}q_{2}\left[ b+a\right] =b\gamma _{2}q_{0} -\partial _{t}q_{1}i\left( S+A\cos {\varOmega }t\right) -bq_{1}i\left( S+A\cos {\varOmega }t\right) . \end{aligned}$$
(33)

All that we need to find the correction term to the stability threshold expression is to apply the solvability condition for this equation, which yields

$$\begin{aligned} Re\left( \gamma _{2}\right) =\frac{S^{2}a}{\left( b+a\right) ^{2}}+\frac{A^{2}a}{2\left\{ {\varOmega }^{2}+\left( b+a\right) ^{2}\right\} }, \end{aligned}$$
(34)

or for \(Re\left( \gamma \right) \approx \varepsilon ^{2}Re\left( \gamma _{2}\right) \) the threshold condition is

$$\begin{aligned} Rp=\frac{\left[ \pi ^{2}n^{2}+k^{2}\right] ^{2}}{k^{2}}+\left[ \pi ^{2}n^{2}+ k^{2}\right] Pe^{2}a\left[ \frac{S^{2}}{\left( b+a\right) ^{2}}+ \frac{A^{2}}{2\left\{ {\varOmega }^{2}+\left( b+a\right) ^{2}\right\} }\right] , \end{aligned}$$
(35)

where \(kPe=\varepsilon \). The stability conditions for the critical perturbations are

$$\begin{aligned} k_\mathrm{min}= & {} \frac{8\pi }{8+aPe^{2}\left[ \frac{2S^{2}}{\left( b+a\right) ^{2}}+ \frac{A^{2}}{{\varOmega }^{2}+\left( b+a\right) ^{2}}\right] },\nonumber \\ Rp_\mathrm{min}= & {} 2\pi ^{2}\left( 2+\frac{Pe^{2}a}{2}\left[ \frac{2S^{2}}{\left( b+a\right) ^{2}}+ \frac{A^{2}}{{\varOmega }^{2}+\left( b+a\right) ^{2}}\right] \right) . \end{aligned}$$
(36)

The modulated external flux leads to an increase in the critical value of the Rayleigh–Darcy number and a decrease in the critical wavenumber. The expression (35) differs from (16) only by the last term. This term is proportional to the amplitude of vibrations and contributes to the growth of the critical value.

4.2.1 High Desorption Rate

The large value of the desorption coefficient tends to weaken the immobilization effect as noted above. Let \(b\gg a\). It means that we should assume in expression (35) that \({\varOmega }^{2}+\left( b+a\right) ^{2}\approx b^{2}\). With this assumption, the critical Rayleigh–Darcy number is

$$\begin{aligned} Rp=\frac{\left[ \pi ^{2}n^{2}+k^{2}\right] ^{2}}{k^{2}}+\frac{\pi ^{2}n^{2}+ k^{2}}{b^{2}}Pe^{2}a\left[ S^{2}+\frac{A^{2}}{2}\right] , \end{aligned}$$
(37)

and the critical perturbations (\(n=1\)) correspond to

$$\begin{aligned} k_\mathrm{min}= & {} \frac{8\pi b^{2}}{8b^{2}+aPe^{2}\left[ 2S^{2}+A^{2}\right] },\nonumber \\ Rp_\mathrm{min}= & {} 2\pi ^{2}\left( 2+\frac{Pe^{2}a}{2b^{2}}\left[ 2S^{2}+A^{2}\right] \right) . \end{aligned}$$
(38)

A high desorption rate is responsible for eliminating the modulation frequency from the expression for threshold conditions. It is similar to expression (18), corresponding to the case when the natural dynamics of the system is very fast and only average effects can affect the threshold.

4.2.2 High Adsorption Rate

A high adsorption rate causes the solute to migrate into the immobile phase, which slows down the sorption kinetics. Let \(a\gg b\). It means that expression (35) should be rewritten in the following form:

$$\begin{aligned} Rp=\frac{\left[ \pi ^{2}n^{2}+k^{2}\right] ^{2}}{k^{2}}+ \frac{\pi ^{2}n^{2}+k^{2}}{a}Pe^{2}\left[ S^{2}+\frac{A^{2}}{2}\right] , \end{aligned}$$
(39)

and the parameter values for the critical perturbations are

$$\begin{aligned} k_\mathrm{min}= & {} \frac{8\pi a}{8a+Pe^{2}\left[ 2S^{2}+A^{2}\right] },\nonumber \\ Rp_\mathrm{min}= & {} 2\pi ^{2}\left( 2+\frac{Pe^{2}}{2a}\left[ 2S^{2}+A^{2}\right] \right) . \end{aligned}$$
(40)

These expressions describe the effect similar to (20) which is related to the case when the natural dynamics of the system is slow and the critical Rayleigh–Darcy number increases because of immobilization.

It is evident from expressions (26) and (35) that the steady and modulated parts of the external flow produces an additive effect on the critical values of parameters. This is the consequence of linearity of the described problem (8)–(9). Since the case of a steady flow is considered in Sect. 3, in the next section we will focus on the case \(S=0\).

4.3 Numerical Analysis for General Case

In this section, the influence of the external flow parameters (which is quite easy to adjust) on the convective modes is considered. Equation (26) is numerically solved by the Runge–Kutta fourth-order method. The critical values of the parameters are defined by the Floquet method. The resulted curves describing the variation of the critical parameters with the Péclet number are presented in Fig. 5.

Fig. 5
figure 5

Dependences of the critical frequency, critical wave number and Rayleigh–Darcy number on Péclet number. The frequency values are: for a, d, g \({\varOmega }=1\); for b, e, h \({\varOmega }=4\); for c, f, i \({\varOmega }=7\). The sorption coefficients values are \(a=4,\; b=4\), the relative strength and amplitude values are \(S=0,\; A=1\)

Full size image

As show in Fig. 5, the parametric excitation of convection is observed. Variation in the Péclet number leads to a change in the excited flow mode. For a small Péclet number the natural mode is excited when the oscillations of concentration is synchronous with the external flow pulsations, this case is described by expressions (36). If the frequency is rather low (Fig. 5a, d, g) and the Péclet number is increasingly growing, the synchronous mode is replaced by a continuous mode. The latter mode corresponds to a monotonous dependence of the oscillation frequency on the Péclet number and independence of the critical Rp and k values on the Péclet number, see formula (29). In this case, the resonant domains cannot be realized because the natural frequency (\(\omega \)) is much higher than the modulation frequency (\({\varOmega }\)). In general, for moderate values of frequency, the main mode is replaced by a zone corresponding to oscillations with nearly twice the frequency of the external flow, followed by oscillations with nearly tripled frequency, etc (see Fig. 5b, c). When one mode is replaced by another, the frequency of oscillations changes continuously. The growth of the modulation frequency leads to an increase in the resonance domain width. These statements can be confirmed by Fig. 6

Fig. 6
figure 6

Dependences of the critical wave number and Rayleigh–Darcy number on modulation frequency. The Péclet number values are: for a, d \(Pe=1\); for b, e \(Pe=7\); for c, f \(Pe=10\). The sorption coefficients values are \(a=4,\; b=4\), the relative strength and amplitude values are \(S=0,\; A=1\)

Full size image

It can be seen from Fig. 6 that for a small Péclet number the natural mode is observed (see 36). At a higher value of the Péclet number the natural mode is replaced by the domains of parametric excitation of the convective flow. The range of the critical wave number and Rayleigh–Darcy number increases with the growth of modulation frequency.

In general, Figs. 5 and 6 demonstrate the possibility of parametric excitation of the convective flow. Additionally, they confirm the possibility of controlling the critical wavelength (i.e., the spatial distribution of the nanoparticles) by varying the external flow parameters.

4.3.1 The Influence of Sorption

The influence of sorption coefficients on the excited convective modes is in their impact on the natural frequency (\(\omega \)). The latter has been discussed in detail in Sect. 3.4. The results of numerical calculations for varying desorption rate are shown in Fig. 7.

Fig. 7
figure 7

Dependences of the critical wave number and Rayleigh–Darcy number on desorption coefficient. The adsorption coefficient values are: for a, d \(a=4\); for b, e \(a=8\); for c, f \(a=12\). The external flow parameter values are \(Pe=7,\;{\varOmega }=4,\; S=0,\; A=1\). Dotted lines show the transition between consecutive modes

Full size image

Figure 7 demonstrates that the system runs through a sequence of modes: First the continuous mode occurs, and then it is replaced by a series of modes with the frequency multiple to the modulation one, and finally the main synchronous mode is observed. For large desorption rates, a small amount of the solute resides in the immobile phase. This case can be described by asymptotic expressions (38).

The analysis of the system state evolution at different adsorption rates has revealed yet another specific feature. Low values of adsorption coefficient correspond to a very slow kinetics of the phase transition and the dependence of the critical parameter values on the desorption rate is smooth. A growth of the adsorption rate may result in the jumps of the wave number and breaks of the Rp(b) curve (see Fig. 7f).

The behavior of critical parameters at increasing adsorption rate is presented in Fig. 8. The case (\(a=0\)) can not be correctly described by Eq. (26). Because of this all plots (Fig. 8) start with the adsorption rate value (\(a=1\)) . The appropriate mode excited at the starting point (\(a=1\)) then it is replaced by the synchronous mode initiated at large values of a (see (39)). The type of excited modes is specified by b value (see Fig. 7).

Fig. 8
figure 8

Dependences of the critical wave number and Rayleigh–Darcy number on desorption coefficient. The desorption coefficient values are: for a, d \(b=4\); for b, e \(b=8\); for c, f \(b=12\). The external flow parameter values are \(Pe=7,\;{\varOmega }=4,\; S=0,\; A=1\). Dotted lines show the transition between consecutive modes

Full size image

In general, the sorption parameters exert considerable effect on the parametric excitation of convection and control the motion regime via the natural oscillation frequency of the system. The most interesting effects are observed at commensurable values of sorption rates, i. e., in the case when the timescale of relaxation to the dynamic equilibrium between the mobile and immobile phases is close to the timescale of the concentration field pulsations.

5 Conclusion

The linear stability problem for solutal convection in a horizontal porous layer under the action of horizontal net mass flow (external flux) with a prescribed vertical concentration gradient is studied. The problem under consideration is complicated by the solute immobilization effect, which is described within the MIM model (Van Genuchten and Wierenga 1976). Two cases are considered: steady and time-modulated external flows.

In the case of a steady external filtration flow, it is shown that the convective threshold increases in contrast to the value presented in work (Prats 1966). The equations determining the frequency of neutral oscillations and critical value of the Rayleigh–Darcy number have been derived (11). The asymptotes of low- and high-intensity flows have been studied analytically. It is shown that at high flow rate the effect of immobilization is in its contribution to the growth of the critical Rayleigh–Darcy number due to a withdrawal of the solute from the flow. In this case, the dependences of the critical Rayleigh–Darcy and wave numbers on the Péclet number vanish (22). For the external flow of low intensity, the critical value of the Rayleigh–Darcy number is increased, and the wave number is decreased in comparison with the case of no external flow (16). The limiting cases of large values of sorption coefficients have been investigated. It has been found that in both cases the effect of immobilization on the convective currents becomes small (18), (20). The stability map for a wide range of system parameters has been obtained numerically (Figs. 2, 3, 4).

The ordinary differential equation, which determines the dynamics of the system near the threshold of convection, has been derived for the case of modulated external flow. The results of our analytical investigation show that at low flow velocity the modulation makes additional positive contribution to the critical value of the Rayleigh–Darcy number. As a result, the formula, which determines the threshold value, consists of three positive terms: The first is the main critical value without external flow, the second describes the impact of the steady external flow (or average flow), and the third is linked to the effect of the external flow modulation (35). Thus the introduction of modulation leads to stabilization. The case of large desorption rates has been investigated analytically. In this case, the solute is transferred to the mobile phase and the effect of immobilization weakens. It has been also found that the correction to the critical Rayleigh–Darcy number is inversely proportional to the square of the desorption rate (37). The parametric excitation of the convection has been investigated numerically in a wide range of parameters. The stability map in the parameter space has been obtained (Figs. 5, 6, 7, 8).

The possibility of controlling the excited convection modes by varying the frequency and strength of the external flow is described. It has been shown that media with commensurable values of adsorption and desorption rates provide wider possibilities for controlling the nanoparticle distribution. A significant variation of the critical wavelength is obtained only in this case. In other cases the effect of immobilization on the convection modes is inessential. The wavelength control allows one to select a suitable distribution of solutes, which is of great practical importance for many industrial applications.