1 Introduction

Most literature on fluid flow in porous media considered the medium as isotropic. However, porous media such as rock formations, cardboard, filters and insulation are usually anisotropic. See Nield and Bejan (2006) for a review, especially on the effects of anisotropy in thermo-convective stability and internal natural convection. It was found that for fully developed internal flow the effect of anisotropy only alters certain constants since the flow is parallel (Dagan et al. 2002, Mobedi et al 2010; Karmakar and Sekhar 2018). For almost parallel boundary layer flows, anisotropy affects the magnitude but not the character of the results (Rees and Storeletten 1995; Vasseur and Degan 1998; Degan et al 2005; 2008; Bachok et al 2010). Of interest is the work of Rees et al (2002) which determines the first-order tilt of a (boundary layer) plume by matching to an outer flow.

This paper studies the effects of permeability anisotropy on forced flow over an obstruction embedded in a porous medium. Specifically, we consider a pressure driven Darcy-Brinkman flow over (or through) an infinite two-dimensional screen composed of thin strips arranged periodically in the same plane. The corresponding Stokes flow problem was solved by Hasimoto (1958) and the isotropic Darcy–Brinkman flow by Wang (2009). Here, we shall concentrate on the effect of anisotropy of the medium.

The Darcy−Brinkman equation for an anisotropic medium is (Bear 2018)

$$ \nabla \cdot \phi \mu_{e} \nabla {{\mathbf{u}}^{\prime}} - \phi \nabla p^{\prime} - \frac{\phi \mu }{{\varvec{K}}}{{\mathbf{u}}^{\prime}} = 0 $$
(1)

Here, \(\phi\) is the porosity, \(\mu_{e}\) is the effective viscosity, u’ is the velocity vector, p’ is the pressure, \(\mu\) is the viscosity of the fluid, and K is the permeability tensor, which when orthotropic would align with each velocity component. Notice porosity and viscosity are scalars, and thus anisotropy would not affect the first term (Brinkman term), and it affects only the last term (Darcy term). For homogeneous (but not isotropic) media, the porosity cancels and \(\mu_{e}\) can be taken out of the gradient operator. Actually \(\mu_{e}\) is very close to \(\mu\) (Breugem 2007).

We assume the principal axes of the permeability tensor are aligned with the Cartesian axes. Equation (1) reduces to

$$ \frac{\partial p^{\prime}}{{\partial x^{\prime}}} = \mu_{e} \nabla^{2} u^{\prime} - \frac{\mu }{{K_{1} }}u^{\prime} = 0 $$
(2)
$$ \frac{\partial p^{\prime}}{{\partial y^{\prime}}} = \mu_{e} \nabla^{2} v^{\prime} - \frac{\mu }{{K_{2} }}v^{\prime} = 0 $$
(3)
$$ \frac{\partial p^{\prime}}{{\partial z^{\prime}}} = \mu_{e} \nabla^{2} w^{\prime} - \frac{\mu }{{K_{3} }}w^{\prime} = 0 $$
(4)

where (\(u^{\prime},v^{\prime},w^{\prime}\)) are velocity components in the (\(x^{\prime},y^{\prime},z^{\prime}\)) directions, respectively. Normalize all lengths by a characteristic length L, the velocities by a characteristic velocity U, the pressure by \(\mu_{e} U/L\) and drop primes. Equations (2–4) become

$$ p_{x} = \nabla^{2} u - k_{1}^{2} u $$
(5)
$$ p_{y} = \nabla^{2} v - k_{2}^{2} v $$
(6)
$$ p_{z} = \nabla^{2} w - k_{3}^{2} w $$
(7)

Here,

$$ k_{1}^{2} = \frac{{\mu L^{2} }}{{\mu_{e} K_{1} }}, k_{2}^{2} = \frac{{\mu L^{2} }}{{\mu_{e} K_{2} }}, k_{3}^{2} = \frac{{\mu L^{2} }}{{\mu_{e} K_{3} }} $$
(8)

are inverse Darcy numbers. The continuity equation is

$$ u_{x} + v_{y} + w_{z} = 0 $$
(9)

These equations, together with boundary conditions specific to the problem, will be solved.

2 Formulation

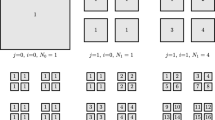
Figure 1a shows the present problem where a screen composed of periodically placed thin strips is embedded in an anisotropic porous medium. The forced velocity far from the screen can be decomposed into (U, V, W) components. Due to the linearity of the Darcy-Brinkman equation, the problem can be separated into three independent problems. Consider first the case of a pressure gradient causing a uniform flow W in the z- direction in a porous medium. Assume the medium is anisotropic, such that the permeabilities in the directions of (x, y, z) are (\(K_{1} ,K_{2} ,K_{3}\)), respectively. In this case, W is a parallel flow and a function of (x, y) only. It only depends on the permeability \(K_{3}\) and does not involve any anisotropy effects. One can use the isotropic results of Wang (2009) with permeability as \(K_{3} ,\) and we shall not discuss this case further.

Fig.1
figure 1

a The screen composed of periodic thin strips. b Cross section of flow due to velocity U.c Cross section of flow due to velocity V

Full size image

The other two directions are not parallel flow and non-trivial. There are two cases: (A) the velocity U parallel to the plane of the screen and in the x direction, whose cross section is shown in Fig. 1b. (B) the velocity V normal the plane of the screen in the y direction, whose cross section is shown in Fig. 1c. In both cases, w is zero and all variables are independent of z. Since the flow is two-dimensional, Eq. (9) suggests a stream function \(\psi\) such that the velocities in the (x,y) directions are \(\left( {\psi_{y} , - \psi_{x} } \right)\). Equations (5,6) become

$$ p_{x} = \nabla^{2} \psi_{y} - k_{1}^{2} \psi_{y} $$
(10)
$$ p_{y} = - \nabla^{2} \psi_{x} + k_{2}^{2} \psi_{x} $$
(11)

Here, \(\nabla^{2}\) is the two-dimensional Laplacian. If pressure is eliminated from Eqs. (10, 11), the stream function satisfies

$$ \nabla^{4} \psi - k_{1}^{2} \psi_{yy} - k_{2}^{2} \psi_{xx} = 0 $$
(12)

The boundary conditions are that the velocities are zero on the slats and approaches uniform flow far from the screen. Note that if \(k_{1} ,k_{2}\) tends to zero, Eq. (12) becomes the biharmonic equation for Stokes flow of Hasimoto (1958). If \(k_{1} ,k_{2}\) are very large, or in the Darcy approximation, Eq. (12) degenerates to a second-order equation, but in general not Laplace's potential flow equation.

3 Case A: The Screen Parallel to the Pressure Gradient

Figure 1b shows the cross section of the screen. Consider a computational domain of \(0 \le x \le b, 0 \le y < \infty\). There are symmetries about x = 0, x = b and anti-symmetry about y = 0 (x > 1). We require the velocities be zero on the solid strip and the velocity approaches 1 at infinity. The boundary conditions are

$$ \psi_{x} = 0, \psi_{xxx} = 0\;on\;x = 0 $$
(13)
$$ \psi_{x} = 0, \psi_{xxx} = 0\;on\;x = b $$
(14)
$$ \psi = 0, \psi_{yy} = 0\;on\;y = 0,\; 1 < x \le b $$
(15)
$$ \psi = 0, \psi_{y} = 0\;on\;y = 0,\; 0 \le x < 1 $$
(16)

and

$$ \psi_{y} = 1\;at\;y \to \infty $$
(17)

Equations (13, 14, 17) suggest the form

$$ \psi = y + \sum \cos (\alpha_{n} x)H\left( y \right) $$
(18)

where \(\alpha_{n} = \frac{n\pi }{b}.\) Equation (12) then gives \(H \sim e^{\lambda y}\) where

$$ \lambda^{4} - \left( {2\alpha_{n}^{2} + k_{1}^{2} } \right)\lambda^{2} + \alpha_{n}^{2} \left( {\alpha_{n}^{2} + k_{2}^{2} } \right) = 0 $$
(19)

or

$$ \lambda_{1,2} = - \left\{ {\left[ {2\alpha_{n}^{2} + k_{1}^{2} \pm \sqrt {(2\alpha_{n}^{2} + k_{1}^{2} )^{2} - 4\alpha_{n}^{2} \left( {\alpha_{n}^{2} + k_{2}^{2} } \right)} } \right]/2} \right\}^{1/2} $$
(20)

Notice that \(\lambda_{1,2}\) are in general complex conjugates. Considering Eqs. (15,16), the stream function is

$$ \psi = y + B_{0} \left( {e^{{ - k_{1} y}} - 1} \right) + \mathop \sum \limits_{n = 1}^{\infty } B_{n} \cos (\alpha_{n} x)\left( {e^{{\lambda_{1} y}} - e^{{\lambda_{2} y}} } \right) $$
(21)

The rest of the boundary conditions Eqs.(15,16) are to be satisfied by point match.

$$ B_{0} k_{1}^{2} + \mathop \sum \limits_{1}^{N - 1} B_{n} \cos (\alpha_{n} x_{j} )\left( {\lambda_{1}^{2} - \lambda_{2}^{2} } \right) = 0, 1 < x_{j} \le b $$
(22)
$$ - B_{0} k_{1} + \mathop \sum \limits_{1}^{N - 1} B_{n} \cos (\alpha_{n} x_{j} )\left( {\lambda_{1} - \lambda_{2} } \right) = - 1,0 \le x_{j} < 1 $$
(23)

Here, we have truncated the series to N terms, and \(x_{j} = \frac{{b\left( {j - 0.5} \right)}}{N}, j = 1 \;{\text{to}}\; N\). Equations (22, 23) are solved for the N unknown coefficients \(B_{n}\).

The normalized shear stress on the strip is

$$ \tau = \psi_{yy} |_{y = 0} = - B_{0} k_{1}^{2} + \mathop \sum \limits_{1}^{N - 1} B_{n} \cos (\alpha_{n} x)\left( {\lambda_{1}^{2} - \lambda_{2}^{2} } \right) $$
(24)

Integrating over the two sides of a slat, the drag per period is

$$ D = 4\left[ {k_{1}^{2} B_{0} + \mathop \sum \limits_{1}^{N - 1} B_{n} \frac{{\sin (\alpha_{n} )}}{{\alpha_{n} }}\left( {\lambda_{1}^{2} - \lambda_{2}^{2} } \right)} \right] $$
(25)

Since Eq. (21) is a Fourier series, convergence as \(N \to \infty\) is assured. Now, let us show the accuracy of the point match method as N is increased. Table 1 shows some typical convergence rates. It is seen that in general three-figure accuracy is attained when N reaches about 100. Up to 1000 terms are used for very small k or when b close to one, or b is very large.

Table 1 The velocity at the center of the gap \(\psi_{y} \left( {b,0} \right)\). Asterisked values indicate the drag per period
Full size table

Another comparison is with an exact solution. When b = 1, the strips are connected and the screen becomes a flat plate. Equation (12) reduces to

$$ \psi_{yyyy} - k_{1}^{2} \psi_{yy} = 0 $$
(26)

The no-slip boundary conditions give

$$ \psi = y - \frac{1}{{k_{1} }}\left( {1 - e^{{ - k_{1} y}} } \right) $$
(27)

The velocity is

$$ u = \psi_{y} = 1 - e^{{ - k_{1} y}} $$
(28)

The drag per period is

$$ D = 4k_{1} $$
(29)

It is interesting this parallel flow solution reduces to uniform flow u = 1 in the Darcy limit \(\left( {k_{1} = \infty } \right)\), but it does not exist in the clear viscous flow limit (\(k_{1} = 0\)) due to Stokes paradox. Table 2 shows a comparison of our point match method to this exact solution as b approaches one. Due to the small gap width, up to 1000 terms are used for accuracy.

Table 2 Mid-gap velocity. Asterisk show the drag per period. Last row entries are from the exact solution Eqs.(28, 29)
Full size table

Figure 2 shows some typical streamlines. It is seen that the streamlines are closer to the screen if \(k_{1} > k_{2}\), than those of \(k_{1} < k_{2}\). It is also reflected in the drag per period in Table 2. The reason is due to the fact that the flow (and drag) is dominated by \(k_{1}\). Of interest is the drag due to a single strip, determined by the asymptote for large b. Table 3 shows the results. Our values for the isotropic case (\(k_{1} = k_{2}\)) agree with those of Wang (2009).

Fig.2
figure 2

Typical streamlines for flow parallel to screen, b = 2. a \(k_{1} = 2, k_{2} = 0.5\) b \(k_{1} = 0.5, k_{2} = 2\)

Full size image
Table 3 Drag on a single slat (\(b \to \infty\)) for a flow parallel to the slat
Full size table

4 Case B: The Screen Normal to the Pressure Gradient

Figure 1c shows the cross section, where a velocity V at \(y = - \infty\) is forced through the gaps of the screen. Our computational domain is also \(0 \le x \le b, 0 \le y < \infty\). There are anti-symmetries about x = 0 and x = b, and symmetry about y = 0 (x > 1). The boundary conditions are

$$ \psi = 0, \psi_{xx} = 0\;on\;x = 0 $$
(30)
$$ \psi = b, \psi_{xx} = 0\;on\;x = b $$
(31)
$$ \psi_{y} = 0, \psi_{yyy} = 0\;on\,y = 0,\;1 < x \le b $$
(32)
$$ \psi_{y} = 0,\psi = 0\;on\;y = 0,\;0 \le x < 1 $$
(33)

and as \(y \to \infty\),

$$ { }\psi_{x} = 1 $$
(34)

Equations (30,31) suggest the form

$$ \psi = x + \sum \sin (\alpha_{n} x)G\left( y \right) $$
(35)

where \(\alpha_{n} \) and \(\lambda_{1,2}\) are same as those in Case A. Using Eqs.(32, 33), the stream function is

$$ \psi = x + \mathop \sum \limits_{n = 1}^{\infty } A_{n} \sin (\alpha_{n} x)\left( {\lambda_{2} e^{{\lambda_{1} y}} - \lambda_{1} e^{{\lambda_{2} y}} } \right) $$
(36)

The coefficients \(A_{n}\) are determined by point match as in Case A. Using the rest of the boundary conditions, Eqs. (32, 33) become, for i = 1 to N,

$$ \mathop \sum \limits_{1}^{N} A_{n} \sin (\alpha_{n} x_{i} )\lambda_{1} \lambda_{2} \left( {\lambda_{1}^{2} - \lambda_{2}^{2} } \right) = 0,\;\;1 < x_{i} \le b $$
(37)
$$ \mathop \sum \limits_{1}^{N} A_{n} \sin (\alpha_{n} x_{i} )\left( {\lambda_{2} - \lambda_{1} } \right) = - x_{i} , \;\;0 \le x_{i} < 1 $$
(38)

The unknowns \(A_{n}\) are inverted from the linear algebraic Eqs.(37, 38) by standard means. The convergence rate is similar to Case A.

From Eqs. (5,6), the pressure is integrated to be

$$ p = - k_{2}^{2} y + \mathop \sum \limits_{1}^{N} A_{n} \cos (\alpha_{n} x)F_{n} \left( y \right) + c $$
(39)

where

$$ F_{n} \left( y \right) = \frac{{\lambda_{1} \lambda_{2} }}{{\alpha_{n} }}\left[ {\left( {\lambda_{1}^{2} - \alpha_{n}^{2} - k_{1}^{2} } \right)e^{{\lambda_{1} y}} - \left( {\lambda_{2}^{2} - \alpha_{n}^{2} - k_{1}^{2} } \right)e^{{\lambda_{2} y}} } \right] $$
(40)
$$ c = \frac{1}{{\left( {b - 1} \right)}}\mathop \sum \limits_{1}^{N} A_{n} \frac{{\sin (\alpha_{n} )}}{{\alpha_{n}^{2} }}\lambda_{1} \lambda_{2} \left( {\lambda_{1}^{2} - \lambda_{2}^{2} } \right) $$
(41)

and we have set the mean pressure at y = 0, \(1 < x \le b\) to zero. Since \(F_{n} \left( \infty \right) = 0\), the extra pressure drop due to the presence of the screen is c. Thus, the normalized drag per period due to the screen is

$$ D = 4b\left| c \right| $$
(42)

Our numerical results can be checked by the exact (clear-fluid) solution found by Hasimoto (1958). In our variables, his drag per period for Stokes flow through a screen is

$$ D = \frac{4\pi }{{\ln \left\{ {\cos \left[ {\frac{{\left( {b - 1} \right)\pi }}{2b}} \right]} \right\}}} $$
(43)

Since our point match method does not admit \(k_{1} ,k_{2}\) identically zero, Table 4 shows the approach to zero. 600 terms are used for four-figure accuracy. It is seen that our results tend to Hasimoto’s solution.

Table 4 Drag per period for small \(k_{1} ,k_{2}\)
Full size table

Of interest is the drag for a single strip which is obtained by extrapolating the half period b to large values. Table 5 shows the drag of a single strip (\(b \to \infty\)). It is clear that the drag is larger if \(k_{1} > k_{2}\) as compared to \(k_{2} > k_{1}\). The values for the isotropic case \(k_{1} = k_{2}\) agree well with those found by Wang (2009).

Table 5 Drag on a single slat (\(b \to \infty\)) for a flow normal to a single strip
Full size table

5 Discussion

The anisotropic permeabilities \(K_{1} ,K_{2} ,K_{3}\) along the principal axes can be experimentally measured, or determined theoretically by pore-level micro fluid dynamics. (e.g., Wang 1996). In this paper, we assumed the principal axes are aligned with the axes of the embedded screen, which occur more often than those inclined at an angle to the solid surfaces. In the latter case, the permeability tensor should be used.

Our point match method is highly efficient, only N linear equations need to be solved in a finite interval. In contrast, finite differences (and boundary integrals) need to tackle an infinite domain, with at least 30 \(N^{2}\) equations. Fourier transforms cannot be applied due to the mixed boundary conditions.

There are many differences between the anisotropic cases of the present paper and the isotropic cases of Wang (2009). For example, the fourth-order partial differential equation, Eq. (12), cannot be factored into two second-order equations as in the isotropic case. Consequently, the eigenvalues Eq. (20) are complex, but the solutions are real. Anisotropy also has non-negligible effects on the streamlines (velocities) and the drag force experienced on the screen as shown in Figs. 2,3.

Fig.3
figure 3

Typical streamlines for flow normal to screen, b = 2. a \(k_{1} = 2, k_{2} = 0.5\) b \(k_{1} = 0.5, k_{2} = 2\)

Full size image

In the limit of \(b \to \infty\), we extrapolated for the drag force on a single strip. Such fundamental results are tabulated for the first time in Tables 3 and 4. The asymmetry of the Tables also shows the effects of anisotropy.

Let us compare the flow parallel to the screen (Case A) with the flow normal to the screen (Case B) illustrated in Fig. 1b and c where \(k_{1} < k_{2}\) as shown. Both Fig. 2 and Fig. 3 show when \(k_{1} < k_{2}\) the velocity is lower. However, Tables 3 and 4 show the drag is lower for flow parallel to the screen, but the drag is higher for the flow normal to the screen. This is because the drag is more sensitive to the permeability in the direction of the flow.

We hope this pilot paper would elicit more research in this interesting area.