1 Introduction

Transport in porous media has been continuously receiving increased attention for the past decades. This stems from its critical importance in many engineering areas, such as oil extraction [1], heat transfer enhancement [2], solar thermal utilization [3], electronics cooling [4], thermal storage [5], chemical reforming [6], modeling of biological tissues [7], as well as many other areas. Another area of interest is the highly conductive porous media, such as metallic/carbon foams with open cells [8], sintered metallic fiber felts [9], packed beds [10], metallic lattice frame structures [11], which facilitates the vast applications of porous media in industry.

The volume averaging technique is a commonly used method for handling transport in porous structures [12]. The Darcy, Brinkman, and Forchheimer models have been used in various research works. The Brinkman model accounts for the viscous effect of an impermeable wall, while the Forchheimer model with quadratic term is appropriate for high velocity flows. For thermal transport in porous media, either local thermal equilibrium (LTE) or local thermal non-equilibrium (LTNE) models are utilized.

For steady convective heat transfer, when the difference between the thermal conductivity of the fluid phase and that of the solid phase is small, the LTE model is an efficient tool for predicting the heat transfer in porous media. Cheng and Hsu [13] numerically studied the fully-developed, forced convective flow and heat transfer through packed bed of spheres in an annular space with Brinkman and LTE models by considering the effects of porosity and permeability variations near the wall. Vafai and Tien [14] performed a theoretical study for moisture transport of fluid in porous materials and the coupling heat/mass transfer process was numerically simulated based on LTE model. Chikh et al. [15] analytically investigated the forced convective heat transfer in an annulus partially filled with a porous medium subject to a constant heat flux, and analyzed the effect of the porous layer thickness on the Nusselt number. Mitrovic and Maletic [16] numerically solved the forced convective heat transfer in a porous annulus with asymmetrical thermal boundary conditions for the inner and outer walls. Mitrovic and Maletic [17] presented a numerical analysis for laminar forced convective heat transfer in a parallel-plate channel filled with a porous medium subject to asymmetrical thermal boundary conditions using the LTE model. Cekmer et al. [18] presented an analytical solution for forced convection in a parallel-plate channel filled with a porous medium when exposed to asymmetrical wall heat fluxes by using LTE model, and analyzed the effect of heat flux ratio on the heat transfer.

LTNE model has received much attention for handling thermal problems in porous media. The importance of using LTNE model was comprehensively established and analyzed in the papers by Vafai and Sozen [19, 20], and Sozen and Vafai [21, 22]. Kuznetsov [23] presented a perturbation solution of heat transfer in a concentric annulus with Darcy model and LTNE model. Lee and Vafai [24] presented a comprehensive analytical study of convective heat transfer in a parallel-plate channel filled with porous media, and presented the parametric analysis for the thermal performance, while analyzing various aspects of the LTNE model. Xu et al. [25] analyzed the LTNE phenomena in metal-foam channel and found there are two main factors affecting thermal transport in porous media: porosity and thermal conductivity ratio of fluid to solid (k r). Using the Brinkman flow model and the LTNE model, Lu et al. [26] presented an analytical solution for forced convection in a tube filled with porous foams, and Zhao et al. [27] presented the analytical solution for forced convection in an annulus filled with porous foams. Shaikh and Memon [28] provided analytical and numerical solutions for forced convective heat transfer in a circular duct with or without porous medium using Darcy–Brinkman–Forchheimer model. Ouyang et al. [29] performed an analytical investigation on developing forced convective heat transfer in a parallel-plate channel filled with a porous medium. Yang and Vafai [30] utilized a comprehensive analysis of the boundary conditions to present an analytical solution for forced convective heat transfer in a porous medium channel and for the first time established the presence of temperature bifurcation in porous media. Xu et al. [31] developed an explicit analytical solution for Brinkman flow and non-equilibrium heat transfer in a parallel-plate channel filled with micro-foams under the condition of asymmetric heat fluxes, and analyzed the effect of basic parameters on Nusselt numbers at the two walls.

Amongst these publications, Refs. [13, 15, 16, 23] consider the forced convection in annular configurations, and Refs. [16,17,18, 31] address the asymmetrical thermal boundary conditions. Tubular configurations with annular space are extensively utilized in industrial applications, such as heat exchangers, solar collectors, chemical reactors, heat accumulators, heat pipes, and electronic heat sinks. Thermal asymmetrical heating is frequently encountered in these applications. As such an analytical investigation of the non-equilibrium heat transfer in an annular space filled with a porous medium under asymmetrical thermal boundary conditions is very important.

To this end, we will employ the LTNE model to obtain analytical solutions for forced convection in an annular duct filled with a porous material subject to a thermally asymmetrical condition. The Darcy and Brinkman models will be used with LTE and LTNE models, and the fin-theory-based model will also be utilized. The effects of key parameters on different models will be analyzed in depth.

2 Physical problem

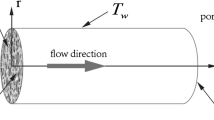
The schematic diagram of forced convective heat transfer in a concentric annulus is shown in Fig. 1. The annulus is filled with a porous medium. The radius of the inner wall is r 1 and that of the outer wall is r 2. Different heat fluxes are imposed on the inner and outer walls. The following commonly used assumptions are imposed: (1) porous medium which fills the annulus is both homogeneous and isotropic; (2) thermophysical properties of the fluid and porous medium are independent of the temperature; (3) hydraulically and thermally fully developed conditions are considered and the fluid is taken to be Newtonian.

Fig. 1
figure 1

Schematic diagram of the problem under consideration

Full size image

3 Analysis

For thermally and hydraulically fully developed forced convection, the following conditions can be imposed:

$$ \begin{array}{*{20}l} {\frac{\partial u}{\partial x} = 0,\;v = 0,\;\frac{\partial p}{\partial r} = 0,\;\frac{dp}{dx} = const,h_{1x} = const,\;h_{2x} = const,} \hfill \\ {\frac{{\partial T_{f} }}{\partial x} = \frac{{\partial T_{s} }}{\partial x} = \frac{{dT_{f,b} }}{dx} = \frac{{dT_{w1} }}{dx} = \frac{{dT_{w2} }}{dx} = const} \hfill \\ \end{array} $$
(1)

The governing equations of the present problem with Brinkman term and LTNE model can be referred from Ref. [19]. The simplified momentum equation with the Brinkman term is

$$ 0 = - \frac{dp}{dx} + \mu_{e} \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial u}{\partial r}} \right) - \frac{{\mu_{f} }}{K}u $$
(2)

For the LTE model, the difference between solid and fluid temperatures is neglected. The energy equation can be presented by

$$ \rho_{f} c_{f} u\frac{{\partial T_{f} }}{\partial x} = k_{e} \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial T_{f} }}{\partial r}} \right) $$
(3)

While, under LTNE condition, the solid and fluid energy equations are as follows:

$$ \left\{ {\begin{array}{*{20}l} {solid:\quad 0 = k_{se} \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial T_{s} }}{\partial r}} \right) - h_{sf} a_{sf} \left( {T_{s} - T_{f} } \right)} \hfill \\ {fluid:\quad \rho_{f} c_{f} u\frac{{\partial T_{f} }}{\partial x} = k_{fe} \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial T_{f} }}{\partial r}} \right) + h_{sf} a_{sf} \left( {T_{s} - T_{f} } \right)} \hfill \\ \end{array} } \right. $$
(4)

The corresponding boundary conditions are

$$ \left\{ {\begin{array}{*{20}l} {r = r_{1} :\quad u = 0,\;T_{s} = T_{f} = T_{w1} ,\;k_{se} \frac{{\partial T_{s} }}{\partial r} + k_{fe} \frac{{\partial T_{f} }}{\partial r} = - q_{1} } \hfill \\ {r = r_{2} :\quad u = 0,\;T_{s} = T_{f} = T_{w2} ,\;k_{se} \frac{{\partial T_{s} }}{\partial r} + k_{fe} \frac{{\partial T_{f} }}{\partial r} = q_{2} } \hfill \\ \end{array} } \right. $$
(5)

In obtaining the analytical solutions, the following dimensionless parameters are employed.

$$ \begin{array}{*{20}l} {R = \frac{r}{{r_{1} }},\;U = \frac{u}{{u_{m} }},\;Da = \frac{K}{{r_{1}^{2} }},\;P = \frac{K}{{\mu_{f} u_{m} }}\frac{dp}{dx},\;M = \frac{{\mu_{e} }}{{\mu_{f} }},\;s = \sqrt {\frac{1}{M \cdot Da}} } \hfill \\ {\theta_{s\left( f \right)} = \frac{{T_{s\left( f \right)} - T_{w1} }}{{q_{2} \cdot r_{1} /k_{se} }},\;B = \frac{{k_{f} }}{{k_{se} }},\;C = \frac{{k_{fe} }}{{k_{se} }},\;D = \frac{{h_{sf} a_{sf} r_{1}^{2} }}{{k_{se} }},\;\xi = \frac{{q_{1} }}{{q_{2} }},\;t = \sqrt {\frac{{D\left( {C + 1} \right)}}{C}} } \hfill \\ \end{array} $$
(6)

3.1 Darcy-LTNE model

In the Darcy flow model, the velocity distribution at the cross-section is uniform. The governing equations for the solid and fluid phases are normalized as

$$ \left\{ {\begin{array}{*{20}l} {solid:\quad 0 = \frac{1}{R}\frac{\partial }{\partial R}\left( {R\frac{{\partial \theta_{s} }}{\partial R}} \right) - D\left( {\theta_{s} - \theta_{f} } \right)} \hfill \\ {fluid:\quad \frac{{2\left( {\xi + R_{2} } \right)}}{{R_{2}^{2} - 1}} = C\frac{1}{R}\frac{\partial }{\partial R}\left( {R\frac{{\partial \theta_{f} }}{\partial R}} \right) + D\left( {\theta_{s} - \theta_{f} } \right)} \hfill \\ \end{array} } \right. $$
(7)

The dimensionless boundary conditions are

$$ \left\{ {\begin{array}{*{20}l} {R = 1:\quad \theta_{s} = \theta_{f} = 0,\;\frac{{\partial \theta_{s} }}{\partial R} + C\frac{{\partial \theta_{f} }}{\partial R} = - \xi } \hfill \\ {R = R_{2} :\quad \theta_{s} = \theta_{f} = \theta_{w2} ,\;\frac{{\partial \theta_{s} }}{\partial R} + C\frac{{\partial \theta_{f} }}{\partial R} = 1} \hfill \\ \end{array} } \right. $$
(8)

The solid and fluid temperature distributions can be obtained analytically as

$$ \theta_{s} = \frac{{2\left( {\xi + R_{2} } \right)}}{{R_{2}^{2} - 1}}\left\{ \begin{aligned} & A_{3} I_{0} \left( {tR} \right) + A_{4} K_{0} \left( {tR} \right) + \frac{1}{{4\left( {C + 1} \right)}}R^{2} \\ & + \frac{{A_{1} }}{C + 1}\ln \left( R \right) + \frac{{A_{2} }}{C + 1} + \frac{C}{{D\left( {C + 1} \right)^{2} }} \\ \end{aligned} \right\} $$
(9a)
$$ \theta_{f} = \frac{{2\left( {\xi + R_{2} } \right)}}{{R_{2}^{2} - 1}}\left\{ \begin{aligned} & - \frac{1}{C}\left[ {A_{3} I_{0} \left( {tR} \right) + A_{4} K_{0} \left( {tR} \right)} \right] + \frac{1}{{4\left( {C + 1} \right)}}R^{2} \\ & + \frac{{A_{1} }}{C + 1}\ln \left( R \right) + \frac{{A_{2} }}{C + 1} - \frac{1}{{D\left( {C + 1} \right)^{2} }} \\ \end{aligned} \right\} $$
(9b)

where the constants A 1, A 2, A 3 and A 4 are as follows

$$ \begin{array}{*{20}l} {A_{1} = \frac{{R_{2}^{3} - R_{2} }}{{2\left( {\xi + R_{2} } \right)}} - \frac{{R_{2}^{2} }}{2}} \hfill \\ {A_{2} = - \frac{1}{4}} \hfill \\ {A_{3} = - \frac{{K_{0} \left( {tR_{2} } \right) - K_{0} \left( t \right)}}{{I_{0} \left( t \right)K_{0} \left( {tR_{2} } \right) - K_{0} \left( t \right)I_{0} \left( {tR_{2} } \right)}} \cdot \frac{C}{{D\left( {C + 1} \right)^{2} }}} \hfill \\ {A_{4} = - \frac{{I_{0} \left( {tR_{2} } \right) - I_{0} \left( t \right)}}{{K_{0} \left( t \right)I_{0} \left( {tR_{2} } \right) - I_{0} \left( t \right)K_{0} \left( {tR_{2} } \right)}} \cdot \frac{C}{{D\left( {C + 1} \right)^{2} }}} \hfill \\ \end{array} $$
(10)

3.2 Darcy-LTE model

For the Darcy model of flow through a porous medium, the effect of impermeable wall on the flow is neglected, and the velocity distribution at a given cross-section is considered to be uniform. In this case, for fully-developed forced convection, the dimensionless energy equation for the LTE model is

$$ \frac{1}{R}\frac{\partial }{\partial R}\left( {R\frac{{\partial \theta_{f} }}{\partial R}} \right) = \frac{{2\left( {\xi + R_{2} } \right)}}{{\left( {C + 1} \right)\left( {R_{2}^{2} - 1} \right)}} $$
(11)

The dimensionless closure conditions can be represented by

$$ \left\{ {\begin{array}{*{20}l} {R = 1:\theta_{f} = 0} \hfill \\ {R = R_{2} :\left( {C + 1} \right)\frac{{\partial \theta_{f} }}{\partial R} = 1} \hfill \\ \end{array} } \right. $$
(12)

The analytical solution for the Darcy-LTE model is obtained as

$$ \theta_{f} = \frac{{2\left( {\xi + R_{2} } \right)}}{{\left( {C + 1} \right)\left( {R_{2}^{2} - 1} \right)}}\left\{ {\frac{1}{4}\left( {R^{2} - 1} \right) + \left[ {\frac{{R_{2} \left( {R_{2}^{2} - 1} \right)}}{{2\left( {\xi + R_{2} } \right)}} - \frac{{R_{2}^{2} }}{2}} \right] \cdot \ln \left( R \right)} \right\} $$
(13)

3.3 Brinkman-LTNE model

With the LTNE model, the dimensionless equations for flow and heat transfer are

$$ \left\{ {\begin{array}{*{20}l} {{\text{momentum}}\;{\text{eq}} .:\quad 0 = \frac{1}{R}\frac{\partial }{\partial R}\left( {R\frac{\partial U}{\partial R}} \right) - s^{2} \left( {U + P} \right)} \hfill \\ {{\text{solid}}\;{\text{energy}}\;{\text{eq}} .:\quad 0 = \frac{1}{R}\frac{\partial }{\partial R}\left( {R\frac{{\partial \theta_{s} }}{\partial R}} \right) - D\left( {\theta_{s} - \theta_{f} } \right)} \hfill \\ {{\text{fluid}}\;{\text{energy}}\;{\text{eq}} .:\quad \frac{{2\left( {\xi + R_{2} } \right)}}{{R_{2}^{2} - 1}}U = C\frac{1}{R}\frac{\partial }{\partial R}\left( {R\frac{{\partial \theta_{f} }}{\partial R}} \right) + D\left( {\theta_{s} - \theta_{f} } \right)} \hfill \\ \end{array} } \right. $$
(14)

The dimensionless boundary conditions are

$$ \left\{ {\begin{array}{*{20}l} {R = 1:\quad U = 0,\;\theta_{s} = \theta_{f} = 0,\;\frac{{\partial \theta_{s} }}{\partial R} + C\frac{{\partial \theta_{f} }}{\partial R} = - \xi } \hfill \\ {R = R_{2} :\quad U = 0,\;\theta_{s} = \theta_{f} = \theta_{w2} ,\;\frac{{\partial \theta_{s} }}{\partial R} + C\frac{{\partial \theta_{f} }}{\partial R} = 1} \hfill \\ \end{array} } \right. $$
(15)

The analytical expression for the velocity is obtained as

$$ U = P\left[ {C_{1} I_{0} \left( {sR} \right) + C_{2} K_{0} \left( {sR} \right) - 1} \right] $$
(16)

where constants C 1, C 2, and P are as follows

$$ \begin{array}{*{20}l} {C_{1} = \frac{{K_{0} \left( s \right) - K_{0} \left( {sR_{2} } \right)}}{{K_{0} \left( s \right) \cdot I_{0} \left( {sR_{2} } \right) - I_{0} \left( s \right) \cdot K_{0} \left( {sR_{2} } \right)}}} \hfill \\ {C_{2} = \frac{{I_{0} \left( s \right) - I_{0} \left( {sR_{2} } \right)}}{{I_{0} \left( s \right) \cdot K_{0} \left( {sR_{2} } \right) - K_{0} \left( s \right) \cdot I_{0} \left( {sR_{2} } \right)}}} \hfill \\ {P = \frac{1}{{\frac{{2\left\{ {C_{1} \left[ {R_{2} \cdot I_{1} \left( {sR_{2} } \right) - I_{1} \left( s \right)} \right] - C_{2} \left[ {R_{2} \cdot K_{1} \left( {sR_{2} } \right) - K_{1} \left( s \right)} \right]} \right\}}}{{s\left( {R_{2}^{2} - 1} \right)}} - 1}}} \hfill \\ \end{array} $$
(17)

The analytical solutions for temperatures of solid and fluid are obtained as follows

$$ \theta_{s} = \frac{{2\left( {\xi + R_{2} } \right)P}}{{R_{2}^{2} - 1}}\left\{ \begin{aligned} & C_{5} I_{0} \left( {tR} \right) + C_{6} K_{0} \left( {tR} \right) - \frac{{\frac{D}{{Cs^{2} }}}}{{s^{2} - \frac{{D\left( {C + 1} \right)}}{C}}}\left[ {C_{1} I_{0} \left( {sR} \right) + C_{2} K_{0} \left( {sR} \right)} \right] \\ & - \frac{1}{{4\left( {C + 1} \right)}}R^{2} + \frac{{C_{3} }}{C + 1}\ln \left( R \right) + \frac{{C_{4} }}{C + 1} - \frac{C}{{D\left( {C + 1} \right)^{2} }} \\ \end{aligned} \right\} $$
(18a)
$$ \theta_{f} = \frac{{2\left( {\xi + R_{2} } \right)P}}{{R_{2}^{2} - 1}}\left\{ \begin{aligned} & - \frac{1}{C}\left[ {C_{5} I_{0} \left( {tR} \right) + C_{6} K_{0} \left( {tR} \right)} \right] + \frac{{1 - \frac{D}{{s^{2} }}}}{{C\left[ {s^{2} - \frac{{D\left( {C + 1} \right)}}{C}} \right]}}\left[ {C_{1} I_{0} \left( {sR} \right) + C_{2} K_{0} \left( {sR} \right)} \right] \\ & - \frac{1}{{4\left( {C + 1} \right)}}R^{2} + \frac{{C_{3} }}{C + 1}\ln \left( R \right) + \frac{{C_{4} }}{C + 1} + \frac{C}{{D\left( {C + 1} \right)^{2} }} \\ \end{aligned} \right\} $$
(18b)

where the constant parameters C 3, C 4, C 5 and C 6 in the above equations are

$$ \begin{array}{*{20}l} {C_{3} = \frac{{R_{2} \left( {R_{2}^{2} - 1} \right)}}{{2\left( {\xi + R_{2} } \right)P}} - \frac{{R_{2} }}{s}\left[ {C_{1} I_{1} \left( {sR_{2} } \right) - C_{2} K_{1} \left( {sR_{2} } \right)} \right] + \frac{{R_{2}^{2} }}{2}} \hfill \\ {C_{4} = \frac{1}{4} - \frac{1}{{s^{2} }}} \hfill \\ {C_{5} = \frac{{K_{0} \left( t \right) - K_{0} \left( {tR_{2} } \right)}}{{K_{0} \left( t \right) \cdot I_{0} \left( {tR_{2} } \right) - I_{0} \left( t \right) \cdot K_{0} \left( {tR_{2} } \right)}}\frac{{Cs^{2} }}{{\left[ {s^{2} - \frac{{D\left( {C + 1} \right)}}{C}} \right]D\left( {C + 1} \right)^{2} }}} \hfill \\ {C_{6} = \frac{{I_{0} \left( t \right) - I_{0} \left( {tR_{2} } \right)}}{{I_{0} \left( t \right) \cdot K_{0} \left( {tR_{2} } \right) - K_{0} \left( t \right) \cdot I_{0} \left( {tR_{2} } \right)}}\frac{{Cs^{2} }}{{\left[ {s^{2} - \frac{{D\left( {C + 1} \right)}}{C}} \right]D\left( {C + 1} \right)^{2} }}} \hfill \\ \end{array} $$
(19)

3.4 Brinkman-LTE model

In this part, the Brinkman model for flow and LTE model for heat transfer are employed. The governing equations are

$$ \left\{ {\begin{array}{*{20}l} {{\text{Momentum}}\;{\text{eq}} . :\quad \frac{1}{R}\frac{\partial }{\partial R}\left( {R\frac{\partial U}{\partial R}} \right) - s^{2} \left( {U + P} \right) = 0} \hfill \\ {{\text{Energy}}\;{\text{eq}} . :\quad \frac{1}{R}\frac{\partial }{\partial R}\left( {R\frac{{\partial \theta_{f} }}{\partial R}} \right) = \frac{{2\left( {\xi + R_{2} } \right)}}{{\left( {C + 1} \right)\left( {R_{2}^{2} - 1} \right)}}U} \hfill \\ \end{array} } \right. $$
(20)

The dimensionless boundary conditions are

$$ \left\{ {\begin{array}{*{20}l} {R = 1:\quad U = 0,\theta_{f} = 0} \hfill \\ {R = R_{2} :\quad U = 0,\left( {C + 1} \right)\frac{{\partial \theta_{f} }}{\partial R} = 1} \hfill \\ \end{array} } \right. $$
(21)

The analytical solution for velocity will be the same as that given in the prior section. The temperature solution is derived as

$$ \theta_{f} = \frac{{2\left( {\xi + R_{2} } \right)P}}{{\left( {C + 1} \right)\left( {R_{2}^{2} - 1} \right)}}\left\{ {\frac{1}{{s^{2} }}\left[ {C_{1} I_{0} \left( {sR} \right) + C_{2} K_{0} \left( {sR} \right)} \right] - \frac{1}{4}R^{2} + C_{7} \ln \left( R \right) + C_{8} } \right\} $$
(22)

where the constants C 7 and C 8 are

$$ \begin{array}{*{20}l} {C_{7} = \frac{{R_{2}^{3} - R_{2} }}{{2\left( {\xi + R_{2} } \right)P}} - \frac{{R_{2} }}{s}\left[ {C_{1} I_{1} \left( {sR_{2} } \right) - C_{2} K_{1} \left( {sR_{2} } \right)} \right] + \frac{{R_{2}^{2} }}{2}} \hfill \\ {C_{8} = \frac{1}{4} - \frac{1}{{s^{2} }}} \hfill \\ \end{array} $$
(23)

3.5 Fin model

For a highly-conductive porous material, the fluid temperature at a cross-section can be approximated to be relatively uniform due to the dominant solid heat conduction. In this case, the thermal conductivity of the fluid does not play a major role. As such, the fin analysis method can be introduced to obtain an approximate solution. The fin model is an approximate tool for evaluating the heat transfer in porous medium. In the fin analysis method, the velocity and fluid temperature is assumed to be uniform, and the heat transfer between the fins and the fluid is usually treated as an equivalent heat source for the heat conduction in the solid. The Darcy flow is considered in the fin model, Darcy-LTE model and Darcy-LTNE model with the assumption of uniform distribution of velocity. In the Brinkman-LTE model and Brinkman-LTNE model, the non-uniform distribution of velocity is considered. The purpose of adopting Darcy model is to be able to compare with the full model so as to examine the effect of non-uniform velocity on heat transfer. For the present problem of forced convection in an asymmetrically heated porous medium, the heat conduction equation for a porous fins can be written as

$$ k_{se} \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{{\partial T_{s} }}{\partial r}} \right) - h_{sf} a_{sf} \left( {T_{s} - T_{f,b} } \right) = 0 $$
(24)

Subject to the following boundary conditions

$$ \left\{ {\begin{array}{*{20}l} {r = r_{1} :\quad k_{se} \frac{{\partial T_{s} }}{\partial r} = - q_{1} } \hfill \\ {r = r_{2} :\quad k_{se} \frac{{\partial T_{s} }}{\partial r} = q_{2} } \hfill \\ \end{array} } \right. $$
(25)

From the energy conservation, the bulk fluid temperature can be obtained as

$$ T_{f,b} \left( x \right) = T_{f,in} + \frac{{2x\left( {q_{1} r_{1} + q_{2} r_{2} } \right)}}{{c_{f} \rho_{f} u_{m} \left( {r_{2}^{2} - r_{1}^{2} } \right)}} $$
(26)

Equation (24) for the porous fin can be normalized as

$$ \frac{1}{R}\frac{\partial }{\partial R}\left( {R\frac{{\partial \theta_{s} }}{\partial R}} \right) - D\left( {\theta_{s} - \theta_{f,b} } \right) = 0 $$
(27)

It should be noted that the dimensionless bulk fluid temperature θ f,b is a quantity that should be determined in the present fin analysis method. The dimensionless boundary conditions are

$$ \left\{ {\begin{array}{*{20}l} {R = 1:\, \theta_{s} = 0,\;\frac{{\partial \theta_{s} }}{\partial R} = - \xi ,\;\theta_{s} = - \theta_{f,b} } \hfill \\ {R = R_{2} :\, \frac{{\partial \theta_{s} }}{\partial R} = 1} \hfill \\ \end{array} } \right. $$
(28)

In the fin analysis method, the dimensionless bulk fluid temperature θ f,b is obtained as

$$ \theta_{f, b} = - \frac{{\left[ {K_{1} \left( {\sqrt D } \right) + \xi K_{1} \left( {\sqrt D R_{2} } \right)} \right]I_{0} \left( {\sqrt D } \right) + \left[ {I_{1} \left( {\sqrt D } \right) + \xi I_{1} \left( {\sqrt D R_{2} } \right)} \right]K_{0} \sqrt D }}{{\sqrt D \left[ {K_{1} \left( {\sqrt D } \right)I_{1} \left( {\sqrt D R_{2} } \right) - I_{1} \left( {\sqrt D } \right)K_{1} \left( {\sqrt D R_{2} } \right)} \right]}} $$
(29a)

The solid temperature can be solved using the above equation to obtain

$$ \theta_{s} = \frac{{\left[ {K_{1} \left( {\sqrt D } \right) + \xi K_{1} \left( {\sqrt D R_{2} } \right)} \right]\left[ {I_{0} \left( {\sqrt D R} \right) - I_{0} \left( {\sqrt D } \right)} \right] + \left[ {I_{1} \left( {\sqrt D } \right) + \xi I_{1} \left( {\sqrt D R_{2} } \right)} \right]\left[ {K_{0} \left( {\sqrt D R} \right) - K_{0} \left( {\sqrt D } \right)} \right]}}{{\sqrt D \left[ {K_{1} \left( {\sqrt D } \right)I_{1} \left( {\sqrt D R_{2} } \right) - I_{1} \left( {\sqrt D } \right)K_{1} \left( {\sqrt D R_{2} } \right)} \right]}} $$
(29b)

As can be seen, the analytical solution based on the fin approximation is much simpler as compared with the full analytical solution incorporating Brinkman and LTNE aspects.

3.6 Parameter definitions

The friction factor for forced convection in a porous annulus is defined as

$$ f = \frac{{2\left( {r_{2} - r_{1} } \right)}}{{\frac{{\rho_{f} u_{m}^{2} }}{2}}} \cdot \frac{dp}{dx} = \frac{{8\left( {R_{2}^{2} - 1} \right)P}}{Re \cdot Da} $$
(30)

The conventional Reynolds number is defined as

$$ Re = \frac{{\rho_{f} u_{m} \cdot 2\left( {r_{2} - r_{1} } \right)}}{{\mu_{f} }} $$
(31)

The friction factor and the Reynolds number based on permeability are defined as:

$$ f_{K} = \frac{\sqrt K }{{\rho_{f} u_{m}^{2} }}\frac{dp}{dx} $$
(32)
$$ Re_{K} = \frac{{\rho_{f} u_{m} \cdot \sqrt K }}{{\mu_{f} }} $$
(33)

Thus, the dimensionless pressure drop can be expressed as

$$ P = \frac{K}{{\mu_{f} u_{m} }}\frac{dp}{dx} = \left( {\frac{\sqrt K }{{\rho_{f} u_{m}^{2} }}\frac{dp}{dx}} \right) \cdot \frac{{\rho_{f} u_{m} \sqrt K }}{{\mu_{f} }} = f_{K} \cdot Re_{K} $$
(34)

The Nusselt numbers at the inner and the outer walls are

$$ \begin{array}{*{20}l} {Nu_{1} = \frac{{h_{1} \cdot 2\left( {r_{2} - r_{1} } \right)}}{{k_{f} }} = \frac{{q_{1} }}{{T_{w1} - T_{fb} }} \cdot \frac{{2\left( {r_{2} - r_{1} } \right)}}{{k_{f} }} = - \frac{{2\xi \left( {R_{2} - 1} \right)}}{{B \cdot \theta_{f,b} }}} \hfill \\ {Nu_{2} = \frac{{h_{2} \cdot 2\left( {r_{2} - r_{1} } \right)}}{{k_{f} }} = \frac{{q_{2} }}{{T_{w2} - T_{fb} }} \cdot \frac{{2\left( {r_{2} - r_{1} } \right)}}{{k_{f} }} = - \frac{{2\left( {R_{2} - 1} \right)}}{{B \cdot \left( {\theta_{w2} - \theta_{f,b} } \right)}}} \hfill \\ \end{array} $$
(35)

The bulk fluid temperature can be obtained from the following integral:

$$ \theta_{f,b} = \frac{{\int_{A} {U\theta_{f} dA} }}{{\int_{A} {UdA} }} = \frac{1}{{\pi \left( {R_{2}^{2} - 1} \right)}}\int_{1}^{{R_{2} }} {\int_{0}^{2\pi } {U\theta_{f} Rd\varphi dR} } = \frac{2}{{R_{2}^{2} - 1}}\int_{1}^{{R_{2} }} {U\theta_{f} RdR} $$
(36)

3.7 Analysis

The dimensionless parameters defined in Eq. (6) are important for estimating the thermal performance of a porous annulus with asymmetrical heat fluxes. Due to the imposed asymmetrical heat load on the annulus, the temperature distribution will be asymmetrical. The structure of annulus will be similar to a parallel-plate channel when the outer radius becomes close to the inner radius (R 2 → R 1).

The derived dimensionless velocity (U = u/u m ) is a function of the shape factor (s), radius ratio (R 2), and dimensionless radial position (R), which can be expressed as

$$ U = F_{U} \left( {s,R_{2} ,R} \right) $$
(37)

For the most complete temperature distribution for the solid and fluid (Brinkman-LTNE model), the derived dimensionless temperatures for the solid and fluid are influenced by several factors, such as s, P, R 2, C, D, t, ξ, and R. This can be expressed as

$$ \theta = F_{\theta } \left( {s,P,R_{2} ,C,D,t,\xi ,R} \right) $$
(38)

The parameters M, and Da are incorporated within the shape factor (s), and expressed as

$$ s = F_{s} \left( {M,Da} \right) $$
(39)

The dimensionless pressure drop (P) can be expressed as

$$ P = \frac{K}{{\mu_{f} u_{m} }}\frac{dp}{dx} = \frac{f \cdot Re \cdot Da}{{8\left( {R_{2}^{2} - 1} \right)}} = F_{P} \left( {R_{2} ,Da,fRe} \right) $$
(40)

It can be seen that dimensionless pressure drop (P) is correlated with radius ratio (R 2), Darcy number (Da), and product of Reynolds number (Re) and friction factor (f).

Since thermal dispersion acts as an additional fluid heat conduction, the parameter C represents the ratio of the effective heat conduction resistance for the solid versus that for fluid, expressed as

$$ C = \frac{{k_{fe} }}{{k_{se} }} = \frac{{R_{se} }}{{R_{fe} }} = \frac{\varepsilon }{1 - \varepsilon }k_{r} = F_{C} \left( {\varepsilon ,k_{r} } \right) $$
(41)

The parameter D in Eq. (6) can be treated as the ratio of solid effective thermal resistance to local convective thermal resistance, shown as

$$ D = \frac{{h_{sf} a_{sf} r_{1}^{2} }}{{k_{se} }} = \frac{{r_{1} /k_{se} }}{{1/\left( {h_{sf} a_{sf} r_{1} } \right)}} = \frac{{R_{se} }}{{R_{cv} }} $$
(42)

The parameter t is a combination of parameters C and D, and can be represented by the ratio of overall thermal resistance to the local convective thermal resistance, given as

$$ t^{2} = \frac{{D\left( {C + 1} \right)}}{C} = \frac{{r_{1} /k_{fe} + r_{1} /k_{se} }}{{1/\left( {h_{sf} a_{sf} r_{1} } \right)}} = \frac{{R_{fe} + R_{se} }}{{R_{cv} }} $$
(43)

The analytical solutions presented in this work can predict the thermal performance of convection in a porous annulus for a wide range of heat flux ratios (ξ ∈ (−∞, −R 2)⋃(−R 2, +∞)). The point ξ = −R 2 is a singular point for the present problem and the analytical values for it can be obtained when the heat flux ratio approaches this point (ξ → −R 2). This singular point corresponds to two special cases for the asymmetrically heated annulus. These are

$$ \xi = - R_{2} \Leftrightarrow \left\{ {\begin{array}{*{20}l} {\vec{q}_{1} = \left| {\vec{q}_{1} } \right|,\vec{q}_{2} = - \frac{{\left| {\vec{q}_{1} } \right|}}{{R_{2} }}} \hfill \\ {\vec{q}_{1} = - \left| {\vec{q}_{1} } \right|,\vec{q}_{2} = \frac{{\left| {\vec{q}_{1} } \right|}}{{R_{2} }}} \hfill \\ \end{array} } \right. $$
(44)

where \( \vec{q}_{1} \) and \( \vec{q}_{2} \) are the heat flux vectors for the inner and outer walls respectively.

Zhao et al. [27] investigated the forced convection in an annulus filled with porous foams using Brinkman model while incorporating the thermal non-equilibrium model. In their study, the inner tube was subjected to a constant heat flux and the outer tube was adiabatic. This is a specific case when the HF ratio is infinite in the present analytical solution. Figure 2 shows a comparison of the present analytical result with the analytical result of Zhao et al. [27]. It can be seen that our analytical temperature distributions of solid and fluid are nearly the same as those obtained by Zhao et al. [27]. At the outer wall of the annulus, the fluid temperature in our solution differs slightly from that in Zhao et al. [27]. This is due to the simplified boundary condition at the outer tube leading to the following solution,

$$ \frac{{\partial T_{s} }}{\partial r} = \frac{{\partial T_{f} }}{\partial r} = 0 $$
(45)

which is different from the present boundary condition used in Eq. (5). Comparing the Brinkman-LTNE model with the Darcy-LTE model in Fig. 2, the solid and fluid temperature of the latter model is slightly closer to the wall temperature than that of the former model. This is expected since the heat transfer obtained by using the Darcy-LTNE model is overestimated due to the uniform velocity in the Darcy model. Thus, the present analytical solution for forced convection in a porous annulus with asymmetrical heat fluxes is validated.

Fig. 2
figure 2

Validation of the present analytical solution (ξ → ∞)

Full size image

4 Results and discussion

4.1 Fluid flow

In the Brinkman model, the viscous force at the solid wall is considered. As such, the velocity distribution at any cross-section is not uniform, as can be seen in Eq. (16). Figure 3 shows the dimensionless velocity profiles of the fluid flow in an annular space filled with a porous medium for different shape factors. It can be seen that an increase in the shape factor can flatten the velocity profile. The velocity profile for small shape factors is nearly parabolic and the peak velocity at the center is relatively large (1.5), which is similar with that for an open channel, while, the velocity profile for large shape factors is quite uniform and the velocity gradient near the solid wall is relatively large.

Fig. 3
figure 3

Velocity profile obtained from the derived analytical solution

Full size image

The dimensionless pressure drop equals to the product of permeability-based friction factor and permeability-based Reynolds number, as can be seen in Eq. (34). Figure 4 shows the effect of shape factor on the absolute value of the dimensionless pressure drop (product of permeability-based friction factor and permeability-based Reynolds number) for different radius ratios. It can be seen that the absolute value of the dimensionless pressure drop decreases with an increase in the shape factor. When the shape factor is sufficiently large, the absolute value for the product of friction factor and Reynolds number based on permeability gradually approaches 1, which is the flow characteristic of the Darcy flow model [12].

Fig. 4
figure 4

Effect of the shape factor on |f K ·Re K |

Full size image

4.2 Temperature profiles

Equations (9), (13), (18), (22), and (29) present the temperature solutions respectively for the Darcy-LTNE, Darcy-LTE, Brinkman-LTNE, Brinkman-LTE and the fin models. In this part, the temperature profiles for different models are analyzed and compared with each other.

Figure 5 shows the temperature profiles for the five models presented in this work for different HF ratios (−R 2, 0, 1, and 100). As can be seen from Eq. (44), when the heat input at one wall is equal to the heat output of the other wall, the net heat imposed on the fluid is zero. In this case, the problem shown in Fig. 1 becomes a pure heat conduction problem. Figure 5a shows the temperature profiles for different models for ξ = −R 2. All the temperature profiles for the solid and fluid with Darcy-LTNE, Darcy-LTE, Brinkman-LTNE, and Brinkman-LTE models are linear and coincide with each other, which is what is expected to occur when the heat conduction is the dominant heat transfer mechanism. Figure 5b shows the temperature profiles for different models for ξ = 0. In this case, the inner wall is adiabatic, as can be seen from Fig. 5b for all the models. Figure 5c shows the temperature profiles for different models for ξ = 1. Due to the geometrical asymmetry of an annular duct, the predicted temperature profiles for different models for ξ = 1 are also asymmetrical, which is different from asymmetrically heated parallel-plate channel [31]. Figure 5d shows the temperature profiles for different models for ξ = 100. In this case, the outer wall can be regarded as adiabatic compared with the inner wall. As can be seen in Fig. 5b–d, the LTE models (including Darcy-LTE and Brinkman-LTE models) always overestimate the heat transfer as compared with LTNE models (including Darcy-LTNE and Brinkman-LTNE models). Simultaneously, the fluid temperature for the Darcy models (including Darcy-LTE and Darcy-LTNE models) is slightly higher than that of Brinkman models (including Brinkman-LTE and Brinkman-LTNE models), respectively. Since the fluid temperature is assumed to be uniform in the fin model, the temperature for the fin model is quite different from those of Darcy-LTNE, Darcy-LTE, Brinkman-LTNE, and Brinkman-LTE models.

Fig. 5
figure 5

Temperature profiles for different HF ratios based on the derived analytical solutions. a ξ = −R 2, b ξ = 0, c ξ = 1, d ξ = 100

Full size image

Figure 6 shows the temperature profiles for the five analytical models at different radius ratios (R 2 = 1.01, 1.3, and 2) with ξ = 2. Figure 6a shows the temperature profiles for the five analytical models at R 2 = 1.01. When the radius ratio approaches 1, the difference between inner and outer radii is small. From Fig. 6a, the temperature profiles for the solid and fluid in an annular channel for R 2 = 1.01 is approximately symmetrical. Figure 6b shows the temperature profiles for the five analytical models for R 2 = 1.3. It can be seen that the asymmetrical aspects have become more prominent. Figure 6c presents the temperature profiles for the five analytical models for R 2 = 2. The LTNE effect in porous media is diminished in this case due to an increase in the width of the annulus, as seen in Fig. 6c. Also as can be seen in Fig. 6, the fluid temperature for the LTE models is greater than those for the LTNE models, and the fluid temperature for the Darcy models is greater than those for the Brinkman models.

Fig. 6
figure 6

Temperature profiles for different radius ratios based on the derived analytical solutions. a R 2 = 1.01, b R 2 = 1.3, c R 2 = 2

Full size image

4.3 Heat transfer assessment

For the asymmetrically heated annular channel, the wall temperature at the inner surface is different from that at the outer surface. Therefore, the Nusselt numbers of the two walls sandwiching the annular channel with a porous medium are different from each other. Equation (35) defines the Nusselt numbers for the inner and outer walls and Eq. (36) presents the bulk mean temperature of the fluid. Since the effect of impermeable wall and the LTNE effect are taken into account in Brinkman-LTNE model as compared to the other models, the Brinkman-LTNE model is treated as the benchmark among the five models. In this section, the effects of the key parameters on thermal performance of asymmetrically heated porous annulus with different models are presented and discussed.

Figure 7 shows the effect of the Reynolds number on the thermal performance of the Brinkman-LTNE, Darcy-LTNE, and the fin models. As expected, an increase in the Reynolds number increases both the inner and outer wall Nusselt numbers. The Brinkman-LTNE result is always slightly less than the Darcy-LTNE result in terms of the Nusselt numbers at the inner and outer walls. For Brinkman-LTNE and Darcy-LTNE models, since the heat flux at the inner wall is greater than that of the outer wall (ξ = 2), the Nusselt number at the inner wall is higher than that of the outer wall for lower Reynolds numbers. However, when the Reynolds number increases, the outer-wall Nusselt number becomes larger than the inner-wall Nusselt number. Further, the difference between the outer and inner wall Nusselt numbers increases with an increase in the Reynolds number. This is due to the larger surface area which results in a larger convective heat transfer at the outer wall. For the fin model with an assumption of uniform fluid temperature, the outer wall Nusselt number is larger than the inner wall Nusselt number, and the difference between these Nusselt numbers increases in the entire range of Reynolds numbers.

Fig. 7
figure 7

Effect of the Reynolds number (Re) on the inner and outer wall Nusselt numbers

Full size image

Figure 8 shows the effect of the shape factor on the thermal performance of an asymmetrically heated annulus filled with a porous medium. The shape factor including the effects of the viscosity ratio and the Darcy number, determines the velocity distribution. Thus, the analytical results for the Darcy-LTE, Darcy-LTNE, and the fin models are independent of the shape factor. As can be seen in Fig. 8, an increase in the shape factor increases the Nusselt numbers for the Brinkman-LTNE, and Brinkman-LTE models. An increased shape factor corresponds to a lower Darcy number, which results in a more uniform Darcy type velocity distribution. As such, as the shape factor increases, the result of the Brinkman-LTE model gradually approaches that of the Darcy-LTE model, while the result for the Brinkman-LTNE model gradually approaches that for the Darcy-LTNE model.

Fig. 8
figure 8

Effect of the shape factor (s) on the inner and outer wall Nusselt numbers

Full size image

Figure 9 shows the effect of the thermal conductivity ratio (k r ) on the thermal performance of asymmetrically heated porous annulus predicted by the five analytical models. The comparisons between the fin model and other models show the applicable scope of the fin model for a thermal performance prediction. The increase in the thermal conductivity ratio, corresponding to a decrease in the solid thermal conductivity, leads to a lower Nusselt number at the inner and outer walls due to the weakened solid heat conduction. As seen in Fig. 9, a decrease in k r increases the difference between LTE and LTNE results for either the Brinkman or the Darcy models. When k r is very large (k r  > 10−2), this difference can be neglected. However, for small k r (k r  < 10−3), LTNE model should be employed for the thermal performance prediction in porous media rather than the LTE model. The difference between the result for the fin model and that for the Brinkman-LTNE model is enlarged as k r increases. In the range of k r  > 10−3, this difference is unacceptable. When k r is less than 10−4, the results for the fin model is closer to that of the Brinkman-LTNE model than that of the Darcy-LTNE model. This indicates that the fin model is useful for predicting thermal performance of porous media for the case of very small thermal conductivity ratios. The fin model is invalid when the thermal conductivity ratio (k r ) is substantial.

Fig. 9
figure 9

Effect of the thermal conductivity ratio (k r ) on the inner and outer wall Nusselt numbers

Full size image

Figure 10 shows the effect of the dimensionless annulus width (R 2 − 1) on the thermal performance of asymmetrically heated porous annulus (ξ = 2) for a set inner wall radius (r 1). The Nusselt numbers at the inner wall increases with an increase in the width of the annulus. An increase in the annulus width leads to a more uniform velocity distribution and relatively smaller temperature difference between solid and fluid phases. It is seen that the fin model can be applicable for a small annulus width. With an increase in the annulus width, the difference between LTE and LTNE results for either Darcy or Brinkman models decreases, and becomes negligible for R 2 – 1 > 3. As such, the LTE model can be applied for predicting the thermal performance of an annulus filled with a porous medium with a substantially large width.

Fig. 10
figure 10

Effect of the dimensionless annulus width (R 2 − 1) on the inner and outer wall Nusselt numbers

Full size image

It should be noted that when HF ratio varies, the temperature of the inner wall may equal to the fluid bulk temperature. From Eq. (35), the corresponding HF ratio for this condition, results in an infinite Nusselt number, which can be defined as the critical value of the inner wall (ξ cr1). A similar feature occurs for the Nusselt number of the outer wall when its temperature becomes the same as the fluid bulk temperature. This results in the critical HF ratio for the outer wall (ξ cr2). The effect of HF ratio on predicting the thermal performance with different models is shown in Fig. 11 and the critical HF ratios for the inner and outer walls for each model can be observed in Fig. 11. Figure 11a, b are for the range of ξ < 0 and for that of ξ > 0 respectively, in logarithmic horizontal coordinate. Figure 11c shows the corresponding overview graph of Fig. 11a, b in linear horizontal coordinate. It can be seen from Fig. 11a that the critical HF ratios at the inner and the outer walls with the fin model are −0.102 and −16.707, respectively. From Fig. 11b, the critical HF ratios at inner wall with Brinkman-LTE, Brinkman-LTNE, Darcy-LTE, and Darcy-LTNE models are approximately 0.549, 0.164, 0.605, and 0.229, respectively. While, the HF ratios at outer wall with these four models are approximately 2.281, 10.165, 2.483, and 7.127, respectively. From Fig. 11c, it can be seen that the LTE result is always greater than the corresponding LTNE result for either Brinkman or Darcy models. The Darcy result is always larger than the corresponding Brinkman result for either LTE or LTNE models.

Fig. 11
figure 11

Effect of the HF ratio (ξ) on the inner and outer wall Nusselt numbers. a ξ < 0, b ξ > 0, c overview

Full size image

5 Summary

Analytical solutions for the fully-developed forced convection in a porous annulus with asymmetrical heat fluxes using five flow/thermal models are presented in this work. These analytical solutions can predict the thermal performance of an asymmetrically heated porous annulus in a wide range of radius and HF ratios. Based on the most comprehensive model, that is, Brinkman-LTNE model, it is found that the thermal performance of asymmetrically heated annulus with porous media can be improved by increasing the Reynolds number, increasing the shape factor, or decreasing the thermal conductivity ratio. An increase in the annulus width can lead to a more uniform velocity field and weakened LTNE effect in porous media. This makes the thermal performance predicted by Brinkman-LTNE model to increase first and then decrease with an increase in the width of the annulus. It is found that the LTE model always overestimates the heat transfer compared to LTNE model, and that when the thermal conductivity ratio is very large (k r  > 10−2), the difference between LTE and LTNE results can be neglected. But the LTE model fails to predict the actual heat transfer for small thermal conductivity ratios. As expected, the Darcy model results in a larger heat transfer than the Brinkman model. The fin solution is found to provide an acceptable approximation to the Brinkman-LTNE result for low thermal conductivity ratios or small annulus widths. Overall, the LTNE phenomena is critical for thermal transport in highly conductive porous media. In addition, the viscous force near the wall has a notable effect on the global thermal performance. Thus, the analytical solution for the Brinkman-LTNE model is more accurate compared to the other simplified models and should be utilized in general. The conventional fin analysis method is generally regarded as a crude model. Finally, the critical HF ratios are found for the inner and outer walls for the five models which were analyzed in this work.