Darcy–Brinkman Flow in a Corrugated Curved Channel

Abstract

A theoretical analysis of a viscous flow in a corrugated curved channel enclosing a porous medium is carried out. The alignment of the corrugations of the outer and the inner curved walls is taken arbitrarily, and the corrugations are considered to be sinusoidal in nature with periodicity. The flow problem is described by Darcy–Brinkman model, derived in the curvilinear coordinates. The effects of the channel curvature, the wall corrugations and the medium permeability are studied through the boundary perturbation technique, for small corrugation amplitude. A substantial effect of the porous medium on the flow is observed when compared to that of the flow in a corrugated curved channel with clear conduit, especially for low permeability medium. Flow enhancement is found to take place for small corrugation wavenumbers, and maximum augmentation is realized for the completely out-of-phase alignment of the two corrugated curved walls. However, the flow reduces for large enough wavenumbers, and the alignment of corrugated curved walls eventually becomes irrelevant, with no influence on the flow. For low permeability medium, the results also show no effect of the wall alignment on the flow. In general, the effect of the channel curvature on the corrugated curved channel flow is discussed relative to a corrugated straight channel flow to demonstrate the implications of the wall geometry enclosing the porous medium.

1 Introduction

Flow through porous media is studied experimentally and theoretically throughout the years, since Darcy’s work, to describe the flow situations and to predict the flow properties in artificial and natural porous media, see for example, Brinkman (1947), Whitaker (1986), Kaviany (1991), Bear and Corapcioglu (1991), Ingham and Pop (2002), Nield and Bejan (2006), Kuznetsov and Nield (2006), Avramenko and Kuznetsov (2008), Kamisli (2009), and Sheikholeslami and Bhatti (2019). The emerging research is fundamental in biological sciences, where the study of flow behaviour in capillary network, for example, in plants and humans, is essential for understanding the transport mechanism of biological fluids. In engineering, applications can be seen in processes which involve cooling, drying, filtration and separation, just to name a few. In geological porous media, practical applications are found in hydrocarbon exploration and production, ground water flow, glaciology transport, geothermal power plant, and so on.

For flow in a porous medium enclosed between two rough straight walls, Ng and Wang (2010) studied the effect of the roughness or the corrugations on the flow characteristics, by using the Darcy–Brinkman model to describe the flow through the porous medium. The authors then showed through boundary perturbation method, that the resulting flow rate in the corrugated channel with porous medium is well affected by the permeability of the channel, when compared with the flow through a corrugated straight channel with clear passage, as studied by Wang (1976). Furthermore, extensions have been made to consider boundaries with three-dimensional roughness, using the Darcy–Brinkman model, see Yu and Wang (2013) and Faltas and Saad (2017). In this context, the modification of the flow field and the underlying phenomenon were analysed by the authors.

Recently, Okechi and Asghar (2019) and Okechi et al. (2020) studied the combined geometrical effects, including curvature and corrugations on viscous flows in corrugated curved channels. The channel curvature was found to influence the flow rate in such a way that is quite different from that of a viscous flow in a corrugated straight channel. For example, in this scenario, the flow rate may not always decrease for the in-phase corrugated curved channel, unlike the flow rate for an in-phase corrugated straight channel (Wang (1976), and Ng and Wang (2010)). However, for the channel radius of curvature, sufficiently large, the results obtained were essentially similar to that of a corrugated straight channel.

In the present study, the objective is to examine and analyse the evolution of the flow characteristics in a corrugated curved channel of an arbitrary phase difference, enclosing a porous medium. The present study is restricted to small amplitude corrugations compared to the channel width. For this problem, the Darcy–Brinkman flow model is adopted as the governing equation for the viscous flow. The parameter characterizing the permeability of the porous medium is defined to determine the effect of the channel porosity on the viscous flow. More also, the effect of the channel radius of curvature on the flow is to be analysed, to elicit the significance of the geometrical parameter, which is rather unexplained in the existing literature.

The study is organized categorically as follows: In the next section, the mathematical model of the physical problem is given in the appropriate coordinate system, with the companying boundary conditions. The boundary perturbation analysis leading to the analytical solution of the model is provided. Section 3 centres on the discussion of the analytical results, while Sect. 4 concludes the study.

2 Mathematical Model and Analysis

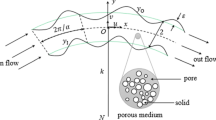
Along the x-direction, a viscous flow is generated by a constant pressure gradient G is considered. The flow moves through pores of the porous medium, which is enclosed by two impermeable corrugated curved walls, separated by a distance 2a, and the channel radius of curvature is k; see Fig. 1. The curvilinear coordinates for the flow geometry are represented by (x, y, z), and (u, v, w) is the velocity in the direction of (x, y, z), respectively. The corrugated walls are defined by the functions $y_{\text{O}} = a + b\sin \left( {2\pi z/L} \right)$ for the outer wall and $y_{\text{I}} = - a + b\sin \left( {2\pi z/L + \varsigma } \right)$ for the inner wall; where b is the corrugation amplitude, L is the wavelength and ς is the arbitrary phase difference between the two corrugated curved walls (ς defines the arbitrary alignment of the two corrugated curved walls, which can be in-phase ς = 0; out-of-phase ς > 0; completely out-of-phase ς = π). For a sparse porous medium, the Darcy–Brinkman model can be used to describe the flow situation. This in vector form reads (Brinkman (1947), Kaviany (1991), Ingham and Pop (2002), Ng and Wang (2010);

Fig. 1

Flow geometry. The outer and the inner walls enclosing the porous medium are indicated by the functions $y_{\text{O}}$ and $y_{\text{I}}$, respectively, which describe the displacement of the corrugations of amplitude b and wavelength L from the smooth walls (dashed lines)

$$ \begin{aligned} & \nabla \cdot \hat{\nu } = 0, \\ & \mu _{E} \nabla ^{2} \hat{\nu } - \frac{\mu }{\kappa }\hat{\nu } - \nabla \hat{p} = 0, \\ \end{aligned} $$

(1)

where $\hat{\nu } = \left( {u, v,w} \right)$ is the pore-averaged velocity vector, $\hat{p}$ is the pressure, κ is the permeability of the porous medium, $\mu_{\text{E}}$ is the effective viscosity of the solid matrix, while μ is the viscosity of the fluid. In the limit κ → ∞, the Stokes model can be obtained and for κ → 0, we get the Darcy model. Equation (1) is well accepted and applicable to high porosity type medium, for example, the fibreglass (also see Lundgren (1972), and Howells (1974)). On normalizing every length by a, velocity by $Ga^{2} /\mu_{E}$, and pressure gradient by G, we can rewrite the dimensionless form of Eq. (1) (without the circumflexes) in the curvilinear coordinates (Schlichting and Gersten (2017), Okechi and Asghar (2019), Okechi et al.(2020)) as:

$$ \left( {{\mathfrak{L}} - \delta^{2} \left( {y + k} \right)^{2} } \right)u = - k\left( {y + k} \right). $$

(2)

Subject to the classical no-slip wall conditions:

$$ \begin{aligned} u\left( {y = y_{o} = 1 + \varepsilon \sin \left( {\alpha z} \right),z} \right) = 0, \hfill \\ u\left( {y = y_{\text{I}} = - 1 + \varepsilon \sin \left( {\alpha z + \varsigma } \right),z} \right) = 0, \hfill \\ \end{aligned} $$

(3)

where ${\mathfrak{L}}$ is defined as:

$$ {\mathfrak{L}} = \left( {y + k} \right)\frac{\partial }{\partial y}\left( {\left( {y + k} \right)\frac{\partial }{\partial y}} \right) + \left( {y + k} \right)^{2} \frac{{\partial^{2} }}{{\partial z^{2} }} - 1 $$

(4)

The parameter $\delta^{2} = \mu a^{2} /\mu_{\text{E}} \kappa$ is a dimensionless parameter, which characterizes the porous medium. The dimensionless corrugation amplitude and wavenumber are now denoted by $\varepsilon = b/a$ and $\alpha = 2\pi a/L$, respectively. However, the limits for the Stokes flow and the Darcian flow are now given, respectively, by δ → 0 and δ ≫ 1. In addition, for k → ∞, Eqs. (2)–(4) reduce to the model of Ng and Wang (2010), whereas, for δ → 0, the model of Okechi and Asghar (2019) is obtained.

For the present analysis, we consider a scenario where the corrugation amplitude is small, i.e., ε ≪ 1, and for this, the boundary perturbation analysis leading to the analytical solution is performed. The procedure follows next. Now, for ε ≪ 1, we conveniently write the solution u as:

$$ u\left( {y,z} \right) = u_{0} \left( y \right) + \varepsilon u_{1} \left( {y,z} \right) + \varepsilon^{2} u_{2} \left( {y,z} \right) + O\left( {\varepsilon^{3} } \right), $$

(5)

which is then substituted in Eq. (2) and also in the Taylor expanded form of Eq. (3) (about y = 1 and y = − 1):

$$ \begin{aligned} & u\left( {y = 1 + \varepsilon \sin \left( {\alpha z} \right),z} \right) = u\left( 1 \right) + \varepsilon \sin \left( {\alpha z} \right)\frac{{\partial u}}{{\partial y}}\left( {1,z} \right) \\ &\quad + \frac{1}{2}\varepsilon ^{2} \sin ^{2} \left( {\alpha z} \right)\frac{{\partial ^{2} u}}{{\partial y^{2} }}\left( {1,z} \right) + O\left( {\varepsilon ^{3} } \right) = 0, \\ \end{aligned} $$

(6)

$$ \begin{aligned} & u\left( {y = - 1 + \varepsilon \sin \left( {\alpha z + \varsigma } \right),z} \right) = u\left( { - 1} \right) + \varepsilon \sin \left( {\alpha z + \varsigma } \right)\frac{{\partial u}}{{\partial y}}\left( { - 1,z} \right) \\ & \quad+ \frac{1}{2}\varepsilon ^{2} \sin ^{2} \left( {\alpha z + \varsigma } \right)\frac{{\partial ^{2} u}}{{\partial y^{2} }}\left( { - 1,z} \right) + O\left( {\varepsilon ^{3} } \right) = 0, \\ \end{aligned} $$

(7)

to obtain the following problems at each order in ε, sequentially;

The zeroth-order governing equation: O ($\varvec{\varepsilon}^{0}$) is

$$ \begin{aligned} & \left( {y + k} \right)\frac{\text{d}}{{{\text{d}}y}}\left( {\left( {y + k} \right)\frac{{{\text{d}}u_{0} }}{{{\text{d}}y}}} \right) - \left( {\delta^{2} \left( {y + k} \right)^{2} + 1} \right)u_{0} = - k\left( {y + k} \right), \\ & u_{0} \left( 1 \right) = 0\; {\text{and }}\;u_{0} \left( { - 1} \right) = 0 \\ \end{aligned} $$

(8)

The solution of Eq. (8) is readily found to be:

$$ u_{0} \left( y \right) = A_{0} I_{1} \left( {\delta \left( {y + k} \right)} \right) + A_{1} K_{1} \left( {\delta \left( {y + k} \right)} \right) + k\left( {\delta^{2} \left( {y + k} \right)} \right)^{ - 1} , $$

(9)

where

$$ A_{0} = \frac{{k\left( {\left( {k + 1} \right)K_{1} \left( {\delta \left( {k + 1} \right)} \right) - \left( {k - 1} \right)K_{1} \left( {\delta \left( {k - 1} \right)} \right)} \right)}}{{\delta^{2} \left( {k^{2} - 1} \right)\left( {I_{1} \left( {\delta \left( {k + 1} \right)} \right)K_{1} \left( {\delta \left( {k - 1} \right)} \right) - K_{1} \left( {\delta \left( {k + 1} \right)} \right)I_{1} \left( {\delta \left( {k - 1} \right)} \right)} \right)}}, $$

(10)

$$ A_{1} = \frac{{k\left( {\left( {k - 1} \right)I_{1} \left( {\delta \left( {k - 1} \right)} \right) - \left( {k + 1} \right)I_{1} \left( {\delta \left( {k + 1} \right)} \right)} \right)}}{{\delta^{2} \left( {k^{2} - 1} \right)\left( {I_{1} \left( {\delta \left( {k + 1} \right)} \right)K_{1} \left( {\delta \left( {k - 1} \right)} \right) - K_{1} \left( {\delta \left( {k + 1} \right)} \right)I_{1} \left( {\delta \left( {k - 1} \right)} \right)} \right)}}. $$

(11)

The functions $I_{\beta }$ and $K_{\beta }$ are modified Bessel functions of order $\beta$ and of the first and second kind, respectively.

The first-order governing equation: O ($\varvec{\varepsilon}^{1}$), with corrugation effect can be written as

$$ \begin{aligned} & \left( {y + k} \right)\frac{\partial }{\partial y}\left( {\left( {y + k} \right)\frac{{\partial u_{1} }}{\partial y}} \right) - \left( {\left( {y + k} \right)^{2} \left( {\delta^{2} - \frac{{\partial^{2} }}{{\partial z^{2} }}} \right) + 1} \right)u_{1} = 0, \\ & u_{1} \left( {1,z} \right) = - \sin \left( {\alpha z} \right)\frac{{{\text{d}}u_{0} }}{{{\text{d}}y}}\left( 1 \right), \\ & u_{1} \left( { - 1,z} \right) = - \sin \left( {\alpha z + \varsigma } \right)\frac{{{\text{d}}u_{0} }}{{{\text{d}}y}}\left( { - 1} \right). \\ \end{aligned} $$

(12)

The differential equation with the boundary conditions in Eq. (12) suggests the solution;

$$ u_{1} \left( {y,z} \right) = g_{1} \left( y \right)\sin \left( {\alpha z} \right) + g_{2} \left( y \right)\cos \left( {\alpha z} \right). $$

(13)

Substituting Eq. (13) in Eq. (12), we have the ordinary differential equations with the boundary conditions at O($\varepsilon^{1}$):

$$ \begin{aligned} & \left( {y + k} \right)^{2} \frac{{{\text{d}}^{2} g_{1} }}{{{\text{d}}y^{2} }} + \left( {y + k} \right)\frac{{{\text{d}}g_{1} }}{{{\text{d}}y}} - \left( {c^{2} \left( {y + k} \right)^{2} + 1} \right)g_{1} = 0, \\ & g_{1} \left( 1 \right) = - \frac{{{\text{d}}u_{0} }}{{{\text{d}}y}}\left( 1 \right), \\ & g_{1} \left( { - 1} \right) = - \cos \left( \varsigma \right)\frac{{{\text{d}}u_{0} }}{{{\text{d}}y}}\left( { - 1} \right), \\ \end{aligned} $$

(14)

and

$$ \begin{aligned} & \left( {y + k} \right)^{2} \frac{{{\text{d}}^{2} g_{2} }}{{{\text{d}}y^{2} }} + \left( {y + k} \right)\frac{{{\text{d}}g_{2} }}{{{\text{d}}y}} - \left( {c^{2} \left( {y + k} \right)^{2} + 1} \right)g_{2} = 0, \\ & g_{2} \left( 1 \right) = 0, \\ & g_{2} \left( { - 1} \right) = - \sin \left( \varsigma \right)\frac{{{\text{d}}u_{0} }}{{{\text{d}}y}}\left( { - 1} \right). \\ \end{aligned} $$

(15)

The solutions of Eqs. (14) and (15) are given, respectively, as:

$$ g_{1} \left( y \right) = A_{2} I_{1} \left( {c\left( {y + k} \right)} \right) + A_{3} K_{1} \left( {c\left( {y + k} \right)} \right), $$

(16)

$$ g_{2} \left( y \right) = A_{4} I_{1} \left( {c\left( {y + k} \right)} \right) + A_{5} K_{1} \left( {c\left( {y + k} \right)} \right), $$

(17)

where $c^{2} = \delta^{2} + \alpha^{2}$ and

$$ A_{2} = \frac{{ K_{1} \left( {c\left( {k - 1} \right)} \right)g_{1} \left( 1 \right) - K_{1} \left( {c\left( {k + 1} \right)} \right)g_{1} \left( { - 1} \right)}}{{K_{1} \left( {c\left( {k - 1} \right)} \right)I_{1} \left( {c\left( {k + 1} \right)} \right) - I_{1} \left( {c\left( {k - 1} \right)} \right)K_{1} \left( {c\left( {k + 1} \right)} \right)}}, $$

(18)

$$ A_{3} = \frac{{ I_{1} \left( {c\left( {k + 1} \right)} \right)g_{1} \left( { - 1} \right) - I_{1} \left( {c\left( {k - 1} \right)} \right)g_{1} \left( 1 \right)}}{{K_{1} \left( {c\left( {k - 1} \right)} \right)I_{1} \left( {c\left( {k + 1} \right)} \right) - I_{1} \left( {c\left( {k - 1} \right)} \right)K_{1} \left( {c\left( {k + 1} \right)} \right)}}, $$

(19)

$$ A_{4} = \frac{{ - K_{1} \left( {c\left( {k - 1} \right)} \right)g_{2} \left( { - 1} \right)}}{{K_{1} \left( {c\left( {k - 1} \right)} \right)I_{1} \left( {c\left( {k + 1} \right)} \right) - I_{1} \left( {c\left( {k - 1} \right)} \right)K_{1} \left( {c\left( {k + 1} \right)} \right)}}, $$

(20)

$$ A_{5} = \frac{{I_{1} \left( {c\left( {k + 1} \right)} \right)g_{2} \left( { - 1} \right)}}{{K_{1} \left( {c\left( {k - 1} \right)} \right)I_{1} \left( {c\left( {k + 1} \right)} \right) - I_{1} \left( {c\left( {k - 1} \right)} \right)K_{1} \left( {c\left( {k + 1} \right)} \right)}}. $$

(21)

The second-order problem: O ($\varvec{\varepsilon}^{2}$) is

$$ \begin{aligned} \left( {y + k} \right)\frac{\partial }{\partial y}\left( {\left( {y + k} \right)\frac{{\partial u_{2} }}{\partial y}} \right) - \left( {\left( {y + k} \right)^{2} \left( {\delta^{2} - \frac{{\partial^{2} }}{{\partial z^{2} }}} \right) + 1} \right)u_{2} = 0, \hfill \\ u_{2} \left( {1,z} \right) = - \frac{1}{2}{ \sin }^{2} \left( {\alpha z} \right)\frac{{{\text{d}}^{2} u_{0} }}{{{\text{d}}y^{2} }}\left( 1 \right) - \sin \left( {\alpha z} \right)\frac{{\partial u_{1} }}{\partial y}\left( {1,z} \right). \hfill \\ u_{2} \left( { - 1,z} \right) = - \frac{1}{2}{ \sin }^{2} \left( {\alpha z + \varsigma } \right)\frac{{{\text{d}}^{2} u_{0} }}{{{\text{d}}y^{2} }}\left( { - 1} \right) - \sin \left( {\alpha z + \varsigma } \right)\frac{{\partial u_{1} }}{\partial y}\left( { - 1,z} \right). \hfill \\ \end{aligned} $$

(22)

Similarly, the solution of Eq. (22) is given as,

$$ u_{2} \left( {y,z} \right) = g_{3} \left( y \right) + g_{4} \left( y \right)\sin \left( {2\alpha z} \right) + g_{5} \left( y \right)\cos \left( {2\alpha z} \right). $$

(23)

Substituting Eq. (23) in Eq. (22), we get the following ordinary differential equations with the boundary conditions at O($\varepsilon^{2}$):

$$ \begin{aligned} & \left( {y + k} \right)^{2} \frac{{{\text{d}}^{2} g_{3} }}{{{\text{d}}y^{2} }} + \left( {y + k} \right)\frac{{g_{3} }}{{{\text{d}}y}} - \left( {\delta^{2} \left( {y + k} \right)^{2} + 1} \right)g_{3} = 0, \\ & g_{3} \left( 1 \right) = - \frac{1}{4}\frac{{{\text{d}}^{2} u_{0} }}{{{\text{d}}y^{2} }}\left( 1 \right) - \frac{1}{2}\frac{{{\text{d}}g_{1} }}{{{\text{d}}y}}\left( 1 \right), \\ & g_{3} \left( { - 1} \right) = - \frac{1}{4}\frac{{{\text{d}}^{2} u_{0} }}{{{\text{d}}y^{2} }}\left( { - 1} \right) - \frac{1}{2}\cos \left( \varsigma \right)\frac{{{\text{d}}g_{1} }}{{{\text{d}}y}}\left( { - 1} \right) - \frac{1}{2}\sin \left( \varsigma \right)\frac{{{\text{d}}g_{2} }}{{{\text{d}}y}}\left( { - 1} \right), \\ \end{aligned} $$

(24)

$$ \begin{aligned} & \left( {y + k} \right)^{2} \frac{{{\text{d}}^{2} g_{4} }}{{{\text{d}}y^{2} }} + \left( {y + k} \right)\frac{{{\text{d}}g_{4} }}{{{\text{d}}y}} - \left( {d^{2} \left( {y + k} \right)^{2} + 1} \right)g_{4} = 0, \\ & g_{4} \left( 1 \right) = - \frac{1}{2}\frac{{{\text{d}}g_{2} }}{{{\text{d}}y}}\left( 1 \right), \\ & g_{4} \left( { - 1} \right) = - \frac{1}{4}\sin \left( {2\varsigma } \right)\frac{{{\text{d}}^{2} u_{0} }}{{{\text{d}}y^{2} }}\left( { - 1} \right) - \frac{1}{2}\sin \left( \varsigma \right)\frac{{{\text{d}}g_{1} }}{{{\text{d}}y}}\left( { - 1} \right) - \frac{1}{2}\cos \left( \varsigma \right)\frac{{{\text{d}}g_{2} }}{{{\text{d}}y}}\left( { - 1} \right), \\ \end{aligned} $$

(25)

and

$$ \begin{aligned} & \left( {y + k} \right)^{2} \frac{{{\text{d}}^{2} g_{5} }}{{{\text{d}}y^{2} }} + \left( {y + k} \right)\frac{{{\text{d}}g_{5} }}{{{\text{d}}y}} - \left( {d^{2} \left( {y + k} \right)^{2} + 1} \right)g_{5} = 0, \\ & g_{5} \left( 1 \right) = \frac{1}{4}\frac{{{\text{d}}^{2} u_{0} }}{{{\text{d}}y^{2} }}\left( 1 \right) + \frac{1}{2}\frac{{{\text{d}}g_{1} }}{{{\text{d}}y}}\left( 1 \right), \\ & g_{5} \left( { - 1} \right) = \frac{1}{4}\cos \left( {2\varsigma } \right)\frac{{{\text{d}}^{2} u_{0} }}{{{\text{d}}y^{2} }}\left( { - 1} \right) + \frac{1}{2}\cos \left( \varsigma \right)\frac{{{\text{d}}g_{1} }}{{{\text{d}}y}}\left( { - 1} \right) - \frac{1}{2}\sin \left( \varsigma \right)\frac{{{\text{d}}g_{2} }}{{{\text{d}}y}}\left( { - 1} \right). \\ \end{aligned} $$

(26)

After some work, the solutions for Eqs. (24)–(25) are:

$$ g_{3} \left( y \right) = A_{6} I_{1} \left( {\delta \left( {y + k} \right)} \right) + A_{7} K_{1} \left( {\delta \left( {y + k} \right)} \right), $$

(27)

$$ g_{4} \left( y \right) = A_{8} I_{1} \left( {d\left( {y + k} \right)} \right) + A_{9} K_{1} \left( {d\left( {y + k} \right)} \right), $$

(28)

$$ g_{5} \left( y \right) = A_{10} I_{1} \left( {d\left( {y + k} \right)} \right) + A_{11} K_{1} \left( {d\left( {y + k} \right)} \right), $$

(29)

where $d^{2} = \delta^{2} + 4\alpha^{2}$, and

$$ A_{6} = \frac{{ K_{1} \left( {\delta \left( {k + 1} \right)} \right)g_{3} \left( { - 1} \right) - K_{1} \left( {\delta \left( {k - 1} \right)} \right)g_{3} \left( 1 \right)}}{{K_{1} \left( {\delta \left( {k + 1} \right)} \right)I_{1} \left( {\delta \left( {k - 1} \right)} \right) - I_{1} \left( {\delta \left( {k + 1} \right)} \right)K_{1} \left( {\delta \left( {k - 1} \right)} \right)}}, $$

(30)

$$ A_{7} = \frac{{I_{1} \left( {\delta \left( {k - 1} \right)} \right)g_{3} \left( 1 \right) - I_{1} \left( {\delta \left( {k + 1} \right)} \right)g_{3} \left( { - 1} \right)}}{{K_{1} \left( {\delta \left( {k + 1} \right)} \right)I_{1} \left( {\delta \left( {k - 1} \right)} \right) - I_{1} \left( {\delta \left( {k + 1} \right)} \right)K_{1} \left( {\delta \left( {k - 1} \right)} \right)}}, $$

(31)

$$ A_{8} = \frac{{ K_{1} \left( {d\left( {k + 1} \right)} \right)g_{4} \left( { - 1} \right) - K_{1} \left( {d\left( {k - 1} \right)} \right)g_{4} \left( 1 \right)}}{{K_{1} \left( {d\left( {k + 1} \right)} \right)I_{1} \left( {d\left( {k - 1} \right)} \right) - I_{1} \left( {d\left( {k + 1} \right)} \right)K_{1} \left( {d\left( {k - 1} \right)} \right)}}, $$

(32)

$$ A_{9} = \frac{{ I_{1} \left( {d\left( {k - 1} \right)} \right)g_{4} \left( 1 \right) - I_{1} \left( {d\left( {k + 1} \right)} \right)g_{4} \left( { - 1} \right)}}{{K_{1} \left( {d\left( {k + 1} \right)} \right)I_{1} \left( {d\left( {k - 1} \right)} \right) - I_{1} \left( {d\left( {k + 1} \right)} \right)K_{1} \left( {d\left( {k - 1} \right)} \right)}}, $$

(33)

$$ A_{10} = \frac{{ K_{1} \left( {d\left( {k + 1} \right)} \right)g_{5} \left( { - 1} \right) - K_{1} \left( {d\left( {k - 1} \right)} \right)g_{5} \left( 1 \right)}}{{K_{1} \left( {d\left( {k + 1} \right)} \right)I_{1} \left( {d\left( {k - 1} \right)} \right) - I_{1} \left( {d\left( {k + 1} \right)} \right)K_{1} \left( {d\left( {k - 1} \right)} \right)}}, $$

(34)

$$ A_{11} = \frac{{I_{1} \left( {d\left( {k - 1} \right)} \right)g_{5} \left( 1 \right) - I_{1} \left( {d\left( {k + 1} \right)} \right)g_{5} \left( { - 1} \right)}}{{K_{1} \left( {d\left( {k + 1} \right)} \right)I_{1} \left( {d\left( {k - 1} \right)} \right) - I_{1} \left( {d\left( {k + 1} \right)} \right)K_{1} \left( {d\left( {k - 1} \right)} \right)}}. $$

(35)

The normalized volumetric flow rate per unit cross-sectional area is defined as:

$$ Q\left( {k,\alpha ,\varsigma ,\delta } \right) = \frac{\alpha }{2\pi }\mathop \smallint \limits_{0}^{2\pi /\alpha } \mathop \smallint \limits_{{y_{\text{I}} }}^{{y_{\text{O}} }} u\left( {y,z} \right){\text{d}}y{\text{d}}z $$

(36)

The expression of Eq. (36) up to second order in $\varepsilon$, by Taylor expansion gives;

$$ \begin{aligned} Q\left( {k,\alpha ,\varsigma ,\delta } \right) & = \int\limits_{{ - 1}}^{1} {u_{0} } \left( y \right){\text{d}}y + \varepsilon \frac{\alpha }{{2\pi }}\int\limits_{0}^{{2\pi /\alpha }}{\int\limits_{{ - 1}}^{1} {u_{1} } } \left( {y,z} \right){\text{d}}y{\text{d}}z \\ & \; + \varepsilon ^{2} \frac{\alpha }{{2\pi }} \left(\int\limits_{0}^{{2\pi /\alpha }} {\int\limits_{{ - 1}}^{1} {u_{2} } } \left( {y,z} \right){\text{d}}y{\text{d}}z\right. \\ & \; + \int\limits_{0}^{{2\pi /\alpha }} {\left( {\sin \left( {\alpha z} \right)u_{1} \left( {1,z} \right) - \sin \left( {\alpha z + \varsigma } \right)u_{1} \left( { - 1,z} \right)} \right)} {\text{d}}z \\ & +\left. \frac{1}{2}\int\limits_{0}^{{2\pi /\alpha }} {\left( {\sin ^{2} \left( {\alpha z} \right)\frac{{{\text{d}}u_{0} }}{{{\text{d}}y}}\left( 1 \right) - \sin ^{2} \left( {\alpha z + \varsigma } \right)\frac{{{\text{d}}u_{0} }}{{{\text{d}}y}}\left( { - 1} \right)} \right)} {\text{d}}z\right) + O\left( {\varepsilon ^{4} } \right). \\ \end{aligned}$$

(37)

Substituting Eqs. (9), (13) and (23), in Eq. (37), we have:

$$ Q\left( {k,\alpha ,\varsigma ,\delta } \right) = q\left( {k,\delta } \right)\left( {1 + \varepsilon^{2} \chi \left( {k, \alpha ,\varsigma ,\delta } \right)} \right) + O\left( {\varepsilon^{4} } \right), $$

(38)

Where

$$ q\left( {k,\delta } \right) = \frac{1}{{\delta^{2} }}\left( {A_{0} \delta \left( {I_{0} \left( { \delta (k + 1} \right)) - I_{0} \left( {\delta (k - 1} \right))} \right) - A_{1} \delta \left( {K_{0} \left( {\delta (k + 1} \right)) - K_{0} \left( {\delta (k - 1} \right))} \right) + k\left( {\ln \left( {k + 1} \right) - \ln \left( {k - 1} \right)} \right)} \right), $$

(39)

is the expression of the volumetric flow rate for a smooth curved channel with no corrugations, containing a porous medium, while the function

$$ \begin{aligned} \chi \left( {k, \alpha ,\varsigma ,\delta } \right) & = \frac{1}{q}\left( {\frac{1}{4}\left( {A_{0} \delta \left( {I_{0} \left( {\delta (k + 1} \right)) - \frac{{I_{1} \left( {\delta \left( {k + 1} \right)} \right)}}{{ \delta \left( {k + 1} \right)}}} \right) - A_{1} \delta \left( {K_{0} \left( {\delta (k + 1} \right)) + \frac{{K_{1} \left( {\delta \left( {k + 1} \right)} \right)}}{{\delta \left( {k + 1} \right)}}} \right) + \frac{k}{{ \delta^{2} \left( {k + 1} \right)^{2} }}} \right)} \right. \\ & \quad - \frac{1}{4}\left( {A_{0} \delta \left( {I_{0} \left( {\delta (k - 1} \right)) - \frac{{I_{1} \left( {\delta \left( {k - 1} \right)} \right)}}{{ \delta \left( {k - 1} \right)}}} \right) - A_{1} \delta \left( {K_{0} \left( { \delta \left( {k - 1} \right)} \right) + \frac{{K_{1} \left( {\delta (k - 1} \right))}}{{ \delta \left( {k - 1} \right)}}} \right) - \frac{k}{{ \delta^{2} \left( {k - 1} \right)^{2} }}} \right) \\ & \quad + \frac{1}{2}\left( {A_{2} I_{1} \left( {c(k + 1} \right)} \right) + A_{3} K_{1} \left( {c(k + 1} \right))) - \frac{1}{2}\left( {A_{2} I_{1} \left( {c\left( {k - 1} \right)} \right) + A_{3} K_{1} \left( {c\left( {k - 1} \right)} \right)} \right)\cos \left( \varsigma \right) \\ & \quad - \frac{1}{2}\left( {A_{4} I_{1} \left( {c\left( {k - 1} \right)} \right) + A_{5} K_{1} \left( {c\left( {k - 1} \right)} \right)} \right)\sin \left( \varsigma \right) \\ & \quad \left. { + \frac{1}{\delta }\left( {A_{6} \left( {I_{0} \left( {\delta (k + 1} \right)) - I_{0} \left( {\delta (k - 1} \right))} \right) - A_{7} \left( {K_{0} \left( {\delta (k + 1} \right)) - K_{0} \left( {\delta (k - 1} \right))} \right)} \right)} \right) \\ \end{aligned} $$

(40)

corresponds to the corrugation function, as a result of the presence of wall corrugations. Note that the contribution of the corrugations takes effect at the second order of approximation, since the first-order solution is periodic in z. The flow rate $Q$ will increase above $q$ or decrease below $q$ by a factor of $\left( {1 + \varepsilon^{2} \chi } \right)$. The function $\chi$ determines the effect of the corrugations on the overall volumetric flow rate $Q$.

3 Results and Discussion

The effect of the permeability of the medium on the velocity distribution in the corrugated curved channel is shown in Fig. 2, through the variation of the parameter δ, when α = 1, k = 1.5, ς = 0.5π and z = 0.5π. As δ is increased, the permeability of the channel takes a decrease, resulting in a decreasing maximum of the axial velocity profile. This simply indicates that as the porosity of the medium decreases, the fluid velocity decreases in turn, for a given constant pressure gradient.

Fig. 2

The effect of the medium permeability on the velocity distribution, when z = π/2, k = 1.5, α = 1, ς = 0.5π, and ε = 0.1

To demonstrate the characteristics of the velocity distribution, due to corrugation effect, the graphical depiction in Fig. 3 is given. For a smooth curved channel (ε = 0) with porous medium, the profile remains independent of z as shown in Fig. 3a (also see Eq. (9)). On the other hand, for a corrugated curved channel (0 < ε ≪ 1), the presence of the sinusoidal variation along the z-direction introduces a dependence of the axial velocity on z. Thus, the peak of the velocity profile no longer remains the same along z, but varies, depending on the alignment of the outer and the inner corrugated walls. The nature of the alignment is determined by the phase difference ς. In Fig. 3b, the peak of the velocity profile is maximum (minimum) at z = 0.5π, when ς = π (ς = 0). This is because, the height of the channel is maximum (minimum) at z = 0.5π, when ς = π (ς = 0). Moreover, at z = π, the maximum peak of the velocity occurs when ς = 0.5π; and the minimum is the same for both ς = 0 and ς = π, see Fig. 3c. A behaviour in reverse to that of Fig. 3b is seen in Fig. 3d, when z = 1.5π is considered. These observations give an insight to the features of the velocity distribution modified by the presence of wall corrugations, with an arbitrary phase difference.

Fig. 3

The effect of the corrugations on the velocity distribution, when δ = 1, k = 1.5, ε = 0 (Fig. 3a) and ε = 0.1 (Figs. 3b–3d)

The graph of zeroth-order volumetric flow rate q specifying the flow rate in porous medium enclosed by two smooth curved walls is given in Fig. 4. In Figs. 4a,b the function q decreases persistently and eventually tends towards zero, as the parameter δ increases. The flow decreases below that of a smooth curved channel with clear conduit (dotted lines), for a given constant pressure gradient. This is due to the decrease in the permeability of the porous medium, as δ is increased. We can see that as we go from the Stokes flow limit to the Darcian flow limit, a tendency of a blockage may be inevitable, due to the decreasing permeability of the porous medium. In particular, for large k, the characteristic behaviour in Fig. 4b agrees with that of Ng and Wang (2010), which is the limiting scenario of the present problem, for sufficiently large k.

Fig. 4

Variation of the volumetric flow rate with the medium permeability, for a smooth curved channel. The dotted lines indicate the volumetric flow rate in a clear conduit for each k

To determine the effect of the wall structure on the flow rate, the variation of the corrugation function χ with the pertinent parameters α, k, ς and δ is examined. In Fig. 5, an illustration of the variation of χ with α, for different ς and δ is given, when k = 1.5. The function χ decreases from positive values (χ > 0) below the horizontal axis (at χ = 0) to negative values (χ < 0), as α increases, irrespective of the values of ς and δ. For a positive χ, and by Eq. (38), the flow rate is increased by the corrugations above that of a smooth curved channel with no corrugations. Note that this increase occurs in the neighbourhood of small wavenumber or large wavelength. On the contrary, a negative χ would consequently result in a decrease in the flow rate, in comparison.

Fig. 5

The effect of corrugations on the volumetric flow rate, shown by the variation of the corrugation function with the corrugation wavenumber, when k = 1.5. The curves for δ = 0 in Fig. 5a agree with the results of Okechi and Asghar (2019) and Okechi et al. (2020)

The characteristic effect of the phase difference ς on the function χ is clearly indicated in Fig. 5: The flow rate is further increased by ς, reaching a maximum when ς = π. This is explained by flow resistance being comparatively the least for the completely out-of-phase (ς = π) alignment of the outer and inner corrugated curved walls. However, for sufficiently large α, this observed feature goes absent, as the flow resistance becomes invariant for all ς. In other words, the phase difference has no influence on the flow, for large corrugation wavenumbers. Furthermore, for δ = 0 (Stokes flow limit), the curves for χ appear distinct for different ς, but as we approach the Darcian flow limit with increasing δ, the medium becomes less permeable, such that the phase difference also becomes immaterial even for small α, see Fig. 5c; when δ = 5. In general, for δ ≥ 5, the phase difference ceases to have effect on the flow.

The significance of the present work is self evident in Figs. 5. The geometrical influence on the flow is captured here, when compared with Ng and Wang (2010). Here, we can clearly notice that the flow rate may not decrease, when the curved corrugated walls are in phase (ς = 0), as reported by Ng and Wang (2010); when the corrugated walls are straight (k → ∞) and in phase. This is due to the effect of the curvature of the channel. Nevertheless, for k ≥ 15, the results agree with the analytical results of Ng and Wang (2010), as illustrated by Fig. 6.

Fig. 6

The effect of corrugations on the volumetric flow rate, shown by the variation of the corrugation function with the corrugation wavenumber, when k = 15, which agrees well with the analytical results of Ng and Wang (2010) (k → ∞)

The effect of the parameter δ on χ is further demonstrated in Fig. 7, taking α = 1. It can be seen that the alignment of the corrugated walls will have the most effect on the flow in the Stokes flow limit, for any given k. When k = 1.5, Fig. 7a shows that the function χ increases above zero as we increase δ, for ς = 0 and ς = 0.5π, whereas, for ς = π, the function χ decreases to a minimum before reaching the curves for ς = 0 and ς = 0.5π, and merging into a single profile in the Darcian flow limit. For k = 15, the variation of the function χ with δ in Fig. 7b is similar in characteristics to the observation of Ng and Wang (2010).

Fig. 7

The variation of the corrugation function with the medium permeability, when α = 1

The variation of χ with k, for δ = 1 is shown in Fig. 8. For α = 0.5, χ is positive for all ς, and for small values of k, implying a flow increase, according to Eq. (38). However, as we move towards the limit of a straight channel with increasing k, only the out-of-phase corrugations will increase the total flow rate, as expected. An increase in the wavenumber, i.e. α = 1, leads to a reduction in the function χ for all values of k, and hence the total flow rate.

Fig. 8

The variation of the corrugation function with the channel radius of curvature, when δ = 1

Figure 9 shows the behaviour of the threshold wavenumber $\alpha_{\text{T}}$ with k for fixed values of δ. The threshold wavenumber indicates the wavenumber at which the function χ cuts across the horizontal line at χ = 0. This wavenumber is a function of both δ and k, such that;

Fig. 9

The variation of the threshold wavenumber with the channel radius of curvature

$$ \chi \left( {k, \alpha ,\varsigma ,\delta } \right) = \left\{ {\begin{array}{*{20}c} { > 0, \quad 0 < \alpha < \alpha_{\text{T}} } \\ { < 0,\quad {\text{elsewhere}}} \\ \end{array} } \right. $$

(41)

For a wavenumber less than $\alpha_{\text{T}}$, the flow rate is enhanced. Thus, to examine the range of flow enhancement, we look at Figs. 9a, 9b. The range of flow enhancement is maximum for ς = π. Furthermore, $\alpha_{\text{T}}$ decreases with increasing k. In particular, the decrease is relatively sharp for ς = 0, tending to zero as k → ∞. For δ = 5, the function $\alpha_{\text{T}}$ decreases with the same curve for all ς, and also tending towards zero as k → ∞. The range for which χ is positive increases further with the increase in δ, but only for sufficiently small values of k.

4 Conclusion

This article initiates the study of a viscous flow through the pores of a porous medium enclosed by two corrugated curved walls, where the corrugations of the curved wall are aligned arbitrarily. The analytical results agree with the limiting case studies in the literature, i.e.: δ → 0, k → ∞, and both δ → 0 and k → ∞. We assume that the porous medium is sparse, and the corrugations are sinusoidal of minute amplitude; such that the Darcy–Brinkman model governs the flow description and the analytical solution is found by perturbation analysis. The velocity and the volumetric flow rate expressions are obtained, and the effects of the medium permeability (with the inclusion of the Stokes flow limit and the Darcian flow limit) and the geometrical features including the radius of curvature and the corrugations have been examined and discussed. A considerable change in the flow behaviour is observed on moving from the Stokes flow limit to the Darcian flow limit, for the same geometry. The flow is increased by the corrugations, when the corrugation wavelength (wave number) is large (small) for an arbitrary alignment, depending on the channel radius of curvature. The flow augmentation maximizes for the completely out-phase alignment of the two corrugated curved walls, in the Stokes flow limit. The alignment has no effect on the flow in the Darcian flow limit. However, the flow decreases with increasing wave number, such that, the alignment of the two corrugated curved walls plays no role for sufficiently large wavenumber. The underlying results of this study may be important and applicable in micro-fluidic situations concerning flows through conduits filled with sparse porous medium, bounded by curved walls with micro-roughness or corrugations.