Darcy-Brinkman Flow Through a Bumpy Channel

Abstract

The forced flow through a channel with bumpy walls which sandwich a porous medium is studied. The problem models micro-fluidics where, due to the small size of the channel width, the surface roughness of the walls is amplified. The Darcy-Brinkman equation is solved analytically through small perturbations on the ratio of bump amplitude to the half width of the channel. The first- order perturbation solutions give the three-dimensional velocity effects of the bumpiness and the second-order perturbation solutions give the increased resistance due to roughness. The problem depends heavily on the non-dimensional porous medium parameter $k$ which represents the importance of length scale to the square root of permeability. Our solutions reduce to the clear fluid limit when $k$ is zero and to the Darcy limit when $k$ approaches infinity.

1 Introduction

The study of the flow in a channel filled with a porous medium is fundamental in the prediction of the various transport properties of porous media. The appropriate governing equation is the Darcy-Brinkman equation which modifies the porous media (Darcy) equation to take into account the non-negligible viscous stress of the walls. Reviews of the many previous references were given by Ingham and Pop (2002), Kaviany (1991) and Nield and Bejan (2006). In what follows, we shall concentrate on the flow through parallel plates enclosing a porous medium. Analytic solutions to the flow in parallel plate channels using the Darcy-Brinkman equation, sometimes with an additional nonlinear Forchheimer term, have been found by Kaviany (1985) and Nakayama et al. (1988). Heat input was considered by Nield et al. (1996), Hung and Tso (2009), Kamisli (2009), Cekmer et al. (2011) and Umavathi and Veershetty (2012). Unsteadiness (starting or oscillatory) was studied by Khodadadi (1991), Kuznetsov and Nield (2006), Wang (2008) and Avramenko and Kuznetsov (2009). In all of the above sources the channel boundaries are assumed to be flat and smooth.

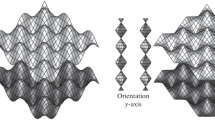
However, in some cases the boundary walls cannot be assumed flat. The uneven bumpiness may be due to surface roughness which is magnified by the small scale of the channel, for example, in micro-fluidic applications. In biology, the problem models forced flow through uneven endothelial clefts (channels) which may be obstructed by hyaluronic acid matrix (Crone and Levitt 1984).

There are few previous works on the effect of uneven walls. Wang (2010) studied the Darcy-Brinkman flow over a boundary with parallel rectangular grooves. It was found that such surface irregularity causes an apparent velocity slip on the boundary wall. Ng and Wang (2010) considered the Darcy-Brinkman flow in a channel with small- amplitude wavy boundary striations. For a given pressure gradient, the surface corrugations, described by both amplitude and phase, affect the net flow rate through the channel. These two papers are pioneer studies of the effect of two dimensional boundary corrugations on Darcy-Brinkman flow.

The present paper considers the Darcy-Brinkman flow in a channel bounded by 3D bumpy walls, which more accurately describe surface roughness. Due to the three-dimensionality, the stream function for 2D flow does not exist and primary variables in terms of velocities and pressure need to be used. We assume the amplitude of the bumps is much smaller than the nominal width of the channel, such that the perturbation method can be used, and that the bumps are much larger than the pore size of the porous medium, such that a continuum (Darcy-Brinkman) description is valid.

Our solution approaches the clear fluid limit as permeability approaches infinity, and the Darcy limit as permeability approaches zero. The clear fluid limit was found by Wang (2004) and the Darcy limit will be developed in this paper.

2 Formulation

The Darcy-Brinkman equation is (e.g. Ingham and Pop 2002; Nield and Bejan 2006)

$$\begin{aligned} \mu _{\text{ e}} \nabla ^{2}\vec {\upsilon ^\prime }-\frac{\mu }{K}\vec {\upsilon ^\prime }=\nabla p^{\prime } \end{aligned}$$

(1)

where $\vec {\upsilon ^\prime }$ is the pore averaged velocity vector, $p^{\prime }$ is the pressure, $\upmu _\mathrm{e}$ is the effective viscosity of the matrix, $\mu$ is the viscosity of the fluid, and $K$ is the permeability. The inertial terms are neglected due to the small velocity and the small scale of the bumps. Let the mean distance between the plates be 2 $L$ and the longitudinal pressure gradient be $G$. Normalize the pressure by $|G|$, all lengths by $L$, the velocity by $|G|L^{2}/\mu _{\text{ e}}$. Let $(u,\upsilon ,w)$ be velocity components in the Cartesian directions $(x,y,z)$, respectively. Eq. (1) becomes

$$\begin{aligned} u_{xx}&+ u_{yy} +u_{zz} -k^{2}u=p_x\nonumber \\ \upsilon _{xx}&+ \upsilon _{yy} +\upsilon _{zz} -k^{2}\upsilon =p_y\nonumber \\ w_{xx}&+ w_{yy} +w_{zz} -k^{2}w=p_z \end{aligned}$$

(2)

where

$$\begin{aligned} k=L\sqrt{\frac{\mu }{\mu _{\text{ e}} K}} \end{aligned}$$

(3)

is the non-dimensional porous medium parameter proportional to the inverse square root of the Darcy number. The continuity equation is

$$\begin{aligned} u_x +\upsilon _y +w_z =0 \end{aligned}$$

(4)

Setting our axes in the middle of the channel, let the top and bottom walls be described by

$$\begin{aligned} z&= 1+\varepsilon \sin (\alpha x)\sin (\beta y)\end{aligned}$$

(5)

$$\begin{aligned} z&= -1\pm \varepsilon \sin (\alpha x)\sin (\beta y) \end{aligned}$$

(6)

Here $\varepsilon$ is the height of the bumps to half width $L$, and $\alpha$ and $\beta$ are wave numbers in the $x$ and $y$ directions, respectively. In Eq. (6), the top sign is used if the walls are in phase, and the bottom sign is used if the walls are out of phase (Fig. 1). The boundary conditions are that the velocities are zero on the bumpy walls described by Eqs. (5) and (6).

Fig. 1

Bumpy parallel plate channel ($\alpha =\beta =1, \varepsilon =0.1$). Left in phase, right out of phase. A porous medium is confined between the plates given by Eqs. (5) and (6) and the flow is forced by a pressure difference in the $x$-direction

The problem is formidable as it stands.

3 First-Order Perturbation Solution

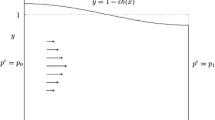
When $\varepsilon$ is zero, the plate is smooth and flat. If the pressure gradient is in the $x$ direction, the solution is the parallel flow

$$\begin{aligned} u_0 =\frac{1}{k^{2}}\left[ {1-\frac{\cosh (kz)}{\cosh k}} \right], \quad \upsilon _0 =w_0 =0, \quad p_0 =-x \end{aligned}$$

(7)

Figure 2 shows the zeroth-order longitudinal velocity profile. As the porous media parameter $k$ is increased, the velocity becomes smaller and more blunted. We shall perturb from this state for small amplitude ratio $\varepsilon$. Any function $f$ can be expanded for small $\varepsilon$

$$\begin{aligned} f=f_0 +\varepsilon f_1 +\varepsilon ^{2}f_2 +\cdots \end{aligned}$$

(8)

Fig. 2

Zeroth-order longitudinal velocity $u_0$. From top $k\,=\,0,\,1,\, 2,\, 5,\, 20$. The velocity is parabolic for $k\,=\,0$ (clear fluid flow) and the velocity is close to plug flow for large $k$ (Darcy limit)

On any boundary $z=a+\varepsilon g(x,y),\,(a=\pm 1)$ the value of $f$ is expanded as a Taylor series

$$\begin{aligned} f\left| {_{a+\varepsilon g} } \right.=f_0 \left|{_a } \right.+\varepsilon (f_1 +gf_{0z} )\left| {_a } \right.+\varepsilon ^{2}(f_2 +gf_{1z} +\frac{g^{2}}{2}f_{0zz} )\left|{_a } \right.+\cdots \end{aligned}$$

(9)

Setting the velocities to zero on the top plate, Eqs. (7), (8) and (9) give, for the first-order,

$$\begin{aligned} u_1 \left| {_1 =-\sin (\alpha x)\sin (\beta y)u_{0z} \left| {_1 =\sin (\alpha x)\sin (\beta y)T_k } \right.} \right., \quad \upsilon _1 \left| {_1 =0} \right., \quad w_1 \left| {_1 =0} \right. \end{aligned}$$

(10)

where

$$\begin{aligned} T_k =\frac{\sinh k}{k\cosh k} \end{aligned}$$

(11)

Equations (2) and (10) and the continuity equation suggest the first-order solution should be in the form

$$\begin{aligned} u_1&= \sin (\alpha x)\sin (\beta y)U(z), \upsilon _1 =\cos (\alpha x)\cos (\beta y)V(z),\end{aligned}$$

(12)

$$\begin{aligned} w_1&= \cos (\alpha x)\sin (\beta y)W(z), p_1 =\cos (\alpha x)\sin (\beta y)P(z) \end{aligned}$$

(13)

where $U,\,V,\,W,\,P$ are amplitude functions to be determined. Then Eqs. (2) and (4) yield the ordinary differential equations

$$\begin{aligned} \begin{aligned} U^{\prime \prime }-\delta ^{2}U&= -\alpha P, V^{\prime \prime }-\delta ^{2}V=\beta P, \\ W^{\prime \prime }-\delta ^{2}W&= P^{\prime }, \alpha U-\beta V+W^{\prime }=0 \end{aligned} \end{aligned}$$

(14)

where

$$\begin{aligned} \delta =\sqrt{\alpha ^{2}+\beta ^{2}+k^{2}} \end{aligned}$$

(15)

The top boundary conditions are

$$\begin{aligned} U(1)=T_k , \; V(1)=0, \; W(1)=0 \end{aligned}$$

(16)

If the bumpiness is in phase, the bottom boundary conditions are

$$\begin{aligned} U(-1)=-T_k , \; V(-1)=0, \; W(-1)=0 \end{aligned}$$

(17)

To simplify the algebra, denote

$$\begin{aligned} \gamma&= \sqrt{\alpha ^{2}+\beta ^{2}}\end{aligned}$$

(18)

$$\begin{aligned} S_\gamma&= \sinh \gamma ,C_\gamma =\cosh \gamma , S_\delta =\sinh \delta , C_\delta =\cosh \delta \end{aligned}$$

(19)

After some work, the solutions are

$$\begin{aligned}&U(z)=\frac{T_k }{S_\delta }\left[ {1+\frac{\alpha ^{2}S_\gamma C_\delta }{\gamma \left(\delta C_\gamma S_\delta -\gamma S_\gamma C_\delta \right)}} \right]\sinh (\delta z)\nonumber \\&\qquad \qquad -\frac{\alpha ^{2}T_k C_\delta }{\gamma \left(\delta C_\gamma S_\delta -\gamma S_\gamma C_\delta \right)}\sinh (\gamma z)\end{aligned}$$

(20)

$$\begin{aligned} V(z)&= \frac{\alpha \beta T_k C_\delta }{\gamma S_\delta \left(\delta C_\gamma S_\delta -\gamma S_\gamma C_\delta \right)}\left[ {S_\delta \sinh (\gamma z)-S_\gamma \sinh (\delta z)} \right]\end{aligned}$$

(21)

$$\begin{aligned} W(z)&= \frac{\alpha T_k }{\left(\delta C_\gamma S_\delta -\gamma S_\gamma C_\delta \right)}\left[ {C_\delta \cosh (\gamma z)-C_\gamma \cosh (\delta z)} \right]\end{aligned}$$

(22)

$$\begin{aligned} P(z)&= -\frac{\alpha T_k C_\delta \left(\gamma ^{2}-\delta ^{2}\right)}{\gamma \left(\delta C_\gamma S_\delta -\gamma S_\gamma C_\delta \right)}\sinh (\gamma z) \end{aligned}$$

(23)

Figure 3 shows the first-order velocity amplitude functions $U(z),V(z),W(z)$. Since $U$ and $V$ are odd and $W$ is even, only the range $0\le z\le 1$ is plotted. It is seen that the porous media parameter greatly depresses the magnitude and changes the shape of these functions.

Fig. 3

a First-order longitudinal function $U(z)$ for in phase case, $\alpha =\beta =1$. From top $k\,=\,0,\,1,\,2,\,5,\,20$. b First-order transverse function $V(z)$for in phase case, $\alpha =\beta =1$. From top $k\,=\,0,\,1,\,2,\,5,\,20$. c First-order transverse function $W(z)$for in phase case, $\alpha =\beta =1$. From top $k\,=\,0,\,1,\,2,\,5,\,20$

If the bumpiness is out of phase, the bottom boundary conditions are

$$\begin{aligned} U(-1)=T_k ,\; V(-1)=0, \; W(-1)=0 \end{aligned}$$

(24)

The solutions are

$$\begin{aligned}&U(z)=\frac{T_k }{C_\delta }\left[ {1+\frac{\alpha ^{2}C_\gamma S_\delta }{\gamma \left(\delta S_\gamma C_\delta -\gamma C_\gamma S_\delta \right)}} \right]\cosh (\delta z)\nonumber \\&\qquad \quad -\frac{\alpha ^{2}T_k S_\delta }{\gamma \left(\delta S_\gamma C_\delta -\gamma C_\gamma S_\delta \right)}\cosh (\gamma z)\end{aligned}$$

(25)

$$\begin{aligned} V(z)&= \frac{\alpha \beta T_k S_\delta }{\gamma \left(\delta S_\gamma C_\delta -\gamma C_\gamma S_\delta \right)}\left[ {\cosh (\gamma z)-\frac{C_\gamma }{C_\delta }\cosh (\delta z)} \right]\end{aligned}$$

(26)

$$\begin{aligned} W(z)&= \frac{\alpha T_k }{\left(\delta S_\gamma C_\delta -\gamma C_\gamma S_\delta \right)}\left[ {S_\delta \sinh (\gamma z)-S_\gamma \sinh (\delta z)} \right]\end{aligned}$$

(27)

$$\begin{aligned} P(z)&= -\frac{\alpha T_k S_\delta \left(\delta ^{2}-\gamma ^{2} \right)}{\gamma \left(\delta S_\gamma C_\delta -\gamma C_\gamma S_\delta \right)}\cosh (\gamma z) \end{aligned}$$

(28)

For the out of phase case, $U$ and $V$ are even and $W$ is odd. The effects of the porous medium parameter $k$ on the functions $U,\,V,\,W$ are shown in Fig. 4 for the out of phase case.

Fig. 4

a First-order longitudinal function $U(z)$ for out of phase case, $\alpha =\beta =1$. From top $k\,=\,0,\,1,\,2,\,5,\,20$. b First-order transverse function $V(z)$for out of phase case, $\alpha =\beta =1$. From top $k\,=\,0,\,1,\,2,\,5,\,20$. c First-order transverse function $W(z)$ for out of phase case, $\alpha =\beta =1$. From top $k\,=\,0,\,1,\,2,\,5,\,20$

4 The Flow Rate

The first-order solution, being periodic in the $y$ direction, would not affect the net flow rate through the channel. Let an over-bar denote the average with respect to the $y$ direction, i.e.,

$$\begin{aligned} \bar{{f}}=\frac{\beta }{2\pi }\int \limits _{-\pi /\beta }^{\pi /\beta } {fdy} \end{aligned}$$

(29)

The normalized volume flow rate per area or mean velocity in the $x$ direction, evaluated at $x$=0 where the cross section is simpler, is

$$\begin{aligned} Q=\frac{1}{2}\int \limits _{-1}^1 {\bar{{u}} \left| {_{x=0} } \right.dz} =\frac{1}{2}\int \limits _{-1}^1 {(\bar{{u}}_0 +\varepsilon ^{2}\bar{{u}}_2 +\cdots )\left| {_{x=0} } \right.dz} \end{aligned}$$

(30)

We see only the $y$-averaged second-order quantities matter in the flow rate. Equations (2) and (4) reduce to

$$\begin{aligned}&\bar{{u}}_{xx}+\bar{{u}}_{zz} -k^{2}\bar{{u}}=\bar{{p}}_x\nonumber \\&\bar{{\upsilon }}_{xx} +\bar{{\upsilon }}_{zz} -k^{2}\bar{{\upsilon }}=0\end{aligned}$$

(31)

$$\begin{aligned}&\bar{{w}}_{xx} +\bar{{w}}_{zz} -k^{2}\bar{{w}}=\bar{{p}}_z\nonumber \\&\bar{{u}}_x +\bar{{w}}_z =0 \end{aligned}$$

(32)

The boundary conditions for the second order are obtained from Eq. (9)

$$\begin{aligned}&\displaystyle u_2 \left| {_1} = -\sin (\alpha x)\sin (\beta y)u_{1z} \Bigg | {_1} -\frac{\left[\sin (\alpha x)\sin (\beta y) \right]^{2}}{2} u_{0zz} \Bigg | {_1 } \right.\nonumber \\&\displaystyle =\frac{1}{4}\left[1-\cos (2\alpha x) \right] \left[1-\cos (2\beta y) \right]\left[ {\frac{1}{2}-U^{\prime }(1)} \right]\end{aligned}$$

(33)

$$\begin{aligned}&\displaystyle \upsilon _2 \left| {_1 =-\frac{1}{4}\sin (2\alpha x)\sin (2\beta y)V^{\prime }(1)} \right.\end{aligned}$$

(34)

$$\begin{aligned}&\displaystyle w_2 \left| {_1 =-\frac{1}{4}\sin (2\alpha x)\left[1-\cos (2\beta y) \right]W^{\prime }(1)} \right. \end{aligned}$$

(35)

Averaging with respect to $y$ gives

$$\begin{aligned}&\displaystyle \bar{{u}}_2 \left| {_1 =\frac{1}{4}[1-\cos (2\alpha x)]\left[ {\frac{1}{2}-U^{\prime }(1)} \right]} \right.\end{aligned}$$

(36)

$$\begin{aligned}&\displaystyle \bar{{\upsilon }}_2 \left| {_1 =0} \right.\end{aligned}$$

(37)

$$\begin{aligned}&\displaystyle \bar{{w}}_2 \left| {_1 =-\frac{1}{4}\sin (2\alpha x)W^{\prime }(1)} \right. \end{aligned}$$

(38)

For the bottom boundary conditions, whether in phase or out of phase, we find similarly

$$\begin{aligned}&\displaystyle \bar{{u}}_2 \left| {_{-1} =\frac{1}{4}[1-\cos (2\alpha x)]\left[ {\frac{1}{2}-U^{\prime }(1)} \right]} \right.\end{aligned}$$

(39)

$$\begin{aligned}&\bar{{\upsilon }}_2 \left| {_{-1} =0} \right.\end{aligned}$$

(40)

$$\begin{aligned}&\displaystyle \bar{{w}}_2 \left| {_{-1} =-\frac{1}{4}\sin (2\alpha x)W^{\prime }(1)} \right. \end{aligned}$$

(41)

Equations (36), (37), (38), (39), (40) and (41) imply the forms

$$\begin{aligned} \bar{{u}}_2 =A(z)+B(z)\cos (2\alpha x), \; \bar{{\upsilon }}_2 =0, \; \bar{{w}}_2 =D(z)\sin (2\alpha x) \end{aligned}$$

(42)

Let

$$\begin{aligned} K_1 =-\frac{1}{4}\left( {\frac{1}{2}-U^{\prime }(1)} \right), \quad K_2 =-\frac{1}{4}W^{\prime }(1) \end{aligned}$$

(43)

The solutions to Eqs. (31) and (32) are

$$\begin{aligned} \begin{aligned}&A(z)=-K_1 \frac{\cosh (kz)}{\cosh k}, \; B(z)=b_1 \cosh (2\alpha z)+b_2 \cosh (\sqrt{\lambda }z) \\&D(z)=2\alpha \left[ {\frac{b_1 }{2\alpha }\sinh (2\alpha z)+\frac{b_2 }{\sqrt{\lambda }}\sinh (\sqrt{\lambda }z)} \right] \end{aligned} \end{aligned}$$

(44)

where $\lambda =4\alpha ^{2}+k^{2}$ and

$$\begin{aligned} b_1 =\frac{2\alpha \sinh \sqrt{\lambda }K_1 -\sqrt{\lambda }\cosh \sqrt{\lambda }K_2 }{2\alpha \cosh (2\alpha )\sinh \sqrt{\lambda }-\sqrt{\lambda }\cosh \sqrt{\lambda }\sinh (2\alpha )},\; b_2 =\frac{K_1 -b_1 \cosh (2\alpha )}{\cosh \sqrt{\lambda }} \end{aligned}$$

(45)

Equation (30) shows the zeroth-order flow rate is

$$\begin{aligned} Q_0 =\frac{1}{2}\int \limits _{-1}^1 {\bar{{u}}_0 dz} =\frac{1}{k^{2}}\left( {1-\frac{\sinh k}{k\cosh k}} \right) \end{aligned}$$

(46)

This is plotted in Fig. 5 showing the rapid decrease of the flow as $k$ is increased. When $k\,=\,0$ (clear fluid) the normalized flow rate is 1/3. The effect of bumpiness is reflected in the second order. Equation (30) is written as

$$\begin{aligned} Q=Q_0 \left[ {1-\varepsilon ^{2}\chi +O\left(\varepsilon ^{4} \right)} \right] \end{aligned}$$

(47)

where $\varepsilon ^{2}\chi$ is the percentage decrease in flow due to bumpiness of the walls. Since the pressure gradient is held fixed, it also represents the percentage increase in resistance due to the bumpiness. After some work, we find

$$\begin{aligned} \chi&= \frac{k^{2}}{(1-T_k )}\left[ {T_k K_1 -a_1 \frac{\sinh \sqrt{\lambda }}{\sqrt{\lambda }}-b_1 \frac{\sinh (2\alpha )}{2\alpha }} \right]\nonumber \\&= \frac{k^{2}}{(1-T_k )}\left( {T_k K_1 -\frac{K_2 }{2\alpha }} \right) \end{aligned}$$

(48)

Equation (48) is valid for both in phase or out of phase cases. The difference is in the form of $K{ }_1$. Let

$$\begin{aligned} T_\gamma =\frac{\sinh \gamma }{\gamma \cosh \gamma }, \quad T_\delta =\frac{\sinh \delta }{\delta \cosh \delta } \end{aligned}$$

(49)

For the in phase case, from Eqs. (20) and (43) we find

$$\begin{aligned} K_1 =-\frac{1}{4}\left\{ {\frac{1}{2}-\frac{T_k \left[(\delta ^{2}-\alpha ^{2})T_\delta -\beta ^{2}T_\gamma \right]}{T_\delta (\delta ^{2}T_\delta -\gamma ^{2}T_\gamma )}} \right\} \end{aligned}$$

(50)

For the out of phase case, from Eqs. (25) and (43) we find

$$\begin{aligned} K_1 =-\frac{1}{4}\left\{ {\frac{1}{2}-\frac{T_k \left[\beta ^{2}\delta ^{2}T_\delta ^{2}+\gamma ^{2}(\alpha ^{2}-\delta ^{2})T_\delta T_\gamma \right]}{\gamma ^{2}(T_\delta -T_\gamma )}} \right\} \end{aligned}$$

(51)

In both cases

$$\begin{aligned} K_2 =\frac{\alpha T_k }{4} \end{aligned}$$

(52)

As $k\rightarrow 0$ the asymptotic limits of Eq. (48) are

$$\begin{aligned} \chi \sim \frac{3\cosh ^{2}\gamma \left[\alpha ^{2}+\beta ^{2}\gamma \coth \gamma -(1+\beta ^{2})\gamma \tanh \gamma +\gamma ^{2}\tanh ^{2}\gamma \right]}{2\gamma \sinh (2\gamma )+4\gamma ^{2}} \end{aligned}$$

(53)

for the in phase case and

$$\begin{aligned} \chi \sim \frac{3\sinh ^{2}\gamma \left[\alpha ^{2}+\beta ^{2}\gamma \tanh \gamma -(1+\beta ^{2})\gamma \coth \gamma +\gamma ^{2}\coth ^{2}\gamma \right]}{2\gamma \sinh (2\gamma )-4\gamma ^{2}} \end{aligned}$$

(54)

for the out of phase case. These expressions agree with the clear fluid problem studied by Wang (2004). In the Darcy limit $k\rightarrow \infty$, the asymptotic forms are

$$\begin{aligned} \chi =\frac{\alpha ^{2}\tanh \gamma }{4\gamma }+\frac{1}{8}\left[ {\beta ^{2}-\alpha ^{2}+2\alpha ^{2}\tanh \gamma \left( {\frac{1}{\gamma }+\tanh \gamma } \right)} \right]\frac{1}{k}+O\left( {\frac{1}{k^{2}}} \right) \end{aligned}$$

(55)

for the in phase case and

$$\begin{aligned} \chi =\frac{\alpha ^{2}\coth \gamma }{4\gamma }+\frac{1}{8}\left[ {\beta ^{2}-\alpha ^{2}+2\alpha ^{2}\coth \gamma \left( {\frac{1}{\gamma }+\coth \gamma } \right)} \right]\frac{1}{k}+O\left( {\frac{1}{k^{2}}} \right) \end{aligned}$$

(56)

for the out of phase case. The first terms on the right hand sides of Eqs. (55) and (56) represent the effect of bumpiness on the flow through a Darcy medium, deduced here for the first time. Figure 6 shows the function $\chi$ as $\beta$ is varied for various constant $\alpha$. Since the function tanh is smaller than coth, the out of phase case has larger flow decrease or resistance than the in phase case. However, for large $\gamma$ or small wavelengths, the differences become negligible.

Fig. 5

The primary flow $Q_0$ as a function of porous media factor $k$. Note the rapid decrease in flow as $k$ is increased (decreased permeability)

Fig. 6

$\chi$as a function of $\beta$ for Darcy flow ($k\rightarrow \infty )$. From bottom $\alpha =1, 2, 3$. Solid curves represent the in phase case, dashed curves represent the out of phase case

For general $k$ the function $\chi$is more complex. Figure 7 show the effect as $k$ is increased from zero. The solid curves are for $k\,=\,0$, the clear fluid case, and they agree with those of Wang (2004). For the in phase case, the porous media factor lowers the percentage decrease in flow (or resistance). For the out of phase case, the effect is mixed. For large $\alpha$, the function $\chi$ is decreased. For small $\alpha$ (long wave lengths in the flow direction) and $k\,=\,0,\,\chi$ is negative, showing an increased flow due to the larger longitudinal pores (of the out of phase case), which more than compensates for the decrease in flow elsewhere. The porous media parameter suppresses this phenomenon of relative increase in flow.

Fig. 7

a $\chi$as a function of $\beta$, in phase case. Bottom curves $\alpha =0$, top curves $\alpha =2$. Solid curves $k\,=\,0$, dashed curves $k\,=\,1$, dot-dashed curves $k\,=\,2$. b $\chi$as a function of $\beta$, out of phase case. Bottom curves $\alpha =0$, top curves $\alpha =2$. Solid curves $k$=0, dashed curves $k\,=\,1$, dot-dashed curves $k\,=\,2$

5 Results and Discussions

The present paper studies the effect of rough or bumpy walls on the flow through a channel filled with a porous medium. We used the Darcy-Brinkman equation, which is well accepted by most researchers in this field. The inertial nonlinear Forchheimer term is not included. The reason is that for low speed applications such as filters, heat exchangers, catalytic converters that term is usually negligible (Khodadadi 1991). Furthermore, we are modeling bumpiness due to surface roughness, which has been magnified by the small size of the channel. In such micro-fluidics the Reynolds number is so small ($O(10^{-3})$ or smaller) that inertial effects are essentially absent.

The effective viscosity of the matrix $\mu _{\text{ e}}$ occurs in the definition of the porous media parameter $k$ and also used in the normalization of the velocity. Our normalized equations (and results) are independent of $\mu _{\text{ e}}$. The value of $\mu _{\text{ e}}$ may be larger or smaller than $\mu$, but they are about the same order of magnitude, and many researchers simply assumed they are equal. See a discussion by Breugem (2007). In this paper we have carefully kept their distinction. The ratio of viscosities only affects the parameter $k$, but not by much.

The problem is governed by the amplitude, wavelength and phase of the bumps and also the important porous media parameter $k$ which is proportional to the inverse square root of the Darcy number or permeability. Perturbation solutions are obtained up to the second order of the small bumpy amplitude to half channel width ratio $\varepsilon$. As $k\rightarrow 0$ our solutions reduce to the clear fluid limit and as $k\rightarrow \infty$ our solutions reduce to the Darcy limit, the latter developed here for the first time.

We perturbed from the smooth plate solution given by Eq. (7), which is also the zeroth-order solution. Figure 2 shows that when the porous medium parameter $k$ is zero, the velocity profile is parabolic (clear fluid flow). An increase in $k$ decreases and flattens the unidirectional primary velocity profile. For large $k$, the velocity profile becomes blunted, and the effects of the wall only extend in a thin layer near the boundary. Consequently, the wall resistance contributes little to the total resistance which is mainly due to the porous medium. In these cases the Darcy equation (without the Brinkman term) is adequate. Note that in our applications, $k$ could be small, even for small permeability, due to small the gap width. For example the length scale $L$ in Eq. (3) could be in $\upmu m$.

The first-order solutions give the complicated three-dimensional corrections. Figures 3 and 4 are the amplitude functions for the three velocity components. Two observations could be made. First, an increase in $k$ (or decrease in permeability) the first- order flow perturbations are suppressed. This is in agreement with the Darcy limit, where the wall effects, including those due bumpiness, become negligible. Second, there is a difference whether the bumpiness of the top plate and the bottom plate is in phase or out of phase. Note the different forms and scales of these functions.

The primary flow rate (zeroth order flow rate) is given by Eq. (46) and shown in Fig. 5. We see the almost exponential decrease in flow rate as $k$ is increased. The flow rate is inversely proportional to the channel resistance for a given pressure gradient. From Fig. 5 we conclude, to within 5 % error, the clear fluid limit can be used if $k<0.35$ and the Darcy limit can be used if $k >7.5$. In between these values the Darcy-Brinkman equation should be used.

The second-order perturbation solutions yield the decrease in flow (or increase in resistance) due to the bumpiness, represented by $\varepsilon ^{2}\chi$. The decrease in flow is proportional to the square of the amplitude of the bumpiness, multiplied by an important function $\chi$ which depends on not only $k$ but also the wavelengths and phase differences of the bumps. From Figs. 6 and 7 we see in general, that the out of phase case has larger $\chi$ than the in phase case, except at long axial wavelengths (low $\alpha$) situations, where $\chi$ may become negative. The influence of the longitudinal wavelength $\alpha$ is much larger than that of the transverse wavelength $\beta$, since the longitudinal direction is aligned with the primary flow. Increase in $k$ decreases the effect of bumpiness through $\chi$.

Since the Darcy-Brinkman equations are linear, in the case the pressure gradient is not aligned with the bumpiness, one can decompose the pressure gradient two orthogonal aligned pressure gradients and superpose the solutions.

To apply our results, first determine the porous medium parameter $k$ through the size of the channel and the permeability. The geometry of the bumps (amplitude, wavelengths, orientation) can be obtained through microscopic observation. Our solution Eqs. (47) and (48) then give the flow rate, or inversely the resistance, of the porous bumpy channel.

The effect of surface bumpiness on the flow through a channel filled with a porous medium is studied. The results are important for micro channels where surface roughness cannot be ignored. In general, we find an increase in flow resistance depending on the relative geometry of the bumps and the porous media factor.