1 Introduction

The effect of irregularities on heat and flow characteristics in channels and tubes has been extensively studied in the literature. One of such studies is the pioneering work of Chow and Soda (1973), in which they investigate the abnormal flow conditions caused by the boundary irregularities in diseased blood vessels. In early studies by Wang (1976, 1979), Stokes’ flow between two corrugated plates was considered. It was found that the flow rate enhancement is a function of the frequency and the relative phase shift of the corrugations. Thus, by varying the relative phase shift, one can, to a limited extent, control the flow through corrugated plates. However, corrugated channels and tubes have long been used in augmentation of heat and mass transfer; see for example Bergles (1988). Wang’s (1976, 1979) results for the flows transverse and parallel to the corrugations have since been extended by Phan-Thien (1980, 1981a, b) to channels and tubes with stationary random surface roughness. Wang’s previous work on corrugated walls has been also extended to three-dimensional bumpy channel (Wang 2006) and bumpy tubes (Wang 2004). Recently, much interest has been found in microflows (Kariandakis and Beskok 2002), basically due to the tiny sizes of flow devices used for manipulating fluids in micromachines. Microchannels exist in the most important part of such systems. The wall irregularities can play a basic role in microchannels (Shen et al. 2006). More recently, Faltas et al. (2017) extend the work of Phan–Thien’s (1981b) to microannuli cylindrical tubes filled with porous medium, allowing for a partial slip at solid boundaries of the annuli.

Another interesting context involving similar problems is the viscous flow through sinusoidal corrugated channels and tubes filled with a porous medium, e.g., Wang (2010), Ng and Wang (2010) and Wang and Yu (2015). Examples of tubes filled with porous medium are many, such as those in filters, catalytic reactors or matrix-filled biological pores. The study of the flow in a channel filled with a porous medium is necessary in the prediction of the various transport properties of porous media. The Brinkman equation (Brinkman 1947) has usually been used as a model for a porous medium. Brinkman equation can be established theoretically by averaging the Stokes flow past a suspension of spherical particles (Tam 1969; Lundgren 1972) or by using renormalization techniques of the Stokes equation for fluid motion past a random assemblage of particles or cylindrical fibers (Howells 1974, 1998). The Brinkman equation is relevant in the low solid fraction limit (Durlofsky and Brady 1987; Phillips et al. 1990). However, in the case of low solid fraction, Allaire (1990) used the method of periodic homogenization to derive Brinkman equations from Stokes equation. In his analysis, the value of the permeability parameter k is determined as the product of the fluid viscosity and a matrix M which is determined by means of the solutions of Stokes problems on the standard periodicity cell. Thus, M takes into account the geometry of the porous medium.

The Brinkman equation has a Newtonian viscous drag term and a Darcy drag term which together balance the pressure gradient. Brinkman equation includes only one parameter characterizing the permeability of the porous medium. Once the permeability has been determined, no need to know knowledge about the detailed structure of the porous media. The dynamic viscosity, \(\tilde{\mu }\), of the fluid constituent in the porous medium which is associated with the viscous drag term in the Brinkman equation is called the effective viscosity. The effective viscosity \(\tilde{\mu }\) is a complicated function of local pore characteristics and fluid viscosity \(\mu .\)Brinkman (1947) proposed that for a high-porosity medium composed of spheres, the effective viscosity can be approximated by Einstein’s formula (Einstein 1956), \(\tilde{\mu }/\mu =1+5\phi /2\), where \(\phi \) is the solid fraction. For low solid fraction, \(\tilde{\mu }\cong \mu \) (Wang and Yu 2015; Lundgren 1972). Later studies indicated that \(\tilde{\mu }\) may be smaller or larger than \(\mu \), depending on the porosity and the type of porous medium (Brinkman 1947; Neale and Nader 1974; Koplik et al. 1983; Kim and Russel 1985; Larson and Higdon 1987; Martys et al. 1994). King (2007) has compared the predictions of the Stokes flow theory for three-dimensional bumpy tubes developed by Wang (2006) to histological measurements of human capillaries and arterioles. It is found that these microvessels exhibit nearly optimal geometry for minimizing the overall flow resistance. The theoretical result that there exists an optimal circumferential wave number which minimizes the flow resistance in capillaries and arterioles with bumpy walls has important implications in the field of tissue engineering. The conclusions of King (2007) motivated us to extend Wang’s (2006) results to Darcy–Brinkman flow through a three-dimensional bumpy tube.

Fig. 1
figure 1

The schematic diagrams of a bumpy tube (\(\epsilon =0.1,\,\alpha =5,\,\beta =3\))

Full size image

In this paper, the problem of flow through a sinusoidal bumpy tube filled with a porous medium is considered. The porous medium is modeled by Brinkman equation with no-slip boundary condition on the lateral surface of the tube. Using a perturbation method with respect to the normalized amplitude of corrugations \((\epsilon \ll 1),\) a closed form of the mean flow rate is obtained in terms of the modified Bessel functions, up to second order in \(\epsilon .\) The mean flow rate approximation depends on the permeability of the medium, the area of a bump and the wave number parameters. In the last part of this paper, the derived approximations are used to study the dependence of the solution on the permeability parameter and the dependence of the mean flow rate on the parameters of the problem. A comparison is made between the results of the present study for clear fluid and the results of Wang (2006) and also between our results and the results of Darcy’s model obtained by Wang and Yu (2015).

2 Mathematical Formulation

In the present mathematical model, we consider the steady flow through a porous structure that is governed by Brinkman equation (Brinkman 1947). The flow is within an infinitely long cylindrical wall with periodic bumps described by

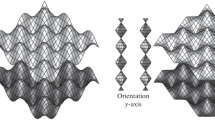
$$\begin{aligned} r'=a+b\,\sin (\alpha \,\theta )\,\sin (2\pi z'/\ell ), \end{aligned}$$
(2.1)

where \((r',\theta ,z')\) are cylindrical coordinates in \(\mathbb {R}^3\), a is the mean radius of the tube, b is the amplitude of the pumps, \(\alpha \) is circumferential wave number and has to be an integer to satisfy the \(2\pi \) periodicity of the annular walls, and \(\ell \) is the longitudinal wavelength (Fig. 1). The tube is filled with a sparse porous material so that the flow can be described by the Darcy–Brinkman model, which tends to the Darcian or Stokes flow limits for small or large permeability of the medium. The Reynolds number is also assumed to be so low that the inertia term can be ignored. Before presenting the equations of motion, it is convenient to non-dimensionalize the coordinates (unprimed) in terms of the dimensional (primed) coordinates as \(r=r'/a,\,z'=z/a,\) such that the dimensionless amplitude of the bumps becomes \(\epsilon =b/a,\) where \(\epsilon \) is a small parameter describing the fact that the amplitude of the oscillations is much smaller than the mean radius of the tube, so that only slight bumps are considered. This small amplitude will be used as a perturbation parameter for the considered problem. The velocity components are expressed in dimensionless form using the mean axial pressure gradient G and the effective viscosity \(\tilde{\mu }\) as

$$\begin{aligned} \vec {u}=\frac{\tilde{\mu }\,\vec {u'}}{G\,a^2}. \end{aligned}$$
(2.2)

The field equations governing an incompressible steady viscous fluid flow through a bumpy tube filled with porous medium according to Darcy–Brinkman model in the absence of body forces under the Stokesian assumption are given in vector forms as

$$\begin{aligned} \nabla \cdot \vec {q}=0,\quad \nabla p+\frac{\mu }{K}\,\vec {q}-\tilde{\mu }\,\nabla ^2\vec {q}=0, \end{aligned}$$
(2.3)

where \(\nabla \) is the gradient operator, \(\vec {q}\) is the volume averaged velocity, p is the pore average pressure, \(\tilde{\mu }\) represents the effective viscosity, and K is the permeability of the porous medium. The permeability K is a scalar for isotropic porous medium; otherwise, K is a second-order tensor (Kaviany 2012). This model has two viscous terms; the first is the usual Darcy term, and the second is analogous to the Laplacian term that appears in the Navier–Stokes equation. This equation is well accepted for porous media of high porosity. When the permeability of the medium is small, \(K\ll 1,\) the viscous term can be neglected and the Darcy–Brinkman equation reduces to Darcy’s law. On the other hand, in the limit of large permeability, \(K\rightarrow \infty ,\) the Brinkman equation reduces to the Stokes equation. Both the continuity and Brinkman equations are actually volume averaged formulations. Let (u, v, w) be velocity components in the dimensionless cylindrical directions \((r,\theta ,z)\), respectively. In terms of velocity components, equations (2.3) become

$$\begin{aligned}&\frac{1}{r}\,\frac{\partial ru}{\partial r}+\frac{1}{r}\,\frac{\partial v}{\partial \theta }+\frac{\partial w}{\partial z}=0,\end{aligned}$$
(2.4)
$$\begin{aligned}&\nabla ^2u-\frac{u}{r^2}-\frac{2}{r^2}\,\frac{\partial v}{\partial \theta }-k^2u=\frac{\partial p}{\partial r},\end{aligned}$$
(2.5)
$$\begin{aligned}&\nabla ^2v-\frac{v}{r^2}+\frac{2}{r^2}\,\frac{\partial u}{\partial \theta }-k^2v=\frac{1}{r}\,\frac{\partial p}{\partial \theta },\end{aligned}$$
(2.6)
$$\begin{aligned}&\nabla ^2w-k^2w=\frac{\partial p}{\partial z}, \end{aligned}$$
(2.7)

where \(k=\sqrt{\mu a^2/(K\tilde{\mu })}\) is a parameter characterizing the porous medium. The parameter k can be defined in terms of Darcy number as \(k=Da^{-1/2}.\) As \(k\rightarrow 0\), the flow reduces to Stokes limit, while for \(k\gg 1\) the flow reduces to Darcian limit.

The no-slip boundary conditions on the lateral surface are

$$\begin{aligned} u=v=w=0,\quad \text {at}\quad r=1+\epsilon \,\sin (\alpha \,\theta )\,\sin (\beta \,z), \end{aligned}$$
(2.8)

where \(\beta =2\pi /(\ell a)\ne 0.\) Also the velocity components must be finite at the axis of the tube.

2.1 Method of Solution

Using a perturbation argument with respect to the small parameter \(\epsilon ,\) the components of velocity and the pressure can be expanded for small \(\epsilon \) as:

$$\begin{aligned} (u\;v\;w\;p)=(u_0\;v_0\;w_0\;p_0)+(u_1\;v_1\;w_1\;p_1)\,\epsilon +(u_2\;v_2\;w_2\;p_2)\,\epsilon ^2+\cdots . \end{aligned}$$
(2.9)

On the boundary of the tube, any function \(f(r,\theta \,z)\) can be expanded about \(r=1\) as

$$\begin{aligned} f|_{r=1+\epsilon \,g}=f_0|_1+\epsilon \,(f_1|_1+g\,f_{0r}|_1)+\epsilon ^2 \left( f_2|_1+g\,f_{1r}|_1+g^2f_{0rr}|_1/2 \right) +\cdots , \end{aligned}$$
(2.10)

where \(g=\,\sin (\alpha \,\theta )\,\sin (\beta \,z).\)

  1. (i)

    \({\varvec{\epsilon }}^{\mathbf {0}}\)–solution

The zero solution is the usual Poiseuille flow in a smooth tube:

$$\begin{aligned} w_0(r)=\frac{1}{k^2}\,\left( 1-\frac{I_0(k\,r)}{I_0(k)}\,\right) ,\quad u_0,\quad v_0=0,\quad p_0=-z, \end{aligned}$$
(2.11)

where \(I_n\) is the modified Bessel function of the first kind of order n.

  1. (ii)

    \({\varvec{\epsilon }}^{\mathbf {1}}\)–solution

The differential equations satisfied by the first-order solution are the same as (2.4)–(2.7) with \((u\;v\;w\;p)\) replaced by \((u_1\;v_1\;w_1\;p_1)\) subject to the boundary condition:

$$\begin{aligned} u_1|_1=0,\;v_1|_1=0,\;w_1|_1=\frac{I_1(k)}{k\,I_0(k)}\,\sin (\alpha \,\theta )\,\sin (\beta \,z) \end{aligned}$$
(2.12)

In view of boundary conditions and the continuity equation, for the first-order solution let

$$\begin{aligned} \begin{array}{ll} u_1=U\,\sin (\alpha \,\theta )\,\cos (\beta \,z), &{} v_1=V\,\cos (\alpha \,\theta )\,\cos (\beta \,z), \\ w_1=W\,\sin (\alpha \,\theta )\,\sin (\beta \,z), &{} p_1=P\,\sin (\alpha \,\theta )\,\cos (\beta \,z). \end{array} \end{aligned}$$
(2.13)

where \(U,\,V,\,W,\,P\) are functions of r to be determined. Substituting from (2.13) into (2.4)–(2.7), we get the following set of differential equation for determining the amplitude functions:

$$\begin{aligned}&\frac{\mathrm{d}U}{\mathrm{d}r}+\frac{U}{r}-\frac{\alpha \,V}{r}+\beta \,W=0,\end{aligned}$$
(2.14)
$$\begin{aligned}&\frac{\mathrm{d}^2U}{\mathrm{d}r^2}+\frac{1}{r}\,\frac{\mathrm{d}U}{\mathrm{d}r}-\left( \frac{1+\alpha ^2}{r^2}+\lambda ^2\right) U+\frac{2\alpha \,V}{r^2}=\frac{\mathrm{d}P}{\mathrm{d}r},\end{aligned}$$
(2.15)
$$\begin{aligned}&\frac{\mathrm{d}^2V}{\mathrm{d}r^2}+\frac{1}{r}\,\frac{\mathrm{d}V}{\mathrm{d}r}-\left( \frac{1+\alpha ^2}{r^2}+\lambda ^2\right) V+\frac{2\alpha \,U}{r^2}=\frac{\alpha }{r}\,P,\end{aligned}$$
(2.16)
$$\begin{aligned}&\frac{\mathrm{d}^2W}{\mathrm{d}r^2}+\frac{1}{r}\,\frac{\mathrm{d}W}{\mathrm{d}r}-\left( \frac{\alpha ^2}{r^2}+\lambda ^2\right) W=-\beta \,P, \end{aligned}$$
(2.17)

where \(\lambda ^2=\beta ^2+k^2,\) and with the boundary conditions

$$\begin{aligned} U|_1=0,\;V|_1=0,\;W|_1=\frac{I_1(k)}{k\,I_0(k)}. \end{aligned}$$
(2.18)

Eliminating \(U,\,V,\,W\) from the set of differential equations (2.14)–(2.17), we find that after much algebraic manipulation, the differential equation satisfied by the amplitude pressure function is

$$\begin{aligned} r^2\frac{\mathrm{d}^2P}{\mathrm{d}r^2}+r\,\frac{\mathrm{d}P}{\mathrm{d}r}-(\alpha ^2+\beta ^2r^2)P=0. \end{aligned}$$
(2.19)

The bounded solution of equation (2.19) is

$$\begin{aligned} P(r)=A\,I_\alpha (\beta \,r), \end{aligned}$$
(2.20)

where A is a constant. If we define the Bessel operator as

$$\begin{aligned} B_\alpha =r^2\frac{\mathrm{d}^2}{\mathrm{d}r^2}+r\,\frac{\mathrm{d}}{\mathrm{d}r}-(\alpha ^2+\lambda ^2r^2), \end{aligned}$$

then the set of differential equations (2.14)–(2.17) has the simplest form

$$\begin{aligned}&B_\alpha \,U-(U-2\alpha \,V)=r^2\frac{\mathrm{d}^2P}{\mathrm{d}r^2},\end{aligned}$$
(2.21)
$$\begin{aligned}&B_\alpha \,V-(V-2\alpha \,U)=\alpha \,r\,P,\end{aligned}$$
(2.22)
$$\begin{aligned}&B_\alpha \,W=-\beta \,r^2P. \end{aligned}$$
(2.23)

Let \(F=U-V\) and \(G=U+V,\) therefore coupled differential equations (2.21) and (2.22) become

$$\begin{aligned}&B_{\alpha +1}\,F=A\,\beta \,r^2I_{\alpha -1}(\beta \,r),\end{aligned}$$
(2.24)
$$\begin{aligned}&B_{\alpha -1}\,G=A\,\beta \,r^2I_{\alpha +1}(\beta \,r). \end{aligned}$$
(2.25)

The bounded general solutions of (2.23), (2.24) and (2.25) are, respectively, as

$$\begin{aligned} W= & {} B\,I_{\alpha }(\lambda \,r)+A\,\beta \,k^{-2}I_{\alpha }(\beta \,r),\end{aligned}$$
(2.26)
$$\begin{aligned} G= & {} C\,I_{\alpha +1}(\lambda \,r)-A\,\beta \,k^{-2}I_{\alpha +1}(\beta \,r),\end{aligned}$$
(2.27)
$$\begin{aligned} F= & {} D\,I_{\alpha -1}(\lambda \,r)-A\,\beta \,k^{-2}I_{\alpha -1}(\beta \,r). \end{aligned}$$
(2.28)

Thus

$$\begin{aligned} 2U(r)= & {} D\,I_{\alpha -1}(\lambda \,r)-A\,\beta \,k^{-2}\bigl (I_{\alpha -1}(\beta \,r)+I_{\alpha +1}(\beta \,r)\bigr )+C\,I_{\alpha +1}(\lambda \,r),\end{aligned}$$
(2.29)
$$\begin{aligned} 2V(r)= & {} D\,I_{\alpha -1}(\lambda \,r)-A\,\beta \,k^{-2}\bigl (I_{\alpha -1}(\beta \,r)-I_{\alpha +1}(\beta \,r)\bigr )-C\,I_{\alpha +1}(\lambda \,r). \end{aligned}$$
(2.30)

Using boundary conditions (2.18) and with the aid of the continuity equation, the unknown coefficients are determined as:

$$\begin{aligned} A= & {} \frac{-2k}{\Delta }\,I_{\alpha +1}(\lambda )\,I_{\alpha -1}(\lambda )\,I_{1}(k),\end{aligned}$$
(2.31)
$$\begin{aligned} B= & {} \frac{\lambda \,I_{1}(k)}{k\,\Delta }\left( I_{\alpha -1}(\lambda )\,I_{\alpha +1}(\beta )+I_{\alpha -1}(\beta )\,I_{\alpha +1}(\lambda )\right) ,\end{aligned}$$
(2.32)
$$\begin{aligned} C= & {} \frac{-2\beta }{k\,\Delta }\,I_{\alpha -1}(\lambda )\,I_{1}(k)\,I_{\alpha +1}(\beta ),\end{aligned}$$
(2.33)
$$\begin{aligned} D= & {} \frac{-2\beta }{k\,\Delta }\,I_{\alpha +1}(\lambda )\,I_{1}(k)\,I_{\alpha -1}(\beta ), \end{aligned}$$
(2.34)

where

$$\begin{aligned} \Delta =I_{0}(k)\Bigl (\lambda \,I_{\alpha }(\lambda )\left( I_{\alpha -1}(\lambda )\,I_{\alpha +1}(\beta )+I_{\alpha -1}(\beta )\,I_{\alpha +1}(\lambda )\bigr )-2\beta \,I_{\alpha }(\beta )\,I_{\alpha -1}(\lambda )\,I_{\alpha +1}(\lambda )\right) . \end{aligned}$$
  1. (iii)

    \({\varvec{\epsilon }}^{\mathbf {2}}\)–solution

Again the differential equations satisfied by the second-order solution are the same as (2.4)–(2.7) with \((u\;v\;w\;p)\) replaced by \((u_2\;v_2\;w_2\;p_2)\) subject to the boundary conditions:

$$\begin{aligned} u_2|_1= & {} -\frac{1}{4}[1-\cos (2\alpha \theta )]\,\sin (2\beta z)\,U_r|_1,\end{aligned}$$
(2.35)
$$\begin{aligned} v_2|_1= & {} -\frac{1}{4}\sin (2\alpha \theta )\,\sin (2\beta z)\,V_r|_1,\end{aligned}$$
(2.36)
$$\begin{aligned} w_2|_1= & {} -\frac{1}{2}[1-\cos (2\alpha \theta )]\,\sin ^2(\beta z)\Bigl (W_r|_1+\frac{w_{0rr}|_1}{2}\Bigr ). \end{aligned}$$
(2.37)

Here, we limit our attention to the mean second-order solution. Let the over bar denote the mean with respect to \(\theta \). Therefore, the differential equations satisfied by the mean second order with respect to \(\theta \) are as follows

$$\begin{aligned}&\frac{1}{r}\,\frac{\partial r\,\bar{u}_2}{\partial r}+\frac{\partial \bar{w}_2}{\partial z}=0,\end{aligned}$$
(2.38)
$$\begin{aligned}&\frac{\partial ^2\bar{u}_2}{\partial r^2}+\frac{1}{r}\,\frac{\partial \bar{u}_2}{\partial r}+\frac{\partial ^2\bar{u}_2}{\partial z^2}-\left( \frac{1}{r^2}+k^2\right) \bar{u}_2=\frac{\partial \bar{p}_2}{\partial r},\end{aligned}$$
(2.39)
$$\begin{aligned}&\frac{\partial ^2\bar{v}_2}{\partial r^2}+\frac{1}{r}\,\frac{\partial \bar{v}_2}{\partial r}+\frac{\partial ^2\bar{v}_2}{\partial z^2}-\Big (\frac{1}{r^2}+k^2\Big )\bar{v}_2=0,\end{aligned}$$
(2.40)
$$\begin{aligned}&\frac{\partial ^2\bar{w}_2}{\partial r^2}+\frac{1}{r}\,\frac{\partial \bar{w}_2}{\partial r}+\frac{\partial ^2\bar{w}_2}{\partial z^2}-k^2\bar{w}_2=\frac{\partial \bar{p}_2}{\partial z}, \end{aligned}$$
(2.41)

with boundary conditions

$$\begin{aligned} \bar{u}_2|_1= & {} -\frac{1}{4}\sin (2\beta z)\,U_r|_1,\end{aligned}$$
(2.42)
$$\begin{aligned} \bar{v}_2|_1= & {} 0,\end{aligned}$$
(2.43)
$$\begin{aligned} \bar{w}_2|_1= & {} -\frac{1}{4}[1-\cos (2\beta z)]\Bigl (W_r|_1+\frac{w_{0rr}|_1}{2}\Bigr ). \end{aligned}$$
(2.44)

We suggest solutions of the above system of equations as follows:

$$\begin{aligned} \bar{u}_2= & {} X(r)\sin (2\beta z),\end{aligned}$$
(2.45)
$$\begin{aligned} \bar{v}_2= & {} 0,\end{aligned}$$
(2.46)
$$\begin{aligned} \bar{w}_2= & {} Y(r)+Z(r)\cos (2\beta z),\end{aligned}$$
(2.47)
$$\begin{aligned} \bar{p}_2= & {} \Pi (r)\sin (2\beta z). \end{aligned}$$
(2.48)

Thus the problem reduces to the solution of the following differential equation:

$$\begin{aligned}&\frac{\mathrm{d}X}{dr}+\frac{X}{r}-2\beta \,Z=0,\end{aligned}$$
(2.49)
$$\begin{aligned}&\frac{\mathrm{d}^2X}{\mathrm{d}r^2}+\frac{1}{r}\,\frac{\mathrm{d}X}{\mathrm{d}r}-\left( \frac{1}{r^2}+\delta ^2\right) X=\frac{\mathrm{d}\Pi }{\mathrm{d}r},\end{aligned}$$
(2.50)
$$\begin{aligned}&\frac{\mathrm{d}^2Y}{\mathrm{d}r^2}+\frac{1}{r}\,\frac{\mathrm{d}Y}{\mathrm{d}r}-k^2Y=0,\end{aligned}$$
(2.51)
$$\begin{aligned}&\frac{\mathrm{d}^2Z}{\mathrm{d}r^2}+\frac{1}{r}\,\frac{\mathrm{d}Z}{\mathrm{d}r}-\delta ^2Z=2\beta \,\Pi , \end{aligned}$$
(2.52)

where \(\delta ^2=4\beta ^2+k^2,\) with the following boundary conditions

$$\begin{aligned} X|_1=-\frac{1}{4}U_r|_1,\quad Y|_1=-\frac{1}{4}\left( W_r|_1+\frac{w_{0rr}|_1}{2}\right) ,\quad Z|_1=\frac{1}{4}\left( W_r|_1+\frac{w_{0rr}|_1}{2}\right) . \end{aligned}$$
(2.53)

It can be shown that the amplitude pressure \(\Pi \) satisfies the differential equation

$$\begin{aligned} \frac{\mathrm{d}^2\Pi }{\mathrm{d}r^2}+\frac{1}{r}\,\frac{\mathrm{d}\Pi }{\mathrm{d}r}-4\beta ^2\Pi =0. \end{aligned}$$
(2.54)

The regular solution of equation (2.54) is

$$\begin{aligned} \Pi (r)=A'\,I_0(2\beta \,r). \end{aligned}$$
(2.55)

After some work, the solutions for the functions \(X(r),\,Y(r)\) and Z(r) are

$$\begin{aligned}&X(r)=B'\,I_1(\delta \,r)-\frac{2\beta \,A'}{k^2}\,I_1(2\beta \,r),\end{aligned}$$
(2.56)
$$\begin{aligned}&Y(r)=C'\,I_0(k\,r),\end{aligned}$$
(2.57)
$$\begin{aligned}&Z(r)=D'\,I_0(\delta \,r)-\frac{2\beta \,A'}{k^2}\,I_0(2\beta \,r). \end{aligned}$$
(2.58)

The unknown constants \(A',\,B',\,C'\) and \(D'\) can be determined using the boundary conditions and with the aid of the continuity equation. In the subsequent work, we need only the value of the constant \(C'\),

$$\begin{aligned} C'= & {} \frac{1}{8I_{0}(k)}\Bigl ( 1-\frac{I_{1}(k)}{\Delta _2k\,I_{0}(k)}\bigl (\lambda \,(2\alpha \,k^2-\beta ^2)\,I_{\alpha }(\beta )+2\beta \,\lambda \,k^2I_{\alpha +1}(\beta )\bigr )I^2_{\alpha +1}(\lambda )\nonumber \\&+\,\bigl (\alpha \,(k^2-\beta ^2)\,(1+2\alpha )\,I_{\alpha }(\beta )+\beta \,(4\alpha \,k^2+\lambda ^2)\,I_{\alpha +1}(\beta )\bigr )I_{\alpha }(\lambda )\,I_{\alpha +1}(\lambda )\nonumber \\&+\,\alpha \,\beta \,\lambda \,(1+2\alpha )\,I^2_{\alpha }(\lambda )\,I_{\alpha +1}(\beta )\Bigr ), \end{aligned}$$
(2.59)

with

$$\begin{aligned} \Delta _2= & {} \bigl (\alpha \,(k^2-\beta ^2)\,I_{\alpha }(\beta )+\beta \,\lambda ^2I_{\alpha +1}(\beta )\bigr )I_{\alpha }(\lambda )\,I_{\alpha +1}(\lambda )-\beta \,\lambda \bigl (\beta \,I^2_{\alpha +1}(\lambda )\,I_{\alpha }(\beta )\\&-\alpha \,I^2_{\alpha }(\lambda )\,I_{\alpha +1}(\beta )\bigr ). \end{aligned}$$

3 The Flow Rate

The change in flow rate due to the unevenness is of second order, i.e.,

$$\begin{aligned}&\displaystyle Q=2\pi \int _0^{1+\epsilon \,g(\theta ,z)}w(r,\theta ,z)\,r\,dr,\end{aligned}$$
(3.1)
$$\begin{aligned}&\displaystyle Q=2\pi \int _0^{1}\left( w_0+w_1\,\epsilon +w_2\,\epsilon ^2\right) \,r\,dr+\frac{\pi \,I_1(k)}{k\,I_0(k)}\,\sin ^2(\alpha \theta )\,\sin ^2(\beta z)\,\epsilon ^2. \end{aligned}$$
(3.2)

The mean rate of flow with respect to \(\theta \) is

$$\begin{aligned} \bar{Q}=2\pi \int _0^{1}\left( w_0+\bar{w}_2\,\epsilon ^2\right) \,r\,dr+\frac{\pi \,I_1(k)}{2k\,I_0(k)}\,\sin ^2(\beta z)\,\epsilon ^2. \end{aligned}$$
(3.3)

Let the over double bar denote the mean with respect to \(\theta \) and then with respect to z. Averaging equation (3.3) with respect to z,  we get

$$\begin{aligned} \bar{\bar{Q}}=\frac{\pi }{k^3I_0(k)}\bigl (k\,I_0(k)-2I_1(k)\bigr )(1+\epsilon ^2\chi ), \end{aligned}$$
(3.4)

where

$$\begin{aligned} \chi =\frac{k^2I_1(k)}{4}\frac{1+8C'\,I_0(k)}{k\,I_0(k)-2I_1(k)}, \end{aligned}$$
(3.5)

which represents the second-order correction of the mean velocity due to the corrugations. The constant \(C'\) is given by equation (2.59).

3.1 Limiting and Asymptotic Results of the Bumpiness Function \(\chi \)

  1. (i)

    For clear fluid \(k\rightarrow 0,\) the bumpiness function \(\chi _c\) (given by equation (3.5)) reduces to the following expression

$$\begin{aligned} \chi _c= & {} \frac{1}{2\Delta _3}\bigl (\alpha \,\beta \,(2\alpha -3)\,I^3_{\alpha }(\beta )+(12\alpha -4\alpha ^3-2\alpha ^2-3\beta ^2)\,I_{\alpha +1}(\beta )\,I^2_{\alpha }(\beta )\nonumber \\&-\beta \,(2\alpha ^2+3\alpha -6)\,I^2_{\alpha +1}(\beta )\,I_{\alpha }(\beta )-\beta ^2I^3_{\alpha +1}(\beta )\bigr )+O(k^2), \end{aligned}$$
(3.6)

where

$$\begin{aligned} \Delta _3= & {} \alpha \,\beta \,I^3_{\alpha }(\beta )+(\beta ^2-2\alpha ^2-4\alpha )\,I_{\alpha +1}(\beta )\,I^2_{\alpha }(\beta )-\beta \,(3\alpha +2)\,I^2_{\alpha +1}(\beta )\,I_{\alpha }(\beta )\\&-\beta ^2I^3_{\alpha +1}(\beta ). \end{aligned}$$

For long and short wavelengths we have, respectively

$$\begin{aligned} \lim _{k\rightarrow 0,\,\beta \ll 1}\chi _c\sim \alpha -\frac{3}{2}+\frac{3\beta ^2}{2(\alpha +1)}+O(\beta ^3),\quad \lim _{k\rightarrow 0,\,\beta \gg 1}\chi _c\sim 2\beta -\frac{3}{2}+O(\beta ^{-1}).\quad \end{aligned}$$
(3.7)

These expressions agree with the clear fluid problem that deduced previously by Wang (2006).

  1. (ii)

    On the other hand, for the Darcy limit \(k\gg 1,\) the asymptotic form is

$$\begin{aligned} \chi _D\approx & {} \frac{\beta \,I_{\alpha }(\beta )}{\Delta _4}-\frac{1}{4}+\left( \frac{2\left( \beta ^2+\alpha ^2\right) \,I^2_{\alpha }(\beta )}{\Delta _4^2}+\frac{\alpha ^2-\beta ^2-2}{4}\right) \frac{1}{k}+O(k^{-2}), \end{aligned}$$
(3.8)

where

$$\begin{aligned} \Delta _4=I_{\alpha -1}(\beta )+I_{\alpha +1}(\beta ). \end{aligned}$$

The \(O(k^{0})\) agrees with that previous result obtained by Wang and Yu (2015) for the Darcy flow in a bumpy tube. Further, if very long and short wavelengths of bumpiness are considered

$$\begin{aligned} \lim _{k\gg 1,\,\beta \ll 1}\chi _D \sim \frac{\alpha ^2-k-2}{4k}+\frac{(\alpha +2k)\,\beta ^2}{4\alpha \,k}+O(\beta ^3),\quad \lim _{k\gg 1,\,\beta \gg 1}\chi _D\sim \frac{\beta ^2+\alpha ^2}{4k} +\frac{(k+1)\,\beta }{2k}+O(\beta ^{-1}).\nonumber \\ \end{aligned}$$
(3.9)
Fig. 2
figure 2

Variation of the first-order radial, tangential and axial velocities at \(\alpha =3\) and \(\beta =6.\)

Full size image
Fig. 3
figure 3

Variation of the bumpiness function \(\chi \) versus the permeability parameter k for different values of the wave number \(\alpha \) and the bump area A.

Full size image
Fig. 4
figure 4

Variation of the bumpiness function \(\chi \) versus the wave number \(\alpha \) for different values of the bump area A and permeability parameter k.

Full size image
Fig. 5
figure 5

Variation of the minimum bumpiness function \(\chi \) versus the bump area A for different values of the wave number \(\alpha \) and permeability parameter k.

Full size image

4 Results and Discussion

The effects of the porous medium parameter k on the typical velocity corrections \(U(r),\,V(r)\) and W(r) are shown in Fig. 2. As the porous media parameter k is increased, the radial and tangential velocities U(r) and V(r) become smaller and more dampen, and the axial velocity correction becomes more dominant. That is, for large k (low permeability) the amplitude of the velocity becomes dampen, and the effect of the wall only extends in a thin layer near the wall. Therefore, the wall resistance has a small effect to the total resistance, which is mostly due to the porosity of the medium. In such cases, the Darcy model is more appropriate. We note also that for all values of k,  the axial velocity W(r) correction may become slightly negative. For clear fluid (\(k\rightarrow 0\)), the velocity profiles coincide with those of Wang (2006). In order to find the values of circumferential wave numbers, for which the flow resistance is minimum, we have to evaluate the volume of a sticking out bump

$$\begin{aligned} V=\int _0^{\pi /\beta }\int _0^{\pi /\alpha }\int _1^{1+\epsilon \,g}r\,dr\,d\theta \,dz=\frac{4}{\alpha \,\beta }\,\epsilon +O(\epsilon ^2), \end{aligned}$$
(4.1)

and its area is \(A=\pi ^2/(\alpha \beta ).\) The volume of each sticking out bump is proportional to its area. Therefore, in our numerical investigation, we replace the two independent parameters (\(\alpha ,\,\beta \)) by the new independent parameters \((\alpha ,\,A).\) Figure 3 exhibits the variation of bumpiness function \(\chi \) against the permeability parameter for different values of A and \(\alpha .\) The function \(\chi \) is monotonically decreasing for the entire range of values of A and \(\alpha ,\) and its relative maximum values occur in the limit of Stokes’ flow (\(k=0\)). This means \(\chi \) tends to zero as k increases to the Darcian limit. The bumpiness will continuously lose their influence on the flow as the permeability decreases. For a specified value of k and for the entire range of \(A,\;\chi \) decreases as \(\alpha \) increases. Figure 4 exhibits the variation of the bumpiness function \(\chi \) against the wave number \(\alpha \) for given values of A and k. It indicates that for the entire range of A and k,  the bumpiness function \(\chi \) decreases as \(\alpha \) increases till it reaches a minimal value at some \(\alpha \) and then it increases for large values of \(\alpha \). Again, as expected, for any specified \(\alpha \) and A, the function \(\chi \) decreases as the permeability decreases. Also, for any specified \(\alpha \) and k,  the function \(\chi \) decreases as the surface area of a bump increases. Figure 5 indicates, for some values of k, the optimum \(\alpha \) (for maximal flow) increases as A is decreased. Note that, the mean flow rate \(\bar{\bar{Q}}\) is directly proportional to the term \((1+\epsilon ^2\chi )\). In Fig. 4 a minimal value of \(\chi \) is found when \(\alpha \) varies from 0 to 30 (and for fixed values of k and A). This \(\chi _\text {min}\) corresponds to a different minimum value of \(\bar{\bar{Q}}\). Table 1 gives the end points of A as \(\alpha \) increases for the values of k. It shows, for fixed \(\alpha \), the values of end points decrease as the permeability parameter increases. In Table 2, a comparison is made between our results for bumpiness function of the clear fluid \((k\rightarrow 0)\) and the results of Wang (2006). It is found that both results are in perfect agreement. Also, this table shows the results of Darcy model obtained by Wang and Yu (2015). It is found that the results almost agree only for large values of the permeability parameter, as expected. Table 2 indicates also the variation of the asymptotic bumpiness function, expression (3.8), compared with exact expression (3.5).

Table 1 Values of the area of a bumpy for various k and \(\alpha .\)
Full size table
Table 2 A comparison of the bumpiness function for the clear fluid, Brinkman’s and Darcy’s limit versus the wave number \(\alpha \) for different values of the bump area A and permeability parameter k.
Full size table

5 Conclusion

The present article extends the work (Wang 2006) to the flow through bumpy tubes filled with a porous medium using Darcy–Brinkman model. The model equation is adequate for high-permeability porous medium and suitable for low velocity applications such as filters and heat exchangers. Moreover, this model is well accepted for microfluidics because the Reynolds number is so small that inertial effects are basically absent. Capillaries can be precisely modeled as a quasi-periodic bumpy tube with a circumferential wave number of \(\alpha =1,\) since in these smallest vessels, a single endothelial cell wraps around the entire tube circumference and the endothelial cell nucleus sticks out into the vessel lumen to provide the occasional large bump. For capillaries of inner diameter 2a ranging from 5.86 to 11.6 \(\upmu \)m, average longitudinal wavelengths \(\ell \) of 38.5–48.4 \(\upmu \)m were measured (King 2007). In this study, we obtained perturbation solutions up to second order of the normalized bumpy amplitude, including the following parameter: the amplitude of the bumpiness, circumferential wave number, the area of a bump and the important porous media parameter k. First-order analytical solutions (2.26)–(2.30) give the complicated part of this study. Our work declares, for every permeability parameter and for given bump area, there exists a circumferential wave number, for which the flow resistance is minimized or the flow rate can be maximized. Numerical investigations are available to extend our study to bumps with large amplitude. Comparisons with the limiting cases available in the literature show excellent agreement, indicating the accuracy and reliability of the results presented in this study.