1 Introduction

Laboratory study of reservoir rock samples of a geologic formation (core analysis) is the direct way to determine reservoir properties and to provide accurate input data for geological models (Andersen et al. 2013). Geoscientists have developed a variety of approaches for measuring properties of reservoir rocks, such as porosity, permeability, residual oil saturation, and many others. The information obtained from core analysis aids in formation evaluation, reservoir development, and reservoir engineering (McPhee et al. 2015; Mahzari et al. 2018). It can be used to calibrate log and seismic measurements and to help with well placement, completion design, and other aspects of reservoir production.

Common applications of core analysis include (Gaafar et al. 2015):

  • definitions of porosity and permeability, residual fluid saturations, lithology and prediction of possible production of gas, condensate, oil, or water;

  • definition of spatial distributions of porosity, permeability, and lithology to characterize a reservoir in macroscale;

  • definition of fluids distribution in a reservoir (estimation of fluids contacts, transition zones);

  • performing special core analysis tests to define the most effective field development plan to maximize oil recovery and profitability.

Unfortunately, core analysis is expensive and tedious. Laboratory study requires careful planning to obtain data with minimum uncertainties (Ottesen and Hjelmeland 2008). Proper results of basic laboratory tests provide the reservoir management team with a vital information for further development and production strategy.

Core analysis is generally categorized into two groups: conventional or routine core analysis (RCA) and special core analysis (SCAL) (Dandekar 2006). RCA generally refers to the measurements for defining porosity, grain density, absolute permeability, fluid saturations, and a lithologic description of the core. Samples for conventional core analysis are usually collected three to four times per meter (Monicard 1980). Fine stratification features and spatial variations in lithology may require more frequent sampling.

Probably, the most prominent SCAL tests are two-phase or three-phase fluid flow experiments in the rock samples for defining relative permeability, wettability, and capillary pressure. In addition, SCAL tests may also include measurements of electrical and mechanical properties, petrographic studies, and formation damage tests (Orlov et al. 2018). Petrographic and mineralogical studies include imaging of the formation rock samples through thin-section analysis, X-ray diffraction, scanning electron microscopy (SEM), and computed tomography (CT) scanning in order to obtain better visualization of the pore space (Dandekar 2006; Liu et al. 2017; Soulaine and Tchelepi 2016). SCAL is a detailed study of rock characteristics, but it is time-consuming and expensive. As a result, the number of SCAL measurements is much less than the number of RCA measurements (5–30% of RCA tests). In this way, SCAL data space requires correct expansion or extrapolation to the data space covered by RCA. To provide the expansion, core samples set used in SCAL tests should be highly representative and contain all the rock types and cover a wide range of permeability and porosity (Stewart 2011). Even then, sometimes it is difficult to estimate correlations between conventional and special core analysis results and expand SCAL data to the available RCA dataset. There are few common approaches on stretching the SCAL data to RCA data space:

  • typification (defining rock types with typical SCAL characteristics in certain ranges of RCA parameters);

  • petrophysical models (SCAL characteristics included as parameters in functional dependencies between RCA characteristics);

  • prediction models based on machine learning (RCA parameters used as features to predict SCAL characteristics).

The first approach leads to a significant simplification of reservoir characterization and is based on subjective conclusions. Petrophysical models allow predicting only a few of SCAL characteristics (basically capillary curves and residual saturations). The last approach looks more promising as it accounts for all the available features (measurements) and builds implicit correlations among the features (Meshalkin et al. 2018; Tahmasebi et al. 2018).

The purpose of this research is to demonstrate the performance of machine learning (ML) at maximizing the effect of RCA and SCAL data treatment. Machine learning is a subarea of artificial intelligence based on the idea that an intelligent algorithm can learn from data, identify patterns, and make decisions with minimal human intervention (Kotsiantis et al. 2007).

Commonly spread feature of fields in Eastern Siberia is salts (the ionic compound that can be formed by the neutralization reaction of an acid and a base) presented in the pore volume of the deposits. Salts distribution in the reservoirs depends on a complex of sedimentation processes. Thus, the key challenge of this work is to develop prediction models, which can characterize the quantity of soluble rock matrix components (sodium chloride and other ionic compounds) and an increase in porosity and permeability after reservoir desalination due to drilling mud or water injection (ablation).

One of the main challenges for geoscientists is forecasting salts distribution in productive horizons together with porosity and permeability alteration due to the salts ablation. It is very important for:

  • estimations of original porosity and permeability in wells as water-based drilling mud can change pore structure during wellbore drilling and coring,

  • RCA and SCAL data validation and correction due to pore structure alteration during core sample preparation and consequent measurements,

  • reservoir engineering (IOR&EOR based on water injection).

In this work, salts content measurements and alteration of porosity and permeability measurements after desalination could be considered as a SCAL experiments because they are expensive and time-consuming. The procedure of alteration estimation includes porosity and permeability measurements before and after water injection in core samples and its desalinization during long-term one-phase water filtration. Porosity and permeability before desalination, sample density, and lithology and texture description are the RCA input data for our predictive models.

The significant benefit of ML predictive models is that one may not have to perform SCAL measurements for all the core samples, but can conduct prediction of the results (Unsal et al. 2005). Once a predictive model of any SCAL results is trained, it could be effectively used for future forecasting. There are a lot of ML algorithms to build a predictive model (Hastie et al. 2001). In our work, we used the following algorithms: linear regression (with and without regularization) (Boyd and Vandenberghe 2004; Freedman 2009), decision tree (Quinlan 1986), random forest (Ho 1995), gradient boosting (Friedman 2001), neural network (Haykin 1998), and support vector machines (Cortes and Vapnik 1995). The choice of algorithm strongly depends on the considered problem, data quality, and size of the dataset. For example, it would be unnecessary to build convolutional or recursive NN in our problem due to the small dataset size and its structure. However, more simple algorithms (mentioned above) could be adopted for discussed cases.

Accordingly, we have two goals in our research. First is to develop a predictive model of salts concentration using information of RCA and some additional data about coring depth and top and bottom depths of productive horizons. Second is to develop relevant predictive models of porosity and permeability.

The main innovation elements of the research are:

  • Special experimental investigations of porosity and permeability increasing in core waterflooding tests;

  • Validation of predictive algorithms to define the best predictive model;

  • Accounting ten features of core samples to predict porosity and permeability after rock desalination and nine features to predict salts content;

  • The high quality of models for the prediction of porosity and permeability after rock desalination and rather good quality of model for the evaluation of rock salinity.

2 Materials and Methods

2.1 Hydrocarbon Reservoir Characterization

The Chayandinskoye oil and gas condensate field is located in the Lensk District of Sakha (Yakutia) Republic in Russia and hosted toward the south of the Siberian platform within the Nepa arch. The field belongs to the Nepa-Botuobinsky oil and gas area, which contains rich hydrocarbons reserves. The main gas and oil resources are associated with the Vendian terrigenous deposits (Talakh, Khamakin, and Botuobinsky horizons) which are overlapped by a thick series of the salt-bearing sediments.

Chayandinskoye field is characterized by a complex geological structure and special thermobaric formation conditions (reservoir pressure of 36–38 MPa, overburden stress of 50 MPa, and temperature of 11–17 \(^{\circ }\)C). The Vendian deposits consist predominantly of quartz sandstones and aleurolits with a low level of cementation and development of indentation and incorporation of grains. Another essential feature of the field is salts presented in the pore volume of the deposits. Salts distribution in the reservoir is exceptionally irregular due to various sedimentation processes: change in thermobaric condition during regional uplifts and erosional destruction of deposits, paleoclimate cooling, and glaciation, in addition to filtration of brines through rock faults and fractured zones (Ryzhov et al. 2014). Usually, the most common salt in rock matrix is sodium chloride (NaCl), but many other salts occur in varying smaller quantities. The same conclusion based on TDS analysis (measurement of the total ionic concentration of dissolved minerals in water) is correct for brine composition. Rocks analysis demonstrates that highly salinized formations are coarse-grain poorly sorted rocks with mass salts concentration—ranging from 4 to 30%. The porosity of the salted rocks is 1–8% (seldom \(\ge \) 10%). After core desalination, permeability could be increased up to 60 times and porosity—up to 2.5 times.

2.2 Dataset

We included the following features to the dataset for our prediction models:

  • measurements of salts mass concentrations for core samples with various values of initial porosity and permeability, lithology, depth, horizons’ ID, and wells’ ID;

  • measurements of porosity and absolute permeability before and after desalination.

All tests are performed on 102 cylindrical core samples with 30 mm radius and 30 mm length. Sample preparation included delicate extraction in the alcohol–benzene mixture at room temperature (to avoid premature desalination) and drying up to constant weight. Absolute permeability was measured at ambient conditions in the steady-state regime of nitrogen flow. Porosity was determined by a gas volumetric method based on Boyle’s Law (API 1998).

Fig. 1
figure 1

Dataset. a Permeability distribution, b porosity distribution, c salts concentration distribution

Full size image

For salts ablation, we injected in each core sample more than ten pore volumes of brine with low salinity (30 mg/cc). To enhance ablation, we also performed additional extraction in the alcohol–benzene mixture to remove oil films preventing salts dissolution. After that, the samples were dried up to a constant weight to measure porosity and permeability after desalination. Results of porosity and permeability measurements (before and after salts ablation) are presented in Fig. 1a, b.

Measurements of salts mass concentrations for core samples were based on the data of sample weighting before and after desalination. The resulting expression for salts concentration could be defined as:

$$\begin{aligned} C_\mathrm{salt} = \frac{\varDelta m}{m_0}, \end{aligned}$$
(1)

where \(\varDelta m\) is the sample mass difference before and after ablation (g); \(m_0\) is the sample mass before desalination (g). All the measurements were made on oven-dry samples. Results of salts mass concentration measurements are presented in Fig. 1c.

For salts concentration predictive model, we have used nine features: formation top depth, formation bottom depth, initial (before desalination) porosity and permeability, sample depth adjusted to log depth, sample density (before desalination), average grain size (by lithology and texture description), sample color, and horizon ID. Average grain size was quantified from textual lithology description in the following way:

  • Gravel—1 mm;

  • Coarse sand—0.5 mm;

  • Medium sand—0.25 mm;

  • Fine sand—0.1 mm;

  • Coarse silt—0.05 mm;

  • Fine silt—0.01 mm;

  • Clay—0.005 mm.

For sample color and horizon type, we have used the classification scheme containing six color types and three horizon types. If the sample has any of the six colors and any of the three horizons, we mark “1”, otherwise, we mark “0”.

For porosity and permeability predictive models, we have used nine previously described features plus salts concentration. All ten features accounting in machine learning algorithms are presented in Table 1.

Table 1 All features used in predictive models
Full size table

2.3 Prediction Models

We have used nine models: linear regression (simple, with L1 and L2 regularization), decision tree, random forest, gradient boosting (two different implementations with and without regularization), neural network, and support vector machines to compare their predictive power.

2.3.1 Linear Regression (Hastie et al. 2001; Freedman 2009)

Simple linear regression expresses predicting value as linear combination of the features:

$$\begin{aligned} y = w_0x_0 + w_1x_1 + \cdots + w_px_p + b, \end{aligned}$$
(2)

where y is the predicting parameter; x is a matrix of features; and \({\mathbf {w}}\) is a matrix of optimizing coefficients.

The optimization problem for regression is given by the expression:

$$\begin{aligned} \min _\mathbf{w , b} F(\mathbf w , b) = \frac{1}{m} \sum _{i=1}^{m} (\mathbf wx _{i} + b - y_i)^2. \end{aligned}$$
(3)

Coefficients \({\mathbf {w}}\) and b are defined from a training set of data (\(y_i\) is the actual value of the predicting parameter; m is the size of the training set). Further, the linear regression model with predefined coefficients could be effectively applied to fit new data. This algorithm is implemented in LinearRegression() method of Python scikit-learn library (Pedregosa et al. 2012).

Sometimes, regression with regularization works better than simple regression. In a case when we have many features, linear regression procedure leads to overfitting: enormous weights \(\mathbf w \) that fit the training data very well, but poorly predict future data. “Regularization” means modifying the optimization problem to prefer small weights. To avoid the numerical instability of the least squares procedure regression with L2 and L1 regularizations is often applied (Hastie et al. 2001).

2.3.2 Linear Regression with L2 Regularization (Ridge) (Boyd and Vandenberghe 2004)

This approach is based on Tikhonov regularization, which addresses the numerical instability of the matrix inversion and subsequently produces lower variance models:

$$\begin{aligned} \min _\mathbf{w , b} F(\mathbf w , b) = \frac{1}{m} \sum _{i=1}^{m} (\mathbf wx _{i} + b - y_i)^2 + \lambda ||\mathbf w ||^2_2. \end{aligned}$$
(4)

All variables have the same meanings as in linear regression case. Optimal regularization parameter \(\lambda \) is chosen in a way to get the best model fitting while weights \(\mathbf w \) are small. This algorithm is implemented in Ridge() method of Python scikit-learn library (Pedregosa et al. 2012).

2.3.3 Linear Regression with L1 Regularization (Lasso) (Boyd and Vandenberghe 2004)

While L2 regularization is an effective approach of achieving numerical stability and increasing predictive performance, it does not address another problem with least squares estimates, parsimony of the model, and interpretability of the coefficient values (Tibshirani 1996). Another trend has been to replace the L2-norm with an L1-norm:

$$\begin{aligned} \min _\mathbf{w , b} F(\mathbf w , b) = \frac{1}{m} \sum _{i=1}^{m} (\mathbf wx _{i} + b - y_i)^2 + \lambda ||\mathbf w ||_1. \end{aligned}$$
(5)

This L1 regularization has many of the beneficial properties of L2 regularization, but yields sparse models that are more easily interpreted (Hastie et al. 2001). L1 regularization algorithm is implemented in Lasso() method of Python scikit-learn library (Pedregosa et al. 2012).

2.3.4 Decision Tree (Quinlan 1986)

Decision tree is a tree representation of a partition of feature space. There are numbers of different types of tree algorithms, but here we will consider only CART (classification and regression trees) (Breiman 2017) approach. A classification tree is a decision tree which returns a categorical answer (class, text, color, and other), while a regression tree is a decision tree which responses with an exact number. Figure 2a demonstrates a simple example of the decision tree in a case of two-dimensional space based on two features X1 and X2.

Fig. 2
figure 2

Examples of prediction algorithms. a Decision tree example, b scheme of artificial neural network with two hidden layers

Full size image

A decision tree consists of sets of leaves and nodes. One may built very detailed deep tree with many nodes; however, such tree will suffer from overfitting. Usually, the maximum depth of the tree is restricted. To build a tree, the recursive partition is applied until a sufficient size of a tree would be obtained. The criteria for tree splitting are often given by Gini index or information gain criteria in classification case and mean squared error or mean absolute error in the regression case. These functions are used to measure the quality of a split and choose the optimal point of partition. Tree construction could involve not all input variables, so tree managed to demonstrate which variables are relatively important, but it could not rank the input variables. Decision tree algorithm exploited in this work is implemented in DecisionTreeRegressor() method of Python scikit-learn library (Pedregosa et al. 2012).

2.3.5 Random Forest (Ho 1995; Breiman 2001)

The main idea of this method is to build many independent decision trees (ensemble of trees), train them on data subset, and receive predictions. The algorithm uses bootstrap re-sampling to prevent overfitting. Bootstrapping is a re-sampling with replacement: bootstrap sets are built on initial data, where several samples are replaced with other repeating samples. Each tree is built on individual bootstrap set (so, for N tree estimators, we need N different bootstrap representations). Consequently, all trees are different as they are built on different datasets and hold different predictions. Then, all trees are aggregated together after training and the final prediction is obtained by averaging (in the case of regression) predictions of each tree. One useful feature of random forest algorithms is that it could rank input features. It is implemented in RandomForestRegressor() method of Python scikit-learn library (Pedregosa et al. 2012).

2.3.6 Gradient Boosting (Friedman 2001)

This method uses “boosting” of the ensemble of weak learners (often decision trees). Boosting algorithm combines trees sequentially in such a way that the next estimator (tree) learns from the error of previous one: this method is iterative, and each next tree is built as a regression on pseudo-remainders. Similar to any other ML algorithm, gradient boosting uses loss function to minimize. Also, gradient descent is applied to minimize error (loss function) associated with adding a new estimator. The final model is obtained by combining the initial estimation with all subsequent estimations with appropriate weights. Gradient boosting method used in this study is implemented in the scikit-learn library in GradientBoostingRegressor() method (Pedregosa et al. 2012). Also, XGBoost library (Chen and Guestrin 2016) was considered because it allows adding regularization to the model.

2.3.7 Support Vector Machine (SVM) (Cortes and Vapnik 1995)

The idea of support vector machine (in case of regression) is to find a function that approximates data in the best possible way. This function has at most \(\epsilon \) deviation out from real train values \(y_i\) and as flat as possible. Such linear function \(f(\mathbf X )\) could be expressed as:

$$\begin{aligned} f(\mathbf X ) = w\mathbf X + b. \end{aligned}$$
(6)

The optimization problem could be formulated in the following form:

$$\begin{aligned} \begin{aligned}&\min _{W} \frac{1}{2}||w||^2 \\ \mathrm{subject}&\, \mathrm{to:} {\left\{ \begin{array}{ll} y_i - w \mathbf X - b \le \epsilon \\ w \mathbf X - b - y_i \le \epsilon \end{array}\right. }. \end{aligned} \end{aligned}$$
(7)

Often, some errors beyond \(\epsilon \) are allowed, which requires introducing of slack variables \(\xi _i, \xi _i^*\) into the problem:

$$\begin{aligned} \begin{aligned}&\min _{W} \frac{1}{2}||w||^2 + C\sum _{i = 1}^{m}(\xi _i + \xi _i^*) \\ \mathrm{subject}&\, \mathrm{to:} {\left\{ \begin{array}{ll} y_i - w \mathbf X - b \le \epsilon + \xi _i\\ w \mathbf X - b - y_i \le \epsilon + \xi _i^*\\ \xi _i, \xi _i^* \ge 0 \end{array}\right. }. \end{aligned} \end{aligned}$$
(8)

The solution of SVR problem is usually given in a dual form (Hsieh et al. 2008), which includes calculation of Lagrange multipliers \(\alpha _i, \alpha '_i\). In this formulation solution looks as follows:

$$\begin{aligned} f(x) = \sum _{i = 1}^{m}(\alpha '_i - \alpha _i)K(x_i, x) + b, \end{aligned}$$
(9)

where \(K(x_i, x)\) is a kernel (Crammer and Singer 2001).

In this work, the standard Gaussian kernel has been applied:

$$\begin{aligned} K(x, x') = exp\left( -\frac{||x - x'||^2}{2 \sigma ^ 2}\right) \end{aligned}$$
(10)

SVM algorithm is implemented in SVR() method of Python scikit-learn library (Pedregosa et al. 2012).

2.3.8 Neural Network (Haykin 1998; Schmidhuber 2015)

Artificial neural network (ANN) is a mathematical representation of biological neural network (Fig. 2b). It consists of several layers with units that are connected by links (McCulloch and Pitts 1943). Each link has associated weight and activation level. Each node has an input value, an activation function, and an output. In ANN, information propagates (forward pass) from first (not hidden) layer with inputs to next hidden layer and then to further hidden layers until the output layer would be achieved. The value of each node of the first hidden layer is obtained after the calculation of activation function for the dot product of inputs and weights. Next hidden layer receives the output of the previous one and puts its dot product with weights to the activation and so on. Initially, all weights for all nodes are assigned randomly. ANN calculates first output with random weights, then compares it with real value, calculates the error, and adopts weights to obtain smaller error on the next iteration via backpropagation (ANN training algorithm). After training, all weights are tuned, and one may make a prediction for a new data by passing them into an ANN which will calculate output via forward propagation through all activations (Rumelhart et al. 1986). Scikit-learn library provides ANN representation in MLPRegressor() method (Pedregosa et al. 2012). This implementation allows to indicate the number of hidden layers, number of nodes in each layer, activation function, learning rate, and some other parameters.

2.4 Methodology of Using Machine Learning Algorithms

2.4.1 Metrics

To evaluate the accuracy of applied methods and compare them between each other, the following metrics have been exploited.

The coefficient of determination R2 is the proportion of the total (corrected) sum of squares of the dependent variable “explained” by the independent variables in the model. R2 score is a part of dispersion of dependent variable that is predictable by independent variables:

$$\begin{aligned} R^2 = 1 - \frac{\sum _{i}(y_i - {\hat{y}}_i)^2}{\sum _{i}(y_i - \bar{y})^2}, \end{aligned}$$
(11)

where \(y_i\) are real values, \({\hat{y}}_i\) are predicted values, and \(\bar{y}\) is a mean value.

Mean squared error corresponds to quadratic errors:

$$\begin{aligned} \mathrm{MSE}(y, {\hat{y}}) = \frac{1}{n_\mathrm{samples}} \sum _{i = 0}^{n_\mathrm{samples} - 1} (y_i - {\hat{y}}_i)^2. \end{aligned}$$
(12)

Mean absolute error corresponds to absolute errors:

$$\begin{aligned} \mathrm{MAE}(y, {\hat{y}}) = \frac{1}{n_\mathrm{samples}} \sum _{i = 0}^{n_\mathrm{samples} - 1} |y_i - {\hat{y}}_i|. \end{aligned}$$
(13)

2.4.2 Cross-Validation

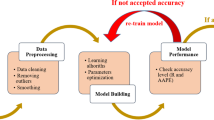
Since this study is limited in the amount of data, cross-validation (CV) has been applied. There are several cross-validation techniques. For example, when we split whole data into k parts, i.e., k-fold, we use first part for testing the performance of ML model after training it on the other \(k-1\) parts. Next, we could take the second part for testing and the rest parts for training and so on k times. In the end, we will have k different values of metrics—R2, MAE, MSE [Eqs. (11)–(13)] calculated for each fold. So, via cross-validation, we could obtain mean values of metrics and their standard deviation. Another cross-validation technique called random permutation supposes random division of data into train and test set, then data shuffle, and we can obtain new division on test and train set. This process repeats n times and each time metrics are calculated. Similarly, in the end, we can evaluate the mean values of metrics and standard deviations. So, cross-validation not only allows to calculate R2 (or MAE and MSE) for the test set but also does it several times by independent data splitting into test and train sets. Since in our task we are restricted in the amount of data, cross-validation was used several times (for hyperparameters tuning, model’s performance estimation, and making predictions to plot predicted results versus real data). Models building and estimation was done in three steps:

  1. 1.

    Hyperparameters tuning was done with the help of exhaustive grid search (Bergstra and Bengio 2012). This process allows to search through given ranges of each hyperparameter and define optimal values which led to the best R2 (or MAE, MSE, etc.) scores. This process is implemented in scikit-learn Python library (Pedregosa et al. 2012) in method GridSearchCV(). The method simply calculates CV score for each combination of hyperparameters in a given range. Random permutation approach with ten repeats was chosen as CV iterator. GridSearchCV() allows not only to find the best hyperparameters, but also calculate metrics in the optimal point. However, just ten repeats are not enough for very accurate final estimation of mean value and deviation; while taking more repeats, more computational time is required. So, final estimation with known hyperparameters would be done next.

  2. 2.

    Evaluation of the ML model with optimal hyperparameters (defined on the first step) was also done via CV with random permutation approach. However, here, we take 100 repeats, and it is enough for a fair result.

  3. 3.

    To plot predictions versus real values, we applied k-fold CV. In our particular case, we took k that equals the number of samples. So, first of all, we train our model on all data without one point and then predict at this point (testing) by trained model. Next, we take the second point, remove it from the dataset and train model from scratch, and then obtain prediction in point. This process was made for all data points (102 times). It allows to obtain predictions for all points and compare them with initial data visually.

Some researchers (Choubineh et al. 2019) suggest the other way to validate the quality of ML models. The data records of the dataset are divided into training, validation, and testing subsets, respectively, where validation set is used for hyperparametres tuning while training set is used for training the model and test set is used for final model evaluation. However, unfortunately, a single random partition of the data on subsets could not be enough for correct model estimation due to non-uniformity of the dataset. Another random partition will give another value of metrics (R2, MAE, MSE, and others). Single partition of the data is reasonable only in case of the big size of the dataset.

2.4.3 Normalization of Data

Some machine learning methods require normalized data to proceed correctly (SVM and neural network), so in these cases, the data have been normalized by using the mean and standard deviation of the training set:

$$\begin{aligned} X_{\mathrm{scaled}_i} = \frac{X_i - {\bar{X}}}{\sigma _X}, \end{aligned}$$
(14)

where \(X_i\) is the feature vector, \({\bar{X}}\) is the mean value of the feature vector, and \(\sigma _X\) is a variance.

3 Results and Discussion

In this section, results of porosity, permeability, and salts concentration predictions are presented, analyzed, and compared. We made predictions of these reservoir properties on the basis of features described in Sect. 2.2 by algorithms described in Sect. 2.3. However, only linear regression with L1 regularization was taken into account out of three linear regression algorithms (because algorithms are very similar and implemented within the same library, results are very close, and regression with L1 regularization performs slightly better in our task). Also, two different libraries for gradient boosting calculation were applied (they reported separately) because XGBoost library allows regularization, while scikit-learn not. So, we reported results for seven different algorithms. Each algorithm was adopted to the experimental data to get the best performance due to the cross-validation procedure.

Since our dataset is not such big from big data point of view and contains different measurements errors, it turns out that the proportion of its splitting via cross-validation procedure is important. We found out via grid search that for our small dataset would be optimal to left 35% of data for testing on each cross-validation pass to obtain the estimation of algorithm performance.

3.1 Porosity Prediction

Porosity model was the first ML model we built. Actually, the material balance equation defines specific dependence between porosity and salts concentration:

$$\begin{aligned} \phi = \phi _0 + \frac{\rho _{r}^{0}}{\rho _\mathrm{ha}}C_\mathrm{salt}, \end{aligned}$$
(15)

where \(\phi \) is the porosity after desalinization; \(\phi _0\) is the porosity before desalinization; \(C_\mathrm{salt}\) is the mass salts concentration; \(\rho _\mathrm{ha}\) is the salt density; and \(\rho _r^0\) is the core sample density before desalinization. Equation 15 allows to estimate performance of ML models. In this case, data-driven algorithms should find hidden correlations within parameters and demonstrate appropriate predictive abilities. The appearance of the physical model gives an opportunity widely to test ML instruments.

For predictive models of porosity, we took into account influence of all ten characteristics of rock samples (Table 1). Almost all surveyed methods (except decision tree) have demonstrated promising results and high values of determination coefficient in the case of porosity prediction. Table 2 demonstrates results of models evaluation via cross-validation process: mean value and standard deviation. Here and further, we reported linear regression only with L1 regularization, because other implementations (without regularization and with L2 regularization) show very close results. However, this algorithm works slightly better. In general, the highest value of R2-metric corresponds to the lowest values of MSE and MAE metrics. In porosity case, SVM, neural network, gradient boosting, and linear regressions have the best scores. The best two models are support vector machines with \(\text {R2} = 0.86 \pm 0.14, \, \text {MAE} = 0.82 \pm 0.19, \, \text {MSE} = 1.63 \pm 1.47\) and neural network with \(\text {R2} = 0.84 \pm 0.1, \, \text {MAE} = 0.94 \pm 0.16, \, \text {MSE} = 1.79 \pm 0.94\).

Table 2 Results for porosity prediction
Full size table

Grid search calculated optimal regularization value of L1 linear regression which equals 0.001. In a similar search process, optimal depth of decision tree was obtained—7—and the optimal number of estimators (trees) for random forest—150—along with the maximum depth of each tree—8. For gradient boosting model, the following parameters were selected: 16,000 estimators (trees), maximum depth of each tree—2, subsample—0.7 (it means that each tree takes only 70% of initial data to fit, the next tree takes another 70% randomly, etc.; this idea helps to prevent overfitting), max-features—0.9 (the concept is similar to subsample; the only difference is that instead of using part of the samples, algorithm takes part of features to fit each tree), and regularization—0.001. Neural network architecture was also defined with the help of grid search since we have the small dataset and can calculate several architectures fast. It has two hidden layers with two and four nodes in each layer. SVM was built with Gaussian kernel which has two parameters to tune: C and gamma. The exhaustive search showed optimal gamma—0.0001—and optimal C—40,000.

Performance of the SVR and MLPRegressor models could be demonstrated by plotting predicted values (via cross-validation) of porosity after ablation versus the actual values (Fig. 3). One can see the data points located along the mean line (bisectrix).

Fig. 3
figure 3

Comparison of actual and predicted porosity. a For SVR algorithm, b for neural network algorithm

Full size image

Python’s XGBoost allows arranging features concerning a degree of their influence on the prediction model (Friedman 2001), as shown in Fig. 4. The importance provides a score (referred as F score) that indicates how useful each feature was in the construction of the boosted decision trees within the model. This metric shows how many times the feature was used to split tree on (Freedman 2009). The feature importance is then averaged across all of the decision trees within the model.

Fig. 4
figure 4

Feature selection in porosity model with XGBoost

Full size image

In Fig. 4, one can see that porosity and permeability before desalination and salts concentration have the most significant influence on the porosity prediction results, which is in a good correspondence with the geometric correlation between porosity and salts concentration (Eq. 15). Core sample density before desalinization (\(\rho _r^0\)) is also among the five influential features in ML algorithms (Fig. 4). These observations demonstrate that predictive ML models simulate the same correlations as the physical model. A strong influence of the permeability before desalinization (\(K_0\)) on the porosity after desalinization (\(\phi \)) can be explained by a strong correlation between \(K_0\) and \(\phi _0\) [as, for example, in Kozeny–Carman equation form (Carman 1956)]. The next few features shown in Fig. 4, which also significantly influence on porosity increase, are depths of sample, formation top, and formation bottom. This fact confirms that the salts are distributed in formation non-uniformly and the distribution strongly depends on the geological condition of the reservoir. The color features and the horizon types have the lowest influence on the prediction models.

3.2 Permeability Prediction

For permeability prediction, all the methods also look promising and demonstrate high values of R2-metrics (Table 3). In this case, support vector machines, neural network, and linear regressions show the best performance. The highest scores were obtained for SVR with \(\text {R2} = 0.86 \pm 0.08, \, \text {MAE} = 105 \pm 20, \, \text {MSE} = 39{,}957 \pm 17{,}906\) and linear regression with \(\text {R2} = 0.85 \pm 0.07, \, \text {MAE} = 118 \pm 20, \, \text {MSE} = 40{,}864 \pm 16{,}434\)

Table 3 Results for permeability prediction
Full size table

Similar to the previous section, one may define optimal hyperparameters of algorithms for permeability prediction via grid search (Bergstra and Bengio 2012). So, for linear regression model, we have used L1 regularization with regularization parameter equal to 10. The decision tree was built with maximum depth—10. Twenty-five trees with the maximum depth of 8 were defined for random forest algorithm. In gradient boosting model, we obtained the following optimal values: 300 estimators with a maximum depth of each tree equal to 2. Only 80% of the samples and 90% of the features have been used for each tree to fit the model and regularization parameter—0.1. Neural network had two hidden layers with 77 and 102 nodes in each layer. SVM parameters included the Gaussian kernel with gamma equal to 0.0001 and C equal to 50,000.

Performance of the SVR and linear regression models is demonstrated on the mean line plots shown in Fig. 5. Similarly, the prediction was made via cross-validation for all points. Data points are mainly located along the bisectrix, but generally matching between observed and predicted permeability is weaker than in porosity case.

Fig. 5
figure 5

Comparison of real and predicted permeability. a For SVR algorithm, b for linear regression algorithm

Full size image

The XGBoost method was also used to arrange features concerning their influence on the predictive model. In Fig. 6, one can see that porosity and permeability before desalination and salts concentration have the most influence on the permeability prediction results. It is very similar to the results of feature selection in porosity model. We also obtained that the next features, which significantly influence permeability increase, are connected with the geological condition of the reservoir (sample depth, formation top, and bottom depths). The color features and the horizon type also occurred in the lowest influencers.

Fig. 6
figure 6

Feature selection in permeability model with XGBoost

Full size image

3.3 Salts Concentration Prediction

The last part of the research is devoted to the prediction of salts concentration. The models work worse and demonstrate rather weak performance with R2-metric hardly reaching 0.6. Only a few methods look promising and demonstrate reasonable values of R2-metrics (Table 4). The best algorithms are neural network, gradient boosting, and random forest. Linear regression and decision tree models are unacceptable with very small R2-metrics. R2 for support vector regression reached almost 0.5. The best two models with the highest scores are neural network (from MLPRegressor model of Scikit-learn) with \(\text {R2} =0.66 \pm 0.25, \, \text {MAE} =0.77 \pm 0.18, \, \text {MSE} = 1.69 \pm 0.96\) and gradient boosting with \(\text {R2} =0.59 \pm 0.27, \, \text {MAE} =0.93 \pm 0.19, \, \text {MSE} = 2.23 \pm 1.13\). Also, in this case, very high standard deviation (up to 100%) in defining R2, MSE, and MAE metrics is obtained. This could be explained by non-uniformity of the experimental data.

Table 4 Results for salts concentration prediction
Full size table

By analogy with porosity and permeability, we defined optimal hyperparameters of algorithms via grid search process (Bergstra and Bengio 2012). Regularization parameter for L1 regression is equal to 1.0. The optimal decision tree has a depth of 9. Random forest performs better with ten estimators of the depth of 1. Gradient boosting model runs with 300 estimators of the depth of 10. 95% of samples and 50% of features have been used for training of each tree. Regularization parameter is small and is equal to 0.00001. The neural network contains three layers and 55, 10, and 86 nodes in each layer, respectively. SVM was performed with gamma which is equal to 0.1 and C which is equal to 25.

Performance of the gradient boosting and neural network models is demonstrated on the mean line plots (Fig. 7). Data points are partially located along the mean line. Accordingly, the correlation between observed and predicted values is much weaker than in porosity and permeability cases.

Fig. 7
figure 7

Comparison of real and predicted salts concentration. a For gradient boosting algorithm, b for neural network algorithm

Full size image

Results of XGBoost features arrangement are shown in Fig. 8. As one can see, porosity before desalination has the most substantial influence on the salts concentration prediction results. The next two features affecting the prediction results are sample depth and permeability before desalination. Results of this feature rating differ from the results obtained for porosity and permeability models. We can state that the prediction of porosity and permeability alteration is primarily controlled by its initial values and amount of salts in the pore volume. Salts concentration, in its turn, strongly depends not only on the initial porosity and permeability but also on the formation pattern characteristics, which are linked with post-sedimentation processes. Therefore, the prediction model attempts to learn from training dataset where and how strong these processes are developed in the certain reservoir beds with various depth and location in the oil field (through the formation top and bottom depths).

Fig. 8
figure 8

Feature selection in salts concentration model with XGBoost

Full size image

3.4 Comparison of the Predictive Models with Traditional Approaches

All obtained R2 scores with its variances for all algorithms are represented in Fig. 9. The worst results could be associated with decision tree method where we obtained not only the lowest values for R2 metric but also the largest standard deviation of R2. Support vector machines and linear regression demonstrate good results only for porosity and permeability prediction, but these methods are inappropriate for salts concentration prediction. The best machine learning method for the prediction of all three petrophysical characteristics is neural network in MLPRegression implementation. This algorithm demonstrates the most significant values of R2 metrics and the smallest standard deviation. Gradient boosting and random forest could also be recommended as effective methods for the prediction of salts concentration and permeability and porosity alteration due to salts ablation.

Fig. 9
figure 9

R2 scores for all models

Full size image

The benefits of using machine learning models to estimate rock properties in comparison with standard one-feature approximation are obvious. When we talk about standard one-feature approximation, we assume the next approach. In case we do not know the law (or physical model) controlling the correlation between core sample characteristics and the target rock property, the simplest and the fastest way to build the petrophysical model of the property is consistent single-variable function analysis—finding consistently the target rock property functional dependence on each variable (characteristic of rock). The best single-variable correlation in this approach could be considered as a one-feature approximation model. Instead of this expert approach, ML algorithms allow building multi-feature approximations, which are more relevant to real rock properties correlations. Using one-feature approximation analysis, we found that porosity and permeability after ablation have the strongest correlation with salts concentration and corresponding dependencies shown in Figs. 10 and 11. However, it does not mean that other core sample characteristics are useless. Over against, ML algorithms accounting all ten characteristics should demonstrate better results. In our case, the one-feature approximation is the cubic polynomial which accounts for the dependency of porosity (permeability) alteration on salt content.

Fig. 10
figure 10

Dependence of real and predicted porosity alteration on salts content. \(\varDelta \phi = \phi - \phi _0\), where \(\phi _0\) is the porosity before salts ablation and \(\phi \) is the porosity after salts ablation

Full size image
Fig. 11
figure 11

Dependence of real and predicted permeability alteration on salts content. \(\varDelta K = K - K_0\), where \(K_0\) is the permeability before salts ablation and K is the permeability after salts ablation

Full size image

To compare ML methods with one-feature approximation approach, predictions of porosity and permeability alterations were performed in three ways:

  • using one-feature approximations for porosity and permeability dependencies on salts content (here we take into account only one feature, solid lines in Figs. 10 and 11);

  • using prediction models based on neural network with all ten predetermined features (dataset with salts concentration measurements, green dots in Figs. 10 and 11);

  • using prediction models based on neural network with only nine predetermined features (dataset without salts concentration measurements, red dots in Figs. 10 and 11).

The last approach includes a two-step procedure. First, we estimate salts concentrations with corresponding prediction model, and second, we use this predicted values in porosity and permeability predictions. This approach is applicable in the case when we do not have experimental measurements of salts concentrations.

Fig. 12
figure 12

Comparison of prediction by ML model and one-feature approximation for porosity

Full size image
Fig. 13
figure 13

Comparison of prediction by ML model and one-feature approximation for permeability

Full size image

The more detailed comparison of machine learning models and standard one-feature approximation is presented in Figs. 12 and 13. Here, the experimentally measured porosity (Fig. 12) and permeability (Fig. 13) were compared with the predicted values from ML (with and without salt content measurements) and one-feature approximation. These plots demonstrate the difference between three applied approaches for the estimation of porosity and permeability after desalinization. Originally, one-feature approximation was obtained from dependency of porosity (permeability) alteration on salt content (Figs. 10,  11). Then, these alterations were used to obtain values of porosity and permeability after desalinization. Blue triangles in Figs. 12 and 13 relate to ML model with known salt content. These points are located near the plot diagonal (ideal case). Black points relate to one-feature approximation, and these points are the most distant from diagonal. Yellow squares are approximation by ML with salt content preliminary predicted by ML. These predictions were made by using the approach described in Sect. 2.4 in cross-validation as a third step (k-fold cross-validation with k equal to the number of samples). This method helps to compare approaches of permeability evaluation between each other and depicts them on the plot. It does not evaluate the performance of ML algorithms well (methods evaluation was given in Tables 2,3,4), because we have only one value of R2 (Eq. 11) and does not have confidence intervals. From Figs. 12 and 13, one can see that machine learning models work better.

Quantitative comparison of models is presented in Table 5. Negative value of R2 for the one-feature approximation of permeability was obtained because of several points, which after recalculation (from normalized permeability to absolute values) lay very far from experimental data and add huge error in R2 calculation (Eq. 11). One may remove these points and obtain much better estimation, but ML models work with satisfying accuracy at these points, so we have left results as they are to demonstrate the superiority of ML over old method. Table 5 confirms that simple polynomial regression taking into account only one feature at the same time works not so well as machine learning models considering many different features. We can also see that restriction of the dataset (case without salts concentration measurements) does not strongly affect prediction quality. However, it makes it possible to predict porosity and permeability alterations using only formation and core sample depths, initial porosity and permeability, rock density and lithology description. Feature ranking for salts concentration and permeability and porosity alterations models with Python’s XGBoost method demonstrate that sample color and horizon have a feeble influence on the predictive models and could be excluded from feature list for further applications.

Table 5 Performance of the prediction models
Full size table

4 Conclusion

In this paper, applicability of various machine learning algorithms for the prediction of some rock properties was tested. We demonstrated that three special properties of salted reservoirs of Chayandinskoye field could be predicted only basing on routine core analysis data. The target properties were:

  • alteration of open porosity,

  • alteration of absolute permeability,

  • salts mass concentration.

After core desalination, permeability could be increased up to 60 times and porosity up to 2.5 times. Usually, these characteristics are out of RCA scope because it is time-consuming and occasional analysis. It is very useful for reservoir development planning to have the predictive models in case of lack of this type of data. Porosity and permeability before desalination, sample density, and lithology and texture description are the RCA input data for our predictive models.

To build relevant predictive models, the dataset with results of 100 + laboratory experiments was formed. The main nine features were: formation top depth, formation bottom depth, initial (before desalination) porosity and permeability, sample depth adjusted to log depth, sample density (before desalination), average grain size (by lithology and texture description), sample color, and horizon ID. These features were used to build the salts concentration predictive model. For porosity and permeability alteration prediction, we additionally used the tenth feature—the salts concentration. From a technical point of view, there is no matter these concentrations measured or predicted with other ML model. We reported seven algorithms:

  • Linear regression with L1 regularization;

  • Decision tree;

  • Random forest;

  • Gradient boosting;

  • XGBoost;

  • Support vector machine;

  • Artificial neural network.

The best two algorithms for porosity and permeability alteration prediction were support vector machines and neural network. For permeability, the linear regression with regularization also showed good results. The best models demonstrate the determination coefficient R2 of 0.85 + for porosity and permeability. High precision of developed models looks to be helpful in decreasing geological uncertainties in modeling of salted reservoirs. It was shown that porosity and permeability before water intrusion along with the matrix density, sample depth, and salts content are the most influencing features on permeability and porosity alteration.

The predictive model of salts concentration has been developed using the results of routine core analysis and data on core depth and top and bottom depths of productive horizons. The best algorithms here were gradient boosting and neural network. The highest coefficient of determination R2 for salts concentration in rocks equals 0.66. The precision of salts model is lower than the precision of porosity and permeability models. Nevertheless, the developed models allow to estimate the salts content in rocks without special experiments.

Combining all three models, it is also possible to make precise porosity and permeability alterations predictions using only a minimal volume of routine core analysis data: formation and core sample depths, initial porosity and permeability, rock density and lithology description. Accordingly, with these instruments geoscientists and reservoir engineers can estimate the porosity and permeability alteration at waterflooding conditions having RCA measurements only.

It was shown that different algorithms work better in different models. However, the best machine learning method for the prediction of all three parameters was two-hidden-layer neural network in MLPRegression implementation. This algorithm gave the highest values of R2 metric and the smallest standard deviation. Gradient boosting and random forest could also be recommended as alternative methods for predictions but with lower precision.

Finally, this work showed that machine learning methods could be applied for the prediction of rock properties, of which laboratory measurements are time-consuming and expensive.