A Numerical Analysis of Permeability Evolution in Rocks with Multiple Fractures

Abstract

This work is devoted to numerical analysis of permeability in rocks with multiple fractures. We propose a discrete approach for porous media with dual porosity. The intact porous rock is first discretized by an assembly of impermeable blocks according to the Voronoi diagram. The pore space of the intact rock is replaced by an equivalent network of interfaces between blocks, which produces the same macroscopic hydraulic conductivity as the intact rock. An induced network of macroscopic fracture or cracks is then introduced into the discrete porous rock. A specific numerical algorithm is developed to solve the obtained dual-porosity discrete porous medium. A series of numerical studies are performed in order to verify the efficiency of the proposed method and to investigate influences of mesh sensitivity, effects of fracture geometry and distribution. The proposed model is then applied to the study of permeability evolution in rock samples submitted to biaxial compression tests with different confining pressures. It is found that the proposed model is able to correctly reproduce the progressive process of initiation and propagation of fractures and the related evolution of permeability.

1 Introduction

The evolution of intrinsic permeability of rocks is an important factor in many engineering applications, such as hydroelectric engineering, deep mining, petroleum engineering, underground storage of oil and gas, and geological disposal of radioactive waste. A number of experimental works have shown that the intrinsic permeability evolution in rocks is highly related to the initiation and propagation of cracks (Bruno 1994; Chen et al. 2000; Schulze and Kern 2001; Berkowitz 2002; Gueguen and Schubnel 2003; Louis et al. 2005). In some cases, the intrinsic permeability can increase by several orders of magnitude due to the onset of connected fractures (Suzuki et al. 1998; Souley et al. 2001; Bossart et al. 2002; Oda et al. 2002; Jiang et al. 2010). Therefore, the permeability evolution in many rocks is inherently coupled with the deformation, damage and failure process. It is then necessary to develop coupled models for the description of hydromechanical behavior of porous rocks.

Based on experimental evidences, various numerical models have been developed by considering the evolution of permeability. Without giving an exhaustive list of such works, we can mention continuous plastic and damage models which consider that the permeability is coupled with plastic deformation or damage state. In some more empirical approaches, the permeability was even directly depending on the applied stress state. All these models give a phenomenological description of experimental data obtained but fail to take into account the relationship between the microstructural modification and macroscopic permeability evolution. In order to improve the phenomenological models, tentative efforts have been made on the micro–macro modeling. The main objective was to develop damage models for modeling the coupled permeability evolution and growth of microcracks. For instance, Oda (1985) and Oda et al. (2002) introduced the concept of crack density tensor to describe the permeability change in granite. Souley et al. (2001) used an anisotropic damage model to account for changes in permeability induced by the growth of microcracks. Some works (Shao et al. 2005; Zhou et al. 2006; Jiang et al. 2010) were devoted to the micromechanics-based anisotropic damage models and tried to establish the relationship between damage variables and microcrack aperture to predict the intrinsic permeability using the cubic law. Pereira and Arson (2013) investigated the influence of deformation and damage on the permeability and retention properties of cracked porous media based on the pore size distribution. These models generally introduced some strong assumptions on the distribution of microcracks and can only consider materials with relatively simple microstructures. Further, the permeability was generally not explicitly calculated from the real aperture of cracks.

During the recent years, discrete models have retained an increasing attention as a promising alternative approach for the explicit description of the microcrack initiation, propagation and coalescence and the related permeability evolution in porous rocks. The basic motivation is not only to improve our understanding of the fundamental mechanisms and physical processes that control the change of permeability, but also to provide a numerical model for quantitatively reproducing the representative experimental data. For instance, Bruno (1994) proposed a conceptual micromechanical model based on the discrete element method and network model. But only qualitative studies have been reported. Tang et al. (2002) presented a coupled model that was able to describe the deformation, fluid flow, damage and failure in rocks. However, in this model, the flow of fluid was governed by the classical Biot’s consolidation theory, and effects of microscopic cracks on the permeability were not explicitly considered. Mansouri et al. (2011) computed the permeability of a cemented granular material based on the discrete element model and the lattice Boltzmann method, but the focus of this work was on the cementation process and no effects of cracks were considered.

In this study, we propose a new discrete approach for the numerical modeling of coupled mechanical damage and failure and fluid flow with the evolution of permeability. The proposed model is based on the rigid block spring method (RBSM) for the mechanical modeling (Yao et al. 2013, 2015) and the discrete fracture network (DFN) model for fluid flow in porous rocks (Yao et al. 2012; Jiang et al. 2013). The outline of the proposed approach is illustrated in Fig. 1. Firstly, we use the randomly and uniformly distributed Voronoi diagram to, respectively, represent preexisting or induced macroscopic fractures and connected pore space of porous rock matrix. Secondly, with an appropriate local failure criterion, the RBSM is employed to model the process of crack initiation, propagation and coalescence of rock material. Finally, we propose a dual-porosity model to describe the fluid flow in both rock matrix and macroscopic fractures.

Fig. 1

Outline of the discrete approach based on RBSM and DFN for modeling hydromechanical coupling

2 DFN-Based Dual-Porosity Model

2.1 Equivalent Interface Network

For the modeling of fluid flow in a porous continuum using Darcy’s conduction law, a permeability tensor is defined and identified. In order to describe the evolution of permeability due to the initiation and propagation of cracks or fractures, we propose here to develop a discrete approach. The porous continuum is discretized by a randomly or uniformly distributed assembly of impermeable blocks based on the so-called Voronoi diagram. The pore space of the porous continuum is hydraulically replaced by the network of interfaces between blocks, preserving the same macroscopic permeability. Therefore, in order to develop the discrete approach for numerical modeling of fluid flow in rock matrix based on this concept, it is first needed to determine the equivalent hydraulic aperture of interfaces so that the macroscopic permeability of the interfaces network is equivalent to that of the rock matrix. In order to determine this aperture and also to investigate its mesh dependency at the same time, we have chosen seven groups of numerical specimens by varying the total number of elements (blocks) as 1010, 2053, 5235, 10,566, 21,329, 53,584 and 107,854. Further, each group contains 10 specimens with different element arrangements. The size of each specimen is 1 m by 1 m. The hydraulic aperture of each interface segment $b_\mathrm{i}$ is set to be $1\times 10^{-6}\,\hbox {m}$; the transmissivity of interface is calculated by using the cubic law:

$$\begin{aligned} T_\mathrm{i} =\frac{gb_\mathrm{i}^{3}}{12v} \end{aligned}$$

(1)

$g$ and $v$ are, respectively, the gravity acceleration and the coefficient of kinematic viscosity of water. The hydraulic boundary conditions are shown in Fig. 2, respectively, for the vertical and horizontal flow. As in many engineering applications, in this paper, we have used the water head as the measure of water pressure. The water head of 1m is equivalent to 9.81 kPa. Accordingly, the unit of hydraulic gradient is set as 1 m/m, which is equivalent to 9.81 kPa/m. For each group of specimens, ten values of flow rate have been obtained from numerical simulations for each flow direction. Based on these values, it was possible to perform a statistical analysis to determine the mean value and coefficient of variance, as listed in Table 1. $Q_\mathrm{h}$ and $Q_\mathrm{v}$ are, respectively, the total horizontal and vertical flow rate, respectively. $\mu$ denotes the mean value while $\lambda _\mathrm{v}$ is the coefficient of variance defined as the ratio of the standard deviation to the mean value. One can see that there is a very small difference between the vertical and horizontal flow rate in all groups of specimens, indicating that the hydraulic isotropy is reproduced by the Voronoi interfaces network. Then, the variance of effective hydraulic conductivity among the same group of specimens is also very small, not exceeding 0.32 %. This means that the mesh arrangement has a negligible impact on the macroscopic results. Further, it seems that the variance in each group trends to decrease when the total number of elements increases.

Fig. 2

Hydraulic boundary conditions for computation of vertical and horizontal conductivity. a Vertical flow, b horizontal flow

Table 1 Statistical analysis of conductivity for different groups of numerical tests

Due to the symmetry, we define the average total flow rate for each group of specimens as $Q_0$:

$$\begin{aligned} Q_0 \cong \hbox {average}(Q_\mathrm{h}) \quad \hbox {or} \quad Q_0 \cong \hbox {average}(Q_\mathrm{v}) \end{aligned}$$

(2)

The relationship between the average total flow rate and the element number of each group $N$ is given in Fig. 3. It can be observed that there is a linear relationship between and the dimensionless parameter $Q_{0}/T_\mathrm{i}$, such as

$$\begin{aligned} Q_{0}/T_\mathrm{i} =0.9473\sqrt{N}-1.0448 \end{aligned}$$

(3)

Then, for the isotropic network of interfaces, we define the macroscopic hydraulic conductivity as $C_{0}$:

$$\begin{aligned} C_{0}= C_\mathrm{h}= Q_\mathrm{h}/h \quad \hbox {or}\quad C_0 =C_\mathrm{v} =Q_\mathrm{v}/w \end{aligned}$$

(4)

$C_\mathrm{h}$ and $C_\mathrm{v}$ are, respectively, the macroscopic horizontal and vertical conductivity, $h$ and $w$ the width and height of the specimen, taken equal to $1\, \hbox {m}$ here. According to Eqs. (1), (2) and (4), if $N$ and $C_0$ are known a priori, the effective hydraulic aperture $b$ can be calculated. It is worth noting that $N$ is the element number in a unit square. If the real size of the specimen $h \hbox {m}\times w \hbox {m}$ and the total number of elements is $N_0$, then the needed value of $N$ in Eq. (2) is given by:

$$\begin{aligned} N=N_0 /(h\times w) \end{aligned}$$

(5)

Fig. 3

Relationship between $Q_0 /T_\mathrm{i}$ and $\sqrt{N}$

2.2 Numerical Method Flow Simulation in Fractured Media

As mentioned above, the failure process of most rocks is controlled by the initiation and propagation of macroscopic fractures or cracks, affecting not only the mechanical behavior but also the hydraulic property. In the framework of discrete fracture network (DFN) method adopted in this work, induced macroscopic fractures are embedded in the Voronoi diagram-based interface network, which represents the initial porous medium. One obtains the so-called dual-porosity medium, respectively, with the initial interface network and induced fracture network. In this way, the fluid flow in both the rock matrix and fractures is treated in the same way based on the discrete fracture network model. However, there is a numerical problem to be solved to apply the DFN-based dual-porosity model in practice. Since the transmissivity of fractures is significantly different from that of interfaces, usually in several orders of magnitude, the global equilibrium equations for the flow simulation may be ill-conditioned, and the PCG method sometimes cannot give the correct solution. Indeed, the global system of equilibrium equations for the flow simulation can be expressed as (Jiang et al. 2013):

$$\begin{aligned}{}[K]\{\phi \}=\{Q\} \end{aligned}$$

(6)

$[K]$ is the global matrix of hydraulic conductivity, $\{ \phi \}$ the vector of water head (or equivalently pore pressure) and $\{Q\}$ the vector of hydraulic charge. For the sake of simplicity, no details on the construction of this system will be given here. Readers can refer to Yao et al. (2012). In the PCG method, one needs the initialization of the vector $\{\phi \}$, noted by $\{ \phi \}^{0}$. $\{ \phi \}^{0}$ is usually chosen according to the boundary condition by experience. The solution of the system can be very sensitive to $\{ \phi \}^{0}$ when $[ K ]$ is very ill-conditioned.

Consider here an example. The geometry of the studied porous medium is shown in Fig. 4. Five fractures are randomly located in the porous medium. The effective conductivity of the rock matrix is set as $C_\mathrm{r} =1\times 10^{-14}\,\hbox {m}/\hbox {s}$, and $N=13,527$. Using the method mentioned above, the equivalent hydraulic aperture of interfaces is calculated and equal to $b_\mathrm{i} =4.79\times 10^{-8}\,\hbox {m}$. The hydraulic aperture of fractures is $b_\mathrm{f} =4.79\times 10^{-5}\,\hbox {m}$, say 1000 times that of interfaces. In this case, the difference between the minor and major component in $[K]$reaches 9 orders of magnitude. Here, the equilibrium between the flow rate on the upstream boundary $(Q_\mathrm{u})$ and that on the downstream boundary $(Q_\mathrm{d})$ is used as an indicator to check the quality of numerical solution. Take $\{ {H_1} \}$ as the initialization of $\{ \phi \}$, so that all elements take the water head of the upstream boundary. Using the PCG method, we get $Q_\mathrm{u} =8.953\times 10^{-14}\, \hbox {m}^{2}/\hbox {s}$ and $Q_\mathrm{d} =9.071\times 10^{-14}\, \hbox {m}^{2}/\hbox {s}$. The solution is totally wrong since the flow rate on the downstream boundary $(Q_\mathrm{d})$ should not be positive.

Fig. 4

Geometry and fracture distribution of the specimen for the verification of the numerical solution for ill-conditioned system of equations

In light of the sensitivity of the solution to $\{ \phi \}^{0}$, a pragmatic procedure is proposed here to improve the solution with PCG. We consider it as pragmatic since we cannot provide here a rigorous mathematical demonstration. The basic idea is to find an initialization $\{ \phi \}^{0}$ to approach gradually to the real solution. The following steps are proposed:

• 1. Suppose the total number of iterative steps of the procedure is $S$, in the first step, we set:

  $$\begin{aligned} \{\phi \}_1^0 =\{H_1 \} \end{aligned}$$

  (7)

• 2. In the $s$th step, assume that $b_\mathrm{f}^{\prime } =({s/S})^{1/3}b_\mathrm{f}$, take this $b_\mathrm{f}^{\prime }$ as the hydraulic aperture of the fractures to construct the global matrix $[D]_s$;

  $$\begin{aligned} \left. {{\begin{array}{c} {b_\mathrm{i}} \\ {b_\mathrm{f}^{\prime } =( {s/S} )^{1/3}b_\mathrm{f}} \\ \end{array} }} \right\} \Rightarrow [D]_s \end{aligned}$$

  (8)

• 3. With the solution in the step ($s-1)$ as the input data for the step ($s)$;

  $$\begin{aligned} \{\phi \}_s^0 =\{\phi \}_{s-1} \end{aligned}$$

  (9)

  Solve the following system of equations:

  $$\begin{aligned}{}[D]_s \{\phi \}_s =\{B\} \end{aligned}$$

  (10)

  In the last step $(S)$, we can get the final solution of the system (6).

Note here that the total number of iteration $(S)$ is set a prior and then a known parameter. We use the gap between $Q_\mathrm{u}$ and $Q_\mathrm{d}$ as the indicator of convergence. When the final gap is under 1 %, we consider that the convergence condition is satisfied. Using the proposed procedure, the results of the example presented above are given in Table 2 with different values of $S$. In this Table, $Q_{32} =1.946\times 10^{-14}\,\hbox {m}/\hbox {s}$, is the flow rate computed when $b_\mathrm{f} =32b_\mathrm{i}$. We can see that the gap between $Q_\mathrm{u}$ and $Q_\mathrm{d}$ generally becomes smaller as $S$ increases, indicating that this procedure can effectively solve this kind of ill-conditioned linear systems of equations. According the results shown in Table 2, the rate of convergence of the numerical method seems to be quite slow. But it is worth noting that the example studied here is an extreme case in which the difference between the minor and major component in the matrix $[K]$ reaches 9 orders of magnitude. Therefore, the convergence rate is very slow. We just use this example here to show the efficiency of the method proposed. In the biaxial compression tests presented later, however, the difference is only 6 orders of magnitude. We will see that the value of $S=100$ is enough for almost all cases, and this is an acceptable convergence rate.

Table 2 Numerical results obtained with the proposed procedure

3 Verification of the DFN-Based Dual-Porosity Model

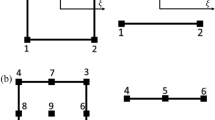
In the proposed DFN-based dual-porosity model, the interfaces representing the intact rock are treated in the same manner as macroscopic fractures, only with a different hydraulic aperture as that of fractures. In order to verify the efficiency of proposed method in predicting the effective conductivity of fractured rocks, we consider here the numerical example reported in Lough et al. (1998). This example considers a unit cube containing a single macroscopic fracture. The fracture with a length of 0.6 units is centered at the cube and oriented at an angle $\alpha$ with respect to the $x$ axis. The initial geometry of the 3D example used by Lough et al. (1998) is illustrated in Fig. 5a. In Fig. 5b, we present the 2D domain studied in the present work. The simplification of the 3D problem to the 2D one is motivated by the fact that in this example the fluid flow occurs essentially in the $x$–$y$ plane, and the main objective here is to study effects of the preexisting fracture on the hydraulic conductivity in $x$ and $y$ directions. The local transmissivity of interface $(T_\mathrm{i})$ is set as 1 unit, and the transmissivity of the fracture is set as $T_\mathrm{f} =2\times 10^{6}\,T_\mathrm{i}$. The Voronoi mesh used is illustrated in Fig. 6.

Fig. 5

Geometry of the specimen with an oriented fracture. a 3D geometry of Lough’s example, b 2D geometry used in this study

Fig. 6

Voronoi mesh for the sample with a fracture orientated at $45^{\circ }$

We know that the effective conductivity will depend on the fracture orientation. Denote the macroscopic horizontal and vertical conductivity as $C_\mathrm{h0}$ and $C_\mathrm{v0}$ for $\alpha =0$. Then, for an arbitrary orientation $\alpha$, the effective conductivity can be written as:

$$\begin{aligned} C_\mathrm{h}&= C_\mathrm{h0}\cos ^{2}\alpha +C_\mathrm{v0} \sin ^{2}\alpha \end{aligned}$$

(11)

$$\begin{aligned} C_\mathrm{v}&= C_\mathrm{h0} \sin ^{2}\alpha +C_\mathrm{v0} \cos ^{2}\alpha \end{aligned}$$

(12)

Take that $C_\mathrm{v0} =1$, the relative value of $C_\mathrm{h0}$ computed by the proposed model is 1.347, with a minor difference of 0.12 % compared to the theoretical prediction of 1.3486 given by Lough et al. (1998). Comparisons between numerical results and theoretical predictions of the relative effective conductivity are presented in Fig. 7 for different orientations of fracture. One can observe that the numerical results are in good agreement with the theoretical predictions.

Fig. 7

Variation of conductivity with fracture orientation-comparisons between theoretical prediction and numerical results

4 Effects of Fracture Geometry on the Effective Conductivity

In this section, we propose to study effects of some geometric parameters of macroscopic fractures on the effective hydraulic conductivity such as hydraulic aperture, length and connectivity.

4.1 Hydraulic Aperture of Fracture

A group of simulations are conducted by varying the hydraulic aperture of preexisting fractures $(b_\mathrm{f})$ to investigate its effect on the effective horizontal conductivity of rock mass $(C_\mathrm{h})$. The geometry used in the simulations is the same as that shown in Fig. 5b, with $\alpha =0$. The hydraulic boundary conditions are those given in Fig. 2b. $N$ is set as 11,458, and the conductivity of rock matrix $C_\mathrm{r}=1\times 10^{-12}\,\hbox {m}/\hbox {s}$. According to Eqs. (1) and (2), the hydraulic aperture of interfaces is computed and equal to $b_\mathrm{i}=2.287\times 10^{-7}\,\hbox {m}$. Numerical results are presented in Fig. 8 for various values of $b_\mathrm{f}$, say from $b_\mathrm{f} =b_\mathrm{i}$ to $b_\mathrm{f}=512b_\mathrm{i}$. It is found that the ration between the horizontal and vertical conductivity $(C_\mathrm{h}/C_\mathrm{r})$ increases as the value of $b_\mathrm{f}$ increases until $b_\mathrm{f} =32b_\mathrm{i}$. After that value, this conductivity ratio becomes constant and the increase in $b_\mathrm{f}$ has no more impacts on this conductivity ratio. The limit value of the ratio $C_\mathrm{h} /C_\mathrm{r}$ is 1.347 in this case. Such a result suggests that an isolated fracture has a limited influence on the enhancement of hydraulic conductivity of porous medium.

Fig. 8

Effective horizontal conductivity for different values of hydraulic aperture of fracture

4.2 Fracture Length

Two different cases are considered to study the effect of fracture length on the effective conductivity. In the first case, the fracture is located in the center of the rock specimen (see Fig. 9a), while in the second case, the fracture is connected to the upstream boundary (see Fig. 9b). The hydraulic boundary conditions are those shown in Fig. 2b. $N$ is set as 11,458 and the hydraulic conductivity of rock matrix is $C_\mathrm{r}=1\times 10^{-12}\,\hbox {m}/\hbox {s}$. The computed values of the ratio $(C_\mathrm{h}/C_\mathrm{r})$ are presented in Fig. 10 by varying the fracture length $l$ from 0.1 to 0.9 units. One can see that the conductivity ratio increases as the length gets larger. In particular, the value of $C_\mathrm{h}/C_\mathrm{r}$ for the case with a connected fracture is overall larger than that with an isolated and centered fracture. Note that when $l=1$, the percolation condition is satisfied, the ratio of transmissivity $(T_\mathrm{h}/T_\mathrm{r})$ abruptly rises to 834, about 300 times the value for $l=0.9$.

Fig. 9

Geometry and fracture disposition for study of length effect. a Fracture located at the center, b fracture connected to the upstream boundary

Fig. 10

Influence of fracture length on effective conductivity for two fracture dispositions

In most constitutive models based on the homogenization procedure, it is generally assumed that the hydraulic pressure gradient is uniform inside the unit cell or equivalent volume element and equal to the prescribed macroscopic pressure gradient. According to the present study, this assumption seems to be debatable. The contour graphs of water head for $l=0.1$, 0.5 and 0.9 are shown in Fig. 11. One can see that the local pressure gradient of the fracture is, respectively, equal to $1.08\times 10^{-4}$, $3.03\times 10^{-4}$ and $1.64\times 10^{-3}$. These values are all much smaller than the prescribed macroscopic hydraulic pressure gradient (1 m/m). Moreover, there seems to be a trend that the shorter the fracture is, the smaller the gradient is. As a result, those models with this assumption may greatly exaggerate the contribution of the isolated fractures to the macroscopic permeability.

Fig. 11

Contours of water head with different values of fracture length. a $l=0.1$, b $l=0.5$, c $l=0.9$, d $l=1$

4.3 Intersection Between Multiple Fractures

Intersections of multiple fractures may result in complex flow behaviors. A simple example containing two fractures is considered here to study the effect of fracture intersection. The geometry conditions are shown in Fig. 12. Two fractures, respectively, extend in the horizontal and vertical direction. They are both 0.4 in length and perpendicular to each other. The horizontal fracture is positioned in the center of specimen. A geometrical parameter $(r)$ is used to define their intersection position. The combined effects of the two fractures are investigated by varying the value of $r$ from 0 to 0.4.

Fig. 12

Geometry of specimen and fracture configuration for study of intersection effect

The computed values of the effective horizontal conductivity are shown in Fig. 13 with different values of $r$. With the increase in $r,\,C_\mathrm{h}$ first goes down before $r$ reaches 0.2, i.e., the middle of the horizontal fracture. Then, it goes up until $r$ reaches the end of the horizontal fracture. In the present case, when $r=0$ and $r=0.4,\,C_\mathrm{h}$ gets to the maximum value as 1.23. And when $r=0.2,\,C_\mathrm{h}$ gets to the minimum value as 1.14.

Fig. 13

Influence of intersection position on effective horizontal conductivity

Note that in Fig. 7, one can see that an isolated vertical fracture $(\alpha =90^{\circ })$ does not affect the horizontal conductivity $(C_\mathrm{h})$. However, as clearly shown in Fig. 13, through the intersection effect with the horizontal fracture, the presence of the vertical fracture can significantly affect the variation of the horizontal conductivity and this effect depends on the position of vertical fracture.

5 Effects of Fracture Initiation and Propagation

In the previous section, we have studied the effects of some preexisting fractures on the macroscopic hydraulic conductivity of porous rock. In many situations, the failure process of rock materials is controlled by the initiation and propagation of fractures. The induced fractures should also affect the macroscopic hydraulic properties of rocks. Therefore, in this section, we propose to investigation the variation of hydraulic conductivity due to the initiation and propagation of macroscopic fractures.

5.1 Failure Criterion of Interfaces

As for the modeling of fluid flow, the mechanical behavior of porous rock is also described by the modified rigid block spring method (RBSM). Since the emphasis of the paper is put on the hydraulic properties, the detailed presentation of the used RBSM is not given here and can be found in the previous works (Kawai 1977; Nagai et al. 2004; Yao et al. 2013, 2015). In this method, the cohesive brittle rock is represented by an assemblage of rigid blocks that are interconnected each other by their interfaces based on the Voronoi diagram. The elastic property of interfaces is characterized by the normal and tangential elastic stiffness, $k_\mathrm{n}$ and $k_\mathrm{t}$. These local elastic properties of interfaces can be directly related to the macroscopic elastic properties (Yao et al. 2015), for instance, the elastic modulus and Poisson’s ratio $E$ and $\nu$. Further, the macroscopic mechanical strength of material is entirely controlled by the local failure process of interfaces. Two modes of failure are considered for each interface, tensile and shear failure. For the tensile failure, an elastic brittle behavior is assumed and characterized by the tensile strength $T$. Once the tensile normal stress of a point on a contact interface reaches the tension strength, say $\sigma _\mathrm{n}=T$, the brittle failure occurs and the local normal and shear stresses ($\sigma _\mathrm{n}$ and $\sigma _\mathrm{s}$) are instantaneously reduced to zero. For the shear failure, a Mohr–Column-type criterion is employed and the shear strength of interface is characterized by the friction angle $\phi$, cohesion coefficient $C$ and the critical normal stress $\sigma _\mathrm{cr}$. The local shear failure criterion is expressed by:

$$\begin{aligned} f&= |\sigma _{\mathrm{s}\max } |+\sigma _\mathrm{n} \tan \phi -C\le 0,\quad \sigma _\mathrm{n} \ge \sigma _\mathrm{cr}\nonumber \\ f&= |\sigma _{\mathrm{s}\max } |+\sigma _\mathrm{cr} \tan \phi -C\le 0,\quad \sigma _\mathrm{n} <\sigma _\mathrm{cr} \end{aligned}$$

(13)

Note that in many rocks, when the confining pressure is high enough, the mechanical strength becomes quasi-independent on the confining pressure. This means that frictional effect progressively vanishes. In order to interpret this phenomenon in a very simply way, the critical normal stress $\sigma _\mathrm{cr}$ is then introduced the failure criterion. When the normal compressive stress is higher than this critical value, the shear strength of interface becomes constant and independent on the normal stress. Further, when the shear failure occurs, the interface exhibits a softening behavior by reducing the frictional angle from the initial value $(\phi _0)$ to the residual one $(\phi _\mathrm{r})$. The list of mechanical parameters used in the present study is given in Table 3.

Table 3 Mechanical parameters for intact rock

5.2 Conductivity Variation During Failure Process of Intact Rock

Consider a representative rock specimen as shown in Fig. 14. The size of the specimen is $0.05\,\hbox {m}\times 0.05\,\hbox {m}$ and the total number of elements is 13,236. Given that the conductivity of the intact rock is $C_\mathrm{r} =1\times 10^{-14}\,\hbox {m}/\hbox {s}$. According to Eqs. (1), (2) and (4), the hydraulic aperture of the interfaces is calculated and equal to $b_\mathrm{i} =1.983\times 10^{-8}\,\hbox {m}$. With this value of interface aperture, the effective vertical conductivity is equal to $C_\mathrm{v} =9.94\times 10^{-15}\,\hbox {m}/\hbox {s}$, which is very close to that of $C_\mathrm{r}$. The influence of local failure on the hydraulic aperture of interface is taken into account in the following simple way. Once the failure is detected on an interface, the hydraulic aperture of the interface is set to be 10 times and 100 times of the original one, respectively, for tensile and shearing failure, i.e. $b_\mathrm{i}=1.983\times 10^{-7}\,\hbox {m}$ and $b_\mathrm{i} =1.983\times 10^{-6}\,\hbox {m}$ in this case. In calculation of the relative conductivity, we use the gap between $Q_\mathrm{u}$ and $Q_\mathrm{d}$ as the indicator of convergence. When the final gap is under 1 %, we consider convergence condition is satisfied. In this test, $S$ is set as 100 and in most cases this can make the final gap under 1 %. In some specific cases, the gap may be larger than 1 %; then, we reset $S$, making $S$ equal 200 or larger and recalculate the conductivity of this case until the convergence condition is met.

Fig. 14

Voronoit mesh for initially intact rock specimen with 13,236 elements

According to the mechanical parameters given in Table 3, we have performed numerical simulations of biaxial compression tests with different values of confining pressures and plane strain conditions. The macroscopic stress–strain curves of the rock specimen are obtained and presented in Fig. 15. One can see that the compressive strength increases when the confining pressure is higher. The post-peak behavior is also depending on the confining pressure. There is a transition from the brittle to ductile behavior as the confining pressure rises up from 0 to 40 MPa. The failure patterns of the specimen are shown in Figs. 17a, 18a, 19a and 20a. It is observed that it is not easy to establish an obvious relationship between the failure mode and confining pressure. The macroscopic cracks can initiate in a random way inside the specimen. In the real situation, the rock specimen is never uniform and contains some initial defeats. As a consequence, the propagation of cracks generally starts from such defeats.

Fig. 15

Stress–strain curves in biaxial compression tests with different confining pressures

In Fig. 16, we present the evolutions of the relative axial conductivity $(C/C_\mathrm{r})$ as functions of the deviatoric stress $(\sigma _1 -\sigma _3)$ and the axial strain $(\varepsilon _1)$ for four confining pressures. We can clearly see that the evolution of conductivity is negligible before the peak stress is reached. Significant increases in conductivity are observed only after the peak strength and can reach five orders of magnitude. These important increases in conductivity are directly related to the initiation and propagation of macroscopic fractures as shown in the failure patterns. The strain and stress threshold for the onset of conductivity increases when the confining pressure is higher. For instance, a sudden increase in conductivity is obtained for the values of axial strain of 0.0017, 0.0018, 0.0021 and 0.0037, respectively, for the confining pressures of 0, 10, 20 and 40 MPa. In Figs. 17b, 18b, 19b and 20b, we show the flow rate distributions at these critical values of axial strain. Main channels for water flow are clearly depicted, indicating that the connectivity of macroscopic fractures is the essential factor of conductivity enhancement.

Fig. 16

Evolution of axial conductivity of initially intact rock as a function of axial strain for different confining pressures

Fig. 17

Distributions of induced fractures and main flow paths in initially intact rock under uniaxial compression $(\sigma _{3}=0)$. a Fracture distribution, b flow rate contours

Fig. 18

Distributions of induced fractures and main flow paths in initially intact rock under biaxial compression $(\sigma _{ 3}=10\, \hbox {MPa})$. a Induced fractures, b flow rate contours

Fig. 19

Distributions of induced fractures and main flow paths in initially intact rock under biaxial compression $(\sigma _ {3}=20\,\hbox {MPa})$. a Induced fractures, b flow rate contours

Fig. 20

Distributions of induced fractures and main flow paths in initially intact rock under biaxial compression $(\sigma _{ 3}=40\,\hbox {MPa})$. a Induced fractures, b flow rate contours

5.3 Conductivity Variation in Rock Specimen with a Preexisting Fracture

In this section, we consider the rock specimen shown in Fig. 21 containing an initial fracture oriented at $45^{\circ }$, subjected to biaxial compression with different confining pressures. The length of the fracture is $l=1.414\times 10^{-2}\,\hbox {m}$, and the hydraulic aperture is $b_\mathrm{f} =1.983\times 10^{-6}\,\hbox {m}$, being 100 times that of the interfaces. The mechanical parameters of the fracture are listed in Table 4. The effective vertical conductivity of the rock specimen is $C_\mathrm{v}=1.02\times 10^{-14}\,\hbox {m}/\hbox {s}$, being slightly higher than $C_\mathrm{r}$ due to the existence of the initial fracture. All other parameters are the same as those used in Sect. 5.1.

Fig. 21

Voronoi mesh for the specimen with an initial fracture

Table 4 Mechanical parameters for the fracture

The stress–strain curves and the evolutions of relative conductivity as functions of axial strains are shown in Fig. 22. It is found that the stress–strain curves exhibit more ductile behaviors than those obtained for the initially intact specimen (see Fig. 15). There is also a sudden rise of the effective conductivity in the axial direction by about 5 orders of magnitude when the confining pressure is 0, 10 and 20 MPa. However, when the confining pressure is equal to 40 MPa, the abrupt conductivity rise is not observed and the increase is only about 1 order of magnitude. Comparisons of the peak deviatoric stress between the intact rock specimen and the pre-cracked rock specimen are shown in Fig. 23 for the different confining pressures. We can see that the mechanical strength of the pre-cracked rock is generally lower than that of the intact one. However, the effect of the preexisting fracture is not influenced by the confining pressure.

Fig. 22

Evolution of axial conductivity of the initially cracked rock as a function of axial strain for different confining pressures

Fig. 23

Peak deviatoric stress as a function of confining pressure comparison between the initially intact and cracked rock specimens

In Figs. 24a, 25a, 26a and 27a, we show the failure patterns and flow rate distributions of the pre-cracked rock specimen after the peak strength is reached. Compared to the intact rock, the effect of confining pressure on the failure mode of the pre-cracked rock specimen is more obvious than in the intact one. Indeed, the preexisting fracture is guiding the propagation of macroscopic fractures inside the specimen. The final failure pattern of the pre-cracked specimen is represented by the formation of an inclined band of crack coalescence. The orientation of the band decreases when the confining pressure increases. In Figs. 24b, 25b, 26b and 27b, we present the flow rate distributions under the vertical hydraulic gradient. Again, the main flow channels are directly correlated with the main fracture bands, demonstrating that the crack propagation and coalescence are the dominating factor for the variation of hydraulic conductivity. For the case of 40 MPa confining pressure, the fracture band is not crossing through the upper and lower surfaces of the specimen due to its high inclination angle. This can explain that the variation of hydraulic conductivity in this case is much smaller than that in other three cases, as shown in Fig. 22.

Fig. 24

Distributions of induced fractures and main flow paths in initially cracked rock under uniaxial compression $(\sigma _{ 3}=0)$. a Induced fractures, b flow rate contours

Fig. 25

Distributions of induced fractures and main flow paths in initially cracked rock under biaxial compression $(\sigma _{ 3}=10\,\hbox {MPa})$. a Induced fractures, b flow rate contours

Fig. 26

Distributions of induced fractures and main flow paths in initially cracked rock under biaxial compression $(\sigma _{ 3}=20\,\hbox {MPa})$. a Induced fractures, b flow rate contours

Fig. 27

Distributions of induced fractures and main flow paths in initially cracked rock under biaxial compression $(\sigma _{ 3}=40\,\hbox {MPa})$. a Induced fractures, b flow rate contours

6 Conclusion

In this study, we have developed a DFN-based dual-porosity model for fluid flow modeling in cracked rocks with multiple cracks. This discrete model is based the randomly and uniformly distributed Voronoi diagram and able to describe the fluid flow in both the porous rock matrix and induced macroscopic fractures. The efficiency of the model is verified by the comparison with Lough’s work and theoretical predictions.

Effects of some geometrical parameters of preexisting fractures on the effective conductivity of the cracked porous rock mass have been investigated, including the orientation, aperture, length and intersection between multiple fractures. Some interesting remarks can be made. Isolated fractures have a significant impact on the local flow field. The hydraulic gradient in these fractures is much smaller than the macroscopic hydraulic gradient. The intersection of fractures also affects the local flow field, and its influence depends on the intersection position. However, the increase in effective conductivity induced by isolated fractures is limited. But when a percolation condition is attained, the increase can be several orders of magnitude.

This DFN-based dual-porosity model has been combined with the improved RBSM to investigate the conductivity variation by the initiation and propagation of fractures in porous rocks. Numerical tests have been conducted on both the intact rock and the pre-cracked rock under biaxial compression with different confining pressures. Typical failure modes and evolutions of conductivity have been investigated. Some conclusions can be drawn down. Typical phases of the macroscopic stress–strain curves for most brittle rocks are reproduced by the improved RBSM, such as linear elasticity, inelastic deformation, softening and residual phase as well as the transition from brittle to ductile behavior as the confining pressure increases. The fracture coalescence bands leading to the final failure of material are also captured. The distribution of such bands is irregular in the initially intact rock. But in the rock specimen with a preexisting fracture, the propagation of fracture band is clearly guided by the preexisting fracture. The orientation of the band depends on the confining pressure. The evolution of hydraulic conductivity is directly related to the onset of macroscopic fractures and can reach about 5 orders of magnitude after the peak strength. The connected fractures constitute the main channels for water flow. There exists a percolation threshold producing a sudden increase of hydraulic conductivity, and this one increases with the confining pressure.