1 Introduction

Permeability in natural fractured rocks is important as it has a major effect on fluid flow. In geothermal projects (Hanano 2004; Nathenson 2000; Slatlem Vik et al. 2018) it is extremely vital to study permeability of fractured medium for modeling of heat flow in heat chambers. It is also of great importance in oil and gas industry (Tayari et al. 2018; Wei et al. 2018) where permeability strongly controls the oil and gas translation and extraction. Another important application is in water reservoirs (Hunt 2005; Wang and Park 2002) the extent and the quality of an aquifer is directly affected by the permeability of the host and surrounding rocks.

Geophysical methods can be an effective nondestructive technique for permeability prediction of a formation (Fabricius et al. 2007; Fang et al. 2018). However, permeability cannot be linked to geophysical responses (such as logging and seismic data) directly and is often indirectly derived from porosity values computed from acoustic impedances. Therefore, understanding the fluid flow of fractured rocks is of great importance for geophysical methods for permeability estimation, which prompted intensive studies of realistic modeling of fractures. Fractures are typically conceptualized as objects with high fluid permeability and high mechanical compressibility (Xu and Yu 2008; Narsilio et al. 2009; Mostaghimi et al. 2013). For reservoirs with extremely low matrix permeability, fracture networks predominant pathways for the migration of fluids (Roy 2019; Szabó et al. 2015). However, the inherent structural randomness of most fractured rocks can result in a complex hydraulic heterogeneity. Therefore, accurate representations of the fractures and efficient evaluation of their influences on permeability are very important for investigation of the fluid flow in fractured rock masses. Although, linking measured large scale permeability directly to exact fracture parameters is difficult, since the fracture sizes are generally much smaller than the scale of Representative Elemental Volume (REV), acquiring an effective value of fractured rocks in REV can be realized. The effective medium approximations and the Kozeny-Carman relationships have been developed for permeability estimation from internal structure information (Xu and Yu 2008). It has been demonstrated that the simple objects, such as the regularly distributed rectangles or ellipsoids, can be reliably estimated but the complicated rock structures remain enigmatic (Mostaghimi et al. 2013; Narsilio et al. 2009). To improve modelling accuracy, there is an urgent need to develop an integrated method for combination of stochastic fracture networks methods and micro-scale fluid flow modelling approaches. Concerning fractured rocks, the ensemble flow response can be quantified by block or equivalent permeability (Amaziane et al. 2001). The flow paths of fractured rocks are mainly controlled by connected fractures, and the hydraulic response of fracture network is of particular importance for characterizing the large scale fluid flow (Huang et al. 2017). In addition, natural fractured rocks usually display a strong hydraulic complexity causing by the internal morphology of fractures (Li et al. 2016; Zhang et al. 2014) and from their distributions in rocks. (Zhang and Yin 2014). (de Dreuzy et al. 2001a, b) conducted numerical tests of water flow through 2D random fracture networks to study the influence of effective connectivity and aperture on hydraulic properties. The 3D DFNs are advantageous to describe the real fracture parameters, such as orientation, connectivity and location, and giving a more reliable permeability result. In recent research, 3D DFNs were used to study how the surface roughness and connectivity of fracture network can affect the nonlinear flow regimes (Xiong et al. 2019). Further progress in fluid flow and mass transport modeling of natural fracture networks, however, requires a better understanding of the relationship between the fracture parameters and permeability. This paper will focus on developing a workflow for estimation of absolute permeability in discrete fracture network rocks using the Darcian continuum theory and single-phase flow velocity in 3D fractured rocks.

Several direct simulation methods are widely used to model fluid flow within heterogeneous fracture spaces (Khirevich et al. 2015; Starnoni et al. 2017). In direct simulations, the governing equations are solved on the real fracture-space of rocks. Finite difference method (FDM) is another popular direct approach allowing for solving the Navier–Stokes equations directly on 3D images. As noted previously, all computational methods have high computational costs when applied to three-dimensional problems. To improve computational efficiency, (Gerke et al. 2018) developed smart and parallel computing software based on FDM scheme to obtain fluid flow velocity and pressure field within heterogeneous medium.

Although many researches have been conducted on fluid flow, studies on the impact of stochastic features of fracture parameters on permeability prediction remains largely unexplored. In this paper, the effects of stochastic properties of fracture networks on absolute permeability are investigated by integrating 3D DFNs generating, fluid flow modeling and permeability calculating. Fluid flow modeling in our study was carried out by solving the Navier–Stokes equations directly using FDM on 3D models with different fracture parameters. Finally, the absolute permeability results and uncertainty analysis for the relationship between permeability and fracture parameters are presented.

2 Fracture model

The geometrical constitution of the natural fracture systems can be described as a set of convex polygons. The shapes, sizes and locations of these polygons are random. Based on this assumption, fractures were represented as a set of 3D irregular convex polygons, and their sizes followed the negative exponential distribution function (Cheng-Haw et al. 2006; Zazoun 2008). The probability density function PDF fX(x) of a negative exponential distribution Exp (λ) with mean μX = λ and variance σX = λ2 can be obtained as follow (Grana et al. 2014):

$$ f_{X} (x) = \left\{ {\begin{array}{*{20}l} {\frac{1}{\lambda }e^{{ - \frac{x}{\lambda }}} , x > 0, } \\ {0, x \le 0.} \\ \end{array} } \right. $$
(1)

where λ > 0. Their locations were determined by means of three dimensional uniform distributions discretely. A fracture plane orientation is given by two angles, dip and strike (or dip direction), see Fig. 1 for details. Fracture orientation is determined by the direction of the fracture, dip angle and strike angle. The intersection line between the fracture and the horizontal plane is OA, and the angle between OA and the Y-axis is the strike angle, which indicates the extension direction of the fracture. OB is a straight line on the fracture and perpendicular to OA, OC is the projection of OB on the horizontal plane, and the angle between OB and OC is dip angle, which shows the inclination degree of fracture. Strike and dip angles were obtained from uniform and Fisher distributions, respectively. For a single fracture, the mean dip angle was π/4 and its variation was π/8. The mean strike angle was π and variation was π/4. For a fracture network, the region of study is a cube bounded by [xmin, xmax, ymin, ymax, zmin, zmax], DFN can be built directly using ADFNE package, see (Fadakar Alghalandis 2017) for more details about 3D DFNs construction.

Fig. 1
figure 1

The fracture orientation parameters in 3D

Full size image

The samples were set to a cube with a side length (L) of 300 μm. To guarantee the integrity of fractured samples, the maximum length value of fractures equaled to lmax = L/2 = 150 μm.

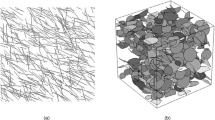
The fracture numbers n were varied from 100 to 500 and consider four mean values of the fracture length (μ) distribution: μ/L = 0.25, μ/L = 0.30, μ/L = 0.35 and μ/L = 0.40. For each combination of the fracture parameters, containing fracture number n, the mean fracture length μ and aperture δ, we generated a DFN. Figure 2 shows 20 realizations of 3D DFNs with different combinations of fracture number and average length value to demonstrate the internal structures of fracture networks. The fracture number n and the ratio μ/L are increased from top to bottom and from left to right, respectively. With respect to a smaller μ/L, smaller fractures dominate the network structure. As μ/L increases, the variance σ increases as well, the relative number of smaller fractures decreases. Increasing the parameter n increases fracture density.

Fig. 2
figure 2

3D DFN models with different fracture numbers and length distributions. The corresponding values of the fracture mean length μ and the fracture numbers n are given in the plot

Full size image

3 Numerical estimation of permeability in discrete fracture network rocks

To study the permeability of Darcian flow for the considered fractured rock sample, we perform single-phase fracture-scale flow tests. In Cartesian coordinate system (x, y, z), let velocity vector v (vx,vy,vz) and pressure field p (px,py,pz) be function of x, y and z. To this end, we solve the Stokes equation (Gerke et al. 2018) formulated for flow velocity field v and pressure field p in 3D space domain.

$$ \left\{ \begin{gathered} \mu \Delta {{\varvec{\upnu}}} - \nabla {\mathbf{p}} = 0 \hfill \\ div{{\varvec{\upnu}}} = 0 \hfill \\ \end{gathered} \right. $$
(2)

under the assumption that Reynolds number (Re) is small:

$$ {\text{Re}} = \frac{\rho \nu l}{\mu },\,Re{ < < 1} $$
(3)

where μ and ρ are the viscosity and density of fluid.

We solved Eq. (2) numerically using the FDMSS open source software (Gerke et al. 2018) to obtain a velocity field under the pressure boundary conditions decided by Δp/L = gradp = 1. According to Darcy's law, the permeability of a given rock sample can be computed as

$$ K = \frac{\mu LQ}{{\Delta pS}} = \frac{\mu Q}{S} $$
(4)

where K is permeability, Δp is the pressure difference generated by the distance L. Consider a cross-sectional area S, the effective area (pores area) and the average velocity over the whole cross-sectional area are Seff and veff respectively, then flow rate Q through it can be computed according to:

$$ Q = \nu_{eff} S_{eff} $$
(5)

So the permeability can be calculated as

$$ K = \frac{{\mu \nu_{eff} S_{eff} }}{S} $$
(6)

In practice, the ratio of effective porosity Vfracture to the volume V is more accurate than Seff to the areas S, we obtain

$$ K = \frac{{\mu \left\langle \nu \right\rangle V_{fracture} }}{V} $$
(7)

Above, the flowchart to determine the permeability of a rock sample containing DFN can be summarized in Fig. 3. The steps are:

  1. 1.

    Input fracture parameters: fracture number, mean length and aperture;

  2. 2.

    Using the ADFNE package (Fadakar Alghalandis 2017) to create 3D DFN;

  3. 3.

    Transform DFN to 3D image;

  4. 4.

    Solving the Stokes equation directly on the voxelized 3D images to obtain flow velocity using the FDMSS software;

  5. 5.

    Substitute the average flow velocity into the Darcian equation to calculate the scalar values of permeability.

Fig. 3
figure 3

Workflow for permeability estimation in a rock sample containing 3D DFN

Full size image

4 Results and discussion

To investigate the influences of length distribution, fracture number and aperture on absolute permeability, we conduct the following numerical experiments. For all the calculations, pressures at every pixel were assigned according to Δp/L = gradp = 1 kg/(vx2 × s2), and μ was fixed to 100 kg/(vx × s), where vx refers to the voxel size. We consider five different values of n, four different values of μ and four different apertures, and obtained 80 different models. The side length L was fixed at 300 μm. Our numerical models were transformed to 301 × 301 × 301 discretized 3D images with an even spatial spacing of 1 μm. In our 3D image files, 0 and 1 represent fractures and solids respectively. The computation results of permeability are given in Table 1. Three numbers of model names represent fracture number, mean length, and aperture, respectively. For example, 300_0.25–1 indicates the computation results of the fracture model with 300 fractures, the ratio of fracture mean length and sample length μ/L and aperture δ equal to 0.25 and 1 μm respectively.

Table 1 Permeability results of 80 different fracture parameter combinations
Full size table

4.1 Permeability as a function of fracture number n

In the first section, the fracture aperture and mean length were fixed to a certain value (μ/L = 0.35 and δ = 3 μm), and fracture number was changed from 100 to 500 to explore how fracture number can affect the permeability of fractured rocks. Figure 4 shows the Darcian permeability as a function of fracture number in the range of 100 to 500 for four different combinations of fracture mean length and aperture. From Fig. 4, the permeability changes hardly with the increase of fracture number when μ/L = 0.25, δ = 1 μm. With μ/L increase to 0.35 and δ keep to 1 μm, it can be found that the permeability also remain almost constant. However, when δ increase to 3 μm, μ/L = 0.25, the permeability is positive correlated with the fracture number. Especially for μ/L = 0.35, the permeability rising tendency remarkably increase with the increase of the fracture number. Hence, on the one hand, it is indicated that the lower level of δ results in the lower permeability in the fracture number range of the 100–500, and for a rock with low fracture aperture the increment of μ/L has subtle influence on the relationship between permeability and the fracture number. The higher δ enhances the positive influence of μ/L on the rising tendency of permeability with the increase of fracture number. On the other hand, the increment of δ reinforces the positive relationship between the permeability and the fracture number a little on the condition of lower μ/L value 0.25. With the larger μ/L value 0.35, the slope of the relationship between the permeability and the fracture number increases when the δ value increases.

Fig. 4
figure 4

Validation and comparison of Darcian permeability as a function of fracture number for four different combinations of fracture mean length and aperture

Full size image
Fig. 5
figure 5

Validation and comparison of Darcian permeability as a function of fracture mean length for four different combinations of fracture number and aperture

Full size image

4.2 Permeability as a function of fracture length distribution

In the second section, the fracture number and aperture were fixed to a certain value (n = 400 and δ = 3 μm), and the ratio of facture mean length and sample length μ/L was changed from 0.25 to 0.40 to explore how fracture mean length can affect the permeability of fractured rocks. Figure 5 represents the Darcian permeability as a function of the ratio μ/L for four different combinations of fracture number and aperture. The permeability keeps a small value (approaching 0) despite the μ/L increases from 0.25 to 0.4 on the condition of δ = 1 μm. Once n = 400, μ/L = 0.25, the permeability increases slowly with the increase of fracture aperture. The rising tendency of the permeability is more obvious when n = 200, μ/L = 0.35. It is indicated that μ/L has more importance on the permeability than the fracture number. While, on the condition of μ/L = 0.35, the increased fracture number 400 enlarge the increasing tendency of permeability apparently.

4.3 Permeability as a function of fracture aperture

In the third section, keeping the fracture number and mean length to a certain value (n = 400 and μ/L = 0.35), and changing the fracture aperture δ from 1 to 4 μm to explore how fracture aperture can affect the permeability of fractured rocks. Figure 6 shows the Darcian permeability as a function of the aperture in the range of 1 to 4 μm for four different combinations of fracture mean length and number. From Fig.  6, the permeability changes hardly with the increase of fracture number when n = 200, μ/L = 0.25. With n increase to 400 and μ/L keep to 0.25, it can be found that the permeability increases slowly with the increase of fracture aperture. However, when μ/L increase to 0.35, n = 200, the permeability is positive correlated with the fracture aperture. Especially for n = 400, the permeability rising tendency remarkably increase with the increase of the fracture aperture.

Fig. 6
figure 6

Validation and comparison of Darcian permeability as a function of aperture for four different combinations of fracture number and mean length

Full size image

4.4 Multivariate regression analysis of fracture parameters and permeability

We increased numerical realizations for each parameter combination to 5.400 results were obtained, and a multivariate regression of the data of fracture number, mean length, aperture and permeability using

$$\begin{aligned} Permeability & = 353.6333 - 160.8944 \cdot \delta - 850.2991 \cdot \left( {\mu /L} \right) \\ & + 277.8966 \cdot \left( {\mu /L} \right) \cdot \delta - 0.6937293 \cdot n + 0.1358125 \cdot n \cdot \delta \\ & + 1.551118 \cdot n \cdot \left( {\mu /L} \right) + 10.86022 \cdot \delta ^{2} \\ \end{aligned} $$
(8)

fits the data quite well. The result clearly shows that in the formation with extremely low matrix permeability, the permeability increases almost linearly with fracture number and length while quadratically with aperture.

4.5 Intersection analysis

In fractured rocks, fracture connectivity controls fluid flow. The intersections between fractures are the key indicator for describing the fracture connectivity in fractured rocks (Dong et al. 2018). Planar polygons were used for fracture representations and therefore the length of fracture intersection becomes the length of the line of intersection between planar polygons in 3D (see Fig. 7). The number of intersections and the total length of intersection lines refer to the number and the total length of the lines of intersections in a DFN models, respectively.

Fig. 7
figure 7

Intersection between two fractures in 3D

Full size image

The range of considered fracture distribution parameters μ and n are closely related to fracture connectivity. In order to facilitate the interpretation of the permeability of the four types of fracture length distributions (μ/L = 0.25, μ/L = 0.30, μ/L = 0.35 and μ/L = 0.40) and three fracture numbers (n = 300, n = 400 and n = 500) considered from the perspective of fracture connectivity, we compared the permeability values for each individual fracture network at a given aperture (δ = 3 μm). For each parameter combination, 5 realizations were conducted. The number and the total length of intersection lines of each fracture network as well as the permeability are plotted in Fig. 8a and b, respectively.

Fig. 8
figure 8

Key results of the hydraulic tests showing the permeability trends with fracture connections: Permeability associated with a The number and b Total length of intersection lines

Full size image

Permeability exhibits an overall increase with an increase in fracture intersection number and total length of intersection lines. The presence of more fracture connectivity increases the fluid flow and, therefore, uppers the permeability. Robust regression was used to compute the fit lines. The correlation coefficients of fitted lines on Fig. 8 a, b are 0.9842 and 0.9940, respectively. Thus, permeability shows a closer link with total length of intersection lines than the intersection number. Figure 8 also presents the variability of permeability is increasing with increasing n and μ. Thus, the larger fracture parameters combination has a larger uncertainty of permeability prediction.

5 Conclusion

The purpose of this study is to investigate the effects of fracture parameters on the absolute permeability of fractured rocks with extremely low matrix permeability by stochastic representation of natural fractures. Series of 3D stochastic fracture networks with different fracture length distribution, aperture and fracture number were established, and the effects of these fracture parameters on the micro-scale fluid flow were systematically investigated. The considered fractures are constituted of homogeneous isotropic convex polygons. The strike, dip angle and length value for each fracture were extracted from Uniform, Fisher and negative Exponential distributions, respectively. The flow velocity field was calculated using Finite-Difference method to solve Stokes equation. Then, the permeability of our rock samples was calculated using Darcy’s law. We numerically acquired permeability of fractured rock samples. We compared the permeability corresponding to changes in the fracture number, aperture, and fracture length distribution of the fractures. From the numerical examples we come to some interesting conclusions.

  1. 1)

    We can see the importance of the fracture parameters to fluid flow in fractured rocks. It is the effective part of the fracture network that directly affects the permeability. The effective part of fracture network is determined by fracture number and the distribution of fracture length and aperture. We found that the fracture number and length variation increased the chances of fracture connection and tended to more fluid flow path, while the fracture aperture increase enhanced this fluid flow and tended to high permeability.

  2. 2)

    From different realization results of the same parameter combination, we found that high value parameters do result in more local distribution patterns of fractures, which can increase the complexity of the fluid flow and making relations between fracture parameters and permeability more complicated and uncertain.

  3. 3)

    The number and the total length of intersections of the fractures are almost linear with permeability. It is indicated that the connectivity features of fractures are a key factor affecting permeability.

These results could contribute to our understanding of the uncertain and nonlinear relationship between fracture parameters and permeability in the natural fractured rocks.