A packet-switched network with On/Off sources and a fair bandwidth sharing policy: state space collapse and heavy-traffic

Abstract

We consider a flow-level model for packet-switched telecommunications networks handling elastic flows with concurrent occupancy of resources, in which digital objects are transferred at a rate determined by capacity allocation on each route. The capacity of each node is dynamically allocated to the routes passing by it through a weighted proportional fair sharing policy, and the arrival request for transfer on each route is generated by N heavy-tailed On/Off sources. Under heavy-traffic, we combine state space collapse (SSC) and an Invariance Principle to show that when $N\rightarrow +\infty$ the conveniently scaled workload and flow count processes converge. SSC establishes a relationship between the corresponding limits by means of a deterministic operator. In Theorem 1 we prove that assuming the other hypotheses hold, SSC is not only sufficient for the convergence, but necessary. In Theorem 2 we prove that when $r\rightarrow +\infty$, r being a scale parameter, the workload limit process converges to a reflected fractional Brownian motion on a polyhedral cone.

1 Introduction

A packet-switched network is a digital telecommunications network that groups all transmitted data, irrespective of content, type or structure into suitably-sized blocks, called packets. The network over which packets are transmitted is a shared network that routes each packet independently from all others and allocates transmission resources as needed.

Routing directs packet forwarding, the transit of logically addressed packets from their source toward their ultimate destination through intermediate nodes, typically hardware devices as routers, bridges, gateways, firewalls or switches, by selecting paths or routes in the network along which to send network traffic. This is performed by means of the packet-switching technology, which is used to optimize the use of the channel capacity available to minimize the transmission latency (i.e., the time it takes for data to pass across the network), and to increase robustness of communication. The best-known use of packet switching is the Internet and most local area networks (LAN).

When dealing with a packet-switched network, it is customary to consider the “packet train” model for which data traffic is essentially composed of individual transactions or flows which can be broadly categorized as “stream” or “elastic”. Elastic flows are established for the transfer of digital objects which can be transmitted at any rate up to the limit imposed by link and system capacity. The digital object in question might be a file, a Web page or a video clip transferred for local playback. We assume that flows are perfectly fluid and ignore problems of granularity due to packet size.

We study a class of packet-switched networks handling elastic flows with concurrent occupancy of resources (nodes and routes connecting them), in which digital objects are transferred at a rate determined by the available bandwidth, which is dynamically shared between flows. The service capacity (bandwidth) on each node is dynamically allocated to the routes passing by the node, and the fraction of capacity assigned to each route is shared at any time among all the flows in progress at the route. This model, which was introduced by Massoulié and Roberts [19], is referred to as a flow-level model by Kang et al. [14], and assumes a “separation of time scales”, which means that the time scale of flow dynamics (digital objects arrivals and departures) is much longer than the time scale of the packet level dynamics on which rate control schemes such as the TCP protocol converge to equilibrium.

The manner in which the bandwidth is allocated to the routes is defined by the network bandwidth sharing policy, and we adopt the usual assumption that traffic to be handled appears as a succession of requests for the immediate transfer of a certain digital object. Due to technical complications of the proposed task, we restrict ourselves to the case of a flow-level model operating under a weighted proportional fair sharing policy, which corresponds to the $\alpha =1$ member of the family of weighted $\alpha$-fair bandwidth sharing policies introduced by Mo and Walrand [20].

The network has a fixed set of nodes and is used by a fixed set of routes and, instead of assuming Poisson arrivals and exponentially distributed digital object sizes, as in De Veciana et al. [4], Bonald and Massoulié [2] and Kang et al. [14], we assume that the arrival process of requests for the digital object transfer on each route is generated by a big number of On/Off sources that during On-periods continuously have data to send and during Off-periods are silent, for which the lengths of the On- and/or of the Off-periods are heavy-tailed (at least one of them). This choice is motivated by the detected presence of long-range dependence and self-similarity in modern high-speed network traffic, especially in the Internet traffic. Indeed, from the work of Taqqu et al. [26] it has been generally accepted that one simple physical explanation for the observed phenomenon of the long-range dependence and self-similarity, consists in the superposition of many On/Off sources with strictly alternating On- and Off-periods and whose lengths are heavy-tailed distributed. This motivation is shared by other recent papers. For example, this is the case of [13], where the asymptotic behavior of the steady-state queue-length distribution, under generalized Max-Weight scheduling in the presence of heavy-tailed traffic, for a system consisting of two parallel queues served by a single server, one of the queues receiving heavy-tailed traffic, and the other receiving light-tailed traffic, is considered. Another example is [18], where the authors examine the impact of the heavy-tailed traffic on the performance of the Max-Weight scheduling in a single-hop switched network with a mix of heavy and light-tailed traffic.

The fact that the superposition of N On/Off sources generates an aggregate cumulative arrival process that conveniently scaled in time by a factor r and in space by a factor of r and $\sqrt{N}$, converges as first N tends to infinity and then, as r tends to infinity, to a fractional Brownian motion process, was proved in Theorem 1 [26], where the authors show the relationship between the parameter describing the heaviness of the tails and the Hurst parameter of the fractional Brownian motion process, $H>1/2$, which measures its degree of self-similarity.

In subsequent work it has been shown that for multi-class networks with FIFO service discipline under heavy-traffic, the convergence of the scaled arrival process carries over to the scaled workload process, which thus also converges to a fractional Brownian motion process but reflected appropriately to be non-negative. See Debicki and Mandjes [5] for the single-station model, and Delgado [6–8] for three different situations in the multi-station scenario. Unlike these works, in this paper we investigate the asymptotic behavior of a family of flow-level models in the heavy-traffic environment, but for networks operating under a weighted proportional fair bandwidth sharing policy. Our motivation was to extend the heavy-traffic limit result of Delgado [7] to this setting. Indeed, in Theorems 1 and 2 we prove that the conveniently scaled workload process converge to a multidimensional reflected fractional Brownian motion process (rfBm) on a polyhedral cone, which is a particular case of convex polytope. By suitably adapting the definition of semimartingale reflecting Brownian motion on a convex polytope of Dai and Williams [3], this process is introduced in Sect. 2, where we also introduce a condition on matrices associated to the polyhedral cone and its directions of constraint at the boundary, named HR, which ensures the existence of such a process. We highlight that when Poisson arrivals and exponential sizes are assumed, a diffusion approximation is obtained instead, a multidimensional reflected Brownian motion (rBm) on a polyhedral cone being the limit of the scaled workload process (see Kang et al. [14]).

By combining the methodology used in Kang et al. [14] with that in Delgado [6–8], we prove in Sect. 4 that under a mild local traffic condition and heavy-traffic, if condition HR holds and a form of state space collapse SSC is met, then the scaled workload converges as $N\rightarrow +\infty$, and then as $r\rightarrow +\infty$, to a multidimensional rfBm process on a polyhedral cone associated to the network (Theorem 2).

The phenomenon of state space collapse SSC was first established by Whitt [28] for a single multi-class station but the term was coined by Reiman [24], and it has been shown to be a key ingredient in the proof of heavy-traffic limit theorems, both in the Poisson-arrivals environment using different service policies (see for instance Peterson [23], Williams [30] and Kang et al. [14]), with a rBm on the positive orthant or on a polyhedral cone as the workload limit process, depending on the service policy, and also in the On/Off heavy-tailed sources context assuming the FIFO service discipline (Delgado [7]) with a rfBm process on the positive orthant instead. Recently, a strong version of SSC has been proved in [21] for an overloaded Markovian queueing system having two customer classes and two service pools, known in the call-center literature as the X-model. This condition has been used by the same authors in [22] in order to develop a refined diffusion approximation for the same model under heavy-traffic. In the present work, for the first time to our knowledge, SSC condition is considered in the context of a heavy-traffic limit theorem in the On/Off heavy-tailed sources context with a fair bandwidth sharing policy, obtaining in the limit a rfBm process on a polyhedral cone.

More specifically, in Theorem 1 we prove that the conveniently scaled workload and flow count processes converge, as $N\rightarrow +\infty$, to processes ${\hat{W}}^r$ and ${\hat{Z}}^r$ respectively, under a mild local traffic condition, heavy-traffic and assumptions HR and SSC, which implies that these limit processes are linked by means of a continuous deterministic operator ${\varDelta }$, obtained by solving an optimization problem, in this way: ${\hat{Z}}^r={\varDelta }({\hat{W}}^r)\,,$ meaning that the flow count process can be approximately recovered as a continuous lifting of the workload process. Actually, in Theorem 1 we prove that assuming the other hypotheses are true, SSC is not only a sufficient condition for the convergence, but also necessary. In Theorem 2 we prove that processes ${\hat{W}}^r$ and ${\hat{Z}}^r$ converge respectively, as $r\rightarrow +\infty$, to W, which is a rfBm process with Hurst parameter H on a polyhedral cone, and $Z={\varDelta }(W)$ .

The main ingredients in the proofs are a combination of Theorem 1 [26] and Theorem 7.2.5 [29] on the one hand, and the Invariance Principle in domains with piecewise smooth boundaries (Theorem 4.3 [15]), for which we set the version we use in Sect. 4.1, on the other. But for applying the Invariance Principle we need some preliminary technical results that can be found in Sect. 5, devoted to a form of multiplicative state space collapse (MSSC). This is a condition trivially implied by SSC but that, in fact, is equivalent to it in our setting, as deduced from Proposition 4. MSSC condition usually appears in relation with heavy-traffic limits in different contexts; for instance, it has been considered in [7] in the context of a fluid queuing network with multiple classes and feedback, fed by a big number of heavy-tailed On/Off sources, where each fluid class is processed at a constant rate by following a FIFO service discipline. More recently, MSSC has been considered in [25] with regard to switched networks (more specifically, single-hop and multihop networks) for a family of scheduling policies related to the maximum-weight policy of Tassiulas and Ephremides [27]. Is worth noting that whereas previous works on switched networks and stochastic processing networks in the diffusion limit have assumed the “complete resource pooling” condition, in [25] this assumption is not required. However, in this work is not shown but it is conjectured that MSSC implies SSC, under an additional hypothesis.

The organization of the rest of the paper is as follows. In Sect. 2 we set up notation and terminology, including definitions of a polyhedral cone and a rfBm process on such a set . The fluid-level model we consider is introduced in Sect. 3, where the network structure, the bandwidth sharing policy, the stochastic processes associated to the model and the heavy-traffic assumption are given. Theorems 1 and 2, which are the main results, are established in Sect. 4, where a simple example to help visualize these mathematical results has been included.

2 Notation and terminology

Let $a,\,b\in \mathbb R$, then $a\vee b$ denotes the maximum of a and b, and $a\wedge b$ the minimum.

For each integer $d\ge 1$, we will denote by $I_d$ the $d-$dimensional identity matrix. Vectors will be column vectors and $v'$ denotes the transpose of a vector (or a matrix) v. Given $v=(v_1,\ldots ,v_d)'\in {\mathbb R}^d,\,$ hereafter we will denote by diag(v) (or by $diag(v_1,\ldots ,v_d)\,$) the $d\times d$ diagonal matrix with diagonal elements $v_1,\ldots ,v_d\,$. Let $\mathbb R^d_{+}$ be the $d-$dimensional positive orthant, $\mathbb R^d_{+} =\{v=(v_1,\ldots ,\,v_d)'\in \mathbb R^d\,:\,v_i\ge 0\,\,\forall i=1,\ldots ,\,d\}.$ For a $d\times d'$ matrix $\,A=(a_{ij})_{i=1,\ldots ,d,\,j=1,\ldots ,d'}\,$, let $|A|\buildrel {\mathrm{def}} \over ={\displaystyle \max _{1\le j\le d'}\big (\sum \nolimits _{1\le i \le d} |a_{ij}|\big )}.$ Note that if $A= diag(v_1,\ldots ,v_d)$, then $|A|=\max \{v_1,\ldots ,v_d\}$. The rank of A will be denoted by rank(A), and if $d'=d$, $A^{-1}$ denotes its inverse, if exists, that is, if the determinant $det(A)\ne 0$. Inequalities between vectors should be interpreted component-wise.

We will say that a sequence of $d\times d'$ matrices $\{A^n\}_n$ converges to a $d\times d'$ matrix A if $|A^n-A|\rightarrow 0$ as n tends to $+\infty$ (this convergence is equivalent to the convergence in the component-wise sense), and we will denote it simply ${\displaystyle \lim _{n\rightarrow +\infty } A^n=A}\,$. The same applies for the particular case $d'=1$, which corresponds to $d-$dimensional vectors, with $|v|\buildrel {\mathrm{def}} \over ={\displaystyle \sum \nolimits _{1\le i\le d} |v_{i}|\,}$ the $\ell _1-$norm. The Euclidean norm on $\mathbb R^d$ is ${\displaystyle ||v||=\big (\sum \nolimits _{1\le i\le d} v_i^2\big )^{1/2}\le |v|}$. The inner product of a couple of vectors $u,\,v\in \mathbb R^d$ is denoted by $\langle \cdot , \cdot \rangle$, that is, ${\displaystyle \langle u,v\rangle = \sum \nolimits _{i=1}^d u_i\,v_i.}$ Let $d(x,\,S)$ denote the distance between $x\in \mathbb R^d$ and $S\subset \mathbb R^d$, $d(x,\,S)=\inf \{\,||x-y||\,:\,y\in S\},$ with the convention $d(x,\,\emptyset )=+\infty$.

Let ${\mathcal C}^d$ be the space of continuous functions $\omega$ from $[0,\,+\infty )$ to $\mathbb R^d$, with the topology of the uniform convergence on compact time intervals, and $\mathcal{D}^d$ the space of continuous on the right with limits on the left functions, endowed with the usual Skorokhod ${\mathcal J}_1-$topology. All stochastic processes in this paper will be assumed to have paths in $\mathcal{D}^d$, for some $d\ge 1$. For each $T\ge 0$ and $\omega \in {\mathcal C}^d$, we define

$$\begin{aligned} \big |\big |\omega (\cdot )\big |\big |_T \buildrel {\mathrm{def}} \over = \sup _{t\in [0,T]}\,\big |\omega (t)\big |= \sup _{t\in [0,T]}\,\Bigg (\,\sum \nolimits _{1\le \ell \le d} |\omega _{\ell }(t)|\,\Bigg ). \end{aligned}$$

We will say that $\omega ^n\rightarrow \omega$ as $n\rightarrow +\infty$ in ${\mathcal C}^d$ (uniformly on compacts, u.o.c.) if for any $T\ge 0$, $||\omega ^n(\cdot )-\omega (\cdot )||_T\rightarrow 0,\,$ and we will denote it ${\displaystyle \lim _{n\rightarrow +\infty }\omega ^n=\omega }.\,$ To measure the oscillation of $\omega$ we make the following definition: for any $T\ge 0,$

$$\begin{aligned} Osc\,\big (\,\omega (\cdot ),\,[0,\,T]\,\big )\buildrel {\mathrm{def}} \over = \sup _{0\le s< t\le T}\, \big |\omega (t)-\omega (s)\big |. \end{aligned}$$

Note that, in general, $Osc\,\big (\,\omega (\cdot ),\,[0,\,T]\,\big )\le 2\,||\omega (\cdot )||_T$ and that $Osc\,\big (\,\omega (\cdot ),\,[0,\,T]\,\big )\ge ||\omega (\cdot )||_T\,$ if $\omega (0)=0$ and $\omega _{\ell }(t)\ge 0$ for any $t\in [0,\,T]$ and any $1\le \ell \le d$.

We let $\mathbf{e}$ be the identity function, that is, $\mathbf{e}(x)=x$.

A sequence of stochastic processes $\{X^n\}_{n\ge 1}$ is said to be tight if the induced measures on $\mathcal{D}^d$ form a tight sequence (that is, the sequence of induced measures is weakly relatively compact in the space of probability measures on $\mathcal{D}^d$).

We will use ${\displaystyle \text {P}-\lim }$ for the convergence in probability (uniformly on compacts), and ${\displaystyle {\mathcal D}-\lim }$ to denote the convergence in distribution on ${\mathcal C}^d$ or ${\mathcal D}^d$ (or weak convergence). That is, we write ${\displaystyle {\mathcal D}-\lim _{n\rightarrow +\infty } X^n=X}$ if the sequence of probability measures induced in $\mathcal{D}^d$ by $\{X^n\}_n$, say $\{P^n\}_n$, converges weakly to that induced by X, P. We denote the weak convergence of probability measures by $P^n \Rightarrow P$. The sequence of processes $\{X^n\}_n$ is called $\mathcal{C}-$ tight if it is tight, and if each weak limit point, obtained as a weak limit along a subsequence, almost surely has sample paths in $\mathcal{C}^d$.

A function $f=(f_1,\,\ldots ,\,f_d)\,:\,[0,\,+\infty )\longrightarrow \mathbb R^d_{+}$ is said to be absolutely continuous if each of its components $f_k$ is absolutely continuous. A regular point for f is a value $t>0$ at which each component of f is differentiable. Let $\frac{d}{dt} f_k(t)$ denote the derivative of function $f_k$ at time t if t is a regular point of f.

The multi-dimensional reflected fractional Brownian motion (rfBm) process on the positive orthant has been introduced, for instance, in Delgado [6, 7] and Konstantopoulos and Lin [17]. Here we extend the definition of this process to a polyhedral cone, which is a particular case of convex polytope. For that we adapt conveniently the definition of a semimartingale reflecting Brownian motion on a convex polytope given in Dai and Williams [3] among others.

Definition 1

(polyhedral cone) For any $d\ge 1$, a $d-$dimensional polyhedral cone S is defined in this way:

for a given set of vectors $v^1,\,\ldots ,\,v^d$ in $\mathbb R^d$, being V the $d\times d$ matrix whose row vectors are $v^1,\,\ldots ,\,v^d$. The fact that the cone is determined by the matrix is made explicit, when convenient, by using the notation S(V).

It is assumed that the interior of the cone is nonempty and that the set $\{v^1,\,\ldots ,\,v^d\}$ is minimal in the sense that no proper subset defines it, that is, for any strict subset $L\subset \{1,\,\ldots ,\,d\}$, the set $\{x\in \mathbb R^d\,:\, \langle v^{\ell }, x\rangle \, \ge 0\quad \text {for all }\ell \in L\}$ is strictly larger than S(V). This is equivalent to the assumption that each of the boundary facets

$$\begin{aligned} \mathtt{F }_{\ell }\buildrel {\mathrm{def}} \over = \big \{x\in S(V)\,:\, \langle v^{\ell }, x\rangle \,= 0\big \},\quad \ell =1,\ldots ,\,d, \end{aligned}$$

has dimension $d-1$. Let $\partial S=\cup _{\ell =1}^d \mathtt{F }_{\ell }$ be the boundary of the cone.

Associated to the cone S(V) we can introduce the directions of constraint u(y) for any y on its boundary, which are constant along each facet, by using a $d\times d$ matrix R whose column vectors are denoted by $u^1,\ldots ,\,u^d$, with the restriction that $\langle v^{\ell },u^{\ell }\rangle >0$ for all $\ell =1,\ldots ,d$, in the following way: we can define $I(y)\buildrel {\mathrm{def}} \over = \{i=1,\ldots ,\,d\,:\,y\in \mathtt{F }_i\}$. Then, if $I(y)=\{\ell \}$ for some $\ell$, u(y) is defined as $u^{\ell }$. Otherwise,

$$\begin{aligned}&u(y)\buildrel {\mathrm{def}} \over = \left\{ \xi \in \mathbb R^d\,:\,\xi =\sum _{i\in I(y)} \delta _{i}\,u^{i},\,\quad \text {with some}\,\,\delta _{i}\ge 0\right. \nonumber \\&\left. \qquad \qquad \quad \text {and such that}\,\,|\xi |=1\,\right\} \end{aligned}$$

(1)

We will say that the cone S(V) with associated matrix of directions of constraint R is “in normal form” if $rank(R)=d$ and it holds that $\langle v^{\ell },u^{\ell }\rangle =1$ for all $\ell =1,\ldots ,\,d,$ that is, the diagonal entries of matrix VR are all equal to 1.

Definition 2

(rfBm on a polyhedral cone) Let S(V) be a d-dimensional polyhedral cone as in Definition 1, with associated matrix of directions of constraint R, and in normal form. A reflected fractional Brownian motion on S(V) associated with data $(x,\,H,\,\theta ,\,{\varGamma },\,R)$, where $x\in S(V)$, $H\in (0,\,1)$, $\theta \in \mathbb R^d$ and ${\varGamma }$ is a $d\times d$ positive definite matrix, is a $d-$dimensional process $W=\{W(t)=(W_1(t),\ldots ,\,W_d(t))',\,t\ge 0\}$ such that

• (i) W has continuous paths and $W(t)\in S(V)$ for all $t\ge 0$ a.s.,

• (ii) $W=X+R\,Y\,$ a.s., with X and Y two d-dimensional processes, defined on the same probability space and verifying:

• (iii) X is a fBm with associated data $(x,\,H,\,\theta ,\,{\varGamma })$, that is, it is a continuous Gaussian process starting from x, with mean function $E\big ( X(t)\big )=x+\theta \,t$ for any $t\ge 0$ ($\theta$ is the drift vector), and with covariance function given by: if $t,\,s\ge 0,\,$

  $$\begin{aligned}&Cov\big ( X(t),X(s)\big )\\&\quad =E\Big (\big ( X(t)-(x+\theta \,t)\big )\big ( X(s)- (x+\theta s)\big )^T\Big )\\&\quad = {\varGamma }_H(s,t) {\varGamma }, \end{aligned}$$

  where ${\displaystyle {\varGamma }_H(s,t)=\frac{1}{2}\, \big (\,t^{2H}+s^{2H}-|t-s|^{2H}\,\big )\,}$, and

• (iv) Y has continuous and non-decreasing paths, and for each $\ell =1,\ldots ,\,d,$ a.s., $Y_{\ell }(0)=0$ and $Y_{\ell }(t)=\int \limits _{0}^{t} 1_{\{W(s)\in \mathtt{F }_{\ell }\}}\,d\,Y_{\ell }(s)\,$ for all $t\ge 0$ (that is, $Y_{\ell }$ can only increase when W is on the boundary facet $\mathtt{F }_{\ell }$).

  If conditions (i), (ii) and (iv) are met, we say that the pair $(W,\,Y)$ is a solution of the (multidimensional) Skorokhod Problem associated to X on the cone S(V) and with associated matrix of directions of constraint R.

To get an idea, rfBm starts in the interior of the cone S and behaves like a fBm being constrained to remain within S in the following way: when the fBm process touches the boundary $\partial S$, it is instantaneous “reflected” preventing its exit from S. For each $\ell$, the $\ell -$th column vector of matrix R, $u^{\ell }$, gives the direction of the reflection on facet $\mathtt{F }_{\ell }$, and $Y_{\ell }$ gives its intensity. On the intersection of two or more facets (ridges and peaks), the direction of reflection is given by a linear combination of the corresponding vectors $u^{\ell }$ of the form given by (1). Two fundamental properties of fBm justify the general interest in it from the modelling point of view: fBm is a self-similar process and has long-range dependent increments, which are positively correlated if $1/2<H<1$.

Remark 1

As usual, we call the map $\pi \,:\,X \mapsto W$ the Skorokhod Map associated to the Skorokhod Problem introduced in Definition 2. It is known that strong existence and uniqueness of the solution of a Skorokhod Problem can be established when the associated Skorokhod Map is Lipschitz continuous on ${\mathcal C}^d$ (see for instance the discussion given in the Introduction of Dupuis and Ramanan [10]). In the couple of papers Dupuis and Ramanan [10, 11] it is shown that the sufficient condition for Lipschitz continuity of the Skorokhod Map given in Dupuis and Ishii [9] is accomplished, in particular, for a class of Skorokhod problems which are there referred as the generalized Harrison–Reimann class. Indeed, Theorem 2.2 [11] ensures the Lipschitz continuity of the Skorokhod Map associated to a Skorokhod Problem in a $d-$dimensional polyhedral cone S(V) with associated matrix of directions of constraint R and in normal form, if matrix VR verifies the following condition (named the generalized Harrison–Reimann condition there) for a $d\times d$ matrix Q:

$$\begin{aligned} \mathbf{HR}&\text { The matrix obtained from }{\varTheta }=Q-I_d\\&\text {by replacing its elements by their absolute} \text {values, has}\\ {}&\text {spectral radius strictly less than}\,\,1. \end{aligned}$$

We highlight that although it is not explicitly written in the statement of Theorem 2.2 [11], there is assumed that the diagonal entries of matrix VR are all equal to 1. Indeed, in order to apply Theorem 2.1 [11] in the proof of Theorem 2.2 [11], it is used that for any $\ell$, $\langle e^{\ell },\,R'\,v^{\ell }\rangle =1$, where $e^{\ell }$ denotes the unit vector in the $\ell$th coordinate direction; taking into account that $\langle e^{\ell },\,R'\,v^{\ell }\rangle =\langle R\,e^{\ell },\,v^{\ell }\rangle =\langle u^{\ell },\,v^{\ell }\rangle$, we obtain that necessarily $\langle u^{\ell },\,v^{\ell }\rangle =1.$ (Observe that notation used here does not match that of Dupuis and Ramanan [11].) Moreover, actually assumption HR as stated in Theorem 2.2 [11] refers to the transpose matrix $(VR)'$ instead of VR, but this makes no difference since the spectral radius of a matrix coincides with that of its transpose.

We discuss briefly two special cases of particular interest:

• Case (a) The positive orthant $\mathbb R^d_{+}$. In this case $\mathbb R^d_{+}=S(V=I_d)$ and let R be any $d\times d$ matrix such that $rank(R)=d$ and all its diagonal entries are 1 (this last requirement can be achieved by normalizing the directions of constraint vectors $u^1,\,\ldots ,\,u^d$). Thus, the cone is in normal form, and if R verifies assumption HR, then strong existence and uniqueness of the solution to any Skorokhod Problem on $\mathbb R^d_{+}$ can be ensured. (This is the case previously considered in Delgado [6–8].)

• Case (b) A cone S(V) with directions of constraint the unit vectors in the coordinate directions, that is, with $R=I_d$. The cone is in normal form if V is such that all its diagonal entries are equal to 1 (this may be achieved through normalization of vectors $v^1,\ldots ,\,v^d$). If that happens and V verifies assumption HR, then strong existence and uniqueness of the solution to any Skorokhod Problem on S(V) is ensured. This is the particular situation we consider in this work.

3 The bandwidth sharing network model

3.1 Network structure

We consider a network with finitely many nodes labeled $\{1,\,\ldots ,\,J\}$. There is also a finite set of routes labeled by $k\in \mathcal{K}$, where each route is interpreted as the non-empty subset of nodes along which network traffic can be transferred. Let K denote the cardinality of $\mathcal{K}$. We assume $J\le K$. We denote by $j\in k$ if node j is used by route k. Each node j has finite (bandwidth) capacity $C_{j}>0$, which is shared among all routes k such that $j\in k$. Let $C=(C_1,\,\ldots ,\,C_J)'$ and A be the $J\times K$ incidence matrix defined by $A_{jk}= 1$ if $j \in k$ and 0 otherwise. Note that in this model A cannot have a column with all entries equal to zero. Hereinafter, we will consider that matrix A satisfies the following condition:

$$\begin{aligned}&\mathbf{LT}\,\text {For each}\, j=1,\,\ldots ,\,J,\, \text {there exists}\, k_j\in \mathcal{K}\nonumber \\&\quad \quad \,\,\,\,\text {such that}\, A_{jk_j}=1\, \text {and}\, A_{\ell k_j}=0\, \text {for all}\, \ell \ne j, \end{aligned}$$

which can be interpreted as a local traffic condition under which each node has at least one route that only uses that node (see Assumption 5.1 [14]). Note that LT implies the full row rank J of matrix A. An example of networks verifying this condition are the so-called linear networks, for which $K=J+1$, there is a common route that goes through all nodes and gets served simultaneously at all of them, and there are J crossing routes: route j going just through node j, $j=1,\ldots ,J$.

Assume that while being transferred, a flow takes simultaneous possession of all nodes on its route, and its transmission time is independent of that of all other flows. Packets wishing to be transferred through route k, arrive at the network from N i.i.d. On/Off external sources, independently of packet arrivals on all other routes, each one with its own $0/1-$valued jump process $\{U_k^{(n)}(t),\,t\ge 0\},\,n=1,\ldots ,\,N$, on a common complete probability space $({\varOmega },\,\mathcal{F},\,P)$, and they are all independent. $U_k^{(n)}(t)=1$ means that at time t, the nth source sending data to route k is On (and it is actually transmitting data at a deterministic data generation or arrival rate $\alpha _k^N>0$), and $U_k^{(n)}(t)=0$ means that it is Off (that is, the nth source is silent). We suppose that independently of k, the lengths of the On-periods are i.i.d., those of the Off-periods are i.i.d., and the lengths of On- and Off-periods are independent of each other.

Let $f^{\mathrm{on}}$ and $f^{{ \mathrm off}}$ be the probability density functions corresponding to the lengths of On- and Off-periods, respectively, which are non-negative, and at least one of them is heavy-tailed. Therefore, their (positive) expected values are

$$\begin{aligned} \mu ^{\mathrm{on}}= & {} \int _0^{+\infty }u\,f^{\mathrm{on}}(u)\,du\,\,{{\text {and}}}\,\,\\ \mu ^{\mathrm{off}}= & {} \int _0^{+\infty }u\,f^{\mathrm{off}}(u)\,du. \end{aligned}$$

Assume that as $x\rightarrow +\infty$,

$$\begin{aligned}&{\left\{ \begin{array}{ll} {\displaystyle \int _x^{+\infty }f^{\mathrm{on}}(u)\,du\sim x^{-\beta ^\mathrm{on}}\,L^\mathrm{on}(x)}\quad \text {and}\\ {\displaystyle \int _x^{+\infty }f^\mathrm{off}(u)\,du\sim x^{-\beta ^\mathrm{off}}\,L^\mathrm{off}(x)}, \end{array}\right. } \end{aligned}$$

(2)

where $1<\beta ^\mathrm{on},\,\beta ^\mathrm{off}\le 2$, $\beta ^\mathrm{on} \wedge \beta ^\mathrm{off}<2$ and $L^\mathrm{on},\,L^\mathrm{off}$ are positive slowly varying functions at infinity such that if $\beta ^\mathrm{on}=\beta ^\mathrm{off}$, then $\lim _{x\rightarrow +\infty }\frac{L^\mathrm{on}(x)}{L^\mathrm{off}(x)}$ exists and belongs to $(0,\,+\infty )$. Note that $\mu ^\mathrm{on}$ and $\mu ^\mathrm{off}$ are finite (and positive) while variances are not if the corresponding beta is $<2$.

The $K-$dimensional (non-deterministic) aggregated cumulative flow arrival process is denoted $E^N=\{E^N(t)=\big (E^N_1(t),$ $\ldots ,\,$ $E^N_K(t)\big )',$ $t\ge 0\}$, with component processes that are all independent and defined by

$$\begin{aligned}&E^N_k(t)\buildrel {\mathrm{def}} \over = \alpha _k^N\,\int _0^t \frac{1}{N}\,\Bigg (\sum _{n=1}^N U_k^{(n)}(u)\Bigg )\,du. \end{aligned}$$

(3)

Note that $\int _0^t \frac{1}{N}\big (\sum _{n=1}^N U_k^{(n)}(u)\big )du$ is the average amount of time that a source of route k is On during the time interval $[0,\,t]$. Let $\alpha ^N=(\alpha _1^N,\ldots ,\,\alpha _K^N)'\,$ and

$$\begin{aligned} \lambda _k^N \buildrel {\mathrm{def}} \over = \frac{\mu ^\mathrm{on}}{ \mu ^\mathrm{on}+\mu ^\mathrm{off}}\,\alpha _k^N,\quad k=1,\ldots ,\,K. \end{aligned}$$

Then, vector $\lambda ^N=(\lambda _1^N,\ldots ,\,\lambda _K^N)'$ can be interpreted as the effective arrival rate.

3.2 Bandwidth sharing policy

How might the capacities $C=(C_1,\,\ldots ,\,C_J)'$ be shared over the routes $\mathcal{K}$ ?

A bandwidth sharing policy is a generalization of the notion of processor sharing discipline from a single resource to a network with several shared links. Bandwidth capacity is allocated dynamically to the routes according to the a weighted proportional fair bandwidth sharing policy explained below.

Typically, the real-time capacity allocation takes the form of a solution to an optimization problem, with the objective function being a utility function (of the state and the allocation), and the constraints enforcing the capacity limit on the nodes. The bandwidth allocated to each route at time t, which is shared equally among all the flows on the route, is given by a function ${\varLambda }(\cdot )=({\varLambda }_1(\cdot ),\ldots ,\,{\varLambda }_K(\cdot ))'$ applied to the amount of flows on each route at this time, defined as follows: ${\varLambda }(\cdot )\,:\,\mathbb R^K_+ \rightarrow \mathbb R^K_+$ and if for $n=(n_1,\ldots ,\,n_K)' \in \mathbb R^K_+$ we denote by $\mathcal{K}_0(n)=\{i\in \mathcal{K}\,:\,n_i=0\}$ and $\mathcal{K}_{+}(n)=\{i\in \mathcal{K}\,:\,n_i>0\}$, ${\varLambda }(\cdot )$ is such that ${\varLambda }_k(n)=0$ for any $k\in \mathcal{K}_0(n)$ and if $\mathcal{K}_{+}(n)\ne \emptyset$, then $({\varLambda }_k(n))_{k\in \mathcal{K}_{+}(n)}$ is the unique vector $({\varLambda }_k)_{k\in \mathcal{K}_{+}(n)}$ that solves the optimization problem

$$\begin{aligned} \text {OP}{\varLambda }{\left\{ \begin{array}{ll}\text {maximize}\,\,\sum \limits _{k\in \mathcal{K}_{+}(n)} \eta _k\,n_k\,\log {\varLambda }_k \\ \text {subject to} \sum \limits _{k\in \mathcal{K}_{+}(n)} A_{jk}{\varLambda }_k\le C_{j},\,1\le j\le J\\ \text {over}\quad {\varLambda }_k\ge 0\quad \text {for any }k\in \mathcal{K}_{+}(n), \end{array}\right. } \end{aligned}$$

where $\{\eta _k,\,k\in \mathcal{K}\}$ is a fixed sequence of strictly positive weights.

We summarize the properties of function ${\varLambda }(\cdot )$ in the following proposition (see Proposition 2.1 [14], which is proved in Appendix A [16]).

Proposition 1

For each $n\in \mathbb R^K_{+}$,

• (i) ${\varLambda }_k(n)>0$ for each $k\in \mathcal{K}_{+}(n)$,

• (ii) ${\varLambda }(\ell \,n)={\varLambda }(n)$ for all $\ell >0$,

• (iii) ${\varLambda }_k(\cdot )$ is continuous on $\{n\in \mathbb R^K_{+}\,:\,n_k>0\}$ but may be discontinuous on $\{n\in \mathbb R^K_{+}\,:\,n_k=0\}$,

• (iv) if $n\ne 0$, there is $p=(p_1,\,\ldots ,\,p_J)'\in \mathbb R^J_{+}$, depending on n, such that for all $k\in \mathcal{K}_{+}(n),\,\sum \limits _{j=1}^J p_j\,A_{jk}>0$ and ${\varLambda }_k(n)=\frac{n_k\,\eta _k}{\sum \nolimits _{j=1}^J p_j\,A_{jk}}$, where the (Lagrange multipliers) $p_1,\ldots ,p_J$ satisfy that for all $j= 1,\,\ldots ,\,J,$

  $$\begin{aligned} p_j\,\big (\,C_j-\sum \limits _{k\in \mathcal{K}_{+}(n)} A_{jk} {\varLambda }_k(n)\,\big )=0. \end{aligned}$$

3.3 Stochastic processes description

Consider an increasing sequence of scale parameters $\{r_i\}_{i=1}^{+\infty }$, with $r_i\ge 1$, which converges to $+\infty$; for ease the notation, we shall simply write r instead of $r_i$, but it is understood that r increases to infinity through a sequence, and consider a sequence of models indexed by (r, N), with N being the number of On/Off sources feeding each route, where the network incidence matrix A and capacity vector C, as well as the distribution of the On/Off sources and the bandwidth sharing policy weights $\{\eta _k,\,k\in \mathcal{K}\}$, do not vary with (r, N). We append a superscript ${}^{r,N}$ to indicate the stochastic processes [all defined on the probability space $({\varOmega },\,\mathcal{F},\,P)$] or parameters in the (r, N)-model, when they are dependent on both r and N. Thus, we have a flow arrival process $E^{r,N}$, an arrival rate $\alpha ^{r,N}>0$ and an effective arrival rate $\lambda ^{r,N}>0$.

For the $(r,N)-$model, each flow at route k requires an i.i.d. service with mean $\frac{1}{\mu ^{r,N}_k}>0$ before it depart from the network; the actual holding time depends on the capacity allocation, that is, $\frac{1}{\mu ^{r,N}_k}$ can be thought of as the mean file size and the fact that the bandwidth is shared equally among all the flows on route k means that if currently the number of flows in transfer across the K routes is $n=(n_1,\ldots ,\,n_K)' \in \mathbb R^K_{+}$, then the mean holding time of each flow is $\big (\mu _k^{r,N}\,\frac{{\varLambda }_k(n)}{n_k}\big )^{-1}$ if $n_k>0$, that is, flow is tranferred at rate $\mu _k^{r,N}\,\frac{{\varLambda }_k(n)}{n_k}$ until there is a change in the network’s state, caused either by a flow transfer being completed, or by a flow arrival occurring.

Let us denote $\mu ^{r,N}=(\mu ^{r,N}_1,\,\ldots ,\,\mu ^{r,N}_K)'$ and $M^{r,N}=diag(\mu ^{r,N})^{-1}$. Assume that $\lim _{N\rightarrow +\infty } \mu ^{r,N}$ exists, does not depend on r and is strictly positive; we denote it by $\mu =(\mu _1,\,\ldots ,\,\mu _K)'.$ Let $M=diag(\mu )^{-1}$. For each j we introduce the node traffic intensity induced by elastic traffic by

$$\begin{aligned}&\rho _j^{r,N}\buildrel {\mathrm{def}} \over = \sum _{k\,:\,j\in k} \frac{\lambda _k^{r,N}}{\mu _k^{r,N}}\quad \bigg (\text { i.e., } \rho ^{r,N}=A\,M^{r,N}\,\lambda ^{r,N}\bigg ). \end{aligned}$$

(4)

Henceforth assume that $\rho ^{r,N} < C$.

Let $Z^{r,N}_k(t)$ be the (random) amount of flows on route k at time t, and $Z^{r,N}(t)=(Z^{r,N}_1(t),\ldots ,\,Z^{r,N}_K(t))'$ $\in \mathbb R^K_{+}$. For simplicity we assume $Z^{r,N}(0)=0$. Then, the bandwidth allocated to route k at time t, which is shared equally among all the flows on this route, is ${\varLambda }_k(Z^{r,N}(t))$. Also define a J-dimensional (average) workload process by

$$\begin{aligned}&W^{r,N} \buildrel {\mathrm{def}} \over =A\,M^{r,N}\,Z^{r,N}, \end{aligned}$$

(5)

that is, for any $j=1,\,\ldots ,\,J$ and $t>0$, $W^{r,N}_j(t)=\sum \limits _{k\,:\,j\in k} \frac{1}{\mu ^{r,N}_k}\,Z^{r,N}_k(t),$ and we introduce the allocated bandwidth $T^{r,N}=\{(T^{r,N}_1(t),\ldots ,\,T^{r,N}_K(t))',\,t\ge 0\}$, defined by: $T^{r,N}_k(t)\buildrel {\mathrm{def}} \over =\int _0^t {\varLambda }_k(Z^{r,N}(s))\,ds$, which is the cumulative amount of bandwidth allocated to route k up to time t. Then, we can introduce the unused bandwidth capacity process $Y^{r,N}=\{(Y^{r,N}_1(t),\ldots ,\,Y^{r,N}_J(t))',\,t\ge 0\}$, which is defined by:

$$\begin{aligned} Y^{r,N}_j(t)\buildrel {\mathrm{def}} \over =C_j\,t-\sum _{k\,:\,j\in k} T^{r,N}_k(t) \end{aligned}$$

(6)

(In matrix form: $Y^{r,N}=C\,\mathbf{e}-A\,T^{r,N}$).

3.4 Scaling

In order to define the scaled processes associated with the $(r,N)-$model we have to introduce some previous notation by following Taqqu et al. [26] (see also Delgado [6]). Set $a^\mathrm{on}=\frac{{\varGamma }(2-\beta ^\mathrm{on})}{(\beta ^\mathrm{on}-1)}$ and $a^\mathrm{off}=\frac{{\varGamma }(2-\beta ^\mathrm{off})}{(\beta ^\mathrm{off}-1)}$, where $\beta ^\mathrm{on}$ and $\beta ^\mathrm{off}$ are defined by (2). The normalization factors used below depend on b, defined by $\,b\buildrel {\mathrm{def}} \over =\lim _{t\rightarrow +\infty } t^{(\beta ^\mathrm{off}-\beta ^\mathrm{on})}\,\frac{L^\mathrm{on}(t)}{L^\mathrm{off}(t)},\,$ which exists although it could be infinite. If $0<b<+\infty$ (implying $\beta ^\mathrm{on}=\beta ^\mathrm{off}$ and $b={\displaystyle \lim _{t\rightarrow +\infty } \frac{L^\mathrm{on}(t)}{L^\mathrm{off}(t)}}$), set $\beta =\beta ^\mathrm{on}=\beta ^\mathrm{off},\,L=L^\mathrm{off}$ and

$$\begin{aligned} \sigma ^{2}\buildrel {\mathrm{def}} \over =\frac{2\,\Big (\big (\mu ^\mathrm{off}\big )^2\,a^\mathrm{on}\,b +\big (\mu ^\mathrm{on}\big )^2\,a^\mathrm{off}\,\Big )}{\big (\,\mu ^\mathrm{on}+\mu ^\mathrm{off}\,\big )^3\,{\varGamma }\big (4-\beta \big )}. \end{aligned}$$

If, on the other hand, $b=+\infty$ ($\beta ^\mathrm{off}>\beta ^\mathrm{on}$), set $L=L^\mathrm{on},\,\beta =\beta ^\mathrm{on}$ and

$$\begin{aligned} \sigma ^{2}\buildrel {\mathrm{def}} \over =\frac{2\big (\mu ^\mathrm{off}\big )^2\,a^\mathrm{on}}{\big (\,\mu ^\mathrm{on}+\mu ^\mathrm{off}\,\big )^3\,{\varGamma }\big (4-\beta \big )}. \end{aligned}$$

If $b=0$ ($\beta ^\mathrm{off}<\beta ^\mathrm{on}$), set $L=L^\mathrm{off},\,\beta =\beta ^\mathrm{off}$ and

$$\begin{aligned} \sigma ^{2}\buildrel {\mathrm{def}} \over =\frac{2\big (\mu ^\mathrm{on}\big )^2\,a^\mathrm{off}}{\big (\,\mu ^\mathrm{on}+\mu ^\mathrm{off}\big )^3\,{\varGamma }\big (4-\beta \big )}. \end{aligned}$$

In either case, $\beta \in (1,\,2)$. Let us define $\,H\buildrel {\mathrm{def}} \over =\frac{3-\beta }{2}.$ Therefore, $H\in (\frac{1}{2},\,1)$.

Now we can introduce the scaled processes associated with the $(r,N)-$model. We use a hat to denote them.

$$\begin{aligned}&\hat{E}^{r,N}(t)\buildrel {\mathrm{def}} \over = \sqrt{N}\,\,\frac{E^{r,N}(r\,t)-\lambda ^{r,N}\,r\,t}{r^{H}\,L^{1/2}(r)}, \end{aligned}$$

(7a)

$$\begin{aligned}&\hat{Z}^{r,N}(t)\buildrel {\mathrm{def}} \over = \sqrt{N}\,\,\frac{Z^{r,N}(r\,t)}{r^{H}\,L^{1/2}(r)}, \end{aligned}$$

(7b)

$$\begin{aligned}&\hat{W}^{r,N}(t)\buildrel {\mathrm{def}} \over = \sqrt{N}\,\,\frac{W^{r,N}(r\,t)}{r^{H}\,L^{1/2}(r)}, \end{aligned}$$

(7c)

$$\begin{aligned}&\hat{Y}^{r,N}(t)\buildrel {\mathrm{def}} \over = \sqrt{N}\,\,\frac{Y^{r,N}(r\,t)}{r^{H}\,L^{1/2}(r)}. \end{aligned}$$

(7d)

Lemma 1

Let $c_1\buildrel {\mathrm{def}} \over = \frac{1}{2\,|M|}>0$ and $c_2\buildrel {\mathrm{def}} \over = {2}\,|M^{-1}|>0$. Then, for any fixed $r\ge 1$ there exists $n_0=n_0(r)\ge 1$ such that for any $T>0$ and any $N\ge n_0$,

$$\begin{aligned}&c_1\big |\big |\hat{W}^{r,N}(\cdot )\big |\big |_T\le \big |\big |\hat{Z}^{r,N}(\cdot )\big |\big |_T\le c_2\big |\big |\hat{W}^{r,N}(\cdot )\big |\big |_T. \end{aligned}$$

(8)

Proof

Since we assume that $\lim _{N\rightarrow +\infty } \mu ^{r,N}=\mu >0$, for any $r\ge 1$ there exists $n_0=n_0(r)$ such that for any $k\in \mathcal{K}$ and $N\ge n_0$, $\mu _k^{r,N}\le 2\, \mu _k$ and $\frac{1}{\mu _k^{r,N}}\le 2\,\frac{1}{\mu _k}.$ First note that by (5), (7c) and (7b), $\hat{W}^{r,N}=A\,M^{r,N}\,\hat{Z}^{r,N}$. Then, for any $T>0,\,N\ge n_0$,

$$\begin{aligned} \big |\big |\hat{W}^{r,N}(\cdot )\big |\big |_T&\le 2\,\max \{\frac{1}{\mu _k}\quad k\in \mathcal{K}\}\big |\big |\hat{Z}^{r,N}(\cdot )\big |\big |_T\\&= 2\,|M|\big |\big |\hat{Z}^{r,N}(\cdot )\big |\big |_T \end{aligned}$$

and we obtain the first inequality in (8).

For the second inequality we note that for any $k\in \mathcal{K}$, there exists at least one index $j_k$ such that $A_{j_k k}=1$, that is, such that $j_k\in k$, and taking into account that for any $j=1,\ldots ,\,J,$ $\hat{W}^{r,N}_{j}=\sum \limits _{\ell \,:\,j\in \ell }\frac{1}{\mu _{\ell }^{r,N}}\,\hat{Z}^{r,N}_{\ell },$ if we take $j=j_k$, we deduce that

$$\begin{aligned} \hat{W}^{r,N}_{j_k}\ge \frac{1}{\mu _k^{r,N}}\,\hat{Z}^{r,N}_k. \end{aligned}$$

Then,

$$\begin{aligned} \hat{Z}^{r,N}_k&\le \mu _k^{r,N}\,\hat{W}^{r,N}_{j_k}\le 2\,\max \big \{\mu _k,\,\,k\in \mathcal{K}\big \}\,\hat{W}^{r,N}_{j_k}\\&= 2\big |M^{-1}\big |\,\hat{W}^{r,N}_{j_k} \end{aligned}$$

and in this way we obtain the second inequality in (8). $\square$

Next proposition shows how using simple algebraic manipulations, a decomposition of process $\hat{W}^{r,N}$ similar to that given by formula (17) [6], which will be used in the proof of Theorem 1, can be obtained.

Proposition 2

For any $r,\,N\ge 1$, we can write

$$\begin{aligned}&\hat{W}^{r,N}=\hat{X}^{r,N}+\hat{Y}^{r,N}, \end{aligned}$$

(9)

where

$$\begin{aligned}&\hat{X}^{r,N}\buildrel {\mathrm{def}} \over = A\,M^{r,N}\,\hat{E}^{r,N}+\frac{\sqrt{N}}{r^{H}\,L^{1/2}(r)}\big (\rho ^{r,N}-C\big )\,r\,\mathbf{e}. \end{aligned}$$

(10)

Moreover, for any $j=1,\,\ldots ,\,J,$

$$\begin{aligned}&\hat{Y}_j^{r,N}(t)=\frac{\sqrt{N}}{r^H L^{1/2}(r)}\int _0^{rt} \bigg (C_j-\sum _{k\in \mathcal{K}} A_{jk}{\varLambda }_k\big (Z^{r,N}(s)\big )\bigg )ds \end{aligned}$$

(11)

and verifies that $\hat{Y}^{r,N}_j(0)=0$, and its paths are continuous and non-decreasing.

Proof

By definition, for any $k\in \mathcal{K},\,t>0$,

$$\begin{aligned} Z^{r,N}_k(t)&=E^{r,N}_k(t)-\mu _k^{r,N}\,T_k^{r,N}(t) \end{aligned}$$

(12)

[that is, $Z^{r,N}=E^{r,N}-(M^{r,N})^{-1}\,T^{r,N}$]. Indeed, the transferred flows up to time t are $\int \limits _0^t D_k^{r,N}(s)\,ds$, where

$$\begin{aligned} D_k^{r,N}(s)= & {} \mu _k^{r,N}\frac{{\varLambda }_k\big (Z^{r,N}(s)\big )}{Z_k^{r,N}(s)} Z_k^{r,N}(s)\\= & {} \mu _k^{r,N}{\varLambda }_k\big (Z^{r,N}(s)\big ) \end{aligned}$$

if $Z_k^{r,N}(s)>0$ and 0 otherwise. Therefore, by (7c), (5) and (12),

$$\begin{aligned} \hat{W}^{r,N}(t)&= \sqrt{N}\frac{W^{r,N}(rt)}{r^{H}L^{1/2}(r)}= \frac{\sqrt{N}}{r^{H}L^{1/2}(r)}AM^{r,N}Z^{r,N} (rt)\\&= \frac{\sqrt{N}}{r^{H}\,L^{1/2}(r)}\, \Big (\,A\,M^{r,N}\,E^{r,N} (r\,t)-A\,T^{r,N} (r\,t)\,\Big )\\&=\frac{\sqrt{N}}{r^{H}\,L^{1/2}(r)}\, \Big (\,A\,M^{r,N}\,(E^{r,N}(r\,t)-\lambda ^{r,N}\,r\,t)\\&\quad +\,A\,M^{r,N}\,\lambda ^{r,N}\,r\,t-A\,T^{r,N} (r\,t)\,\Big )\\&= A\,M^{r,N}\,\hat{E}^{r,N}(t)+\frac{\sqrt{N}}{r^{H}\,L^{1/2}(r)}\,\rho ^{r,N}\,r\,t\\&\quad -\,\frac{\sqrt{N}}{r^{H}\,L^{1/2}(r)}\,A\,T^{r,N} (r\,t)\\&= A\,M^{r,N}\,\hat{E}^{r,N}(t)+\frac{\sqrt{N}}{r^{H}\,L^{1/2}(r)}\,\big (\rho ^{r,N}-C\big )\,r\,t\\&\quad +\,\frac{\sqrt{N}}{r^{H}\,L^{1/2}(r)}\,\big (C\,\mathbf{e}-A\,T^{r,N}\big )(r\,t)\\&= AM^{r,N}\hat{E}^{r,N}(t)+\frac{\sqrt{N}}{r^{H}L^{1/2}(r)}\big (\rho ^{r,N}-C\big )rt\\&\quad +\, \hat{Y}^{r,N}(t), \end{aligned}$$

which uses (7a), (4), (6) and (7d). The proof ends considering that for any j, the paths of $\hat{Y}_j^{r,N}$, which have the expression (11), verify that start from zero and are continuous. Moreover, these paths are non-decreasing since the integrand in (11) is nonnegative by the restriction of the optimization problem OP${\varLambda }$. $\square$

3.5 Heavy-traffic condition

Our main result will be proved under heavy-traffic, which establishes that the total load imposed on each node (that is, its traffic intensity) tends to be equal to its capacity. This node’s capacity saturation assumption can be splitted into two parts, namely conditions HTa and HTb:

$$\begin{aligned}&\mathbf{HTa}\quad \lim _{N\rightarrow +\infty } \sqrt{N}(\rho ^{r,N}-C)=-{ {\hat{\gamma }}}^r\\&\qquad \quad \text {for some }{ {\hat{\gamma }}}^r\in \mathbb R^J_{+},\,\,\text {and }\lim _{r\rightarrow +\infty } { {\hat{\gamma }}}^r\,\,\text {exists in }\mathbb R^J_{+}.\\&\mathbf{HTb}\quad \gamma \in \mathbb R^J_{+} \,\,\text {exists such that} \lim _{r\rightarrow +\infty } \frac{r^{1-H}}{L^{1/2}(r)}{\hat{\gamma }}^r=\gamma . \end{aligned}$$

Formulation of the heavy-traffic assumption here is formally the same as in Delgado [8], where it was motivated through thin control, which applies to systems with processing rates of the form $\mu _j^{r,N}=\lambda _j^{r,N}\,(\frac{1}{C_j}+\frac{1}{\sqrt{N}}\,{\hat{\gamma }}_j^r)\,$ (see Remark 5 [8] for the particular case $C_j=1$, and references therein).

Remark 2

Note that from HTa, (4) and the assumption that $\lim _{N\rightarrow +\infty } M^{r,N}=M$, we deduce the existence of $\lambda \buildrel {\mathrm{def}} \over =\lim _{N\rightarrow + \infty } \lambda ^{r,N}$, which is independent of r and verifies that $C=A\,M\,\lambda$. Here and subsequently assume that $\lambda >0$. Moreover, since $\lambda ^{r,N}=\frac{\mu ^\mathrm{on}}{\mu ^\mathrm{on}+ \mu ^\mathrm{off}}\,\alpha ^{r,N}$, the (independent of r) limit of the data generation rate as $N\rightarrow +\infty$ needed to achieve the maximum capacity of the network is

$$\begin{aligned} \alpha =\lim _{N\rightarrow +\infty }\alpha ^{r,N}=\frac{\mu ^\mathrm{on}+\mu ^\mathrm{off}}{\mu ^\mathrm{on}}\,\lambda >0 \end{aligned}$$

with $\lambda$ such that $C=A\,M\,\lambda .$

The following result shows the convergence of the scaled flow arrival process $\hat{E}^{r,N}$, first as $N\rightarrow +\infty$ and then as $r\rightarrow +\infty$ to a multidimensional fractional Brownian motion process (see Definition 1 [6]). As a consequence and assuming heavy-traffic, we obtain the convergence of process $\hat{X}^{r,N}$ defined by (10), which is a component of the decomposition (9) of the scaled workload process $\hat{W}^{r,N}$.

Proposition 3

If there exists $\lim \limits _{r\rightarrow +\infty } \lim \limits _{N\rightarrow +\infty } \alpha ^{r,N}=\alpha$ and $\alpha >0$, then there exist the limits

$$\begin{aligned} {\hat{E}}^r={\mathcal D}-{\lim _{N\rightarrow +\infty }} \hat{E}^{r,N}\quad \text {and}\quad {\mathcal D}-{\lim _{r\rightarrow +\infty }} {\hat{E}}^r=B^H, \end{aligned}$$

where $B^H$ is a $K-$dimensional fractional Brownian motion with associated data $(x=0,\,H,\,\theta =0,\,\sigma ^2\,diag(\alpha )^2)$, where H and $\sigma ^2$ were introduced in Sect. 3.4.

Moreover, assuming that HTa holds, we have that there exists the limit

$$\begin{aligned} {\hat{X}}^r&={\mathcal D}-{\lim _{N\rightarrow +\infty }} \hat{X}^{r,N}\\ \nonumber&=A\,M\,{\hat{E}}^r -\frac{r^{1-H}}{L^{1/2}(r)}\,{\hat{\gamma }}^r\,\mathbf{e}, \end{aligned}$$

(13)

which has continuous paths. In addition, if HTb holds, there also exists the limit

$$\begin{aligned} X= & {} {\mathcal D}-{\lim _{r\rightarrow +\infty }} {\hat{X}}^r\\ \nonumber= & {} A\,M\,B^H-\gamma \,\mathbf{e}, \end{aligned}$$

which is a $J-$dimensional fractional Brownian motion process with associated data $(x=0,\,H,\,\theta =-\gamma ,\,{\varGamma })$, being

$$\begin{aligned}&{\varGamma }\buildrel {\mathrm{def}} \over =\sigma ^2\,A\,M\,diag(\alpha )^2\,M\,A'. \end{aligned}$$

(14)

Proof

Fixed $r,\,N\ge 1$, for any $k\in {\mathcal K}$ we have by (7a) and (3) that $\hat{E}^{r,N}_k(t)$ can be written as

$$\begin{aligned} \frac{\alpha _k^{r,N}}{r^HL^{1/2}(r)}\frac{1}{\sqrt{N}}\sum _{n=1}^N \Bigg ( \int _0^{rt} U_k^{(n)}(u)du-\frac{\mu ^{\text {on}}}{\mu ^{\text {on}}+\mu ^{\text {off}}}r\,t\Bigg ), \end{aligned}$$

and then using Theorem 1 [26] and Theorem 7.2.5 [29], jointly with the joint convergence for independent random elements (see Theorem 11.4.4 [29]), we have that in $\mathcal{D}^K$ there exists the limit

$$\begin{aligned}&{\hat{E}}^r={\mathcal D}- {\lim _{N\rightarrow +\infty }} \hat{E}^{r,N}, \end{aligned}$$

(15)

which has paths in $\mathcal{C}^K$, and in $\mathcal{C}^K$ there exists the limit

$$\begin{aligned}&{\mathcal D}- {\lim _{r\rightarrow +\infty }} {\hat{E}}^r=B^H. \end{aligned}$$

(16)

Then, by (10), (15), HTa and the continuous mapping theorem (see Corollary 1 of Theorem 5.1 [1]), we deduce that ${\hat{X}}^r={\displaystyle {\mathcal D}- {\lim _{N\rightarrow +\infty }}\hat{X}^{r,N}}$ exists and obtain (13).

If we also assume condition HTb, then by (16) the limit $X={\mathcal D}-{\lim _{r\rightarrow +\infty }} {\hat{X}}^r$ exists and $X=A\,M\,B^H-\gamma \,\mathbf{e}$, which is a $J-$dimensional fBm with associated data $(x=0,\,H,\,\theta =-\gamma ,\,{\varGamma })$, where ${\varGamma }$ is the matrix (14). $\square$

3.6 Fluid model solution and invariant manifold

From Sect. 4 [14] (see also Sect. 5 [16]) we adapt the following two definitions that are used to introduce the polyhedral cone where the limit of the scaled workload process lives, as will be proved in Sect. 4.

Definition 3

(Fluid model solution) A fluid model solution is an absolutely continuous function

$$\begin{aligned} z\,:\,[0,\,+\infty )\longrightarrow \mathbb R^K_{+} \end{aligned}$$

such that at each regular point $t>0$ for z, we have that for each $k\in \mathcal{K}$,

$$\begin{aligned}&\frac{d}{dt}\,z_k(t)={\left\{ \begin{array}{ll} \lambda _k-{\mu _k}\,{\varLambda }_k(z(t)) &{}\quad \text {if } z_k(t)>0,\\ 0 &{}\quad \text {if } z_k(t)=0, \end{array}\right. } \end{aligned}$$

and for each $j=1,\,\ldots ,\,J$,

$$\begin{aligned}&\sum _{k\in \mathcal{K}_{+}\big (z(t)\big )} A_{jk}\,{\varLambda }_k\big (z(t)\big ) + \sum _{k\in \mathcal{K}_0\big (z(t)\big )} A_{jk}\,\frac{\lambda _k}{\mu _k} \le C_j. \end{aligned}$$

For an intuitive idea we refer the reader to the comments following Definition 5.1 [16].

Definition 4

(Invariant manifold) A state $z_0\in \mathbb R^K_{+}$ is called invariant if there exist a fluid model solution $z(\cdot )$ and $t_0\ge 0$ such that $z(t)=z_0$ for all $t\ge t_0$. Let $\mathcal{M}$ denote the set of invariant states of the network. We call $\mathcal{M}$ the invariant manifold.

For each $z\in \mathbb R^K_{+}$, we define $\omega (z)=(\omega _1(z),\ldots ,\,\omega _J(z))'$, to be given by

$$\begin{aligned}&\omega _j(z)\buildrel {\mathrm{def}} \over =\sum _{k\in \mathcal{K}} A_{jk}\,\frac{z_k}{\mu _k},\quad \text {for all } j=1,\,\ldots ,\,J. \end{aligned}$$

That is, $\omega (z)=A\,M\,z$. We call $\omega (z)$ the workload associated with z.

For each $\omega \in \mathbb R^J_{+}$, define ${\varDelta }(\omega )$ to be the unique value $z\in \mathbb R^K_{+}$ that solves the following optimization problem:

$$\begin{aligned} \text {OP} \,{{\varDelta }}\quad {\left\{ \begin{array}{ll} \text {minimize} \quad F(z)\buildrel {\mathrm{def}} \over = \frac{1}{2}\,\sum \limits _{k\in \mathcal{K}} \eta _k\,\frac{z_k^2}{\lambda _k}\\ \text {subject to} \sum \limits _{k\in \mathcal{K}} A_{jk}\frac{z_k}{\mu _k}\ge \omega _j,\,1\le j\le J\\ \qquad \qquad \quad \text {(that is }, A\,M\,z\ge \omega ),\\ \text {over}\quad z_k\ge 0,\quad k\in \mathcal{K}, \end{array}\right. } \end{aligned}$$

Function F was introduced in Bonald and Massoulié [2] as a Lyapunov function for the fluid model solution. Note that as we assume $\lambda >0$, function F is well defined. Since A has full row rank and its only entries are zeros and ones, for each $\omega \in \mathbb R^J_{+}$ the feasible set of the optimization problem $\{z\in \mathbb R^K_{+}\,:\,\sum _{k\in \mathcal{K}} A_{jk}\,\frac{z_k}{\mu _k}\ge \omega _j\quad \forall j=1,\ldots ,J\}$ is nonempty, and then since F is nonnegative in $\mathbb R^K_{+}$ and $F(z)\longrightarrow +\infty$ as $|z|\rightarrow +\infty$, OP${\varDelta }$ has an optimal solution, which is unique by the strict convexity of F (see Remark 5.2 [16]).

As stated in Proposition 4.1 [14] (see also Kelly and Williams [16]), function ${\varDelta }(\cdot )$ defined in this way has two main properties: it is continuous and verifies that ${\varDelta }(c\,\omega )=c\,{\varDelta }(\omega )$ for each $\omega \in \mathbb R^J_{+}$ and $c>0$. Moreover ${\varDelta }(0)=0$, as can be readily seen. Theorem 4.1 [14] gives some characterizations of the invariant states which we reproduce in the following lemma, for the sake of completeness.

Lemma 2

The following are equivalent for $z\in \mathbb R^K_{+}$ :

• (i) $z\in \mathcal{M}$ ;

• (ii) ${\varLambda }_k(z)=\frac{\lambda _k}{\mu _k}$ for all $k\in \mathcal{K}_{+}(z)$ ;

• (iii) there exists some $q\in \mathbb R^J_{+}$ such that

  $$\begin{aligned}&z_k=\frac{\lambda _k}{\mu _k}\,\frac{1}{\eta _k}\,\sum _{j=1}^J q_j\,A_{jk}\quad \text {for all}\,\,k\in \mathcal{K}\,; \end{aligned}$$

• (iv) $z={\varDelta }(\omega (z)).$

In Sect. 5 we will use the following result, which is analogous to Proposition 4.2 [14]. We reproduce it, as well as its proof, for convenience of the reader:

Lemma 3

For each $\omega \in \mathbb R^J_{+},\,{\varDelta }(\omega )\in \mathcal{M}$ (that is, ${\varDelta }(\omega )$ is an invariant state).

Proof

Fixed $\omega \in \mathbb R^J_{+},\,{\varDelta }(\omega )$ is the unique solution to OP${\varDelta }$. Then, by Lemma 6.4 [16], there exists $q\in \mathbb R^J_{+}$ such that ${\varDelta }(\omega )_k=\frac{\lambda _k}{\mu _k}\,\frac{1}{\eta _k}\,\sum _{j=1}^J q_j\,A_{jk}$ for all $k\in \mathcal{K}$. By Lemma 2, this is equivalent to say that ${\varDelta }(\omega )\in \mathcal{M}.$ $\square$

From Lemma 2 we can write the invariant manifold $\mathcal{M}$ as:

$$\begin{aligned} \left\{ z\in \mathbb R^K_{+}:\exists q\in \mathbb R^J_{+} \,\text {and}\, z_k=\frac{\lambda _k}{\mu _k}\frac{1}{\eta _k}\sum _{j=1}^J q_jA_{jk},\,\,\forall k\in \mathcal{K}\right\} , \end{aligned}$$

and for any j, let us introduce

$$\begin{aligned} \mathcal{M}_j&= \left\{ z\in \mathbb R^K_{+}:\exists q\in \mathbb R^J_{+}\,\text {with }q_j=0\, \text {and}\right. \\&\qquad \qquad \qquad \left. z_k=\frac{\lambda _k}{\mu _k}\,\frac{1}{\eta _k}\,\sum _{j=1}^J q_jA_{jk},\,\,\forall k\in \mathcal{K}\right\} . \end{aligned}$$

Let us define

$$\begin{aligned}&\mathcal{W}\buildrel {\mathrm{def}} \over = A\,M\,\mathcal{M}=\big \{A\,M\,z\,:\,z\in \mathcal{M}\big \}. \end{aligned}$$

(17)

Then, $\mathcal{W}$ is a J-dimensional polyhedral cone as introduced in Definition 1, since it can be expressed in the form

$$\begin{aligned} \mathcal{W}= \big \{A\,B\,A'\,q\,:\,q\in \mathbb R^J_{+}\big \}, \end{aligned}$$

with $B=diag(b_1,\ldots ,\,b_K)$ and $b_k=\frac{\lambda _k}{\mu _k^2\,\eta _k}$. Actually, as matrix A has full row rank and B is diagonal with strictly positive diagonal entries, $A\,B\,A'$ is a linear bijection between $\mathbb R^J_{+}$ and $\mathcal{W}$, and it follows that

$$\begin{aligned} \mathcal{W}&=S(V) \end{aligned}$$

(18)

with V being a $J\times J$ matrix whose diagonal entries are taken to be all equal to 1, obtained from matrix $(A\,B\,A')^{-1}$ by normalizing its row vectors.

Moreover, the jth facet of $\mathcal{W}$ is given by

$$\begin{aligned} \mathtt{F }_j= A\,M\,\mathcal{M}_j=\big \{A\,M\,z\,:\,z\in \mathcal{M}_j\big \}, \end{aligned}$$

and if we denote by $n^j$ the vector of the jth row of matrix $(A\,B\,A')^{-1}$, then

$$\begin{aligned}&\mathtt{F }_j= \big \{\omega \in \mathcal{W}\,:\, \langle n^j,\,\omega \rangle =0\big \}. \end{aligned}$$

(19)

4 The heavy-traffic limit

4.1 The invariance principle

A key ingredient in the proof of our heavy-traffic limit result is what is known as the Invariance Principle. This result is stated and proved for Semimartingale reflecting Brownian motions (SRBMs) living in the closures of domains with piecewise smooth boundaries in Theorem 4.3 [15]), a crucial ingredient in its proof being an oscillation inequality for solutions of perturbed Skorokhod problems (Theorem 4.1 [15]). However, this important result does not depend, actually, on the specific law of the processes, as can be checked following the steps of the proof. This enables it, in particular, to be applied to reflected fractional Brownian motion processes. For convenience of the reader we present below a simplified version of this result.

Lemma 4

(Version of Theorem 4.3 [15]) Let $d\ge 1$. Given a $d-$dimensional polyhedral cone S(V) in normal form and associated matrix of directions of constraint $I_d$, assume that matrix V verifies condition HR in Sect. 2, and that there exists a sequence of strictly positive constants $\{\delta ^n\}_n$ such that for each positive integer n, there are processes $W^n,\,\tilde{W}^n,\,X^n,\,\varphi ^n,\,Y^n$ defined on some probability space $({\varOmega }^n,\,\mathcal{F}^n,\,P^n)$ and having paths in ${\mathcal D}^d$, such that

$\mathrm{(i)}$ $P^n-$a.s., $W^n=\tilde{W}^n+\varphi ^n$, $\tilde{W}^n(0)=\varphi ^n(0)=0$ and $d(\tilde{W}^n(t),\,S(V))\le \delta ^n$ for all $t\ge 0$,

$\mathrm{(ii)}$ $P^n-$a.s., $W^n=X^n+Y^n,$

$\mathrm{(iii)}$ $\{X^n\}_n$ is $\mathcal{C}-$tight,

$\mathrm{(iv)}$ $Y^n$ has non-decreasing paths, and for each $j=1,\ldots ,d,\,\,P^n-$a.s., $Y^n_j(0)=0$ and

$$\begin{aligned} Y_j^n(t)=\int \limits _{0}^{t} 1_{\big \{d(\tilde{W}^n(s),\,\mathtt{F }_j)\le \delta ^n\big \}}\,d\,Y_j^n(s), \end{aligned}$$

where $\mathtt{F }_j$ denotes the jth facet of the cone S(V),

$\mathrm{(v)}$ $\varphi ^n\rightarrow 0$ in probability, and $\delta ^n\rightarrow 0$, as $n\rightarrow +\infty$.

Then, the sequence $\{(W^n,\,X^n,\,Y^n)\}_n$ is ${\mathcal C}-$tight, and any weak limit point of this sequence, of the form $(W,\,X,\,Y)$, has continuous paths almost surely, and additionally verifies conditions (i), (ii) and (iv) of Definition 2 (with $W(0)=X(0)=Y(0)=0$ and $R=I_d$), that is, $(W,\,Y)$ is a solution of the Skorokhod Problem associated to X on the cone S(V) and with associated matrix of directions of constraints $I_d$.

If, in addition,

$\mathrm{(vi)}$ $\{X^n\}_n$ converges in distribution to a $d-$dimensional fBm process with associated data $(x,\,H,\,\theta ,\,{\varGamma })$, then W is a rfBm process on S(V) with associated data $(x,\,H,\,\theta ,\,{\varGamma },\,I_d)$.

Brief justification of Lemma 4: First, note that we use Theorem 4.3 [15] in a particular situation in which the domain G is a cone $S(V)=\cap _{\ell =1}^d S_{\ell }$ with $S_{\ell }=\{x\in \mathbb R^d\,:\, \langle v^{\ell },x\rangle \,\ge 0\}$, with directions of constraint the unit vectors in the coordinate directions $e_1,\ldots ,\,e_d$. In Assumption 4.1 [16], we take $\beta ^n\equiv 0$ and for any $i=1,\ldots ,\,d$, $\gamma ^{i,n}(y,\,x)=\gamma ^i(x)=e_i$.

The proof of Theorem 4.3 [15] does not uses any specific property of the Brownian motion process. Indeed, the $\mathcal{C}-$tightness of sequence $\{X^n\}_n$, which is assumption $\mathrm{(iii)}$, is a consequence of $\mathrm{(vi)}$, and $\{(W^n,\,X^n,\,Y^n)\}_n$ inherits ${\mathcal C}-$tightness from it as showed in Theorem 4.2 [15]. Let $(W,\,X,\,Y)$ be a (weak) limit point of this sequence. Then, a subsequence $\{(W^{n_k},\,X^{n_k},\,Y^{n_k})\}_k$ exists such that

$$\begin{aligned} {\mathcal D}-\lim _{k\rightarrow +\infty } \big (W^{n_k},\,X^{n_k},\,Y^{n_k}\big )=\big (W,\,X,\,Y\big ). \end{aligned}$$

Then, the Skorokhod representation theorem (Theorem 3.1.8 [12]) is used to replace the above sequence of processes by one that is term-by-term equivalent in distribution to the original one and that a.s. converges uniformly on compact intervals. With this simplification, it is seen that the limit triplet $(W,\,X,\,Y)$ inherits properties (i), (ii) and (iv) of Definition 2.

Now, instead of use hypothesis $\mathrm{(viii)}$ of Theorem 4.3 [15] in order to ensure that all (weak) limit points of $\{(W^n,\,X^n,\,Y^n)\}_n$ have the same law, as done in the proof of this result, we use that by assumption HR on matrix V, the law of the pair $(W,\,Y)$ is unique (see Remark 1), which gives the desired result. Combining this uniqueness with tightness, it follows that the whole sequence $\{(W^n,\,X^n,\,Y^n)\}_n$ converges in distribution to a triplet $(W,\,X,\,Y)$ which satisfies conditions (i), (ii) and (iv) of Definition 2 (with $W(0)=X(0)=Y(0)=0$ and $R=I_d$) and, moreover, that if condition $\mathrm{(vi)}$ is satisfied, then W is a rfBm process on S(V) with associated data $(x,\,H,\,\theta ,\,{\varGamma },\,I_d).\,\,\,\,\square$

4.2 The heavy-traffi limit results

Before stating our main result, the heavy-traffic limit, which has been split into two theorems, we introduce a key assumption, that is a form of state space collapse since it expresses the relationship between the scaled workload and flow count processes through the deterministic lifting operator ${\varDelta }$ obtained by solving the optimization problem OP${\varDelta }$, in this way: for any $r\ge 1$,

$$\begin{aligned} \mathbf{SSC}\qquad \mathrm{P-}\lim _{N\rightarrow +\infty } \bigg (\hat{Z}^{r,N}-{\varDelta }\big (\hat{W}^{r,N}\big )\bigg )=0. \end{aligned}$$

In Theorem 1 below we prove that in the heavy-traffic environment, concretized by assumption HTa, condition SSC is not only sufficient, but also necessary for the existence of the limits of the scaled workload and flow count processes, when $N\rightarrow +\infty$, denoted by ${\hat{W}}^r$ and ${\hat{Z}}^r$, respectively.

Theorem 1

Assume that HTa holds, and that matrix V in (18) verifies assumption HR (Sect. 2). Then, condition $\mathbf{SSC}$ is necessary and sufficient for the existence of the limits

$$\begin{aligned} {\hat{W}}^r={\mathcal D}-{\lim _{N\rightarrow +\infty }} \hat{W}^{r,N}\quad \text {and}\quad {\hat{Z}}^r={\mathcal D}-{\lim _{N\rightarrow +\infty }} \hat{Z}^{r,N} \end{aligned}$$

and, if the limits exist, ${\hat{Z}}^r={\varDelta }({\hat{W}}^r)$ and for any $t>0$, ${\hat{Z}}^r(t)\in \mathcal{M}$ or, equivalently, ${\hat{W}}(t)\in \mathcal{W}=S(V),$ a.s.

Proof

Step 1: Sufficiency.

Let us introduce notations $\hat{\gamma }^{r,N}(t)\buildrel {\mathrm{def}} \over = -\sqrt{N}(\rho ^{r,N}-C)t$ and $\hat{\varepsilon }^{r,N}(t)\buildrel {\mathrm{def}} \over =\hat{Z}^{r,N}(t)-{\varDelta }(\hat{W}^{r,N}(t)).$ We first mention that by Proposition 3 and hypotheses HTa and SSC, we actually have that for any $r\ge 1$ there exists

$$\begin{aligned} {\mathcal D}- {\lim _{N\rightarrow +\infty }}\big (\hat{E}^{r,N},\,\hat{X}^{r,N},\, {\hat{\gamma }}^{r,N},\,{\hat{\varepsilon }}^{r,N}\big )= \big ({\hat{E}}^r,\,{\hat{X}}^r,\,{\hat{\gamma }}^r,\,0\big ), \end{aligned}$$

where ${\hat{E}}^r$ and ${\hat{X}}^r$ are processes with continuous paths related by means of expression (13).

We proceed now to show the corresponding convergence for processes $\hat{W}^{r,N}$ and $\hat{Y}^{r,N}.$ For that we use (9) and hypothesis HR on matrix V to apply the Invariance Principle in domains with piecewise smooth boundaries (Theorem 4.3 [15]) in the version given by Lemma 4, with $\varphi ^n=\hat{\xi }^{r,N}$ and using that for any $j=1,\ldots ,\,J$, $r\ge 1$, $t>0$ and N big enough, $P^{r,N}-a.s.$

$$\begin{aligned}&\hat{Y}^{r,N}_j(t)=\int _0^t 1_{\big \{d(\tilde{W}^{r,N}(s),\mathtt{F }_j)\le \delta ^{r,N}\big \}} d\hat{Y}_j^{r,N}(s) \end{aligned}$$

(20)

for a sequence of positive numbers $\delta ^{r,N}\rightarrow 0$ as $N\rightarrow +\infty$ and a sequence of probability measures $P^{r,N}\Rightarrow P$ as $N\rightarrow +\infty$, where $\tilde{W}^{r,N}$ and $\hat{\xi }^{r,N}$ are introduced in (28), with $\hat{\xi }^{r,N}(0)=0$. Indeed, (20) is proved in Corollary 1 (Sect. 5), under the MSSC assumption, which is implied by SSC. Actually, these two conditions are equivalent under HTa, as shown in Proposition 4 (Sect. 5), from which it follows that $\mathrm{P-}\lim _{N\rightarrow +\infty } \hat{\xi }^{r,N}=0$, and for any $t>0$ a.s. $\tilde{W}^{r,N}(t)\in \mathcal{W}$ is shown in its proof.

Then, sequence $\{(\hat{W}^{r,N},\,\hat{X}^{r,N},\,\hat{Y}^{r,N})\}_N$ is $\mathcal{C}-$tight (inherits tightness from $\{\hat{X}^{r,N}\}_N$), and in $\mathcal{D}^{3J}$ there exists

$$\begin{aligned} \mathcal{D}-\lim _{N\rightarrow +\infty }\big (\hat{W}^{r,N},\,\hat{X}^{r,N},\,\hat{Y}^{r,N}\big )=\big ({\hat{W}}^r,\,{\hat{X}}^r,\,{\hat{Y}}^r\big ) \end{aligned}$$

and the limit satisfies conditions (i), (ii) and (iv) of Definition 2 on the cone S(V) with $R=I_J.$ That is, $({\hat{W}}^r,\,{\hat{Y}}^r)$ is a solution of the Skorokhod Problem associated to ${\hat{X}}^r$ on the cone S(V) with associated matrix of directions of constraints $I_J$. Then,

$$\begin{aligned}&{\hat{W}}^r={\hat{X}}^r+ {\hat{Y}}^r \end{aligned}$$

(21)

and ${\hat{Y}}^r$ has continuous and non-decreasing paths, starting from zero, and

$$\begin{aligned}&{\hat{Y}}^r_j(t)=\int _0^t 1_{\big \{{\hat{W}}^r(s)\in \mathtt{F }_j\big \}}\,d{\hat{Y}}_j^r(s). \end{aligned}$$

(22)

Taking into account that $\hat{Z}^{r,N}=\hat{\varepsilon }^{r,N} +{\varDelta }(\hat{W}^{r,N})$, SSC and the continuous mapping theorem, the existence of

$$\begin{aligned}&{\displaystyle {\hat{Z}}^r={\mathcal D}- {\lim _{N\rightarrow +\infty }} \hat{Z}^{r,N}},\quad \text {with}\quad {\displaystyle {\hat{Z}}^r={\varDelta }\big ({\hat{W}}^r\big ),} \end{aligned}$$

(23)

follows from

$$\begin{aligned} \hat{Z}^{r,N}-{\varDelta }\big ({\hat{W}}^r\big )=\hat{\varepsilon }^{r,N}+\bigg ({\varDelta }\big (\hat{W}^{r,N}\big )-{\varDelta }\big ({\hat{W}}^r\big )\bigg ), \end{aligned}$$

since ${\varDelta }(\cdot )$ is a continuous function. Finally, by (23) we have that for any $t>0$, ${\hat{Z}}^r(t)={\varDelta }({\hat{W}}^r(t))={\varDelta }(A\,M\,{\hat{Z}}^r(t))={\varDelta }(\omega ({\hat{Z}}^r(t)))$ a.s., which by Lemma 2 is equivalent to writing ${\hat{Z}}^r(t)\in \mathcal{M}$ a.s., and by definition (17) this in turn is equivalent to ${\hat{W}}^r(t)\in \mathcal{W}=S(V)$  a.s.

Step 2: Necessity.

Note that for any fixed $r\ge 1$, ${\displaystyle {\mathcal D}-\lim _{N\rightarrow +\infty }\hat{\varepsilon }^{r,N}=0}\,$ by the continuous mapping theorem and the fact that by hypotheses, there exist $\mathcal{D}-\lim _{N\rightarrow +\infty } \hat{Z}^{r,N}={\hat{Z}}^r$ and $\mathcal{D}-\lim _{N\rightarrow +\infty } \hat{W}^{r,N}={\hat{W}}^r$, and ${\hat{Z}}^r={\varDelta }({\hat{W}}^r).$ Then, assumption SSC follows if we prove tightness of sequence ${\displaystyle \{\hat{\varepsilon }^{r,N}\}_N}$. First, we have that for any $T>0$,

$$\begin{aligned} ||\hat{\varepsilon }^{r,N}(\cdot )||_T&=||\hat{Z}^{r,N}(\cdot )-{\varDelta }(\hat{W}^{r,N})(\cdot )||_T\nonumber \\&\le ||\hat{Z}^{r,N}(\cdot )||_T+||{\varDelta }(\hat{W}^{r,N})(\cdot )||_T, \end{aligned}$$

(24)

and by Lemma 1, $n_0\ge 1$ exist such that $||\hat{Z}^{r,N}(\cdot )||_T\le c_2\,||\hat{W}^{r,N}(\cdot )||_T$ for any $N\ge n_0$. Besides, by (9) and (13) we have that $\mathcal{D}-\lim _{N\rightarrow +\infty } \hat{Y}^{r,N}={\hat{Y}}^r$ exists and

$$\begin{aligned} {\displaystyle {\hat{W}}^r=A\,M\,\hat{\hat{E}}^r-\frac{r^{1-H}}{L^{1/2}(r)}\,{\hat{\gamma }}^r\,\mathbf{e} + {\hat{Y}}^r}, \end{aligned}$$

and hence ${\hat{W}}^r$ has continuous paths. Then, for any $\varepsilon >0$ a positive constant $K'_{\varepsilon }>0$ exists such that for N big enough,

$$\begin{aligned}&P\,\Big (\,||\hat{Z}^{r,N}(\cdot )||_T\le K'_{\varepsilon }\,\Big )\ge 1-\frac{\varepsilon }{2}. \end{aligned}$$

(25)

Note that the existence of ${\displaystyle {\hat{E}}^r}$ and ${\displaystyle {\hat{X}}^r}$, which was shown in Proposition 3, does not require hypothesis $\mathbf {SSC}$. Analogously, taking into account that function ${\varDelta }(\cdot )$ is continuous, we have that a positive constant $K''_{\varepsilon }>0$ exists such that for N big enough,

$$\begin{aligned}&P\,\Bigg (\,||{\varDelta }(\hat{W}^{r,N})(\cdot )||_T\le K''_{\varepsilon }\,\Bigg )\ge 1-\frac{\varepsilon }{2}. \end{aligned}$$

(26)

Let $K_{\varepsilon }\buildrel {\mathrm{def}} \over =K'_{\varepsilon }+K''_{\varepsilon }$. Then, by (24), (25) and (26),

$$\begin{aligned} P\,\Big (||\hat{\varepsilon }^{r,N}(\cdot )||_T&>K_{\varepsilon }\Big )\le P\,\Big (||\hat{Z}^{r,N}(\cdot )||_T>K'_{\varepsilon }\Big )\\&\quad + \,P\,\big (||{\varDelta }(\hat{W}^{r,N})(\cdot )||_T>K''_{\varepsilon }\big )\le \varepsilon \end{aligned}$$

for N big enough, that is, $P\,\big (||\hat{\varepsilon }^{r,N}(\cdot )||_T\le K_{\varepsilon }\big )\ge 1-\varepsilon$, which proves the tightness of ${\displaystyle \{\hat{\varepsilon }^{r,N}\}_N}$ and finishes the proof. $\square$

Remark 3

In Theorem 2 below quantity H plays the role of the Hurst parameter of the reflected fractional Brownian motion process (rfBm), to which the scaled workload process converges. Note that $\beta \in (1,\,2)$ implies $H\in (\frac{1}{2},\,1)$. In particular, $H>\frac{1}{2}$ (the condition on the Hurst parameter corresponding to the long-range dependence behavior of the rfBm process) is due to the fact that $\beta <2$, that is, that the On- and/or Off-period lengths (at least one of them) have infinite variance (heavy tails). As mentioned in Taqqu et al. [26], if both period lengths were light-tailed (with finite variances), then $\beta ^{\text {on}}=\beta ^{\text {off}}=\beta =2$ and $H=\frac{1}{2}$, which would correspond to the case of the ordinary Brownian motion process, whose increments are independent.

Theorem 2

Under the assumptions of Theorem 1, suppose in addition that HTb and $\mathbf{SSC}$ hold. Then, the following conditions are fulfilled:

(i) ${\displaystyle W={\mathcal D-}\lim _{r\rightarrow +\infty }\, {\hat{W}}^{r},\,X= {\mathcal D-}\lim _{r\rightarrow +\infty }\hat{\hat{X}}^{r}\,\, \text { and }}$

${\displaystyle Y= {\mathcal D-}\lim _{r\rightarrow +\infty } {\hat{Y}}^{r}\,}$ exist,

(ii) $W= X+Y$ and it is a rfBm on the polyhedral cone $\mathcal{W}=S(V)$ with associated data

$$\begin{aligned} (x=0,\,H,\,\theta =-\gamma ,\, {\varGamma },\,I_J), \end{aligned}$$

with ${\varGamma }=\sigma ^2\,A\,M\,diag(\alpha )^2\,M\,A',$ and H and $\sigma ^2$ introduced in Sect. 3.4, and

(iii) ${\displaystyle Z={\mathcal D-}\lim _{r\rightarrow +\infty } {\hat{Z}}^{r}}$ also exists, and ${\displaystyle Z={\varDelta }(W).}$

Proof

By (13), (21) and (22) we have that

$$\begin{aligned}&{\hat{X}}^r(t) =A\,M\, {\hat{E}}^r (t)-\frac{r^{1-H}}{L^{1/2}(r)}\,{\hat{\gamma }}^r\,t, \quad {\hat{W}}^r={\hat{X}}^r+{\hat{Y}}^r,\\&{\hat{Y}}^r_j(t)=\int _0^t 1_{\{{\hat{W}}^r(s)\in \mathtt{F }_j\}}\,d{\hat{Y}}_j^r(s), \end{aligned}$$

that is, $({\hat{W}}^r,\,{\hat{Y}}^r)$ is the solution of the Skorokhod problem associated to ${\hat{X}}^r$ on the cone $\mathcal{W}=S(V)$ and with associated matrix of directions of constraints $I_J$ (see Definition 2). Moreover by Proposition 3 it follows ${\displaystyle {\mathcal D-}\lim _{r\rightarrow +\infty }{\hat{E}}^{r}= B^H}$ and

$$\begin{aligned} X= {\mathcal D-} {\lim _{r\rightarrow +\infty }} {\hat{X}}^{r}=A\,M\,B^H-\gamma \,\mathbf{e} \end{aligned}$$

by HTb, which is a $J-$dimensional fBm process. Therefore, we can apply the Invariance Principle of Theorem 4.3 [15] again in the version of Lemma 4, to processes ${\hat{W}}^r,\,{\hat{X}}^r$ and ${\hat{Y}}^r$, taking into account that V verifies assumption HR and that

$$\begin{aligned} {\displaystyle {\mathcal D-}\lim _{r\rightarrow +\infty } {\hat{X}}^{r}=X}, \end{aligned}$$

with $\varphi ^r=\delta ^r\equiv 0$, obtaining that $\big \{\big ({\hat{W}}^r,\, {\hat{X}}^r,\,{\hat{Y}}^r\big )\big \}_r$ inherits tightness from sequence $\big \{ {\hat{X}}^r\big \}_r\,$ and consequently,

$$\begin{aligned} {\displaystyle {\mathcal D-}\lim _{r\rightarrow +\infty } \Big ( {\hat{W}}^{r},\, {\hat{X}}^{r},\, {\hat{Y}}^{r}\Big )=\big (W,\,X,\,Y\big )}\quad \text {exists}, \end{aligned}$$

where $W=X+Y$, and conditions of Definition 2 are satisfied. Hence W is a $J-$dimensional rfBm on the simple polyhedral cone $\mathcal{W}=S(V)$ with associated data $(x={0},\,H,\,\theta =-\gamma ,\,{\varGamma },\,I_J),$ and (i) and (ii) are proved.

Finally, we deduce (iii) from (23). Indeed, ${\hat{Z}}^r={\varDelta }({\hat{W}}^r)$ and ${\mathcal D-}\lim \limits _{r\rightarrow +\infty } {\varDelta }({\hat{W}}^r)={\varDelta }(W)$ by the continuity of function ${\varDelta }\,$. $\square$

4.3 An example

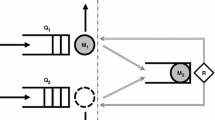
For easy viewing of these mathematical results, consider the following illustrative example of a network with $J=2,\,K=3$ and $A=\left( \begin{matrix} 1 &{} 0 &{} 1\\ 0 &{} 1 &{} 1 \end{matrix}\right)$, which verifies LT. Indeed, this network is the example of linear network depicted in Fig. 1, in which each resource has a route that passes only through that resource and there is also a route (route 3) that passes through both resources. This example was introduced in [14], from which we reproduce some elements of interpretation.

Fig. 1

A linear network with two resources and three routes

In this case,

$$\begin{aligned} A\,B\,A'&=\left( \begin{matrix} b_1+b_3 &{}\quad b_3\\ b_3 &{}\quad b_2+b_3 \end{matrix}\right) ,\\ (A\,B\,A')^{-1}&=\frac{1}{b_1b_2+b_1b_3+b_2b_3}\left( \begin{matrix} b_2+b_3 &{}\quad -b_3 \\ -b_3 &{}\quad b_1+b_3 \end{matrix}\right) \end{aligned}$$

and $V=\left( \begin{matrix} 1&{}\quad -\frac{b_3}{ b_2+b_3} \\ -\frac{b_3}{ b_1+b_3} &{}\quad 1 \end{matrix}\right)$, which verifies HR if and only if the spectral radius of matrix $\left( \begin{matrix} 0&{} \frac{b_3 }{ b_2+b_3} \\ \frac{b_3}{b_1+b_3} &{}0 \end{matrix}\right)$ is strictly less than 1, but this can be checked directly since $b_3^2<(b_1+b_3)\,(b_2+b_3).$

The workload cone in this example is the polyhedral cone in $\mathbb R^2_{+}$ $\mathcal{W}=A\,M\,\mathcal{M}=\{A\,M\,z\,:\,z\in \mathcal{M}\}$. Taking into account that

$$\begin{aligned} \mathcal{M}=\big \{z&=(z_1,z_2,z_3)'\in \mathbb R^3_{+}\,:\, \exists q=(q_1,q_2)\in \mathbb R^2_{+}\,\,\text {and}\\ z_1&=b_1q_1,\,z_2=b_2q_2,\,z_3=b_3(q_1+q_2)\big \} \end{aligned}$$

we see that the cone has the following representation:

$$\begin{aligned} \mathcal{W}&=\big \{ \omega =(\omega _1,\omega _2)' \in \mathbb R^2_{+}\,:\, \exists q=(q_1,q_2)\in \mathbb R^2_{+}\,\,\text {and}\\&\qquad \omega _1=(b_1+b_3)q_1+b_3q_2,\,\, \omega _2=b_3q_1+(b_2+b_3)q_2\big \}\\&=\left\{ \omega =(\omega _1,\omega _2)' \in \mathbb R^2_{+}\,:\, \omega _1\ge \frac{b_3}{b_2+b_3}\omega _2,\right. \\&\left. \qquad \qquad \qquad \qquad \qquad \quad \,\,\omega _2\ge \frac{b_3}{b_1+b_3}\omega _1\right\} \end{aligned}$$

and the two boundary facets of the cone are:

$$\begin{aligned} F_1&=\left\{ \omega =(\omega _1,\omega _2)' \in \mathcal{W}\,:\, \omega _1=\frac{b_3}{b_2+b_3}\omega _2\right\} ,\\ F_2&=\left\{ \omega =(\omega _1,\omega _2)' \in \mathcal{W}\,:\, \omega _2=\frac{b_3}{b_1+b_3}\omega _1\right\} \end{aligned}$$

(see Fig. 2). On the other hand, the lifting map ${\varDelta }$ is a linear map on $\mathcal{W}$ given by: if $\omega =(\omega _1,\omega _2)'\in \mathcal{W}$, ${\varDelta }(\omega )=(z_1,z_2,z_3)'\in \mathbb R^3_{+}$ with

$$\begin{aligned} z_1&=\frac{b_1}{b_1b_2+b_1b_3+b_2b_3}\,\big ((b_2+b_3)\omega _1-b_3\omega _2\big )\\ z_2&=\frac{b_2}{b_1b_2+b_1b_3+b_2b_3}\,\big ((b_1+b_3)\omega _2-b_3\omega _1\big )\\ z_3&=\frac{b_3}{b_1b_2+b_1b_3+b_2b_3}\,(b_2 \omega _1+b_1\omega _2). \end{aligned}$$

As a consequence, points $(\omega _1,\omega _2)'$ on the boundary facets $F_1$ or $F_2$ are mapped respectively to points

$$\begin{aligned} \left( 0,\,b_2 \,\omega _2,\,\frac{b_3}{b_2+b_3} \,\omega _2\right) '\,\,\text {and}\,\, \left( b_1\,\omega _1,\,0,\,\frac{b_3}{b_1+b_3}\,\omega _1\right) '. \end{aligned}$$

(27)

Fig. 2

The workload cone for the linear network with two resources and three routes

Roughly speaking we can say that condition SSC establishes that in the limit, not only the workload process is a function of the amount of flows on each route, as is deduced from definition (5), which in this example results in the conditions

$$\begin{aligned} W_1^r(t)=\frac{Z_1^r(t)}{\mu _1}+\frac{Z_3^r(t)}{\mu _3}\quad \text {and}\quad W_2^r(t)=\frac{Z_2^r(t)}{\mu _2}+\frac{Z_3^r(t)}{\mu _3}, \end{aligned}$$

but that with the knowledge of the workload process at each node we can retrieve all the information about the amount of flows on each of the routes by means of the lifting map ${\varDelta }$ in this way:

$$\begin{aligned} Z_1^r(t)&=\frac{b_1}{b_1b_2+b_1b_3+b_2b_3}\,\big ((b_2+b_3)\,W_1^r(t)-b_3\,W_2^r(t)\big )\\ Z_2^r(t)&=\frac{b_2}{b_1b_2+b_1b_3+b_2b_3}\,\big ((b_1+b_3)\,W_2^r(t)-b_3\,W_1^r(t)\big )\\ Z_3^r(t)&=\frac{b_3}{b_1b_2+b_1b_3+b_2b_3}\,(b_2 \,W_1^r(t)+b_1\,W_2^r(t)). \end{aligned}$$

This condition plays a key role in the proof of the heavy traffic limit. Indeed, by assuming conditions HTa and HR hold, SSC is sufficient and, what is more important, also necessary for the existence of the limits in conclusion of Theorem 1, that is, it cannot be weakened nor dropped.

The conclusion of Theorem 2, which is our heavy traffic limit result, applies provided assumptions of Theorem 1 plus condition HTb are satisfied. If moreover SSC holds, we obtain that the limiting workload process when $r\rightarrow +\infty$ is a rfBm process W living in the polyhedral cone $\mathcal{W}$, which is confined there by reflection at the boundary, with associated data $(x=0,\,H,\,\theta =-\gamma ,\,{\varGamma },\,I_2)$ where

$$\begin{aligned} {\varGamma }=\sigma ^2\, \left( \begin{array}{cc} \frac{\alpha _1^2}{\mu _1^2}+\frac{\alpha _3^2}{\mu _3^2} &{}\quad \frac{\alpha _3^2}{\mu _3^2}\\ \frac{\alpha _3^2}{\mu _3^2} &{}\quad \frac{\alpha _2^2}{\mu _2^2}+\frac{\alpha _3^2}{\mu _3^2} \end{array} \right) . \end{aligned}$$

The direction of reflection on the boundary facets is defined by the columns of the matrix $R=I_2$, that is, reflection occurs in the horizontal direction (corresponding to node 1 underutilizing capacity) on the bounding facet $F_1$. The interpretation of this is that although there is no work for node 1 on route 1, there is work for this resource on route 3, but that by the nature of the bandwidth sharing policy, congestion at node 2 is preventing node 1 from working at its full capacity. Similarly, vertical reflection (node 2 underutilizing capacity) on $F_2$ is interpreted to mean that congestion at node 1 is preventing node 2 from working at its full capacity. Thus, the shape of the workload space $\mathcal{W}$ indicates the entrainment of the nodes, whereby congestion at one of the nodes may prevent the other node from working at its full capacity. Note that when $\eta _3\rightarrow +\infty$ (implying $b_3\rightarrow 0$), $F_1$ and $F_2$ tend respectively to the vertical and the horizontal axes, expanding the polyhedral cone to the whole first quadrant, that is, approaching the situation with full utilization resources.

Moreover, given W in Theorem 2, define process $\tilde{Z}=diag(b_1,\,b_2)\,(ABA')^{-1}\,W$, that is,

$$\begin{aligned} \tilde{Z}_1(t)&=\frac{b_1}{b_1b_2+b_1b_3+b_2b_3}\,\big ((b_2+b_3)\,W_1(t)-b_3\,W_2(t)\big )\\ \tilde{Z}_2(t)&=\frac{b_2}{b_1b_2+b_1b_3+b_2b_3}\,\big ((b_1+b_3)\,W_2(t)-b_3\,W_1(t)\big ). \end{aligned}$$

Then, process $\tilde{Z}$ (corresponding to take the first two components of process $Z={\varDelta }(W)$ in Theorem 2) inherits an rfBm structure from W. Indeed,

$$\begin{aligned} \tilde{Z}&=diag(b_1,\,b_2)\,(ABA')^{-1}\,X \\&\quad +\, diag(b_1,\,b_2)\,(ABA')^{-1}\,Y \end{aligned}$$

is a rfBm process living on the two-dimensional first orthant $\mathbb R^2_{+}$, with associated data $(x=0,\,H,\,\tilde{\theta },\,\tilde{\varGamma },\,\tilde{R}),$ where

$$\begin{aligned} \tilde{\theta }&=-diag(b_1,\,b_2)\,(ABA')^{-1}\,\gamma \\ \tilde{\varGamma }&=diag(b_1,\,b_2)\,(ABA')^{-1}\,{\varGamma }\,\,(ABA')^{-1}\,diag(b_1,\,b_2)\\ \tilde{R}&= diag(b_1,\,b_2)\,(ABA')^{-1}, \end{aligned}$$

since $Y_j$ increases when $W_j$ is in $F_j$, that is, when $\tilde{Z}_j$ is zero [by (27)]. The directions of reflection on the axes of $\mathbb R^2_{+}$ are defined by the columns of matrix $\tilde{R}$.

5 Multiplicative state space collapse

In this section we introduce a condition that is a kind of MSSC, and it has appeared in different contexts regarding heavy-traffic limits (see for instance Williams [30], Kang et al. [14] and Delgado [7]):

$$\begin{aligned}&\mathbf{MSSC}\quad \quad \mathrm{P}-\lim _{N\rightarrow +\infty } \frac{\hat{Z}^{r,N}-{\varDelta }(\hat{W}^{r,N})}{||\hat{W}^{r,N}(\cdot )||_{T}\vee 1}=0\\ {}&\quad \text {for any }T>0,\, r\ge 1. \end{aligned}$$

It is obvious that state space collapse SSC (see Sect. 4) implies MSSC. Somewhat surprisingly, under heavy traffic they are, in fact, equivalent. That is, MSSC also implies SSC as can be seen from Proposition 4 below. This proposition presents similarities with Lemma 7.5 [14]. Let us introduce the following notations:

$$\begin{aligned}&\tilde{W}^{r,N}\buildrel {\mathrm{def}} \over =A\,M\,{\varDelta }\big (\hat{W}^{r,N}\big )\quad \text {and}\quad \hat{\xi }^{r,N}\buildrel {\mathrm{def}} \over =\hat{W}^{r,N}-\tilde{W}^{r,N}. \end{aligned}$$

(28)

Proposition 4

Under assumption HTa (see Sect. 3.5), assume MSSC holds. Then, for each $r\ge 1$, $T>0$ and $\delta >0$, there exist constants K and $N_0$ (depending on $r,\,T$ and $\delta$) such that for each $N\ge N_0$,

$$\begin{aligned} P\Big (&||\hat{\xi }^{r,N}(\cdot )||_{T}\le \delta ,\,||\hat{Z}^{r,N}(\cdot )-{\varDelta }(\hat{W}^{r,N}(\cdot )||_{T}\le \delta ,\nonumber \\&||\hat{W}^{r,N}(\cdot )||_{T}\le K,\,||\hat{Y}^{r,N}(\cdot )||_{T}\le K\Big ) \ge 1-\delta . \end{aligned}$$

(29)

Moreover, for each $j=1,\,\ldots ,\,J$ and $t\in [0,\,T]$, on a set of probability $\ge 1-\delta$,

$$\begin{aligned}&\hat{Y}^{r,N}_j(t)=\int _0^t 1_{\big \{d(\tilde{W}^{r,N}(s),\,\mathtt{F }_j)\le \delta \big \}} \,d\,\hat{Y}_j^{r,N}(s). \end{aligned}$$

(30)

Note that from (29) we obtain that the sequences $\{\hat{W}^{r,N}\}_N$ and $\{\hat{Y}^{r,N}\}_N$ are tight, and also that $\text {P}-\lim \limits _{N\rightarrow +\infty } \hat{\xi }^{r,N}=0$ and $\text {P}-\lim \limits _{N\rightarrow +\infty } \big (\,\hat{Z}^{r,N}-{\varDelta }(\hat{W}^{r,N})\,\big )=0$, that is, under HTa we have that

$$\begin{aligned} {\mathbf{MSSC }}\Rightarrow {\mathbf{SSC }}. \end{aligned}$$

Proof

For better understanding, we split the proof into several steps.

Step 1:

First, fixed $r,\,N\ge 1$ and $j=1,\ldots ,\,J$, in order to prove (30) we have to find out where $\hat{Y}_j^{r,N}(\cdot )$ increases. By making a change of variable in the integral of (11), we have that for any $t>0,\,\hat{Y}^{r,N}_j(t)$ can be written as

$$\begin{aligned} \sqrt{N}\frac{r^{1-H}}{L^{1/2}(r)}\int _0^{t} \Big (C_j-\sum _{k\in \mathcal{K}} A_{jk}{\varLambda }_k\big (Z^{r,N}(r\,s)\big )\Big )\,ds, \end{aligned}$$

and taking into account that $C_j-\sum _{k\in \mathcal{K}} A_{jk}\,{\varLambda }_k(Z^{r,N})\ge 0$ by the restriction of the optimization problem OP${\varLambda }$ in Sect. 3.2, we concentrate on finding out where this expression is strictly positive. For that, fix $T,\,\delta >0$, $t\in [0,\,T]$ and $\omega \in {\varOmega }$, and take $s\in [0,\,t]\subset [0,\,T]$ such that

$$\begin{aligned} 0&<C_j-\sum _{k\in \mathcal{K}} A_{jk}\,{\varLambda }_k\big (Z^{r,N}(r\,s,\,\omega )\big )\\&=C_j-\sum _{k\in \mathcal{K}} A_{jk}\,{\varLambda }_k\big (\hat{Z}^{r,N}(s,\,\omega )\big ), \end{aligned}$$

where we have used (7b) and Proposition 1(ii). By Proposition 1(iv), if $\hat{Z}^{r,N}(s,\,\omega )\ne 0$,

$$\begin{aligned} p^{r,N}\big (s,\,\omega \big )=\big (p^{r,N}_1(s,\,\omega ),\,\ldots ,\,p^{r,N}_J(s,\,\omega )\big )^\prime \in \mathbb R^J_{+} \end{aligned}$$

exists such that $p^{r,N}_j(s,\,\omega )=0$, and

$$\begin{aligned}&\hat{Z}^{r,N}_k\big (s,\omega \big )={\varLambda }_k\big (\hat{Z}^{r,N}(s,\omega )\big )\frac{1}{\eta _k}\sum _{\ell =1}^J p_{\ell }^{r,N}\big (s,\omega \big )A_{\ell k} \end{aligned}$$

(31)

for any $k\in \mathcal{K}_{+}(\hat{Z}^{r,N}(s,\,\omega )).$ By assumption LT on matrix A (Sect. 3.1), there exists $k_j$ such that $A_{jk_j}=1$ and $A_{\ell k_j}=0$ for all $\ell \ne j$, and using (31) with $k_j$ we have that $\hat{Z}^{r,N}_{k_j}(s,\,\omega )=0$.

For any $\varepsilon >0$, we introduce the following subset of ${\varOmega }$, denoted by $\mathcal{B}^{r,N}_{T,\varepsilon }$,

$$\begin{aligned}&\Big \{||\hat{Z}^{r,N}(\cdot )-{\varDelta }(\hat{W}^{r,N}(\cdot ))||_T\le \varepsilon \big (||\hat{W}^{r,N}(\cdot )||_T\vee 1\big )\Big \}. \end{aligned}$$

(32)

By MSSC we have that $n_1(\delta )$ exists such that if $N\ge n_1(\delta )$, then $P(\mathcal{B}^{r,N}_{T,\varepsilon })\ge 1-\delta /2$, and if $\omega \in \mathcal{B}^{r,N}_{T,\varepsilon }$, then as $\hat{Z}^{r,N}_{k_j}(s,\,\omega )=0$,

$$\begin{aligned} \Big ({\varDelta }\big (\hat{W}^{r,N}(s,\,\omega )\big )\Big )_{k_j}\le \varepsilon \Big (\,||\hat{W}^{r,N}(\cdot )(\omega )||_{T}\vee 1\,\Big ). \end{aligned}$$

(33)

On the other hand, from Lemmas 3 and 2 we know that there exists some $q^{r,N}(s,\,\omega ) \in \mathbb R^J_{+}$ of the form $q^{r,N}(s,\,\omega )=(q^{r,N}_1(s,\,\omega ),\,\ldots ,\,q^{r,N}_J(s,\,\omega ))'$, such that

$$\begin{aligned} \Big ({\varDelta }\big (\hat{W}^{r,N}(s,\,\omega )\big )\Big )_{k_j}&=\frac{\lambda _{k_j}}{\mu _{k_j}}\,\frac{1}{\eta _{k_j}}\,\sum _{\ell =1}^J q^{r,N}_{\ell }(s,\,\omega )\,A_{\ell k_j}\nonumber \\&=\frac{\lambda _{k_j}}{\mu _{k_j}}\,\frac{1}{\eta _{k_j}}\,q_{j}^{r,N}(s,\,\omega ), \end{aligned}$$

(34)

and then, by (33), if $\omega \in \mathcal{B}^{r,N}_{T,\varepsilon }$,

$$\begin{aligned} q_j^{r,N}(s,\,\omega )&\le \varepsilon \,\eta _{k_j}\,\frac{\mu _{k_j}}{\lambda _{k_j}}\, \Big (\,||\hat{W}^{r,N}(\cdot )(\omega )||_{T}\vee 1\,\Big ). \end{aligned}$$

(35)

Note that if $\hat{Z}^{r,N}(s,\,\omega )= 0$ the same applies.

Besides, by using notations (28) we can write

$$\begin{aligned} \hat{W}^{r,N}=A\,M^{r,N}\,\hat{Z}^{r,N} \end{aligned}$$

as $\hat{W}^{r,N}=\tilde{W}^{r,N}+\hat{\xi }^{r,N}$, where

$$\begin{aligned} \hat{\xi }^{r,N}&=\hat{W}^{r,N}-\tilde{W}^{r,N} =A\,M\,\big (\hat{Z}^{r,N}-{\varDelta }(\hat{W}^{r,N})\big )\nonumber \\&\quad +\,A\,\big (M^{r,N}-M\big )\,\hat{Z}^{r,N}. \end{aligned}$$

(36)

By Lemma 3 and definition (17), $\tilde{W}^{r,N}(s,\,\omega )\in \mathcal{W}$, and by (34) $\tilde{W}^{r,N}(s,\,\omega )=A\,B\,A'\,q^{r,N}(s,\,\omega )$, and if $\omega \in \mathcal{B}_{T,\varepsilon }^{r,N}$, taking into account the definition of vector $n^j$ (see (19)),

$$\begin{aligned} d(\tilde{W}^{r,N}(s,\,\omega ),\,\mathtt{F }_j)&=\frac{\langle n^j,\,\tilde{W}^{r,N}(s,\,\omega )\rangle }{|n^j|}\\&=\frac{\langle n^j, A\,B\,A'\,q^{r,N}(s,\,\omega )\rangle }{|n^j|}=\frac{q_j^{r,N}(s,\,\omega )}{|n^j|}\\&\le \frac{\varepsilon \,\eta _{k_j}\,\frac{\mu _{k_j}}{\lambda _{k_j}}\, \big (\,||\hat{W}^{r,N}(\cdot )(\omega )||_{T}\vee 1\,\big )}{|n^j|}\\&\le D\,\varepsilon \,\big (\,||\hat{W}^{r,N}(\cdot )(\omega )||_{T}\vee 1\,\big ) \end{aligned}$$

with $D=\max \limits _{j=1,\ldots ,J} \big (\eta _{k_j}\,\frac{\mu _{k_j}}{\lambda _{k_j}}\,\frac{1}{|n^j|}\big )$, where in the first inequality we used (35). And then, we have proved that on $\mathcal{B}_{T,\varepsilon }^{r,N}$, if $t\in [0,\,T],\,\hat{Y}^{r,N}_j(t)$ can be written as

$$\begin{aligned}&\int _0^t 1_{\big \{d(\tilde{W}^{r,N}(s),\mathtt{F }_j)\le D\varepsilon (||\hat{W}^{r,N}(\cdot )||_{T}\vee 1)\big \}} d\hat{Y}_j^{r,N}(s), \end{aligned}$$

(37)

which is not yet the desired expression (30), but from which we will get it in Step 3. For the moment, (37) is what we need to prove (29) in the next step of the proof.

Step 2:

Secondly we will show (29). For that, note that fixed $r,\,N\ge 1$ and $T,\,\delta ,\,\varepsilon >0$ in Step 1, there exists $n_2(\varepsilon ,\delta )\ge n_1(\delta )$ such that for any $N\ge n_2(\varepsilon ,\delta )$,

$$\begin{aligned}&P(||\hat{X}^{r,N}(\cdot )||_{T}\le K_0)\ge 1-\frac{\delta }{2}\quad \text {and}\quad |M^{r,N}-M|\le \varepsilon \end{aligned}$$

for some constant $K_0>0$ depending on $\delta$ although not specify in the notation. This is a consequence of assuming the convergence of $M^{r,N}$ to M as $N\rightarrow +\infty$, and of the fact that sequence $\{\hat{X}^{r,N}\}_N$ is $\mathcal{C}-$tight, since by Proposition 3, under HTa there exists ${\hat{X}}^r=\mathcal{D}-\lim \limits _{N\rightarrow +\infty } \hat{X}^{r,N}=A\,M\,{\hat{E}}^r-\frac{r^{1-H}}{L^{1/2}(r)}\,{\hat{\gamma }}^r\,\mathbf{e}$, which has continuous paths. Let

$$\begin{aligned}&{{\varOmega }}^{r,N}_{T,\varepsilon ,\delta }=\{||\hat{X}^{r,N}(\cdot )||_{T}\le K_0\}\cap \mathcal{B}^{r,N}_{T,\varepsilon ,\delta }. \end{aligned}$$

Then, for all $N\ge n_2(\varepsilon ,\delta ),\,P({{\varOmega }}^{r,N}_{T,\varepsilon ,\delta })\ge 1-\delta$. On ${{\varOmega }}^{r,N}_{T,\varepsilon ,\delta }$, using (36) and Lemma 1, we have that for all $N\ge n_2(\varepsilon ,\delta )\vee n_0,$

$$\begin{aligned}&||\hat{\xi }^{r,N}(\cdot )||_{T}\le c_3\,\varepsilon \,\big (||\hat{W}^{r,N}(\cdot )||_{T}\vee 1\big ), \end{aligned}$$

(38)

where $c_3=|A\,M|+|A|\,c_2>0$. We introduce notation

$$\begin{aligned}&N_0\buildrel {\mathrm{def}} \over =n_2(\varepsilon ,\delta )\vee n_0. \end{aligned}$$

(39)

Note that $N_0$ depends on fixed $r\ge 1$, and on $T,\,\delta ,\,\varepsilon >0$, and that if $N\ge N_0$, then $P({{\varOmega }}^{r,N}_{T,\varepsilon ,\delta })\ge 1-\delta$.

On the other hand, by (37) we can apply the Oscillation inequality (Proposition 7.1 [14]) to $\tilde{W}^{r,N}=\hat{W}^{r,N}-\hat{\xi }^{r,N}=( \hat{X}^{r,N}-\hat{\xi }^{r,N})+\hat{Y}^{r,N}$, and then we have that some constant $\hat{C}_0>0$ exists such that on ${\varOmega }_{T,\varepsilon ,\delta }^{r,N}$,

$$\begin{aligned} Osc(\tilde{W}^{r,N}&(\cdot ),\,[0,\,T])\nonumber \\&\le \hat{C}_0 \Big (Osc(\hat{X}^{r,N}(\cdot )-\hat{\xi }^{r,N}(\cdot ),\,[0,\,T])\nonumber \\&\qquad \quad +D\,\varepsilon \,\big (\,||\hat{W}^{r,N}(\cdot )||_{T}\vee 1\,\big )\,\Big )\nonumber \\&\le \hat{C}_0\,\big (2\,||\hat{X}^{r,N}(\cdot )||_{T}+2\,||\hat{\xi }^{r,N}(\cdot )||_{T}\nonumber \\&\qquad \quad +D\,\varepsilon \,\big (\,||\hat{W}^{r,N}(\cdot )||_{T}\vee 1\,\big )\,\big ) \end{aligned}$$

(40)

and the same bound applies to $Osc(\hat{Y}^{r,N}(\cdot ),\,[0,\,T])$, that is,

$$\begin{aligned} Osc(\hat{Y}^{r,N}(\cdot ),\,[0,\,T])&\le \hat{C}_0\,\big (2||\hat{X}^{r,N}(\cdot )||_{T}+2||\hat{\xi }^{r,N}(\cdot )||_{T}\nonumber \\&\quad +D\varepsilon \big (||\hat{W}^{r,N}(\cdot )||_{T}\vee 1\big )\big ). \end{aligned}$$

(41)

By using that

$$\begin{aligned}&||\hat{W}^{r,N}(\cdot )||_{T}\vee 1\le Osc(\hat{W}^{r,N}(\cdot ),\,[0,\,T])+1\\&\quad \le Osc(\tilde{W}^{r,N}(\cdot ),\,[0,\,T])+ Osc(\hat{\xi }^{r,N}(\cdot ),\,[0,\,T])+1\\&\quad \le Osc(\tilde{W}^{r,N}(\cdot ),\,[0,\,T])+2\,||\hat{\xi }^{r,N}(\cdot )||_{T} + 1, \end{aligned}$$

(40) and (38), we have that if $N\ge N_0$, on ${\varOmega }^{r,N}_{T,\varepsilon ,\delta }$,

$$\begin{aligned} ||\hat{W}^{r,N}(\cdot )||_{T}\vee 1 \le&2\,\hat{C}_0\,K_0+\big (\hat{C}_0\,(2\,c_3+D)+2\,c_3\big )\,\varepsilon \nonumber \\&\big (\,||\hat{W}^{r,N}(\cdot )||_{T}\vee 1\,\big )+1. \end{aligned}$$

(42)

From now define $\varepsilon =\varepsilon (\delta )$ by

$$\begin{aligned} \min&\left\{ \frac{1}{2\big (\hat{C}_0(2c_3+D)+2c_3\big )},\right. \nonumber \\&\left. \frac{\delta }{2\max \{D,c_3,1\}(2\hat{C}_0 K_0+1)}\right\} . \end{aligned}$$

(43)

With such an $\varepsilon >0$, (42) implies that if $N\ge N_0$, on ${\varOmega }^{r,N}_{T,\varepsilon ,\delta }$,

$$\begin{aligned} ||\hat{W}^{r,N}(\cdot )||_{T}\vee 1 \le 2\,(2\,\hat{C}_0\,K_0+1), \end{aligned}$$

(44)

and then, by (32), (44) and (43),

$$\begin{aligned} ||\hat{Z}^{r,N}(\cdot )-{\varDelta }(\hat{W}^{r,N}(\cdot ))||_{T}\le \varepsilon \,(||\hat{W}^{r,N}(\cdot )||_{T}\vee 1)\le \delta , \end{aligned}$$

which by using the bound in (41) and (38) gives that

$$\begin{aligned} ||\hat{Y}^{r,N}(\cdot )||_{T}&\le Osc(\hat{Y}^{r,N}(\cdot ),\,[0,\,T])\\&\le 2\,\hat{C}_0\,K_0+\hat{C}_0\,(2\,c_3+D)\,\delta . \end{aligned}$$

Then, with

$$\begin{aligned} K\buildrel {\mathrm{def}} \over =\max \{2\,(2\,\hat{C}_0\,K_0+1),\,2\,\hat{C}_0\,K_0+\hat{C}_0\,(2\,c_3+D)\,\delta \}, \end{aligned}$$

which is a function of $r,\,T$ and $\delta$, we obtain that on ${\varOmega }^{r,N}_{T,\varepsilon (\delta ),\delta }$, if $N\ge N_0$, $||\hat{W}^{r,N}(\cdot )||_{T}\le K,\,||\hat{Y}^{r,N}(\cdot )||_{T}\le K.$ Finally, from (38), (44) and (43), on ${\varOmega }^{r,N}_{T,\varepsilon (\delta ),\delta }$ and if $N\ge N_0$, $||\hat{\xi }^{r,N}(\cdot )||_{T}\le \delta ,$ which completes the proof of (29).

Step 3:

Thirdly, we return to the expression (37), and by (44) and (43), we obtain that if $N\ge N_0$, on ${\varOmega }^{r,N}_{T,\varepsilon (\delta ),\delta }$ it holds that if $t\in [0,\,T],$

$$\begin{aligned}&\hat{Y}^{r,N}_j(t)=\int _0^t 1_{\big \{d(\tilde{W}^{r,N}(s),\,\mathtt{F }_j)\le \delta \big \}} \,d\,\hat{Y}_j^{r,N}(s), \end{aligned}$$

(45)

which finishes the proof. $\square$

Corollary 1

Under assumption HTa, assume in addition that MSSC holds. Then, for each $r\ge 1$ there exists a sequence of positive numbers $\{\delta ^{r,N}\}_N$ such that $\delta ^{r,N}\rightarrow 0$ as $N\rightarrow +\infty$, and a sequence of probability measures $\{P^{r,N}\}_N$ on $({\varOmega },\,\mathcal{F})$ with $P^{r,N}\Rightarrow P$ as $N\rightarrow +\infty$, such that for each $t>0,\,j=1,\,\ldots ,\,J$ and N big enough, $P^{r,N}-a.s.$

$$\begin{aligned} \hat{Y}^{r,N}_j(t)=\int _0^t 1_{\big \{d(\tilde{W}^{r,N}(s),\,\mathtt{F }_j)\le \delta ^{r,N}\big \}} \,d\,\hat{Y}_j^{r,N}(s). \end{aligned}$$

Proof

(This proof follows the arguments of Theorem 5.2 [14].) Fix $r\ge 1$. To make explicit its dependency on $T,\,\varepsilon$ and $\delta$, we denote by $N_0(T,\varepsilon ,\delta )$ the constant defined by (39), where $\varepsilon =\varepsilon (\delta )$ is the function of $\delta$ given by expression (43). Choose a strictly increasing sequence of positive constants $\{N_{\ell },\,\ell \ge 1\}$ such that $\lim _{\ell \rightarrow +\infty } N_{\ell }=+\infty$ and for each $\ell$, $N_{\ell }\ge N_0(\ell ,\,\varepsilon (1/{\ell }),\,\frac{1}{\ell }),$ and define the sequence $\{\delta ^{r,N}\}_N$ in this way:

$$\begin{aligned} \delta ^{r,N}\buildrel {\mathrm{def}} \over = {\left\{ \begin{array}{ll} 1 &{}\quad \text {if } N\le N_1\\ \frac{1}{\ell } &{}\quad \text {if } N\in (N_{\ell },\,N_{\ell +1}]. \end{array}\right. } \end{aligned}$$

Then, $\lim _{N\rightarrow +\infty } \delta ^{r,N}=0$ and $\lim _{\ell \rightarrow +\infty } \varepsilon (1/\ell )=0$. Using notation introduced in the proof of Proposition 4, for any $N>N_1$ let us define ${\varOmega }^{r,N}\buildrel {\mathrm{def}} \over = {\varOmega }^{r,N}_{\ell ,\varepsilon (1/\ell ),\frac{1}{\ell }}$ if $N\in (N_{\ell },\,N_{\ell +1}]$. With this definition, as seen in the proof of Proposition 4, $P({\varOmega }^{r,N})\ge 1-\delta ^{r,N}$, which is $>0$ since $N>N_1$. Now define a sequence of probability measures $\{P^{r,N}\}_{N> N_1}$ on $({\varOmega },\,\mathcal{F})$ by:

$$\begin{aligned} \forall A\in \mathcal{F},\quad P^{r,N}(A) \buildrel {\mathrm{def}} \over = \frac{P\big (A\cap {\varOmega }^{r,N}\big )}{P\big ({\varOmega }^{r,N}\big )} \end{aligned}$$

(that is, $P^{r,N}(\cdot )=P(\cdot \,/\,{\varOmega }^{r,N})$). If a property holds $\forall \omega \in {\varOmega }^{r,N}$, then it holds $P^{r,N}-$a.s. since $P^{r,N}({\varOmega }^{r,N})=1$, and moreover $P^{r,N}\Rightarrow P$ as $N\rightarrow +\infty$.

For any $t>0$ and N big enough, there exists $\ell \ge t$ such that $N\in (N_{\ell },\,N_{\ell +1}]$ and then, from (45) with $T=\ell ,\,\delta =1/\ell$ and $\varepsilon =\varepsilon (1/\ell )$ we have that for any $j=1,\ldots ,\,J$, $P^{r,N}-$a.s.,

$$\begin{aligned} \hat{Y}^{r,N}_j(t)&=\int _0^t 1_{\big \{d(\tilde{W}^{r,N}(s),\,\mathtt{F }_j)\le \frac{1}{\ell }\big \}} \,d\,\hat{Y}_j^{r,N}(s)\\&=\int _0^t 1_{\big \{d(\tilde{W}^{r,N}(s),\,\mathtt{F }_j)\le \delta ^{r,N}\big \}} \,d\,\hat{Y}_j^{r,N}(s). \end{aligned}$$

$\square$

6 Conclusion

A heavy-traffic limit theorem (split into to parts: Theorems 1 and 2) for a flow-level model of a packet-switched network handling elastic flows, with local traffic and fed by a huge number of heavy-tailed On/Off sources, is proved in this paper. The service capacity (bandwidth) on each node of the network is dynamically allocated to the routes passing by the node by following a weighted proportional fair sharing policy, and the fraction of capacity assigned to each route is shared at any time among the flows in progress at the route. The choice of the arrival process has been made by coherency with the long-range dependence and self-similarity observed in modern high-speed network traffic.

In the proof of this result, state space collapse SSC plays a key role: in the heavy-traffic environment and under some other technical conditions, if SSC holds we prove that the limit of the conveniently scaled workload process (associated to each node) W is a rfBm process on a polyhedral cone determined by the bandwidth sharing policy. SSC implies that the limit of the scaled amount of flows process (associated to each route) can be expressed in terms of W by means of a deterministic lifting map. The novelty lies in the fact that it is for the first time that SSC has been considered in the context of a heavy-traffic limit theorem in the On/Off heavy-tailed sources model, with a fair bandwidth sharing policy. We also prove that SSC is equivalent, under heavy traffic, to the a priori weaker condition known as MSSC.

Another important ingredient in the proof of the heavy-traffic limit is the version we introduce of the Invariance Principle in domains with piecewise smooth boundaries by Kang and Williams [15]. An illustrative example consisting of a linear network with two resources and three routes, is introduced to assist in the understanding of the results presented in the paper.

In this work, we restrict ourselves to the member $\alpha =1$ of the family of weighted $\alpha$-fair bandwidth sharing policies introduced in [20], but other members of the family, that is, extensions of the model to other network bandwidth sharing policies than the weighted proportional fair, could be considered for future research.