Abstract
In previous papers we developed a deterministic fluid approximation for an overloaded Markovian queueing system having two customer classes and two service pools, known in the call-center literature as the X model. The system uses the fixed-queue-ratio-with-thresholds (FQR-T) control, which we proposed as a way for one service system to help another in face of an unexpected overload. Under FQR-T, customers are served by their own service pool until a threshold is exceeded. Then, one-way sharing is activated with customers from one class allowed to be served in both pools. The control aims to keep the two queues at a pre-specified fixed ratio. We supported the fluid approximation by establishing a functional weak law of large numbers involving a stochastic averaging principle. In this paper we develop a refined diffusion approximation for the same model based on a many-server heavy-traffic functional central limit theorem.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we establish a many-server heavy-traffic functional central limit theorem (FCLT) for an overloaded large-scale Markovian queueing system having two classes and two service pools, known as the \(X\) model [7], using the fixed-queue-ratio with thresholds (FQR-T) routing, which we proposed in [21].
In particular, we consider a system in which each class has its own designated service pool, but with all agents, in both pools, capable of serving customers from both classes. The control aims to prevent sharing of customers (i.e., sending customers from one class to be served at the other class pool) when both classes are normally loaded, and to activate sharing when the system unexpectedly experiences an overload, due to an unforseen shift in the arrival rates.
When sharing is taking place, the control aims at keeping a pre-specified fixed ratio between the two queues, both as the overload develops over time and in the overload steady-state. This ratio is chosen according to an optimization problem for the approximating stationary deterministic “fluid” model, assuming a convex holding cost is incurred on the two queues during the overload incident; see §5.3 in [21], where it is also shown that sharing should not be allowed at both directions simultaneously, i.e., at any time there should be at most one pool working with both classes. In general, there are two different ratios: If class 1 is overloaded, then an optimal ratio \(r_{1,2}\) should hold between the queues. If class 2 is overloaded, then an optimal ratio \(r_{2,1}\) should hold between the queues. In [24] we showed that the FQR-T control achieves the target ratios asymptotically as the scale increases (in the fluid limit), for the time-dependent transient performance as well as in steady- state. Moreover, the FQR-T control produces a tractable fluid limit. Here, we show that the FQR-T control also produces a tractable refined stochastic limit.
The FQR-T control here is a modification of the FQR control (without the thresholds), which is a special case of the queue-and-idleness ratio (QIR) controls suggested by Gurvich and Whitt [11]. These QIR and FQR controls were analyzed in [10–12] for critically loaded systems, operating in the quality and efficiency driven (QED) many-server heavy-traffic regime; see [8, 13]. Heavy-traffic limits for networks having cyclic graphs, such as the X model, were obtained under the condition that the service rates are class or pool-dependent; see Theorem 3.1 in [11]. In general, when the service rate depends on both the class and the pool, FQR can perform badly in cyclic networks, creating severe congestion even if each pool is not congested by itself; see §4.1 in [21] and §EC.2 in [22].
We suggested the FQR-T control in [21], and analyzed the X model using a stationary fluid approximation. In [22] we determined the transient behavior of that same fluid model, based on a stochastic averaging principle (AP), but that AP was introduced there as a heuristic engineering principle (i.e., used without proof), supported only by simulation. This heuristic analysis and the AP were made rigorous in our subsequent papers. In particular, the purpose of [23, 24] was to establish key mathematical properties of the fluid model, expressed as an ordinary differential equation (ODE), and show that the fluid model in [21, 22], arises as the many-server heavy traffic limit of a sequence of \(X\) models in the many-server efficiency driven (ED) regime. That FWLLN is challenging, because the fluid limit depends critically on the AP. For each \(n\), the system evolves as a 6-dimensional continuous-time Markov chain (CTMC), but there is a (somewhat complicated) statistical regularity associated with the many-server heavy-traffic limit. In particular, the limiting fluid approximation is a deterministic function characterized by an ODE (and an initial condition), which is driven by the time-varying instantaneous average behavior of a family of fast-time-scale stochastic processes (FTSP’s), which produces the AP. See §1.3 of [24] for a discussion of the literature on AP’s; notable contributions in the queueing literature are by Coffman et al. [4] and Hunt and Kurtz [15]. See [6] for a (quite different) FCLT involving an AP, building on [15].
We now build on the FWLLN and the AP to describe the distribution of the stochastic fluctuations about the fluid path; i.e., we establish the corresponding FCLT, which is Theorem 4 here. There is technical novelty in properly treating the FTSP’s alluded to above. The limit process involves an independent Brownian motion (BM) term with deterministic time scaling involving the asymptotic variance of the FTSP; see §4.1 and \({\hat{L}}_2, {\hat{I}}, \gamma _2\) and \(\gamma _3\) in Theorem 4. A key step in establishing the main result—the FCLT in Theorem 4—is a FCLT for the family of FTSP’s, Theorem 6, which is of independent interest. This challenging step proves a FCLT for a sequence of CTMC’s having time-varying parameters depending on the fluid limit. The new methods developed here should prove useful for analyzing related problems.
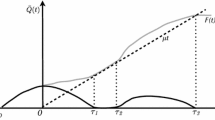
From an engineering perspective, Corollary 1 is especially useful for understanding the performance of the FQR-T control. It describes the stochastic-process limit once the fluid has stabilized (i.e., when the fluid is stationary). With a constant fluid state, the key limit process becomes the well-studied bivariate Ornstein-Uhlenbeck (BOU) process, which has a Gaussian distribution for each \(t\); see Corollary 1 below. Consequently, the approximating steady-state distribution during the overload is a Gaussian distribution, with mean values equal to the stationary fluid point in Theorem 2 multiplied by \(n\), and variance and covariance terms in (24) multiplied by \(\sqrt{n}\).
The FCLT extension is essential for truly understanding the system performance under overloads, because the actual performance is not nearly deterministic, as described by the fluid approximation, unless the scale is extremely large. This phenomenon is well- illustrated by the example here in §11. For that example, the standard deviations of the queue lengths are about equal to (half of) the mean queue lengths when the number of servers in each pool is 25 (100).
Here is how the paper is organized: after preliminaries in §2, we briefly state the FWLLN and the associated WLLN for the stationary distributions in §3. We state the FCLT and our other main results in §4. We prove the FCLT in §5 except for Lemma 6, establishing joint convergence of the driving processes. We give the proof of Lemma 6 in §6 except for two supporting results. The key supporting result is a FCLT for the FTSP with time-varying parameter state function in Theorem 6. We prove Theorem 6 in §7. Our proof of Lemma 14 to prove Theorem 6 exploits the martingale FCLT for triangular arrays. We state these supporting martingale results in §8. We then prove five remaining Lemmas in §9. A key technical step in the proofs is approximating the given process with time-varying parameters over appropriate subintervals by associated frozen processes, where the parameters are fixed (frozen) at designated values. Those approximation steps are justified in §10 using coupling constructions. In particular, we prove Lemmas 8 and 12 there. Finally, we evaluate the quality of the approximations by making comparisons with simulations in §11.
2 Preliminaries
2.1 Notation
Let \(\mathbb{R },\, \mathbb{Z }\) and \(\mathbb{N }\) denote the real numbers, integers, and non-negative integers, respectively. Let \(\equiv \) denote equality by definition. For a subinterval \(I\) of \([0,\infty )\), let \(\mathcal{D }\equiv \mathcal{D }(I) \equiv \mathcal{D }(I, \mathbb{R })\) be the space of all right-continuous \(\mathbb{R }\)-valued functions on \(I\) with limits from the left everywhere, endowed with the familiar Skorohod \(J_1\) topology [31]. Let \(\mathcal{C }\) be the subset of continuous functions in \(\mathcal{D }\). Let a subscript \(k\) appended to one of these spaces denote the set of all \(k\)-dimensional vectors with components from the space, endowed with the corresponding product topology, e.g., \(\mathbb{R }_k\) and \(\mathcal{D }_k\).
Let \(d_{J_1}\) denote a metric on \(\mathcal{D }_k(I)\) inducing the convergence. Since we will be considering continuous limits, the topology is equivalent to uniform convergence on compact subintervals of \(I\). Let \(e\) be the identity function in \(\mathcal{D }\equiv \mathcal{D }_1\); i.e., \(e (t) \equiv t, t \in I\). Let \(\circ \) be the composition function, i.e., \((x\circ y) (t) \equiv x(y(t))\). Let \(\Rightarrow \) denote convergence in distribution [31].
We use the familiar big-\(O\) and small-\(o\) notation for deterministic functions: For two real functions \(f\) and \(g\), we write
(note that our definition of \(O(g(x))\) deviates from the standard definition which allows for the \(\limsup \) in the right-hand side to be equal to \(0\)). For a function \(x : [0, \infty ) \rightarrow \mathbb{R }\) and \(0 < t < \infty \), let \(\Vert x\Vert _t \equiv \sup _{0 \le s \le t} | x(s)|\).
For a stochastic process \(Y \equiv \left\{ Y(t) : t \ge 0\right\} \) and a deterministic function \(f : [0, \infty ) \rightarrow [0, \infty )\), we say that \(Y\) is \(o_P(f(t))\) if \(\Vert Y\Vert _t/f(t) \Rightarrow 0 \quad \text{ as }\quad t \rightarrow \infty \).
For a sequence of stochastic processes or random variables, \(\left\{ Y^n : n \ge 1\right\} \), we denote its fluid-scaled version by \(\bar{Y}^n \equiv Y^n / n\). We let \(\breve{Y}^n \equiv Y^n/\sqrt{n}\) be the \(\sqrt{n}\)-scaled processes without the centering about the fluid limit, and \(\hat{Y}^n\) denote the diffusion-scaled processes centered about the fluid limit, as in (15) below.
2.2 A sequence of overloaded Markovian X models
We consider a sequence of overloaded Markovian X models, indexed by superscript \(n\). There are two customer classes and two service pools. We are looking at these models during the overload incident, after the arrival rates have changed. The arrival rates are considered fixed, but the system is typically not yet in its new steady-state during the overload (assuming that the overload would persist). For each \(n\) and \(i = 1, 2\), there is a class-\(i\) Poisson arrival process with rate \(\lambda ^n_i\). Customers have limited patience, and may abandon when waiting in queue. The times to abandon are i.i.d. exponential variables with rate \(\theta _i\) for each class-\(i\) customer in queue. Service pool \(j\) has \(m^n_j\) homogeneous agents (servers). Service times of class-\(i\) customers by pool-\(j\) agents are mutually independent and exponentially distributed with rate \(\mu _{i,j},\; i,j = 1,2\). The abandonment and service rates are independent of \(n\). We mention that we make no assumptions on the four service rates and, in particular, we do not assume that the weak inefficiency condition holds, namely, that \(\mu _{1,1}\mu _{2,2} \ge \mu _{1,2} \mu _{2,2}\). This condition was key to our analysis in [21], but here we study a more general system.
Since we are considering an overload incident, we will scale to achieve an ED many-server heavy-traffic regime.
Assumption 1
(Many-server heavy-traffic scaling) For \(\lambda _i,\, m_i > 0,\, i = 1,2\),
We could instead obtain a modified, more general, FCLT if there were non-degenerate limits in Assumption 1, but we consider our choice natural, because the system operates in an overload regime (the modified limit includes a deterministic term \(ct\) in the diffusion limit, but there is no difference in the variability of the limit process, as can be seen from (30). For the FWLLN, it is sufficient that \(\lambda ^n_i/n \rightarrow \lambda _i\) and \(m^n_i/n \rightarrow m_i\) as \(n \rightarrow \infty ,\, i = 1,2\)). Let
where, for \(y \in \mathbb{R }, y^+ \equiv \max \left\{ 0, y\right\} \). Then \(\rho _i\) is the traffic intensity for pool \(i\) and \(q_i^a\) is the stationary class-\(i\) fluid-limit queue, when both pools operate independently. We say that pool \(i\) is overloaded if \(\rho _i > 1\). However, with sharing allowed, pool \(i\) can be overloaded even if \(\rho _i < 1\) provided that enough class \(j\) customers are routed to be served there, \(j \ne i\). The next assumption makes precise our notion of system overload.
Assumption 2
(System overload, with class 1 more overloaded)The rates in the system are such that
Clearly, \(\rho _1 > 1\) by Condition \((I)\), so that class 1 is overloaded. However, Condition \((I)\) also ensures that pool 2 is overloaded if sharing is taking place. That is so because, even if \(\rho _2 < 1\), there is not enough extra service capacity in pool 2 to take care of all the class-1 customers that pool 1 cannot serve. Condition \((II)\) in the assumption implies that even if pool 2 is overloaded by itself (i.e., if \(\rho _2 > 1\)), then class 1 is the one that should receive help from pool 2.
2.3 The FQR-T control
We now describe the FQR-T control for each system \(n\). The purpose of the FQR-T control is: (i) to prevent sharing under normal loads, (ii) to activate sharing as soon as an overload incident begins, and (iii) to keep close to the desired ratio between the two queues, making sure that sharing takes place in the needed direction only. The control is based on two positive thresholds, \(k^n_{1,2}\) and \(k^n_{2,1}\), and the two ratio parameters discussed above, \(r_{1,2}\) and \(r_{2,1}\), which satisfy \(r_{1,2} \ge r_{2,1}\); see Proposition EC.2 and Eq. (EC.11) in [21].
Let \(Q^n_i (t)\) be the number of customers in the class-\(i\) queue and let \(Z^n_{i,j} (t)\) be the number of class-\(i\) customers being served in service pool \(j\), at time \(t, i,j = 1,2\) (in the \(n\)th system). The FQR-T routing is based on the queue-difference stochastic processes
As long as \(D^n_{1,2} (t) \le 0\) and \(D^n_{2,1} (t) \le 0\), no sharing of customers is allowed, i.e., a server in pool \(j\) takes only class \(j\) customers, \(j = 1,2\). It follows from [8] that thresholds of order larger than \(O(\sqrt{n})\) will prevent sharing (asymptotically, as \(n \rightarrow \infty \)) when both pools are normally loaded, because normally loaded systems, that are not overloaded, have stochastic fluctuations that are of order \(O(\sqrt{n})\). Once one of the queue-difference processes in (1) becomes strictly positive (so that one of the thresholds is crossed) sharing is initiated. It follows from the Corollary 2.1 in [32], that thresholds of size \(o(n)\) will detect an overload relatively quickly (instantly, asymptotically as \(n \rightarrow \infty \)). This is because overloaded queues are of order \(n\) asymptotically. We thus choose the thresholds according to the following assumption.
Assumption 3
(Scaling of the thresholds) For \(k_{1,2}, k_{2,1} > 0\) and a sequence of positive numbers \(\left\{ c_n : n \ge 1\right\} \), where \(c_n/n \rightarrow 0\) and \(c_n/\sqrt{n} \rightarrow \infty \) as \(n \rightarrow \infty \),
Finally, only one-way sharing is allowed at any time. For example, a newly available pool-2 agent at time \(t\) serves a class-1 customer if \(D^n_{1,2} (t) > 0\), provided no class-2 customers are served in pool 1 at that same time \(t\); otherwise he serves a class-2 customer.
2.4 Dimension reduction
For the X model operating under FQR-T, the six-dimensional process
is a CTMC for each \(n \ge 1\). However, there is an important dimension reduction established in §6 of [24]. It was shown, under the assumptions above and with appropriate initial conditions, that asymptotically the two service pools remain fully occupied with no pool-1 servers serving class 2; i.e., for each \(T > 0\),
Thus, the system is characterized by an essentially three-dimensional process
having the vector of essential components
whose evolution is directly specified, and will be specified here in Theorem 1. Theorem 1 concludes that \({\bar{X}}^{n,*}_6\) and \({\bar{X}}^n_6\) are asymptotically equivalent, so that \({\bar{X}}^n\) is sufficient to characterize the FWLLN and, in turn, to prove the FCLT. That implies that \({\bar{X}}^n_6 \Rightarrow x_6\) in \(\mathcal{D }_6\) if and only if \({\bar{X}}^n \Rightarrow x\) in \(\mathcal{D }_3\) as \(n \rightarrow \infty \), with \(x(t) \in \mathbb{S }\equiv [0, \infty )^2 \times [0, m_2]\), for \(t \ge 0\); see Theorem 1 below. We thus restrict attention to the space \(\mathbb{S }\).
2.5 The fast-time-scale process
Given that the system is overloaded with class 1 needing help from pool 2, as determined by Assumptions 1 and 2, the FQR-T control is driven by the process \(D^n_{1,2}\) in (1). Since the queue lengths are asymptotically of order \(O(n)\), the queue-difference process \(D^n_{1,2}\) has transitions at rate \(O(n)\). However, Theorem 4.5 in [24] shows that, under regularity conditions, the sequence \(\{D^n_{1,2} (t): n \ge 1\}\) is stochastically bounded in \(\mathbb{R }\), so that the difference process should be analyzed without any spatial scaling. On the other hand, Theorem 4.4 in [22] also shows that this sequence is not \(\mathcal{D }\)-tight. Thus, these difference processes do not converge to non-degenerate limits in \(\mathcal{D }\) as \(n \rightarrow \infty \) without spatial scaling. Nevertheless, both the FWLLN and FCLT depend heavily on the asymptotic behavior of functionals of that driving queue-difference process and on the analysis of a related family of fast time scale process (FTSP’s).
Fix \(t_0 \ge 0\) and consider the time expanded queue-difference process
where \(\Gamma ^n\) is a random vector in \(\mathbb{R }_3\), representing a possible state of \(X^n\), and we condition on \(X^n(t_0) = \Gamma ^n\). Theorem 4.4 in [24] shows, under the assumptions of the FWLLN in Theorem 1 below, that
if \(\Gamma ^n/n \Rightarrow \gamma \in \mathbb{S }\) and \(D^n_e (\Gamma ^n, 0) \Rightarrow D(\gamma , 0)\) in \(\mathbb{R }\) as \(n \rightarrow \infty \). The limit process \(D(\gamma ,\cdot )\) is the FTSP, an irreducible pure-jump (time homogeneous) Markov process having transition rates that are the limit of the instantaneous rates of \(D^n_{1,2} (t_0)\) at time \(t_0\) (given the state of the CTMC \(X^n_6 (t_0)\)), divided by \(n\). Since the distribution of the FTSP is determined by \(\gamma \), we obtain a different FTSP \(D(\gamma , \cdot )\) for each \(\gamma \in \mathbb{S }\), and thus for each \(t \ge 0\). The name “FTSP” becomes clear when observing that it arises as the limit in (5) achieved by “slowing” time in the neighborhood of each time point \(t_0\) in \(D^n_{1,2}(t_0)\).
As explained in §2.3, the purpose of the FQR-T control during overload periods (with class 1 receiving help) is to keep the two queues approximately fixed at the target ratio \(r\). In this paper we will be concerned with the region of the state space in which \(q_1 = r q_2\) and the FTSP is positive recurrent. In particular, for \(\gamma \equiv (q_1,\, q_2,\, z_{1,2})\) we let
denote the “boundary” set of points in \(\mathbb{S }\) which is part of the state space to which the control drives the process. We then let \(\mathbb{A }\) denote the set of all \(\gamma \in \mathbb{S }^b\), such that \(D(\gamma ,\cdot )\) is positive recurrent, with \(D(\gamma , \infty )\) denoting a random variable distributed as the stationary distribution of the FTSP \(D(\gamma , \cdot )\). For each \(\gamma \in \mathbb{S }^b\), let
By Lemma 3.1 in [24], \(\pi _{1,2}(\gamma )\) is well-defined for all \(\gamma \in \mathbb{S }\), but \(D(\gamma , \cdot )\) is positive recurrent if and only if \(0 < \pi _{1,2}(\gamma ) < 1\) and \(\gamma \in \mathbb{S }^b\). By Theorem 6.1 of [23],
where \(\delta _{+} (\gamma )\) and \(\delta _{-} (\gamma )\), respectively, are the constant drift rates in the positive region \(\{s:D(\gamma , s) > 0\}\) and the non-positive region \(\{s:D(\gamma , s) \le 0\}\).
Both the FWLLN and the FCLT depend critically on distributional and topological characteristics of the FTSP’s. A simplification is achieved by representing the FTSP as a quasi-birth-and-death (QBD) process, which can be done by assuming that \(r_{1,2}\) is rational. The QBD representation is not straightforward, thus we refer to §6.2 in [23] for more details on the QBD representation of the FTSP, and to [18] for the general theory of QBD processes. See also Theorem 6.1 and Eq. (7.2) in [23] for how the QBD representation simplifies the characterization of \(\mathbb{A }\), as well as §11 in [23], where an efficient algorithm for computing the fluid limit numerically is developed, based on that QBD representation. For our purposes here, it only matters that the FTSP can be analyzed as a QBD, provided that the queue ratios are rational number. We thus make the following assumption.
Assumption 4
(Queue ratios parameters) The queue ratios \(r_{1,2}\) and \(r_{2,1}\) are positive rational numbers.
Since we are considering the case when sharing is taking place with class-1 customers receiving help, we essentially need only consider \(r_{1,2}\), which we henceforth denote by \(r\), i.e., \(r \equiv r_{1,2}\).
3 The fluid limit
We now review the FWLLN for the process \({\bar{X}}^n_6\) in (2) and the WLLN for the associated sequence of stationary random variables \({\bar{X}}^n_6 (\infty )\), established in [24]. For these, we assume that the fluid \(x(t)\) is in the set \(\mathbb{A }\), where the FTSP is positive recurrent. We conclude by reviewing a result stating that the fluid model eventually remains in \(\mathbb{A }\).
3.1 The FWLLN
We now describe the fluid limit, i.e., the limit of \({\bar{X}}^n_6\) for \(X^n_6\) in (2). The FWLLN requires an assumption about the initial conditions. In [24] we considered a (more general) version of the following.
Assumption 5
Assume that
where \(L\) is a finite random variable, \(x(0)\) is deterministic and \(\{a_n : n \ge 1\}\) is a sequence of numbers satisfying \(a_n/c_n \rightarrow a,\; 0 < a \le \infty \), for \(c_n\) in Assumption 3.
We note that in [24] \(x(0)\) was not necessarily in \(\mathbb{A }\). The following theorem is a version of the main result—Theorem 4.1—in [24], adapted to our needs here.
Theorem 1
(FWLLN) Under Assumptions 1–5,
for \(X^n_6\) in (2), where \(x_6 \equiv (q_i,\; z_{i,j}; i,j = 1,2)\), is a deterministic element of \(\mathcal{C }_{6}\), with \(z_{1,1} = m_1\text{ e },\; z_{2,1} = 0\text{ e }\) and \(z_{2,2} = m_2\text{ e } - z_{1,2}\) and \(x \equiv (q_1,\, q_2,\, z_{1,2})\) being the unique solution to the three-dimensional ODE
for \(\pi _{1,2}(x(t)) \equiv P(D(x(t), \infty ) > 0)\) in (7). Moreover, there exists \(\delta , 0 < \delta \le \infty \), such that \(x(t) \in \mathbb{A }\), so that \(0 < \pi _{1,2} (x(t)) < 1\) and \(q_1 (t) = r q_2 (t)\), for all \(t \in [0, \delta )\).
Just as the routing of customers at each time \(t \ge 0\) in the prelimit is determined by whether \(D^n_{1,2}(t) > 0\) or \(\le 0\), so also the instantaneous future evolution of the fluid limit \(x(t)\) at time \(t \ge 0\), is determined by whether the FTSP corresponding to \(x(t),\, D(x(t), \cdot )\), is positive or non-positive. However, that evolution is determined by the long-run average behavior of the FTSP corresponding to time \(t\), i.e., by \(\pi _{1,2}(x(t))\), giving rise to the term “averaging principle”. Loosely speaking, \(D^n_{1,2}(t)\) achieves a local steady-state (the steady-state of the FTSP) instantaneously as \(n \rightarrow \infty \), at each time \(t \ge 0\).
Observe that Theorem 1 concludes that if \(x(0) \in \mathbb{A }\), then \(x(t) \in \mathbb{A }\) for all \(t\) over some interval \([0, \delta )\) (that part of the theorem follows from Theorem 4.5 in [24]), so that we have SSC in the sense that the original six-dimensional process is a deterministic function of a two-dimensional process. More importantly for the FCLT, we also have that \(Q^n_1(t) - k^n_{1,2} - r Q^n_2(t) = o(\sqrt{n})\) for \(t \in (t_1, t_2)\) if \(x(t) \in \mathbb{A }\) over \([t_1, t_2)\), so the SSC to two dimensions holds in diffusion scale as well; see Lemma 2 below.
3.2 The stationary fluid limit
Our main theorem here will be establishing the FCLT about the fluid trajectory, given that the trajectory is in \(\mathbb{A }\). An important consequence will be the BOU limit when the fluid limit is stationary. Since the fluid limit of \({\bar{X}}^n\) in (3) is the unique solution to the ODE (9), there is an immediate equivalence between stationarity of the fluid limit and stationarity of the dynamical system in (9), and we do not distinguish between the two.
Recall that \(e\) denotes the identity function, i.e., \(e(t) = t, t \ge 0\).
Definition 1
(Fluid stationarity) A point \(x^{*} \in \mathbb{S }\) is a stationary point of the unique solution \(x \equiv \left\{ x(t) : t \ge 0\right\} \) to the ODE (9) if \(x(0) = x^{*}\) implies \(x = x^{*} e\). If \(x = x^{*} e\), then \(x\) is said to be stationary.
Since the ODE is autonomous (i.e., time invariant), we can replace time 0 with any \(t > 0\) in Definition 1. That is, if \(x(T) = x^{*}\) for some \(T > 0\), then \(x(t) = x^{*}\) for all \(t > T\). Time invariance also implies that \(x(t)\) is stationary at time \(t\) (\(x(t) = x^{*}\)) if and only if \(\dot{x} (t) \equiv (\dot{q}_1 (t),\; \dot{q}_2 (t),\; \dot{z}_{1,2}(t)) = (0, 0, 0)\); see §8 of [23].
There are several issues regarding stationarity, which we addressed in [23]. In advance, neither existence of a stationary point to the fluid limit nor uniqueness are immediate. Even if there exists a unique stationary point, it needs to be identified. Moreover, it must be shown that the fluid limit converges to a stationary point as \(t \rightarrow \infty \) (there are still other issues regarding stability of the dynamical system in (9), and we refer to §8.3 in [23] for a discussion). Finally, the fluid limit of \({\bar{X}}^n_6\) in (2) is characterized by the fluid limit of the three-dimensional \({\bar{X}}^n\) in (4), but that does not directly imply any relation between the stationary fluid limit and the stationary stochastic prelimit.
We now present the most relevant results for the FCLT regarding fluid stationarity.
Theorem 2
(Fluid stationarity) Under Assumptions 1–5, the following hold:
-
(i)
For each \(n, {\bar{X}}^n_6 (t) \Rightarrow {\bar{X}}^n_6 (\infty )\) in \(\mathbb{R }\) as \(t \rightarrow \infty \), with \({\bar{X}}^n_6 (\infty )\) being the unique stationary distribution of the CTMC, and \({\bar{X}}^n_6 (\infty ) \Rightarrow x^{*}_6\) in \(\mathbb{R }\) as \(n \rightarrow \infty \) for
$$\begin{aligned} x^{*}_6 \equiv \big (q^{*}_1,\; q^{*}_2,\; m_1,\; z^{*}_{1,2},\; 0,\; m_2 - z^{*}_{1,2}\big ), \end{aligned}$$(10)where
$$\begin{aligned} z_{1,2}^{*}&= \frac{\theta _2\big (\lambda _1 - m_1\mu _{1,1}\big ) - r \theta _1\big (\lambda _2 - m_2\mu _{2,2}\big )}{r \theta _1\mu _{2,2} + \theta _2\mu _{1,2}} \wedge m_2, \\ q_1^{*}&= \frac{\lambda _1 - m_1\mu _{1,1} - \mu _{1,2} z_{1,2}^{*}}{\theta _1} \quad \text{ and }\quad q_2^{*} = \frac{\lambda _2 - \mu _{2,2} \big (m_2 - z_{1,2}^{*}\big )}{\theta _2}. \end{aligned}$$ -
(ii)
\(x^{*} \equiv (q^{*}_1,\, q^{*}_2,\, z^{*}_{1,2})\) is the unique stationary point of \(x\), the unique solution to the ODE (9).
-
(iii)
\(\pi _{1,2}(x^{*}) \equiv P(D(x^{*}, \infty ) > 0) = \pi ^{*}_{1,2}\), where \(D(x^{*}, \infty )\) is a random variable with the stationary distribution of the FTSP \(D(x^{*}, \cdot )\) and
$$\begin{aligned} \pi ^{*}_{1,2} \equiv \frac{\mu _{1,2}z^{*}_{1,2}}{\mu _{1,2}z^{*}_{1,2} + \big (m_2 - z^{*}_{1,2}\big ) \mu _{2,2}}. \end{aligned}$$(11) -
(iv)
\(x(t) \rightarrow x^{*}\) as \(t \rightarrow \infty \) exponentially fast.
Proof
Parts \((i),\; (ii)\) and \((iii)\), and \((iv)\), respectively, are covered by Theorem 4.2 in [24], §8 of [23] and Theorem 9.2 in [23]. Explicit exponential bounds on the rate of convergence to stationarity in \((iv)\) are given in [23]. We now elaborate on \((ii)\) and \((iii)\). First, if \(x^{*} \notin \mathbb{A }\), then the fact that \(x^{*}\) is a stationary point of \(x\) follows immediately from the fact that \(\pi _{1,2}(x^{*}) = 0\) or \(= 1\). In that case, it is also easy to see that \(\pi ^{*}_{1,2}\) in (11) is equal to \(\pi _{1,2}(x^{*})\); see Corollary 8.1 in [23]. It is the unique stationary point by Theorem 8.1 in [23]. The more challenging case, in which \(x^{*} \in \mathbb{A }\) and the existence of a stationary point is non-trivial, is proved in Theorem 8.2 in [23].\(\square \)
3.3 Eventually remaining in the set where the FTSP is positive recurrent
The FCLT will be stated under the assumption that the associated fluid limit lies in the set \(\mathbb{A }\). Thus, we now explain why this makes sense and introduce an additional assumption.
Note that \(x^{*}_6\) in (10) is completely characterized by \(x^{*}\), which involves only the rates in the system, and does not require any knowledge of the transient fluid limit or the initial condition (in particular, SSC to three dimensions holds for the WLLN of the stationary distributions). Simple algebra shows that if \(0 < z^{*}_{1,2} < m_2\), then \(q^{*}_1 = r q^{*}_2\). Together with (8) and (11) we see that \(x^{*} \in \mathbb{A }\) if and only if \(0 < z^{*}_{1,2} < m_2\). It follows from Assumption 2 and from (10) that \(z^{*}_{1,2} > 0\) (see also Corollary 8.2 in [23]), so that, under Assumption 2,
The next theorem, which follows from Theorem 10.2 in [23], shows that there is not much loss in assuming that the limit \(x\) lies entirely in \(\mathbb{A }\) whenever \(x^{*} \in \mathbb{A }\).
Theorem 3
If \(x^{*} \in \mathbb{A }\) then there exists \(T_A < \infty \) such that \(x (t) \in \mathbb{A }\) for all \(t \ge T_A\).
Since we are interested in the case \(x^{*} \in \mathbb{A }\), which is the main case, as is clear from (12), we make the following assumption
Assumption 6
For all \(t \ge 0, x(t) \in \mathbb{A }\).
Assumption 6 is not essential for our results; we make it only for simplicity of the exposition. Without this assumption, the FCLT can be proved over a finite interval over which \(x \in \mathbb{A }\). In applications, the fluid limit is likely to hit \(\mathbb{A }\) immediately after the overload begins, and remain in \(\mathbb{A }\) thereafter; see §11.3 in [23].
4 The main results
In preparation for the FCLT, we indicate how the limit is affected by the FTSP in §4.1. We then state the main FCLT and important corollaries in §4.2 and §4.3. We conclude in §4.4 by indicating how the results simplify in the special case \(r \equiv r_{1,2} = 1\), where FQR reduces to serving the longer queue.
4.1 The role of the FTSP’s in the stochastic limit
Just as the limiting ODE in (9) arising in the FWLLN depends on the FTSP’s \(D(\gamma , \cdot )\) (through the probability \(\pi _{1,2} (x(t))\)), the stochastic limit process arising in the FCLT refinement depends on these same FTSP’s. Since the FTSP \(D(\gamma , \cdot )\) depending on the state \(\gamma \) is a positive recurrent QBD under the assumption that \(\gamma \in \mathbb{A }\), the stochastic refinement depends on the asymptotic variability of the FTSP. In particular, since the FTSP \(D(\gamma , \cdot )\) is a regenerative process (which can be represented as a QBD whenever the ratio \(r\) is rational), the associated cumulative process obtained by integrating the indicator functions \(1_{\left\{ D(\gamma , s) > 0\right\} }\) obeys a FCLT; i.e.,
in the functions space \(\mathcal{D }\) as \(n\rightarrow \infty \), where \(B\) is a standard BM for each \(\gamma \in \mathbb{A }\).
The constant \(\sigma ^2 (\gamma )\) appearing inside the BM on the right in (13) is often called the asymptotic variance (see [3, 9, 30]) of the regenerative process \(D(\gamma ,s)\) (and the function \(f\) with \(f(D(\gamma ,s)) \equiv 1_{\left\{ D(\gamma ,s) > 0\right\} }\)). For each \(\gamma \in \mathbb{A }\), it is defined as the limit
In this paper we will be making extensive use of the regenerative structure; see [3, 9] for background. In our QBD context, the underlying regenerative cycles can be determined by successive visits of \(D(\gamma , \cdot )\) to any fixed state, i.e., starting at a transition into the state and ending at the next transition into that state after first leaving that state (the next transition into the state after leaving is the beginning of the next cycle; the cycles are closed on the left and open on the right). The asymptotic behavior is determined by the random length of a cycle, \(\tau (\gamma )\), and either the random integral over a cycle, \(\tilde{Y} (\gamma )\), or the random centered integral over a cycle, \(Y(\gamma )\), where
The key asymptotic quantities here can be expressed in terms of the means of the first two variables and the variance of \(Y(\gamma )\) via
see [3, 9]. Of course, \(Y(\gamma ) = \tilde{Y} (\gamma ) - \pi _{1,2} (\gamma ) \tau (\gamma )\), so that \({\text{ Var }}(Y(\gamma ))\) can be expressed in terms of the means, variances, and the covariance of the variables \(\tau (\gamma )\) and \(\tilde{Y}(\gamma )\), where \(0 \le \tilde{Y} (\gamma ) \le \tau (\gamma )\) w.p.1. Here we have strong regularity, with the random variable \(\tau (\gamma )\) having a finite moment generating function and all these quantities being continuous functions of the state \(\gamma \), by virtue of Lemma C.5 of [24].
4.2 The FCLT
Let \(A^n_i (t)\) count the number of class-\(i\) customer arrivals, let \(S^n_{i,j} (t)\) count the number of service completions of class-\(i\) customers by agents in pool \(j\), an let \(U^n_i (t)\) count the number of class-\(i\) customers to abandon from queue, all in model \(n\) during the time interval \([0,t]\). Let \(D^n_{1,2} (t)\) be the queue-difference process in (1) and let \(Q^n_s (t) \equiv Q^n_1 (t) + Q^n_2 (t)\), all at time \(t\). Let \(p_1 \equiv r/(1+r)\) and \(p_2 \equiv 1 - p_1 = 1/(1+r)\), where \(r \equiv r_{1,2}\). For \(t \ge 0\) and \(i,j = 1,2\), let the diffusion-scaled processes be
where \(x \equiv (q_1, q_2, z_{1,2})\) is the customary three-dimensional representation of the fluid limit, \(z_{1,1} \equiv m_1\text{ e }, z_{2,1} = 0\text{ e }\,z_{2,2} \equiv m_2\text{ e } - z_{1,2}, q_s \equiv q_1 + q_2\) and \(\pi _{1,2} (x(s)) \equiv P(D(x(s), \infty ) > 0)\), with \(D(x(s), \infty )\) being a random variable with the steady-state distribution of the FTSP \(\{D(x(s), t): t \ge 0\}\) associated with the fluid limit \(x(s)\) at time \(s\).
Here is the main result of this paper: the FCLT for the overloaded X model operating under FQR-T. Since the limit is clearly a Markov process with continuous sample paths, it is by definition a diffusion process. Most of the rest of the paper is devoted to its proof.
Theorem 4
(FCLT) If, in addition to Assumptions 1–6,
then, for \(i,j = 1,2\),
in \(\mathcal{D }_{17}\), where the processes depending on \(n\) on the left are defined in (15) and the limit process has continuous paths w.p.1. The initial \(10\)-dimensional component \(({\hat{A}}_i,\, {\hat{U}}_i,\,{\hat{S}}_{i,j},\, {\hat{D}},\, {\hat{I}})\) is a vector of independent Brownian motions, time scaled by increasing continuous deterministic functions (for the first 8, the fluid limits in the translation terms of (15)), with two null components \({\hat{S}}_{2,1} \equiv 0\text{ e }\) and \({\hat{D}}\equiv 0\text{ e }\). Five components of the limit are determined by the relations \({\hat{Q}}_{i} \stackrel{\mathrm{d}}{=}p_i {\hat{Q}}_{s},\; {\hat{Z}}_{2,1} \equiv {\hat{Z}}_{1,1}\equiv 0\text{ e }\) and \({\hat{Z}}_{2,2}\equiv -{\hat{Z}}_{1,2}\). Finally, \(({\hat{Q}}_s, {\hat{Z}}_{1,2})\) is the unique solution of the following two-dimensional stochastic integral equation:
where, for \(i = 1,2\),
with \(B_1,\; B_{1,2},\; B_{2,2},\; B_{1,3},\; B_{2,3}\) and \(B_2\) being six independent standard BM’s, while \(\gamma _i,\, \gamma _{i,2}\) and \(\phi _{i,2}\) are strictly increasing continuous deterministic functions. Specifically,
where
with \(\pi _{1,2} (x(u))\) and \(\sigma ^2 (x(u))\) being the quantities associated with the FTSP \(D(x(u), \cdot )\), defined in (7) and (13), respectively, and characterized in (14).
Since the FCLT describes a refinement of the transient behavior of the fluid limit, it should not be surprising that the limiting stochastic process \(({\hat{Q}}_s,\; {\hat{Z}}_{1,2})\) would be difficult to analyze. On the positive side, we can solve for \({\hat{Z}}_{1,2}\) in (17) without having to simultaneously solve for \({\hat{Q}}_s\), but we need \({\hat{Z}}_{1,2}\) to solve for \({\hat{Q}}_s\). An additional complication for \({\hat{Q}}_s\) is the dependence between the driving Brownian motions for the two processes \({\hat{Q}}_s\) and \({\hat{Z}}_{1,2}\); note that the time-transformed Brownian terms \(\hat{L}_{i,2}\) appear in both.
The FCLT shows the impact of system variability on the stochastic limit. First, and perhaps of greatest interest, there is a Brownian contribution \({\hat{L}}_2 \stackrel{\mathrm{d}}{=}B_{2} (\gamma _2 (t))\) from the FTSP appearing in the equation for \({\hat{Z}}_{1,2}\); note the dependence between \({\hat{L}}_2\) and \({\hat{I}}\). However, \(({\hat{L}}_2,\, {\hat{I}})\) is independent of all other Brownian terms. We thus see that the fluctuations about the fixed target ratio \(r\) in the queue-difference process (1) due to FQR do have an impact on the stochastic limit.
On the other hand, we see that the stochastic fluctuations associated with external arrivals and abandonments only affect \({\hat{Q}}_s\); they have no impact on \({\hat{Z}}_{1,2}\). The same is true for the stochastic fluctuations of service facility 1, which is always busy, without any sharing. These fluctuations are captured by the Brownian term \({\hat{L}}_1 \stackrel{\mathrm{d}}{=}B_1 (\gamma _1(t))\). However, as noted above, in distinct contrast, the stochastic fluctuations in the service processes at service facilty 2 have a more complicated impact, because they appear in the Brownian driving processes of both equations.
4.3 Important corollaries
The stochastic limit in the FCLT depends critically on the fluid limit \(x\), which typically must be computed numerically, but an efficient algorithm was developed in [23], exploiting the QBD structure of the FTSP \(D\) when \(r_{1,2}\) is rational. Since we are mainly interested in the steady-state variance of the diffusion limits, and since the stochastic fluctuations become more significant when the fluid is nearly constant (which happens when it is close to its stationary point) it is reasonable to initialize the fluid model at this fluid stationary point to simplify the expressions in (17) and (19). We do this in the next corollary.
From an application point of view, the fluid limit is “more important” than the refined stochastic limit during the fluid transient period, since then the changes in the prelimit are of order \(O (n)\). It follows from Theorem 2 that after some (relatively short) time, the fluid stabilizes close to its unique stationary point \(x^{*}_6\) in (10). After that happens, the refined stochastic limits become the significant approximation to consider.
When we consider the stochastic refinement of the stationary fluid limit \(x^{*}\), the stochastic limit process becomes much more tractable: it is a bivariate Ornstein-Uhlenbeck (BOU) process centered at the origin, as in [2, 29]. Consequently, the random vector \(({\hat{Q}}_s (t),\; {\hat{Z}}_{1,2} (t))\) has a bivariate normal distribution with zero means for all \(t\), and the associated steady-state random vector \(({\hat{Q}}_s (\infty ),\; {\hat{Z}}_{1,2} (\infty ))\) can be very useful in applications. It is characterized by three parameters: the two variances and the covariance, which we exhibit explicitly in (24) below.
For a matrix \(M\), let \(M^t\) denote its transpose. The following is the key result for applications. It gives explicit Gaussian approximations for the steady-state distributions of all quantities of interest.
Corollary 1
(FCLT with a stationary fluid) If, in addition to the conditions of Theorem 4, \(x(0) = x^{*}\) for the stationary point \(x^{*}\) in (10) so that \(x\) is stationary, then the time transformations in (19) simplify by having \(\gamma _i(t) = \xi _i t, \gamma _{i,2} (t) = \xi _{i,2} t\), and \(\phi _{i, 2} (t) = \eta _{i,2} t, i = 1,2\), where
for \(\sigma ^2 (x^{*})\) and \(\psi (x^{*})\) defined in (13) and (20) with \(x(u) = x^{*}\). Then \(({\hat{Q}}_s, {\hat{Z}}_{1,2})\) becomes a BOU process, satisfying the two-dimensional stochastic differential equation \((sde)\)
where \(\mathcal{{X}}\equiv ({\hat{Q}}_s, {\hat{Z}}_{1,2})^t, \mathcal{{B}}\equiv (B_1,\, B_2)^t\), with \(B_1\) and \(B_2\) being two independent standard BM’s, and
As a consequence, \(({\hat{Q}}_s (t),\;{\hat{Z}}_{1,2} (t))\) has a bivariate normal distribution with zero means for each \(t\). The covariance matrix of the steady-state random vector \(({\hat{Q}}_s (\infty ),\;{\hat{Z}}_{1,2} (\infty ))\) has elements
Proof
By the definition of a stationary point, if \(x(0) = x^{*}\) then \(x(t) = x^{*}\) for all \(t > 0\) given in (10); then \(\pi _{1,2} (x^{*})\) appears in (11). The expressions in (21) follow directly from the expressions in (19), by replacing the time-dependent fluid quantities by their stationary counterparts. The resulting pair of integral equations for \(({\hat{Q}}_s (t), {\hat{Z}}_{1,2} (t))\) is known to be equivalent to the BOU sde in (22). The covariance matrix of the stationary distribution, \(\Sigma \), is known to satisfy the matrix equation \(\mathcal{{M}}\Sigma + \Sigma \mathcal{{M}}^t = -\mathcal{{V}}\), where \(\mathcal{{V}}\equiv \mathcal{{S}}\mathcal{{S}}^t\), from which (24) follows; e.g., see [2] and [16]. Algebra shows that \(\xi _4/2|\mathcal{{M}}_{2,2}| = (1 - (z^{*}_{1,2}/m_2))\). \(\square \)
Remark 1
(When components become null) Notice that the results in Corollary 1 simplify greatly with pool-dependent service rates, i.e., when \(\mathcal{{M}}_{1,2} \equiv \mu _{2,2} - \mu _{1,2} = 0\). Then \(\mathcal{{Q}}_2 = 0\) and \(\xi _5 = 0\), so that \(\sigma ^2_{Q_s,Z_{1,2}} (\infty ) = 0\).
We now see how Theorem 4 simplifies under the condition of pool-dependent service rates (no longer assuming that \(x(0) = x^{*}\)).
Corollary 2
(FCLT with pool-dependent service rates) If, in addition to the assumptions of Theorem 4, \(\mu _{2,2} = \mu _{1,2} \equiv \nu \), then the two diffusion-limit processes \({\hat{Q}}_s\) and \({\hat{Z}}_{1,2}\) can both be represented as separate one-dimensional processes, which satisfy the following integral equations
where
with \(\gamma _2 (t)\) defined in (19),
but \(B_1\) and \(B_2\) are dependent standard BM’s.
Proof
It is immediate from the expression for \({\hat{Q}}_s\) in (17) that when \(\mu _{1,2} = \mu _{2,2}\) the diffusion process \({\hat{Q}}_s\) can be analyzed separately from \({\hat{Z}}_{1,2}\). Since \(q_i = p_i q_s\) and \(\mu _{1,2} = \mu _{2,2}\), it follows from (9) that \(\dot{q}_s(t)\) satisfies the simple ODE
whose solution is
for \(\tilde{\eta }_1\) and \(\tilde{\eta }_2\) in the statement of the lemma. Notice that \(\tilde{\gamma }_1(t)\) here corresponds to \(\gamma _1 (t) + \gamma _{1,2} (t) + \gamma _{2,2} (t)\) in (19). Inserting \(q_s(t)\) above into \(\gamma _1(t)\) in (19) gives \(\tilde{\gamma }_1(t)\). Notice that \(\tilde{\gamma }_2 (t)\) corresponds to \(\phi _{1,2} (t) + \phi _{2,2} (t) + \gamma _2 (t)\) in (19). Again substituting yields the conclusion.
Remark 2
(Equivalence with the single-class model) If, in addition to the conditions of both Corollaries 1 and 2, we also have \(\theta _1 = \theta _2 \equiv \theta \), then the diffusion-limit process \({\hat{Q}}_s\) is the same as the limit obtained for the \(M/M/n + M\) model in the ED regime, see [32]. That is, \({\hat{Q}}_s\) is an Ornstein-Uhlenbeck process with infinitesimal mean equal to \(\theta \) and infinitesimal variance \(2\lambda \equiv 2(\lambda _1 + \lambda _2\)). Thus, its steady-state distribution is normal with mean zero and variance \(\lambda / \theta \). However, \(\hat{Z}_{1,2}\) remains somewhat complicated involving \(\gamma _2 (t)\) in (19).
4.4 The case r = 1: longer queue first (LQF)
The most complicated feature in the FWLLN and FCLT asymptotic results in the previous two sections, inhibiting application, is the need to analyze the FTSP. Specifically, both the approximating fluid model and the stochastic refinement depend critically on the FTSP \(D \equiv D(\gamma ) \equiv \{D(\gamma , s) : s \ge 0\}\) at each point \(\gamma \in \mathbb{A }\). In particular, both limits depend on \(D(\gamma )\) through the two functions \(\pi _{1,2}(\gamma )\) and \(\sigma ^2 (\gamma )\). These two functions can be computed numerically, as indicated above. For the stationary fluid point \(x^{*},\; \pi _{1,2} (x^{*})\) is given explicitly in (11).
However, there is an important special case, itself of practical value, in which the analysis simplifies greatly, which can provide insight more generally. When the target queue ratio is \(r = 1\), the FTSP \(D(\gamma )\) becomes an ordinary birth-and-death (BD) process for each \(\gamma \in \mathbb{A }\). Then the quantities \(\pi _{1,2} (\gamma )\) and \(\sigma ^2 (\gamma )\) are both easily expressed. It turns out that they can be expressed in terms of the first two moments of the busy-period distributions of two \(M/M/1\) queues. We consider that case now.
We now assume that \(r = 1\), and take \(\gamma \in \mathbb{A }\). In this case, the FTSP evolves as one BD process when \(D(\gamma ) > 0\) and evolves as another BD process when \(D(\gamma ) \le 0\). We call zero the boundary state. Let \(\lambda _1 (\gamma )\) denote the constant rate up (away from the boundary) and let \(\mu _1 (\gamma )\) denote the constant rate down (toward the boundary) of \(D(\gamma )\) when \(D(\gamma ) > 0\). Focusing on the movement relative to the boundary, let \(\lambda _2 (\gamma )\) denote the constant rate down (away from the boundary) and let \(\mu _2 (\gamma )\) denote the constant rate up (toward the boundary) of \(D(\gamma )\) when \(D(\gamma ) \le 0\).
Note that we need to analyze \(D(\gamma )\) only through the associated stochastic process
which records which region \(D(\gamma , t)\) is in at each time \(t\). The stochastic process \(X \equiv X(\gamma ) \equiv \left\{ X(\gamma , t): t \ge 0\right\} \) is a \(\left\{ 0, 1\right\} \)-valued process associated with an alternating renewal process. Let \(T_1 (\gamma )\) denote a time interval between the instant of a state change from state 0 to state 1 until the next instant of a state change from state 1 back to state 0. Similarly, let \(T_2 (\gamma )\) denote a time interval between instant of a state change from state 1 to state 0 until the next instant of a state change from state 0 back to state 1. The successive times in the alternating renewal process are independent random variables distributed as \(T_1 (\gamma )\) and \(T_2 (\gamma )\). The process \(X(\gamma )\) is a regenerative process in which the regeneration times can be the successive instant of a state change from state 0 to state 1 until the next instant of the same state change again at a later time. The intervals between successive regenerations are distributed as \(T_1 (\gamma ) + T_2 (\gamma )\).
Now observe that \(T_i (\gamma )\) is distributed as a busy period in an \(M/M/1\) queue with arrival rate \(\lambda _i (\gamma )\) and service rate \(\mu _i (\gamma ),\; i = 1,2\). In this context, the condition \(\gamma \in \mathbb{A }\) is equivalent to \(\lambda _i (\gamma ) < \mu _i (\gamma ),\; i = 1,2\). Under this condition, \(T_i (\gamma )\) is known to have a finite moment generating function with a positive radius of convergence, so that all moments of \(T_i (\gamma )\) are finite. Let
Then, from basic \(M/M/1\) theory, we have
Finally, we are interested in the cumulative process associated with \(X(\gamma )\),
We can apply (14) to obtain the following result.
Theorem 5
(The FTSP when \(r=1\)) When \(r = 1\) and \(\gamma \in \mathbb{A }\), the FTSP becomes a recurrent BD process. Hence the key FTSP quantities can be expressed directly in terms of the four BD rates \(\lambda _i (\gamma )\) and \(\mu _i (\gamma )\) via
for \(E[T_i (\gamma )]\) and \(E[T_i (\gamma )^2]\) in (26) and (25), \(i = 1,2\).
In the more general QBD setting arising with \(r \not = 1\), the analysis is more complicated, because the excursions of \(\int _{0}^{t} 1_{\left\{ D(\gamma ,s) > 0\right\} }\) above and below 0 depend on the entering and exit states from level 0; thus these excursions are not simply independent. Theorem 5 can be the basis for heuristic extensions to non-Markovian models in which the arrival, service, and abandonment processes are non-Markovian. We may then exploit approximations for the busy period in \(GI/GI/1\) queues, e.g., [1] and [25].
5 Proof of Theorem 4
First observe that the assumed convergence in \(\mathbb{R }_2\) at time zero is actually equivalent to the full convergence in \(\mathbb{R }_{17}\) of the process in (16) at time zero because of Assumption 5. Our proof has four main steps: The first step is to exploit SSC results established in [24]. In particular, we first give an asymptotically equivalent three-dimensional representation of \(X^n_6\) (without any scaling) involving rate-1 Poisson processes. Then, we observe that the essential dimension is actually two (when scaling by \(\sqrt{n}\)) because the queue lengths are asymptotically in the fixed ratio. Thus, we deduce that it is sufficient to directly prove convergence of the two-dimensional process \(({\hat{Q}}^n_{s},\; {\hat{Z}}^n_{1,2})\).
The second step is to facilitate application of the continuous mapping theorem by showing that an essential mapping is continuous. The third step is to construct appropriate martingale representations, allowing application of the continuous mapping theorem. The fourth and final hardest step is to show that the driving stochastic terms in this martingale representation converge to the specified limits. This final step uses a new result of independent interest, Theorem 6, the generalization of the classical FCLT for cumulative processes in (13) to the case where the QBD parameters at time \(t\) are given by the fluid limit \(x(t)\), which in general is time-varying.
5.1 Representation and SSC
Following common practice, as reviewed in §2 of [20], we represent the processes \(A^n_i (t),\; S^n_{i,j} (t)\) and \(U^n_i (t)\) introduced at the beginning of §4.2 in terms of mutually independent rate-1 Poisson processes; let
where \(N^{a}_i,\; N^{s}_{i,j}\) and \(N^{u}_i\) for \(i = 1,2;\; j = 1,2\) are eight mutually independent rate-1 Poisson processes. Theorem 5.1 of [24] gives a representation of the CTMC in terms of these processes. Corollaries 6.1–6.3 plus Theorem 6.4 of [24] then establish state space collapse (SSC) results yielding an asymptotically equivalent three-dimensional representation of \(X^n_6\) involving these mutually independent rate-1 Poisson processes plus two others. Since we exploit that representation, we state it here. Directly, the representation of \(Z^n_{1,2}\) below keeps it in the interval \([0,\, m^n_2]\). However, the representation directly allows the queue lengths \(Q^n_i\) to become negative. The results in [24] show that the occurrence (anywhere in a a bounded interval) is asymptotically negligible. Recall that \(d_{J_1}\) denotes the Skorohod \(J_1\) metric.
Lemma 1
(Representation via SSC of the service process) Under the assumptions in Theorem 1, \(d_{J_1}(X^n_6, X^{n,*}_6) \Rightarrow 0\) in \(\mathcal{D }_6\) as \(n \rightarrow \infty \), with the three determining components of \(X^{n,*}_6\) in (3), i.e., in \(X^n\) in (4), being represented via
where \(N^{s,2}_{1,2}\) and \(N^{s,2}_{2,2}\) are two additional rate-1 Poisson processes, independent of the others.
The representation in Lemma 1 provides important simplification, but it also shows the difficulty in proving heavy traffic limit theorems; the integrals contain the indicator functions depending on \(D^n_{1,2}\). We now show that the essential dimension can be reduced from three to two when we introduce scaling. The next result follows from Corollary 4.1 of [24].
Lemma 2
(SSC to two dimensions) Under the conditions of Theorem 1, the essential dimension can be reduced from \(3\) established in Lemma 1 to 2, because \(d_{J_1}(Q^n_1,\; rQ^n_2)/a_n \Rightarrow 0\) in \(\mathcal{D }([0, \delta ))\) for \(\delta \) in Theorem 1 whenever \(a_n/\log n \rightarrow \infty \) as \(n \rightarrow \infty \). If \(x \in \mathbb{A }\) over an interval \([t_1, t_2),\; 0< t_1 < t_2 \le \infty \), then the conclusion holds in \(\mathcal{D }((t_1,\, t_2))\).
Due to Assumption 6 and Lemma 2, it is sufficient to directly prove convergence of the two-dimensional process \(({\hat{Q}}^n_{s}, {\hat{Z}}^n_{1,2})\); the more general 16-dimensional limit in (16) can be obtained as a byproduct of the analysis, and in particular, \({\hat{Q}}_i \stackrel{\mathrm{d}}{=}p_i {\hat{Q}}_s, i = 1,2\).
5.2 A continuous mapping
As in [20], our proof exploits the continuous mapping theorem. However, in our case, the stochastic processes describing the evolution of the system (the queue length and service processes) cannot be expressed directly as a continuous mapping of the primitive processes. We next establish the continuity of the mapping that we will eventually apply.
Lemma 3
(Continuity of the two-dimensional integral representation) Consider the two-dimensional integral representation
where \(g : \mathbb{R }\rightarrow \mathbb{R }\) satisfies \(g(0) = 0\) and is Lipschitz continuous with a Lipschitz constant \(c_g\). That integral representation has a unique solution \((x_1,\, x_2)\), so that the integral representation constitutes a function \(f : \mathcal{D }_2 \times \mathbb{R }_2 \rightarrow \mathcal{D }_2\) mapping \((y_1,\, y_2,\, b_1,\, b_2)\) into \((x_1,\, x_2) \equiv f(y_1,\, y_2,\, b_1,\, b_2)\). In addition, the function \(f\) is a continuous mapping from \(\mathcal{D }_2 \times \mathbb{R }_2\) to \(\mathcal{D }_2\). Moreover, if \(y_2\) is continuous then \(x_2\) is continuous. If both \(y_1\) and \(y_2\) are continuous, then \(x_1\) is also continuous.
Proof
By the conditions on the function \(g\) we have for all \(T \ge 0\)
Note that \(x_2\) does not depend on \(x_1\), hence we can prove the lemma iteratively by first showing that the function \(f_2 : \mathcal{D }\times \mathbb{R }\) mapping \((y_2, b_2)\) into \(x_2 \equiv f_2(y_2, b_2)\) is continuous, and then use this result to show that the function \(f_1 : \mathcal{D }_2 \times \mathbb{R }\) mapping \((y_1,\, x_2,\, b_1)\) into \(x_1 \equiv f_1(y_1,\, x_2,\, b_1)\) is continuous.
To show that \(f_2\) is continuous we use Theorem 2.11 in [27] with \(h(x_2(u),\, u) \equiv g(u)x_2(u)\). For that purpose, choose \(T > 0\) and let \(\lambda \) be a homeomorphism on \([0, T]\) with strictly positive derivative \(\dot{\lambda }\). Then, for every \(\varphi _1,\, \varphi _2 \in \mathcal{D }\)
where \(c_1 \equiv c_g T \Vert \varphi _2 \Vert _T\) and \(c_2 \equiv \Vert g \Vert _T\). For \(x_1 = f_1(y_1,\, x_2,\, b_1)\) we can apply Theorem 4.1 in [20] with input \(y \equiv y_1 + \alpha _2\int \nolimits _0^t{x_2(u) \, {{\mathrm{d}}}u}\). It follows from Theorem 2.11 in [27] that if \(y_2\) is continuous then so is \(x_2\). If, in addition, \(y_1\) is continuous, then \(y\) is continuous and, by Theorem 4.1 in [20], so is \(x_1\). \(\square \)
5.3 Martingale representations
As in Theorem 6.3 of [24], we next apply the representation in Lemmas 1 and 2 to obtain martingale representations for \(\hat{Q}^n_s\) and \(\hat{Z}^n_{1,2}\), but now we are interested in the FCLT instead of the FWLLN. We exploit martingale representations for the counting processes appearing in Lemma 1 constructed from the rate-1 Poisson processes \(N^a_i,\; N^s_{i,2},\; N^{s,2}_{i,2}\) and \(N^u_i,\; i = 1,2\), in particular,
Lemma 4
(Martingale representation for \(\hat{Q}^n_s\))
where \(\hat{M}^n_s \equiv M^n_s/\sqrt{n}\) for
The terms in (28) can be shown to be martingales with respect to an appropriate filtration, so that \(M^n_s\) in (29) is also a martingale. However, since our proofs will not employ the martingale property, we do not specify the filtration and only use the term “martingale” for convenience. See §2.1 and §3.4 of [20] for background on the construction and the martingale property, including the appropriate filtration.
Proof
By Lemma 1,
for \(M^n_s(t)\) in (29). Observe that the indicator functions in the representation of \(X^n\) in Lemma 1 do not appear in the representation of \(Q_s^n(t)\). That simplifies the analysis.
From (9) it follows that \(q_s \equiv q_1 + q_2\), the fluid counterpart of \(Q^n_s\), evolves according to the integral equation:
so that, substituting \(q_1\) with \(p_1 q_s(u)\) and \(q_2(u)\) with \(p_2 q_s(u)\),
Then, by centering about \(n q_s\) and dividing by \(\sqrt{n}\) as in (15), we have
By Assumption 1, the second and third terms in the expression above converge to zero. By Corollary 6.2 and Theorem 6.4 in [24], \(n^{-1/2} \Vert Z^n_{2,2} - (m^n_2 - Z^n_{1,2})\Vert \Rightarrow 0\) in \(\mathcal{D }\) as \(n \rightarrow \infty \) so that \(z_{2,2} = m_2 - z_{1,2}\). Also, \((m_2^n - n m_2)/\sqrt{n} \rightarrow 0\) as \(n \rightarrow \infty \) by Assumption 1. Hence,
Define
By applying the SSC result in Lemma 2, we conclude that \(\Vert {\hat{Q}}_s^n - \hat{Q}^n_{a,s} \Vert _T \Rightarrow 0\) in \(\mathcal{D }\) as \(n \rightarrow \infty \) for any \(T > 0\). That completes the proof. \(\square \)
We now turn to the process \(Z^n_{1,2}\). As in Lemma 4, we call \(M^n_Z\) in (33) below a “martingale” for convenience, although we do not employ any martingale property.
Lemma 5
(Martingale representation for \(\hat{Z}^n_{1,2}\))
where \(\hat{L}^n \equiv L^n/\sqrt{n}, \hat{M}^n_{Z} \equiv M^n_{Z}/\sqrt{n}\),
and
for \(M^n_{2,2}\) and \(M^n_{1,2}\) in (28).
Proof
We start by rewriting the representation of \(Z^n_{1,2}\) in Lemma 1 as
To achieve the diffusion-scaled process, we center \(Z^n_{1,2}\) about \(n z_{1,2}\) and divide by \(\sqrt{n}\), where, by (9), the fluid limit \(z_{1,2}\) satisfies the equation
We get the representation (31) with the \(o(1)\) term replacing the deterministic term \([(m^n_2 - n m_2)\int \limits _{0}^{t} \pi _{1,2} (x(s)) \, {\mathrm{d}}s]/\sqrt{n} \le (m^n_2 - n m_2) t/\sqrt{n}\), which converges to zero by Assumption 1. \(\square \)
5.4 Convergence of stochastic driving terms
Given the representations in Lemmas 4 and 5, we can complete the proof of the convergence of \((\hat{Q}^n_s,\; \hat{Z}^n_{1,2})\) in Theorem 4 by establishing convergence of the driving terms and applying the continuous mapping theorem with the mapping in Lemma 3, i.e., with the following lemma, proved in the next section. We add an extra process, \(\hat{I}^n\), also defined in (15), which is closely related to \(\hat{L}^n\), but not directly needed to treat \((\hat{Q}^n_s, \;\hat{Z}^n_{1,2})\).
Lemma 6
(Convergence of driving terms) Under the assumptions of Theorem 4,
where
\(B_1,\, B_{1,2},\, B_{2,2},\, B_{1,3},\, B_{2,3}\) and \(B_2\) are independent standard BM’s as in the statement of Theorem 4 and \(\gamma _1(t),\, \gamma _2 (t),\, \gamma _3 (t),\, \gamma _{1,2}(t),\, \gamma _{2,2}(t),\, \phi _{1,2}(t)\) and \(\phi _{2,2}(t)\) are the increasing continuous functions defined in (19).
5.5 Overall Proof of Theorem 4
We prove convergence of \((\hat{Q}^n, \hat{Z}^n_{1,2})\) by applying the continuous mapping theorem with the continuous function in Lemma 3, exploiting the representations in Lemmas 4 and 5 and the convergence established in Lemma 6. In applying Lemma 3, we rely heavily on Theorem 7.1 in [23], which establishes that \(\pi _{1,2}(\cdot )\) is locally Lipschitz continuous in \(\mathbb{A }\) as a function of the fluid state \(x\) and is thus Lipschitz continuous over compact sets. Moreover, \(x (\cdot )\) is itself Lipschitz continuous, as a function of the time argument \(s\) by Corollary 5.1 in [24]. It follows that \(\pi _{1,2} (x(s))\) is Lipschitz continuous as a function of the time argument \(s\) as well (using Assumption 6 implying that \(x\) lies entirely in \(\mathbb{A }\)). Thus, the proof of Theorem 4 is complete with the exception of the proof of Lemma 6. The next four sections are devoted to that proof.
5.5.1 Difficulties in the Proof of Lemma 6
The first two terms in the left-hand side of (34), which we refer to as “martingales”, are relatively easy to deal with, using the standard Poisson FCLT; see [20]. This is done in Lemma 7 below.
However, the limits of the last two terms in (34) is far more complicated to derive. These two terms are not martingales, and the process \(D^n_{1,2}\) is neither Markov nor regenerative. Moreover, as was shown in §4 of [24], the number of jumps of the process \(D^n_{1,2}\) grows to \(\infty \) as \(n\rightarrow \infty \) w.p.1 over any interval, and this process is not stochastically bounded (in particular, it is not \(\mathcal{D }\)-tight). An additional complication stems from the fact that the two martingale terms are not independent from the last two terms in (34), so the joint convergence in the statement of the lemma is not immediate. Joint convergence is proved via an asymptotic independence result, which is proved in Lemma 10. Therefore, we elaborate on the steps that are required to identify the limit of \(({\hat{L}}^n,\, \hat{I}^n)\).
The main intuition comes from the convergence in (6) of the time-expended process \(D^n_e\) in (5). Loosely speaking, the convergence in (6) implies that the process \(D^n_{1,2}(t)\) is approximately distributed as the FTSP \(D(x(t), \cdot )\) at a small neighborhood of time \(t\), for any \(t \ge 0\) and for large \(n\). Since (13) holds for each of the (uncountably-many) FTSP’s \(\left\{ D(x(t), \cdot ) : t \ge 0\right\} \), the main idea is to bound the sample paths of the process \(D^n_{1,2}\) appropriately for each \(n\) with a countable number of time-scaled FTSP’s processes, each operating in the same time scale as \(D^n_{1,2}\). More specifically, we bound \(D^n_{1,2}\) over short intervals with processes that have the same structure as the FTSP’s, but with scaled rates (their generators are scaled by \(O(n)\)); see \(\tilde{D}^n_f\) in (42) below. Since scaling the rates of a time-homogeneous CTMC by \(n\) without scaling time is equivalent to scaling its time argument by \(n\) and keeping the rates fixed, the bounds \(\tilde{D}^n_f\) in (42) below, having \(O(n)\) rates, are distributed the same as versions of the FTSP with \(O(1)\) rates, but with the time scaled by \(O(n)\).
Now, for the cumulative processes associated with each of these bounding FTSP’s there exists an FCLT as in (13), and we need to “paste together” all the bounding FTSP’s (each having random rates) and their FCLT’s so as to achieve the Brownian limit of \(\hat{I}^n\) in (18) and (19). This final step includes Theorem 6 below, which is a generalization of the FCLT for cumulative processes. In particular, Theorem 6 states an FCLT for a cumulative processes associated with the FTSP having time-varying parameters.
6 Proof of Lemma 6
This section is devoted to proving Lemma 6. In §6.1 we apply standard arguments to establish the convergence of the first two terms \((\hat{M}^n_s,\; \hat{M}^n_Z)\). In preparation for treating the last two terms, in §6.2 we state two key results that we will use; they are proved in the following three sections. In §6.3 we establish convergence of the last two terms \((\hat{L}^n,\; \hat{I}^n)\). Finally, in §6.4 we establish joint convergence of all four terms by proving asymptotic independence of the last two terms from the first two terms.
6.1 The first two terms in (34)
We start by establishing convergence of the first two terms in Lemma 6.
Lemma 7
There is joint convergence of the processes
where the processes are defined in (29), (33) and Lemma 6.
Proof
Let
for the processes in (28). To compress the notation, for \(x \in \mathcal{D }_k\) and \(t \in [0,\infty )^k\), let \(x(t) \equiv (x_1(t_1),\; x_2(t_2), \ldots , x_k(t_k))\). We start by proving that
as \(n \rightarrow \infty \), where
for \(\phi _{i,2}\) and \(\gamma _{i,2}\) defined in (19). Here \(B_A(t),\; B_S(t)\) and \(B_U(t)\) are vectors of independent standard Brownian motions. Using our compressed notation, we have \(\lambda t \equiv (\lambda _1 t,\, \lambda _2 t)\) and \(\theta q(s) \equiv (\theta _1 q_1(s),\, \theta _2 q_2(s))\). For example, \(B_A(\lambda t) = (B_{A_1} (\lambda _1 t),\, B_{A_2} (\lambda _2 t) )\), and similarly for \(B_S(\cdot )\) and \(B_U (\cdot )\).
To prove (35), we apply the FCLT for Poisson processes. For the Poisson processes in Lemma 1, let
Let \(\tilde{M}^n_A(t), \tilde{M}^n_S(t)\) and \(\tilde{M}^n_{U}(t)\) be the corresponding vector-valued processes. By the independence of all the unit-rate Poisson processes \(N^a_i(\cdot ),\, N^s_{i,j}(\cdot )\) and \(N^u_i(\cdot )\), and the FCLT for a Poisson process, the following joint convergence holds:
where \(\tilde{B}_A,\; \tilde{B}_S\) and \(\tilde{B}_U\) are, respectively, 2-dimensional, 5-dimensional, and 2-dimensional independent Brownian motions; see Theorem 4.2 and §9.1 in [20].
We now introduce random time changes. Let
By Assumption 1 on the arrival rates, \(\Phi ^n_{A_i} \rightarrow \lambda _i \text{ e }\) in \(\mathcal{D }, i = 1,2\). From the initial conditions in the statement of Theorem 4, the fluid limit and the continuity of the integral mapping, it follows that \(\Phi ^n_{S,i} \Rightarrow \phi _i, 1 \le i \le 5\), and \(\Phi ^n_{U,i} (t) \Rightarrow \theta _i \int \nolimits _0^t{q_i(s)\, {\mathrm{d}}s}\) in \(\mathcal{D }\) as \(n \rightarrow \infty \).
Let \(\Phi ^n_{A}(t), \Phi ^n_{S}(t)\) and \(\Phi ^n_{U}(t)\) be the corresponding vector-valued processes. By Theorem 11.4.5 of [31], these limits hold jointly, yielding
as \(n \rightarrow \infty \). By Theorem 11.4.5 of [31], the limits in (37) and (39) also hold jointly. By definition,
Thus, the convergence in (35) follows from the continuity of the composition mapping at continuous limits, Theorem 13.2.1 in [31]. Finally, the conclusion of the lemma itself then follows from the definition of \(\hat{M}^n_s\) and \(\hat{M}^n_Z\) in (29) and (33), and the continuity of addition under continuous limits, e.g., Corollary 12.7.1 in [31]. \(\square \)
6.2 Key supporting results for the last two terms
In §4.1 we indicated that the stochastic limit will depend on the FCLT for cumulative processes associated with the FTSP, as stated in (13). As indicated in §6 of [23], the FTSP with fixed state \(\gamma \) is a QBD; its parameters (transition rates) are given explicitly in (13)–(16) of [24]. Since the FTSP \(D(\gamma , \cdot )\) is a QBD for each state \(\gamma \), it is a relatively simple regenerative stochastic process for each state \(\gamma \), assuming that \(\gamma \) makes the QBD positive recurrent. However, in our application, the fluid state is not fixed at \(\gamma \), but is instead given by the fluid limit \(x(t)\), which is a function of time \(t\). That means that the parameters of the FTSP are actually time-varying. By Assumption 6, the FTSP with fluid state \(x(t)\) is a positive recurrent QBD for all states \(x(t)\) considered. Moreover, by Lemma C.5 of [24], the infinitesimal generator and the asymptotic variance of the QBD are continuous functions of the underlying state \(x(t)\). Since the essential matrix structure (e.g., the dimension of the matrices) of the QBD’s depends only on the rational ratio parameter \(r_{1,2}\), and thus does not change, the QBD is characterized by only finitely many parameters. As a consequence, we can establish a variant of the FCLT in (13), allowing the FTSP to have a time-varying state.
In our remaining proof of Lemma 6, in particular for Lemma 8 below, we will want to generalize the state of the QBD. The parameters of the QBD not only depend on the fluid state \(\gamma \equiv (q_1,\, q_2,\, z_{1,2})\), but also on the rest of the QBD parameters, in particular, also upon \(\zeta \equiv (\lambda _i, m_j;\; i, j = 1,2)\). In order to establish Lemma 8 below, we will want to allow the parameters \(\lambda _i\) and \(m_j\) to vary, because they vary with \(n\) in the many-server heavy-traffic scaling in Assumption 1. The QBD also depends on the other model parameters \(\theta _i\) and \(\mu _{i,j}\), but they are fixed, so we do not include them. Thus, we will consider the more general “full” parameter state function \(\eta \equiv (\zeta , \gamma )\) for \(\eta \equiv \eta (t)\) and \(\gamma \equiv \gamma (t)\) above, which we understand to be an element of the functions space \(\mathcal{{D}}\). We obtain a conventional stationary QBD model for each full parameter state \(\eta (t)\).
Now we will establish a FCLT for
where the state function \(\eta \) is an element of \(\mathcal{D }\) and \(D(\eta (0), 0)\) is some fixed finite initial value. Note that in the special case of a constant parameter state function, with \(\eta (t) = \gamma , 0 \le t \le T\), this new process reduces to the previous one in §4.1; i.e.,
for \(\hat{C}^n_\mathrm{{QBD}} (t; \gamma )\) in (13).
However, more generally, the process \(\hat{C}^n (t; \eta )\) in (40) is more complicated, so that the new FCLT is by no means immediate. The non-constant function \(\eta \) makes the new process \(\left\{ D (\eta (s/n),s): s \ge 0\right\} \) appearing in the integrand of (40) neither a QBD nor a regenerative process. Nevertheless, we establish the following generalization of the FCLT in (13). The proof is given in §7.
Theorem 6
(FCLT for FTSP with time-varying parameter state) Consider the FTSP \(D\) as a function of its parameter state function \(\eta \) specified above, where \(\eta \) is an element in \(\mathcal{C }\). Suppose that the QBD \(D(\eta (t), \cdot )\) is positive recurrent for all \(\eta (t), 0 \le t \le T\). Then
where \(\hat{C}^n (\cdot ; \eta )\) is given in (40) and
with \(B\) being a standard BM and, for each \(u,\, \sigma ^2 (\eta (u))\) is the asymptotic variance of the cumulative process with constant full parameter state \(\eta (u)\), as in (13)–(14).
For Lemma 8 below, we will also want to extend the FCLT in Theorem 6 to full parameter state functions that are suitably near a given deterministic one. For that purpose, we use the following elementary corollary to Theorem 6 and its proof (also see §6 of [23] and §C.3 of[24]). We use the Prohorov metric \(d_{\mathcal{{P}}, T} (Y_1, Y_2)\) characterizing convergence in distribution in \(\mathcal{D }([0,T])\); see p. 77 of [31]. We say that a parameter-state function \(\eta \) is positive recurrent if the associated FTSP \(D(\eta , \cdot )\) is positive recurrent.
Corollary 3
(Continuity of the FCLT for the FTSP with time-varying parameter state) Consider the FTSP \(D\) as a function of its parameter state function \(\eta \) specified above, where the parameter state function \(\eta \) is continuous and positive-recurrent. For all \(\epsilon > 0\) and \(T>0\), there exists \(\delta > 0\) such that, if \(\eta ^{\prime } \in \mathcal{D }\) is a parametric state function satisfying \(\Vert \eta - \eta ^{\prime }\Vert _T < \delta \), then \(\eta ^{\prime }\) is positive recurrent for all \(t\) in \([0,T]\) and \(d_{\mathcal{{P}}, T} (\hat{C} (\cdot ; \eta ),\hat{C} (\cdot ,\,\eta ^{\prime })) < \epsilon \) where \(\hat{C} (\cdot ; \eta )\) is the limit process associated with \(D(\eta , \cdot )\) in Theorem 6.
Proof
We exploit the criterion for recurrence in terms of the drift rates given in (8). The drift rates \(\delta _{+} (\eta )\) and \(\delta _{-} (\eta )\) for constant \(\eta \) in the regions \(\left\{ s: D(\eta , s) > 0\right\} \) and \(\left\{ s: D(\eta , s) \le 0\right\} \), respectively, are linear functions of the components of the vector \(\eta \). We can thus express the drifts as the inner products \(\delta _{\pm } (\eta ) = a_{\pm } \cdot \eta \), where \(a_{+}\) and \(a_{-}\) are constant vectors. Hence, if \(|\eta - \eta ^{\prime }| \le \epsilon \), then \(| \delta _{\pm } (\eta ) - \delta _{\pm } (\eta ^{\prime })| \le \epsilon (|a_{\pm }|\cdot 1)\), where here 1 is a vector of 1’s of the appropriate dimension. This property for constant parameter states extends immediately to more general state functions in \(\mathcal{D }\) using the uniform norm; i.e., if \(\Vert \eta - \eta ^{\prime }\Vert _T \le \epsilon \), then \(\Vert \delta _{\pm } (\eta ) - \delta _{\pm } (\eta ^{\prime })\Vert _T \le \epsilon (|a_{\pm }|\cdot 1)\). Thus, for any positive recurrent state function \(\eta \), there exists \(\epsilon > 0\) such that \(\delta _{+} (\eta ^{\prime }) < 0\) and \(\delta _{-} (\eta ^{\prime }) > 0\) if \(\Vert \eta - \eta \Vert _T < \epsilon \), implying that \(\eta ^{\prime }\) is also positive recurrent. \(\square \)
In Lemma 8 below, we will apply Corollary 3 to random state functions \(\tilde{\eta }_n\) which converge weakly to a continuous function \(\eta \) as \(n \rightarrow \infty \), i.e., for which \(\tilde{\eta }_n \Rightarrow \eta \) in \(\mathcal{D }\) as \(n \rightarrow \infty \). To do so, we need to connect the queue-difference processes \(D^n_{1,2}\) appearing in \(\hat{I}^n\) in (15) to the FTSP. We do that via the associated frozen processes, introduced in §A.1 of [24]. The frozen process \(\left\{ D^{n}_{f}(X^n (t), s): s \ge 0\right\} \) corresponds to the queue-difference process \(D^n_{1,2}\) starting at time \(t\), conditioned on the state \(X^n(t)\) at time \(t\) under the assumption that the transition rates are fixed (“frozen”) at the rates associated with the initial state \(X^n (t)\). A key property, for applying Theorem 6 and Corollary 3 above, is that the frozen process can be represented as the FTSP with modified parameters. To express the connection, we write the frozen process and the FTSP as functions of the parameters \((\lambda _i,\, m_j, \gamma , s)\). As in equation (74) of [24], we have the representation
where \(D^n_f\) on the left of (41) is the frozen process described above, and \(D\) on the right of (41) is the FTSP.
Like the queue-difference process, the frozen process has \(O(n)\) transition rates, whereas the FTSP has \(O(1)\) transition rates, because of the time scaling in (5). Thus, the time variable \(s\) on the right in (41) is scaled by \(n\).
However, we need to construct a process that is made up of different frozen processes over different subintervals. Thus, for each \(n \ge 1\), we will construct a process that is a different frozen process over each successive interval of length \(1/n\), but identical to the queue-difference process at each interval endpoint. In particular, we will construct the overall frozen process by setting
\(0 \le t \le T\), where \(D^n_f\) is the frozen process defined above. That is, we use a different frozen state and thus frozen process for each interval \([(k-1)/n, k/n)\) in \([0,T]\). As a consequence, the frozen process state for the process \(\tilde{D}^{n}_{f}\) as a function of \(t\) is thus
As a consequence of (41)–(43) above, we can simply write
where \(\tilde{\eta }_n\) is a random full parameter state function with the special parameter function given in (41) above, with the frozen state at time \(t\) given by (43). Corollary 3 is relevant because, by virtue of Assumption 1 and Theorem 1, for each \(T > 0\), we have
where \(\eta \) has fixed components \(\lambda _i, m_j\) and \(x(t), t \ge 0\).
Hence, the FCLT for fixed positive recurrent state function \(\eta \), which holds by Theorem 6, also holds with \(\eta \) replaced by \(\tilde{\eta }_n\) by virtue of Corollary 3. However, it remains to show that the newly constructed frozen processes approximate the queue-difference processes suitably well. For that, we will use a special coupling construction, similar to the coupling constructions used in [24]. The following result is proved in §10.
Lemma 8
For each \(n\), we can construct the new frozen processes \(\tilde{D}^n_f\) defined by (41)–(44) on the same underlying probability space with the queue-difference processes \(D^n_{1,2}\) so that \(\Delta ^n \Rightarrow 0\) in \(\mathcal{D }\) as \(n \rightarrow \infty \), where
6.3 The last two terms in (34)
We now establish joint convergence of the last two terms in Lemma 6.
Lemma 9
There is joint convergence of the last two terms in Lemma 6, i.e.,
where the converging processes \(\hat{L}^n\) and \(\hat{I}^n\) are defined, respectively, in (32) and (15), while the vector limit process is \((\hat{L}_2 (t),\, \hat{I} (t)) \equiv (B_2 (\gamma _2 (t),\, B_2 (\gamma _3 (t))\) for \(B_2\) a standard Brownian motion and \((\gamma _2 (t),\, \gamma _3 (t))\) in (19), as in (18).
Proof
We start by considering just \(\hat{I}^n\). We make a change of variables in (15) to get
From either the original representation of \(\hat{I}^n\) in (15) or the equivalent alternative expression in (46), the main line of the proof should be evident: We show that the time-scaled queue-difference process \(D^{n}_{1,2}(s/n)\) in (46) is asymptotically equivalent to the scaled FTSP \(D(x(s/n), s)\), making the expression in (46) be essentially of the form of \(\hat{C}^n\) in (40). If we could just directly make that substitution, then the desired limit \(\hat{I}^n \Rightarrow \hat{I}\) would be an immediate consequence of Theorem 6. However, the desired substitution is only valid asymptotically. We actually achieve the desired approximation by the FTSP indirectly by approximating the queue-difference process and applying Lemma 8 and Corollary 3 in addition to Theorem 6. In particular, we can write
We then apply Lemma 8 to the first component in the RHS of the equality, and Corollary 3 to the second component, using (44).
Having established the limit for \(\hat{I}^n\), we turn to \(\hat{L}^n\). From (32), we know that \(\hat{L}^n\) differs from \(\hat{I}^n\) by having the extra term \(\bar{\Psi }^n\) in the integrand. However, by the FWLLN, Theorem 1, \(\bar{\Psi }^n \equiv \Psi ^n/n \Rightarrow \psi \) as \(n \rightarrow \infty \), where \(\psi (t) \equiv \mu _{2,2} (m_2 - z_{1,2} (t)) + \mu _{1,2} z_{1,2} (t)\). Hence, we can reduce the proof of joint convergence of \((\hat{I}^n,\; \hat{L}^n)\) to the convergence of \(\hat{I}^n\) established above, as we now show.
By the uniform continuity of \(\psi \) over \([0,T]\), for any \(\epsilon > 0\), we can choose \(K\) sufficiently large that we can find a partition of \([0,T]\,0 = t_0 < t_1 < t_2 < \cdots < t_{K-1} < t_K = T\) such that \(|\psi (s) - \psi (t_{k-1})| < \epsilon \) for all \(s\) with \(t_{k-1} \le s \le t_{k}, 1 \le k \le K\). Of course, \(K \equiv K(\epsilon )\) depends upon \(\epsilon \). However, since the fluid limit \(x\) is Lipschitz continuous by Corollary 5.1 of [24], \(\psi \) is also Lipschitz continuous, so that there exists a constant \(K_1\) independent of \(\epsilon \) such that \(K \le K_1/\epsilon \).
Let \(\psi _{\epsilon }\) be the piecewise-constant function on \([0,T]\) mapping \(s\) into \(\psi (t_{k-1})\) for all \(s\) with \(t_{k-1} \le s \le t_{k}, 1 \le k \le K\). As noted above, we apply the FWLLN to obtain \(\bar{\Psi }^n \equiv \Psi ^n/n \Rightarrow \psi \) as \(n \rightarrow \infty \). For simplicity, we now invoke the Skorohod representation theorem, and assume the convergence is w.p.1. Then, we choose \(n_0\) sufficiently large that \(\Vert \bar{\Psi }^n - \psi \Vert _T < \epsilon \) for all \(n \ge n_0\) (w.p.1, no longer mentioned). As a consequence, \(\Vert \bar{\Psi }^n - \psi _{\epsilon }\Vert _T \le 2\epsilon \) for all \(n \ge n_0\).
Now, for \(n \ge n_0\) and any subinterval \([t_{k-1},t_k]\), we have either
or
In either case,
where
and \(\hat{I}^n_{k} (t) \equiv 0\) elsewhere in \([0,T]\). Hence, \(\Vert \hat{L}^n - \hat{L}^n_1\Vert _T \le 2\epsilon \hat{I}^n_{*}\), where
and \(\hat{I}^n_{*} \equiv \sum \nolimits _{k = 1}^{K} \Vert \hat{I}^n_k \Vert _T\).
By essentially the same argument as for \(\hat{I}^n\), we can establish convergence of \(\hat{I}^n_k\) for all \(k, \hat{L}^n_1 \) and \(\hat{I}^n_{*}\) jointly with \(\hat{I}^n\) as \(n \rightarrow \infty \). However, it is important to note that the upper bound on the error \(\Vert \hat{L}^n - \hat{L}^n_1\Vert _T\) involves \(\hat{I}^n_{*}\), which is the sum of \(K\) terms, where \(K \equiv K(\epsilon )\) depends on \(\epsilon \).
To show that the error bound \(2\epsilon \hat{I}^n_{*}\) is small, we use our previous observation that \(K (\epsilon ) \le K_1/\epsilon \), where \(K_1\) is a constant independent of \(\epsilon \), and the form of the Brownian limit established for \(\hat{I}\); see Theorems 4 and 6. As can be seen from the statement of Theorem 4, for any \(K\), the limit of \(|\hat{I}^n_k|\) over the interval of length \(T/K\) where it is positive is stochastically bounded above by a quantity distributed as \(\Vert B(c \cdot )\Vert _{T/K} \stackrel{\mathrm{d}}{=}\sqrt{t/K} \Vert B(c \cdot )\Vert _1\), where \(B\) is a standard BM, for a constant \(c\) that depends on the continuous fluid limit over the finite interval \([0,T]\). Thus, we can apply Markov’s inequality to deduce that, for any \(\eta > 0\),
where \(K_1\) and \(K_2\) are constants independent of \(\epsilon \) and \(\eta \). Hence, for any \(\eta > 0, \epsilon > 0\) can be chosen to make the right side small.
Thus, for any \(\eta > 0\), we can choose \(n_1 > n_0\) so that \(P(\Vert \hat{L}^n - \hat{L}^n_1\Vert _T > \eta ) < \eta \) for all \(n \ge n_1\). Hence, we have proved the joint convergence of \((\hat{I}^n,\;\hat{L}^n)\) as claimed. \(\square \)
6.4 Joint convergence in Lemma 6
To complete the proof of Lemma 6, it remains to show that the two limits established in Lemmas 7 and 9 actually hold jointly. To that end, we next prove that the sequences \((\hat{M}^n_s,\; \hat{M}^n_Z)\) and \((\hat{L}^n,\; \hat{I}^n)\) are asymptotically independent in the sense that
for any two Borel sets \(B_1\) and \(B_2\) in \(\mathcal{D }_2\). In particular, the limits \((\hat{M}_s, \hat{M}_Z)\) and \((\hat{L}, \hat{I})\) are independent.
Lemma 10
(Asymptotic independence) The sequences \((\hat{M}^n_s, \hat{M}^n_Z)\) and \((\hat{L}^n, \hat{I}^n)\) are asymptotically independent.
In order to prove Lemma 10, we use the following lemma.
Lemma 11
(Basis for asymptotic independence) If \(\hat{D}^n \Rightarrow 0\text{ e },\; \hat{I}^n \Rightarrow \hat{I}\) and \(\hat{V}^n \Rightarrow \hat{V}\) as \(n \rightarrow \infty \) for random vectors \((\hat{I}^n,\; \hat{D}^n, \hat{V}^n)\) in \(\mathcal{D }_3\), where \(\hat{D}^n = f(\hat{V}^n)\) for some function \(f\) and \(P(\hat{I}^n \in B| \hat{V}^n = v) = P(\hat{I}^n \in B| \hat{D}^n = f(v))\) for all Borel sets \(B\) almost surely with respect to \(dP(\hat{V}^n = v)\), then \(\hat{I}^n\) is asymptotically independent of \(\hat{V}^n\).
Proof
Let \(g_i\) be a continuous bounded real-valued function on \(\mathcal{D }\) for \(i = 1, 2 , 3\). By the assumptions above,
Since \({\hat{I}}^n \Rightarrow {\hat{I}}\) and \({\hat{D}}^n \Rightarrow 0\text{ e }\), we also have \(({\hat{I}}^n, {\hat{D}}^n) \Rightarrow ({\hat{I}}, 0\text{ e })\) by Theorem 11.4.5 of [31]. Thus, \(E[g_1 ({\hat{I}}^n) g_2 ({\hat{D}}^n)] \Rightarrow E[g_1 ({\hat{I}}) g_2 ({\hat{D}})] = g_2 (0\text{ e }) E[g_1 ({\hat{I}})]\) as \(n\rightarrow \infty \), so that \({\hat{I}}^n\) is asymptotically independent of \({\hat{D}}^n\) and therefore also of \({\hat{V}}^n\)
By Theorem 11.4.5 of [31] once again,
so that, applying the continuous mapping theorem with the function \(h: \mathbb{R }\times \mathcal{D }\rightarrow \mathbb{R }\) defined by \(h(x,y) \equiv x g_3(y)\), we obtain
Since the random variables in (48) are bounded, we can apply the bounded convergence theorem, combined with (47) and (48), to get
From the special case \(g_2 \equiv 1\text{ e }, E[g_1 ({\hat{I}}^n) g_3 ({\hat{V}}^n)] \rightarrow E[g_1 ({\hat{I}})] E[g_3 ({\hat{V}})]\) as \(n\rightarrow \infty \). Since the product \(g_1 g_3\) is a continuous bounded real-valued function, we also have \(E[g_1 ({\hat{I}}^n) g_3 ({\hat{V}}^n)] \rightarrow E[g_1 ({\hat{I}}) g_3 ({\hat{V}})] \quad \text{ as }\quad n\rightarrow \infty \). Hence,
for all continuous bounded real-valued functions \(g_1\) and \(g_3\), so that \({\hat{I}}\) is independent of \({\hat{V}}\). \(\square \)
Proof of Lemma 10
We show that the conditions of Lemma 11 are satisfied in our case. For that, we rely strongly on the SSC result in Corollary 4.1 of [24]. We first observe that, for each \(n\), the stochastic process \(\{D^n_{1,2} (t): t \ge 0\}\), and thus also the stochastic processes \(\{1_{\{D^n_{1,2} (t) > 0\}}: t \ge 0\}\) and \({\hat{I}}^n\) in (15) are directly functions of \({\hat{D}}^n\) in (15). Thus, for each \(n\), the conditional distribution of \({\hat{I}}^n\) in \(\mathcal{D }\) conditional on \({\hat{V}}^n \equiv ({\hat{A}}^n_i, {\hat{U}}^n_i,{\hat{S}}^n_{i,j}, {\hat{D}}^n, {\hat{Q}}^n_{i}, {\hat{Q}}^n_{s}, {\hat{Z}}^n_{i,j} )\) in (15) coincides with the conditional distribution of \({\hat{I}}^n\) in \(\mathcal{D }\) conditional on \(\hat{D}^n\). Moreover, \({\hat{D}}^n\) is scaled in the same way as the other processes in \({\hat{V}}^n\) in (15). However, Theorem 4.5 (iii) and its Corollary 4.1, both from [24], imply that \({\hat{D}}^n \Rightarrow 0\text{ e }\). Thus all the conditions of Lemma 11 are satisfied, and the statement of the Lemma follows. \(\square \)
7 Proof of Theorem 6
First, if the parameter state function \(\eta \) is a constant function, with \(\eta (t) = \gamma , \,10 \le t \le T\), then \(\hat{C}^n (t; \eta ) = \hat{C}^n_\mathrm{{QBD}} (t,\gamma )\) for \(\hat{C}^n (t; \eta )\) in (40) and \(\hat{C}^n_\mathrm{{QBD}} (t,\gamma )\) in (13), as noted in §6.2. Moreover, if the QBD \(D(\gamma , \cdot )\) is positive recurrent, then the conclusion in Theorem 6 reduces to the standard FCLT for a cumulative process in (13). To consider more general time-varying parameter state functions \(\eta \equiv \left\{ \eta (u) : 0 \le u \le T\right\} \), we require that \(\eta \) be positive recurrent where, as before, we say that a state function \(\eta \) is positive recurrent if the associated FTSP \(D(\eta (t),\, \cdot )\) is positive recurrent for all \(t,\, 0 \le t \le T\).
Next, we observe that the conclusion in Theorem 6 is also valid for all positive-recurrent piecewise constant parameter state functions, where we include the condition that there may be only finitely many discontinuities in each bounded interval. Let \(\mathcal{{D}}_{pc}\) be the subspace of \(\mathcal{{D}}\) containing all such piecewise constant functions. To see that the conclusion holds for each positive recurrent \(\eta \in \mathcal{{D}}_{pc}\), note that, because of the time scaling, each subinterval \([a,b)\) of length \(O(1)\) for the state function \(\eta \) corresponds to an interval of length \(O(n)\) for the stochastic process \(\left\{ D(\eta (s/n), s): s \ge 0\right\} \), which has transition rates of \(O(1)\). Moreover, the convergence on each successive interval implies that the initial distributions converge on the next interval. Hence, the initial conditions on each subinterval do not alter the limit. Thus, the separate subintervals can be treated separately, as if we were considering the first case of a constant parameter state function.
Intuitively, it should be evident that the result extends to positive recurrent state functions \(\eta \) in \(\mathcal{D }\) because each such function is the uniform limit over bounded intervals of piecewise-constant state functions; see p. 393 of [31]. However, a complete proof for this seemingly minor extension seems quite complicated. The remaining proof will be based on a series of lemmas, which are proved in the next section.
First, we exploit Corollary 3 showing that the subset of positive recurrent state functions in \(\mathcal{D }\) is an open subset. With Corollary 3, we then exploit the continuity of QBD’s established in Lemma C.5 of [24] to complete the proof. We complete the proof in several steps, requiring further lemmas. In doing so, we will exploit frozen processes to simplify the argument. As before, we use a coupling construction to show that they serve as suitable asymptotic approximations.
Here we consider a modification of the process \(\hat{C}^n\) in (40), having a parameter state that is frozen over each successive cycle, where as before a cycle is the period between successive visits to a fixed state. As remarked before, in the case of a constant parameter state function \(\eta \), with \(\eta (t) = \gamma , 0 \le t \le T\), these are the regeneration cycles associated with the regenerative process \(D(\gamma , \cdot )\), as in §4.1, but here we have a more general case. For each \(n\), let \(\hat{C}^n_f\) denote this modification of \(\hat{C}^n\), having a parameter state that is frozen over each successive cycle. We use a coupling construction to show that it suffices to consider \(\hat{C}^n_f\) to establish the desired convergence of \(\hat{C}^n\) in (40).
Lemma 12
(Frozen cumulative processes) The processes \(\hat{C}^n_f\) and \(\hat{C}^n\) can be constructed on the same underlying space so that \(d_{J_1} (\hat{C}^n_f, \;\hat{C}^n) \Rightarrow 0\).
Now we want to establish the convergence \(\hat{C}^n_f \Rightarrow \hat{C}\) as \(n \rightarrow \infty \). To do so, we apply modified versions of the reasoning used to prove the FCLT in (13), as given in [9]. In particular, as in (1.1–1.4) of [9], we observe that \(\hat{C}^n_f\) is asymptotically equivalent to a random sum, ignoring remainder terms, and we then establish convergence for the sequence of random sums. To set the stage, let the \(i\)th full cycle in system \(n\) end at time \(T^n_i\) (recall that the cycle begins upon transition into the designated state, while the next cycle begins upon first returning to that state after first leaving the state, which is well-defined because the processes are pure-jump processes).
As in §4.1, the key random variables associated with these cycles are the cycle lengths
and the integrals of the centered process over the cycle, which we call the cycle variables,
where \(\gamma _i \equiv \eta (T^n_{i-1})\), with \(T^n_{i-1}\) being the random time at which the \(i^\mathrm{th}\) full cycle begins and \(T^n_{0} =0\), so that \(Y^n_0\) is the cycle variable for the first partial cycle. We do not need to make additional assumptions for the analog of the variables \(W_i (f)\) in (1.2) of [9] because
With this construction, we can write
for
Unlike for a regenerative process, as in [9], here the random cycle vectors \((\tau ^n_i,\, Y^n_i)\) are in general neither independent nor identically distributed. However, the sequence of cycle variables \(\{(\tau ^n_j, \, Y^n_j) : j \ge i\}\) is conditionally independent of the entire system history up to time \(T^n_{i-1}\), which we denote by \(\mathcal{{F}}^n_{i-1}\), given only \(T^n_{i-1}\), for each \(i \ge 0\) and \(n \ge 1\). Of course, in general these conditional distributions vary with \(i\) because the parameter state function \(\eta \) is not constant, but they change little if \(\eta \) changes little, by the QBD continuity.
Let \(N^n (t)\) count the number of full cycles up to time \(t\). As in (1.4) of [9], we can write
where \(\hat{R}^n (t)\) is the random sum
while \(\hat{R}^n_1 (t)\) and \(\hat{R}^n_2 (t)\) are remainder terms involving the initial and final partial cycle, if any, also scaled by dividing by \(\sqrt{n}\).
Just as in the standard regenerative setting, we are able to show that \(\hat{C}^n_f\) is asymptotically equivalent to \(\hat{R}^n\), so that it suffices to work with \(\hat{R}^n\).
Lemma 13
(Reduction to random sums) As \(n \rightarrow \infty , \hat{R}^n_1 \Rightarrow 0\text{ e }\) and \(\hat{R}^n_2 \Rightarrow 0\text{ e }\), so that \(d_{J_1} (\hat{R}^n, \; \hat{C}^n_f) \Rightarrow 0\).
It now suffices to show that \(\hat{R}^n (\cdot ; \eta ) \Rightarrow \hat{C} (\cdot ; \eta )\) as \(n \rightarrow \infty \) for each continuous positive recurrent \(\eta \). By virtue of Corollary 3, given such an \(\eta \), we can find a sequence of piecewise-constant state functions \(\{\eta _{pc}^m: m \ge 1\}\) in \(\mathcal{D }\) where \(\Vert \eta _{pc}^m - \eta \Vert _T \rightarrow 0\) as \(m \rightarrow \infty \) with \(\eta _{pc}^m\) being positive recurrent for all sufficiently large \(m\). For those \(m\), we have the desired convergence \(\hat{C}^n (\cdot ; \eta ^m_{pc}) \Rightarrow \hat{C} (\cdot ; \eta ^m_{pc})\) as \(n \rightarrow \infty \), as observed in the beginning of the proof. Thus, by Lemma 12 and 13 above, we also have \(\hat{R}^n (\cdot ; \eta ^m_{pc}) \Rightarrow \hat{C} (\cdot ; \eta ^m_{pc})\) as \(n \rightarrow \infty \) for these \(m\) as well. We now want to show that the established convergence also holds when \(\eta ^m_{pc}\) is replaced by \(\eta \). For that purpose, we need to establish convergence as \(n \rightarrow \infty \) and \(m \rightarrow \infty \) jointly. In order to justify that joint convergence, we establish the following result.
Lemma 14
(Tightness and bounds for the random sums) Consider a continuous parameter state function \(\eta \) and a piecewise-constant parameter state function \(\eta _{pc}\), where both \(\eta \) and \(\eta _{pc}\) are positive recurrent. Let \(T>0\) and \(\delta > 0\) be such that \(\Vert \eta - \eta _{pc}\Vert _T < \delta \). Then the sequence \(\{\hat{R}^n (\cdot , \eta )\}\) is \(\mathcal{C }\)-tight in \(\mathcal{D }([0,T^{*}])\) for some constant \(T^{*} > 0\) and there exist functions \(\sigma _l (\eta _{pc}(\cdot ), \delta )\) and \(\sigma _u (\eta _{pc}(\cdot ), \delta )\) such that the limit, say \(\hat{R} (\cdot , \eta )\), of any convergent subsequence of \(\{\hat{R}^n (\cdot , \eta )\}\) can be represented as
where \(B\) is standard BM and \(\bar{W}\) can be bounded above and below by
for all \(t_1\) and \(t_2\) with \(0 \le t_1 < t_2 \le T^{*}\), where \(0 \le \sigma ^2_{l} (\eta _{pc} (s), \delta ) \le \sigma ^2_{u} (\eta _{pc} (s), \delta ) < \infty \) for all \(s, 0 \le s \le T\), and having the form in (14) determined by the state \(\eta _{pc} (s)\). Moreover, for any \(\epsilon > 0\) and \(T^{*} > 0\), there exist \(\delta > 0\) and \(T > 0\) as above, such that
Lemma 14 is based on associated lemmas for partial sums from triangular arrays of the cycle lengths and cycle variables \(\tau ^n_i\) and \(Y^n_i\), exploiting martingale structure; these results are stated in §8 and proved in §9. Given these lemmas, we now can complete the proof of Theorem 6. First, we have observed that \(\hat{C}^n (\cdot ,\, \eta _{pc}) \Rightarrow \hat{C} (\cdot ,\, \eta _{pc})\) in \(\mathcal{D }\) for any positive-recurrent piecewise-constant parameter state function \(\eta _{pc}\). By Lemmas 12 and 13, \(\hat{R}^n (\cdot , \eta _{pc}) \Rightarrow \hat{C} (\cdot , \eta _{pc})\) in \(\mathcal{D }\) as well. We can then apply Lemma 14 to deduce that the sequence of random sums \(\{\hat{R}^n (\cdot ,\,\eta )\}\) is tight. Hence, each subsequence has a convergent subsequence. Let \(\hat{R} (\cdot , \eta )\) be the limit of such a convergent subsequence. Next, we construct a sequence \(\{\eta ^m_{pc}\}\) of positive-recurrent piecewise-constant state functions with \(\Vert \eta ^m_{pc} - \eta \Vert _T \rightarrow 0\) as \(m \rightarrow \infty \). As shown above, for each of them, we have \(\{\hat{R}^n (\cdot , \eta ^m_{pc})\} \Rightarrow \hat{C} (\cdot , \eta ^m_{pc})\) as \(n \rightarrow \infty \). However, again by Lemma 14, we have \(\hat{R} (\cdot , \eta )\) bounded above and below by the limits \(\hat{C} (\cdot , \eta ^m_{pc})\) which converge to \(\{\hat{C} (\cdot , \eta )\}\) as \(m \rightarrow \infty \). Hence, we must have \(\hat{R} (\cdot , \eta ) = \{\hat{C} (\cdot , \eta )\}\). Hence all convergent subsequences must have the same limit, which implies that we must have the full convergence, \(\hat{R}^n (\cdot , \eta ) \Rightarrow \hat{C} (\cdot , \eta )\) in \(\mathcal{D }\) as \(n \rightarrow \infty \). By Lemmas 12 and 13, we must also have \(\hat{C}^n (\cdot , \eta ) \Rightarrow \hat{C} (\cdot , \eta )\) in \(\mathcal{D }\). Hence, Theorem 6 is proved. \(\square \)
8 Proof of Lemma 14: using the martingale FCLT
We have indicated that Lemma 14 is based on associated lemmas for partial sums from triangular arrays of the cycle lengths and cycle variables \(\tau ^n_i\) and \(Y^n_i\), exploiting martingale structure; in particular, we apply the martingale FCLT for triangular arrays. We can treat these two components of \(\hat{R}^n (\cdot , \eta )\) separately because, just as in the familiar setting of renewal reward processes discussed in §§7.4 and 13.2 of [31], the FCLT for \(\hat{R}^n (\cdot , \eta )\) depends on a FCLT for partial sums of \(Y^n_i\) and a FWLLN for \(N^n (t)\) separately. By the inverse relation discussed in §§7.3 and 13.6 of [31], a FWLLN for \(N^n (t)\) is equivalent to a corresponding FWLLN for the partial sums of \(\tau ^n_i\). Since we can reduce the case of piecewise-constant \(\eta _{pc}\) to the case of constant \(\eta _c\) by focusing on the subintervals separately, we now relate the given \(\eta \) to a constant \(\eta _c\).
Consider the cycle variables \(Y^n_i\) in (50) associated with a parameter state function \(\eta \). Let \(\mathcal{{F}}^n_k\) be the \(\sigma \)-field generated by \(X^n_6 (t): 0 \le t \le T^n_k,\; k \ge -1\). Let
For \(i \ge 0\), let
We will be strongly exploiting the QBD continuity to obtain regularity in the variables \(Y^n_i\).
Lemma 15
(Sums of cycle variables) Consider a continuous parameter state function \(\eta \) in \(\mathcal{D }\) and an associated constant parameter state function \(\eta _c\), where \(\Vert \eta - \eta _{c}\Vert _T < \delta \) for some \(T > 0\) and \(\delta >0\), and both \(\eta \) and \(\eta _c\) are positive recurrent. Consider the cycle variables \(Y^n_i\) in (50) and the associated variables in (55) and (56), all associated with \(\eta \). Then there exist constants \(\sigma ^2_l (\eta _c, \delta ), \; \sigma ^2_u (\eta _c, \delta )\) and \(\delta ^{\prime } > 0\) such that, for all \(i\) and \(n\),
for \(\sigma ^2_{n,i}\) in (56), associated with \(\eta \), so that
for all \(n \ge 1\) and \(0 \le t_1 < t_2 \le T\), for \(\bar{V}^n\) in (56). As a consequence,
for all \(n \ge 1\) and \(0 \le t_1 < t_2 \le T^{\prime }\) for \(T^{\prime } \equiv T/\sigma ^2_u (\eta , \delta )\). Hence, the sequences \(\left\{ \bar{V}^n\right\} \) and \(\left\{ \mathcal{V }^n\right\} \) associated with \(\eta \), defined in (56), are \(\mathcal{C }\)-tight in \(\mathcal{D }([0,T])\) and \(\mathcal{D }([0,T^{\prime }])\), respectively. Moreover, the limits of convergent subsequences, say \(\bar{V}\) and \(\mathcal{V }\) must satisfy corresponding inequalities, i.e.,
for the same ranges of \(t_1\) and \(t_2\) above, so that \(\bar{V}\) and \(\mathcal{V }\) are both continuous and strictly increasing. In addition,
for \(\hat{M}^n_{Y}\) in (55), where \(B\) is standard BM. Thus, the sequence \(\left\{ \hat{M}^n_{Y}\right\} \) is \(\mathcal{C }\)-tight in \(\mathcal{D }([0,T])\) with the limit of any convergent subsequence, say \(\hat{M}_{Y}\), being of the form
where \(\bar{V}\) is bounded above and below over all subintervals as in (60). If we are free to choose the bounding constant \(\delta \) above, then for any \(\epsilon > 0\), we can find \(\delta > 0\) so that \(\delta ^{\prime } < \epsilon \) for \(\delta ^{\prime }\) in (57).
We now state the corresponding result for the partial sums of the cycle lengths.
Lemma 16
(Sums of cycle lengths) Consider a continuous parameter state function \(\eta \) and a constant state function \(\eta _c\), where both \(\eta \) and \(\eta _c\) are positive recurrent. Let \(T>0\) and \(\delta > 0\) be such that \(\Vert \eta - \eta _{c}\Vert _T < \delta \). Consider the cycle lengths \(\tau ^n_i\) in (49) associated with \(\eta \). Let \(U^n_k \equiv \tau ^n_1 + \cdots + \tau ^n_k,\; k \ge 1\), and \(\bar{U}^n (t) \equiv n^{-1} U^n_{\lfloor nt \rfloor },\; t \ge 0\). Let \(M^n_{U,i} \equiv E[\tau ^n_i|\mathcal{{F}}^n_{i-1}],\; \bar{M}^n_{U} (t) \equiv n^{-1} (M^n_{U,1} + \cdots + M^n_{U,\lfloor nt \rfloor })\). Then the sequence \(\{\bar{U}^n\}\) is \(\mathcal{C }\)-tight in \(\mathcal{{D}}([0,T^{\prime \prime }])\) for an appropriate time \(T^{\prime \prime } > 0\), and if \(\bar{U}\) is the limit of a convergent subsequence, then necessarily it is bounded above and below with probability 1 by linear functions, i.e.,
where \(m_l (\eta _c, \delta )\) and \(m_u (\eta _c, \delta )\) are constants depending on \(\delta \) such that \(0 < m_l (\eta _c, \delta ) \le m_u (\eta _c, \delta ) < \infty \). If we are free to choose the time \(T > 0\) and the bounding constant \(\delta \) above, then for any \(\epsilon > 0\) and \(T^{\prime \prime }, 0 < T^{\prime \prime } < \infty \), we can find \(\delta > 0\) so that the conclusions above hold with \(m_u (\eta _c, \delta ) - m_l (\eta _c, \delta ) < \epsilon \).
As a consequence of the inverse relation between the partial sums and the associated counting processes, as in Chapter 13 of [31], we obtain the following corollary for the counting processes associated with the partial sums. Let \(\bar{N}^n (t) \equiv n^{-1} N^n (nt), t \ge 0\). In the next section we combine Corollary 4 below with Lemma 15 to prove Lemma 14.
Corollary 4
(Counting process for cycle lengths) Under the assumptions of Lemma 16, the sequence of scaled counting processes \(\{\bar{N}^n\}\) is \(\mathcal{C }\)-tight in \(\mathcal{{D}}([0,T^{\prime \prime \prime }])\) for any time \(T^{\prime \prime \prime } < T^{\prime \prime }/m_l (\delta )\), where \(T^{\prime \prime }\) is as in Lemma 16. If \(\bar{N}\) is the limit of a convergent subsequence of \(\{\bar{N}^n\}\), then necessarily it is bounded above and below with probability 1 by linear functions, i.e.,
where \(m_l (\eta _c,\delta )\) and \(m_u (\eta _c,\delta )\) are the constants depending on \(\delta \) from Lemma 16 above. If we are free to choose the time \(T > 0\) and the bounding constant \(\delta \) above, then for any \(\epsilon > 0\) and \(T^{\prime \prime \prime }\), we can find \(\delta > 0\) so that the conclusions above hold with \(m_u (\eta _c,\delta ) - m_l (\eta _c,\delta ) < \epsilon \).
9 Remaining Proofs of Lemmas in §§7 and 8
In this section we prove five lemmas in the previous two sections, which were used in the proof of Theorem 6. We prove them in the order needed for the proof. We prove the one remaining lemma, Lemma 12 justifying the approximation by the frozen process \(\hat{C}^n_f\), afterwards in §10.
Proof of Lemma 15
The key observation is that the sequence of random vectors \(\{(\tau ^n_j, Y^n_j): j \ge i\}\) associated with the general parametric state function \(\eta \) is conditionally independent of the entire system history up to time \(T^n_{i-1}\) for each \(i\), which we have denoted by \(\mathcal{{F}}^n_{i-1}\), given only \(T^n_{i-1}\). As a consequence, paralleling the regenerative case in [9] and (14),
for \(i \ge 1\), where \(\eta _i \equiv \eta (T^n_{i-1})\), so that \(E[Y^n_i|\mathcal{{F}}^n_{i-1}] = 0\) for each \(i\). Hence, the stochastic process \(\{M^n_{Y} (k): k \ge 1\}\) is a square integrable martingale with respect to the filtration \(\{\mathcal{{F}}^n_k: k \ge 1\}\).
Moreover, by the QBD continuity, the variances \(\sigma ^2_{n,i} \equiv E[(Y^n_i)^2|\mathcal{{F}}^n_{i-1}]\) in (56) cannot differ too much from the corresponding variance for the constant parameter function \(\eta _c\). For a fixed \(t \ge 0\), let \(\sigma ^2_Y (\eta (t))\) be \(\sigma ^2_{n,i}\) under the condition that \(T^n_{i-1} = t\), so that \(\eta _i \equiv \eta (T^n_{i-1}) = \eta (t)\). Since \(\Vert \eta - \eta _c\Vert _T < \delta \), we can apply the QBD continuity to obtain the relations in (57), where
These in turn imply that the inequalities in (58) and (59) hold for \(\bar{V}^n\) and \(\mathcal{V }^n\) for all \(n\), implying the tightness of the sequences \(\{\bar{V}^n\}\) and \(\{\mathcal{V }^n\}\) and the inequalities stated in (60) for the limits of all convergent subsequences. However, we cannot conclude that in general either \(\bar{V}^n\) or \(\mathcal{V }^n\) converges.
Nevertheless, we can apply an appropriate martingale FCLT to deduce that the limit in (61) holds; e.g., see Theorems 2.1 and 2.2 of [5], Theorem 5 of [26] and p. 98 of [14]. The QBD continuity and the bounds in (57) imply that the technical regularity conditions are satisfied in this case. Hence, for any \(\delta > 0\), we can apply the martingale FCLT to get the convergence in (61).
Given that \(\mathcal{V }\) is a strictly increasing continuous function with bounded slope, as in (60), we can deduce from the tightness of \(\{\hat{M}^n_{Y} \circ \mathcal{V }^n\}\), which follows from the convergence in (61), that the sequence \(\{\hat{M}^n_{Y}\}\) itself must be tight. That is most easily done by letting \(\mathcal{V }^n\) be a continuous function constructed by linear interpolation under which we still have the convergence in (61). Then, \(\bar{V}^n\) itself is a continuous strictly increasing function with modulus bounds in (60). Hence, we can deduce that the sequence \(\{\hat{M}^n_{Y}\}\) must be tight.
The sequence \(\{(\hat{M}^n_{Y}, \;\mathcal{V }^n,\; \bar{V}^n)\}\) is tight because the component sequences are all tight. Starting from the joint convergence \((\hat{M}^n_{Y},\; \mathcal{V }^n,\; \bar{V}^n) \Rightarrow (\hat{M}_Y,\; \mathcal{V },\; \bar{V})\) in \(\mathcal{{D}}_3\) for any convergent subsequence, we can deduce from (61) that \(\hat{M}_Y = B \circ \bar{V}\), as claimed in (62). The final \(\epsilon \) bound follows from the QBD continuity in Lemma C.5 of [24]. \(\square \)
Proof of Lemma 16
The proof is similar to the proof of Lemma 15 above, but now we need a FWLLN instead of a FCLT. However, it is convenient to apply the FCLT to deduce the FWLLN. Indeed, by the same reasoning used to prove Lemma 15 above, we can obtain a martingale FCLT for the sums of the centered variables \(\tau ^n_i - E[\tau ^n_i|\mathcal{{F}}^n_{i-1}]\), paralleling (61). Here, we use the conditional variances and their sums, defined by
instead of (56). We then obtain analogs of (57), (58) and (60).
Given that FCLT, we scale further, essentially dividing by \(\sqrt{n}\), to get the associated FWLLN for the centered variables. As a consequence, we obtain the FWLLN \(\bar{U}^n - \bar{M}^n_U \Rightarrow 0\text{ e }\) in \(\mathcal{D }([0,T^{\prime \prime }])\) as \(n \rightarrow \infty \), for an appropriate finite time \(T^{\prime \prime }\), not necessarily equal to \(T\) or \(T^{\prime }\) in the previous proof above. Then, in direct analogy with (64), we apply the QBD continuity to obtain \(m_l (\eta _c, \delta ) \le M^n_{U,i} \le m_u (\eta _c, \delta )\) for all \(i\) and \(n\). Hence, \(m_l (\eta _c,\delta ) t \le \bar{M}^n_U (t) \le m_u (\eta _c,\delta ) t\) for all \(n\) and \(t, 0 \le t \le T\). We can then combine these bounds with the FWLLN to obtain the conclusions stated in the lemma. By the QBD continuity, \(m_u (\eta _c,\delta ) - m_l (\eta _c,\delta ) \rightarrow 0\) as \(\delta \downarrow 0\). \(\square \)
Proof of Lemma 14
First, Lemmas 15 and 16 and Corollary 4 can be extended directly to piecewise-constant state functions as well as constant state functions. Thus, for \(\eta \) in \(\mathcal{D }\), they imply that the sequences \(\{\hat{M}^n_{Y}\}\) and \(\{\bar{N}^{n}\}\) are each \(\mathcal{C }\)-tight in \(\mathcal{D }\). Consequently, the associated sequence of vector processes \(\{(\hat{M}^n_{Y},\;\bar{N}^{n})\}\) is \(\mathcal{C }\)-tight in \(\mathcal{D }_2\). Hence, every subsequence has a further convergent subsequence. Moreover, by Lemma 15 and Corollary 4, any limit, say \((\hat{M}_{Y},\;\bar{N})\), can be represented as \((B \circ \bar{V},\; \bar{N})\), where \(\bar{V}\) and \(\bar{N}\) are bounded as in (60) and (63) over each subinterval where the piecewise-constant parametric state function is constant. Hence, overall they can be bounded above and below by
where \((\bar{V}_{Y,l}(0),\bar{N}_l(0)) = (\bar{V}_{Y,u}(0),\bar{N}_u(0)) = (0, 0)\) and
for \(t_{i-1} \le t < t_i\), where \(0 \equiv t_0 < t_1 < \ldots < t_k \equiv T\), so that \(t_i\) are the endpoints of a piecewise constant state function \(\eta _{pc}\), with \(\sigma ^2_{l,i}\) and \(1/m_{u,i}\) being the lower bounds and \(\sigma ^2_{u,i}\) and \(1/m_{l,i}\) being the upper bounds on the \(i\)th subinterval, depending on \(\eta _{pc}\) and \(\delta \). Hence, we can apply the continuous mapping theorem to obtain the corresponding convergence for the random sum for all convergent subsequences, with the limit of all convergent subsequences represented as claimed in (52) with \(\bar{W}\) there bounded as in (53). The bounding variance functions are given explicitly by \(\sigma ^2_u (\eta _{pc} (s), \,\delta ) = \sigma ^2_{u,i}/m_{l,i}\) and \(\sigma ^2_l (\eta _{pc}(s),\, \delta ) = \sigma ^2_{l,i}/m_{u,i}\) for \(t_{i-1} \le s < t_i\). Thus, by having \(\Vert \eta - \eta _{pc}\Vert _T < \delta \) and choosing \(\delta \) sufficiently small, we can obtain the desired variance inequality (54). \(\square \)
Proof of Lemma 13
The reasoning follows the regenerative case as in [9]. First, the remainder term \(\hat{R}^n_1 (t)\) is relatively easy to treat since it involves the initial cycle and is thus independent of \(t\). Since \(D(\eta (0),0)\) has been specified as some fixed state after (40), the initial partial cycle until hitting time of the designated state is clearly \(O(1)\) and becomes asymptotically negligible when we divide by \(\sqrt{n}\).
As in [9], to treat the second remainder term, we exploit the representation
for \(W^n_i\) and \(\tau ^n_i\) defined in (51) and (49). However, the last term in (65) is asymptotically negligible because of the FCLT for the cycle lengths used in the proof of Lemma 16 above. The last term is the maximum discontinuity in the prelimit process indexed by \(n\). Since the limit is continuous, that term is asymptotically negligible. \(\square \)
10 Proof of Lemmas 8 and 12: coupling constructions
In this section we prove the two lemmas justifying approximation by frozen processes, using coupling constructions.
Proof of Lemma 8
By the construction in (42), we have forced the new frozen processes \(\tilde{D}^n_{f}\) to coincide with the queue-difference processes \(D^n_{1,2}\) for all time points \(t\) of the form \(k/n\). To complete the proof, we employ a special coupling construction to construct these two processes on the same underlying probability space to make the processes have the same transitions within each interval \([(k-1)/n,\, k/n)\) with high probability. As usual [19, 28], this coupling construction produces an artificial joint distribution, but leaves the distributions of each of the two processes individually unchanged.
We start by focusing on a single interval \([(k-1)/n,\, k/n)\). It suffices to focus on one of these intervals, because we will show that the construction is uniform over the \(n\) intervals. Since the transition rates in system \(n\) are of order \(O(n)\) and the interval is of length \(1/n\), it is convenient to start by rescaling time as in the fluid limit in Theorem 1. By doing a change of variables, we have
Then recall that both processes inside the integral converge appropriately to the FTSP. To expose the connection, let \(k\) go to infinity with \(n\) so that \(k/n \rightarrow t\) as \(n \rightarrow \infty \). First, by Theorem 1, \({\bar{X}}^n ((k-1)/n) \Rightarrow x_6 (t)\). Then, by Theorem 4.4 of [24],
Second, by (41),
The main point for the coupling is that, after the change of time scale, both processes have transition rates of order \(O(1)\) that differ by \(O(1/n)\). Moreover, the processes are identical w.p.1 at the left end point of the interval \([0,1]\).
However, we need to apply the argument above to all \(n\) intervals, where \(n \rightarrow \infty \). It is thus important that the conclusions are valid uniformly over the \(n\) subintervals. Those conclusions are justified because the fluid limit in Theorem 1 implies that \(\bar{X}^n_6 \Rightarrow x_6\) uniformly over each finite interval. Moreover, the limit \(x_6\) is a continuous function over a bounded interval with values in a compact subset of \(\mathbb{A }\). Finally, the limiting transition rates are a continuous function of the state.
Let \(\nu ^n (T)\) be the number of \(k\) for which the \(nk \le T\) and the sample paths of \(\tilde{D}^n_{f}\) and \(D^n_{1,2}\) fail to be identical over the interval \([(k-1)/n, k/n)\). As a consequence of the asymptotically equivalent transition rates after changing the time scale above, we show below that \(\nu ^n (T) = O(1)\) as \(n \rightarrow \infty \). Thus, to complete the proof, we use the elementary bound \(\Vert \Delta ^n \Vert _T \le \nu ^n (T+ \epsilon )/\sqrt{n}\) for all \(n \ge 1/\epsilon \), where \(T>0\) and \(\epsilon > 0\) are arbitrary constants.
We now discuss the coupling in more detail. Since the transitions in the queue-difference process \(D^n_{1,2}\) are generated from state changes in the CTMC \(X^n_6\), we do the special construction from the perspective of the CTMC \(X^n_6\). We use the device of uniformization to generate the transitions of the CTMC; i.e., we construct the transitions by thinning a Poisson process. Without loss of generality, we use different independent Poisson processes to generate potential transitions for each kind of transition, each interval \([(k-1)/n, k/n)\) and each \(n\). Since the transition rate of the CTMC is not uniformly bounded, there is a possibility that this direct construction will be invalid, but by choosing these Poisson process rates sufficiently high, we can make the likelihood of a violation asymptotically negligible. In the actual construction, we can change the Poisson process when the constructed process hits a state from which a further transition could lead to a violation. The detailed construction does not matter because we declare a difference occurring throughout the entire subinterval if the Poisson rate needs to be adjusted, thus contributing the maximum possible to the bound above. Since the integrand in (45) is bounded by one, the total impact upon (45) by such rate violations can clearly be made asymptotically negligible.
The coupling is achieved using the same Poisson processes to generate the transitions in both \(D^n_{1,2}\) and \(\tilde{D}^n_{f}\) over each subinterval \([(k-1)/n,\, k/n)\). These are done with respect to the states of \(X^n_6 (t)\) and \(X^n_6 ((k-1)/n)\). For \(D^n_{1,2}\), the transitions rates of the various transitions (arrivals, abandonments from each queue and service completions of each class from each pool) are determined by the actual state \(X^n_6 (t)\), which changes throughout the interval \([(k-1)/n, k/n)\). For, \(\tilde{D}^n_{f}\), we do the same construction, but we leave the state fixed at its initial value \(X^n_6 ((k-1)/n)\) throughout the interval \([(k-1)/n, k/n)\), so that the transition rates do not change. However, we match the transitions in the two systems as much as possible. We make the transitions differ only to the extent that the state of \(X^n_6 (t)\) differs from \(X^n_6 ((k-1)/n)\).
As stated above, we use different independent Poisson processes for each kind of transition. We have one Poisson process generate potential arrivals for each \(n\). Since the arrival rates are unaffected by the state, the Poisson process for generating potential arrivals of class \(i\) can have rate \(\lambda _i^n\), so that every potential arrival corresponds to an actual arrival in both systems. Thus no difference is caused by any arrival. That arrival in turn affects the constructed processes \(D^n_{1,2}\) and \(\tilde{D}^n_{f}\) in the obvious way: an arrival of class 1 increases them by one, while an arrival of class 2 decreases them by \(r\).
For service completions of class 1 by pool 2, we let the Poisson process generating potential transitions have rate \(\mu _{1,2} m^n_2\). The actual transition rate at time \(t\) for \(X^n_6 (t)\) is \(\mu _{1,2} Z^n_{1,2} (t)\), so that the Poisson rate is an upper bound on the actual transition rate for all states. If the Poisson process with rate \(\mu _{1,2} m^n_2\) has a transition at time \(t\), where \((k-1)/n \le t < k/n\), then we let both systems have an actual service completion of class 1 by pool 2 at time \(t\) with probability \((Z^n_{1,2} (t) \wedge Z^n_{1,2} ((k-1)/n)/ m^n_2\); we let only the system associated with \(D^n_{1,2}\) have an actual service completion of class 1 by pool 2 at time \(t\) with probability \([Z^n_{1,2} (t) - (Z^n_{1,2} (t) \wedge Z^n_{1,2} ((k-1)/n)]/m^n_2\); we let only the system associated with \(D^n_{f}\) have an actual service completion of class 1 by pool 2 at time \(t\) with probability \([Z^n_{1,2} ((k-1)/n) - (Z^n_{1,2} (t) \wedge Z^n_{1,2} ((k-1)/n)]/ m^n_2\); and we let neither system have an actual service completion of class 1 by pool 2 with probability \([m^n_2 - (Z^n_{1,2} (t) \vee Z^n_{1,2} ((k-1))/n)]/ m^n_2\). Thus, a difference in the sample path is caused by this transition with probability \([(Z^n_{1,2} (t) \vee Z^n_{1,2} ((k-1)/n) - (Z^n_{1,2} (t) \wedge Z^n_{1,2} ((k-1)/n)]/m^n_2\), which clearly is of order \(O(1/n)\).
We do similar constructions with independent Poisson processes for each of the other transitions. The abandonments are where the transition rate is unbounded, because the queue lengths \(Q^n_i (t)\) are unbounded above. However, the maximum queue length over the interval is bounded above by the initial queue length plus the number of arrivals over the interval, so that the probability of violation is easily controlled by the Poisson arrival process for that class. Hence, for the Poisson process generating potential abandonments from the class-\(i\) queue over the interval \([(k-1)/n,k/n)\), we can give it rate \((Q^n_i ((k-1)/n) + cn^3)\theta _i\) for \(c > \lambda _i\) (the exponent 3 is chosen to make careful calculations unnecessary). This is sufficient, because the initial number in queue \(i\) is \(Q^n_i ((k-1)/n)\) and new class-\(i\) arrivals occur at rate \(\lambda ^n_i\), which is \(O(n)\). The higher power of \(n\) ensures that a violation of the rate-order uniformization condition is asymptotically negligible as \(n \rightarrow \infty \). If the Poisson process generates a potential abandonment at time \(t\), then it is a real abandonment for at least one system with probability \(a_n/c_n = O(1/n^2)\), a real abandonment for both systems with probability \(b_n/c_n = O(1/n^2)\) and a real abandonment for only one of the two systems with probability \((a_n - b_n)/c_n = O(1/n^3)\), where \(a_n \equiv Q^n_i ((k-1)/n) \vee Q^n_i (t),\, b_n \equiv Q^n_i ((k-1)/n) \wedge Q^n_i (t)\) and \(c_n \equiv Q^n_i ((k-1)/n) + cn^3\). The main point is that \((a_n - b_n) = O(1)\) because the two queues differ by arrivals at rate \(O(n)\) over the interval of length \(1/n\). Hence, the probability that a real transition at \(t\) (not counting transitions from a state to itself, which are generated by the common Poisson process) produces an abandonment for only one of the two systems is \((a_n - b_n)/a_n = O(1/n)\). At the same time, the probability that the uniformization condition is violated during the entire interval is \(o(1/n)\), so that it is asymptotically negligible in the relevant scale.
We now assess the impact of this construction. Both processes have transition rates of order \(O(n)\) because the relevant processes \(Q^n_i\) and \(Z^n_{i,j}\) in \(X^n_6\) are \(O(n)\). Thus, the processes \(D^n_{1,2}\) and \(\tilde{D}^n_{f}\) have \(O(1)\) transitions over each interval of length \(1/n\). Hence, the state of \(X^n (t)\) will only change an amount of order \(O(1)\) within each interval \([(k-1)/n,\, k/n)\). Consequently, the probability of any one transition being different is \(O(1/n)\), and the probability that there is any difference over the interval \([(k-1)/n, k/n)\) is also of \(O(1/n)\). Hence, \(\nu ^n (T)\)—the total number of intervals having any difference over the interval \([0,T]\)—will be of order \(O(1)\), as claimed at the beginning of the proof.
Elaborating on the last step, observe that conditional upon \(\bar{X}^n_6\), which converges to \(x_6\), we can regard \(\nu ^n (T)\) as the sum of at most \(\lfloor nT \rfloor + 1\) independent Bernoulli random variable, assuming the value 1 with probability \(p_{n,i}\) and 0 otherwise, where \(p_{l}/n \le p_{n,i} \le p_{u}/n\) for all \(i = 1, \dots , \lfloor nT \rfloor + 1\), provided that \(n\) is suitably large, where \(p_{l}/n\) and \(p_{u}/n\) are the minimum and maximum “success probabilities” among those Bernoulli random variables. The bounds hold because \(t \mapsto x_6(t)\) is a continuous function that is considered over a compact interval. Hence, all the transition rates described above, producing the probabilities \(p_{n,i}\) over each interval \(i\), also have continuous limits which can be bounded uniformly for all \(n\) large enough. Using the upper bound, we can bound \(\nu ^n (T)\) above stochastically by \(\nu ^n_{u} (T)\), defined as the partial sum of i.i.d. Bernoulli random variables. taking the value one with probability \(p_{u}/n\). By the LLN for partial sums from triangular arrays \(\nu ^n_{u} (T) \Rightarrow p_{u}T\) as \(n \rightarrow \infty \), which implies that \(\nu ^n (T)\) is indeed properly \(O(1)\) as \(n \rightarrow \infty \). Hence, the proof is complete. \(\square \)
Proof of Lemma 12
The reasoning here is similar to the proof of Lemma 8. As before, we can use a coupling construction to make the two processes have identical sample paths over the vast majority of the cycles. We exploit the oscillation property for functions in \(\mathcal{D }([0,T])\), Corollary 12.2 of [31], concluding that, for any \(\epsilon > 0\), there are \(k\) time points \(t_i\) with \(0 \equiv t_0 < t_1 < \cdots < t_{k-1} < t_k \equiv T\) such that \(|\eta (s_1) - \eta (s_2)| < \epsilon \) for all \(s_1,\, s_2 \in [t_{i-1},\, t_i)\) for all \(i\). Hence, with the time scaling by \(1/n\) in (40), we see that, except for at most \(k\) cycles in \([0,T]\) containing the \(k\) boundary points \(t_i\), the oscillation of \(\eta \) over the cycle is at most \(\epsilon /n\). Hence, the coupling can be performed as in the proof of Lemma 8, making the probability that the sample paths differ over any one cycle among all except the \(k\) be of order \(O(1/n)\). Since there are \(O(n)\) cycles in \([0,T]\), as substantiated by Corollary 4, there are order \(O(1)\) among the \(O(n)\) cycles that have any difference in the sample paths. Hence, with the spatial scaling by \(\sqrt{n}\), we clearly have \(d_{J_1} (\hat{C}^n_f,\, \hat{C}^n) \Rightarrow 0\) as \(n \rightarrow \infty \) as claimed. \(\square \)
11 Comparisons with simulation
To both support the validity of the theorems and their applicability to the intended engineering problems, we now compare the approximations stemming from the FWLLN and the FCLT to the results of simulation experiments. Specifically, we will compare the Gaussian approximations for the steady-state queue lengths with simulation estimates of these quantities, obtained by simulating the actual queueing model over a large time interval. The approximate mean values come directly from the stationary point of the fluid limit, \(x^{*}\) in Theorem 2; the approximate variances come from Corollary 1, specifically, from (24).
Our simulation examples will have parameters related to a base case. First, scale is described by the parameter \(n\), which is the scaling parameter in our limit theorems. The abandonment and service rate parameters, which describe the behavior of individual customers and servers, are independent of \(n:\,\theta _1 = \theta _2 = 0.2,\, \mu _{1,1} = \mu _{2,2} = 1.0\) and \(\mu _{1,2} = \mu _{2,1} = 0.8\). The service rates are chosen so that it is less efficient to serve a customer from a different class.
The parameters that scale as the service system grows depend on \(n\); they are chosen to be directly proportional to \(n:\,m^{(n)}_i \equiv n m_i, \lambda ^{(n)}_i \equiv n \lambda _i\) and \(k^{(n)}_{1,2} \equiv n k_{1,2}\). We take \(k^n_{1,2}\) to be order \(O(n)\) so it is easy to compare different system sizes (note that the scaling of the thresholds is different than in Assumption 3. This alternative choice facilitates comparing the three different cases simulated). Our base case then has \(m_1 \equiv m_2 \equiv 1,\, \lambda _1 = 1.3,\, \lambda _2 = 0.9\) and \(k_{1,2} = 0.1\). The arrival rates are chosen to put class 1 in a focused overload, while class 2 is initially normally loaded or slightly underloaded, but becomes overloaded too after the sharing (these model parameters satisfy case 1 of Assumption 3.1 of [24]). We use the FQR-T control with ratio parameter \(r = 1.0\), which allows us to apply the simple asymptotic formulas from §4.4.
From (10) and (11), we see that the stationary fluid solution for this base case yields \(z^{*}_{1,2} = 0.2111, q_1^{*} = 0.6556, q^{*}_2 = 0.5556\) and \(\pi ^{*}_{1,2} \equiv \pi _{1,2} (x^{*}) = 0.1763\). Without any sharing, the fluid approximation for queue 1 would be 1.5000. Hence the sharing reduces the first fluid queue from 1.5000 to 0.6556, at the expense of causing the second class to have a fluid queue of 0.5556.
We now turn to the variances, for which we need to analyze the FTSP more carefully. The FTSP has BD parameters: \(\lambda _1 (x^{*}) = 1.411, \mu _1 (x^{*}) = 2.989,\, \lambda _2 (x^{*}) = 2.031\) and \(\mu _2 (x^{*}) = 2.369\). The associated \(M/M/1\) traffic intensities are \(\rho _1 (x^{*}) = 0.472\) and \(\rho _2 (x^{*}) = 0.8574\). The associated mean busy periods are \(E[T_1 (x^{*})] = 0.6338\) and \(E[T_2 (x^{*})] = 2.9603\). Hence, the alternative formula for \(\pi _{1,2} (x^{*})\) in (27) agrees with the value 0.1763 given above (providing a check on our calculations).
Turning to the FCLT, from (20), we see that \(\psi (x^{*}) \!=\! 0.6200\), so that \(\psi ^2 (x^{*}) \!=\! 0.3844\). For \(\sigma ^2 (x^{*})\), from (26), we see that \(E[T_1 (x^{*})^2] \!=\! 1.5218\), so that \({\text{ Var }}(T_1 (x^{*})) \!=\! 1.1201\), and \(\sigma ^2 (x^{*}) \!=\! 1.1201/3.5941 \!=\! 0.3116\). Then \(\xi _2 \equiv \psi ^2(x^{*})\sigma ^2 (x^{*}) = 0.1198\). Since \(|\mathcal{{M}}_{2,2}| = 0.176, \,\mathcal{{Z}}_2 = 0.3403\). Hence, \(\sigma ^2_{Z_{1,2}} (\infty ) = 1 - 0.2111 + 0.3403 = 1.1292\).
As a consequence, \(\sigma ^2_{Q_s, Z_{1,2}} (\infty ) = (1.1292)(0.5319) = 0.6006\). Since \(\mu _{2,2} - \mu _{1,2} = p_1 \theta _1 + p_2 \theta _2 = 0.2, \mathcal{{Q}}_2 = \sigma ^2_{Q_s,\, Z_{1,2}} (\infty ) = 0.6006\). Since \(\mathcal{{Q}}_1 = 11.0\), we have \(\sigma ^2_{Q_{s}} (\infty ) = 11.6006\), so that the associated standard deviation is 3.41 (without \(\mathcal{{Q}}_2\), we would approximate the standard deviation by \(\sqrt{11} = 3.32\), so \(\mathcal{{Q}}_2\) contributes only \(3\,\%\) to the standard deviation approximation in this case).
By the SSC, the diffusion approximations for \(Q_1\) and \(Q_2\) are linearly related to \(Q_s\); in particular, \(\sigma ^2_{Q_{i}} (\infty ) = (p_i)^2 \sigma ^2_{Q_{s}} (\infty )\), so that \(\sigma ^2_{Q_{i}} (\infty ) = 11.6006/4 = 2.900\) and the associated standard deviation is 1.70.
We now turn to the simulations. We simulate the actual queueing system obtained by scaling up the appropriate parameters by \(n\). We consider three cases: \(n = 25,\; n = 100\), and \(n = 400\) (since \(k_{1,2}^n\) must be an integer, we let \(k_{1,2}^n = 3\) when \(n = 25\)).
In all our simulation experiments, we used five independent runs, each with 300,000 arrivals. We report averages together with the half widths of the 95 % confidence intervals, based on a \(t\) statistic with four degrees of freedom. Simulation results for the base case above are presented in Table 1 below.
The first four rows of Table 1 show mean values. We display both the steady-state mean values and the associated scaled values (i.e., divided by \(n\)). The unscaled values helps us evaluate the performance of the actual system, while the scaled values show the convergence in the FWLLN. Table 1 clearly shows that the accuracy improves as \(n\) gets larger, but even for relatively small systems, the fluid approximation gives reasonable results.
Rows 5–10 of Table 1 show the standard-deviations of the total queue length \(Q_{s} = Q_1+Q_2\) as well as the two queues. As before, we treat both the actual values and the scaled values, but now we are scaling in diffusion scale (dividing by \(\sqrt{n}\) after subtracting the order-\(O(n)\) mean), as in (15), so that we will be substantiating the FCLT, specifically Corollary 1 and the variance formulas in (24). To save space, we omit the confidence intervals for the scaled standard deviations; these can be computed from the confidence intervals of the actual queues by dividing the half widths by \(\sqrt{n}\).
Overall, we conclude that Table 1 shows that the approximations are remarkably accurate.
12 Conclusions and further research
In this paper we characterized the diffusion-limit refinements for the fluid limit of the X model operating under FQR-T. Establishing the weak limits is non-standard due to the effect of the stochastic AP, which contributes an additional Brownian term that is independent of all other terms in the diffusion equation.
There are many open problems and directions for future research, to which we hope to contribute. One extension, mentioned at the end of §4.2, is to establish limits for corresponding non-Markovian \(X\) models. A second extension is to establish asymptotic optimality for the FQR-T control within the optimization framework of [21], including a separable quadratic cost function, under which FQR-T was shown to be optimal for the fluid model. A third extension is to design corresponding overload controls for more complicated systems, possibly involving several customer classes and service pools. A fourth extension is to study the current system in a time-varying environment, in which arrival rates and/or staffing levels are assumed to be time-dependent. Finally, it remains to seek new applications of the AP. We anticipate that it will have many more applications in the future.
References
Abate, J., Whitt, W.: Limits and approximations for the busy-period distribution in single-server queues. Probl. Eng. Inf. Sci. 9, 581–602 (1995)
Arnold, L.: Stochastic Differential Equations: Theory and Applications. Wiley, New York (1974)
Asmussen, S.: Applied Probability and Queues, 2nd edn. Wiley, New York (2003)
Coffman, E.G., Puhalskii, A.A., Reiman, M.I.: Polling systems with zero switchover times: a heavy-traffic averaging principle. Ann. Appl. Probab. 5, 681–719 (1995)
Durrett, R., Resnick, S.I.: Functional limit theorems for dependent random variables. Ann. Probab. 6(5), 829–846 (1978)
Fricker, C., Robert, P., Tibi, D.: A degenerate central limit theorem for single resource loss systems. Ann. Appl. Probab. 13(2), 561–575 (2003)
Gans, N., Koole, G., Mandelbaum, A.: Telephone call centers: tutorial, review and research prospects. Manuf. Serv. Oper. Manag. 5, 79–141 (2003)
Garnet, O., Mandelbaum, A., Reiman, M.: Designing a call center with impatient customers. Manuf. Serv. Oper. Manag. 4(3), 208–227 (2002)
Glynn, P.W., Whitt, W.: Limit theorems for cumulative processes. Stoch. Process. Appl. 47, 299–314 (1993)
Gurvich, I., Whitt, W.: Scheduling flexible servers with convex delay costs in many-server service systems. Manuf. Serv. Oper. Manag. 11, 237–253 (2009)
Gurvich, I., Whitt, W.: Queue-and-idleness-ratio controls in many-server service systems. Math. Oper. Res. 34, 363–396 (2009)
Gurvich, I., Whitt, W.: Service-level differentiation in many-server service systems via queue-ratio routing. Oper. Res. 58, 316–328 (2010)
Halfin, S., Whitt, W.: Heavy-traffic limits for queues with many exponential servers. Oper. Res. 29(3), 567–588 (1981)
Hall, P., Heyde, C.C.: Martingale Limit Theory and Its Applications. Academic Press, New York (1980)
Hunt, P.J., Kurtz, T.G.: Large loss networks. Stoch. Process. Appl. 53, 363–378 (1994)
Karlin, S., Taylor, H.M.: A Second Course in Stochastic Processes. Academic Press, New York (1981)
Karr, A.F.: Weak convergence of a sequence of Markov chains. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 33, 41–48 (1975)
Latouche, G., Ramaswami, V.: Introduction to Matrix Analytic Methods in Stochastic Modeling. SIAM and ASA, Philadelphia (1999)
Lindvall, T.: Lectures on the Coupling Method. Wiley, New York (1992)
Pang, G., Talreja, R., Whitt, W.: Martingale proofs of many-server heavy-traffic limits for Markovian queues. Probab. Surv. 4, 193–267 (2007)
Perry, O., Whitt, W.: Responding to unexpected overloads in large-scale service systems. Manag. Sci. 55(8), 1353–1367 (2009)
Perry, O., Whitt, W.: A fluid approximation for service systems responding to unexpected overloads. Oper. Res. 59(5), 1159–1170 (2011)
Perry, O., Whitt, W.: An ODE for an overloaded X model involving a stochastic averaging principle. Stoch. Syst. 1, 17–66 (2011)
Perry, O., Whitt, W.: A fluid limit for an overloaded X call center via a stochastic averaging principle. Math. Oper. Res. 38 (2013) (articles in advance online, December 20, 2012)
Salminen, P., Norros, I.: On busy periods of the unbounded Brownian storage. Queueing Syst. 39, 317–333 (2001)
Rootzen, H.: On the functional central limit theorem for Martingales. Zeit. Wahrscheinlichkeitsth. werv. Gebiete 38, 199–210 (1977)
Talreja, R., Whitt, W.: Heavy-traffic limits for waiting times in many-server queues with abandonment. Ann. Appl. Prob. 19(6), 2137–2175 (2009)
Whitt, W.: Comparing counting processes and queues. Adv. Appl. Prob. 13(1), 207–220 (1981)
Whitt, W.: On the heavy-traffic limit theorem for GI/G/infinity queues. Adv. Appl. Probab. 14(1), 171–190 (1982)
Whitt, W.: Asymptotic formulas for Markov processes with applications to simulation. Oper. Res. 40(2), 279–291 (1992)
Whitt, W.: Stochastic-Process Limits. Springer, New York (2002)
Whitt, W.: Efficiency-driven heavy-traffic approximations for many-server queues with abandonments. Manag. Sci. 50(10), 1449–1461 (2004)
Acknowledgments
This research is part of the first author’s doctoral dissertation in the IEOR Department at Columbia University. Additional work was done subsequently, including while the first author had a postdoctoral fellowship at CWI in Amsterdam. This research was partly supported by NSF Grants DMI-0457095, CMMI 0948190 and CMMI 1066372.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Perry, O., Whitt, W. Diffusion approximation for an overloaded X model via a stochastic averaging principle. Queueing Syst 76, 347–401 (2014). https://doi.org/10.1007/s11134-013-9363-9
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11134-013-9363-9
Keywords
- Averaging principles
- Many-server queues
- Heavy-traffic limits
- Diffusion limits
- Functional central limit theorem
- Overload control