If structured propositions are logical procedures then how are procedures individuated?

Abstract

This paper deals with two issues. First, it identifies structured propositions with logical procedures. Second, it considers various rigorous definitions of the granularity of procedures, hence also of structured propositions, and comes out in favour of one of them. As for the first point, structured propositions are explicated as algorithmically structured procedures. I show that these procedures are structured wholes that are assigned to expressions as their meanings, and their constituents are sub-procedures occurring in executed mode (as opposed to displayed mode). Moreover, procedures are not mere aggregates of their parts; rather, procedural constituents mutually interact. As for the second point, there is no universal criterion of the structural isomorphism of meanings, hence of co-hyperintensionality, hence of synonymy for every kind of language. The positive result I present is an ordered set of rigorously defined criteria of fine-grained individuation in terms of the structure of procedures. Hence procedural semantics provides a solution to the problem of the granularity of co-hyperintensionality.

1 Introduction

It is good and well that we philosophers of language and logicians invoke structured meanings as cornerstones of our respective semantic theories. But, first, what is the structure of structured meanings? And, second, how are structured meanings individuated? In this paper, I am going to investigate structured procedures in the role of structured linguistic meanings. The framework I will use is Tichý’s transparent intensional logic (TIL) that comes with a procedural semantics, according to which the structured meaning of an expression is explicated as a procedure that produces at most one object, which is denoted by the expression.¹ In well-defined cases procedures fail to produce anything, which reflects the fact that there are meaningful terms that do not refer to anything, like ‘the greatest prime number’. When an object is produced, the produced object is a possible-world semantic (PWS) intension in the case of empirical expressions, and an extension in the case of logical/mathematical expressions, or a (lower-order ‘displayed’) procedure, which is especially the case with the complements of hyperintensional attitudes. These procedures are rigorously defined in TIL as so-called constructions. The main points I will be arguing for below are these two:

• Structured meanings are procedurally structured. TIL constructions are procedurally structured wholes that are assigned to expressions as their meanings, and their constituents are sub-procedures occurring in executed mode (as opposed to displayed mode).

• There is no universal criterion of the structural isomorphism of meanings, hence of co-hyperintensionality, hence of synonymy for every kind of language.² Though the individuation of TIL constructions is rigorously defined, the individuation of structured meanings does not coincide seamlessly with the individuation of constructions. The positive result of this paper is that we can put forward an ordered set of rigorously defined criteria of fine-grained individuation in terms of procedural structure. Hence procedural semantics offers a principled solution to the problem of the granularity of co-hyperintensionality.

My starting point is provided by King (2014, p. 1).

It is a truism that two speakers can say the same thing by uttering different sentences, whether in the same or different languages. For example, when a German speaker utters the sentence ‘Schnee ist weiß’ and an English speaker utters the sentence ‘Snow is white’, they have said the same thing by uttering the sentences they did. Proponents of propositions hold that, speaking strictly, when speakers say the same thing by means of different declarative sentences, there is some (non-linguistic) thing, a proposition, that each has said.

The question that many logicians and philosophers have been worried about is what kind of object is this ‘same thing’, the ‘proposition’, that sentences can have in common. The two sentences ‘Schnee ist weiß’ and ‘Snow is white’ in the quote by King certainly have the same meaning, hence they are synonymous: the same thing they have in common is their meaning. Logically or analytically equivalent sentences also have something in common, though they may fail to be synonymous. For instance, sentences of the form “It is not true that if A then B” and “A and not B” are logically equivalent, yet I take it to be obvious that they do not have the same meaning. Otherwise we would not have to teach students how to negate implicative sentences: linguistic competence would do. These two sentences share the same truth-conditions: whenever one is true, so is the other.³

Propositions should arguably perform many other functions in addition to being bearers of truth or falsity and being the things expressed by declarative sentences. They are commonly thought to be:⁴

• the meanings of sentences

• the objects that can be true or false

• the objects that are necessary, possible, or contingent, that is, bearers of modal properties

• the objects that can be true with a certain likelihood or to a certain degree, that is, bearers of probabilities or fuzzy degrees of truth

• the complements of propositional attitudes, that is, objects that can be understood, known, believed, desired, etc.

• the informational content of sentences

Obviously, one and the same ‘thing’ can hardly play all of these roles. Thus, several conceptions of propositions have been developed. While PWS-propositions modelled as functions from possible worlds and times to truth-values are the objects that can be true or false at this or that world and time, true to a certain degree, and arguably also objects that are necessary, (merely) possible or contingent, they are not the structured meanings of sentences, because as set-theoretical mappings they are not structured. Furthermore, they are too coarse-grained to serve as meanings in the first place, and as the complements of explicit propositional attitudes (which the agents are aware of having and can manipulate logically, as when acquiring inferential knowledge), because they are individuated only up to analytical equivalence.⁵ Moreover, in Duží (2010) it has been shown that PWS-propositions cannot be bearers of the so-called analytic information content of sentences, because if they were the paradox of inference would be inevitable and analytically true sentences would convey no information and thus be useless.⁶

One straightforward way to accommodate both fine-grained, structured propositions and coarse-grained, flat PWS-propositions within one and the same theory is to operate with two different levels with the former at the top and the latter ones below. This is the way we proceed in TIL. At the top, hyperintensional level, we explicate fine-grained propositions as algorithmically structured procedures that are assigned to sentences as their meanings. At the lower, intensional level are the PWS-propositions produced by these procedures as their products.

One might wonder what kind of an object our abstract structured procedure is, and what motivates us to explicate meanings as structured procedures. As for the former, let me say this. Procedures are neither set-theoretical mappings (Church’s functions-in-extension), nor properties or types. Rather, they might be compared to functions-in-intension, as suggested by Church in (1941, pp. 2–3). To anticipate a possible misunderstanding, note that in the semantics of mathematics, the terms ‘function-in-intension’ and ‘function-in-extension’ are used in this sense: function-in-extension corresponds to the modern notion of a function as a set-theoretical mapping, and function-in-intension could arguably correspond to our notion of procedure producing a mapping. Thus function-in-intension is a structured way or rule laying down how to obtain a function-in-extension. Only I am hesitant to push the parallel, since function-in-intension remains a poorly-understood notion. See also Church (1956, pp. 2–3).

Maybe the best explanation of the character of abstract procedures is provided in Duží et al. (2010, §1.3, pp. 54–56). Briefly, abstract procedures are generalized algorithms, as suggested in Moschovakis (1994, 2006), see also van Lambalgen and Hamm (2004). In Moschovakis (2006) a procedure is an “(abstract, idealized, not necessarily implementable) algorithm” (2006, p. 27). Algorithms are normally understood to be effectively computable.⁷ But not every procedure can be evaluated in an effective way. This is in particular the case of procedures that are assigned as meanings to empirical expressions. Their evaluation calls for an ‘oracle’ that supplies empirical facts.⁸ For the most recent account of abstract procedures, I agree with Jespersen (2017a) which characterizes procedures in this way:

[${\ldots }$] I identify structured propositions with particular kinds of objective logical (as opposed to, say, psychological or pragmatic) molecular procedures whose parts are sub-procedures (as opposed to entities such as mountains or numbers). The underlying logic is a typed function/argument logic that specifies which functions of which logical types are lined up to be applied to which arguments of which types to obtain values (if any) of which types. [${\ldots }$] Though modelled on a function/argument logic, procedures are not functions-in-extension, i.e., mappings. Nor are they set-theoretic sequences, nor, for that matter, the formulae of a symbolic notation. Instead they are Platonic, higher-order, fine-grained structures. Procedures, as I understand them, are neither set-theoretic, nor inscriptional, nor linguistic entities. They are mereological entities, because they are wholes with parts. Furthermore, procedures are governed by a mereology that cannot be fully extensional, because their parts interact with one another.

As for the latter question, i.e. the motivation to explicate the meanings of sentences, or generally of any linguistic terms, procedurally, I’d like to refer to Duží (2014a). To summarise the main ideas, there are two main reasons. The first one is obvious. That the structured meaning of a sentence cannot be a possible-world semantics proposition (PWS-proposition) should be obvious. A PWS-proposition is a set of possible worlds (and times); in this set, there is no trace of the structure of the respective sentence. For instance, Westerhoff (2005) criticizes the opinion that possible-world semantics is a proper tool for explaining the semantics of structures:

Consider the sense in which states of affairs (possible worlds) could be taken to have parts. It is straightforward to argue that the state of affairs that John loves Becca has John as a part. But it is equally straightforward to argue that John’s brain is part of the state of affairs that John loves Becca. But the mere parts (John’s brain as opposed to John) are just any parts of that particular bit of the world we happen to be talking about, whether they take part in our conceptualization or not. (Ibid., p.  609).⁹

The second argument is this. How is it possible that we are able to learn a (new) language? On its standard conception, a language is a (potentially) infinite set of expressions. In order to obtain such an infinity, we need a sequence of instructions detailing which operations to apply to which operands that would make it feasible to get to know any (as opposed to every) element of the infinite set in a finite number of operational steps. I am in favour of the idea that this sort of sequence of instructions is exactly the sort of structured procedure I have been talking about so far.

The procedural character of structured meanings in mathematics should be obvious. For instance, when one is seeking the solution of the equation sin(x) = 0 he/she is not related to the infinite set {..., $-2\uppi$, $-\uppi$, 0, $\uppi$, 2$\uppi$, ...}, because otherwise the seeker would immediately be a finder and there would be nothing to solve. On the other hand, relating the seeker to a particular syntactic term is not general enough. The Ancient Greek or Babylonian mathematicians, for instance, would solve such an equation using a different syntactic system. Rather, the seeker is related to the very procedure consisting of these constituents: applying the function sine to a real number x, checking whether the value of the function is zero, and, if so, abstracting over the value of the input number x. When solving the equation, the seeker aims to execute this procedure to potentially produce the infinite set of multiples of $\uppi$.

For an empirical example, consider the sentence “The Pope is a Pole”. The sentence encodes an instruction how, in any possible world w at any time t, to evaluate its meaning procedure producing the reference of the sentence at the world w and time t of evaluation, i.e., a truth-value. This instruction consists of a few simple steps: take the individual office Pope; take the property of being a native of Poland; extensionalize the papal office, i.e., find out empirically who (if anybody) is the Pope at the world w and time t of evaluation (if there is no such individual, then finish with no truth-value); and finally, check (empirically) whether the individual occupying the papal office is a native of Poland in the world w and time t of evaluation; if so, produce the truth-value T, otherwise F.

One might object that procedures cannot be true or false, and thus procedurally structured hyperpropositions cannot be intrinsically connected with truth-conditions.¹⁰ But the same objection would be applicable to sentences themselves. A sentence is a piece of syntax endowed with meaning. Neither a piece of syntax, nor a PWS-proposition understood as a set of worlds and times, is true or false. What then does it mean that, for instance, the sentence “The Pope is a Pole” is true or false, or, as the case may be, has a truth-value gap? There is no mystery, however. It means that the evaluation of its procedural meaning in a given state-of-affairs as described above yields a truth-value or no truth-value. If evaluating the meaning procedure of the sentence “The Pope is a Pole” in the actual world in the period between October 16, 1978 and April 2, 2005, one obtains T. If evaluating after April 2 and before April 19, 2005, one obtains a truth-value gap. Later on, one obtains F.

Hence hyperpropositions that are typed to produce PWS-propositions, or truth-values in the case of mathematics, unambiguously produce truth-conditions, or truth-values, upon being executed, and in this way, they are intrinsically connected with truth-conditions. Hence, this objection has little purchase.

Thus, I take it for granted that formal semantics demands a notion of hyperintensionality and that meanings of sentences, or generally of any expressions, are structured procedures. The focus of my research below is to put forward a formally precise and philosophically persuasive theory of fine-grained, structured meanings.

My background theory is TIL, as set out in Tichý (1988) and Duží et al. (2010). The formal apparatus of TIL will be fairly familiar to those who are acquainted with typed $\lambda$-calculi or Montague’s IL system¹¹, because from the formal point of view TIL is a hyperintensional, partial, typed $\lambda$-calculus. It is partial, because we embrace properly partial functions; and hyperintensional, because TIL terms are interpreted procedurally, which is to say that they denote abstract procedures (roughly, Church’s functions-in-intension) producing set-theoretical functions/mappings (Church’s functions-in-extension) rather than the mappings themselves. This is actually in good harmony with the original interpretation of the terms of the $\lambda$-calculus, which was indeed procedural. For instance, Barendregt (1997, p. 184) says,

[I]n this interpretation the notion of a function is taken to be intensional, i.e., as an algorithm.

I would prefer to say, “... is taken to be hyperintensional”, because the term ‘intensional’ is currently reserved for mappings from possible worlds (if not among proof-theoretic semanticists, then at least among model-theoretic semanticists).

Thus, $\lambda$-Closure, [$\lambda x_{1}$...$x_{n} X$], transforms into the very procedure of producing a function by abstracting over the values of the variables $x_{1}$, ..., $x_{n}$. Similarly, Composition, [$X X_{1}$...$X_{n}$], transforms into the very procedure of applying a function produced by the procedure X to the tuple-argument (if any) produced by the procedures $X_{1}$, ..., $X_{n}$. The procedural semantics of TIL makes it possible to explicitly deal with those features that are otherwise hidden if dealing only with the products of the procedures, i.e. functions-in-extension. These features concern in particular operations in a hyperintensional context where the very procedure denoted by a term is being operated on. For instance, if Tilman calculates the cotangent of the number $\uppi$, he is not related to a non-existing number. He is related to the procedure of applying the function cotangent to the number $\uppi$, aiming to uncover the product of this procedure. And even if the function cotangent were defined at this number, it still makes no sense to compute a number without any procedure specifying how to obtain that number. Hence the procedure of applying the cotangent function at the number $\uppi$ is here the object of predication, making the context of calculating a hyperintensional one. In TIL we strictly distinguish between procedures producing set-theoretical functions and the functions (-in-extensions) themselves (including sets and atomic objects such as truth-values, numbers and individuals viewed as zero-place functions). Not to lose one’s way in this stratified ontology all entities (including procedures) receive a type within a ramified hierarchy of types.

The rest of this paper is organised as follows. In Sect. 1 I introduce the relevant basic principles and definitions of TIL. Section  2 introduces the three kinds of context, namely hyperintensional, intensional and extensional ones, in which a TIL construction can occur. Section  3 deals with the mereological structure of TIL constructions. In Sect.  4 I deal with the problem of the individuation of structured procedures and the problem of synonymy. Section  5 contains some concluding remarks.

2 Basic principles of TIL

As mentioned above, the terms of the TIL symbolism denote abstract procedures that produce set-theoretical mappings (functions-in-extension) or lower-order procedures. These procedures are defined as TIL constructions.

Definition 1

(Construction)

• (i) Variables x, y, ... are constructions that construct objects (elements of their respective ranges) dependently on a valuation v; they v-construct.

• (ii) Where X is an object whatsoever (even a construction), $^{0}X$ is the construction Trivialization that constructsXwithout any change of X.

• (iii) Let $X, Y_{1}$, ..., $Y_{n }$ be arbitrary constructions. Then Composition [$X Y_{1}{\ldots } Y_{n}$] is the following construction. For any v, the Composition [$X Y_{1}{\ldots }Y_{n}$] is v-improper if at least one of the constructions$X, Y_{1}, {\ldots }, Y_{n}$ is v-improper by failing to v-construct anything, or if Xdoes not v-construct a function that is defined at the n-tuple of objects v-constructed by $Y_{1}$,...,$Y_{n}$. If Xdoes v-construct such a function, then [$X Y_{1}{\ldots }Y_{n}$] v-constructs the value of this function at the n-tuple.

• (iv) ($\lambda$-) Closure [$\lambda x_{1}{\ldots }x_{m} Y$] is the following construction. Let $x_{1}, x_{2}, {\ldots }, x_{m}$ be pair-wise distinct variables and Ya construction. Then [$\lambda x_{1}{\ldots }x_{m} Y$] v-constructs the function f that takes any members $B_{1}, {\ldots }, B_{m }$ of the respective ranges of the variables $x_{1}, {\ldots }, x_{m }$ into the object (if any) that is $v(B_{1}/x_{1},{\ldots },B_{m}/x_{m})$constructed by Y, where $v(B_{1}/x_{1},{\ldots },B_{m}/x_{m})$ is like v except for assigning $B_{1}$ to $x_{1}, {\ldots }, B_{m}$ to $x_{m}$.

• (v) Where X is an object whatsoever, $^{1}\!X$ is the construction Single Execution that v-constructs what X v-constructs. Thus, if X is a v-improper construction or not a construction as all, $^{1}\!X$ is v-improper.

• (vi) Where X is an object whatsoever, $^{2}X$ is the construction Double Execution. If X is not itself a construction, or if Xdoes not v-construct a construction, or if X v-constructs a v-improper construction, then $^{2}\!X$ is v-improper. Otherwise $^{2}$X v-constructs what is v-constructed by the constructionv-constructed by X.

• (vii) Nothing is a construction, unless it so follows from (i) through (vi).$\square$

Comments Being procedural objects, constructions can be executed in order to operate on input objects (of a lower-order type) and produce the object (if any) they are typed to produce, while non-procedural objects, i.e. non-constructions, cannot be executed. Hence the constituents of constructions cannot be non-procedural objects; non-procedural objects must be presented, or referred to, by atomic constructions. Trivialization and Variables are the two atomic constructions that present input objects (which can also be lower-order constructions) to be operated on. The operational sense of Trivialization is similar to that of constants in formal languages. A Trivialization presents an object X without the mediation of any other procedures. Using the terminology of programming languages, the Trivialization of $X, `^{0}X$’ in symbols, is just a pointer referring to X. Variables produce objects dependently on valuations; they v-construct. We adopt an objectual variant of the Tarskian conception of variables. To each type (see Def. 2) are assigned countably many variables that range over this particular type. Objects of each type can be arranged into infinitely many sequences. The valuation v selects one such sequence of objects of the respective type, and the first variable v-constructs the first object of the sequence, the second variable v-constructs the second object of the sequence, and so on. Hence the execution of a Trivialization or a variable never fails to produce an object; these constructions are not v-improper for any valuation v. The ($\lambda$-) Closure [$\lambda x_{1}{\ldots }x_{m} Y$] is also not v- improper for any v, as it always v-constructs a function. Even if the constituent Y is v-improper for every valuation v, the Closure is not v-improper. Yet in such a case the constructed function is a bizarre object; it is a degenerate function that lacks a value at any argument. However, the other molecular constructions, namely Composition, Single and Double Execution, can fail to present an object of the type they are typed to produce, they can be v-improper. The main source of improperness is an application of a function to an argument at which the function is not defined.¹²

With constructions of constructions, constructions of functions, functions, and functional values in our stratified ontology, we need to keep track of the traffic between multiple logical strata. The ramified type hierarchy does just that. The type of first-order objects includes all non-procedural objects. Therefore, it includes not only the standard objects of individuals, truth-values, sets, functions, etc., but also functions defined on possible worlds (i.e., the intensions germane to possible-world semantics). The type of second-order objects includes constructions of first-order objects and functions with such constructions in their domain or range. The type of third-order objects includes constructions of first- and second-order objects and functions with such constructions in their domain or range; and so on, ad infinitum.

Definition 2

(Ramified hierarchy of types). Let B be a base, where a base is a collection of pair-wise disjoint, non-empty sets. Then:

T$_{1 }$(types of order 1).

• (i) Every member of B is an elementary type of order 1 over B.

• (ii) Let $\upalpha , \upbeta _{1}$,..., $\upbeta _{m} (m >0)$ be types of order 1 over B. Then the collection ($\upalpha \upbeta _{1 }\ldots \upbeta _{m})$ of all m-ary partial mappings from $\upbeta _{1} \times \ldots \times \upbeta _{m}$ into $\upalpha$ is a functional type of order 1 over B.

• (iii) Nothing is a type of order 1 over B unless it so follows from (i) and (ii).

C$_{n}$(constructions of order n)

• (i) Let x be a variable ranging over a type of order n. Then x is a construction of order n over B.

• (ii) Let X be a member of a type of order n. Then ${^{0}}\!{X}, {^{1}}\!{X}, {^{2}}\!{X}$ are constructions of order n over B.

• (iii) Let $X, X_{1},\ldots , X_{m} (m > 0)$ be constructions of order nover B. Then [$X X_{1}\ldots X_{m}$] is a construction of order n over B.

• (iv) Let $x_{1},\ldots , x_{m}, X (m > 0$) be constructions of order nover B. Then [$\lambda x_{1}\ldots x_{m} X$] is a construction of order n over B.

• (v) Nothing is a construction of order n overB unless it so follows from C$_{n}$ (i)–(iv).

T$_{n+1 }$(types of order n + 1)

Let *$_{n}$ be the collection of all constructions of order nover B. Then

• (i) *$_{n}$ and every type of order n are types of order n + 1.

• (ii) If $m>$ 0 and $\upalpha , \upbeta _{1}, \ldots , \upbeta _{m}$ are types of order n + 1 over B, then ($\upalpha \upbeta _{1} \ldots \upbeta _{m})$ (see T$_{1}$ ii)) is a type of order n + 1 over B.

• (iii) Nothing is a type of order n + 1 over B unless it so follows from (i) and (ii).$\square$

For the purposes of natural language analysis, we are assuming the following base of ground types:

o: the set of truth-values {T, F};

$\upiota$: the set of individuals (the universe of discourse);

$\uptau$: the set of real numbers (doubling as discrete times);

$\upomega$: the set of logically possible worlds (the logical space).

We model sets and relations by their characteristic functions. Thus, for instance, (o $\upiota )$ is the type of a set of individuals, while (o $\upiota \upiota )$ is the type of a relation-in-extension between individuals. Empirical expressions denote empirical conditions that may or may not be satisfied at the particular world/time pair of evaluation. These empirical conditions are modelled as possible-world-semantic (PWS) intensions. PWS intensions are entities of type ($\upbeta \upomega )$: mappings from possible worlds to an arbitrary type $\upbeta$. The type $\upbeta$ is frequently the type of the chronology of $\upalpha$-objects, i.e., a mapping of type ($\upalpha \uptau )$. Thus $\upalpha$-intensions are frequently functions of type (($\upalpha \uptau )\upomega )$, abbreviated as ‘$\upalpha _{\uptau \upomega }$’. Extensional entities are entities of a type $\upalpha$ where $\upalpha \ne$ ($\upbeta \upomega )$ for any type $\upbeta$. Where w ranges over $\upomega$ and t over $\uptau$, the following logical form essentially characterizes the logical syntax of empirical language: $\lambda w\lambda t [{\ldots }w{\ldots }.t{\ldots }]$.

Examples of frequently used PWS intensions are: propositions of type o$_{\uptau \!\upomega }$, properties of individuals of type (o$\upiota )_{\uptau \! \upomega }$, binary relations-in-intension between individuals of type (o$\upiota \upiota )_{\uptau \!\upomega }$, individual offices (or roles) of type $\upiota _{\uptau \!\upomega }$, attitudes to constructions of type ($\mathrm{o}\upiota *_{n})_{\uptau \! \upomega }$.

Logical objects like truth-functions are extensional: $\wedge$ (conjunction), $\vee$ (disjunction) and $\supset$ (implication) are of type (o o o), and $\lnot$ (negation) of type (o o). Below all type indications will be provided outside the formulae in order not to clutter the notation. The outermost brackets of the Closure will be omitted whenever no confusion arises. Furthermore, ‘$X/\upalpha$’ means that an object X is (a member) of type $\upalpha . `X \rightarrow _{v} \upalpha$’ means that X is typed to v-construct an object of type $\upalpha$, if any. We write ‘$X \rightarrow \upalpha$’ if what is v- constructed does not depend on a valuation v. Throughout, it holds that the variables $w \rightarrow _{v} \upomega$ and $t \rightarrow _{v} \uptau$. If $C \rightarrow _{v} \upalpha _{\uptau \! \upomega }$ then the frequently used Composition [[Cw]t], which is the intensional descent (a.k.a. extensionalization) of the $\upalpha$-intension v-constructed by C, will be encoded as ‘$C_{wt}$’. Whenever no confusion arises, we use traditional infix notation without Trivialisation for truth-functions and the identity relation, to make the terms denoting constructions easier to read.

3 Displayed versus executed constructions

Here I go through the two modes in which constructions (procedures) can occur, either displayed or executed. This distinction is a crucial ingredient of my account of the constituents of structured propositions, as they themselves are also procedures.

When a construction occurs displayed, then the construction itself becomes the object on which other constructions can operate; we say that it occurs hyperintensionally. When a construction occurs executed, then the product of the construction is the object to operate on.¹³ In this case the executed construction is a constituent of its super-construction, and an additional distinction can be found at this level. The constituent presenting a function may occur either intensionally (de dicto) or extensionally (de re). If intensionally, then the produced function is the object of predication; if extensionally, then the value of the produced function is the object of predication. The two distinctions, between displayed/executed and intensional/extensional occurrence, enable us to distinguish between three kinds of context. The rigorous definitions of the three kinds of contexts can be found in Duží et al. (2010, §2.6). The exact details are rather complicated, though the basic ideas are fairly simple. Thus, here I only explain the main ideas, with the rigorous definition of displayed vs. executed occurrence of a construction coming afterwards.

• Hyperintensional context a construction occurs in displayed mode (though another construction at least one order higher needs to be executed in order to produce the displayed construction)

• Intensional context a construction occurs in executed mode in order to produce a function rather than its value (moreover, the executed construction does not occur within another hyperintensional context)

• Extensional context a construction occurs in executed mode in order to produce a particular value of a function at a given argument (moreover, the executed construction does not occur within another intensional or hyperintensional context).

The basic idea underlying the above trifurcation is that the same set of logical rules applies to all three kinds of context, but these rules operate on different complements: procedures, produced functions, and functional values, respectively. Having defined the three kinds of context, we are thus in a position to build up TIL as an extensional logic of hyperintensions.¹⁴

The analysis of the meaning of an expression consists in furnishing the expression with the construction encoded by it. The meaning of an empirical sentence is a construction that is typed to produce a PWS-proposition, and the meaning of a mathematical/logical sentence is a construction that is typed to produce a truth-value. If a construction C is typed to produce a truth-value ($C\rightarrow _{v}\mathrm{o}$) or a PWS-proposition ($C \rightarrow _{v}\mathrm{o}_{\uptau \! \upomega }$) then C is a hyperproposition.

When assigning a construction to a sentence (or generally to a piece of language), we apply a three-step method of analysis. First, we assign types to the objects that receive mention in the sentence. Second, we combine constructions of these objects so that to obtain a hyperproposition that constructs the PWS-proposition or a truth-value denoted by the sentence. Finally, we apply type-theoretical control to check whether the resulting hyperproposition is composed in a type-theoretically coherent way. To this end, we often draw a derivation tree; yet the tree is not the structure, it is just a graphic representation of the hyperpropositional structure.

Since the distinction between executed and displayed occurrence of a construction plays a significant role in particular in attitudinal sentences, I will use as a paradigmatic example the attitude of calculating. When a calculates something, for instance $2+5$ or cotangent of the number $\uppi$, a is not related to the number 7 or to a non-existing number, respectively. It makes no sense to calculate a number without any mathematical operation. Rather, a is related to the very procedure expressed by the terms ‘$2+5$’ or ‘cotangent of $\uppi '; a$ wants to find out what the procedure in question produces. Thus, Calculate is of type ($o\upiota *_{1})_{\uptau \! \upomega }$: relation-in-intension of an individual to a construction of a number. Here is the analysis of the sentence “Tom calculates the cotangent of $\uppi$” followed by its derivation tree accompanied by type assignments.

• (i) Typeanalysis.Tom/$\upiota$; Calculate/($o \upiota *_{1})_{\uptau \! \upomega }$; Cot(angent)/($\uptau \uptau ); \uppi /\uptau$.

• (ii) Synthesis. In order to apply the relation-in-intension Calculate to its two arguments, we have to extensionalize it first: [[$^{0}{} \textit{Calculate\, w}] t$], or $^{0}$Calculate$_{wt}$ for short. Since Tom is related to the very procedure [$^{0}{} { Cot}\,{^{0}}{\uppi }$] of applying the function Cotangent to the number $\uppi$ rather than to its non-existing product, the Composition [$^{0}$Cot${^{0}}{\uppi }$] must be Trivialized in order to become displayed: $^{0}[^{0}$Cot ${^{0}}{\uppi }$]. The agent, Tom, also must be pinpointed by Trivialization, as explained above. Thus, we have [$^{0}$Calculate$_{wt}$$^{0}$Tom$^{0}$[$^{0}$Cot $_{ }{^{0}}{\uppi }$]] $\rightarrow _{v }o$. Finally, abstracting over the values of the variables w, t, we construct the PWS-proposition denoted by the sentence: $\lambda w \lambda t [^{0}$Calculate$_{\,wt}$$^{\,0}{} \textit{Tom}$$^{0}[^{0}$Cot ${^{\,0}}{\uppi }]] \rightarrow _{v }o_{\uptau \! \upomega }$

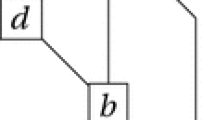
• (iii) Derivation tree.

The resulting type is the type of a PWS-proposition.

Note that the types of the objects that the constructions $^{0}\!\uppi , ^{0}$Cot and [$^{0}$Cot  ${^{0}}{\uppi }$] are typed to produce (i.e., $\uptau$, ($\uptau \uptau )$ and $\uptau$, respectively) are irrelevant here. This is since Composition [$^{0}$Cot  $_{ }{^{0}}{\uppi }$] occurs here only displayed as an argument of the relation $^{0}$Calculate$_{wt}$. In any world w and time t, the evaluation of the truth-conditions of the analysed sentence amounts just to checking whether Tom does calculate Cotangent of $\uppi$, i.e. the execution of the Composition

[${^{0}}$Calculate$_{wt}$$^{0}$Tom$^{0}$[$^{0}$Cot$_{ }\,{^{0}}{\uppi }$]];

yet execution of this Composition does not involve the execution of the procedure [$^{0}$Cot$^{\,\,0}\uppi$]; this is the futile activity Tom is trying to do.

To put these ideas on more solid grounds, we define:

Definition 3

(Subconstruction). Let C be a construction. Then

• (i) C is a subconstruction of C.

• (ii) If C is $^{0}\!X, ^{1}\!X$ or $^{2}\!X$ and X is a construction, then X is a subconstruction of C.

• (iii) If C is [$X X_{1}{\ldots }X_{n}$] then X, $X_{1}, {\ldots }, X_{n}$ are subconstructions of C.

• (iv) If C is [$\lambda x_{1} {\ldots }x_{n} Y$] then Y is a subconstruction of C.

• (v) If A is a subconstruction of B and B is a subconstruction of C then A is a subconstruction of C.

• (vi) A construction is a subconstruction of C only if it so follows from (i)–(v).$\square$

As mentioned above, it is important for our theory of procedurally structured constructions that a construction can be not only executed as a procedural whole to produce an object (if any) but can itself figure as an argument or value of a function produced by another construction of a higher order. Yet the constituents of a construction are not the particular material or abstract objects that the construction operates on. Rather, the constituents are only those sub-constructions that occur in executed mode; those that occur as objects to be operated on are displayed as arguments or values. To define the distinction between displayed and executed mode, we must take the following into account:

• a construction C can occur in displayed mode only as a subconstruction of another construction D that operates on C;

• C itself has, therefore, to be constructed by another subconstruction $C'$ of D; and

• it is necessary to define this distinction for occurrences of constructions, because one and the same construction Ccan occur executed in D and at the same time serve as an input/output object for another subconstruction $C'$ of D that operates on C.

The distinction between displayed and execution mode of a construction is characterised as follows, with a rigorous definition following afterwards.

Displayed versus executed subconstruction Let C be a subconstruction of a construction D. Then an occurrence of Cisdisplayed in D if the execution of D does not involve the execution of this occurrence of C. Otherwise, an occurrence of Cis executed in D and C occurs as a constituent of D.

A simple example to illustrate the situation. Consider this argument.

The conclusion is obviously unreasonable, and probably even nonsensical, for how could anybody be calculating anything in the absence of an arithmetical operation? The reason why the substitution within the first premise based on the identity specified by the second premise is invalid is this. There is a substantial difference between using the term ‘2 + 5’ in the first and the second premise. The first premise expresses Tilman’s relation(-in-intension) to the very procedure of applying the function plus to the arguments 2 and 5. Tilman is trying to execute this procedure, and the procedure, which is the meaning of ‘2 + 5’, is displayed as an argument of calculating in the first premise. The evaluation of the truth-conditions expressed by the first premise consists in any possible world w at any time t in checking whether Tilman is in the extensionalized relation of calculating to the procedure of adding 2 and 5. Hence the execution of the hyperproposition expressed by the first premise does not involve the execution of the procedure of adding 2 and 5; this is something Tilman is responsible for. On the other hand, in the second premise the procedure of adding 2 and 5 is executed to identify the result with the number 7.

The analyses of premises P$_{1}$, P$_{2 }$ are:

P$_{1}$: $\lambda w\lambda t [^{0}$Calculate$_{wt}$$^{0}$Tilman$^{0}[^{0}+^{0}2\,^{0}5]] \,\,\,\,\,\,\,/*_{2}, \rightarrow \quad$ o$_{\uptau \! \upomega }$

P$_{2}$: [$^{0}\!\!= [^{0}+\,^{0}2\, ^{0}5]\, ^{0}7] \,\,\,\,\,\,\,/*_{1}, \rightarrow \quad$ o.

Types: Tilman/$\upiota$; Calculate/(o$\upiota$*$_{1})_{\uptau \! \upomega }$; +/($\uptau \uptau \uptau )$; 2, 5, 7/$\uptau$; =/(o$\uptau \uptau )$.

It should be obvious that the identity specified by P$_{2}$, namely the identity of the number presented by the Trivialization $^{0}$7 and by the Composition [$^{0}\!+\,^{0}2\,^{0}5$], does not make the substitution of $^{0}$7 for the Trivialization $^{0}[^{0}+\,^{0}2\,^{0}5$] in P$_{1}$ possible. Such a substitution would constitute a type-theoretical category mistake, attempting as it would to substitute an entity of one type for an entity of another type, because $^{0}$7 constructs the number 7 while $^{0}[^{0}\!+\,^{0}2\,^{0}5$] constructs the Composition [$^{0}\!+\,^{0}2 \,^{0}5$]. This goes to show that the occurrence of [$^{0}\!+\,^{0}2 \,^{0}5$] is displayed in the P$_{1}$ premise by another constituent of P$_{1}$, namely the Trivialization $^{0}[^{0}+\,^{0}2 \,^{0}5$], whereas it is executed in P$_{2}$. This particular occurrence of $^{0}[^{0}+\,^{0}2 \,^{0}5$], in turn, occurs executed in P$_{1}$.

The execution steps specified by P$_{1}$, i.e., the constituent parts of P$_{1}$, are as follows.

• (1) $\lambda w\lambda t [^{0}$Calculate$_{wt}$$^{0}$Tilman$^{0}$[$^{0}+^{0}$2 $^{0}$5]]

• (2) $\lambda t$ [$^{0}$Calculate$_{wt}$$^{0}$Tilman$^{0}$[$^{0}+^{0}$2 $^{0}$5]]

• (3) [$^{0}$Calculate$_{wt}{} ^{0}$Charles$^{0}$[$^{0}+^{0}$2 $^{0}$5]]

• (4) $^{0}$ Calculate $_{wt}$

• (5) [$^{0}$Calculate w]

• (6) $^{0}$ Calculate

• (7) w

• (8) t

• (9) $^{0}$ Tilman

• (10) $^{0}$[$^{0}+^{0}$2 $^{0}$5]

Note that each construction is a part of itself, hence the Closure (1) is a constituent of itself. The other constituents are proper parts of (1). The Composition [$^0\!\!+\,^{0}2\,^05$] is not a part of (1), it occurs displayed in (1) as an object on which the other constituent parts operate.

Constructions are displayed by Trivialization. As the above examples illustrate, all the subconstructions of a displayed construction occur displayed as well. A context in which a construction occurs displayed is a hyperintensional context. It might seem that in order to define rigorously the distinction between displayed and executed occurrence it would suffice to say that a construction occurs displayed if it occurs within the scope of a Trivialization. Alas, matters are more complex than that. The complicating factor is this. Trivialization has a dual operation, namely Double Execution. It follows from Definition 2, (vi) that while Trivialization raises the context to the hyperintensional level, Double execution cancels the effect of Trivialization, because this law is valid: $^{20}C = C$. Therefore, the effect of Trivialization is voided by Double Execution.

Thus, we define:

Definition 4

(Displayed vs. executed occurrence of a construction) Let C be a construction and Da subconstruction of C.

• (i) If D is identical to C then the occurrenceofDis executed inC.

• (ii) If C is identical to [$X_{1} X_{2}$...$X_{m}$] and D is identical to one of the constructions $X_{1}$, $X_{2}$,..., $X_{m}$, then the occurrence of D is executedinC.

• (iii) If C is identical to [$\lambda x_{1}$...$x_{m} X$] and D is identical to X, then the occurrence of D is executed in C.

• (iv) If C is identical to $^{1}\!X$ and D is identical to X, then the occurrence of D is executed inC.

• (v) If C is identical to $^{2}\!X$ and D is identical to X, or $^{0}\!D$ occurs executed in X and this occurrence of D occurs executed in $Y \quad v$-constructed by X, then the occurrence of D is executed in C.

• (vi) If an occurrence of D is executed in C’ and this occurrence of C’ is executed in C, then the occurrence of D is executed inC.

• (vii) If an occurrence of a subconstruction D of C is not executed in C then the occurrence of D  is displayed inC.

• (viii) No occurrence of a subconstruction D of C is executed/displayed in C unless it so follows from (i)–(vii).

Remark

If a construction D is displayed in C then all the variables occurring in D are Trivialization-bound in C, i.e. bound by Trivialization. Proof follows from Definition 4; if D is displayed in C then there is a construction $D^\prime$ such that $^{0}D^\prime$ is, and $D^\prime$ is not, executed as a constituent of C, and D is a subconstruction of $D^\prime$.

Definition 5

(Constituent part of a construction) Let C be a construction and D a subconstruction of C. Then any occurrence of D is a constituent part of C if the occurrence is executed in C.

Corollary

Since a construction C occurs executed in itself (as per Def. 4, i), C is a constituent part of C. Other subconstructions of C occurring in the execution mode (as per Def. 4, ii, iii, iv, v) are proper constituent parts of the construction C.

Claim 1

The relation of being a constituent part of a construction is a partial order on the collection of constructions.

Proof

• (a) Reflexivity follows immediately from Def. 4, (i)

• (b) Transitivity follows immediately from Def. 4, (vi)

• (c) Antisymmetry Suppose that $C_{1}$ is a part of $C_{2}$ and $C_{2}$ is a part of $C_{1}$, and $C_{1}$ is not identical with $C_{2}$. Then Def. 4, i) is not applicable. Hence $C_{1}$ is a proper part of $C_{2}$ and $C_{2}$ is a proper part of $C_{1}$. This contradicts the corollary of Def. 5, because none of the items (ii), (iii), (iv) and (v) of Def. 4 is applicable. Hence $C_{1}$ is identical to $C_{2}$.

Definition 6

(Atomic and molecular constructions). A construction is atomic if it does not contain any other constituents but itself. If a construction has at least one proper constituent part, then the construction is molecular.

Corollary

A construction C is atomic if C is

• a variable, or

• a Trivialization $^{0}X$, where X is an object of any type, even a construction

• a Single execution $^{1}\!X$ where X is an object of a type of order 1, that is, X is not a construction

• a Double execution $^{2}\!X$ where X is an object of a type of order 1, that is, X is not a construction.

4 On the mereological structure of constructions

Above we saw that each construction is a structured whole with unambiguously determined constituent parts. Moreover, each construction can be executed as a whole to yield at most one object, and each construction can itself figure as a whole object on which other constructions operate. That an atomic construction is a whole is trivially true, because an atomic construction is a constituent part of itself (Def. 4, i). Now the question arises what unifies the proper parts of a molecular construction. The proper constituents of a molecular construction interact by producing functions and their values. The product of one or more constituents becomes an argument of the function produced by another constituent. If one or more constituents fail to produce an object (that is, if they are v-improper) the whole construction which is typed to operate on this object fails as well (that is, the whole construction comes out v-improper), because the process of producing an output object has been interrupted. Hence, constructions (or procedures in general) are not mere aggregates of their proper parts. The elements of an aggregate lack ‘direct connection inter se’ even when they are organised in an ordered sequence or list. And direct connection inter se is exactly what makes something parts of a whole.¹⁵

A simple example to illustrate the interaction in question. The Composition [$^{0}\!+\,^{0}$2 $^{0}$5] is the procedure of applying the function + to the couple of numbers 2 and 5 (in this order) to produce the value of + at this couple. Using programming-language jargon, the execution of this procedure can be described as follows. Since the constituent part $^{0}$+ is composed with $^{0}$2 and $^{0}$5, it calls the other two constituent parts, $^{0}$2, $^{0}$5, to yield their respective products, namely the numbers 2 and 5, so that the couple (2, 5) can serve as the argument of the function + produced by $^{0}$+. In this way, the execution of the whole Composition produces the value of the function + at the argument (2, 5), to wit, the number 7.¹⁶

Similarly, the Closure $\lambda x$[$^{0}+x^{0}$1], when executed, produces the successor function. Again, using programming jargon, it is a procedure with the formal parameter x. Whenever the actual argument n is substituted for x into the procedural ‘body’ [$^{0}\!+x^{0}$1], the body produces n’s successor, the number $n+1$. Since this process can be executed for any number n, by abstracting over the values of n the mapping from naturals to their successors is produced.

Now we can compare the structure of abstract procedures (TIL constructions) with Classical Extensional Mereology (CEM). Cotnoir (2013) recapitulates the three main principles of CEM as follows.

Extensionality If x and y have the same mereological make-up, then x and y are identical.

Antisymmetry If x is part of y and y part of x, then x and y are identical.

Idempotency If x is a proper part of y, then the sum of x and y is identical to y.

The principle of antisymmetry has been proved in Claim 1.

The principle of idempotency can be formulated like this. It is not possible to add a further occurrence of a proper part x to y, because any such ‘addition’ would be ‘swallowed up’ by the existing occurrence of x. In other words, one thing cannot be part of the same whole twice or more times over. This seems to be a valid principle for material entities, but obviously does not hold for abstract entities such as structured procedures. One and the same constituent sub-construction can occur twice or more times in a whole construction. A simple example: the Composition [$^{0}\!\!+\, ^{0}$2 $^{0}$2] of applying the addition function + to the couple (2, 2) has two occurrences of the part $^{0}$2.¹⁷ Moreover, we cannot simply add another proper part to an unambiguously determined structured whole. If we wish to iterate a part (i.e. add another instance of a part already found in the whole), we must also determine the way this additional part is composed with the other parts; this addition makes for another construction. For a simple example, consider the constructions A, $B \rightarrow$ o that are typed to produce a truth-value. Then the constructions [$A \supset B$], [[$A \wedge A$] $\supset B$] are not identical, though they are equivalent by producing the same truth-value. These two Compositions are two distinct procedures, because the latter instructs us to process a conjunction whereas the former contains just one of the conjuncts. The truth-conditional idempotency between A and [$A \wedge A$] is irrelevant to the absence of mereological idempotency between them.

Extensionality, as expressed by “Same parts = same whole”, is in classical mereology of material objects a subject of much dispute.¹⁸ In this paper I am disregarding the mereology of concrete entities, such as bronze statues and the chunks of bronze they are made of, and focusing on the mereology of abstract logical procedures. In the mereology of abstract procedures (TIL constructions, in my case), the principle of extensionality is trivially valid if it is applied both to proper and improper parts, because it is tantamount to reflexivity, as has been proved above. The stronger principle

“The same proper parts = the same whole”

is, however, not valid. The failure of the stronger extensionality axiom was obvious already to Bernard Bolzano. In his (1837) Bolzano shows that the mere sum of the components of the content of a concept does not define the concept.¹⁹ We have to take into account the way of composing these components.²⁰ Bolzano worked out a systematic realist theory of concepts (Vorstellungenan sich), construing concepts as objective entities endowed with structure. Our theory is continuous with this conception. Traditional theories of concepts built on the Port Royal school define a concept as a couple consisting of an extension (Umfang) and an intension (Inhalt, or content). The intension of a concept Cis the sum of features or sub-concepts $C_{1}$,...,$C_{n}$, while the extension of Cis the intersection of the sets of objects having these features by falling under the sub-concepts $C_{1}$,...,$C_{n}$. Thus, the so-called Law of inverse proportion of extension and intension (the more components in the intension, the fewer elements in the extension, and vice versa) is valid within the framework of Port Royal logic. For instance, the extension of the concept Prague inhabitants is greater than that of Prague inhabitants speaking German. Bolzano criticizes this Law in (1837: §120). He adduces an example of a pair of concepts for which the Law is not valid.

• 1. A man who understands all European languages

• 2. A man who understands all living European languages

The first concept contains fewer components than the second one but (contra the Law) its extension is smaller than the extension of the second concept. This is due to the fact that the actual-world set of all European languages that ever existed, currently exist or once will exist is greater than the set of all living (i.e. currently spoken) European languages, hence there are fewer people falling under this more exacting concept. By this example, Bolzano wants to show that the way of composing particular components is important. The classical Port Royal theory of concepts presupposes only a conjunctive method of composition.²¹ The ‘sum’ of the components of an intension is meant as their conjunctive connection. Then, of course, the Law is an elementary consequence of set theory. However, if the way of composing is not conjunctive, the Law does not hold. For instance, the Law holds for the concepts expressed by ‘Prague citizens speaking Czech’ and ‘Prague citizens speaking Czech and German’. However, it obviously does not hold for the concepts expressed by ‘Prague citizens speaking Czech’ and ‘Prague citizens speaking Czech or German’.

Not only that; Bolzano also shows that a concept is not the same thing as its intension/content. As an example, Bolzano considers two mathematical concepts, 3$^{5}$ and 5$^{3}$. These concepts have exactly the same proper parts, namely the respective concepts of the numbers 3 and 5, and the concept of the power function. Yet 3$^{5}$ and 5$^{3}$ are different concepts. This is due to the fact that the procedure of raising 3 to the power of 5 is different from the procedure of raising 5 to the power of 3.

$^{0}$[$^{0}$Power $^{0}$3 $^{0}$5] $\ne \, ^{0}$[$^{0}$Power $^{0}$5 $^{0}$3]

TypesPower/($\uptau \uptau \uptau )$; 3,5/$\uptau$; [$^{0}$Power $^{0}$3 $^{0}$5], [$^{0}$Power $^{0}$5 $^{0}$3]/*$_{1 }\rightarrow \uptau$; $^{0}$[$^{0}$Power $^{0}$3 $^{0}$5]/*$_{2} \rightarrow$ *$_{1}$; $^{0}$[$^{0}$Power $^{0}$5 $^{0}$3]/*$_{2} \rightarrow$ *$_{1}$; $\ne$/(o*$_{1}$*$_{1})$: the relation of not being identical between constructions of order 1.

Even if constructions $C_{1}$ and $C_{2 }$ produce the same object and have the same proper parts, they can be non-identical. For instance, according to Def. 1, Compositions [$^{0}\!+\,^{0}$2 $^{0}$5] and [$^{0}\!+\,^{0}$5 $^{0}$2] are not identical, though they consist of the same proper parts and produce the same number:

[$^{0}\!+\, ^{0}$2 $^{0}$5] = [$^{0}\!+\, ^{0}$5 $^{0}$2]

but

$^{0}$[$^{0}\!+\, ^{0}$2 $^{0}$5] $\ne$$^{0}[^{0}\!+\, ^{0}$5 $^{0}2]$

Types +/($\uptau \uptau \uptau )$; 2,5/$\uptau$; [$^{0}+\,$$^{0}2$  $^{0}5$], [$^{0}+\,$$^{0}5$  $^{0}2$]/*$_{1} \rightarrow \uptau$; =/(o$\uptau \uptau ); ^{0}[^{0}\!+\, ^{0}2\,\, ^{0}5], ^{0}[^{0}+\, {^{0}5}\,\, {^{0}2}]/*_{2} \rightarrow *_{1}; \ne /(o*_{1}*_{1})$.

Again, this is as it should be. The respective meanings of the terms ‘$2+5$’ and ‘$5+2$’ are insufficient in order to prove that they are equivalent. It must, furthermore, be proved that the addition function is commutative, using, for instance, the axioms of Peano arithmetic.

5 Hyperintensionality and inferences

As mentioned above, the basic idea underlying our distinction between the three kinds of context in which a construction can occur is that the same set of logical rules applies to all three kinds of context, but these rules are properly applicable to objects of different types. In an extensional context, the relevant objects are the values of the constructed functions; in an intensional context, the produced functions themselves; and in a hyperintensional context, the constructions themselves.

The rules that operate in an extensional or intensional context are easy to specify, for instance, in the standard manner of the $\lambda$-calculi, because in an intensional context equivalent constructions are substitutable, that is, constructions v-constructing the same object for every valuation v.²² However, applying logical rules into a hyperintensional context is far from being straightforward. The technical complications we are confronted with are rooted in displayed constructions, because a displayed construction cannot at the same time be executed. The original motivation for hyperintensionality was a negative one. Whenever substitution of logically/analytically equivalent terms fails, the context was declared hyperintensional. Thus, the main reason for introducing hyperintensionality was originally to block various inferences that were argued on philosophical grounds to be invalid. Naturally, the converse question arises as to which arguments involving hyperintensional contexts are valid. I am going to deal with these two issues now.

5.1 Invalid inferences

Consider this argument:²³

$$\begin{aligned} \frac{\hbox {Tilman is seeking his brother}}{\hbox {Tilman is seeking his male sibling}} \end{aligned}$$

Is this argument valid? In my opinion, it is not. Tilman can be seeking his brother without him seeking his male sibling, though both ‘male sibling of’ and ‘brother of’ denote one and the same attribute.²⁴ To get the example of Tilman seeking his brother and not seeking his male sibling off the ground, I am stipulating that ‘is a brother of’ and ‘is a male sibling of’ are a pair not of synonymous but merely equivalent predicates. Their respective meanings are co-intensional, but not co-hyperintensional. The rationale for this stipulation is that the latter predicate has a molecular structure thanks to the application of the modifier denoted by ‘male’ to the attribute denoted by ‘sibling’, whereas the former predicate is atomic.²⁵ Hence this is a case where the mode of presentation of one and the same intension matters.²⁶ In this case an intensional analysis will yield a contradiction, because Tilman would be related, and at the same time not related, to one and the same property by the seeking relation.²⁷

Here is the proof of the contradiction. First, the property to which Tilman is related is constructed by this Closure: $\lambda w\lambda t [^{0}$Brother_of$_{wt }\,\,^{0}$Tilman]. Thus, the analysis of the premise is this construction:²⁸

$\lambda w\lambda t [^{0}$Seek$_{wt }\,\,^{0}$Tilman $\lambda w\lambda t [^{0}$Brother_of$_{wt }\,\,^{0}$Tilman]]

Types: Seek/(o$\upiota$(o$\upiota )_{\uptau \!\upomega })_{\uptau \!\upomega }$: the relation-in-intension of an individual to a property the instance of which the seeker wants to find; Tilman/$\upiota$; Brother_of/((o$\upiota )\upiota )_{\uptau \! \upomega }$: attribute, i.e., an empirical function associating an individual with a set of individuals, his or her brothers.

The proof of the contradiction is this:

• (1) $\lambda w\lambda t$ [$^{0}$Seek$_{wt }\,\,^{0}$Tilman $\lambda w\lambda t$[$^{0}$Brother_of$_{wt }\,\,^{0}$Tilman]] $\varnothing$

• (2) $\lambda w\lambda t \lnot [^{0}$Seek$_{wt }\,\,^{0}$Tilman $\lambda w\lambda t$[[$^{0}$Male $^{0}$Sibling_of]$_{wt }\,\,^{0}$Tilman]] $\varnothing$

• (3) [$^{0}$Seek$_{wt }\,\,^{0}$Tilman $\lambda w\lambda t$[$^{0}$Brother_of$_{wt }\,\,^{0}$Tilman]] $\lambda$-elimination, 1)

• (4) $\lnot [^{0}$Seek$_{wt }\,\,^{0}$Tilman $\lambda w\lambda t$[[$^{0}$Male $^{0}$Sibling_of]$_{wt }\,\,^{0}$Tilman]] $\lambda$-elimination, 2)

• (5) [$\lambda w\lambda t$[[$^{0}$Brother_of]$_{wt }\,\,^{0}$Tilman] = $\lambda w\lambda t$[[$^{0}$Male $^{0}$Sibling_of]$_{wt }\,\,^{0}$Tilman]] $\varnothing$

• (6) [$^{0}$Seek$_{wt }\,\,^{0}$Tilman $\lambda w\lambda t$[[$^{0}$Male $^{0}$Sibling_of]$_{wt }\,\,^{0}$Tilman]] Leibniz’s Law, 3, 5)

• (7) Contradiction! 4, 6, $\wedge$I

Additional types. Sibling_of/((o$\upiota )\upiota )_{\uptau \! \upomega }$; Male/(((o$\upiota )\upiota )_{\uptau \! \upomega }$((o$\upiota )\upiota )_{\uptau \! \upomega })$: an attribute modifier.

To block the above invalid inference, a hyperintensional analysis must be applied. Here is how.

• (1) $\lambda w\lambda t$ [$^{0}$Seek*$_{wt }\,^{0}$Tilman $^{0}$[$\lambda w\lambda t$[$^{0}$Brother_of$_{wt }\,\,\,^{0}$Tilman]]] $\varnothing$

• (2) $\lambda w\lambda t \lnot [^{0}$Seek*$_{wt }\,^{0}$Tilman $^{0}$[$\lambda w\lambda t$[[$^{0}$Male $^{0}$Sibling_of]$_{wt }\,\,\,^{0}$Tilman]]] $\varnothing$

• (3) $\lnot [^{0}=\!*\, ^{0}[\lambda w\lambda t [^{0}$Brother_of$_{wt }$ $^{0}$Tilman]] $^{0}$[$\lambda w\lambda t$[[$^{0}$Male $^{0}$Sibling_of]$_{wt }{}^{0}$Tilman]]] $\varnothing$

Additional types Seek*/(o$\upiota$*$_{n})_{\uptau \! \upomega }$: the relation-in-intension of an individual to a construction of a property; =*/(o*$_{n}$*$_{n})$: the identity of constructions.

No contradiction arises. When construed hyperintensionally, Tilman’s search is only ostensibly inconsistent. One could object that it seems reasonable to assume that there is a meaning postulate in place to the effect that ‘is a brother of’ is shorthand for, or a notational variant of, ‘is a male sibling of’, the same way ‘lasts a fortnight’ is arguably short for ‘lasts two weeks’. Yet it is questionable what semantic and inferential gain may be accrued from introducing a redundant predicate as a mere notational variant of another predicate.²⁹ What speaks against this assumption, at least through the lens of TIL, is that the Trivialization $^{0}$Brother_of and the Composition [$^{0}$Male $^{0}$Sibling_of] are not co-hyperintensional but only equivalent constructions. Furthermore, the latter is a refinement of the former providing more analytic information than just the Trivialization of the attribute.³⁰

5.2 Valid inferences in hyperintensional contexts

Above I illustrated how invalid inferences can be blocked in hyperintensional contexts. But there is the other side of the coin, which is the positive topic of which inferences should be validated.

For instance, an argument like this:

$$\begin{aligned} \frac{{ Tilman }\,\, \mathrm{calculates}\,\, \mathrm{the}\,\, \mathrm{cotangent}\,\, \mathrm{of}\,\, \uppi }{\mathrm{There}\,\, \mathrm{is}\,\, \mathrm{a}\,\,\mathrm{number}\,\, x\,\, \mathrm{such}\,\, \mathrm{that}\,\, \mathrm{Tilman}\,\, \mathrm{calculates}\,\, \mathrm{the}\,\, \mathrm{cotangent}\,\, \mathrm{of}\,\, x} \end{aligned}$$

is obviously valid. Surely, if Tilman calculates the cotangent of $\uppi$, then there is such a number, namely the number $\uppi$, the cotangent of which Tilman calculates. But careless existential generalization into a hyperintensional context is not valid:

$$\begin{aligned} \frac{\lambda w\lambda t[^{0}{\textit{Calculate}_{wt}} {^{0}\!\textit{ Tilman\! }^{0}}[^{0}{} { Cot}^{\,0}\!\uppi ]]}{\lambda w\lambda t [^{0}\exists \lambda x [^{0}{{ Calculate}_{wt}} {^{0}\!\textit{Tilman \!}^{0}}[^{0}{} { Cot}\,x]]]} \end{aligned}$$

The reason is this. The Trivialisation $^{0}[^{0}$Cotx] constructs the Composition [$^{0}$Cotx] independently of any valuation v. Thus, from the fact that at $\langle w$, $t\rangle$ it is true that Tilman calculates [$^{0}$Cot  $^{0}\!\uppi$], we can not validly infer that Tilman calculates [$^{0}$Cotx], because Tilman calculates the cotangent of $\uppi$ rather than of an arbitrary value of x. Put differently, the variable xoccurring displayed in a hyperintensional context is not amenable to the logical operation of $\lambda$-binding, because it is bound by Trivialization (‘$^{0}$-bound’). In other words, the Composition [$^{0}$Cotx] is not a constituent of the whole construction. The problem just described of $\lambda x$ being unable to catch the occurrence of x inside the displayed construction is TIL’s way of phrasing the standard objection to quantifying-in (i.e. the impossibility of reaching across an attitude operator). Yet in TIL we are able to overcome this obstacle. To validly infer the conclusion, we need to apply our substitution method that pre-processes the Composition [$^{0}$Cotx] and substitutes the Trivialization of $\uppi$ for x. Only then can the conclusion be inferred. To this end we deploy the polymorphic functions Sub/(${*_n}\!*_{n}\!*_{n}\!*_{n})$ and Tr/($*_{n} \upalpha )$ defined as follows.

The function Sub of type ($*_{n}\!*_{n}\!*_{n}*_{n})$ operates on constructions in this way. When applied to constructions $C_{1},C_{2}, C_{3}$, Sub returns as its value the construction D that is the result of substituting $C_{1}$ for $C_{2}$ in $C_{3}$. The likewise polymorphic function Tr returns as its value the Trivialization of its argument.

For instance, if the variable x ranges over $\upiota$, the Composition [$^{0}$Tr x] v(John/x)-constructs $^{0}$John. Note one essential difference between the function Tr and the construction Trivialization. Whereas the variable x is free in [$^{0}$Tr x], the Trivialization $^{0}$x displays the variable x by constructing just x independently of valuation. Thus, for instance, the Composition

[$^{0}$Sub [$^{0}$Tr x]  $^{ 0}$him $^{0}[^{0}$Wife_of$_{wt}$   him]]

v(John/x)-constructs the Composition [$^{0}$Wife_of$_{wt} ^{\ 0}$John], while the Composition

[$^{0}$Sub $^{0}x^{ 0}$him $^{0}$[$^{0}$Wife_of$_{wt}$  him]]

constructs the Composition [$^{0}$Wife_of$_{wt} x$] independently of valuation.

Consequently, the following inference comes out valid:³¹

$$\begin{aligned} \frac{\lambda w\lambda t [^{0}{} { Calculate}_{wt}\, ^{0}{ Tilman }\ ^{0}[^{0}{} { Cot}^{\,\,0}\!\uppi ]]}{\lambda w\lambda t [^{0}\exists \lambda x [^{0}{} { Calculate}_{wt} \, ^{0}{ Tilman }\,\,[^{0}{} { Sub }[^{0}{} { Tr\, x}]\,\, ^{0}y \ ^{0}[^{0}{ Cot}\,y]]]]} \end{aligned}$$

Gloss. Since the variable x occurs free as a constituent of [$^{0}$Tr x], it v-constructs the Trivialization of the number v-constructed by x. Hence [$^{0}$Sub [$^{0}$Tr x] $^{0}y\,\, ^{\!0}$[$^{0}$Cot$_{ }y$]] v($\uppi$/x)-constructs the Composition [$^{0}$Cot   $_{ }^{0}\!\uppi$], to which Tilman is related according to the premise. For this reason, it follows from the premise that the class of numbers v-constructed by $\lambda x$[$^{0}$Calculate$_{wt}\, ^{0}$Tilman [$^{0}$Sub [$^{0}$Tr x] $^{\!0}y\, ^{\,0}$[$^{0}$Cot$_{\, }y$]]] is non-empty; the function $\exists$ can be validly applied.

Hence existential generalization into a hyperintensional context is just a technical issue that is easily solvable by our substitution method. Another fundamental rule that is universally valid and should thus be applicable even in hyperintensional contexts is Leibniz’s Law of indiscernibility of identicals, which translates into a rule of substitution of identicals. However, there is a philosophical rather than technical problem here. At the linguistic level, a hyperintensional context is such a context where the very meaning is the object of predication, and the problematic issue is the individuation of procedures. That is, how hyper are hyperintensionally individuated structured meanings? If there is one central question permeating hyperintensional logic and semantics then it is arguably this one.

There is a simple answer, which, unfortunately, also happens to be simplistic. Since we assign constructions to expressions as their meaning, then if a construction C occurs displayed in a hyperintensional context, then, trivially, an identical (not merely equivalent) construction is substitutable.³² So the answer is simplistic because trivial because self-substitution is trivially valid.

Example. Suppose that ‘cerulean’ and ‘azure’ are synonymous terms. Since synonymous terms have the same meaning, they express the same construction; thus, the Trivializations $^0$Cerulean/*$_{1} \rightarrow$ (o$\upiota )_{\uptau \! \upomega }$ and $^{0}$Azure/*$_{1} \rightarrow$ (o$\upiota )_{\uptau \! \upomega }$ are identical. One and the same property has been Trivialized, regardless of the name we use for that property.³³ Let now Believe*/(o$\upiota$*$_{n})_{\uptau \! \upomega }$ be a hyperintensional relation-in-intension of an individual to a hyperproposition (i.e., to a construction of the proposition). Then the following argument is valid:

$$\begin{aligned} \frac{\hbox {Tilman believes\,* that the Italian national football team wear azure shirts; Cerulean is azure}}{\hbox {Tilman believes\,* that the Italian national football team wear cerulean shirts}} \end{aligned}$$

The standard objection would be that the argument is not valid, because it can be true that Tilman believes that the shirts are azure without him believing them to be cerulean. But no, this is not possible. For sure, Tilman can assent to a sentence and fail to assent to another sentence, though the two sentences that report his attitude are synonymous but deploy two different predicates. But then the problem has to do with Tilman’s linguistic incompetence (be it a restricted vocabulary or failure to recognize a pair of synonyms). Richard’s principle of Transparency bears directly on this objection:

... It is impossible for a (normal, rational) person to understand expressions which have identical senses but not be aware that they have identical senses. (Richard 2001, pp. 546–7)

Hence the paradox of analysis is not a problem of hyperintensionality. Rather, it is a matter of linguistic incompetence and not of logical incompetence.

On the other hand, this example is from the logical point of view too trivial. It is obvious that identical constructions are always mutually substitutable, because there is nothing to substitute; there is just one construction.³⁴

At the linguistic level, strictly synonymous expressions (expressions encoding one and the same procedure) are substitutable in any hyperintensional context. Synonymy of semantically simple expressions is a matter of linguistics. Now we are, however, interested in the synonymy of complex expressions.³⁵ Since semantically complex expressions encode molecular procedures, the issue of synonymy of complex expressions transforms into the problem of the identity of their composed meanings, i.e., the problem of the identity of molecular procedures. To this end we introduce the relation of procedural isomorphism.

5.3 Procedural isomorphism and synonymy

For a simple example, consider the analysis of the sentence

“Tilman is solving the equation Sin(x)=0”

As explained at the outset, when solving this equation, Tilman is not related to the infinite set of multiples of the number $\uppi$, because then there would be nothing to solve: Tilman would have the solution straightaway. In his effort to solve the equation he is related to the very procedure

$\lambda x [^{0}= [^{0}$Sin x] $^{0}$0];

he wants to find out what the procedure produces. Hence, Solving is of the type ($\mathrm{o}\upiota *_{n})_{\uptau \! \upomega }$. The analysis amounts to this construction:

$\lambda w\lambda t [^{0}$Solving$_{wt }\,^{0}$Tilman$^{0}[\lambda x [^{0}= [^{0}$Sin x] $^{0}$0]]]

But couldn’t we equally well assign to the above sentence as its meaning the following construction?

$\lambda w\lambda t [^{0}$Solving$_{wt }\,^{0}$Tilman$^{0}[\lambda y [^{0}= [^{0}$Sin y] $^{0}$0]]]

Both constructions $\lambda x [^{0}= [^{0}$Sin x] $^{0}$0] and $\lambda y [^{0}= [^{0}$Sin y] $^{0}$0] seem to play the same procedural role in this hyperintensional context, because they are $\upalpha$-equivalent. When aiming to find the solution Tilman must perform these procedural steps:

• Take the function sine ($^{0}$Sin)

• Take any real number (x, or y, ...)

• Apply the sine function to this number to obtain its value ([$^{0}$Sin x]; or [$^{0}$Sin y]; ...)

• Compare the value with the number 0 ([$^{0}$= [$^{0}$Sin x] $^{0}$0]]; or [$^{0}$= [$^{0}$Sin y] $^{0}$0]]; ...)

• If the value is equal to zero, assign the number (x, y, ...) to the resulting set. In other words, abstract over the value of the variable ($\lambda x$, $\lambda y$, ...)

Any difference there might be between x, y, or any other variable ranging over the reals, does not translate into a procedural difference. This amounts to a distinction without a difference.³⁶

We furnish non-synonymous terms with different constructions, i.e., different procedures. Hence, two terms are synonymous if they express one and the same procedure. This is trivial, but the deep issue is this. From the semantic point of view constructions are in some cases too fine-grained so that their difference cannot be expressed in a given language. This is usually the case with $\lambda$-bound variables that are not used in an ordinary vernacular. We need a slightly less fine-grained criterion of synonymy in order to weed out certain distinctions without a semantic difference. My thesis is that synonymous expressions share structurally isomorphic meanings. Meaning being a procedure, we need to define the relation of procedural isomorphism holding between constructions.

The problem of how fine-grained hyperintensional entities, hence meanings, should be was important already for Carnap who introduced in (1947: §§13ff) the relation of intensional isomorphism. However, Church (1954) found a counterexample of two terms that are obviously not synonymous, yet intensionally isomorphic. Church himself considered several so-called Alternatives of how to constrain these entities so as to develop a notion of synonymous isomorphism.³⁷ Senses are identical if the respective expressions are (A0) ‘synonymously isomorphic’, (A1) mutually $\lambda$-convertible, (A2) logically equivalent. (A2), the weakest criterion, was refuted already by Carnap, and was not acceptable to Church, either. (A1) was considered to be the right criterion of synonymy. Yet it has been subjected to a fair amount of criticism, in particular due to the inclusion of unrestricted $\upbeta$-reduction (‘by name’). For instance, Salmon (2010) adduces examples of expressions that should intuitively not be taken to be synonymous, yet their meanings are mutually $\upbeta$-convertible.³⁸ Moreover, partiality throws a spanner in the works; $\upbeta$-conversion by name is not guaranteed to be an equivalent transformation as soon as partial functions are involved.³⁹ Church also considered Alternative (A1$^\prime$), which is (A1) plus $\eta$-convertibility. Yet $\eta$-convertibility is plagued by similar defects as those of $\upbeta$-convertibility by name. The alternative (A0) arose from Church’s criticism of intensional isomorphism, and it is synonymy resting on $\upalpha$-equivalence and meaning postulates for semantically simple terms. Of course, we need meaning postulates to fix synonymy for pairs of semantically simple terms (possibly even of different languages). Now we are, however, interested in the synonymy of molecular terms, which depends on structural isomorphism.⁴⁰

In TIL similar work has been done by Materna (1998, §5.3) and (2004, §1.4.2.2) where the relation of quasi-identity of closed constructions is defined. It includes $\upalpha$- and $\eta$- conversion. This criterion has been later coined procedural isomorphism and incorporated into Duží (2010) as Alternative (A ). Duží and Jespersen (2013) and Duží (2014b) put forward a new definition of the criterion of structured synonymy called (A ). It includes $\upalpha$-equivalence, $\eta$-equivalence, and so-called restricted $\upbeta _{r}$-conversion. Finally, in Duží and Jespersen (2015) and Duží (2014) alternative ($\hbox {A1}^{\prime \prime }$) is introduced. Close to Church’s (A1), it includes an adjusted version of $\upalpha$-conversion and $\upbeta$-conversion by value, while $\eta$-conversion is excluded. ($\hbox {A1}^{\prime \prime }$) arguably counts at present as the right calibration of procedural isomorphism, hence of co-hyperintensionality, from the point of view of TIL. However, there can be no such thing as a transcendental argument for the necessity and sufficiency of ($\hbox {A1}^{\prime \prime }$). It is perfectly conceivable, indeed likely that (A1$^{\prime \prime })$ is going to face cogent counterexamples.

It should be obvious now that the problem of co-hyperintensionality is not simple, and the question arises whether there is a unique universal solution. I am going to formulate several conditions that should be met by constructions Cand D in order for them to qualify as procedurally isomorphic, hence substitutable in hyperintensional contexts. Yet before doing so, let me summarize the definitions of particular conversions; $\upalpha$-conversion, $\upbeta$-conversion by name, and $\eta$-conversion are defined in the ordinary manner of the $\lambda$-calculi. In the TIL formalism they are as follows.⁴¹

${\varvec{\upalpha }}$-conversion. Constructions C and D are $\upalpha$-equivalent if they differ at most by using different $\lambda$-bound variables. Formally, let a construction Ycontain at most $x_{1}, {\ldots }, x_{n }$ as free variables. Then:

[$\lambda x_{1}{\ldots }x_{n} \quad Y$] ${{\Rightarrow }}_{\upalpha }\,\,[\lambda y_{1}{\ldots }y_{n} \quad Y(y_{1}/x_{1}{\ldots } y_{n}/x_{n})$]

where $Y(y_{1}/x_{1}{\ldots } y_{n}/x_{n})$ is the construction that arises from Y by collision-less substitution of $y_{1}$ for all the occurrences of $x_{1}, {\ldots }, y_{n}$ for all the occurrences of $x_{n}$, is $\upalpha$-conversion.

${\varvec{\upbeta }}$-conversion by name. Let $Y \rightarrow _{v}\,\, \upalpha$; $x_{1}$,$D_{1}\,\, \rightarrow _{v} \,\, \upbeta _{1}$,..., $x_{n}$,$_{ }D_{n }\rightarrow _{v }\upbeta _{n}$; [$\lambda x_{1}{\ldots }x_{n} \,\, Y] \rightarrow _{v }(\upalpha \upbeta _{1} \ldots \upbeta _{n})$. Then :

[[$\lambda x_{1}{\ldots }x_{n} \,\, Y] D_{1}{\ldots }D_{n}$] ${ \Rightarrow }_{\upbeta {\mathrm{n}} }\,\,\,Y(D_{1}/x_{1}{\ldots }D_{n}/x_{n})$,

where $Y(D_{1}/x_{1}{\ldots } D_{n}/x_{n})$ is the construction that arises from Y by collision-less substitution of $D_{1}$ for all the occurrences of $x_{1}, {\ldots }, D_{n}$ for all the occurrences of $x_{n}$, is $\upbeta$-conversion by name.

As a special case of $\upbeta$-conversion by name we define restricted${{\upbeta }}_{r}$-conversion. Let $Y \rightarrow _{v} \,\, \upalpha ; x_{1}, y_{1} \,\, \rightarrow _{v} \,\, \upbeta _{1},{\ldots }, x_{n},y_{n }\rightarrow _{v }\upbeta _{n;} [\lambda x_{1}{\ldots }x_{n} \,\, Y] \rightarrow _{v }(\upalpha \upbeta _{1} \ldots \upbeta _{n})$. Then :

[[$\lambda x_{1}{\ldots }x_{n} \,\, Y] y_{1}{\ldots }y_{n}$] ${{\Rightarrow }}_{\upbeta {\mathrm{r}} }\,\,\,Y(y_{1}/x_{1}{\ldots }y_{n}/x_{n})$,

where $Y(y_{1}/x_{1}{\ldots }y_{n}/x_{n})$ is the construction that arises from Y by collision-less substitution of $y_{1}$ for all the occurrences of $x_{1}, {\ldots }, y_{n}$ for all the occurrences of $x_{n}$, is restricted$\upbeta$-conversion by name.

Using the functions Sub and Tr introduced above, $\upbeta$-conversion by value is defined as follows.

${\varvec{\upbeta }}$ -conversion by value.

Let $Y \rightarrow _{v} \upalpha ; x_{1}, D_{1} \rightarrow _{v} \upbeta _{1},{\ldots }, x_{n},D_{n }\rightarrow _{v }\upbeta _{n}, [\lambda x_{1}{\ldots }x_{n} Y] \rightarrow _{v }(\upalpha \upbeta _{1} \ldots \upbeta _{n})$. Then

[[$\lambda x_{1}{\ldots }x_{n} Y] D_{1}{\ldots }D_{n}]\Rightarrow _{\upbeta v} {}^{2}[^{0}$Sub [$^{0}$Tr D$_{1}$] $^{0}x_{1}$ ... [$^{0}$Sub [$^{0}$Tr D$_{n}$] $^{0}x_{n }\,{^{0}Y}$]]

is $\upbeta$-conversion by value.

Duží and Jespersen (2015) proves that this conversion is strictly equivalent in the sense that for any valuation v the left-hand and right-hand side constructions v- construct the same object or both are v-improper, unlike unrestricted $\upbeta$-conversion by name.⁴²

${\varvec{\eta }}$-conversion. Let $Y\rightarrow _{v }(\upalpha \upbeta _{1} \ldots \upbeta _{n}); x_{1} \rightarrow _{v} \upbeta _{1},{\ldots }, x_{n }\rightarrow _{v }\upbeta _{n}$. Then:

[$\lambda x_{1}{\ldots }x_{n} [Y \,\, x_{1}{\ldots }x_{n}$]] ${{\Rightarrow }}_{\eta }\ Y$

is $\eta$-conversion.

Next, I put forward and assess several conditions to be met by constructions C and D in order to qualify as procedurally isomorphic, hence substitutable in hyperintensional contexts.

• (a) Strict equivalence; for any valuation v constructions C and $D\, v$-construct the same object or are both v-improper.

• (b) Constructions C and D have the same number of constituents.

Both conditions are met only by $\upalpha$-conversion and by meaning postulates. Condition (a) is met by $\upbeta _{\mathrm{r}}$-conversion (i.e. the restricted $\upbeta$-conversion by name that only substitutes variables for $\lambda$-bound variables of the same type) and by $\upbeta _{\mathrm{v}}$-conversion by value. However, both $\upbeta _{\mathrm{r}}$-conversion and $\upbeta _{\mathrm{v}}$-conversion by value do not meet condition (b). Finally, $\eta$-conversion fails to meet either of them.⁴³

It is a well-known fact that $\upbeta$-conversion by name does not preserve equivalence in a logic of partial functions. Yet the fact that $\eta$-conversion also does not preserve logical equivalence in a logic of partial functions such as TIL might be surprising. To see why, consider the following example. Let F v-construct a function of type (($\upalpha \upbeta )\gamma )$ that is not defined at the argument v-constructed by $A~\rightarrow _{v} \gamma$. Then the Composition [$F~A] \rightarrow _{v} (\upalpha \upbeta )$ is v-improper. However, the $\eta$-expanded construction $\lambda x~[[F~A]~x] \rightarrow _{v} (\upalpha \upbeta ), x \rightarrow \upbeta , v$-constructs a degenerate function, which is a function undefined at all its arguments. To be sure, due to the v-improperness of [F A] the Composition [[F A] x] is also v-improper. But $\lambda$-abstraction raises the context to an intensional one, hence the Closure $\lambda x~[[F~A]~x$] v-constructs a degenerate function, which is an object, if a bizarre one. Hence the constructions [F A] and $\lambda x~[[F~A]~x$] are not strictly equivalent.

We might formulate weaker requirements like the following two.

• (c) Weak equivalence; for any valuation v constructions C and $D\, v$-construct the same object, provided neither of them is v-improper.

• (d) Constructions C and D have the same number of closed constituents.

Both of these requirements are met by $\eta$-conversion, while $\upbeta$-conversion by name meets only (c). $\upbeta$-conversion by value meets, of course, (c) because it satisfies (a), but it does not meet (d).

However, if we postulated that the term ‘[[$\lambda x_{1}{\ldots }x_{n} \quad Y] D_{1}{\ldots }D_{n}$]’ is just a notational shorthand for ‘$^{2}[^{0}$Sub [$^{0}$Tr D$_{1}]\, ^{0}x_{1} \ldots [^{0}$Sub [$^{0}$Tr D$_{n}]\, ^{\,0}x_{n }{^{0}Y}$]]’, then $\upbeta$-conversion by value would trivially meet also the condition (d).⁴⁴ Such a notational convention is well justified, because conversion by value specifies the correct and proper way of executing the procedure of applying a function to its argument, unlike the $\upbeta$-conversion by name.

But then an adjusted version of $\upalpha$-conversion is called for. Consider, for instance, the constructions

[$\lambda x [^{0}\!+\,x {^{\,0}1}] \,{^{0}}{5}$] and [$\lambda y\, [{^{0}}\!\!+\!\!{y}\, {^{0}1}] ^{0}5$]

They are $\upalpha$-equivalent according to the standard definition. Yet their respective $\upbeta _{v}$-reduced forms

$^{2}[^{0}$Sub [$^{0}$Tr $^{0}5] ^{0}x ^{0}[{^{0}}\!+\,{x} {^{0}}{1}$]] and $^{2}[^{0}$Sub [$^{0}$Tr $^{0}5] ^{0}y ^{0}[^{0}\!+\,y ^{0}1$]]

would not be $\upalpha$-equivalent. Yet they ought to be, because from the procedural point of view it is irrelevant which bound variables are used as formal parameters of the respective procedure.

Thus, the adjusted version of ${ \upalpha }$-conversion is defined as follows. Let C, D be constructions. Then C, D are $\upalpha$-equivalent, if either C, D differ at most by using different $\lambda$-bound variables, or their $\upbeta _{\mathrm{v}}$-expanded forms differ at most by using different $\lambda$-bound variables.

Let us next reflect on meaning postulates. Above we wondered what semantic and inferential gain can be obtained from introducing a redundant predicate like ‘is a brother of’, on its construal as a mere notational variant of ‘is a male sibling of’, and we did not stipulate those terms to be synonymous. In my opinion, we can accept only very few meaning postulates for semantically simple terms as assigning to these simple terms complex synonymous terms. It is usually just the case of introducing a shorthand for something frequently used, like ‘fortnight’ for ‘a period of fourteen days’. In mathematics, it can be the case of introducing a new term as a shorthand for a long definition; for instance, ‘group’ for an ‘algebraic system consisting of a set, an identity element, one binary operation and its inverse operation’. Once we introduce such a shorthand into a language, the two terms become automatically synonymous. Yet a problem can arise that for one and the same mathematical object there are more non-synonymous definitions. For instance, ‘lattice’ can be defined either as a partially ordered set L such that every two-element subset of L has an infimum and supremum in L, or as an algebra with two binary operations meet and join satisfying the axioms of commutativity, associativity and absorption. Then we must decide which of them is the primary definition of ‘lattice’ and prove that the other one is just equivalent.⁴⁵

Now I am in the position to specify a series of criteria for procedural isomorphism partially ordered from the strongest (most restrictive) to the weakest (most liberal). Of course, there is no warranty that the list as specified below is exhaustive. Nonetheless, I provide good reasons for each of these criteria and specify conditions under which this or that criterion is applicable. Hence, when one needs to pick this or that criterion, he/she knows the conditions under which the criterion can be safely applied.

Where ‘MP’ abbreviates ‘meaning postulates’, the proposed criteria are as follows. First, I adduce the criteria that apply none or only one kind of conversion. Afterwards, I consider variants of applying more than one conversion.

C0   MP (and nothing else)

This is the most restrictive criterion that would be applicable in any language, provided the above specified conditions are met. Recall Mates’s puzzle and the paradox of analysis. As mentioned above, it is not a problem of hyperintensionality and synonymy; rather, it is a problem of linguistic competence.

C1   MP, $\upalpha$-conversion

This criterion is applicable in any non-professional, ordinary language where $\lambda$-bound variables are not explicitly used.

Yet, for instance, it cannot be carelessly applied in a functional programming language where a $\lambda$-bound variable plays the role of a formal parameter of a procedure for which an actual argument should be substituted when calling the procedure.

Consider, for instance, the easy procedure $\lambda x\, [^{0}+x\, {^01}], x \rightarrow _{v} \uptau ,$ computing the successor function. Whenever we call this procedure to compute the successor of a number n we must substitute this number n for the formal parameter x. If we applied $\upalpha$-conversion to this procedure, for instance, $\lambda y \,[^{0}+\,y {^{\,0}1}], y \rightarrow _{v} \uptau ,$ every calling procedure deployed to obtain the successor of the number n would have to be adjusted. Thus, in such a language $\lambda x [^{0}\!+\,x\, {^01}]$ is not procedurally isomorphic with $\lambda y\,[^{0}\!+\,y\, {^01}]$.

C2    MP, $\upbeta _{\mathrm{r}}$-conversion

This criterion is applicable in any non-professional, ordinary language where$\lambda$-bound variables are not explicitly used.

Yet, for instance, in a slightly more technical jargon $\upbeta _{\mathrm{r}}$-conversion is not applicable as a criterion of procedural isomorphism. For instance, is there any semantic difference between the following sentences?

• (1) “The president of the USA is a Republican”

• (2) “The holder of the office of President of the USA is a Republican”

• (3) “The president of the USA has the property of being a Republican”

• (4) “The holder of the office of President of the USA has the property of being a Republican”

In my opinion, there is. These sentences do not have, strictly speaking, the same meaning, though their respective analyses reveal that they express constructions that are just $\upbeta _{\mathrm{r}}$-equivalent. For instance, (1*) is a $\upbeta _{r}$-reduced form of (2*):

(1*)   $\lambda w\lambda t [^{0}$Republican$_{wt} [^{0}$President_of$_{wt}{}^{0}$USA]]

(2*)   $\lambda w\lambda t [^{0}$Republican$_{wt} \lambda w_{1}\lambda t_{1}[^{0}$President_of$_{w1t1}{}^{0}$USA]$_{wt}$]

Types.:

Republican/(o$\upiota )_{\uptau \! \upomega }$; President_of/($\upiota \upiota )_{\uptau \! \upomega }$; USA/$\upiota$; [$^{0}$President_of$_{wt}$$^{0}$USA] $\rightarrow _{\!v}\! \upiota$; $\lambda w_{1}\lambda t_{1}[^{0}$President_of$_{w1t1}$$^{0}$USA] $\rightarrow \upiota _{\uptau \! \upomega }$.

C3   MP, $\upbeta _{\mathrm{v}}$-conversion

This criterion is applicable in any language, provided we postulate, as proposed above, that the term ‘[[$\lambda x_{1}{\ldots }x_{n} Y] D_{1}{\ldots }D_{n}$]’ is just a notational shorthand for

‘$^{2}[^{0}$Sub [$^{0}$Tr D$_{1}]\, ^{0}x_{1} {\ldots } [^{0}$Sub [$^{0}$Tr D$_{n}]\, ^{0}x_{n }^{0}Y$]]’.

C4   MP, $\eta$-conversion

This criterion is not applicable in any logic of partial functions, because it does not preserve strict equivalence. In an ordinary language, the exclusion of $\eta$-conversion from the definition of procedural isomorphism might seem to be harmless. When analysing expressions in TIL we apply our method of literal analysis according to which semantically simple terms are furnished with the Trivialisation of the denoted object as their meaning. For instance, the literal analysis of “The Pope is wise” (when understood de re) is the Closure

$\lambda w\lambda t [^{0}$Wise$_{wt }{}^{0}$Pope$_{wt}$]

rather than the Closure

$\lambda w\lambda t [\lambda w\lambda t [\lambda x [^{0}$Wise$_{wt }x]]_{wt }{}^{0}$Pope$_{wt}$],

because the literal analysis of the predicate ‘is wise’ is the Trivialization $^{0}$Wise rather than the Closure $\lambda w\lambda t [\lambda x [^{0}$Wise$_{wt }x$]], which should be glossed as ‘is someone who is wise’ or ‘is one of the wise ones’. The types are Wise/(o$\upiota )_{\uptau \! \upomega }$; Pope/$\upiota _{\uptau \! \upomega }; x \rightarrow \upiota$. Yet the sentences “The Pope is wise” and “The Pope is one of the wise ones” can hardly be taken as strictly speaking synonymous, as the latter makes a detour via the population of wise individuals at the indices of evaluation.

C5   MP, $\upbeta _{\mathrm{n}}$-conversion

This criterion is in general not applicable in any logic of partial functions, because it does not preserve strict equivalence; nor is it applicable in an ordinary language, because we do use non-referring terms like ‘the King of France’. Moreover, as Duží and Jespersen (2013) shows, $\upbeta _{\mathrm{n}}$-conversion by name has other serious defects which include the loss of analytic information and non-effectiveness.

C6   MP, $\upalpha$-conversion, $\upbeta _{\mathrm{r}}$-conversion

The applicability rests on the assumptions as those of C1 and C2

C7   MP, adjusted $\upalpha$-conversion, $\upbeta _{\mathrm{v}}$-conversion

The applicability rests on the same assumptions as those of C1 and C3

C8   MP, adjusted $\upalpha$-conversion, $\upbeta _{\mathrm{r}}$-conversion, $\upbeta _{\mathrm{v}}$-conversion

The applicability rests on the same assumptions as those of C1, C2 and C3

C9   MP, adjusted $\upalpha$-conversion, $\upbeta _{\mathrm{r}}$-conversion, $\upbeta _{\mathrm{v}}$-conversion, $\eta$-conversion

The applicability rests on the same assumptions as those of C1, C2 and C3, provided semantically simple terms are analysed as mere references to the denoted object (i.e., Trivialization of the denoted object)

C10   MP, $\upalpha$-conversion, $\upbeta _{\mathrm{r}}$-conversion, $\upbeta _{\mathrm{v}}$-conversion, $\upbeta _{\mathrm{n}}$-conversion, $\eta$-conversion

The applicability rests on the same assumptions as those of C1, C2,C3, C9, provided properly partial functions are not involved

To illustrate mutual dependences and ordering of these criteria, here is a graph (in the form of a Hasse diagram).

To sum up, in an ordinary language without explicitly used $\lambda$-bound variables, the most liberal criterion for procedural isomorphism includes meaning postulates for semantically simple terms, adjusted $\upalpha$-conversion, $\upbeta _{\mathrm{r}}$-conversion, and $\upbeta _{\mathrm{v}}$-conversion, which is the criterion C8. The more technical the language, the less liberal a criterion can be applied, so that, at the other extreme, the most restrictive criterion includes just meaning postulates defining semantically simple terms (criterion C0). Criterion C9 is applicable, provided one strictly applies the method of literal analysis, i.e., provided semantically simple terms are conceived as mere references to the objects denoted by the terms. The most liberal criterion C10 is applicable only in a logic of total functions. Other variants combining particular conversions are thinkable, of course, yet, for an ordinary vernacular we recommend as the most suitable the criterion C8.

As a result, the rule of substitution of co-hyperintensional terms in hyperintensional contexts can be formulated only conditionally:

If constructions C, D are procedurally isomorphic per one of the existing criteria of procedural isomorphism thenC, D can be validly substituted within a hyperintensional context, provided the discourse has been so defined as to obey that particular calibration of procedural isomorphism.

The methodological take-home is that it is a philosophical and linguistic decision—not one based on pure logic—which sorts of discourse obey which calibrations of procedural isomorphism.

6 Conclusion

In this paper, I have discussed structured propositions explicated as algorithmically structured logical procedures. I have put forward a number of reasons in favour of a procedural semantics that furnishes expressions with meaning procedures encoded by those expressions. There are two issues I dealt with in this paper. The first one concerns the mereological structure of procedures, while the second one concerns the granularity of structured meaning procedures.

Concerning the former, I explicated the fundamental distinction between the occurrence of a procedure in the executed mode and the displayed mode. If a procedure occurs in the executed mode, then the procedure is a constituent part of another procedure (and of itself), while if a procedure occurs in the displayed mode, then the procedure itself figures as an object on which other procedures operate. Yet the input object(s) on which a procedure operates and the output object (if any) that a procedure produces are not constituent parts of the procedure. The constituent parts of a procedure are defined as those sub-procedures that occur in the executed mode. Thus, I have also demonstrated that procedures are structured wholes consisting of unambiguously determined parts, which are those sub-procedures each of which must be individually executed whenever the whole procedure is to be executed to produce at most one object. Moreover, I have proposed a solution to the problem of what unifies the proper parts of a molecular procedure. The proper constituents of a molecular procedure interact in the process of producing an object. The product of one or more constituents becomes an argument of the function produced by another constituent. If one or more constituents fail to produce an object, the whole procedure, which is typed to operate on an object of an already specified type, fails as well, because the process of producing an output object has been interrupted. Hence, procedures are not mere set-theoretical aggregates of their proper parts. The elements of an aggregate lack direct connection inter se, even when they are organised in an ordered sequence or list. And direct connection inter se is exactly what makes some things parts of a whole. As another novel result, I proved that this part-whole relation is a partial order. On the other hand, the mereology of structured procedures is non-classical, because the principles of extensionality and idempotence do not hold; and it is desirable that they should not, as already Bolzano demonstrated.

In the second part of the paper I dealt with the problem of co-hyperintensionality, and in general with the problem of valid inferences in a hyperintensional context, where such a context is defined in terms of a procedure occurring in the displayed mode. I demonstrated that the problem of validly applying extensional rules of inference (such as the rule of existential generalization and substitution of identicals) in a hyperintensional context is closely connected with the problem of the structural isomorphism of meanings, hence of co-hyperintensionality, hence of synonymy. I demonstrated that the individuation of procedures assigned to expressions as their structured meaning cannot be decided in virtue of a universal criterion applicable to every language. Yet, the positive result of this paper is that I have specified a set of rigorously defined criteria of fine-grained procedural individuation, partially ordered according to the degree of their being permissive with respect to synonymy. It turned out that the formalization of procedures in my background theory Transparent Intensional Logic (TIL) may become a bit too fine-grained from the point of view of the semantics of natural language. Yet the same problem must be met in any formalization that makes use of $\lambda$-bound variables, i.e. in any $\lambda$-calculus, because in an ordinary vernacular we do not use $\lambda$-bound variables. For this reason, I proposed a criterion that is the most suitable for an ordinary, non-professional language. It is the criterion that declares that procedural isomorphism of TIL constructions obtains whenever the differences between constructions consist just in technical manipulations with $\lambda$-bound variables. Thus, the rule of co-hyperintensionality (i.e. the rule for substitution of synonymous terms in hyperintensional contexts) has been formulated only conditionally.