1 Introduction

There has been a lot of research interest in analyzing chaotic systems and their possible cryptographic structures in recent years [1,2,3]. Specific cryptographic primitives behave in a way that is fundamentally similar to chaotic frameworks, which are described by their sensitivity to random operations and initial conditions in the vicinity [4,5,6]. Many remote clients exchange their details with one another due to the relative ease of using the Internet, and the widespread popularity of the Internet of Things (IoT) [7]. The mechanism of remote user authentication ensures that a remote server verifies the legitimacy of a user over an insecure or open communication channel [8,9,10]. It is crucial to verify the identity of remote clients in this situation. In order to address this issue, Lamport [11] suggested the first authentication procedure for use in open network channels in 1981. However, it is worth mentioning that the Lamport system allows the server to keep a verification table for remote clients.

Consequently, hackers could be able to access sensitive information. The password-enabled authentication procedure is an important technique for determining the authenticity of a remote user in a client/server environment [12,13,14,15]. For instance, Sun et al. [16] posit that password-supported authentication procedures have a significant flaw because humans are not specialists at memorizing text strings. As a result, even though they know that their passwords could be insecure, most users would likely select easy-to-remember passwords.

Researchers have recently suggested several biometric-based remote client authentication procedures [17,18,19,20]. The work in [17] in particular presented an improved biometric-based authentication procedure for telecare medicine information systems (TMIS) based on an elliptic curve cryptosystem. By comparison, the work in [18] projected an improved and robust biometrics-based three-factor authentication procedure for applications in multi-server environments. In a similar fashion to work in [18], a robust biometrics-based authentication procedure for a multi-server setting has been presented [19]. Due to Odelu et al. [20], the work presented a secure biometrics-based multi-server authentication procedure using smart cards. Essentially, the biometric system, based on pattern recognition, collects biometric data from an individual. The system accomplishes this by extracting and comparing a feature set from the information to a database template set [21,22,23,24]. According to Das [25], biometric keys have several advantages listed as follows. Biometric keys cannot be lost or forgotten. They are complicated to share or copy. They are also tough to distribute or forge, not easy to break, and cannot be guessed easily.

Additionally, biometric-supported remote client authentication procedures are highly efficient and safer than predictable password-based remote client authentication procedures. In 2014, Chuang et al. [26] introduced a trust computing-based anonymous multi-server authentication with key agreement procedure, leveraging smartcards and biometrics. According to Chuang et al. [26], the procedure is quite simple to use and allows for multi-server authentication and user anonymity. Later, in 2014 and 2015, Mishra et al. [27] and Lin et al. [28] examined Chuang et al. [26] procedure and found several flaws. In order to address these issues, they suggested a stable anonymous three-factor authentication procedure with superior capabilities. In 2015, Lu et al. [29] demonstrated that Mishra et al.’s [27] approach is highly vulnerable to replay attacks and includes an insecure password altering process. For multi-server architecture, they suggested a robust biometric-based authentication procedure.

In 2015, Mir et al. [30] projected an authentication procedure using Elliptic Curve Cryptography (ECC) for telemedicine networks. Also, Chaudhry et al. [31] demonstrated that Mir et al.’s procedure [30] is vulnerable to a misplaced smart card attack and fails to provide the required user anonymity. In 2016, Zhu [32] proposed a multi-server procedure for privacy security focused on chaotic map operations. However, their procedure is limited due to their vulnerability to a privileged insider attack. This is because an RC system insider operating as an attacker can guess a client's password using stored information on the client's device and registration appeal information throughout the registration process.

In 2018, Qi et al. [33] showed that Chaudhry et al.’s [31] procedure could not achieve the perfect forward secrecy and failed a denial-of-service attack. Qi et al. [33] proposed a new procedure to address the limitations inherent in Chaudhry et al.’s procedure [31]. It is worthy of note that the scheme due to Qi et al. [33] can withstand various attacks. Recently, Sahoo et al. [34] presented remarkable results that show the limitations of Qi et al.’s procedure. Sahoo et al. [34] noted that Qi et al.’s procedure [33] could not protect against the key compromise impersonation attack, known session-specific temporary information attack, and offline password guessing attack. In order to address these issues, Sahoo et al. [34] advised an enhanced new procedure based on ECC and demonstrating the strengths to resist various attacks. A summary of some related works is given in Table 1.

Table 1 Related works
Full size table

The preceding works of literature demonstrate that current biometric-empowered remote client authentication with key agreement procedures has varying security strengths and lower computational overheads. However, when exposed to several high-level adversarial attacks, most of the existing schemes show limited existential unforgeability.

Additionally, remote user authentication using biometric applications with key agreement procedures is critical to the design of future security systems. However, the idea of employing convolution-Chebyshev chaotic maps for biometric-based remote user authentication has not been addressed adequately. Addressing this problem is critical to overcoming the vast limitations of current remote user authentication using biometric with key agreement procedures.

Also, modern cryptography focused on chaos theory, such as signature techniques [35,36,37,38], authentication [9, 39, 40], information hiding techniques [41,42,43], encryption techniques for cloud computing environments [44,45,46,47,48], mobile healthcare [49], secure and adaptive intelligent learning [50,51,52,53], and hash functions [54], which has received a lot of attention in recent years. Thus, the idea of using cryptographic-based chaotic maps to create a robust authentication scheme is not out of place.

Based on chaos theory, the projected procedure will allow a client to communicate with a server anonymously while providing mutual authentication among the client and the server. Thus, the current paper introduces an efficient convolution-Chebyshev chaotic maps-based remote client authentication with key agreement procedure using biometric to address the shortcomings of the related procedures in the literature.

1.1 Contributions

The following are the main contributions of this paper:

  • We projected an effective remote user authentication using biometric with a key agreement procedure, leveraging convolution-Chebyshev chaotic maps.

  • We demonstrated that the proposed remote user authentication using biometric with key agreement procedure has the lowest storage expense in contrast to other procedures in the literature.

  • We showed that our projected scheme gives high-level security. The key innovation in our proposed work is that while maintaining high performance, the proposed remote user authentication using biometric with key agreement procedure provides high-level security.

  • We demonstrate that the proposed remote user authentication using biometric with key agreement procedure can be easily implemented in various low-power and low-processing-power devices.

1.2 Roadmap

The remainder of this article is planned as follows. In Sect. 2, we introduce the definitions of Chebyshev chaotic maps and their extension. In Sect. 3, we developed the new version of chaotic maps and discussed their properties. Then, the projected procedure is presented in Sect. 4. In Sect. 5, we review the projected procedure and prove that it can withstand various sophisticated attacks. In Sect. 6, we examined the performance of the presented procedure. Finally, Sect. 7 concludes the paper and discusses future prospects.

2 Preliminaries

The Chebyshev polynomial and extended chaotic maps are discussed in this section. The symbolizations used in our projected procedure are presented in Table 2.

Table 2 Symbolizations used in the presented procedure
Full size table

2.1 Chebyshev chaotic maps

This section looks at Chebyshev polynomials (CP) [55] and examines their functionalities, as shown in Fig. 1. The CP \({\mathtt{T}}_{r} \left( \chi \right)\) is a polynomial with degree n in the variant of \(\chi\). Let \(n\) be an integer, and \(\chi\) \(\in \left[ { - 1, 1} \right]\) be the version. The CP is defined as follows:

$$\begin{aligned} {\mathtt{T}}_{\mathrm{n}} \left( \chi \right) & = \cos \left( {\text{n} \times \cos^{ - 1} \left( \chi \right)} \right), \\ {\mathtt{T}}_{0} \left( \chi \right) & = 1 \\ {\mathtt{T}}_{1} \left( \chi \right) & = \chi \\ {\mathtt{T}}_{\mathrm{n}} \left( \chi \right) & = 2\chi {\mathtt{T}}_{\mathrm{n} - 1} \left( \chi \right) - {\mathtt{T}}_{\mathrm{n} - 2} \left( \chi \right); \ \text{n} \ge 2 \\ \end{aligned}$$

where \(\cos^{ - 1}\) and \(\cos \left( x \right)\) are trigonometric functions [56] considered as \(\cos^{ - 1} : \left[ { - 1, 1\left] { \to } \right[0, \pi } \right]\) and \(\cos : \text{R} \to \left[ { - 1, 1} \right].\) Figure 1 shows a few examples of CPs for \(n = 1,2,3,4,5\).

Fig. 1
figure 1

Chebyshev polynomials

Full size image

2.2 Properties of Chebyshev polynomials

Two significant properties characterize Chebyshev polynomials [38, 45, 49, 57]. These are the chaotic and semi-group properties.

  1. (a)

    The chaotic property:


The Chebyshev polynomial map defined as \({\mathtt{T}}_{r} : \left[ { - 1, 1\left] \to \right[ - 1, 1} \right]\) with degree \(n > 1\), is a chaotic map having its invariant density function given as \(f^{*} \left( \chi \right) = \frac{1}{{\left( {\pi \sqrt {1 - \chi^{2} } } \right)}}\) for some positive Lyapunov exponent \(\lambda = {\text{In }} n > 0\).

  1. (b)

    The semi-group property:

$$\begin{aligned} {\mathtt{T}}_{{\text{w}}} \left( {{\mathtt{T}}_{{\text{l}}} \left( \chi \right)} \right) & = \cos \left({{\text{w}}\cos^{ - 1} \left( {\cos \left( {{\text{l}}\cos^{ - 1} \left( \chi \right)} \right)} \right)} \right) \\ & = \cos \left( {{\text{wl}}\cos^{ - 1} \left( \chi \right)} \right) \\ & = {\mathtt{T}}_{{{\text{lw}}}} \left( \chi \right) \\ & = {\mathtt{T}}_{{\text{l}}} \left( {{\mathtt{T}}_{{\text{w}}} \left( \chi \right)} \right), \\ \end{aligned}$$

where \({\text{l}}\) and \({\text{w}}\) are positive integers and \(\chi \in \left[ { - 1, 1} \right].\)

2.3 Computational problems

Two challenges that are known to be quite hard to handle within polynomial time are observed in Chebyshev polynomials [35, 36, 38, 39, 45]. These are defined as follows:

  1. (1)

    Given two exponents \(\chi\) and Y, the task of the discrete Log (DL) is to estimate the integer \(w\) with the end goal \({\mathtt{T}}_{{\text{w}}} \left( \chi \right) = {\text{Y}}\).

  2. (2)

    Given three exponents \(\chi\), \({\mathtt{T}}_{{\text{w}}} \left( \chi \right)\), and \({\mathtt{T}}_{\ell } \left( \chi \right)\), the task of the Diffie–Hellman problem (DHP) is to estimate the exponent \({\mathtt{T}}_{{{\text{w}}\ell }} \left( \chi \right)\).

2.4 Extended chaotic maps

It was established by Zhang [58] that the above semigroup property holds for CPs within the interval \(\left( { - \infty , + \infty } \right)\). This can be strengthened by:

$${\mathtt{T}}_{\mathrm{n}} \left( \chi \right) = \left( { 2\chi {\mathtt{T}}_{\mathrm{n} - 1} \left( \chi \right) - {\mathtt{T}}_{\mathrm{n} - 2} \left( \chi \right)} \right) \left( {\bmod \, q_{1} } \right)$$

where \(\chi \in \left( { - \infty , + \infty } \right)\), \(\text{n} \ge 2\) and \(q_{1}\) is a large prime. Now, we reflect on the recurrence relations \({\mathtt{T}}_{\mathrm{n}} \left( \chi \right) = \left( {12{\mathtt{T}}_{\mathrm{n} - 1} \left( \chi \right) - {\mathtt{T}}_{\mathrm{n} - 2} \left( \chi \right)} \right) \left( {\bmod 13} \right)\) with \({\mathtt{T}}_{0} \left( \chi \right) = 1\) and \({\mathtt{T}}_{1} \left( \chi \right) = 6\), where \(q_{1} = 13.\) Then, \({\mathtt{T}}_{\mathrm{n}} \left( \chi \right)\) created by this recurrence is 1, 6, 6, 1, 6, 6, …… with \({\mathtt{T}}\) = 3 period [45, 59]. Obviously,

\({\mathtt{T}}_{{\text{w}}} \left( {{\mathtt{T}}_{{\text{l}}} \left( \chi \right)} \right) \equiv {\mathtt{T}}_{{{\text{lw}}}} \left( \chi \right) \equiv {\mathtt{T}}_{{\text{l}}} \left( {{\mathtt{T}}_{{\text{w}}} \left( \chi \right)} \right) \left( {\bmod \, q_{1} } \right)\),

As a result, the semigroup assets holds and the improved Chebyshev polynomials commute as well.

3 Main results for convolution-Chebyshev chaotic maps

In this section, we briefly familiarize the convolution-Chebyshev summation (CCS). Also, we developed a new version of Chebyshev chaotic maps, known as convolution-Chebyshev chaotic maps (CCCM).

3.1 Convolution-Chebyshev summation (CCS)

Convolution-Chebyshev summation (CCS) is a formula of several variations of any summation method for summing possibly divergent formal power series, introduced by Chebyshev summation.

3.1.1 Convolution-Chebyshev chaotic maps

Definition 1

For two power series in \(z\), the convolution product (Hadamard product) is defined as follows [60]:

$$\phi \left( \varsigma \right)*\psi \left( \varsigma \right) = \mathop \sum \limits_{n = 0}^{\infty } \phi_{n} \psi_{n} \varsigma^{n} ,$$

where \(\phi \left( \varsigma \right) = \mathop \sum \nolimits_{n = 0}^{\infty } \phi_{n} \varsigma^{n}\) and \(\psi \left( \varsigma \right) = \mathop \sum \nolimits_{n = 0}^{\infty } \psi_{n} \varsigma^{n} .\)

We define a transform called convolution-Chebyshev summation (CCS) by using the convolution product and the summation formula of Chebyshev polynomials.

$${\mathbb{T}}_{\chi } \left( \varsigma \right): = \mathop \sum \limits_{n = 0}^{\infty } {\mathtt{T}}_{n} \left( \chi \right)\varsigma^{n} = \frac{1 - \varsigma \chi }{{1 - 2\varsigma \chi + \varsigma^{2} }}.$$

Note that

$${\mathtt{T}}_{n} \left( \chi \right) = n\mathop \sum \limits_{k = 0}^{n} ( - 2)^{k} \frac{{\left( {n + k - 1} \right)!}}{{\left( {n - k} \right)! \left( {2k} \right)!}}(1 - \chi )^{k} ,\quad n > 0,$$

where

$$\begin{aligned} & {\mathtt{T}}_{0} \left( \chi \right) = 1 \\ & {\mathtt{T}}_{1} \left( \chi \right) = \chi \\ & {\mathtt{T}}_{n + 1} \left( \chi \right) = 2\chi \,{\mathtt{T}}_{n} \left( \chi \right) - {\mathtt{T}}_{n - 1} \left( \chi \right). \\ \end{aligned}$$

as follows:

Definition 2

Define a power series in \(\varsigma\)

$$\phi \left( \varsigma \right) = \mathop \sum \limits_{n = 0}^{\infty } \phi_{n} \varsigma^{n} .$$

Define the transform \({\mathcal{T}}_{\chi }\) of \(\phi\) by

$${\mathbf{T}}_{\chi } \left( \varsigma \right): = {\mathbb{T}}_{\chi } \left( \varsigma \right)*\phi \left( \varsigma \right) \equiv \mathop \sum \limits_{n = 0}^{\infty } \phi_{n} T_{n} \left( \chi \right)\varsigma^{n} .$$

Note that

$${\mathbf{T}}_{\chi }^{k} \left( \varsigma \right) = {\mathbf{T}}_{\chi } \left( \varsigma \right)*,\underbrace { \ldots }_{{k{\text{-times}}}},*{\mathbf{T}}_{\chi } \left( \varsigma \right)$$

and for all \(\chi ,\) The CCS \({\mathbf{T}}_{\chi } \left( \varsigma \right)\) satisfies the recurrent convolution

$${\mathbf{T}}_{\chi } \left( \varsigma \right) = \mathop \sum \limits_{n = 0}^{\infty } \phi_{n} \left[ {2\chi \,{\mathtt{T}}_{n - 1} \left( \chi \right) - {\mathtt{T}}_{n - 2} \left( \chi \right)} \right]\varsigma^{n} .$$

Finally, the dynamic plot of the suggested CCS is shown in Fig. 2.

Fig. 2
figure 2

Three-dimensional plot and the contour plot for the functions \({\mathbb{T}}_{\upchi } \left( z \right),\upphi \left( \varsigma \right) = \frac{\varsigma }{{\left( {1 - \text{x}\varsigma } \right)}},{\mathbb{T}}_{\chi } \left( \varsigma \right)*\upphi_{\chi } \left( \varsigma \right)\) of first order and \(\phi_{{\upchi }} \left( \varsigma \right) = \frac{\varsigma }{{(1 - {\text{x}}\varsigma )^{2} }}\) and \({\mathbb{T}}_{\upchi } \left( \varsigma \right),\phi_{\chi } \left( \varsigma \right)\) for the second order, respectively

Full size image

3.1.2 Extended chaotic maps by using convolution product

Zhang [58] established that the above semigroup properties hold for Chebyshev polynomials defined on the \(\left( { - \infty , + \infty } \right)\) interval, which can improve the assets, as follows (see Sect. 2):

$${\mathtt{T}}_{\mathrm{n}} \left( \chi \right) = \left( { 2\chi {\mathtt{T}}_{\mathrm{n} - 1} \left( \chi \right) - {\mathtt{T}}_{\mathrm{n} - 2} \left( \chi \right)} \right) \left( {\bmod \, q_{1} } \right)$$

Obviously, \({\mathtt{T}}_{n} \left( {{\mathtt{T}}_{l} \left( \chi \right)} \right) \equiv {\mathtt{T}}_{nl} \left( \chi \right) \equiv {\mathtt{T}}_{l} \left( {{\mathtt{T}}_{n} \left( \chi \right)} \right)\) (mod \(q_{1} )\) , so the semigroup possessions hold and the enhanced Chebyshev polynomials commute under composition.

Using the convolution approach for all \(\chi \in \left( { - \infty , + \infty } \right)\), we get the following result:

Theorem 3.1

Consider the power series \(\phi \left( \varsigma \right) = \sum\nolimits_{n = 0}^{\infty } {\phi_{n} \varsigma^{n} }\) . The recurrent and semi-group relations for all \(\chi \in \left( { - \infty , + \infty } \right)\) are given by

  1. (1)
    $$\left( {{\mathbf{T}}_{\chi }^{m} \left( \varsigma \right)} \right) = {\mathbf{T}}_{\chi }^{m - 1} \left( {{\varvec{T}}_{\chi } \left( \varsigma \right)} \right) = {\varvec{T}}_{\chi }^{m - 2} \left( {{\varvec{T}}_{\chi }^{2} \left( \varsigma \right)} \right)$$
  2. (2)
    $${\mathbf{T}}_{\chi }^{k} \left( {{\mathbf{T}}_{\chi }^{m} \left( \varsigma \right)\,} \right) = {\mathbf{T}}_{\chi }^{km} \left( \varsigma \right).$$

Proof

For the first part, it is easy to verify the result directly from the convolution product. For the second part, we use the definition of the generalized formula, we get

$$\begin{aligned} {\mathbf{T}}_{\chi }^{k} \left( {{\mathbf{T}}_{\chi }^{m} \left( \varsigma \right)} \right) & = {\mathbf{T}}_{\chi } \left( {{\mathbf{T}}_{\chi }^{m} \left( \varsigma \right)} \right)*,\underbrace { \ldots }_{{k{\text{-times}}}},*{\mathbf{T}}_{\chi } \left( {{\mathbf{T}}_{\chi }^{m} \left( \varsigma \right)} \right) \\ & = {\mathbf{T}}_{\chi } \left( {{\mathbf{T}}_{\chi } \left( \varsigma \right)*,\underbrace { \ldots }_{{m{\text{-times}}}},*{\mathbf{T}}_{\chi } \left( \varsigma \right)} \right)*,\underbrace { \ldots }_{{k{\text{-times}} \mathbf{T}_{\chi } \left( \varsigma \right)}},*{\mathbf{T}}_{\chi } \left( {{\mathbf{T}}_{\chi } \left( \varsigma \right)*,\underbrace { \ldots }_{{m{\text{-times}}}},*{\mathbf{T}}_{\chi } \left( \varsigma \right)} \right) \\ & = {\mathbf{T}}_{\chi } \left( \varsigma \right)*,\underbrace { \ldots }_{{km{\text{-times}}}},*{\mathbf{T}}_{\chi } \left( \varsigma \right) \\ & = {\mathbf{T}}_{\chi }^{km} \left( \varsigma \right). \\ \end{aligned}$$

4 The proposed procedure

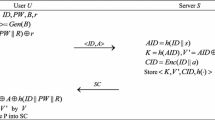
In this section, the proposed scheme using the convolution-Chebyshev chaotic maps is presented. The flowchart of authentication using biometric is shown in Fig. 3. The registration center \({\mathcal{R}\mathcal{C}}_{i}\) starts by picking a random number \(w\) and an arbitrary integer \(b\), then computing \(p{\mathtt{k}} \equiv {\varvec{T}}_{b} \left( w \right) \left( {\bmod \, q_{1} } \right)\). The master secret key \(b\) is held secretly by the registration center \({\mathcal{R}\mathcal{C}}_{i}\). The registration, authentication, login, and password change stages are all part of our presented scheme. The detailed steps of these stages will now be outlined in the subsections as follows.

Fig. 3
figure 3

Flowchart of authentication using biometric

Full size image

4.1 Registration stage

The remote \({\mathcal{U}}_{i}\) user must follow the steps below to register and become new authorized users in the framework, as shown in Fig. 4.

  1. (1)

    The user enters their password \(pwd_{i}\), identity \(id_{i}\), a \({\text{n}}\) arbitrary number, and her/his personal biometric \({\varvec{B}}_{i}\) on a specific computer, then estimates \(\psi_{i} = {\mathcal{H}}\left( {{\varvec{B}}_{i} } \right)\). \({\mathcal{U}}_{i}\) then sends {\(id_{i}\), \(\psi_{i} = {\mathcal{H}}\left( {{\varvec{B}}_{i} } \right)\), \({\mathcal{H}}\left( {pwd_{i} \parallel {\varvec{B}}_{i} \parallel {\text{n}}} \right)\)} via a protected channel to the \({\mathcal{R}\mathcal{C}}_{i}\) registration center.

  2. (2)

    The registration center calculates the succeeding \({\mathcal{R}\mathcal{C}}_{i}\):

    \(\begin{aligned} & \Omega_{i} = {\mathcal{H}}\left( {id_{i} \parallel b} \right), \\ & {\mathcal{W}}_{i} = {\mathcal{H}}\left( {pwd_{i} \parallel {\varvec{B}}_{i} \parallel \text{n}} \right) \oplus \psi_{i} , \\ & {\mathcal{Y}}_{i} = \Omega_{i} \oplus {\mathcal{W}}_{i} . \\ \end{aligned}\)

    \({\mathcal{R}\mathcal{C}}_{i}\) embeds \(\left( {id_{i} , {\mathcal{H}}\left( . \right),{\mathcal{Y}}_{i} ,w,p{\mathtt{k}},q_{1} } \right)\) in the user's smart card (SC) and sends it over a protected channel to the user \({\mathcal{U}}_{i}\).

  3. (3)

    \({\mathcal{U}}_{i}\) calculates \({\varvec{B}}pwd = {\varvec{B}}_{i} \oplus {\mathcal{H}}\left( {pwd_{i} } \right)\) after obtaining the smart card and inserting \({\text{n}}\) and \({\varvec{B}}pwd\) into the SC to complete the registration.

Fig. 4
figure 4

Registration stage of the projected procedure

Full size image

4.2 Login stage

When a legal user \({\mathcal{U}}_{i}\) wishes to access the server \({\mathcal{S}}_{i}\) in this process, as shown in Fig. 5, they must do the following:

  1. (1)

    \({\mathcal{U}}_{i}\) inserts their SC into the card reader and select a specific device for their biometric template \({\varvec{B}}_{i}\) and password \(pwd_{i}\).

  2. (2)

    The values \({\varvec{B}}_{i} ^{\prime} = {\varvec{B}}pwd \oplus {\mathcal{H}}\left( {pwd_{i} } \right)\) is computed and \({\varvec{B}}_{i} = {\varvec{B}}_{i} ^{\prime}\) is checked by the SC. The smart card would refuse the request if \({\varvec{B}}_{i} \ne {\varvec{B}}_{i} ^{\prime}\).

  3. (3)

    The SC creates a \({\mathtt{u }}\) and calculates

    \(\begin{aligned} & \psi_{i} = {\mathcal{H}}\left( {{\varvec{B}}_{i} } \right), \\ & {\mathcal{W}}_{i} ^{\prime} = {\mathcal{H}}\left( {pwd_{i} \parallel {\varvec{B}}_{i} \parallel {\text{n}}} \right) \oplus \psi_{i} \\ & \Omega_{i} ^{\prime} = {\mathcal{Y}}_{i} \oplus {\mathcal{W}}_{i} ^{\prime}, \\ & {\mathfrak{W}}_{1} \equiv {\varvec{T}}_{\mathrm{u}} \left( w \right) \left( {\bmod \, q_{1} } \right), \\ & {\mathfrak{W}}_{2} \equiv {\varvec{T}}_{\mathrm{u}} \left( {p{\mathtt{k}}} \right) \left( {\bmod \, q_{1} } \right), \\ & {\text{n}}id_{i} = id_{i} \oplus {\mathcal{H}}\left( {{\mathfrak{W}}_{1} \parallel {\mathfrak{W}}_{2} } \right) \\ & \gamma = {\mathcal{H}}\left( {id_{i} \parallel {\text{n}}id_{i} \parallel \Omega_{i} ^{\prime}\parallel {\mathfrak{W}}_{1} \parallel {\mathfrak{W}}_{2} \parallel \tau_{1} } \right). \\ \end{aligned}\)

  4. (4)

    The user \({\mathcal{U}}_{i}\) sends {\({\text{n}}id_{i}\), \({\mathfrak{W}}_{1}\), \(\gamma\), \(\tau_{1}\)} to \({\mathcal{S}}_{i}\).

Fig. 5
figure 5

Login stage of the projected procedure

Full size image

4.3 Authentication stage

The server \({\mathcal{S}}_{i}\) carries out the following phases to access mutual authentication after receiving the login appeal messages, as shown in Fig. 6.

  1. (1)

    Upon receiving {\({\text{n}}id_{i}\), \({\mathfrak{W}}_{1}\), \(\gamma\), \(\tau_{1}\)}, \({\mathcal{S}}_{i}\) tests the legitimacy of \(\tau_{1}\) by the examination, if the equation \(\tau^{\prime} - \tau_{1} > \Delta \tau\) holds, where \(\tau^{\prime}\) is the time when the server obtains the messages from \({\mathcal{U}}_{i}\) and \(\Delta \tau\) represents the predetermined permissible time period of transmission delay. \({\mathcal{S}}_{i}\) rejects \({\mathcal{U}}_{i}\) if the equation holds.

  2. (2)

    \({\mathcal{S}}_{i}\) calculates \({\mathfrak{W}}_{2}^{^{\prime}} \equiv {\varvec{T}}_{b} \left( {{\mathfrak{W}}_{1} } \right) \left( {\bmod \, q_{1} } \right)\), \(id_{i} ^{\prime} = {\text{n}}id_{i} \oplus {\mathcal{H}}\left( {{\mathfrak{W}}_{1} \parallel {\mathfrak{W}}_{2} ^{\prime}} \right)\) and checks the legitimacy of \(id_{i} ^{\prime}\).

  3. (3)

    \({\mathcal{S}}_{i}\) calculates \(\Omega_{i} ^{\prime\prime} = {\mathcal{H}}\left( {id_{i} ^{\prime}\parallel b} \right)\) and \(\gamma ^{\prime} = {\mathcal{H}}\left( {id_{i} ^{\prime}\parallel {\text{n}}id_{i} \parallel \Omega_{i} ^{\prime\prime}\parallel {\mathfrak{W}}_{1} \parallel {\mathfrak{W}}_{2} ^{\prime}\parallel \tau_{1} } \right)\).

  4. (4)

    Then, \({\mathcal{S}}_{i}\) verifies whether \(\gamma ^{\prime}\) equals to \(\gamma\). If \(\gamma ^{\prime} \ne \gamma\), \({\mathcal{S}}_{i}\) stops the session.

  5. (5)

    If \(\gamma^{\prime} = \gamma\), \({\mathcal{S}}_{i}\) arbitrarily selects an integer \({\mathtt{v}}\) and calculates \({\mathfrak{W}}_{3} \equiv {\varvec{T}}_{{\mathtt{v}}} \left( w \right) \left( {\bmod \, q_{1} } \right)\) and \(\mu = {\mathcal{H}}\left( {id_{i} ^{\prime}\parallel \Omega_{i} ^{\prime\prime}\parallel {\mathfrak{W}}_{2} ^{\prime}\parallel {\mathfrak{W}}_{3} \parallel \tau_{2} } \right)\). Then, \({\mathcal{S}}_{i}\) sends {\({\mathfrak{W}}_{3}\), \(\mu\), \(\tau_{2}\)} to \({\mathcal{U}}_{i}\).

  6. (6)

    \({\mathcal{U}}_{i}\) tests the validity of \(\tau_{2}\) by testing, if the equation \(\tau^{\prime} - \tau_{2} > \Delta \tau\) holds after obtaining {\(\mathfrak{W}_{3}\), \(\mu\), \(\tau_{2}\)}. \({\mathcal{U}}_{i}\) rejects \({\mathcal{S}}_{i}\) if the equation holds.

  7. (7)

    \({\mathcal{U}}_{i}\) checks whether \(\mu^{\prime}? = \mu\) by computing \(\mu ^{\prime} = {\mathcal{H}}\left( {id_{i} \parallel \Omega_{i} ^{\prime}\parallel {\mathfrak{W}}_{2} \parallel {\mathfrak{W}}_{3} \parallel \tau_{2} } \right)\). \({\mathcal{U}}_{i}\) will terminate the session if they are not equal. Otherwise, \({\mathcal{U}}_{i}\) computes \({\mathfrak{W}}_{4} \equiv {\varvec{T}}_{{\mathtt{u}}} \left( {{\mathfrak{W}}_{3} } \right) \equiv {\varvec{T}}_{{{\text{uv}}}} \left( w \right) \left( {\bmod \, q_{1} } \right)\) and \(\xi = {\mathcal{H}}\left( {id_{i} \parallel \Omega_{i} ^{\prime}\parallel {\mathfrak{W}}_{2} \parallel {\mathfrak{W}}_{4} \parallel \tau_{3} } \right)\). Then, \({\mathcal{U}}_{i}\) sends {\(\xi\), \(\tau_{3}\)} to \({\mathcal{S}}_{i}\).

  8. (8)

    \({\mathcal{S}}_{i}\) tests the validity of \(\tau_{3}\) by testing, if the equation \(\tau^{\prime} - \tau_{3} > \Delta \tau\) holds as it receives {\(\xi\), \(\tau_{3}\)}. \({\mathcal{S}}_{i}\) rejects \({\mathcal{U}}_{i}\) if the equation holds. Otherwise, \({\mathcal{S}}_{i}\) computes \({\mathfrak{W}}_{4}^{^{\prime}} \equiv {\varvec{T}}_{{\mathtt{v}}} \left( {{\mathfrak{W}}_{1} } \right) \equiv {\varvec{T}}_{{{\text{uv}}}} \left( w \right) \left( {\bmod \, q_{1} } \right)\) and \(\xi ^{\prime} = {\mathcal{H}}\left( {id_{i} ^{\prime}\parallel \Omega_{i} ^{\prime\prime}\parallel {\mathfrak{W}}_{2} ^{\prime}\parallel {\mathfrak{W}}_{4} ^{\prime}\parallel \tau_{3} } \right)\) and tests if \(\xi^{\prime}? = \xi\).

  9. (9)

    \({\mathcal{S}}_{i}\) approves \({\mathcal{U}}_{i}\)’s login appeal if it holds, and the verification is complete. Then, using a symmetric cryptosystem, both \({\mathcal{U}}_{i}\) and \({\mathcal{S}}_{i}\) will connect with each other using the session key \({\mathfrak{W}}_{4}\) and \({\mathfrak{W}}_{4}^{^{\prime}}\).

Fig. 6
figure 6

Authentication stage of the presented procedure

Full size image

Subsequently \(p{\mathtt{k}} \equiv {\varvec{T}}_{b} \left( w \right) \left( {\bmod \, q_{1} } \right)\), \({\mathfrak{W}}_{1} \equiv {\varvec{T}}_{{\mathtt{u}}} \left( w \right) \left( {\bmod \, q_{1} } \right)\), \({\mathfrak{W}}_{2} \equiv {\varvec{T}}_{{\mathtt{u}}} \left( {p{\mathtt{k}}} \right) \left( {\bmod \, q_{1} } \right)\), and \({\mathfrak{W}}_{3} \equiv {\varvec{T}}_{{\mathtt{v}}} \left( w \right) \left( {\bmod \, q_{1} } \right)\) so that we can originate

$${\mathfrak{W}}_{2}^{^{\prime}} \equiv {\varvec{T}}_{b} \left( {{\mathfrak{W}}_{1} } \right) \equiv {\varvec{T}}_{b} \left( {{\varvec{T}}_{{\mathtt{u}}} \left( w \right)} \right) \equiv {\varvec{T}}_{{\mathtt{u}}} \left( {{\varvec{T}}_{b} \left( w \right)} \right) \equiv {\varvec{T}}_{{\mathtt{u}}} \left( {p{\mathtt{k}}} \right) \equiv {\mathfrak{W}}_{2} \left( {\bmod \, q_{1} } \right)$$

and

\({\mathfrak{W}}_{4}^{^{\prime}} \equiv {\varvec{T}}_{{\mathtt{u}}} \left( {{\mathfrak{W}}_{3} } \right) \equiv {\varvec{T}}_{{\mathtt{u}}} \left( {{\varvec{T}}_{{\mathtt{v}}} \left( w \right)} \right) \equiv {\varvec{T}}_{{\mathtt{v}}} \left( {{\varvec{T}}_{{\mathtt{u}}} \left( w \right)} \right) \equiv {\varvec{T}}_{{\mathtt{v}}} \left( {{\mathfrak{W}}_{1} } \right) \equiv {\mathfrak{W}}_{4} \left( {\bmod \, q_{1} } \right)\).

As a result, the correctness of the scheme is established.

4.4 Password change stage

The smart card confirms the user's previously entered password before updating the newly updated password during this process. The user \({\mathcal{U}}_{i}\) goes through the following steps to update the password:

  1. (1)

    Inserts the SC and suggestions both the \({\varvec{B}}_{i}\) biometric template and \(pwd_{i}\) old password.

  2. (2)

    \({\varvec{B}}_{i} ^{\prime} = {\varvec{B}}pwd \oplus {\mathcal{H}}\left( {pwd_{i} } \right)\) is computed by the smart card, and \({\varvec{B}}_{i} = {\varvec{B}}_{i} ^{\prime}\) is checked. If \({\varvec{B}}_{i} \ne {\varvec{B}}_{i} ^{\prime}\) is true, \({\mathcal{U}}_{i}\) has entered the incorrect old password or biometric template. The SC then declines the order.

  3. (3)

    \({\mathcal{U}}_{i}\) enters their new password \(pwd_{i}^{new}\), if the biometric verification is effective.

  4. (4)

    The smart card is capable of computing the following:

    \(\begin{aligned} & \psi_{i} = {\mathcal{H}}\left( {{\varvec{B}}_{i} } \right), \\ & {\mathcal{W}}_{i} \,^{\prime} = {\mathcal{H}}\left( {pwd_{i} \parallel {\varvec{B}}_{i} \parallel {\text{n}}} \right) \oplus \psi_{i} , \\ & {\mathcal{W}}_{i} \,^{\prime\prime} = {\mathcal{H}}\left( {pwd_{i}\,^{new} \parallel {\varvec{B}}_{i} \parallel {\text{n}}} \right) \oplus \psi_{i} , \\ & \Omega_{i} \,^{\prime} = {\mathcal{Y}}_{i} \oplus {\mathcal{W}}_{i} ^{\prime}, \\ & {\mathcal{Y}}_{i} \,^{\prime} = \Omega_{i}\, ^{\prime} \oplus {\mathcal{W}}_{i} \,^{\prime\prime}. \\ \end{aligned}\)

  5. (5)

    Finally, replaces \({\mathcal{Y}}_{i}\) with \({\mathcal{Y}}_{i} ^{\prime}\) on the smart card.

5 Security Analysis and Discussion

This segment contains a check to ensure that the procedure under consideration supports mutual authentication, perfect forward secrecy, and user anonymity. Furthermore, we tested the proposed protocol against a variety of attacks, including privileged insider attack, replay attack, offline password guessing attack, perfect forward secrecy, stolen-verifier attack, known-plaintext attack, and Bergamo et alattack.'s [56].

Proposition 1

The proposed procedure can achieves privileged insider attacks.

Proof

The remote user \({\mathcal{U}}_{i}\) sends \({\mathcal{H}}\left( {pwd_{i} \parallel {\varvec{B}}_{i} \parallel {\text{n}}} \right)\) to the registration center \({\mathcal{R}\mathcal{C}}_{i}\) during the registration procedure of the presented scheme. Without \({\varvec{B}}_{i}\) and \({\text{n}}\), the privileged insider cannot deduce the password \(pwd_{i}\). As a result, our system will withstand a privileged insider attack.

Proposition 2

The presented procedure can achieve user anonymity.

Proof

The attacker can listen in on a user \({\mathcal{U}}_{i}\)'s communication with a server \({\mathcal{S}}_{i}\) and attempt to track down the user's true identity to obtain info about the user. The real identity \(id_{i}\) is secured in our scheme by \({\mathfrak{W}}_{2} \equiv {\mathfrak{W}}_{2}^{^{\prime}} \equiv {\varvec{T}}_{b} \left( {{\varvec{T}}_{{\mathtt{u}}} \left( w \right)} \right) \left( {\bmod \, q_{1} } \right)\) from \(p{\mathtt{k}} \equiv {\varvec{T}}_{b} \left( w \right) \left( {\bmod \, q_{1} } \right)\) and \({\mathfrak{W}}_{1} \equiv {\varvec{T}}_{{\mathtt{u}}} \left( w \right) \left( {\bmod \, q_{1} } \right)\). The attacker would need to deal with the convolution-Chebyshev chaotic maps-based DHP to compute \(\mathfrak{m}_{2}\). As a result, our presented scheme will guarantee user anonymity.

Proposition 3

The proposed procedure can achieves mutual authentication.

Proof

The mutual authentication among the user \({\mathcal{U}}_{i}\) and server \({\mathcal{S}}_{i}\) is possible with our presented scheme. To authenticate \({\mathcal{U}}_{i}\), server \({\mathcal{S}}_{i}\) must check the validity of \(\gamma\) and \(\xi\) during the authentication process of our presented scheme. To authenticate \({\mathcal{S}}_{i}\), the user \({\mathcal{U}}_{i}\)'s smart card must also check the validity of \(\mu\). If an attacker attempts to forge messages, she/he will be faced with the convolution-Chebyshev chaotic maps-based DLP and the convolution-Chebyshev chaotic maps-based DHP. As a result, both the server and the user will authenticate, resulting in mutual authentication.

Proposition 4

The presented procedure can achieve an off-line password guessing attack.

Proof

The messages {\({\text{n}}id_{i}\), \({\mathfrak{W}}_{1}\), \(\gamma\), \(\tau_{1}\)} and {\({\mathfrak{W}}_{3}\), \(\mu\), \(\tau_{2}\)} may be intercepted by the attacker. The attacker can also gain access to the smart card's \({\mathcal{Y}}_{i}\). Then, she/he will try to guess the \(pwd_{i} ^{\prime}\) password. However, since the attacker lacks knowledge of the elements \({\mathcal{W}}_{i}\), \(\psi_{i}\), \({\varvec{B}}_{i}\) and \(\Omega_{i}\), the attacker is unable to check the correctness of the password \(pwd_{i} ^{\prime}\). The attacker will also have to deal with the convolution-Chebyshev chaotic maps-based DHP if he tries to derive the random integers \({\mathtt{u}}\) and \({\mathtt{v}}\). As a result, our system can withstand an offline password guessing attack.

Proposition 5

The presented procedure can achieve replay attacks.

Proof

In the next run, the attacker might intercept contact messages from \({\mathcal{U}}_{i}\) and replay them to the server \({\mathcal{S}}_{i}\). With the wrong timestamps, however, the intruder is unable to pass the verification. So, by using the timestamps \(\tau_{1}\), \(\tau_{2}\), and \(\tau_{3}\), our presented procedure is safe against the replay attack.

Proposition 6

The proposed procedure can achieves a stolen-verifier attack.

Proof

The stolen-verifier attack occurs when an intruder good deals with the server's security-sensitive verification table and uses it to impersonate a genuine user during the authentication process. In our presented system, the server does not need to keep any security-subtle verification tables. As a result, our procedure is immune to the stolen-verifier attack.

Proposition 7

The projected procedure can achieve perfect forward secrecy.

Proof

According to perfect forward secrecy, even if a session key or long-term key is compromised in some way, the foe will be unable to extract all other session keys from the cracked one [61, 62]. In our proposed procedure, the smart card and server \({\mathcal{S}}_{j}\) compute the existing session key \(\xi = {\mathcal{H}}\left( {id_{i} \parallel \Omega_{i} ^{\prime}\parallel {\mathfrak{W}}_{2} \parallel {\mathfrak{W}}_{4} \parallel \tau_{3} } \right)\), where \({\mathfrak{W}}_{3} \equiv {\varvec{T}}_{{\mathtt{v}}} \left( w \right) \left( {\bmod \, q_{1} } \right)\), and \({\mathfrak{W}}_{4} \equiv {\varvec{T}}_{{\mathtt{u}}} \left( {\mathfrak{m}_{3} } \right) \left( {\bmod \, q_{1} } \right)\) use random numbers \({\mathtt{v}}\) and \({\mathtt{u}}\) and \(\Omega_{i} ^{\prime} = {\mathcal{Y}}_{i} \oplus {\mathcal{W}}_{i} ^{\prime}\), where \({\mathcal{W}}_{i} ^{\prime} = {\mathcal{H}}\left( {pwd_{i} \parallel {\varvec{B}}_{i} \parallel {\text{n}}} \right) \oplus \psi_{i}\). Even if a foe knew the current session key, they would be unable to use it to calculate any of the other valid session keys because the random numbers in each contact session are unique. With our presented procedure, this procedure aids in maintaining complete forward confidentiality.

Proposition 8

The projected procedure can achieves lost smart card attacks.

Proof

Assume that a side-channel attack will remove all of the data from the smart card [63, 64]. The attacker may attempt to deduce the password from the data, but the elements protect the password \({\mathcal{W}}_{i}\), \(\psi_{i}\), \({\varvec{B}}_{i}\), and \(\Omega_{i}\), which the attacker does not have access to it. Furthermore, if the biometric template of the user \({\varvec{B}}_{i}\), is not provided, the attacker is unable to pass biometric authentication. As a result, our presented procedure is impervious to smart card theft.

Proposition 9

The presented procedure can achieves Bergamo et al.’s attack [56].

Proof

Bergamo et al.’s attack [56] is predicated on a foe being able to obtain the related variables \(b\), w, \({\mathfrak{W}}_{1}\), and \({\mathfrak{W}}_{3}\) and derive u and v from them. The adversary may be able to quickly obtain \(b\), w, \({\mathfrak{W}}_{1}\), and \({\mathfrak{W}}_{3}\), but there is no way in our presented procedure to extract \({\mathtt{u}}\) and \({\mathtt{v}}\) from those values. Convolution-Chebyshev chaotic maps encrypt the elements, which can only be identified by the client and server. In addition, we use enhanced convolution-Chebyshev chaotic maps to avoid the periodicity of the cosine function by extending the \({\mathcal{Y}}\) interval to \(\left( { - \infty , + \infty } \right)\). As a result, Bergamo et al. attack’s [56] have no bearing on our proposed procedure.

6 Performance analysis and discussion

We demonstrate how well the proposed procedure works in this section of the paper. Table 3 compares the security futures of our projected procedure to those of Lee et al. [65], He et al. [61], Lee and Hsu [66], Fan et al. [67], Qi and Chen [33], and Sahoo et al. [34] existing procedures. Under critical considerations, our proposed procedure provides more security than the other existing procedures. Furthermore, we compared the computational primitives used in our proposed procedure for positioning the user and server to those used in other related procedures. We assume that the hash output of \(h\left( . \right)\) is 160 bits (if we use the SHA-1 hash algorithm [68]) and that both the clear identity \(\varvec{id}_{i}^{^{\prime}}\) and the check value are 160 bits. As a result, a sensor node's total storage requirement is 480 bits.

Table 3 Comparisons of security characteristics among the projected and other related procedures
Full size table

In this comparison, we used the four-time complexity notations: \({\mathtt{t}}_{ch} ,\;{\mathtt{t}}_{s}\),\({\mathtt{t}}_{h} ,\) and \({\mathtt{t}}_{{{\text{ec}}}}\) which described the performance time for a Chebyshev chaotic map operation, one elliptic curve scale multiplication, a one-way hash function, and a symmetric encryption/decryption operation, respectively. Several works [35,36,37, 69] have recognized the relationships between \({\mathtt{t}}_{{\text{h}}} ,{\mathtt{t}}_{{{\text{ch}}}} ,{\mathtt{t}}_{{\text{s}}}\) and \({\mathtt{t}}_{{{\text{ec}}}}\) with respect to \({\mathtt{t}}_{{\text{h}}}\) \(\left( {{\mathtt{t}}_{{\text{h}}} = 0.32\,{\text{ms}}} \right)\). The relationship and order of computational complexity among the metrics are as follows: \({\mathtt{t}}_{s} \approx {\mathtt{t}}_{h} , {\mathtt{t}}_{{{\text{ch}}}} \approx {\mathtt{t}}_{{\text{h}}} ,{\mathtt{t}}_{{{\text{ec}}}} \approx 72.5{\mathtt{t}}_{{\text{h}}} ,\) and \({\mathtt{t}}_{ch} \approx {\mathtt{t}}_{{\text{h}}} \approx {\mathtt{t}}_{{\text{s}}} < {\mathtt{t}}_{{{\text{ec}}}}\). Table 4 shows the proposed procedure as well as the most time-consuming operations of the existing procedures. Figure 7 also compares total processing costs in milliseconds (ms).

Table 4 Performance evaluation of the presented and other relevant procedures
Full size table
Fig. 7
figure 7

Overall processing cost (ms)

Full size image

By comparison, due to the use of Chebyshev chaotic maps and hash functions, our proposed procedure can provide comprehensive security assurance at a very low computation cost while demonstrating very high efficiency.

Remote user authentication is an essential part of accessing valuable services or resources in healthcare, the Internet of Things (IoT), multi-server environments, and cloud applications. Remote user authentication [70] is an essential part of any security architecture. Authorization grants identity-based privileges, and audit trails are not transparent without authentication. The presented procedure is lightweight; therefore, it is very useful for the development of lightweight authentication protocols for Internet of Things (IoT), multi-server environments, and cloud applications.

The convolution is a mathematical operation on two functions, formulas (polynomials, expressions, etc.) (X and Y) that yields a third function X*Y = Z) that states how the outline of one is improved by the other. The term convolution indicates to both the consequence function and to the procedure of calculating it. Understanding discrete convolution as polynomial multiplication, which is a necessary operation in digital signal and image processing. The summation on k-times is known as a periodic summation of the function X with respect to Y. The proposed procedure is based on the convolution-Chebyshev chaotic maps and its security is based on the hardness of convolution-Chebyshev chaotic maps.

7 Conclusions

This article projected an efficient convolution-Chebyshev chaotic maps-enabled remote user authentication with key agreement procedure using biometric. We developed the extended convolution-Chebyshev chaotic maps over the interval \(\left( { - \infty , + \infty } \right)\) and derived the required properties to establish the proposed procedure. The procedure shows significant biometric authentication without verification tables, enhances user anonymity, gives perfect forward secrecy, and has less computational and communication costs. Finally, formal and informal security and performance analyses revealed that the proposed procedure performs better than related procedures in the literature. Future work would focus on harnessing the potentials of the proposed procedure to provide a secure biometric authenticated key agreement for telemedicine-based information systems.