1 Introduction

Solving optimization problems is complex and time-consuming for central processing units (CPUs), especially for large-scale problems. Metaheuristics are efficient methods to obtain satisfactory resolution (approximate optimum) in a reasonable time, and widely applied in solving science, engineering, economics and technology problems [13, 24, 29, 30, 40]. Recently, efficient parallel metaheuristic algorithms have been a topic of considerable interest [1, 28, 44]. Local search metaheuristics (LSMs) are one of the most widely researched single solution-based approaches with many variants such as iterated local search (ILS) [26], tabu search (TS) [10] and simulated annealing (SA) [20]. LSMs share a common feature that the candidate solution is iteratively selected from its neighborhood. LSMs could solve combinatorial optimization problems such as the Travelling Salesman Problem (TSP) [37] and the Quadratic Assignment Problem (QAP) [21], both of which have been proved NP-hard. Many works are dedicated to improve its performance by parallel computing technology from algorithmic level, iteration level and solution level [38]. As a result, parallelism is a way not only to reduce the time complexity but also to improve the quality of the solutions provided [1].

Today, graphics processing units (GPUs) have evolved from fixed function rendering devices to programmable and parallel processors [18]. The demand from the market for real-time, high-definition 3D graphics motivates GPUs to become highly parallel, multithreaded, many-core processors with tremendous computational power and high-bandwidth memory. Therefore, the GPU architecture is designed such that more transistors are devoted to data processing than to data caching and flow control [32]. With the rapid development of general-purpose GPU (GPGPU) techniques in many areas, major companies promote programming frameworks for GPUs, such as CUDA [32], OpenCL [18] and Direct Compute. Recently, the use of GPGPU has been extended to other domains such as numerical computing, computational finance and life science. The field of metaheuristics also follows this trend, and GPU accelerated LSMs have been reported more computational efficient than CPU-based LSMs [9, 17, 28, 35]. However, little work is known about the quantitative comparison between the proposed approaches which is a challenging task [4]. As a result, we should pay great efforts on trying different optimization strategies on several generations of GPUs. Although several studies are dedicated to the quantitative performance analysis of parallel algorithms on GPUs [19, 39], it is still missing in the field of metaheuristics, including LSMs. Furthermore, it is an important problem to make LSM algorithms on GPU optimized for the best efficiency.

In this paper, we propose an optimized parallel ILS algorithm on GPUs and test the algorithm with a typical and open issue of the TSP in computational science. We present an efficient mapping between a neighborhood and a GPU thread. We do quantitative comparison between previous parallel local search operators, by using the Roofline performance model [41]. We analyze the performance of existing GPU-based 2-opt kernels in the ILS. Based on the performance analysis, we propose an optimized 2-opt kernel. We evaluate the performance of these algorithms with the standard TSP problems with sizes as many as 4461 cities. We obtain a speedup factor of 279\(\times \) compared to the CPU sequential version. We also compare our algorithm with two state-of-the-art GPU-based local search algorithms in literature, and the results demonstrate our approach is effective.

The rest of the paper is organized as follows: First, we briefly introduce the GPU architecture, the Roofline model and the ILS for the TSP in Sect. 2. Second, related works are discussed in Sect. 3. Third, our methods for the design and analysis of parallel ILS are discussed in Sect. 4. Our experimental methodology is outlined in Sect. 5, and we describe the performance evaluation of our algorithm in this section. Finally, we summarize our findings and conclude with suggestions for future work.

2 Background

2.1 GPU computing

For the purpose of understanding our work, a brief description of GPU architecture and programming framework is required. GPUs have evolved from fixed function rendering device to a highly parallel and many-core general purpose computing device which work in a single instruction, multiple data (SIMD) manner. They are very suitable for compute-intensive and highly data parallel computation, because more transistors are devoted to data processing than to data caching and flow control. More detailed materials about the GPU architecture could be found in [2, 16, 31].

The programming framework that we adopt to implement the parallel ILS algorithm is OpenCL. OpenCL is an open royalty-free standard for general-purpose parallel programming across CPUs, GPUs and other processors, providing software developers with portable and efficient access to the power of these heterogeneous processing platforms [18]. OpenCL consists of APIs for coordinating parallel computation across heterogeneous processors and a cross-platform programming language with a well-specified computation environment.

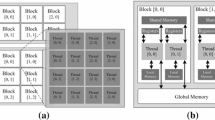
Figure 1 illustrates that an OpenCL device is divided into one or more compute units (CUs), which are further divided into one or more processing elements (PEs). Computations on a GPU occur within the processing elements. Generally, a CPU in OpenCL architecture could be named a host. The OpenCL application submits commands from the host to execute computations on the PEs within a GPU.

Fig. 1
figure 1

OpenCL compute device architecture [18]

Full size image

A CU supports the SIMD model with multiple PEs that perform the same operation on multiple data points simultaneously. Work-items in OpenCL are the smallest execution units and more generally called threads. We use the term thread and work-item interchangeably. The host calls the GPU function by the kernel, which defines the computation to be executed by many work-items organized in work-groups. In a work-group, work-items are further grouped into batches (or warps) coordinated by a scheduler at runtime. They execute concurrently on the PEs of a single CU.

The memory model of the GPU is hierarchical and could be classified into on-chip memory and off-chip memory. The on-chip memory consists of local memory and private memory. Work items in a work-group share data through the local memory, which has a limited memory space typically within 64 K. The private memory is a private memory region of a work item that cannot be observed by other work-items. This memory contains registers used by each PE. The global memory, constant memory and texture memory together represent the off-chip memory of GPUs. The largest memory region is the global memory, which can be accessed by all work items. The size of this memory is typically larger than 1 GB, but it is much slower than the local memory. The constant memory that can only be allocated and initialized on a host is a read-only region in the global memory. The texture memory space also resides in global memory and are cached in texture cache. A texture can be any region of linear memory, so we could write arrays into texture memory for efficient data fetch.

2.2 Roofline performance model

Roofline model is a performance analysis model for modern processors, especially focusing on the floating point performance of parallel processors [41]. This model is based on the relation of processor performance to off-chip memory traffic. The terminology operational intensity is used to mean operations per byte of DRAM traffic, for example, the floating point operations per byte (FLOP/byte). The theoretical performance of a kernel on a device could be calculated by multiplying operational intensity by the main memory bandwidth (byte/s). The performance is bounded by two types of ceilings: computational ceilings and bandwidth ceilings. We could assume that the operational intensity is a column. If it hits the computational ceiling, which represents the theoretical peak performance of the device, the kernel is compute-bound; otherwise, it is memory-bound. This model offers us with insights for algorithm optimization on parallel processors.

2.3 Iterated local search for the TSP

The TSP is an NP-hard problem in combinatorial optimization and plays a prominent role in research as well as in a number of application areas [14]. The objective of the TSP is to find a minimum-weight Hamilton cycle in a complete weighted directed graph \(G = (V, A, d)\), where \(V = {1, 2, \ldots , n}\) is a set of vertexes (cities), \(A = \{(i, j)|(i, j) \epsilon V \times V\}\) is the set of arcs, and \(d : A \rightarrow \mathbb {N}\) is a function assigning a weight or distance (positive integer) \(d_{ij}\) to every arc (i, j).

The local search operator for TSP could be formally descried as follows. Let s be the candidate solution of a TSP problem. N(s) presents for neighborhoods of s which could be generated by simply change k edges in s, also named as k-opt. The most well-known neighborhood generation methods for the TSP are the 2-opt and 3-opt. Let \(s'\) be the best neighborhood in N(s). If the fitness value of \(s'\) which is \(f(s')\) is smaller than f(s), then \(s'\) replace the candidate solution s. This process is done iteratively until there is no improvement to candidate solution and the local search gets stuck at a locally optimal point. The basic local search is also known as the hill climbing. To get global optimal solution, some approaches are incorporated into it to jump out of the local optimal point. In the ILS, a perturbation function is made to the local optimal solution \(s^*\) by performing a random change of edges that is enough to guide to another local optima. The double-bridge move (also known as 4-opt move), first introduced by Lin and Kernighan in [25], is a typical perturbation method that used widely in many modern algorithms. The ILS executes the local search operator and the perturbation iteratively until the termination criterion condition is reached. The outline of the algorithm is given in Algorithm 1.

figure a

3 Related work

Recently, the GPU has become a major accelerator with the ease of programming and the need for computing power. It is attractive to researchers who are interested in solving computationally hard optimization problems. Since LSMs are popular and efficient methods for solving these problems, accelerating LSMs on GPUs is of course a reasonable choice. Following works have been dedicated to the parallel implementation of LSMs on GPUs.

For solving the Quadratic three-dimensional Assignment Problem (Q3AP), Luong et al. [27] present an iterated tabu search on GPUs. They design a new large neighborhood structure in their algorithm. They obtain speedups up to 6.1 with convinced quality and robustness. They later focus on the design and implementation of effective LSMs on GPU [28]. They propose efficient approaches for CPU-GPU data transfer optimization, thread control, mapping of neighboring solutions to GPU threads and memory management. Their experiments are performed using four well-known combinatorial and continuous optimization problems. The results achieve 80\(\times \) speedup in large combinatorial problems and 240\(\times \) speedup in a continuous problem. They demonstrate that the performance GPU-based LSMs is even better than the cluster and grid-based parallel architectures in some cases.

Rocki and Suda propose high-performance 2-opt [36] and 3-opt [35] algorithms on GPUs for the TSP. Their results demonstrate that the local search operator execution time is 90 % of the whole, and the GPU algorithm is approximately over 500\(\times \) faster in case of 3-opt compared to a sequential CPU code. Their major contribution is the classification of distance calculation strategies. They name the strategy Look Up Table (LUT) that the distances are pre-computed once and reused later reading from memory. They identify that the space complexity of LUT is \(O(n^2)\), which is not suitable for the GPU memory architecture. Therefore, they present a better strategy that reads coordinates of the vertexes and recalculates the distance each time. We name it CALC. We also observe that Fosin et al. [9] propose a parallel ILS implementation with 2-opt and 3-opt operators for the TSP, in which the distance is calculated at the GPU run-time. This strategy is the same as CALC. They have reported a 27\(\times \) speedup with the same solution quality as the sequential CPU version.

Delévacq et al. [8] present an ILS on GPUs with considering processing hardware and memory structure. They propose two models for ILS, named \(\mathrm{ILS}_{\mathrm{thread}}\) and \(\mathrm{ILS}_{\mathrm{block}}\), which exploit parallelism in different levels. They report speedups of up to 6.02 with solution quality similar to the sequential CPU implementation on TSPs ranging from 100 to 3038 cities. They later integrate the GPU-based local search algorithm into new GPU-based Max–Min Ant System algorithms [7] to achieve competitive computational efficiency and solution quality. Similar as Delévacq et al., Arbelaez and Codognet [3] present the ideas of parallelizing constraint-based local search in single-walk and multi-walk manners. Their experiments indicate speedups up to 17 times.

O’Neil and Burtscher [33] present a GPU-accelerated random-restart hill climbing embedded with 2-opt local search to solve TSP. They emphasize more on computational efficiency by as fully as possible exploiting GPUs hierarchical hardware parallelism. They introduce an intra-parallelism scheme and a shared memory tiling approach, which yield eight times faster than an OpenMP-based counterpart on a 20 cores CPU.

The previous works have researched the parallel ILS implementation on GPUs and demonstrate that GPUs could accelerate ILS algorithms significantly. However, little attention is paid to the performance analysis model for the design of LSM algorithms on GPUs. Further, the analysis could motivate us to optimize the performance of the parallel ILS on GPUs.

4 Parallel ILS algorithms on GPUs

4.1 Parallel ILS design

Following the terminology defined by Talbi [38] in parallel metaheuristics, we design a parallel ILS focusing on the iteration level. In this case, we parallelize the local search process in Algorithm 1. Figure 2 illustrates the parallel local search accelerated by GPU in the iteration level. In this design, a host that contains CPU and system memory handles the major algorithm control flow and memory management. The most time-consuming part of the local search is the evaluation of neighborhoods, which could be accelerated by a GPU. The host copies TSP problem data structures such as the city distance matrix to the GPU memory. Because the problem data are constant during the local search process, it could be transferred into the constant memory or texture memory on GPUs only once. The solution structure should be transferred into the GPU global memory before each iteration of the local search process. The other processes in Algorithm 1 are calculated on the host.

Fig. 2
figure 2

The parallel local search accelerated by GPU in the iteration level

Full size image

The local search operator we choose is the 2-opt. Figure 3 shows the generation of a neighborhood in the 2-opt kernel for the TSP. The edges \((i,i+1)\) and \((j,j+1)\) in the original solution (at the left of Fig. 3) are broken and the fragments are reconnected to a neighborhood solution (at the right of Fig. 3). Each neighborhood (i, j) is associated with a unique id wid (work id), which is the number identity of a neighbor instead of number pairs.

Fig. 3
figure 3

Illustration of generation a neighborhood in 2-opt operator for the TSP

Full size image

As depicted in Fig. 4, neighborhoods are processed in parallel on GPU. There are two phases: the improvement computation and selection of the best neighborhood. In the first phase, the key issue is the mapping between a neighborhood and a GPU thread which is explained in the next subsection. Each GPU thread performs the improvement computation of a neighborhood. In terms of task parallelism, each GPU thread could also be assigned with m neighborhoods and process them sequentially. In the second phase, we select the best improved neighborhood. In terms of data parallelism, the improvement results in each GPU work-group are processed to find the best improving neighborhood by parallel reduction in \(O(\mathrm{log}n)\) steps [12]. Then, we select the best neighborhood from all work-groups by atomic operations.

Fig. 4
figure 4

Parallel evaluation of neighborhoods on GPU

Full size image

4.2 Mapping strategy of neighborhood structures on GPU

Assuming that there are n cities in a TSP, the size of neighborhoods is \(\frac{n*(n-1)}{2}\) in the 2-opt. In our algorithm, we evaluate all of the neighborhoods on GPU and choose the best improved one. This strategy is also regarded as the best improvement. For the mapping between a neighborhood and a GPU thread that is not straightforward, a conversion between them should be considered for efficiency. Figure 5 illustrates our mapping scheme. First, we use a mapping table in which each row is associated with a city i and each element in a row represents the combination with other cities. In each row, the first element is set with \(i+1\) and the next value increases by 1 until the last element is reached. If the value of element j is greater than \(n-1\), we use \(j\%n\) instead. Second, since the neighbor (i, j) is equal to (j, i), we eliminate the repeated combinations with column id greater than or equal to n / 2. Further, if n is an even number, the neighborhoods with row id ranging from n / 2 to \(n-1\) and column id \(n/2-1\) are also repeated. We keep them for padding to avoid divergent code path on GPUs. Finally, based on the work id wid, the 2-opt neighborhood indexes could be calculated by

$$\begin{aligned} {\left\{ \begin{array}{ll} i=\frac{\mathrm{wid}}{\mathrm{width}}\\ j=(i+1+\mathrm{wid}\%\mathrm{width})\%n,\\ \end{array}\right. } \end{aligned}$$
(1)

where width is the size of a row which is equal to n / 2.

Because 32-bit integer arithmetic on GPU is more costly than single-precision floating-point arithmetic [32], less number of integer operations should be considered for efficiency. By simple calculation, we find that our mapping calculation contains only five integer operations which is relatively small compared to that in [28, 35]. Each thread calculates the improvement \(\Delta (i,j)\). Then, we select the minimal \(\Delta \) in all the threads and get the corresponding neighborhood (i, j).

Fig. 5
figure 5

Neighbors and threads mapping on GPU

Full size image

To achieve higher hardware utilization, we assign m neighborhoods to a thread. Each thread processes m neighborhoods sequentially and stores the best neighborhood to local memory for the reduction process. In this case, the work id can be calculated by \(\mathrm{wid}=\mathrm{tid}*m+\mathrm{offset}\), where tid is the thread id and offset is the private work id in thread tid.

4.3 Performance analysis of 2-opt kernels

We introduce Roofline model for GTX780 to analyze 2-opt kernels in Fig. 6. The vertical line (the dashed line in the figure) is started from the operational intensity of an algorithm on the x-axis and ended with the intersect point on the y-axis. The performance of the 2-opt kernel on GTX780 lies somewhere along that line. The key points behind the Roofline model are to calculate the operational intensity (FLOPs/Byte, also named arithmetic intensity) of a GPU kernel and then to determine if the kernel is compute-bound or memory-bound for further algorithm optimization.

Fig. 6
figure 6

Performance analysis of 2-opt kernels on a GTX780 by Roofline model. The graph is on a logClog scale. The diagonal roof is the bound by memory bandwidth, and the horizontal roof is the bound by computational performance. We add a ceiling, named no FMA (fused multiply-add), for which there is no FMA operation in these kernels

Full size image

First, we introduce major steps in the 2-opt kernel. In Fig. 3, the edge \((i,i+1)\) and edge \((j,j+1)\) are broken and then the four fragments are reconnected. The improvement of the neighborhood is the length changed by these two new edges. To reuse the distance of cities, a pre-calculated matrix d with size \(O(n^2)\) is used as a lookup table. The Euclidean distance of (i, j) is calculated by

$$\begin{aligned} d(i,j)=\sqrt{(x_i-x_j)^2+(y_i-y_j)^2}, \end{aligned}$$
(2)

where (x, y) is the coordinate of a city. Because the distance matrix d is too large to fit in GPU local memory, it is always put into global memory. So, we name this kernel 2-opt-glm.

Second, we measure the performance of the 2-opt-glm kernel by floating-point operations per second (FLOP/s). The operational intensity of the 2-opt-glm kernel is calculated as follows: We consider a neighborhood (i, j). First, four cities at positions \(i, i+1, j\) and \(j+1\) are loaded from solution s. Now we have four cities c1, c2, c3, c4. Second, the lengths of four edges (\((i,i+1),(j,j+1),(i,j),(i+1,j+1)\)) are loaded from d. Until now, there are totally eight float values loaded. Third, the improvement of neighborhood (i, j) is calculated by \(\Delta (i,j)=d[c1][c3]+d[c2][c4]-d[c1][c2]-d[c3][c4]\) which contains three floating point operations (FLOPs). By simple calculations, we can get the operational intensity OI\(_{\mathrm{2opt}}=\frac{3}{8*4}=0.09375\) FLOPs/Byte. Figure 6 illustrates that the theoretical throughput of 2-opt-glm is only 27 GFLOP/s on a GTX780 with memory bandwidth of 288.4 GB/s. As a result, we conclude that the 2-opt-glm kernel is memory-bound. Additionally, the memory access pattern of the 2-opt kernel is irregular. The GPU memory bandwidth could hardly be fully exploited because of these non-coalesced accesses.

4.4 Analysis of previous optimization approaches

There are two existing optimization approaches. The first one is to utilize the GPU texture memory that proposed by Luong et al. [28]. Since the memory access pattern of 2-opt-glm is irregular and could hardly coalesce, this would degrade the performance of the global memory accesses. Therefore, the use of GPU texture memory is well suited for the following reasons:

  1. 1.

    The data structures used in the improvement computation phase are read-only values.

  2. 2.

    The texture memory space reside in global memory is cached in texture cache. There is no need to consider noncoalesced accesses.

We call the strategy 2-opt-tex. This could also be explained by aforementioned performance analysis. The 2-opt-glm kernel is memory-bound, so the global memory traffic should be optimized to approach the theoretical performance.

Rocki and Suda [35] also have noticed the memory bandwidth limitation of the 2-opt kernel. They present a repeated computing data strategy to better utilize the GPU computing power. They utilize the on-chip local memory on GPU. We name this kernel 2-opt-shm. In fact, this approach increases the operational intensity of the 2-opt kernel. Two data structures are stored in local memory: the solution array and city coordinates. For the size of a TSP solution that is n, it is easy to use local memory. But the size of the city distance matrix that is \(n^2\) that exceeds the capacity of GPU local memory (48 KB). It is unable to load the whole city distance matrix into GPU local memory. The alternative method is to load the city coordinates (2n) into GPU local memory, and the Euclidean distances between cities are calculated on-the-fly. Fosin et al. [9] also suggest using this strategy.

We can learn from Eq. (2) that there are seven FLOPs for computing d(i, j). Four city distance entries are calculated for each neighborhood, so there are additional 28 FLOPs to the 2-opt kernel. As the number of work-items in a work-group is limited to 1024, for achieving higher operational intensity, we could assign m neighbors to each thread. Considering a work-group, we compute the operational intensity by total FLOPs dividing total bytes accessed in

$$\begin{aligned} \mathrm{OI}_{2\mathrm{optE}}=\frac{w*m*(3+28)}{(n+2n)*4}=\frac{31wm}{12n}, \end{aligned}$$
(3)

where w is the number of work-items in a work-group, m is the number of neighbors processed by a work-item and n is the number of cities. Given a work-group size 1024 and each work-item process ten neighbors, the operational intensity for a TSP with size 1024 is 25.83 FLOPs/Byte. Figure 6 shows that the 2-opt-shm kernel is compute-bound. Because there are no simultaneous floating-point additions and multiplications in the 2-opt kernel, we could hardly exploit the FMA operation supported by GPU. Thus, we add a performance ceiling, named no FMA, which is half of the peak computation performance (see Fig. 6).

The theoretical throughput of the 2-opt-shm kernel reaches 1988.5 GFLOP/s. This kernel makes a tradeoff between the data transfer from global memory and the computation of city distance. However, it is also bounded by the local memory size. Due to this the 2-opt-shm kernel is unable to apply to TSP instances that is larger than 4096 cities [\((4096+4096*2)*4=49,152\,\mathrm{Bytes}=48\,\mathrm{KB}\)].

4.5 Our optimization approaches

We optimize the 2-opt kernel motivated by the above performance analysis. In the following sections, we present the optimization approaches aiming at two strategies of the Euclidean distance calculation: pre-calculation once (LUT) or recalculation every time (CALC). In order to clearly demonstrate the optimizations in the parallel implementation, the major pseudo-code of the two kernels used to implement the OpenCL version of the algorithm is shown in Listings 1 and  2.

figure b

4.5.1 Optimization of the 2-opt kernel based on the LUT strategy

Our major idea is to increase the operational intensity of the 2-opt kernel. Because the city distance matrix is too large to fit into local memory, we still store it in the texture memory for efficient data reuse (e.g., line 24 in Listing 1). We name this kernel 2-opt-tex-shm. Here, i and j stand for the position in the solution array (lines 17–18 Listing 1). Similar to the 2-opt-shm kernel, we use local memory to store the solution array s (lines 4–7 in Listing 1). Further, we load the length of edges in solution s to a local memory array \(\mathrm{break}\_\mathrm{edges}\) so that we can later use it for the improvement computation of neighborhoods (lines 9–13 in Listing 1). For example, the length of edge \((b,b+1)\) is saved to \(\mathrm{break}\_\mathrm{edges}[b]\). Thus, the improvement computation of the neighbor (i, j) could use the length \(\mathrm{break}\_\mathrm{edges}[i]\) and \(\mathrm{break}\_\mathrm{edges}[j]\) that reside in local memory (line 26 in Listing 1).

We keep the number of FLOPs for computing improvement of neighborhoods but reduce the overall data size load from global memory. For each work-group, the size of local memory used is 2n (the s and \(\mathrm{break}\_\mathrm{edges}\) array). For each neighborhood, there are still two edges to be loaded from texture memory. Similar to the analysis method of the 2-opt-shm kernel. We compute the operational intensity by total FLOPs dividing total bytes accessed in

$$\begin{aligned} \mathrm{OI}_{2\mathrm{optTS}}=\frac{w*m*3}{2n*4 + w*m*2*4}=\frac{3wm}{8(n+wm)}, \end{aligned}$$
(4)

where w is the number of work-items in a work-group, m is the number of neighbors processed by a work-item and n is the number of cities. Given a work-group size 1024 and each work-item process ten neighbors, the operational intensity for a TSP with size 1024 is 0.34 FLOPs/Byte. So, the theoretical performance is 98 GFLOP/s (see Fig. 6).

4.5.2 Optimization of the 2-opt kernel based on the CALC strategy

Since the neighbors are mapping to a 2D matrix as illustrated in Fig. 5 before, we could assign several rows of neighbors to a work-group and the work-items within the work-group execute evaluation of each neighbor in a data-parallel fashion (Fig. 7). We name this kernel 2-opt-coord. Here, i and j stand for the position in the ordered coordinate array (coords) of a solution (Listing 2). We use two loops in the kernel. In the outer loop (lines 3–7 in Listing 2), each work-item reads the data of city in position i from global memory. In the inner loop (lines 8–13 in Listing 2), each work-item reads the data of city in position j in parallel from global memory. Then, we optimize the operational intensity of the kernel. First, similar to 2-opt-tex-shm, we create a global memory buffer, named buf, to store the length of break edges. Therefore, the number of distances to compute for each neighbor reduces from 4 to 2. Second, the coordinates for cites at position i could be reused, so for each neighbor, the number of the coordinates loaded is 2 and the number of break edges is 1. We compute the operational intensity by \(\frac{3+14}{(2*2+1)*4}=0.85\). The theoretical peak performance of 2-opt-coord is 245 GFLOP/s (see Fig. 6).

Fig. 7
figure 7

Optimization of global memory access pattern in 2-opt-coord kernel

Full size image
figure c

We could learn from the Roofline model analysis (Fig. 6) that the kernel is memory-bound. Therefore, our other optimization is to improve the performance of global memory accesses. Note that in Fig. 7, the j value is not continuous when the j index is \(n-1\). This would cause uncoalesced global memory accesses. For example, the neighbor (\(i=5,j=7\)) and its next one (\(i=5,j=0\)) are not continuous in the index of j. Our strategy is to expand the size of the coordinate array to 2n and copy the first n elements of the array to fill the expanded space. Thus, if j exceeds \(n-1\), the access of index \(j\%n\) is replaced by j. For instance, we could use (\(i=5,j=8\)) to retrieve the coordinate data of the next neighbor. Thus the global memory access is coalesced (lines 13–15 in Listing 2) and, therefore, higher memory bandwidth is achieved. Furthermore, because the kernel accesses the data without use of the local memory, the size of the TSP problems to be solved is not limited by the hardware resource.

5 Performance evaluation

We have experimented our algorithm implemented using C\(++\) and OpenCL on a PC. The detailed hardware specifications are given in Table 1. The OS is Microsoft Windows 7 64-bit ultimate edition. Our experiment uses a standard set of benchmark instances from the TSPLIB library [34]. The sizes of these TSP problems are varying from 198 to 4461 cities which could represent samples from small to medium and large scale [11]. The perturbation method in Algorithm 1 we choose is a double-bridge move, like nearly all ILS algorithms for the TSP [14].

Table 1 Hardware specifications of our test platform
Full size table

Similar to Rocki and Suda [35], we use single-precision float-point numbers for the city distance. Each TSP instance tests a fixed number of iterations 1000 times in ten tries, and we use the average value for comparison. We record the 2-opt kernel execution time of the sequential CPU version and parallel GPU-accelerated version, respectively, and the speedup is calculated by dividing the sequential CPU time with the parallel GPU time.

5.1 Thread configuration optimization

As we state that the 2-opt-shm kernel is compute-bound, a proper configuration of m in Eq. (5) should be considered to achieve higher GPU hardware utilization. The number of work-groups g is calculated by the total number of neighbors divided by the number of neighbors in a work-group,

$$\begin{aligned} g=\left\lceil \frac{\frac{n*(n-1)}{2}}{1024*m}\right\rceil =\left\lceil \frac{n*(n-1)}{2048*m}\right\rceil . \end{aligned}$$
(5)

If g is small than the number of CUs on a GPU, it makes some CUs idle during the kernel execution, thus lowering the hardware utilization. To keep all CUs busy and map each work-group to a dedicated CU, we set \(g=12\) and solve m for each TSP instance. The configuration of m for each TSP instance is presented in Table 2.

Table 2 Configuration of parameter m for each TSP instances
Full size table
Fig. 8
figure 8

Performance measured in terms of GFLOP/s

Full size image

5.2 Floating point performance comparison among 2-opt kernels

Figure 8 shows the performance results obtained by measuring the execution time of each kernel. We use the theoretical performance depicted in Fig. 6 for comparison. Due to the uncoalesced global memory accesses, the 2-opt-glm only achieves 41 % of the theoretical performance in pr2392. With the help of the GPU texture memory, the 2-opt-tex kernel reaches 81 % of the theoretical performance in pcb3038 and performs better than the 2-opt-glm kernel. The 2-opt-tex-shm kernel improves the performance of the 2-opt-tex kernel significantly. Because the city distance is calculated on GPU, the 2-opt-shm and 2-opt-coord kernels have a much higher floating point operation throughput than the 2-opt-glm, 2-opt-tex and 2-opt-tex-shm.

However, the performance analysis results (see Fig. 6) are too rough, especially for the 2-opt-shm kernel (see Fig. 8). To achieve more accurate performance prediction, we could add memory bandwidth and computational ceilings to the Roofline model [41]. In this paper, we focus on the performance optimization of the GPU-based ILS algorithm. So, the performance prediction is left for the future work.

5.3 Speedup comparison among 2-opt kernels

Figure 9 shows speedups of 2-opt kernels. The 2-opt-tex kernel outperforms 2-opt-glm significantly in large datasets. We notice that the speedups of 2-opt-tex drop to 67.6 in fnl4461. This is explained in two different ways. On the one hand, due to large data arrays being accessed randomly, texture memory cache efficiency is decreased drastically. On the other hand, because the 2-opt-tex kernel is memory-bound, its performance is highly related to the attainable memory bandwidth.

The 2-opt-shm kernel performs as high as 182\(\times \) speedup in pcb3038 which is 65 % faster than 2-opt-tex. This demonstrates that the pressure on global memory access is relieved in 2-opt-shm, and the GPU computing power is better utilized. Our 2-opt-tex-shm kernel also delivers promising performance even approaching the 2-opt-shm kernel. However, because 2-opt-tex-shm avoids repeated calculation of city distances, the algorithm is more work-efficient than 2-opt-shm. The best performed one is 2-opt-coord which achieves a speedup of 279\(\times \). Since the global memory access of 2-opt-coord is coalesced, its attainable memory bandwidth is very high. And it also reads the pre-calculated length of two edges for each neighbor to avoid re-computations. Therefore, this kernel is balanced with memory bandwidth and floating point computation.

Fig. 9
figure 9

Kernel speedups comparison results

Full size image
Table 3 Solution quality comparison result
Full size table

5.4 Solution quality

To ensure the solution quality of our approach is the same as the CPU implementation, we run ILS with a fixed 1000 iterations for each kernel, and we get average results in ten tries. Table 3 lists the result of TSP instances ranging from 198 to 4461 cities for all algorithms.

The results indicate that the solution quality of the GPU versions is similar to that of the sequential CPU. Our GPU algorithm has the same principal as the sequential CPU version; thus, the solution quality is preserved.

5.5 Comparisons with existing high performance GPU-based local search algorithms

We also make a comparison with two high-performance GPU-based local search algorithms in existing literatures (“State-of-the-art”): Logo [36] and TSP-GPU [33]. Both of them are publicly available. The algorithms are based on ILS and random-restart hill climbing, respectively, which embed the 2-opt local search operator. Since a parallel heuristic method has to be efficient both in execution speed and in solution quality, we provide computational performance and solution accuracy results for comparison. We measure the computational performance by calculating the number of 2-opt neighbors evaluated (referred to as GigaNBs) per second. We also give mean percentage deviations from optimal solution to demonstrate the solution accuracy (the lower the better).

Fig. 10
figure 10

Throughput comparison with high performance GPU-based local search algorithms

Full size image

The version of Logo is 0.62 and it is built with OpenCL 1.2. The version of TSP-GPU is 2.2 and it is built with CUDA 7.5. We choose our best performing kernel, 2-opt-coord, to compare with them. All of the algorithms are set to run with a fixed number of local search iterations or restarts (1000) in ten tries. And they are compiled without fast math option to make the comparisons as fair as possible. We also observe from the 2-opt code of Logo that n neighbors are not evaluatedFootnote 1. This has a subtle impact on the intensification strength of the local search, but may influence the solution quality. Therefore, we change n to \(n-1\) in Listing 2 (line 3) to align our code with Logo.

Table 4 Solution quality comparison with high performance GPU-based local search algorithms
Full size table

The computational performance of TSP-GPU is the best one (Fig. 10). This could be explained in two different ways. On the one hand, TSP-GPU exploits the independency of each restart to achieve very high GPU hardware utilization (i.e. a restart per block). On the other hand, since all neighbors of a restart computed in a block, more fine-grained parallelism could be achieved by intra-parallelization and shared memory tiling. Our approach is up to 1.7\(\times \) faster than Logo. This demonstrates that our analysis and optimization are effective.

The solution quality comparison results illustrate that the TSP-GPU is the worst one (Table 4). This is because the major differences between ILS and multi-start hill climbing is the exploring manner in solution space (single-walk and multi-walk respectively). Although both of them embed a 2-opt local search operator, the high-level algorithm frameworks are different. In ILS, perturbation plays a very important role in escaping from local optima. On the contrary, multi-start hill climbing is based on a “random restart” approach that each climber is independent in execution and thus solution improved by each climber is limited. Table 4 also demonstrates that our solution quality is as competitive as that of Logo.

6 Conclusions and future work

We present a parallel ILS design and adopt the Roofline model to analysis the performance of previous 2-opt kernels. Based on the analysis, we identify the disadvantages of the 2-opt kernels. We utilize the texture memory for optimizing memory transfer and use the local memory as a user-managed cache for LUT. Furthermore, we also enhance data parallelism and coalesce global memory access for CALC. All algorithms use TSP as a case study and are tested with a large range of instances varying from 198 to 4461 cities. The experimental results demonstrate that our optimization strategies toward GPU platforms are effective. The solution result is also evaluated to guarantee that the quality is similar to the sequential CPU version. We also compare our algorithm with existing high-performance GPU-based local search algorithms. The proposed algorithm is efficient in computation and effective in solution quality.

Research on parallel LSMs remains in development. We acknowledge that we have experimented on a basic LSM algorithm. There are variants of LS, such as the tabu search, simulated annealing and guided local search, which still need to be optimized on GPU. And since ILS could also solve combinatorial optimization problems other than TSP, the GPU-based ILS algorithm should be reconsidered for its differences in data structure. Furthermore, the local search kernel could be combined with other population-based metaheuristic algorithms, such as ant colony optimization (ACO), particle swarm optimization (PSO) and honey bee mating optimization (HBMO) to more efficiently find optimum solutions. This combination should also be analyzed to utilize the full potential of the GPU parallelism power [23, 43].

In future work, we will try to extend the optimization method of GPU accelerated metaheuristics algorithms to the fields of CAD, graphics and images [5, 6, 15, 22, 42, 45]. We will also conduct comparative study of GPU-based ILS algorithms on different GPU platforms to analyze the differences in ratios of cores to memory [11].