1 Introduction

Metaheuristics are widely acknowledged as essential tools for solving, within a reasonable time frame, optimization problems that are often NP-hard (Garey and Johnson 1979), time-consuming and complex (Alba et al. 2009). However, the limits of what may be solved in a “reasonable” time frame can be different, at least considered excessive, for the growing needs of research and industry alike. Therefore, parallelism appears to be a natural way to not only reduce the search time, but also to improve the quality of the solutions provided.

In recent years, graphics processing units (GPUs) have emerged as a powerful platform for massively parallel computing, achieving high performance on long-running scientific applications (Owens et al. 2007). Thus, several researchers have presented ideas to modify existing optimization algorithms running on CPUs for the new GPU architecture: genetic algorithms (Cavuoti et al. 2013), cellular genetic algorithms (Vidal and Alba 2010), particle swarm optimization (Rabinovich et al. 2012) and others (Langdon 2010; Maitre et al. 2012).

However, most of the existing GPU optimization algorithms still fail to take full advantage of the available CPU–GPU simultaneous, collaborative computing power. Moreover, in much work the CPU is simply left as a controller and its computing power is wasted. In general, when running a GPU application in a heterogeneous CPU–GPU system to solve large-scale complex problems, only one thread is assigned to a CPU core to control the GPU. The rest of CPU cores are in idle state, while the GPU performs the optimization of many computing tasks. This wastes a large amount of available CPU resources. Therefore, developing an effective method to make full use of all the available computational resources of both CPUs and GPUs has become extremely relevant and has recently drawn the attention of many application developers. Some approaches (Daga et al. 2011; Yu et al. 2011; Agulleiro et al. 2012; Cardellini et al. 2014) have been developed to simultaneously use both multi-core CPUs and GPUs to perform a specific task, instead of the CPU-only or GPU-only alternatives. Several approaches have also elaborated on the concept of hybridization to take advantage of both the algorithmic design and hardware available platforms (Chamberlain et al. 2008). In this way, the design of efficient hybrid CPU–GPU optimization algorithms encompasses many challenges with both software and hardware issues.

The key challenge that arises when working with hybrid systems is how to assign the most suitable optimization processes to CPUs and GPUs. Thus, each approach has to maximize the utilization of all the computational resources without losing the computational power that each architecture provides and enhance the capacity of resolution of high complexity problems. However, to the best of our knowledge, very few implementations (Luong et al. 2010; Pospichal et al. 2010; Krömer et al. 2011; Coelho et al. 2012) follow the cooperation model between CPUs and GPUs to solve a diverse group of complex optimization problems where parallelism can be exploited in a transparent way.

We propose a novel hybrid CPU–GPU implementation in a heterogeneous system that is able to provide a robust and cooperative behavior based on two complementary optimization algorithms. We implement our proposal on multi-core CPUs plus a GPU using OpenMP (OpenMP Architecture Review Board 2008) and CUDA (NVIDIA Corporation 2012), respectively. We call the resulting algorithm HySyS (hybrid systolic search). The principal objective is to make HySyS both numerically effective (in terms of the final fitness value obtained) and parallel efficient (short execution times). We combine two optimization techniques, each one running in a CPU and a GPU platform, respectively. The solutions of the CPU technique are used to replace—to improve—some of the solutions in the GPU algorithm. Each optimization technique has been selected, considering its performance and suitability for the hardware architecture where it will work. We combine these two algorithms into one CPU–GPU hybrid algorithm for optimization.

The algorithmic component of HySyS that runs in the CPU is a micro-genetic algorithm [\(\upmu \mathrm{GA}\) (Goldberg 1989)] which can use explicit strategies to improve the generated solutions not only for search intensification but also for search diversification, thereby avoiding getting stuck in local optima. The \(\upmu \mathrm{GA}\) incorporates a set of genetic operators that modify a small population that is used to give a set of solutions capable of providing information on the search in the GPU component of HySyS. This GPU component is a systolic neighborhood search (SNS) (Vidal and Alba 2012). SNS considers the GPU as a container of structured optimization units that search in the problem space by passing data between adjacent computing cell units (in our case each cell unit is a GPU-thread).

Previous works (Vidal and Alba 2012; Pedemonte et al. 2012, 2014a, b; Vidal et al. 2014) have already introduced a first approximation of the SNS approach, which has proven to be effective in several optimization problems. However, none of them are targeted to engineering a hybrid GPU-CPU parallel algorithm (the main processes are executed on GPU). Indeed, in (Vidal and Alba 2012; Vidal et al. 2014), the SNS algorithm (the GPU component of HySyS) is presented and evaluated. The work of Pedemonte et al. (2014a, b) elaborates on the systolic genetic search (SGS). It is also an algorithm that follows the systolic paradigm, but one that develops a more complex flow of solutions (both vertically and horizontally) which allows a recombination operator to be included within the cells. That is, none of the published approaches above use hybridization with other techniques nor are they targeted to profit from two different hardware architectures.

The potential of HySyS is that it is able to maintain the diversity in SNS, using a CPU algorithm with strong intensification capabilities (using evolutionary operators). It does so by transferring solutions between the CPU and the GPU, thus reducing the chance of getting stuck prematurely. HySyS has also been designed to avoid communication bottlenecks (between the two sides of the CPU–GPU platform), which may degrade the performance of the algorithm.

To evaluate the behavior and performance of HySyS, we use a test suite composed of instances from three NP-hard problems: namely the massively multimodal deceptive problem (MMDP), the sum set problem (SSP), and the maximum cut problem (MAXCUT). We have compared our proposal to both a CPU version of random search as a sanity check test, and the standalone components of HySyS: \(\upmu \mathrm{GA}\) and SNS.

The comparison has been carried out on the basis of: (1) an exhaustive experimental evaluation has been undertaken plus a statistical analysis of the results to provide the reader with insights into both the search capabilities of the HySyS algorithm and its parallel performance when deployed a CPU–GPU cooperative model, (2) the computational effort, to evaluate the time gains of HySyS in relation to the other techniques, and finally (3) a scalability analysis, investigating the effects of an increasing problem size on the two features above.

The main contributions of this work are:

  • We propose a novel CPU–GPU cooperative hybrid implementation to efficiently solve a set of combinatorial optimization problems in a heterogeneous parallel computing system.

  • We show how two complementary optimization algorithms can be engineered to use the best mechanisms on each architecture to create a cooperative model that can be used in commodity machines.

  • We have conducted a series of experiments to compare the performance of the CPU–GPU cooperative implementation against the optimized CPU-only implementation and the GPU-only implementation providing experimental results that show the effectiveness of the proposed model.

The rest of this paper is structured as follows: Sect. 2 reviews of the literature on hybrid optimization over heterogeneous architectures. Section 3 explains in detail the proposed algorithm and its components. The implementation details are presented in Sect. 4. Section 5 is divided into two parts: the first includes the test suite used, the parameter settings of the algorithms and, the statistical tests used. The second presents the experimental results and analyzes the values obtained. Finally, Sect. 6 presents the main conclusions of the work done and future lines of research.

2 Related work

The combination of components from different algorithms is currently one of the most successful trends in optimization, and it is one, well-known way of hybridization (Davis 1991; Cotta and Troya 1998; Talbi 2002).

The main motivation has been to engineer enhanced algorithms that exploit and combine the advantages of the pure individual strategies. In particular, combinations of local search (LS), simulated annealing (SA), evolutionary algorithms (EAs) and others have provided very powerful search algorithms that are considered to be hybrid metaheuristics (Sinha and Goldberg 2003). We want, however, to use the term hybrid to refer to not only the combination of different pieces of software, but also the involvement of a heterogeneous computing platform (e.g., one using CPUs and GPUs trying to profit from their own individual strong points). In our case, the GPU can easily handle massively parallel tasks by profiting from its extremely large number of cores, while the CPU has been especially designed for non-data-parallel tasks, such as the initializations, starting routines, data transfers, and final result management. Effectively combining these two fairly different computing platforms into one single algorithm is the goal of the work shown here. But this is challenging because of the different features each one has and, especially, because the communication between the CPU and the GPU is highly time consuming in comparison with their actual processing speed. This entire context can lead to a poor utilization of the CPU itself, restrict the creativity of the designer when looking for new algorithms, and might waste a lot of time in transferring data.

There are, however, several related papers, that have already been published in the literature that deserve further analysis so as to demonstrate in a clearer way the contributions of the work presented here. Earlier approaches with a combined use of devices started using a model in which the CPU managed the whole sequential search process and the GPU was dedicated to executing a time-consuming task (usually the evaluation of the quality of solutions for an optimization problem). Once the computing tasks on the GPU had been performed, the information was transferred back to the CPU to continue with the algorithm (Robilliard et al. 2008; Maitre et al. 2009; Pospichal et al. 2010; Krömer et al. 2011). A recent approach has been presented by Tsutsui and Fujimoto (2011), using a multiple GPU architecture that implements an ant colony optimization (ACO) with the CPU as a mere controller. They propose a parallel ACO to solve quadratic assignment problems (QAPs) by combining Tabu Search (TS) with ACO on GPU. This approach obtained a maximum acceleration of \(21\times \).

As the time for transferring information between the CPU and GPU is very long and the function evaluation has to be carried out many times during the execution, the computing time in the GPU was not enough to permit such communication times. The next evolution of the CPU–GPU algorithms was to deploy all the search procedures on the GPU, keeping the CPU merely as a simple controller. In Munawar et al. (2009), the authors introduced a contribution that incorporated a local search (LS) into an EA (a GA), using the GPU as main processor. The communication between them was therefore performed within the GPU. This approach obtained a maximum speedup of \(25\times \) over the selected MAXSAT instances. Research along the same lines was presented by Coelho et al. (2012), where they introduced a distribution of LS tasks between CPU and GPU for the unrelated parallel machine scheduling problem with sequence dependent setup times (UPMSPST). The speedup ranged from \(10\times \) to \(27\times \).

Similarly, a novel approach was introduced by Luong et al. (2010). They presented interesting guidelines relating to the distribution of the search process between the CPU and the GPU, minimizing the data transfer between them. The algorithmic proposal indicates that the CPU manages the whole hybrid evolutionary process and lets the GPU be used as a coprocessor dedicated to intensive calculations. The hybridization model used in their work included an EA and an LS. This approach obtained a maximum speedup of \(14\times \). The proposal certainly made clear that hybridization is a powerful way to achieve high computational efficiency in both architectures. In (Luong et al. 2013), the authors used the GPU to solve a variety of problems using the GPU to evaluate an LS per GPU, while the CPU was used to control the algorithm (a hybrid algorithm with multiple GPUs). The algorithms report a speedup of up to \(50\times \) for the instances used with respect to the sequential version.

While our goal is to work with hybrid metaheuristics, the implementation of techniques in a cooperative architecture of CPU–GPU is spreading to other scientific applications, such as algebra problems (Wang et al. 2014) and sparse matrix-vector multiplication (Yang et al. 2015). They have designed a class of heterogeneous algorithms to maximize the degree of parallelism, to minimize the communication volume, and to accommodate the heterogeneity between CPUs and GPUs. These algorithms have wide adaptability for different types of problem instances.

After analyzing all these contributions, it seems clear that very few approaches use CPU–GPU as a tandem to numerically search along the problem space. The few partial approaches related to using both devices have reported very good results. All this makes it clear that combined CPU–GPU is worthy of further investigation, which we do here, by adding a new recent idea: that of systolic computing on GPUs.

From the published material, it can be seen that the contribution of this paper refers to the combination of two algorithms (namely, \(\upmu \mathrm{GA}\) and SNS). They have been carefully selected to create a hybridization on a CPU–GPU computing platform that effectively performs both numerically and in parallel. This unification results in a hopefully efficient and innovative way of hybridizing over heterogeneous hardware.

3 HySyS

This section describes of our CPU–GPU cooperative optimization technique called HySyS, which can make full use of all the available computational resources of both CPUs and GPUs. After briefly presenting the working principles of the main technique, both algorithmic components (SNS and \(\upmu \mathrm{GA}\)) are detailed and the pattern of explorations of the search space carried out by each method is explained. The final design of the proposal with a detailed explanation of the entire process is given afterwards.

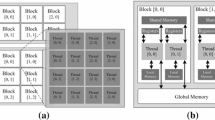
Hybrid systolic search is aimed at exploring the parallelization in a hybrid CPU–GPU computing architecture. The main idea is as follows: CPU thread 1 executes the \(\upmu \mathrm{GA}\), while CPU thread 2 is dedicated to communicating with the GPU and managing the execution of the SNS algorithm on the GPU side. The typical flow of this CPU–GPU computing method is shown in Fig. 1. Briefly, a dedicated CPU thread firstly starts the data transfer operation and then, the input data are allocated into the GPU to be copied to the global memory. After the data transfer operation has been completed, CPU thread 2 invokes the CUDA kernel and all GPU threads run the Systolic Search defined in parallel. The purpose of this first step of HySyS, that initializes the search on the GPU, is to avoid wasting computational time. Then, CPU thread 1 is launched in parallel with the systolic search with a \(\upmu \mathrm{GA}\). When the \(\upmu \mathrm{GA}\) finishes, a series of routines has generated a set of new solutions. They are inserted into the population of the Systolic Search. We use the CPU solutions to look for an overall quality improvement of the systolic population and to help in the search for the optimal value of a problem. With this approach, we seek an improvement in the space of solutions of the SNS algorithm. From the \(\upmu \mathrm{GA}\) we try to use the genetic operators because their complexity and behavior are not suitable for implementation on a GPU. In the context of \(\upmu \mathrm{GA}\), we try to use their genetic operators on a CPU due to their behavior and because the complexity of some operations makes them unsuitable for their use on a GPU.

Fig. 1
figure 1

Hybrid systolic search

Full size image

In the following subsections we explain the algorithms that comprise our approach and finish with a more detailed explanation of HySyS operation.

3.1 Systolic neighborhood search (SNS)

Systolic neighborhood search has its roots in systolic computation (Kung 1979) which shows a realistic model of computation that captures the concept of pipelining, parallelism, and interconnected structures. There is an exciting set of concepts that can be translated into optimization if one sees systolic computation from a high level and broad point of view. Systolic computation works on a large array of connected data processing units called cells. These cells can be small processing elements, hardware elements (software elements in our case, GPU threads), where each of them performs the same task, calculating simple functions like multiplications, additions, or other such low-level operations. The purpose of this architecture is to keep a constant flow of data throughout the entire network after an initial data input and, as a consequence, it produces an elaborated (optimized in our case) output. This concept was used to create a new class of algorithms in GPU broadly known as the systolic neighborhood search (SNS) (Vidal et al. 2014). The new concept of algorithms has also been inspired by the idea of animal heart working principles from the point of view of circulating blood in the animal’s body.

The main approach of SNS is to define a mesh where the solution flows in a toroidal mesh. Taking into account the systolic philosophy, SNS presents a model based on interconnected cells, threads in our case. Each one is capable of performing a small modification in all solutions using the same optimization operator method. The crux of this approach is to ensure that once a solution (data item) is brought out from the memory it can be used effectively at each cell it passes while being “pumped” from cell to cell along the rows of the mesh. Being able to use each input solution a number of times (and thus achieving high computation throughput with only modest memory bandwidth) is just one of the many advantages of the systolic approach (Kung and Leiserson 1978). Similarly, advantages such as modular extensibility, data flow simply and constantly, elimination of global broadcasting, and fast response time structure (Kung 1984, 2003), represent substantial advantages over more complicated ones in design and implementation.

The operations of the SNS are presented in Algorithm 1. The algorithm starts by defining the size of a mesh M of size \(m \times n\), where m is the number of rows and n is the number of columns. These two values depend on the size s of the problem instance to be solved. Value s is used to define these two variables for two reasons. Firstly, we define a perturbation pattern where each row and column has an important role. The row indicates the number of perturbations to be performed on each element of the vector solution. The column in the mesh indicates the starting position at which SNS proceeds to create perturbations. Indeed, with n columns we can perform changes on each element of a solution. The row in the mesh indicates the size of the neighborhood, i.e., how many elements undergo changes. Secondly, as the aim of SNS is to perform controlled perturbations on solutions when they flow through the mesh, the cell position is used to define a simple modification pattern that they all follow. SNS generates \(m \times n\) solutions assigned initially to each cell in M at position (x, y). Each solution is generated randomly and is then evaluated. Values x and y contain the coordinates of a solution inside the mesh.

Then, some operations are carried out to improve the quality of the solution currently located in each cell. Subsequently, with a synchronous movement a solution can move to the next cell where SNS can make several modifications to the incoming solution with the aim of improving it.

figure a

Algorithm 2 presents the operations performed by each cell in SNS. It starts by creating a copy \(sol'_{(x,y)}\) of the original \(sol_{(x,y)}\) (line 2). Then, \(sol'_{(x,y)}\) undergoes a perturbation process that depends on the parameters x and y, i.e., its location in M (line 3). Parameter x defines the number of values to be changed in the vector solution, while parameter y indicates the left position in the array where changes start (line 3). Once all the changes have been made, and as the total re-evaluation of \(sol'_{i}\) could be very time consuming, we have used a partial function evaluation, thus re-evaluating only the changed section in the vector solution copy (line 4). Finally, if \(sol'_{(x,y)}\) is better than \(sol_{(x,y)}\), the latter is replaced by the former; otherwise, the original solution remains unchanged (lines 5–7). When all the cells of the mesh have performed the changes on their respective solutions, SNS synchronously moves all solutions in each cell to the next one in the row (lines 8–9).

figure b

A variant of the previous canonical approach is used in here: \(\mathrm{SNS}^{\mathrm{exp}}\). This variant has demonstrated a stable behavior in a wide variety of sizes of instances (Vidal et al. 2014). By reducing the number of rows we can generate a larger flow of solutions, reducing the number of evaluations. However, we cannot use the same mechanism as in the canonical SNS of incremental changes in the solutions per line, so we need to define two things: the number of rows and how many components are changed in each line. The first factor is computed by using the problem size: \(\mathrm{SNS}^{\mathrm{exp}}\) will have \(\log _2 s\) rows. Second, \(\mathrm{SNS}^{\mathrm{exp}}\) indicates the number of elements to perturb using the result of exponentiation with number two as the base and the row number as the exponent. This result is used as the reference in the changes per row. With this approach, the number of values to be changed increases in multiples of two until reaching the total number of elements in a solution.

3.2 A micro-genetic algorithm (\(\upmu \mathrm{GA}\))

In our quest for an algorithm to run in the CPU we first list the requirements that it should meet so as to be used inside the hybrid framework of this approach:

  • It must be a fast/light algorithm, capable of interacting with the GPU several times during the systolic computing.

  • Accurate, in computing the optimum or a quasi-optimum solution.

  • Flexible enough, to plug into the best operators known for optimization problem solving in the literature.

With these requirements in mind, one algorithm seems particularly suitable: a micro-Genetic Algorithm (\(\upmu \mathrm{GA}\)). The “micro” term (\(\upmu \)) refers to a “small population” GA that operates with the same genetic operators as standard GAs. Therefore, as the population size increases GAs find better solutions. However, larger population sizes require more computational time to find the optimal solution. To avoid these problems, Krishnakumar proposed micro-Genetic Algorithm (\(\upmu \mathrm{GA}\)) (Krishnakumar 1989), based on the theoretical work by Goldberg (1989).

The \(\upmu \mathrm{GA}\) uses a relatively smaller population size than the sequential genetic algorithm, resulting in less computational time. By virtue of the small populations, convergence can be achieved faster and less memory is required to store the population. Moreover, \(\upmu \mathrm{GA}\) uses elitism to prevent extinction of the best solution in the next generation. Different approaches using \(\upmu \mathrm{GA}\)s have demonstrated their effectiveness in different fields finding optimal (or very near-optimal) solutions in landscapes with multiple local optima (Pu et al. 2010; Kim et al. 2013; Batres 2013; Kahn and Tangorra 2013).

The \(\upmu \mathrm{GA}\) process starts by creating a randomly small population (named P) formed by \(p_{i}\) solutions with \(i=\{1, 2, \ldots , g\}\). Then, \(\upmu \mathrm{GA}\) chooses the parents with a selection operator, which undergoes evolution (crossover, mutation) afterwards. Finally, the offspring is evaluated. These steps are repeated until an auxiliary population (called auxP) is filled with the newly generated tentative solutions. We call all these aforementioned steps to fill auxP the “\(\upmu \mathrm{GA}\) cycle”. Once auxP has been completed, \(\upmu \mathrm{GA}\) replaces P with auxP. This process is shown in Algorithm 3.

figure c

To better control the intensification capabilities of \(\upmu \mathrm{GA}\), a local search procedure has been included to locally improve the solutions found. In our case, we have used a Hill climbing search (HC) (Russell and Norvig 2003). HC is an iterative search that works by starting with an initial arbitrary solution to a problem, then it attempts to aiding a computationally faster and more accurate solution by making local changes incrementally until either the solution is found or the heuristic gets stuck in a local optimum. If the change produces a better solution, an incremental change is made to the new solution, and the process is repeated until no further improvements can be found.

3.3 Detailed outline of HySyS

In this subsection, we describe our proposal named HySyS in more detail. Algorithm 4 shows the distribution task scheme. We can observe the following three steps:

  • Set all the variables and determine the number of required CPU threads and GPU threads, respectively, according to the previously defined variables. Additionally, we create and evaluate the population for each component on the CPU and the GPU respectively, according to the algorithmic scheme determined.

  • Execute each process taking into account the platform used. For the case of the CPU, a \(\upmu \mathrm{GA}\) cycle is executed and for the GPU we run a \(\mathrm{SNS}^{\mathrm{exp}}\) approach.

  • Once a \(\upmu \mathrm{GA}\) cycle has finished, we stop all the processes and replace some tentative solutions from M with P. Finally, HySyS restarts the whole process back to run the \(\upmu \mathrm{GA}\) cycle and continues the \(\mathrm{SNS}^{\mathrm{exp}}\) process.

figure d

In the beginning of the evolutionary process, HySyS starts with the initialization on the host and device sides. During the initialization phase, we first set parameters for both components \(\upmu \mathrm{GA}\) and \(\mathrm{SNS}^{\mathrm{exp}}\) (lines 1–3). Then, we launch the \(\upmu \mathrm{GA}\) process for creating and evaluating P (lines 4–6). Also, the kernel is launched in the device side creating and evaluating the population in the mesh M (lines 7–9).

In the host side we start evolving a small population composed of five tentative solutions, \(P = \{p_1,\ldots ,p_5\}\). First, \(p_1\) and \(p_2\) undergo HC (local search). Each newly generated individual is allocated \(auxP_1\) and \(auxP_2\). Then, \(p_3\) and \(p_4\) are crossed over and two offsprings are generated. The best child replaces \(auxP_3\) and the other one undergoes mutation. The goal is to introduce as much new genetic material as possible (diversification). Finally, in \(auxP_5\) the best solution of P is stored to preserve the best solution in the last iteration (line 16). This process is explained in Algorithm 3.

While \(\upmu \mathrm{GA}\) is running on CPU, HySyS proceeds to evolve \(m \times n\) solutions for \(\mathrm{SNS}^{\mathrm{exp}}\) on the GPU (line 22 of Alg. 4), which takes them all and starts the cell computations and the solution flow as shown in Algorithm 1. \(\mathrm{SNS}^{\mathrm{exp}}\) is executed without any interruption until a \(\upmu \mathrm{GA}\) cycle is completed. At this point, HySyS replaces u solutions in M, with the solutions coming from P, the population of \(\upmu \mathrm{GA}\). The replacement is performed if the copy (random solution selected from P) is better than the previous one (random solution selected from M), otherwise the old solution remains intact. The value for the parameter u is usually greater than the size of P, i.e., \(u > 5\). The value of u must be carefully chosen because a high value (i.e., \(u = m \times n\)) could generate considerable bias in the \(\mathrm{SNS}^{\mathrm{exp}}\) population. Once it has been done, HySyS re-launches both \(\upmu \mathrm{GA}\) and \(\mathrm{SNS}^{\mathrm{exp}}\). We can see a general model of the proposal algorithm in Fig. 1. This figure presents the three steps mentioned above in this section. It can be seen that processes are executed on the host and the device side.

A clear consequence of the movement of solutions between CPU and GPU is the necessity of copying structures to the GPU. This movement, in return, has the benefit of eliminating the necessity to make an efficient algorithm on GPU with the main characteristics of \(\upmu \mathrm{GA}\) (that implies divergence). We try to create a balanced workload between the two architectures (CPU and GPU). Our approach aims to improve the quality of solutions without increasing the cost in terms of execution time and provides better and more robust solutions using collaborative methods that fully utilize modern, heterogeneous PC architectures.

4 Implementation details

In this section, we focus on the low-level implementation details. These features actually have a deep impact on the performance of HySyS, as the algorithm for GPUs must be fine-tuned to profit from the massive parallelism of the card. Three main issues are discussed: random number generation, memory deployment, and thread control of the HySyS components.

The performance of any stochastic algorithm, such as an evolutionary algorithm, highly depends on the quality of its random numbers generation. During the execution, \(\mathrm{SNS}^{\mathrm{exp}}\) generates the initial solutions randomly. To avoid transferring any data between CPU and GPU, \(\mathrm{SNS}^{\mathrm{exp}}\) passes a global seed as a parameter on to the kernel only once at the beginning, which is then used by each GPU local thread. The local seed is used to generate random numbers with a fast Mersenne Twister version kernel provided within the CUDA SDK. A GPU version of the Mersenne Twister generator (Podlozhnyuk 2007; Howes and Thomas 2009) is used in some PSO implementations (Rabinovich et al. 2012; Ding and Tan 2014). For more information about GPU-based random numbers generators see (Couturier and Guyeux 2013).

To avoid the continuous communication between the CPU and the GPU, HySyS uses the global memory of the GPU device to store the entire population of the \(\mathrm{SNS}^{\mathrm{exp}}\) algorithm. The size of the problems addressed usually prevents the algorithm from using the shared memory of the SMPs. All the optimization problems considered as the testbed can use a binary string representation. This has allowed us to use bit-level operations so as to save memory space, thereby addressing very large problem instances, which can be allocated within the GPU in one batch of communication.

Regarding thread management on HySyS, we use open multi-processing (OpenMP) (OpenMP Architecture Review Board 2008). OpenMP has established itself as an important method and language extension for programming shared-memory parallel computers. There are several advantages to OpenMP as a programming paradigm for GPGPUs:

  • OpenMP is efficient at expressing loop-level parallelism in applications, which is an ideal target for utilizing GPU’s highly parallel computing units to accelerate data-parallel computations.

  • Incremental parallelization of applications, which is one of OpenMP’s features, can add the same benefit to GPGPU programming.

In this way, OpenMP has allowed us to have a clean and efficient management of the resources by using one CPU thread to handle the computation of the \(\mathrm{SNS}^{\mathrm{exp}}\) algorithm and its resources in GPU, and another CPU thread to manage the \(\upmu \mathrm{GA}\) computation (as can be seen in Fig. 1).

Additional information of the paper such as the details of the CUDA kernels and the datasets employed are available for downloading at http://www.uaco.unpa.edu.ar/pjvidal/

5 Experimentation

This section comprises the experimentation performed to assess the efficiency of HySyS: the testbed, the methodology, and, finally, the analysis of the obtained results.

5.1 Test suite

To analyze the behavior and performance of the algorithms, this section describes the three benchmark problems selected and the features of the instances used.

  • Massively Multimodal deceptive problem (MMDP): is a problem that has been specifically designed to be difficult for an EA (Goldberg et al. 1992). The MMDP problem is composed of k subproblems (\(subp_{i}\), where \(i =\{ 1,2,\ldots ,k \}\)), each one has 6 bits that can take the values 0 or 1. Thus, the degree of multimodality is defined by k. In relation to the subproblems, each one contributes to the overall fitness according to the value resulting from the sum of the 6 bits (accordingly the number of ones present is the result of each one). Table 1 shows the possible values that the sum of each subproblem can take (from 0 to 6). This is known as unitation (number of ones in the solution, regardless of their position). Unitation functions (represented in our case by \(unitation(subp_{i})\)) are also important because they allow the study of the behavior of optimization algorithms in the presence of multiple local and global optima. It is easy to see (plot on Fig. 2) that these subproblems have two global maxima and a deceptive attractor in the middle point. The objective function to be maximized is shown in Eq. 1. We here use considerably larger instances with \(k = \{20,30,40\}\) subproblems.

    $$\begin{aligned} f(\overrightarrow{x})= \sum \limits _{i=1}^k (unitation({subp_{i}))} \end{aligned}$$
    (1)
    Fig. 2
    figure 2

    Basic deceptive bipolar function (\(s_i\)) for MMDP

    Full size image
    Table 1 Unitation values
    Full size table

  • Subset sum problem (SSP): is a special class of binary knapsack problem which interests both theoreticians and practitioners. This problem has several interesting applications (Dietrich and Escudero 1993; Chakravarty et al. 2000; Thomas et al. 2009). In the formal definition of the SSP we are given a set \(W=\{w_1,w_2,w_3,\ldots ,w_n\}\) of n integers and a large integer C. We would like to find a vector solution \(x=(x_1,x_2,\ldots ,x_n)\) where \(x_i\, \epsilon \,\{0,1\}\), such that:

    $$\begin{aligned} f(\mathbf {x})=\sum _{i=1}^{n} w_i x_i \le C\quad \text{ with } i =1,2,\ldots ,n \end{aligned}$$
    (2)

    We used the same coding and objective function as suggested by Khuri et al. (1994). To guarantee that all infeasible solutions yield larger (worse) objective function values than the feasible ones, the following function was used as a fitness function:

    $$\begin{aligned} f(\mathbf {x})= w * (C - P(\mathbf {x}))+(1-w) * P(\mathbf {x}) \end{aligned}$$
    (3)

    where \(w=1\) when the vector solution is feasible \((C - x \ge 0)\), and \(w=0\) when x is infeasible. We created our problem instances in a similar way to the method used by Khuri et al. (1994). The size of vector W was set to \(\{1000,5000,10{,}000\}\) and the elements in W were created randomly with a uniform distribution from the interval \([0,10^4]\) to obtain a large variance. Three problem instances were generated (called \(\mathrm{SSP}\_i\) where i is the index of the size of the test suite of W).

  • Maximum cut problem (MAXCUT): The MAXCUT problem is just one of the many NP-hard graph theory problems which have attracted a great number of researchers over the years. The problem looks for a partition of the set of vertices (V) of a weighted graph \(G_w = (V, E)\). In this case, \(G_w = (V,E)\) stands for a weighted undirected graph, and \(w_{ij} \ge 0\) is the weight of edge \(e_{ij}\) \(\epsilon \) E. The result of the division is two disjoint subsets \(V_0\) and \(V_1\) where the sum of the weights of the edges with one endpoint in \(V_0\) and the other in \(V_1\) is maximized. To encode the problem we use a binary string \((x_1, x_2, \ldots , x_n)\) of length n where each position corresponds to a vertex. If \(x_i = 0\) then vertex i is in \(V_0\); otherwise, it is in \(V_1\). The function to be maximized (Khuri et al. 1994) is:

    $$\begin{aligned} f(\overrightarrow{x})=\sum _{i=1}^{n-1} \sum _{j=i+1}^{n}w_{ij}[x_i (1-x_j)+x_j (1-x_i)] \end{aligned}$$
    (4)

    Note that \(w_{ij}\) contributes to the sum only if nodes i and j are in different partitions. While one can generate different random graph instances to test the algorithm, here we have used three cases tested in the literature (Khuri et al. 1994) with a size of 20 and 100 elements (called \(20\_01\), \(20\_09\), and 100). In addition, we have selected one instance called G1Footnote 1 with an instance size of 800.

5.2 Methodology

This section describes the methodology adopted in the experiments carried out in the course of this work.

First, we introduce the motivation for selecting each one of the algorithms to be compared with our HySyS algorithm. Then, we validate our results. Finally, a description of the hardware used in the tests is included.

Nowadays, the comparison between different algorithms in any study is mandatory. We have done so here, by examining the obtained results by a random search (RS) on CPU, \(\upmu \mathrm{GA}\) on CPU, and \(\mathrm{SNS}^{\mathrm{exp}}\) on GPU; then, we have provided numerical evidence of the highly competitive results of our proposal. RS is used as a way to provide a sanity check with respect to the results of HySyS, just to test if our algorithmic proposal is more intelligent than a pure random sampling.

Likewise, \(\upmu \mathrm{GA}\) and \(\mathrm{SNS}^{\mathrm{exp}}\) are used because they are the algorithmic components of HySyS and we want to test whether the emergent behavior of hybridization outperforms the parts separately. Moreover, we consider \(\upmu \mathrm{GA}\) as a classical advanced intelligent search that will serve to contextualize HySyS results in optimization. The main features of the above mentioned algorithms are the following:

  • Random search: RS initializes a solution \(sol_x\) randomly and evaluates it. Then, until a termination criterion is met, RS repeats the process of creating and evaluating a new solution \(sol_y\). If \(sol_y\) is better than \(sol_x\), \(sol_x\) is replaced with \(sol_y\); otherwise, \(sol_x\) is left unchanged.

  • micro-genetic algorithm (\(\upmu \mathrm{GA}\)): The \(\upmu \mathrm{GA}\) is described in Sect. 3.

  • Exponential systolic neighborhood search (\(\mathrm{SNS}^{\mathrm{exp}}\)): The \(\mathrm{SNS}^{\mathrm{exp}}\) algorithm is presented in Sect. 3.

Our work aims at providing experimental findings on the performance and robustness of HySyS, showing that it is especially worthy of future study and use. Apart from comparing our proposal to three canonical algorithms from the literature, the conducted experimentation has also been designed to show the scalability capabilities (a key issue seldom reported in the literature) of this hybrid CPU–GPU algorithm.

We have carried out a thorough statistical procedure to provide the results with confidence. Firstly, we performed 30 independent runs for every problem instance in the test suite. Then, a Kolmogorov–Smirnov test was performed to check whether the values of the results follow a normal (Gaussian) distribution or not. If the distribution was normal, then we applied the Levene test to check the homogeneity of the variances. If samples had equal variances (positive Levene test), an ANOVA test was done; otherwise, a Welch test was performed. For non-Gaussian distributions, the non-parametric Kruskal-Wallis test was used to compare the medians of the algorithms. Here we have always considered a confidence level of 95 % in the statistical tests. This means we can guarantee that the differences between the compared algorithms are significant or not with 95 % probability and the observed algorithmic differences are unlikely to have occurred by chance with 95 % probability.

The experiments were run on a host with a CPU Intel (R) i7 CPU 920, with a total physical memory of 8192 MB. The operating system was Ubuntu Lucid 12.10. In the case of the GPU, we had two GPU models to prove the performance behavior for HySyS. Details of each model are presented in Table 2. The HySyS approach tested in each GPU model is called \(\mathrm{HySyS}\_n650\) and \(HySyS\_n780\), respectively. They are composed by the name of the algorithm followed by an n (from the card manufacturer NVIDIA) and the card model.

Table 2 Parameter settings for the GPU models used
Full size table

5.3 Parameterization

As usual, stopping criterion is necessary so as to ensure an adequate termination condition for an evolutionary process (Aytug and Koehler 2000; Greenhalgh and Marshall 2000; Oliveto et al. 2007). We have chosen a stop condition to guarantee a similar exploration of the search space for all the problem instance sizes. Thus, the function evaluation reflects the time complexity of the algorithms. We have estimated an upper bound for the number of evaluations required to ensure convergence taking into account previous work related to the problems (Dorronsoro et al. 2004; Wang 2004; Martí et al. 2009; Kochenberger et al. 2013). We have examined HySyS efficiency with a maximum number of objective function evaluations (up to 600,000 evaluations) to investigate algorithmic behavior and time complexity. To evaluate algorithmic performance directly, we have kept the effort constant and compared the quality of the obtained results. We have selected a sufficiently large, but not excessive, number of evaluations to monitor the behavior and evolution up to large instances. Evaluations’ control occurs by counting the evaluations performed in each component controlled by a particular CPU thread. Specifically, the GPU kernel is managed by a thread in the CPU, as can be seen in Fig. 1, that controls the number of SNS iterations. Each SNS kernel performs one single iteration of the algorithm; in this way this thread knows the total number of evaluations that have been performed, and can be stopped at any moment. Therefore, when HySyS detects that the stop condition has almost been reached (i.e., 600,000 evals) these actions are triggered: the \(\upmu \mathrm{GA}\) thread is stopped; its number of function evaluations is summed up; the number of evaluations that have not yet been performed is passed on to the SNS kernel, which only performs this number of evaluations.

As our approach uses two components with several differences in the number of evaluations performed by cycle, HySyS separately calculates the evaluations performed by each component and a third CPU thread is responsible for checking whether it has reached the stop condition.

The rest of the \(\upmu \mathrm{GA}\) parameters included in Table 3 have been reached through several preliminary pilot tests. We first design an analysis using a simplified design with three discrete values for every parameter (small, medium, high) taking into account the existing literature (Kahn and Tangorra 2013; Batres 2013) on \(\upmu \mathrm{GA}\)s.

Table 3 Parameter settings for \(\upmu \mathrm{GA}\)
Full size table
Table 4 Average fitness and hit rates for MMDP instances over 30 independent runs
Full size table

Hybrid systolic search introduces a few additional parameters: those related to the search configuration, and those associated with the GPU parallelization. On the one hand, the experiments have allowed us to set the percentage of solutions replaced in \(\mathrm{SNS}^{\mathrm{exp}}\), u, to 15 %. This value is based on tests previously performed to adjust this parameter. On the other hand, the configuration of the GPU kernels uses a static size; 512 threads per block. The number of blocks varies depending on the instance size. If this size is greater than 512, the number of blocks is computed as \(\mathrm{round}(s/512)\) where s is the instance size.

5.4 Results

In this section, we provide a detailed study of the results for the problems presented above. For further analysis of the outcome of using our approach regarding the other algorithms, we present different evaluations, focusing on both the numerical and the real-time performances. Then, a scalability analysis of the HySyS is presented.

5.4.1 Numerical analysis

The quality of the solutions reached by the algorithms is examined in this section. The first three tables include the average fitness values and the hit rate (percentage of successful runs that obtain the best known optimum value) for the different instances of the three benchmarking optimization problems.

Table 5 Average fitness and hit rates for SSP instances over 30 independent runs
Full size table
Table 6 Average fitness and hit rates for MAXCUT instances in 30 independent runs
Full size table

With respect to the MMDP problem, Table 4 shows the average fitness and hit rate obtained results over 30 independent runs. The subindex on each MMDP instance gives the number of subproblems used (defined by the k value). It can be clearly seen that both HySyS models obtain the best (highest) values for all the instances considered, the differences with respect to the other algorithms becoming greater as the problem size grows. Indeed, our proposal hits the optimum value in all these instances at least once. The second best algorithm for this instance group is \(\upmu \mathrm{GA}\), where the best fitness is found at least once. In the case of \(\mathrm{RS}_{\mathrm{CPU}}\), the results are the worst ones with respect to the other algorithms. These results indicate that the HySyS approach can perform a more intelligent exploration of the search space than a pure random search.

Having evaluated the performance of HySyS against each technique separately, HySyS is always above 95 % of the optimum solution. The results obtained clearly indicate that HySyS can explore the search space better than each technique acting separately, thus showing a promising emergent behavior.

Fig. 3
figure 3

Hit rates reached by all the algorithms

Full size image

Table 5 displays the results for SSP instances averaged over 30 independent runs. For this group of instances the name of each one consists of the name problem and a number from 1 to 3. The first conclusion that can be drawn from Table 5 is that almost all algorithms found the best known solution at least once (except for \(\mathrm{RS}_{\mathrm{CPU}}\), for instance \(\mathrm{SSP}\_3\)). Concretely, accurate solutions have been computed by HySyS, which obtains 100 % hit rate for all the instances. However, for the SSP problem, it is worth noting that \(\mathrm{SNS}^{\mathrm{exp}}\) reaches 100 % numerical accuracy for \(\mathrm{SSP}\_1\) and \(\mathrm{SNS}\_2\). The \(\upmu \mathrm{GA}\) is the third in performance as regards its effectiveness. As can be seen in Table 5, HySyS finds the optimum value in all the runs for all the instance sizes (Avg. columns). On the other hand, the other algorithms gradually get worse (higher) solutions as the instance size increases. In conclusion, for the SSP instances the HySyS algorithm obtains competitive results and has overcome all the other algorithms in our comparison. In the case of \(\mathrm{RS}_{\mathrm{CPU}}\) and \(\upmu \mathrm{GA}_{\mathrm{CPU}}\), there is a statistical difference with respect to the quality of the solutions found.

Table 6 shows the average fitness values for the MAXCUT instances. In this case, the results are also clear. HySyS proves to be the best algorithm out of all those involved in this comparison as it finds the best (the highest) average fitness values in the four instances considered. In the context of this work, HySyS has been able to obtain higher quality solutions by combining both techniques (\(\upmu \mathrm{GA}\) and \(\mathrm{SNS}^{\mathrm{exp}}\)), rather than using each one separately. The two approaches using different GPU card models obtain the best optimum in all the executions.

Fig. 4
figure 4

Average fitness value through the evolution process with HySyS in the three MMDP instances. a \(\mathrm{MMDP}\_20\), b \(\mathrm{MMDP}\_30\), c \(\mathrm{MMDP}\_40\)

Full size image
Fig. 5
figure 5

Average fitness value through the evolution process with HySyS in the three SSP instances. a \(\mathrm{SSP}\_1\), b \(SSP\_2\), c \(\mathrm{SSP}\_3\)

Full size image

To illustrate the effectiveness of our approach more clearly, Fig. 3 contains the hit rates of all the algorithms for all tested instances (i.e., taking into account the instances for the three problems). The figure shows a clear fact: HySyS is able to find the optimal solution in 9 out of 10 instances used, and in the remaining instances it obtains the best (highest) hit rates. The rest of the algorithms reach the optimal solution only for the SSP instances, the first MAXCUT instance, and the two first MMDP instances.

As a final remark on the numerical performance of HySyS, we would like to point out that the hybrid cooperation of the HySyS is able to generate accurate solutions and explore the search space effectively so as to identify the region where the optimal solution is located. The benefits of HySyS are principally justified by two factors: (1) the long flow of solutions within the \(\mathrm{SNS}^{\mathrm{exp}}\) mesh, which allows the algorithm to perform deep search intensification and (2) the injection of high quality solutions from \(\upmu \mathrm{GA}\) within the mesh, which prevents \(\mathrm{SNS}^{\mathrm{exp}}\) from being stuck by increasing the diversity with high quality and diverse solutions.

The charts in Figs. 4,  5 and 6 show the evolution for a simple execution of the average fitness solutions during the evolutionary process for the MMDP, SSP and MAXCUT problems, respectively. For the x-axis each chart displays the percentage of the number of completed evaluations, versus the fitness value for each instance. There are three lines that indicate the evolution of each algorithm. The solid line with plus signs is the reference for HySyS, the dashed line with circles denotes the \(\upmu \mathrm{GA}\), and the dash-dot line with asterisks is for \(\mathrm{SNS}^{\mathrm{exp}}\). The \(\mathrm{HySyS}\_n650\) model is used as a reference to create the plots.

For the MMDP problem, we can see in Fig. 4a, b that in the early evolution (from 0 to 40 %) the fitness increases abruptly in the first generations reaching the optimum value at 80 % of the completed evaluations. The \(\upmu \mathrm{GA}\) component starts out, having a superior quality fitness to the one presented by \(\mathrm{SNS}^{\mathrm{exp}}\). However, continuous data exchanges between components allow the \(\mathrm{SNS}^{\mathrm{exp}}\) to acquire higher quality solutions; therefore, the search can be refined through the pattern of exploration and exploitation. In Fig. 4c we can see a sharp increase in fitness value as in Fig. 4a, b, but subsequent stagnation occurs revealing no significant improvements. Once 70 % of evaluations have been completed, \(\mathrm{SNS}^{\mathrm{exp}}\) values have reached \(\upmu \mathrm{GA}\) average fitness solutions and finally finds the best optimum.

Fig. 6
figure 6

Average fitness value through the evolution process with HySyS in the three MAXCUT instances. a \(20\_09\), b 100, c 800

Full size image

Figure 5a–c shows the evolution of the components for the three instances of the SSP problems. We can clearly see the differences between the start and end of the process evolution. At the start, the two components scale in a similar manner. However, the \(\upmu \mathrm{GA}\) component improves gradually during the first steps of the process but as the algorithm progresses, either the solutions converge prematurely or get stuck at a local optimum. Fig. 5c, which represents the fitness evolution for the largest MMDP instance, the fitness scaling is similar to the one in the other two figures. At first, the value of best average fitness is obtained by the \(\upmu \mathrm{GA}\), but as the process continues, \(\mathrm{SNS}^{\mathrm{exp}}\) reaches a value that is very close to the optimal fitness.

As can be observed in Fig. 6a–c, the communications between components allow \(\mathrm{SNS}^{\mathrm{exp}}\) to reach the optimum value in the first two figures. In fact, \(\mathrm{SNS}^{\mathrm{exp}}\) can execute a greater number of cycles (for the same number of visited points in the search space) and in the last steps of the evolution process it has quality solutions from the CPU component. This scenario allows each new incoming solution to be modified extensively (higher exploitation) until it reaches a stage that is very close to the optimal.

For the three groups of figures, we can say that, it can be seen comparatively that HySyS improves solutions very fast in the early evolution, taking advantage of the small group of high quality solutions provided by \(\upmu GA\).

5.4.2 Execution time analysis

Table 7 presents the average time results measured in seconds for the MMDP instances over 30 independent runs. It shows that \(\mathrm{HySyS}\_n780\) obtains the shortest times for all the instances. \(HySyS\_n650\) does not fall very far behind the \(\mathrm{HySyS}\_n780\), especially in smaller instances. We find that for the \(\mathrm{MMDP}\_20\) instance the times are very similar between \(\mathrm{SNS}^{\mathrm{exp}}\) and the two HySyS models. Even if HySyS includes the behaviors of \(\upmu GA\) and \(\mathrm{SNS}^{\mathrm{exp}}\), the number of performed steps and the execution time of the HySyS algorithm is less than the amounts taken by each component separately (i.e., \(\upmu GA\) and \(\mathrm{SNS}^{\mathrm{exp}}\) algorithms).

We can see that for small instances (few items), the execution times are similar. In larger instances it is clear that both HySyS runtimes are lower than \(\mathrm{SNS}^{\mathrm{exp}}\). This is justified because the performance of \(\upmu GA\) with HC consumes part of the evaluations, finishing the HySyS run at almost the same time as \(\mathrm{SNS}^{\mathrm{exp}}\). By considering the numerical performance, it can be stated that HySyS exhibits the most robust behavior, being able to reach or be close to the optimum in the shortest execution time.

Table 7 Average time (in s) for MMDP instances in 30 independent runs
Full size table

Now, we turn to analyzing the run times for the SSP instances. Table 8 shows that the shortest times are obtained by \(\mathrm{HySyS}\_n780\) in all instances. In these kinds of problems, we observe a clear difference in time between both HySyS tests. The results reveal a faster performance for the newer GPU architecture. Particularly, with the larger instances \(\mathrm{SNS}^{\mathrm{exp}}\) has a shorter computation time than \(\upmu GA\)’s. Finally, \(\mathrm{RS}_{\mathrm{CPU}}\) has the longest performance times for each SSP instance.

The average execution times for 30 independent runs in the MAXCUT instances are presented in Table 9. \(\mathrm{RS}_{\mathrm{CPU}}\) has the longest execution times compared to the rest of the algorithms. We have observed in the two smaller instances (20 items) that the \(\upmu \mathrm{GA}\) is executed in a shorter time, when compared to the others. HySyS and \(\mathrm{SNS}^{\mathrm{exp}}\) also have similar execution times. As the instance size grows, HySyS has the shortest execution times compared to the other algorithms.

Table 8 Average time (in s) for SSP instances in 30 independent runs
Full size table
Table 9 Average time (in s) for MAXCUT instances in 30 independent runs
Full size table

Below, we show the run time for the processes of \(\mathrm{HySyS}\_n650\) and demonstrate the necessity to report memory transfer overhead costs for CPU–GPU performance comparisons so as to understand the behavior of a CPU–GPU algorithm better. We have selected the first GPU model since the execution times between the two models are similar and it is also interesting to evaluate the behavior of this approach in commodity video graphics cards.

We have focused on three major operations: (1) The time spent by the main CPU–GPU process of evolution. (2) The measurement of transferred data (no solution) between the two architectures. (3) Finally, the time taken to move solutions between host and device. The first operation measures the time that the two processes (i.e., \(\mathrm{SNS}^{\mathrm{exp}}\) and \(\upmu GA\)) apply to operators over the solutions. The second operation is a very important point because it allows us to know whether \(\mathrm{HySyS}\_n650\) is consuming too much time when the information is transferred between CPU and GPU. It is well known that the CPU–GPU communication of data can be a bottleneck in the performance of algorithms. The latter operation is related to the total runtime that \(\mathrm{HySyS}\_n650\) uses to move solutions between host and GPU devices. The control of these times provides information about the behavior of the different processes involved in the algorithm. It also allows us to analyze whether or not there is a bottleneck or a significant delay in the execution of some processes.

Figure 7 presents the percentage of time spent on each relevant operation in our CPU–GPU implementation. The figure shows (for each instance) the time percentage used with respect to the total execution times for the three operations explained above.

Fig. 7
figure 7

Average percentage of the time spent by \(\mathrm{HySyS}\_n650\) in the three time-consuming operations

Full size image

As a first observation, in Fig. 7 we can appreciate the high times related to the communication and data transfer. This time is longer in those instances with a lower number of elements. For example, the MMDP instances have the longest time percentage, which decreases with the instance sizes. In fact, for MMDP instances the time percentage ranges from 25 to 30 % of the total run time; for SSP instances, from 5 to 19 % and finally, it reaches 1 % for the largest MAXCUT instance.

As a second observation, the time to exchange solutions in most of the instances is less than 10 %; only for the MMDP cases, does the algorithm reach a maximum of 13 %. These values indicate that the exchange of solutions uses around 10 % of the total run time. These times can be explained by taking into account that the number of iterations decreases as the number of elements increases. So, the chance to transfer solutions between devices is greatly reduced.

As a concluding remark regarding Fig. 7, we can state that the advantage of a full distribution of tasks over the CPU and GPU shows that the algorithm is still fast and effective even though some time is lost in the data transfer operations. Data transmission performed by the algorithmic model is efficient with respect to the runtime. Moreover, this process is also less time consuming, which can lead us to devise new variants based on this methodology. As a result, we can conclude that the time associated with the communication/transfer directly affects the execution time in smaller instances but is negligible for the largest instances.

Fig. 8
figure 8

Runtime reduction for MMDP instances

Full size image
Fig. 9
figure 9

Runtime reduction for SSP instances

Full size image
Fig. 10
figure 10

Runtime reduction for MAXCUT instances

Full size image

Figure 8 shows the acceleration values for MMDP instances. We can see that in all cases the values are greater than 1, which means that \(\mathrm{HySyS}\_n780\) is faster than the rest of the algorithms. Likewise, we have noticed that as the instance size grows, so does the time gained, ranging from 1\(\times \) to 118\(\times \). The results for SSP instances are presented in Fig. 9. The runtime reduction ranges from 1\(\times \) to \(365\times \). These values suggest a good scalability of our algorithm. Finally, Fig. 10 shows a surprising similarity between \(\mathrm{HySyS}\_n780\) and \(\mathrm{SNS}^{\mathrm{exp}}\), which do not exhibit any clear differences. As the problem size grows, the time gained is better with \(\mathrm{HySyS}\_n780\). Finally, \(\mathrm{HySyS}\_n780\) obtains a greater time reduction against RS; this difference ranges from \(8\times \) to \(129\times \). For the comparison of graphic accelerators in particular, the results are quite interesting. A GeForce GTX 650 with 384 cores showed nice execution times, falling not too far behind the GTX 780 with 2880 cores. The mid-end card was even faster in all instances. This might be influenced by a slightly larger scheduling overhead with the more complex GPU. Of course, if we think about problems that increase in size, GTX 780 could be used to full capacity and the speedup would be significantly higher. However, the features of low-end cards should be considered for scientific computing.

In summary, we can draw some interesting conclusions. As expected, parallel implementation outperforms the serial one in the largest instances. The time consumed by a CPU algorithm does not increase exponentially as the instance dimension rises. The high runtime reductions demonstrated in this study for the largest instances are encouraging and indicate the usefulness of practical hybrid applications on CPU/GPU-based computing platforms for large size problems. Moreover, our approach has succeeded in solving large academic problems in a shorter time with respect to other algorithms. These experiments provide guidelines on how to work with real problems (computationally demanding in terms of time).

5.4.3 Scalability analysis

This section is dedicated exclusively to summarizing the scalability behavior of the HySyS and its observed performance. For this analysis, we have also taken into account the time and numerical results explained above.

The first conclusion that can be easily drawn from the results is that there is a better scalability of the HySyS approach with respect to the execution time. Furthermore, communication times are quite short compared to the running processes in most of the cases (as can be noted in Fig. 7). Therefore, we can state that the numerical performance is not penalized by the communication time. However, this may be a direct effect of the number of steps that the algorithm executes.

As for the numerical performance, HySyS presents really accurate values when the instance sizes grow. Indeed, as the instance size grows, it forces both \(\upmu \mathrm{GA}\) and \(\mathrm{SNS}^{\mathrm{exp}}\) to face major difficulties to hit the optimal solutions of the instances (this is proved by the hit rates showed in Fig. 3). In the SSP instance, we have observed that HySyS obtains a full hit rate, while the rest of algorithms are always below. Therefore, HySyS can work efficiently with very large problem instances. This is further supported by the results of the other two problem instances as HySyS finds the optimal value at least once. Thus, our proposal is likely to provide a more robust search under these experimental conditions.

6 Conclusions

In this paper, we have proposed a new hybrid parallel optimization algorithm: the Hybrid Systolic Search algorithm, its acronym being HySyS. This is just the first of many other approaches that can be derived from using the same methodology as HySyS. We have tried to adapt the concept of hybrid metaheuristics exhibiting complementary behaviors, to improve the effectiveness and robustness in an architecture of CPU–GPU.

The main scientific contribution of the work presented here is the novel hybrid model which exploits two computational optimization methods with a specific focus on each architecture. In addition, systolic computing on GPUs is novel, and this work reinforces its potential. HySyS constitutes an original model where it is possible to introduce and reuse new optimization components designed for each computing platform.

Our study has considered three different combinatorial optimization problems commonly employed in the EA field. The preliminary results of our experiments are very promising with respect to the effectiveness of the method that we have developed.

On the one hand, the experimental results show that the hybrid CPU–GPU cooperative implementation yields significant performance improvements by fully utilizing all the available computational resources of both CPUs and GPUs. The runtime reduction of the HySyS approach with respect to other algorithm implementations is up to \(118\times \) for the MMDP, \(365\times \) for the SSP and \(166\times \) for the MAXCUT. The computational experience corroborates the effectiveness of the parallel metaheuristics. These parallelizations provide the basic advantages of the parallel procedures. On the other hand, the \(\upmu \mathrm{GA}\) operators do matter as they do not need such heavy computation, since they achieve an increase of either the efficiency or the exploration.

When applied to a hybrid scheme, the first-improvement strategy resulted in an effective use of the resources, reaching the best known fitness value in very short times and with good scalability behavior when solving high-dimension problem instances.

As future work, we are now exploring this line of research by introducing new optimization techniques in the CPU component. The use and testing of other algorithms will uncover evidence of HySyS versatility in allowing an easy integration with additional components from the literature.