Introduction. The problems of the vibration-based diagnosis surface cracks in rods of rectangular [1] and circular [2, 3] cross section, which have been considered by us before, concerned, as in most known papers, the analysis of bending vibrations. In literature, however, certain attention is also given to the evaluation of the vibrodiagnostic indicators of the presence of cracks under longitudinal vibration excitation. In this case, both the best known and simple methods of vibration-based diagnosis, which are based on the evaluation of change in natural vibration frequencies [4,5,6] and the methods based on the assessment of nonlinear effects, caused by crack breathing, in the time and frequency characteristics of measured vibrations at the main resonance are employed [7, 8].

For instance, Niwarkar et al. [7] consider a cantilever rod of rectangular cross section under main resonance excitation, in one of the three eigenmodes, by a longitudinal axial harmonic force applied to the free end of the rod. In the analytical-numerical solution of the corresponding differential equation of rod vibration, the crack is modeled as a limiter of longitudinal displacement of the free end of the rod, and in the experiment, an aluminum rod with an edge crack grown in the center of the specimen (without indication of its depth) is used. The research is limited to a rather general qualitative assessment of the observed change in the time and frequency characteristics of longitudinal displacements and strains measured in different rod cross sections.

In the study [8], longitudinal vibrations of a cantilever rod of rectangular cross section with a breathing edge crack of different depth and at different location were investigated using a finite element (FE) model developed in ABAQUS. The vibrations were excited by a longitudinal harmonic force, which was applied to the free end of the rod at the frequency corresponding to the first eigenmode of the longitudinal vibration of the undamaged rod.

The main attention was given to the analysis of the level of the nonlinearity associated with higher harmonic generation in acceleration frequency spectrum, which is recorded at different sites along the rod on its surface on the crack side. The level of nonlinearity was evaluated from the value of the relative amplitudes of the second and third harmonics, i.e., normalized with respect to the fundamental harmonic amplitude.

The results of the calculations of the relative amplitudes of these harmonics in eight cross sections of a cantilever rod for three depth values and three locations of the crack along the rod length showed in all cases a very pronounced increase in the relative amplitude of second harmonic near the crack and its value to be independent of the level of excitation and friction between the crack surfaces. It has also been shown that the results obtained using a simplified crack model based on bilinear elasticity are in good agreement with the results of the model with a breathing crack.

To check the results of numerical simulation, the authors have carried out a series of experimental investigations on a cantilever aluminum specimen and a freely suspended aluminum specimen at different crack depth and location with the evaluation of nonlinearity from the more sensitive amplitude of second harmonic. However, the effect of localization of the relative amplitude of this harmonic was much less pronounced than in the numerical solution.

In this paper, attention is given to the analysis of the level of relative second harmonic amplitudes at the main resonance and of the more pronounced value at the superharmonic resonance of the order of 1/2 of the first mode of longitudinal vibration of rods of rectangular and circular cross section with an edge crack and with different boundary conditions using the analytical and numerical methods presented in [1, 2] for the case of bending vibrations. The presence of a second harmonic at the main resonance and the possibility of exciting superharmonic resonance are determined by the nonlinearity of the vibrating system, which is due to the presence of a mode I breathing surface crack.

Main Resonance. At the main resonance of a single-mass system with a bilinear asymmetric characteristic of restoring force, which models an elastic body with a breathing crack under its vibrations in some jth eigenmode on the assumption that it does not change at crack opening, the relative amplitude of the originating second harmonic \( {\overline{A}}_{2/j}={A}_{2j}/{A}_{1j} \) and the relative change in eigenfrequency \( \varDelta {\overline{\upomega}}_j=\left({\upomega}_{cj}-{\upomega}_j\right)/{\upomega}_j \) (ωj is the eigenfrequency of the jth vibration mode of an integral bode and ωcj is the vibration eigenfrequency with a breathing crack) can be determined through the nonlinearity parameter of the vibrating system αj [1, 9]:

$$ {\overline{A}}_{2/j}=\frac{2{\upalpha}_j\left(1+0.6{\upalpha}_j\right)}{9\uppi}\approx \frac{2{\upalpha}_j}{9\uppi},\kern0.5em \varDelta {\overline{\upomega}}_j=\frac{1-\sqrt{1-{\upalpha}_j}}{1+\sqrt{1-{\upalpha}_j}}. $$
(1)

It is convenient to express the parameter αj, corresponding to the relative change in the stiffness of the system at crack opening, in terms of the damage energy characteristic χj [1]:

The characteristic χj is equal to the ratio of the strain energy increment of the body ∆Πcj , which is caused by crack opening and determined through the tensile stress intensity factor (SIF) K1, to the potential energy of deformation in the jth vibration mode under consideration of the integral body Πj.

For the rods under consideration (Fig. 1) at the known stress intensity factor K 1 along the tension crack front and the known amplitude function of longitudinal displacements of integral rods uj (x) at the resonance of their jth longitudinal vibration mode, the characteristic χj can be determined, similarly to the bending vibration method considered in [1], from the relation:

$$ {\chi}_j=\frac{\varDelta {\varPi}_{cj}}{\varPi_j}=\frac{2}{EE^{\prime }F}\frac{\underset{\left({F}_T\right)}{\int }{K}_1^2d{F}_c}{\underset{0}{\overset{l}{\int }}{\left(\frac{d{u}_j}{dx}\right)}^2 dx}, $$
(3)
Fig. 1.
figure 1

Schematic of a cantilever rod with a crack, loaded with an exciting longitudinal force.

Full size image

where E is the elastic modulus of the rod material, E′=E under the plane stress state along the crack front, E′=E/(1−μ2) under plane strain, F is the cross section area of the rod, Fc is the crack area, and μ is Poisson’s ratio.

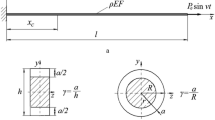
For a rod of rectangular cross section, a strip with an edge crack located in the cross section x=xc [10]:

$$ {K}_1=\frac{Q_j\left({x}_c\right)\sqrt{\pi \upgamma}}{b{h}^{1/2}}{F}_1\left(\upgamma \right), $$
(4)

where Qj(xc) is the nominal longitudinal force in the cross section xc of the rod, which equals \( EF{\left(\frac{\partial {u}_j}{\partial x}\right)}_{x={x}_c} \),

$$ {\displaystyle \begin{array}{cc}{F}_1\left(\upgamma \right)=1.12-0.231\upgamma +10.55{\upgamma}^2-21.72{\upgamma}^3+30.39{\upgamma}^4,& \upgamma =\frac{a}{h}\end{array}}. $$

In the case of a rod of circular cross section with a crack with strictly rectilinear front [11]:

$$ {K}_1=\frac{4{Q}_j\left({x}_c\right)\sqrt{\uppi \upgamma}}{\uppi {D}^{3/2}}{F}_1\left(\upgamma, \overline{z}\right), $$
(5)

where

$$ {\displaystyle \begin{array}{ccc}{F}_1\left(\upgamma, \frac{z}{z_C}\right)=\sum \limits_{m=0}^7\sum \limits_{n=0}^2{N}_{mn}{\left(\upgamma \right)}^m{\left(\overline{z}\right)}^n,& \upgamma =\frac{a}{D},& \overline{z}\end{array}}=\frac{z}{z_C},\kern1em {z}_C=\sqrt{a\left(D-a\right)}. $$

The values of the coefficients Nmn are found from Table 1 in the cases of cantilever rod and rod with the ends free for longitudinal displacements [11].

Table 1. The Values of the Coefficients Nmn for Cantilever Rod (numerator) and Rod with Free Ends (denominator)
Full size table

Some advantage should be noted of studying longitudinal vibrations of rods of circular cross section because of the ambiguity of possible circumferential crack position in the cross section, e.g., in the case of damage of rotating rod, which makes difficult more sensitive vibration-based diagnosis under bending vibrations. However, the study of longitudinal vibrations can also be limited to the assessment of the possibility of the presence of a crack based on integral indicators (1), i.e., without determination of its location.

Using expressions (4) and (5), we find the characteristic (3) by analogy with (7) [1], considering that at the main resonance ui ≠ j for a rod of rectangular cross section:

$$ {\chi}_j=2\uppi h\underset{0}{\overset{a/h}{\int }}\upgamma {\left({F}_1\left(\upgamma \right)\right)}^2d\upgamma {\varTheta}_j\left({x}_c\right), $$
(6)

and by analogy with (21) [3], for a rod of circular cross section:

$$ {\chi}_j=16D\left(1-{\upmu}^2\right)\underset{0}{\overset{a/D}{\int }}\underset{0}{\overset{1}{\int }}\upgamma \sqrt{\upgamma \left(1-\upgamma \right)}{\left({F}_1\left(\upgamma, \overline{z}\right)\right)}^2d\upgamma d\overline{z}{\varTheta}_j\left({x}_c\right), $$
(7)

where

$$ {\varTheta}_j\left({x}_c\right)=\frac{{\left(\frac{d{u}_j}{dx}\right)}_{x={x}_c}^2}{\underset{0}{\overset{l}{\int }}{\left(\frac{d{u}_j}{dx}\right)}^2 dx}. $$
(8)

At the jth eigenmode resonance of an undamaged rod, the amplitude functions of longitudinal displacements of the rod uj(x) = const ⋅ Uj(x) , where the eigenmode for a cantilever rod \( {U}_j(x)=\sin \frac{\left(2j-1\right)\uppi}{2l}x \) a rod with the ends free for longitudinal displacements \( {U}_j(x)=\cos \frac{j\uppi}{l} \), and for a cantilever rod with mass M at the free end \( {U}_j(x)=\sin {k}_il\frac{x}{l} \), where kil is the roots of the frequency equation \( {k}_il\tan {k}_il=\frac{\uprho Fl}{M},\uprho \) is the density of the material.

It should be noted that at the main resonance, the value of the characteristic χj and, hence, of the parameter αj and the vibrodiagnostic indicator \( {\overline{A}}_{2,j} \) depends neither on the level and site of application of exciting force nor on the damping capacity of the vibrating system.

For rods with the ratio \( \frac{h}{l}=\frac{D}{l}=\frac{0.02}{0.23} \), Fig. 2 shows, using (1), (2), (6)–(8), calculated values of the relative second harmonic displacement amplitude \( {\overline{A}}_{2/1} \) and relative change in the eigenfrequency \( \left(\varDelta {\overline{\upomega}}_1\right) \) of the first (j =1) eigenmode for different boundary conditions, relative depths γ and the crack location xc.

Fig. 2.
figure 2

Calculated plots of the relative amplitude of the second harmonic of displacement (solid lines) and acceleration (dashed lines) \( {\overline{A}}_{2/1},{\overline{A}}_{2/1}^a \)(□, ○) and relative change in eigenfrequency \( \varDelta {\overline{\upomega}}_1 \) (■, ●), on the relative depth γ of a crack at xc =0.1l (a, c) and 0.5l (e) and the crack location xc at γ = 0.2 (b, d, f) in a cantilever rod without mass (a, b) and with a mass at the end (c, d) and with free ends (e, f) of rectangular (□, ■) and circular (○, ●) cross section.

Full size image

As can be seen, the value of \( {\overline{A}}_{2/1} \) in the case of main resonance depends largely on γ, xc and boundary conditions, which determine the eigenmode, and is much lower than the value of relative change in eigenfrequency, \( \varDelta {\overline{\upomega}}_1 \). The commonly determined relative acceleration amplitudes \( {\overline{A}}_{2/1}^a=4{\overline{A}}_{2/1} \) (in Fig. 2 dashed lines) almost correspond to the value of \( \varDelta {\overline{\upomega}}_1 \).

However, the relative second harmonic amplitude of longitudinal displacements at the main resonance, determined via Eq. (1), depends neither on the site of application of the disturbing force P nor on the site of measurement of longitudinal displacements of rod cross sections, i.e., it does not reflect its change along the rod length, considered in [8], and corresponds to the value of \( {\overline{A}}_{2/1} \) far from the crack.

To determine the nature of possible change in the relative second harmonic amplitude of displacements along the length of rods, let us consider their FE models.

Figure 3 shows FE models of rods of rectangular (b × h = 0.004 × 0.02 m) and circular (D = 0.02 m) cross section of length l = 0.23m, which were constructed in accordance with the procedures presented in [2, 12] by means of 8-node finite elements. Mechanical characteristics of the rods: elastic modulus E = 200 GPa, density of the material ρ = 7800 kg/m3, and logarithmic decrement of vibrations δ = 0.01. The breathing crack of relative depth γ = 0.2 was represented as a mathematical cut and was located in the cross section xc = 0.1l. Mutual nonpenetration between crack faces was ensured by solving a contact problem.

Fig. 3.
figure 3

FE models of rods under investigation.

Full size image

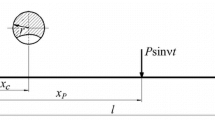
The longitudinal vibrations of cantilever rods were excited by a concentrated harmonic force P sin vt applied to their free end (xP = l). The determination of the vibration amplitude spectrum and afterwards vibrodiagnostic indicators (relative second harmonic acceleration amplitudes \( {\overline{A}}_{2/1}^a \)) was performed using the Newmark method and FFT analysis.

The dependence of the relative amplitude of displacement second harmonic acceleration on the upper face of a cantilever rod on the crack side on the site of measurement (x = x0) of vibrations of the rod of rectangular cross section is shown in Fig. 4: the figure also presents the results [8] obtained for rods (b × h × l = 0.01 × 0.025 × 0.3 m) with a crack of relative depth γ = 0.16 and 0.24, located in the cross section xc = 0.1667l.

Fig. 4.
figure 4

Dependence of the relative amplitude of the displacement second harmonic on the site of measurement of vibrations of rods of rectangular cross section, obtained numerically (▲), analytically (dashed line) and from the results presented in [8] at γ = 0.16 (□) and 0.24 (○).

Full size image

As can be seen, the plots of \( {\overline{A}}_{2/1}^a \) agree in general trend. Some difference is due to the different relative thickness of the rods and to some difference in the location of the crack and its relative depth.

As can be seen, the plots of \( {\overline{A}}_{2/1}^a\left({x}_0\right) \) agree in general trend. Some difference is due to the different relative thickness of the rods and to some difference in the location of the crack and its relative depth.

For the investigated rods, the displacements were determined both on the upper face, i.e., on the crack side, and along the neutral line. The obtained plots of \( {\overline{A}}_{2/1}^a\left({x}_0\right) \) for rods of rectangular and circular cross section, which are shown in Fig. 5, show a pronounced effect of localization of surface displacement acceleration amplitude hear the crack and a much smaller effect for displacements along the neutral line of cross sections, especially in the case of rod of circular cross section.

Fig. 5.
figure 5

Plots of the relative acceleration amplitude of the displacement second harmonic vs the site of measurement of vibrations of rods of rectangular (a) and circular (b) cross section, obtained using FE models for the nodes on the upper face (●) and on the neutral line (▲) of a rod.

Full size image

As was already pointed out, however, the results of an experimental examination of plots of \( {\overline{A}}_{2/1}^a\left({x}_0\right) \) [8] showed, on the whole, a much weaker manifestation of the effect of localization of relative displacement amplitude near the crack, and a significant difference between the results of several measurements was observed. Moreover, the detection of a crack in cantilever specimens proved to be possible only when measuring vibration near their free (excited) end because the measurement data in other cross sections were close together and sometimes smaller than for undamaged specimen; this may be attributed to the presence of a parasitic second harmonic in the excitation signal and, perhaps, to different amplitude value in different measurements. At the same time, for a freely suspended specimen with a crack in the middle, the measurement data at one end turned out to be smaller than for undamaged specimen and at the other end, to be slightly larger. Thus, the problem of experimental investigation apparently consists in the difficulty of generating strictly harmonic excitation. However, it is the subject of a separate investigation.

Noteworthy is that the deviation between experimental and numerical results is also affected by bending forms of vibrations, which are controlled by the crack depth and location.

More sensitive methods for the vibration-based diagnosis of breathing crack are nonlinear effects in the excitation of super- and subharmonic resonances, which have been studied under bending vibrations by many researchers, including us [1,2,3]. Because of subharmonic resonance frequencies that are too high for practical use in the case of longitudinal vibrations of rod elements, we shall confine ourselves here to considering the results of an analytical and a numerical determination, made using the FE models of rods shown in Fig. 3, of the vibrodiagnostic indicator of the presence of a crack at the superharmonic resonance.

Superharmonic Resonance. The vibrodiagnostic indicator of the presence of a breathing crack in the rod at the above resonance of some jth vibration mode is, as under bending vibrations [1, 3], the value of the relative amplitude of resonant harmonic displacement of the chosen rod cross section in the vibration spectrum.

At the superharmonic resonance of the order \( 1/2\left(v=\frac{1}{2}{\upomega}_{cj}\right) \) it is the ratio of the displacement amplitude of the second harmonic to that of the first harmonic \( {\overline{A}}_{2/1}={A}_{2j}/{A}_{1\varSigma } \). This ratio is calculated as at the main resonance through the nonlinearity parameter αj (2), but at the known logarithmic decrement of vibration δi of the system, it is calculated from formulas derived before for the case of relatively small cracks [1, 3]:

$$ {\displaystyle \begin{array}{lllllll}{\overline{A}}_{2,j}\cong 0.58\frac{\upalpha_j}{\delta_j}{\uplambda}_{1j}& \mathrm{for}& {\overline{A}}_{2,j}\le 0.9& \mathrm{and}& {\overline{A}}_{2,j}\cong 0.725{\uplambda}_{1j}\sqrt{\frac{\upalpha_j}{\updelta_j}}& \mathrm{for}& {\overline{A}}_{2,j}>0.9\end{array}}, $$
(9)

where the coefficient λ1j is determined from the results of calculation of the amplitude functions of longitudinal displacements ui (x) by the method of normal modes or principal coordinates of forced vibrations of an integral rod at the superharmonic resonance frequency of the jth vibration mode as the ratio of the amplitudes of displacements in the resonating mode at its frequency ωcj and in the sum N of the first modes in the rod cross section x = x0 of interest at the excitation frequency v:

$$ {\lambda}_{1j}={u}_{1j}\left({x}_0\right)/\sum \limits_{i=1}^N{u}_{1i}\left({x}_0\right). $$
(10)

At the known damping capacity of the vibrating system, i.e., δj value, the main goal is to find the parameter αj through the damage energy characteristic χj of the vibrating system under its deformation not in one isolated jth mode, as at the main resonance [(6)–(8)], but in the other excited vibration modes at the frequency of the corresponding superharmonic resonance.

As it follows from [1], this necessitates the representation of the factor Θj(xc) in (6) and (7) in the form

$$ {\varTheta}_j\left({x}_c\right)=\frac{{\left(\frac{d{u}_j}{dx}\sum \limits_{i=1}^N\frac{d{u}_i}{dx}\right)}_{x={x}_c}}{\underset{0}{\overset{1}{\int }}{\left(\frac{d{u}_j}{dx}\right)}^2 dx}. $$
(11)

Longitudinal displacement amplitude functions of an undamaged rod ui under vibration excitation by a longitudinal harmonic force P sin vt applied in the cross section with the coordinate xP:

$$ {u}_i(x)=\frac{2P{U}_i\left({x}_P\right){U}_i(x)}{\rho Fl{\omega}_i^2{\beta}_i}, $$
(12)

under kinematic excitation through a harmonic displacement B sin vt of the fixed end of the cantilever (x = 0):

$$ {u}_i(x)=\frac{2B{v}^2}{l{\upomega}_i^2}\frac{U_i(x)\underset{0}{\overset{l}{\int }}{U}_i(x) dx}{\upbeta_i} $$
(13)

and under vibration excitation of the cantilever by a longitudinal harmonic force P sin vt applied to the localized mass M at the free end of the rod:

$$ {u}_i(x)=\frac{P{U}_i(l){U}_i(x)}{\left(\frac{1}{2}\rho Fl+M{\sin}^2{k}_il\right){\upomega}_i^2{\upbeta}_i}. $$
(14)

Here βi = 1 − (v/ωi)2, v ≅ 0.5ωj, Ui(x) and ωi are the ith eigenmode and self-resonant frequency of longitudinal vibration of the rod \( \left({\upomega}_i={k}_i\sqrt{E/\uprho}\right) \). For a cantilever rod, ki = [(2i − 1)π]/2l, for a freely supported rod, ki = iπ/l, and for a cantilever rod with a mass at the end M, where the value of ki is determined from the frequency equation \( {k}_il\tan \left({k}_il\right)=\frac{\rho Fl}{M} \). In the examples of calculation given below, the ratio ρFl/M = 0.5 is adopted.

Figure 6 shows plots, using formulas (2), (6), (7) and (11)–(14), of the nonlinearity parameter α j vs the relative depth γ of a crack located in the cross section xc=0.1l and the location xc of the crack of relative depth γ = 0.2 for a cantilever rod of rectangular and circular cross section in the cases of excitation of the superharmonic resonance of the first eigenmode (j = 1) by a force P sin vt, applied to the free end of the rod (xP =l), and a fixity displacement B sin vt.

Fig. 6.
figure 6

Dependence of the nonlinearity parameter α1 on the relative depth γ (a, c) of a crack located in the cross section xc = 01l and on the crack location (b, d) in the cases of vibration excitation by a force P sin vt (solid symbols), applied to the free end of the rod (xP = l), and a fixity displacement B sin vt (open symbols) for cantilever rods without mass (a, b) and with a mass at the end (c, d) of rectangular (■, □) and circular (●, ○) cross section.

Full size image

Figure 7 shows, as an example, analytical plots of \( {\overline{A}}_{2,1}^a \) vs the relative depth γ and location xc of a crack for a cantilever rod of different cross sections under different types of vibration excitation and their registration in cross section x0 = l. The shape of the plots corresponds to that of the plots of the nonlinearity parameter α1 considered before (Fig. 6) and depends largely on the boundary conditions for the fastening of the rod (Fig. 8). In Fig. 7, the solid symbols indicate the corresponding values of \( {\overline{A}}_{2,1}^a \), obtained from the results of a numerical solution for the nodes on the upper face. As can be seen, there is a significant difference from the results of the analytical solution. Earlier, e.g., in [3], we pointed out possible causes of this: neglect of the change in the vibration mode of rods at crack opening in the analytical solution and difference in SIF value in the crack, which is determined from known reference data [10, 11] and actually reflected in the FE models used.

Fig. 7.
figure 7

Dependence of the vibrodiagnostic indicator \( {\overline{A}}_{2,1}^a \), on the relative depth γ (a, b) of a crack located in the cross section xc = 01l and the location xc (c, d) of a crack of relative depth γ = 0.2 in the cases of vibration excitation by a force P sin vt (a, c) and a fixity displacement B sin vt (b, d) for rods of rectangular (□, ■) and circular (○, ●) cross section. (Solid symbols correspond to numerical solution and dashed lines to specified analytical solution.)

Full size image
Fig. 8.
figure 8

Dependence of the vibrodiagnostic indicator \( {\overline{A}}_{2,1}^a \), on the normalized location xc/l of a crack of relative depth γ = 0.2 in the cases of vibration excitation by a force P sin vt for cantilever-supported rods (solid symbols) without mass (solid line) and with a mass at the end (dashed line) and rods with free ends (open symbols) of rectangular (□, ■) and circular (○, ●) cross section.

Full size image

For instance, the results of determinations of the SIF value from crack opening displacement in the FE models used proved to be 20% lower for the rod of rectangular cross section and 12.3% lower for the round rod. The appropriate correction of the analytical plots of \( {\overline{A}}_{2,1}\left({x}_c\right) \), which is indicated by dashed lines, reduces greatly the difference in the results of analytical and numerical solutions.

By analogy with the consideration of the main resonance, plots of \( {\overline{A}}_{2,1}^a \), against the site of measurement x0 of longitudinal displacements and accelerations corresponding to them for the case γ = 0.2, xc = 0.1l. have also been determined for the nodes on the upper face; they are shown in Fig. 9. As in Fig. 7, the specified analytical dependences in Fig. 9 are marked by dashed lines. A significant difference from the analogous plots in the case of main resonance should be emphasized here. As can be seen, at the superharmonic resonance, the value of \( {\overline{A}}_{2,1}^a \), does not increase as the site of measurement approaches the crack, i.e., there is no pronounced effect of localization, and the shape of the analytical and numerical plots of \( {\overline{A}}_{2,1}^a \) is much the same.

Fig. 9.
figure 9

Dependence of the vibrodiagnostic indicator \( {\overline{A}}_{2,1}^a \), on the site of measurement x0 of longitudinal displacements, derived analytically (■) and numerically for the nodes on the upper face (●) and on the neutral line (●). (Dashed lines correspond to specified analytical solution.)

Full size image

However, the plot of the absolute value of the second harmonic amplitude of longitudinal displacements A2 on the upper face vs the site of their measurement exhibits some disturbance of its smooth shape at the crack location. Figure 10 shows for cantilever rods the dependence of the normalized value of \( {\overline{A}}_2\left({x}_0\right)={A}_2\left({x}_0\right)/{A}_2(l) \),

Fig. 10.
figure 10

Dependence of the normalized amplitudes of the longitudinal displacement second harmonic \( {\overline{A}}_2 \) on the site of measurement of displacements x0 for rods of rectangular (a) and circular (b) cross section, obtained for the nodes on the upper face (solid symbols) and on the neutral line (open symbols) and from the results of an analytical solution (dashed line).

Full size image

determined from the results of a numerical solution for the nodes both on the upper face and on the neutral line and from the results of an analytical solution, on the site of measurement x0 for \( {A}_2={\overline{A}}_{2,1}\left({A}_1\equiv \sum \limits_{i=}^N{u}_i\right) \):

$$ {\overline{A}}_{2\left({x}_0\right)}=\sin \frac{\uppi}{2l}{x}_0. $$
(15)

It is natural that the most pronounced effect of localization near the crack is to be expected for the longitudinal strain ε on the upper face of rods. For instance, the plots of the half value of the total strain range per cycle (εav) and the first (ε1) and second (ε2) harmonic amplitude of strain vs the site of its measurement x0 obtained from the results of a numerical solution for the upper face nodes of cantilever rods, show a pronounced effect of localization (Fig. 11).

Fig. 11.
figure 11

Dependence of the normalized amplitudes of longitudinal strains \( \overline{\upvarepsilon}=\upvarepsilon /{\upvarepsilon}_{av\;\max } \) on the site of measurement of displacements x0 for the nodes on the upper face of cantilever rods of rectangular (a) and circular (b) cross section: (1) εav/εav max, (2) ε1/εav max , and (3) ε2/εav max.

Full size image

The obtained values of the nonlinearity parameter α1 and hence the vibrodiagnostic indicator \( {\overline{A}}_{2,1}^a \), under longitudinal vibrations are, on the whole, much lower than under bending vibrations. Figure 12 shows the comparison of analytical plots of \( {\overline{A}}_{2,1}^a\left({x}_c\right) \) ,in the case of longitudinal and bending vibrations obtained from the data presented in [1, 3], for a cantilever rod and a freely supported rod of rectangular and circular cross section, in the case of vibration excitation by a concentrated force P sin vt. Under bending vibrations, the harmonic force for the cantilever rod was applied to the free end and for the supported rod in the middle. The difference in the results is determined by the difference in the value of the characteristic χ1 and, hence, the parameter α1, as well as of the coefficient λ11, which depend at the constant value of δ on the vibration eigenmode, the site of application of exciting force and the chosen site of measurement of vibrations.

Fig. 12.
figure 12

Dependence of the vibrodiagnostic indicator \( {\overline{A}}_{2,1}^a \), on the relative depth γ (a, c) of a crack, located in the cross section xc = 01l, and the location xc (b, d) of a crack of relative depth γ = 0.2 in the cases of excitation of the superharmonic resonance of the first longitudinal (solid symbols) and bonding (open symbols) modes for rods of rectangular (■, □) and circular (●, ○) cross section.

Full size image

However, the peculiarity of the vibrodiagnostic indicator \( {\overline{A}}_{2,1}^a \), under longitudinal vibrations should be emphasized here once more. The presence of a central transverse crack or two symmetric edge cracks in the rod of rectangular cross section (strip) and the presence of a surface ring crack in the rod of circular cross section (Fig. 13) do not cause the nonlinearity of the vibrating system, but only change its stiffness under bending vibrations (the parameter α in vibration half-cycles of different sign has the same value), and hence the impossibility of the vibration-based diagnosis of cracks at both super- and subharmonic resonance. At the same time, under longitudinal vibrations, the nonlinearity caused by the above cracks is well determined from (2) and (3) at known SIFs [10]:

$$ {\displaystyle \begin{array}{ll}{K}_1=\frac{Q\left({x}_c\right)}{bh}\sqrt{\pi a}{F}_1\left(\upgamma \right),& {F}_1\left(\upgamma \right)=\sqrt{\sec \left(\frac{\upgamma \uppi}{2}\right)}\end{array}} $$
(16)
Fig. 13.
figure 13

Cross sections of rods with a central crack (a), two symmetric edge cracks (b), and a ring crack (c).

Full size image

for a central crack,

$$ {\displaystyle \begin{array}{cc}{K}_1=\frac{Q\left({x}_c\right)}{bh}\sqrt{\uppi a}{F}_1\left(\upgamma \right),& {F}_1\left(\upgamma \right)\end{array}}=\left(1+0.122{\cos}^2\frac{\uppi \upgamma}{2}\right)\sqrt{\frac{2}{\uppi \upgamma}\tan \frac{\uppi \upgamma}{2}} $$
(17)

for two symmetric cracks, and

$$ {\displaystyle \begin{array}{ccc}{K}_1=\frac{Q\left({x}_c\right)}{\uppi {r}^2}\sqrt{\uppi r}{F}_1\left(\upbeta \right),& \mathrm{where}\;\upbeta =1-\upgamma, & {F}_1\end{array}}\left(\upbeta \right)=0.5\left(1+0.5\upbeta -0.37{\upbeta}^2-0.36{\upbeta}^3+0.731{\upbeta}^4\right)\sqrt{\upgamma} $$
(18)

for a ring crack.

Figure 14 shows the comparison of calculated plots of \( {\overline{A}}_{2,1}^a\left(\upgamma \right) \) for the case of vibration excitation by a concentrated force P sin vt applied to the cross section \( {x}_P=l\;\mathrm{at}\kern0em \frac{h}{l}=\frac{D}{l}=\frac{0.02}{0.23} \) for all types of cracks considered in this paper, of relative depth γ = 0.2, located in the cross section xc = 0.1l of a cantilever rod.

Fig. 14.
figure 14

Dependence of the vibrodiagnostic indicator \( {\overline{A}}_{2,1}^a \), on the relative depth γ of a crack located in the cross section xc = 0.1l , in the cases of vibration excitation by a force P sin _t for cantilever-supported rods of rectangular (1, 3, 4) and circular (2, 5) cross section with an edge crack (1, 2), a central crack (4), a ring crack (5), and two symmetric cracks (3).

Full size image

Conclusions. At the main resonance of some jth eigenmode of longitudinal vibration of rods, an explicit vibrodiagnostic indicator of the presence of a breathing crack in them is the appearance of the displacement second harmonic. The relative amplitude of this harmonic \( {\overline{A}}_{2/1} \) depends neither on the level of vibration excitation nor on the damping capacity of the vibrating system. However, far from the crack, the value of even relative acceleration \( {\overline{A}}_{2/1}^a=4{\overline{A}}_{2/1} \) is small, and the results of analytical solutions are much the same and correspond to the relative change in vibration eigenfrequency.

However, numerical solution shows that on the surface on the crack side, the values of \( {\overline{A}}_{2/1} \)increase greatly with approaching the crack, i.e., the possibility of determining the crack location from the pronounced effect of localization of longitudinal displacements is confirmed.

At the superharmonic resonance of the order 1/2, an explicit vibrodiagnostic indicator of the presence of a breathing crack is the excitation level independent acceleration amplitude of longitudinal displacements of the second resonant harmonic \( {\overline{A}}_{2,j}^a \) for which in the case of j = 1 and the given damping capacity of the system, a strong dependence of \( {\overline{A}}_{2/1} \) on the relative depth γ and location xc of the crack and on the site of measurement of displacements x0 has been shown for a cantilever rod without mass and with a mass at the end and a freely supported rod of rectangular and circular cross section. At a large localized mass, the value of \( {\overline{A}}_{2,1}^a \), practically (or weakly) depends on the crack location.

In comparison with the main resonance, the values of \( {\overline{A}}_{2,1}^a \), are about two orders of magnitude higher than \( {\overline{A}}_{2/1}^a \), but they are practically independent of the site of measurement of vibrations, i.e., there is no effect of localization, which is important for the determination of crack location. However, the absolute values of the resonant harmonic exhibit the effect of localization near the crack.

In spite of the lower values of the vibrodiagnostic indicator of the presence of a breathing crack under longitudinal vibrations than under bending vibrations, they have an important peculiarity, viz allow one to diagnose the presence of symmetric both surface and internal cracks.