Introduction. In further elaboration on the works [1, 2], where consideration was limited to beams of rectangular cross section with an edge crack, we will present here the results of analytical and numerical solutions to determine vibrodiagnostic parameters of the presence of a breathing semielliptic surface crack in a circular bar under various types of harmonic excitation of 2-order superharmonic resonance and 1/2-order subharmonic resonance in any jth mode of bending vibration due to the crack-induced initial nonlinearity of the vibrating system.

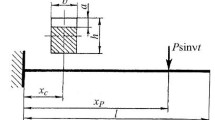
Analytical Solution Procedure. For the main vibrodiagnostic parameter of the presence of a semielliptic surface crack in any section x c of a bar (Fig. 1) we use the following harmonic amplitude ratios: between the second (resonating) amplitude and the first one under superharmonic resonance (Ā 2/1 = A 2j /A 1Σ ), and between the first (resonating) amplitude and the second one under subharmonic resonance (Ā 1/2 = A 1j /A 2Σ ). They are determined in terms of the nonlinearity parameter α and the logarithmic decrement δ of the system by the formulas [1, 3, 4]

Fig. 1
figure 1

A circular bar with a semielliptic surface crack, which is loaded with an exciting harmonic force.

Full size image
$$ {\overline{A}}_{2/1}\cong 0.58\left(\upalpha /\updelta \right){\uplambda}_{1j}\kern1em \mathrm{f}\mathrm{o}\mathrm{r}\kern1em {\overline{A}}_{2/1}\le 0.9, $$
(1a)
$$ {\overline{A}}_{2/1}\cong 0.725{\uplambda}_{1j}\sqrt{\upalpha /\updelta}\kern1em \mathrm{f}\mathrm{o}\mathrm{r}\kern1em {\overline{A}}_{2/1}>0.9, $$
(1b)
$$ {\overline{A}}_{2/1}\cong \frac{4\upalpha}{3\updelta}{\left({\uplambda}_{2j}^2+\frac{1}{9}{\left(\frac{8{\upalpha}^2}{9\uppi \updelta}\right)}^2\right)}^{-1/2}, $$
(2)

where λ1j is the ratio between the amplitude of the first harmonic of the jth mode A 1 j and the peak-to-peak amplitude of the first harmonic A 1Σ for an intact bar under forced vibration at a superharmonic resonance frequency, λ2j is the ratio of the peak-to-peak amplitude of the second harmonic A 2Σ to the amplitude of the second harmonic of the jth mode A 2 j for an intact bar under forced vibration at a subharmonic resonance frequency.

The parameter α is equal to a possible relative change of the bar bending stiffness due to the crack opening under fundamental forced vibrations by the jth mode until its resonance occurs, among other excitable modes at a frequency of super- or subharmonic resonances, and is determined via the energy characteristic of damage χ:

$$ \upalpha =\frac{v}{1+\upchi}. $$
(3)

The characteristic χ is computed, using the data of calculation of fundamental steady-state forced vibrations of an intact bar, as a ratio of the crack-induced possible increment of potential energy of the bar deformation ΔΠ jc in vibrations by the jth mode under consideration, among other excitable modes, to the potential energy of the bar deformation Π j in the jth-mode vibration at a super- or subharmonic resonance:

$$ \upchi =\frac{\Delta {\varPi}_{jc}}{\varPi_j}. $$
(4)

The forced vibrations of the bar will be calculated by the normal mode method or the method of principal coordinates of the linear vibration theory. Considering that it is acceptable to neglect the difference in the phase shift of vibrations along the principal coordinates at frequencies of the resonances under study and the possible levels of damping, the amplitude function of the bar deflections is represented in the form of the finite sum of natural-mode deflection amplitudes:

$$ y(x)={\displaystyle \sum_{i=1}^N{y}_i(x).} $$
(5)

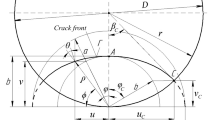
In the case of a mode I crack of surface area S and contour Γ (Fig. 2) present in the bar cross section, theincrement of potential energy ΔΠ jc is determined in terms of the normal stress intensity factor K 1 by the formula [5]

Fig. 2
figure 2

Geometry of a semielliptic surface crack in a circular bar.

Full size image
$$ \Delta {\varPi}_{jc}=\frac{1}{E}{\displaystyle \underset{(s)}{\iint }{K}_1^2\updelta \overline{\uprho} \cos \uptheta d\varGamma, } $$
(6)

where \( \mathrm{o}\overline{\uprho} \) is the vector of a possible displacement of a point of the crack front contour Γ and θ # is the angle between \( \updelta \overline{\uprho} \) and the normal to the crack contour.

Consider two variants of a possible change of the crack front. In the first one, the crack front is assumed to undergo changes at a constant ratio of semiaxes, i.e., at a/b const. From the schematic representation in Fig. 2, with the radius vector \( \overline{\uprho} \) preset in polar coordinates (ρ and ϕ ), we have \( \cos \uptheta =\uprho \frac{d\upphi}{d\varGamma },\kern0.5em \updelta \overline{\uprho}=\frac{\uprho}{b}db \), and \( d\upphi =\frac{ab}{\uprho^2}d\upvarphi \), and formula (6) takes on the form

$$ \Delta {\varPi}_{jc}=\frac{2}{E}\frac{a}{b}{\displaystyle \underset{0}{\overset{b}{\int }}{\displaystyle \underset{0}{\overset{\varphi_c}{\int }}{K}_1^2 bdbd\upvarphi}.} $$
(7)

For the crack case at hand, the normal stress intensity factor is found, according to [6, 7], by the formula

$$ {K}_1={\upsigma}_{cj}\sqrt{\uppi \mathrm{c}}{F}_1, $$
(8)

where σ cj is the nominal maximum normal stress in the crack location section x = x c in the case of the bar bending by the jth mode of its deformation, among other modes (hereinafter denoted by an asterisk) of forced vibrations \( \left({\upsigma}_{cj}=Er{\left(\frac{d^2{y}_j^{*}}{d{x}^2}\right)}_{x={x}_c}\right) \), c is the half the length of the arc of a circle of the section that encloses the crack (c = rβ c ), and F 1 is the dimensionless intensity factor.

Using the tabulated values [6, 7] for F 1 at points A and C of the crack contour for different ratios b/a and b/r as well as the diagrams of F 1 vs. the relative angle \( \overline{\upvarphi}=\upvarphi /{\upvarphi}_c \), we can write, as an approximation for the given

values of the ellipse semiaxes a, b and the bar cross-sectional radius r, the factor F 1 as a function of two variables: the relative angle \( \overline{\upvarphi} \) that varies from 0 to unity and the relative current crack depth \( z=\tilde{b}/r \) that varies from zero to b/r,

$$ {F}_1\left(z,\overline{\upvarphi}\right)={F}_{1A}(z)+0.511\Delta {F}_1\overline{\upvarphi}-1.511\Delta {F}_1{\overline{\upvarphi}}^2, $$
(9)

where ΔF 1 = F 1A (z) − F 1C (z), F 1A and F 1C are given in the form of power series of the variable z.

For instance, for the first variant of the crack front variation with a/b = 2.5 we have

$$ \begin{array}{l}\kern2em {F}_{1A}(z)=0.56-0.027z-0.058{z}^2+0.382{z}^3,\hfill \\ {}{F}_{1C}(z)=4.426z-20.9{z}^2+45.18{z}^3-43.7{z}^4+15.75{z}^5,\hfill \end{array} $$
(10)

for the second variant with a/r = 1 we have

$$ \begin{array}{l}{F}_{1A}(z)=0.4505+0.4457z-0.425{z}^2+0.0521{z}^3,\hfill \\ {}\kern2em {F}_{1C}(z)=0.8186z+0.33{z}^2+0.037{z}^3.\hfill \end{array} $$
(11)

In view of the orthogonality condition of natural modes of vibration, the potential energy of the bar deformation by the jth mode, among other vibration modes, is determined as if this mode is isolated,

$$ {\varPi}_j=\frac{\uppi}{8}E{r}^4\left[{{\displaystyle \underset{0}{\overset{l}{\int }}\left(\frac{d^2{y}_j^{*}}{d{x}^2}\right)}}^2={\displaystyle \underset{0}{\overset{l}{\int }}{\left(\frac{d^2{y}_j}{d{x}^2}\right)}^2}\right]dx. $$
(12)

Then, we find

$$ \upchi =16\frac{a}{b}r{\displaystyle \underset{0}{\overset{b/r}{\int }}z{\upvarphi}_c(z){\upbeta}_c(z){\displaystyle \underset{0}{\overset{l}{\int }}{\left({F}_1\left(z,\overline{\upvarphi}\right)\right)}^2dzd\overline{\upvarphi}}}\frac{{\left(\frac{d^2{y}_j^{*}}{d{x}^2}\right)}_{x={x}_c}^2}{{\displaystyle \underset{0}{\overset{l}{\int }}{\left(\frac{d^2{y}_j}{d{x}^2}\right)}^2dx}}, $$
(13)

where

$$ {\upvarphi}_c(z)= \arccos \left(\left.\frac{-1}{\left(\frac{a^2}{b^2}-1\right)z}\right|1-\left.\sqrt{1+\frac{a^2}{b^2}\left(\frac{a^2}{b^2}-1\right){z}^2}\right|\right), $$
(14)
$$ {\upbeta}_c(z)= \arccos \left(1-z \cos {\upvarphi}_c\right). $$
(15)

By way of example, let us consider a bar with a crack of relative depth b/r = 0.4 and an ellipse semiaxes ratio b/a = 0.4.

The integration of the functions of z and \( \overline{\upvarphi} \) in (13) using (10), (14), and (15) gives

$$ \upchi =0.4224r\frac{{\left(\frac{d^2{y}_j^{*}}{d{x}^2}\right)}^2}{{\displaystyle \underset{0}{\overset{l}{\int }}{\left(\frac{d^2{y}_j}{d{x}^2}\right)}^2dx}}. $$
(16)

The value of \( \left(\frac{d^2{y}_j^{*}}{d{x}^2}\right) \) is determined, as in [1] earlier, for the case of the bar deformation by the jth mode, among other vibration modes considered, by the formula

$$ {\left(\frac{d^2{y}_j^{*}}{D{x}^2}\right)}^2=\left(\frac{d^2{y}_j}{d{x}^2}\right){\displaystyle \sum_{i=1}^N\left(\frac{d^2{y}_i}{d{x}^2}\right).} $$
(17)

For the amplitude functions of deflection y i (x), in the case of a cantilever bar, we have

$$ {y}_i\left({x}_p,x\right)=\frac{P{l}^3}{EI{\left({k}_jl\right)}^4}{X}_i\left({x}_P\right){X}_i(x){\upbeta}_i $$
(18)

for the vibrations excited by a point force P sin vt applied in the section x = x P , and

$$ {y}_i(x)=\frac{Bm{v}^2{l}^3}{EI{\left({k}_jl\right)}^4}{X}_i(x){\displaystyle \underset{0}{\overset{l}{\int }}{X}_i(x)dx{\upbeta}_i} $$
(19)

for the displacement of the restraint (x = 0) B sin vt, where

$$ \begin{array}{l}\kern8em {\upbeta}_i={\left[{\left(\frac{k_il}{k_jl}\right)}^4-{\left(\frac{v}{\upomega_j}\right)}^2\right]}^{-1},\hfill \\ {}{X}_i(x)=\left( \cosh {k}_ix- \cos {k}_ix\right)-\frac{ \cosh {k}_il+ \cos {k}_il}{ \sinh {k}_il+ \sin {k}_il}\left( \sinh {k}_ix- \sin {k}_ix\right),\hfill \end{array} $$
(20)

k i l is the ith root of the frequency equation, m is the mass of the bar unit length, and EI is the cross-sectional bending stiffness.

For the second variant of the crack front variation (a/r = const), disregarding the second-order (of smallness) terms, we have \( \updelta \overline{\uprho}\approx \frac{\uprho}{b\left(1+{ \tan}^2\upvarphi \right)}db \), and formulas (7) and (13) become

$$ \Delta {\varPi}_{jc}=\frac{2a}{E}{\displaystyle \underset{0}{\overset{b}{\int }}{\displaystyle \underset{0}{\overset{\upvarphi_c}{\int }}{K}_1^2}\frac{1}{1+{ \tan}^2\upvarphi}}dbd\upvarphi, $$
(21)
$$ \upchi =16a{\displaystyle \underset{0}{\overset{b/r}{\int }}{\upvarphi}_c(z){\upbeta}_c(z){\displaystyle \underset{0}{\overset{l}{\int }}\frac{{\left({F}_1\left(z,\overline{\upvarphi}\right)\right)}^2}{1+{ \tan}^2\left({\upvarphi}_c(z)\overline{\upvarphi}\right)}dzd\overline{\upvarphi}}\frac{{\left(\frac{d^2{y}_j^{*}}{d{x}^2}\right)}_{x={x}_c}^2}{{\displaystyle \underset{0}{\overset{l}{\int }}{\left(\frac{d^2{y}_j}{d{x}^2}\right)}^2dx}}}, $$
(22)

where

$$ {\upvarphi}_c(z)= \arccos \left(\frac{-z}{\left({\left(\frac{a}{r}\right)}^2-{z}^2\right)}\left[1-\sqrt{1+{\left(\frac{a}{r}\right)}^2\frac{\left({\left(\frac{a}{r}\right)}^2-{z}^2\right)}{z^2}}\right]\right), $$
(23)

\( {F}_1\left(z,\overline{\upvarphi}\right) \) and β c (z) are found from expressions (9) and (15).

For the example a/r = 1 and b/r = 0.4 under consideration, after the functions of \( \overline{\upvarphi} \) in (22) have

been integrated using (11), (15), (23) we have

$$ \upchi =0.425a\frac{{\left(\frac{d^2{y}_j^{*}}{d{x}^2}\right)}_{x={x}_c}^2}{{\displaystyle \underset{0}{\overset{l}{\int }}{\left(\frac{d^2{y}_j}{d{x}^2}\right)}^2dx}}. $$
(24)

For the specified condition a = r the results obtained by (24) are almost coincident with those found by (16).

Numerical Solution Procedure. The problem is solved numerically by means of a finite-element (FE) model of a bar with a breathing crack (Fig. 3), which enables one to take into account the object geometry and physical-mechanical characteristics. For the FE mesh modeling we use an eight-node finite element Solid45 and its modifications [8]. The breathing crack is represented in the form of a mathematical cut; the relative positions of the crack contacting faces are traced by means of surface four-node contact elements Conta174 that exclude mutual penetrations and collisions of the crack faces.

Fig. 3
figure 3

The finite-element model of a bar with a semielliptic surface crack.

Full size image

Thus, the cracked bar system under consideration will be nonlinear for its stiffness, depending on the contact interaction between the crack faces, varies with time and is found by solving the static equilibrium equation:

$$ \left[C\right]\left\{\tilde{u}\right\}=\left\{\tilde{P}\right\}, $$
(25)

where {ũ} is the column vector of nodal displacements, [C] is the stiffness matrix, and \( \left\{\tilde{P}\right\} \) is the vector of angular forces arising from contact interaction between the faces.

Vibration of the bar FE model is described by the matrix equation

$$ \left[M\right]\left\{\overset{..}{u}\right\}+\left[D\right]\left\{\overset{.}{u}\right\}+\left[C\right](u)=\left\{P(t)\right\}, $$
(26)

where [M] and [D] are the inertial and dissipative matrices of the system, {P(t )},{u}, \( \left\{\overset{.}{u}\right\} \), and {ü} are the column vectors of the exciting force, displacement, velocity, and acceleration, respectively.

The dissipative matrix is taken in the form

$$ \left[D\right]=\upeta \left[M\right], $$
(27)

for which, with the decrement δ j (independent of the displacement amplitude) of the resonating jth mode of the bar vibration under study, the constant η is found by

$$ \upeta ={\updelta}_j\frac{\upomega_j}{\uppi}. $$
(28)

For the chosen form of the [D] matrix and the value of η, the decrement of vibrations in any other ith mode is derived as

$$ {\updelta}_i={\updelta}_j\frac{\upomega_i}{\upomega_j}, $$
(29)

i.e., with i > j we take δ i  < δ j .

Equation (26) is solved by time integrating using the Newmark method.

For processing the obtained time dependence of displacements of the neutral line in the bar free end section, we apply the fast Fourier transform (FFT) procedure and eventually determine the harmonics of the vibration process at hand.

Results of Analytical and Numerical Solutions. The solutions were carried out for super- (v/ω j  = 1/2) and subharmonic (v/ω j  = 1/2) resonances in the first ( j = 1) mode of bending vibrations for the ratios a/b = 2.5, l/r = 23, and values

$$ {\uplambda}_{1l}=\frac{y_l(l)}{\varSigma {y}_i(l)},\kern1em {\uplambda}_{2l}=\frac{\varSigma {y}_i(i)}{y_l(l)}. $$
(30)

Consider the characteristic dependences of the crack-induced nonlinearity of the vibrating system at super-and sub-harmonic resonances on the relative crack depth b/r, on the crack location x c , and on the point of application x P of the exciting force P sin vt.

By way of illustration, Fig. 4 shows the dependence of the nonlinearity parameter α, which is determined by (3) in view of (13) and (16) for the case of x P  = l, on b/r at x c  = 0.1l and on x c at b/r = 0.4. Figure 5 gives α vs. x P at b/r = 0.4 and x c  = 0.1l. In all the cases, the parameter α is seen to depend significantly on b/r, x c , and x P ,and this dependence can be different at super- and subharmonic resonances.

Fig. 4
figure 4

The parameter α as a function of the relative depth b/r of the crack located in the section x c  = 0.1l (a) and of the crack location x c for the crack relative depth b/r = 0.4 (b), with the vibrations excited by the force P sin vt applied to in the section x P  = l, with a frequency v = 0.5ω1 (solid lines) and v = 2ω1 (dash lines).

Full size image
Fig. 5
figure 5

The parameter α vs. the point of application of the exciting force P with a frequency v = 0.5ω1 (solid lines) (solid line) and v = 2ω1 (dash line) for a bar with a crack of relative depth b/r = 0.4 located in the section x c  = 0.1l.

Full size image

Using the found values of α, we determined [by formulas (1) and (2)] the corresponding dependences of the

vibrodiagnostic parameters Ā 2/1 and Ā 1/2 on the relative crack depth b/r at x c  = 0.1l in the case of super- and subharmonic resonances excited by a force applied to the section x P  = l (Fig. 6) and in the case of kinematic excitation (Fig. 7). The dependences of Ā 2/1 and Ā 1/2 on the crack location x c for the relative crack depth b/r = 0.4 in the force and kinematic excitations are shown in Figs. 8 and 9, respectively.

Fig. 6
figure 6

The vibrodiagnostic parameters Ā 2/1 and Ā 1/2 as functions of the relative crack depth b/r for the crack location x c  = 0.1l at super- (a) and subharmonic (b) resonances excited by a point harmonic force applied to the section x P  = l. (Here and in Figs. 7–10: open symbols are the analytical solution data, solid symbols are the numerical solution data.)

Full size image
Fig. 7
figure 7

The vibrodiagnostic parameters Ā 2/1 and Ā 1/2 vs. the relative crack depth b/r for the crack location x c  = 0.1l at kinematically excited super- (a) and subharmonic (b) resonances, taking into account the absolute (1) and relative (2) displacements of the bar by a harmonic with the vibration excitation frequency.

Full size image
Fig. 8
figure 8

The vibrodiagnostic parameters Ā 2/1 and Ā 1/2 vs. the crack location for the relative crack depth b/r = 0.4 with the exciting force applied to the section x P  = l in the case of super- (1) and subharmonic (2) resonances.

Full size image
Fig. 9
figure 9

The vibrodiagnostic parameters Ā 2/1 and Ā 1/2 vs. the crack location for the relative crack depth b/r = 0.4, at kinematically excited super- (a) and subharmonic (b) resonances, taking into account the absolute (1) and relative (2) displacements of the bar by a harmonic with the excitation frequency.

Full size image

The dependences of the vibrodiagnostic parameters Ā 2/1 and Ā 1/2 on the point of force application x P for the same crack located in the section x c  = 0.1l are given in Fig. 10 for super- and subharmonic resonances.

Fig. 10
figure 10

The vibrodiagnostic parameter Ā 2/1 (a) and Ā 1/2 (b) as a function of the point of application x P of the exciting force P sin vt for the crack of relative depth b/r = 0.4 in the section x c  = 0.1l.

Full size image

Note that if we take into consideration the bar deformation by only one resonating mode of vibration, i.e., with \( {\left(\frac{d^2{y}_j^{*}}{d{x}^2}\right)}_{x={x}_c}={\left(\frac{d^2{y}_j}{d{x}^2}\right)}_{x={x}_c} \), the values of the parameter α, and thus of Ā 2/1 and Ā 1/2, are independent of the point of application x P of the exciting force or the method of excitation of this resonating mode. The calculated values of these parameters, which correspond to the above-mentioned condition, for the case of vibrations excited by a point force are shown by horizontal lines in Figs. 5 and 10.

The results of determination of Ā 2/1 and Ā 1/2 in kinematic excitation of vibrations are presented for the cases of computation of amplitudes A 1Σ or A 2Σ by the relative displacement of the bar end (x 0 = l) (points 2 in Figs. 7 and 9), i.e., by displacements due to deformation of the bar during its vibration, as well as by the absolute displacement (points 1) that consists of the relative displacement and the displacement of the bar as a rigid body due to the displacement of the restraint. For relative frequencies of the resonances at hand and the possible values of the decrement the bar displacement due to forced vibrations and its displacement as a rigid body are in the same phase at superharmonic resonance and in phase opposition at subharmonic resonance. This enables us to consider, much like in (5), the amplitude functions of deflections and easily determine the amplitude of the absolute displacement.

At subharmonic resonance the amplitude of vibrations of the bar as a rigid body is also influenced by the resonating second harmonic with an amplitude \( {A}_{2P}=\frac{2\upalpha}{9\uppi}{A}_1 \), which has a phase shift relative to the second one by π/2 and is allowed for by the second term in the radicant in (2) [3]Footnote 1.

The results shown in Figs. 6–10 demonstrate that the vibrodiagnostic parameters Ā 2/1 and Ā 1/2 essentially depend on the crack relative depth b/r and location x c as well as on the point of application x P of the exciting force. The dependence of these parameters on b/r and x c is mostly monotonic, while their dependence on x P has extremum points whose number and location essentially depend on the crack location. Noteworthy is also the finding that the trend of these dependences is mainly governed by the nonlinearity parameter α of the vibrating system.

Figures 6–10 give also the results of numerical solutions – the respective dependences of the parameters Ā 2/1 and Ā 1/2 are shown as dark points. It is evident that though these dependences closely correlate in their trend

with the analytical solutions, the values of these parameters differ substantially. For the models considered for these solutions, the discrepancy in the data is conventionally attributed to the fact that the analytical solution disregards the change of vibration mode during the crack opening and assumes the crack opening/closing transition to be a stepwise process.

The numerical solutions performed additionally demonstrate that for the small relative crack depth the change of the vibration mode is insignificant but the contact of the cut nodes along the crack height occurs, strictly speaking, nonsimultaneously. This will be taken into account in further investigations.

Also, we considered the assumption of a possible difference in values of the mode I stress intensity factor (SIF) K 1, which are involved in the analytical solution as per [6, 7] and computed from the crack opening displacement in the numerical solution for the present FE model of a cracked bar and for its deformation behavior. In the second case, using the well-known expression for normal displacements υ of contacting crack faces near the crack front in terms of K 1 [9, 10] and expressing the displacement in terms of the crack opening magnitude Δυ we have

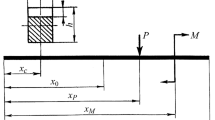
$$ {K}_1=\frac{\Delta \upsilon E}{1+\upmu}\sqrt{\frac{\uppi}{8p}}{\left[ \sin \frac{\upgamma}{2}\left(2-2\upmu -{ \cos}^2\frac{\upgamma}{2}\right)\right]}^{-1}, $$
(31)

where p and γ are the coordinates of contacting nodes nearest to the crack front nodes (Fig. 11).

Fig. 11
figure 11

For determination of stress intensity factors K 1 by the crack opening displacement Δv.

Full size image

The values of K 1 were computed by (31) from displacements of nodes 1′,2′,3′ (Fig. 11) for a bar with its free end statically loaded by a force (x P  = l), with a crack located in the section x c  = 0.1l.

Table 1 gives the K 1 values found for two force values (100 and 200 N). It is evident that the K 1 values in the numerical solutions essentially differ from those involved in the analytical solution using data [6, 7] for the case of simple bending of a bar element. The computations of K 1 by means of the FE model of a bar of length 0.2l with a crack located in the section x c  = 0.1l, with the free end nodes loaded by longitudinal forces whose distribution along the bar height correspond to the distribution of normal stresses in bending, have yielded the data close to those in [6, 7], the difference being 5.8%.

Table 1 Results of Analytical and Numerical Calculations
Full size table

The arithmetic mean of the K 1 values found by the present FE model is about 76% of that as per [6, 7]. If we assume, just formally, that in (8) the values of the dimensionless intensity factor F 1 are 24% smaller than those actually used, the agreement between the results of analytical and numerical solutions for determination of the parameters Ā 2/1 and Ā 1/2 would be significantly improved, even with such a formal refining. In Figs. 6–10, the refined data are shown by dot-and-dash lines.

The numerical solution has confirmed a characteristic feature (as revealed earlier [11] for a single-degreeof-freedom system) in the formation of the amplitude-frequency response (AFR) at a strong superharmonic resonance. Specifically, at a weak resonance (Fig. 12a), much like at any subharmonic resonance, the AFR, if expressed in terms of relative values of the vibration amplitude A/A max, almost fully coincides with the fundamental resonance, while at a strong superharmonic resonance (Fig. 12b) the resonance peak is noted to be more narrow and, therefore, is more difficult to find.

Fig. 12
figure 12

Amplitude-frequency responses of a bar at a weak (a) and strong (b) superharmonic resonances \( \left(\overline{v}=2v/{\upomega}_1\right) \). [Dash lines are the amplitude-frequency responses at fundamental resonance \( \left(\overline{v}=v/{\upomega}_1\right) \).]

Full size image

Conclusions

1. We have discussed here the approximate methods of determination of the vibrodiagnostic parameters of the presence of a mode I semielliptic crack in a circular bar at super- and subharmonic resonances: the analytical solution based on the calculated data of forced transverse vibrations of an intact bar, and the numerical solution by means of the bar FE model.

2. The results of the calculations for the case of resonance of the first-mode bending vibrations have revealed a substantial dependence of the vibrodiagnostic parameters on the crack location and relative depth, on the type and features of vibration excitation. In particular, in the case of vibrations excited by point force the values of the vibration parameters depend on the location of the force application x P along the bar length and exhibit some extremum points whose number and locations are governed by the crack location.

3. A good agreement has been found between the data of the analytical and numerical solutions after a substantiated adjustment was applied to the stress intensity factor values involved in the analytical solution.

4. We have revealed a special feature in the formation of the amplitude-frequency response at a strong superharmonic resonance, which differs from that at other resonances; this makes it more difficult to find.