Introduction. Most of structural elements, in particular, the rotor blades of turbomachinery, operate under conditions of a wide range of dynamic loads, which are the main reason for the occurrence of fatigue cracks. To ensure a reliable operation of machinery, it is necessary to timely detect such damages and estimate their parameters. The presence of a crack affects the elastic properties of a structure, and as a consequence, its vibration characteristics whose variation is one of the possible reasons for the considered damages.

Among the vibration methods of damage diagnostics, those that are based on the monitoring of the modal (frequency and vibration mode) [1, 2] and dissipative [3] characteristics of the objects of investigation and also on the occurrence of the resonances (both sub-harmonic and superharmonic) [4, 5] are worthy of note. It has been found that the former methods are low sensitive to the presence of faults in the object of investigation, require strict setting of the initial state and are efficient only provided that faults occupy more than 20% of the height of its cross section [2, 6]. The results of the analytical [7] and numerical [8] calculation of the vibration-diagnostic parameters to identify the presence of a crack in beams with different boundary conditions, depending on the exciting force application point and location of the damage along their length, are indicative that the methods based on the analysis of the occurrence of non-linear resonances are more sensitive.

In the solution of the crack detection problem by these methods, various approaches to its modeling are used.

Thus, open cracks are represented in the form of elastic elements [9], notches [10], and grooves [11]. However, the models with open cracks do not give rise to the system nonlinearity and are valid for more serious faults [5]. In the case of a breathing crack, which is opened during one half-cycle of the system vibration and is closed during the other half-cycle of such vibration, the variation in its rigidity modeled by the non-symmetrical piecewise linear response of the restoring force is observed under deformation [2, 8, 12–14]. Nonetheless, this assumption does not reflect to a considerable extent the state of the crack, since its opening and closure do not occur instantly. Therefore, in [4, 5, 15] it is proposed to model this kind of crack in the form of a contact interaction of its faces, which enables one to take into account their mutual non-penetration as well as the partial crack closure.

The 2D finite element (FE) model of a cantilever beam of rectangular cross section that allows the consideration of the surface interaction of the breathing crack whose front is perpendicular to its axis is proposed in [16]. The comparison of the calculation results obtained using the 2D FE model and the models in the form of elastic elements and a bilinear oscillator has shown their qualitative agreement and, at the same time, a considerable quantitative difference.

A more general approach to the FE modeling of the crack located at a certain angle to the beam axis in the assumption of the contact interaction of its faces is proposed in [15, 17]. In this case, the advantage of the 3D model is noted, since, as compared to the 2D model, it allows all the vibration modes of the beam to be taken into account.

The goal of the present work is to determine the influence of the point of the exciting force application on the amplitude spectrum of flexural vibrations in a beam of a constant cross section using the three-dimensional finite element modeling and contact interaction of the mode I breathing crack faces under excitation at sub- and superharmonic resonances of the first vibration mode.

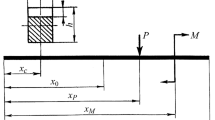
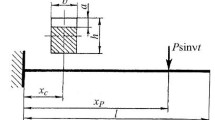
Object of Investigation and Its Modeling. Consider a cantilever beam of length L = 230 mm with a constant rectangular cross section, of height b = 4 mm and width h = 20 mm (Fig. 1). It is assumed that the beam vibration comes from a harmonic transverse force applied at the distance L P from the support. The breathing crack perpendicular to the beam axis whose depth a does not change (4 mm) with its deformation is located at a distance L c from the support. The mechanical characteristics of the beam are as follows: the elastic modulus E = 200 GPa, material density ρ = 7800 kg/m3 , and logarithmic decrement of vibrations δ = 0.01. The choice of this object of investigation allows a comparison of the obtained calculation results with those given in [7, 8].

Fig. 1
figure 1

Cantilever beam of a constant cross section with a breathing crack and applied finite element mesh.

Full size image

The finite element modeling of the beam under consideration proceeds in two steps: creation of the FE model and definition of contact conditions between the crack faces.

The 8-node linear finite element of type Solid45 and its modifications (Fig. 2) are used to construct the FE mesh of the beam (Fig. 1), allowing sufficient accuracy of the solution to be obtained at a relatively high speed of computation.

Fig. 2
figure 2

8-node linear finite element of type Solid45 (a) and its modifications (b).

Full size image

The beam is divided into uniform finite elements (Fig. 2a). As seen from Fig. 1, by analogy with [17], the FE mesh is thickened in the vicinity of the crack. To go to a finer mesh, the modifications of the chosen finite element are used (Fig. 2b).

The breathing crack is represented as a mathematical cut, and the mutual “non- closure” of the crack faces is provided by solving the contact problem using the 4-node surface-to-surface contact elements Conta174 [18], which are used to monitor the relative positions of the contact surfaces (Fig. 3). In this case, the collision of crack faces is eliminated.

Fig. 3
figure 3

A schematic of the interaction between the nodes of the contact surfaces.

Full size image

Calculation Procedure. The matrix equation describing the flexural vibrations of the proposed FE model of the beam with a breathing crack (Fig. 1) is of the form

$$ \left[M\right]\left\{\overset{\cdot \cdot }{u}\right\}+\left[D\right]\left\{\overset{\cdot }{u}\right\}+\left[K\right]\left\{u\right\}=\left\{P(t)\right\}, $$
(1)

where [M], [D], and [K] are the inertial, dissipative and elastic matrices of the system, respectively, {u}, \( \left\{\overset{\cdot }{u}\right\}, \) and {ü}, are the column vectors of displacements, velocity and acceleration, respectively, and {P(t)} is the column vector of external loads acting on the system.

The system under consideration is nonlinear since the elastic matrix [K] varies with time depending on the contact interaction of the crack faces. For its definition, the Newton–Raphson procedure [19] is used, the basis for which is the solution of the nonlinear contact problem described here by the equation

$$ \left[K\right]\left\{u\right\}=\left\{P(t)\right\} $$
(2)

with the result that the contact surface nodes p and q (Fig. 3) interacting with each other are defined.In the general case, the dissipative matrix [D] is of the form

$$ \left[D\right]={\upalpha}_1\left[M\right]+{\upalpha}_2\left[K\right], $$
(3)

i.e., the energy dissipation in the system is due to external and internal friction. This case involves only the presence of energy losses due to the interaction with the external environment of the beam, which does not limit the generality of the problem solution. Therefore, it was assumed that α1 ≡ 0, and α2 was chosen such that δ = 0.01.

The above-mentioned non-linearity of dynamic behavior of the beam under consideration, even under monoharmonic excitation of the steady-state vibration mode at the fundamental resonance of any jth natural mode, allows the detection of higher harmonics using the Fourier analysis and possible occurrence of sub- and superharmonic resonances.

The solution of non-linear equation (1) is performed by the integration in time using the Newmark scheme.

The main essence of the scheme is that the time of the solution under consideration T is divided by N steps with a time step ∆ t = T/N. Next, for each instant of time 0, ∆ t , 2∆t, …, T, the approximate solution is found with consideration of the solution at each sub-step for the previous value of time:

$$ \begin{array}{l}{\left\{\overset{\cdot }{u}\right\}}_{t+\varDelta t}={\left\{\overset{\cdot }{u}\right\}}_t+\left[\left(1-\upgamma \right){\left\{\overset{\cdot \cdot }{u}\right\}}_t+\upgamma {\left\{\overset{\cdot \cdot }{u}\right\}}_{t+\varDelta t}\right]\varDelta t,\hfill \\ {}{\left\{u\right\}}_{t+\varDelta t}={\left\{u\right\}}_t+{\left\{\overset{\cdot }{u}\right\}}_t\varDelta t+\left[\left(\frac{1}{2}-\upbeta \right){\left\{\overset{\cdot \cdot }{u}\right\}}_t+\upbeta {\left\{\overset{\cdot \cdot }{u}\right\}}_{t+\varDelta t}\right]\varDelta {t}^2,\hfill \end{array} $$
(4)

where β and γ are the Newmark integration parameters that determine the accuracy and stability of integration.Here, the initial conditions were chosen as follows: {u}0 = 0, \( {\left\{\overset{\cdot }{u}\right\}}_0=0, \) and {ü}0 = 0.

The next step of the problem solution is the Fourier analysis of the obtained results in the form of the time t dependence of the neutral line displacement in the free-end cross section of the beam. The fast Fourier transformation according to which the set of handled values should be multiple of 2n where n is the integer and the number of the mentioned function periods should be no less than three, is used to handle the u(t) dependence. In our case, this is achieved by way of interpolation of the given dependence corresponding to the steady-state mode of forced vibrationand the representation of its three periods in the form of 8192 points.

The amplitudes of the displacement harmonics A k , where k is the number of the harmonic are determined from the harmonic analysis.

Calculation Results and Their Discussion. According to the problem statement using the developed FE model of the beam with a breathing crack, a comprehensive set of computational experiments was performed to determine the influence of the application point L P of the harmonic exciting force P 0 sin ωt along the beam length on the amplitude spectrum of its flexural vibrations in the excitation frequency range ω equal to the doubled and the half the natural frequency of the first (j = 1) vibration mode of the beam, that is, subharmonic resonance of order 1/2 and superharmonic resonance of order 2 were studied. Two versions of application of the exciting force along the beam height were considered: on the neutral line and at the nodes of its lower face. As in [20], the ratio of the maximum amplitudes of the first A 1 (resonant) and second A 2 harmonics at subharmonic resonance and that of the second A 2 (resonant) and first A 1 harmonics at superharmonic resonance was chosen as a vibration-diagnostic parameter.

The dependences of the chosen ratios of the maximum harmonic amplitudes at sub- (Fig. 4) and superharmonic (Fig. 5) resonances on the application point L P of the exciting force on the neutral line obtained for two locations of the crack L c = 0.1L and 0.5L were plotted from the calculation results. The similar dependences determined by the analytical [7] and numerical [8] methods are presented in Figs. 4 and 5 with the aim of comparing the results.

Fig. 4
figure 4

Dependence of the ratio of the maximum amplitudes of displacement harmonics at subharmonic resonance on the application point L c of the exciting force for L c = 0.1L (a) and L c = 0.5L (b). (Here and in Fig. 5: solid lines correspond to the three-dimensional FE model, dashed lines – analytical solution [7], and dot-and-dash lines – numerical calculation [8].)

Full size image
Fig. 5
figure 5

Dependence of the maximum amplitudes of displacement harmonics at superharmonic resonance on the application point L c of the exciting force for L c = 0.1L (a) and L c = 0.5L (b).

Full size image

The presented results lend support to a strong dependence of the vibration-diagnostic parameters on the exciting force application point whose nature is defined by the crack location and the resonance mode of the beam, which should be taken into account in the diagnostics of the damage location. Thus, firstly, in the application of the force in the cracked cross section of the beam, the maximum of the ratio of the maximum amplitudes A 1/A 2 (Fig. 4) is observed in the case of the subharmonic resonance excitation, and the minimum of A 2/A 1 (Fig. 5) is observed in the case of the superharmonic resonance excitation. Secondly, there exist points of the exciting force application where the subharmonic resonance practically is not excited. This phenomenon discussed in [7] manifests itself if in the cracked cross section, the value of the second derivative of the beam deflection component according to the resonant vibration mode under consideration is equal to zero. It is noteworthy that at subharmonic resonance, the values of the ratio of the maximum amplitudes A 1/A 2 are calculated by both the analytical [7] and the numerical method using the finite element model of the beam and the determination of the change in stiffness of the cracked element at crack opening in terms of the stress intensity factor [8]. At superharmonic resonance, the difference in the values of the ratio of the maximum amplitudes A 1/A 2 is essentially less significant. All the presented dependences agree quite well with each other. It is also of note the established invariance for both the exciting force application on the neutral line and the analytical solution of some vibration-diagnostic parameters indicating the presence of a crack.

Consider the influence of the point of the exciting force application along the height of the cross section on the results of the investigations conducted. The calculations were performed for the crack location at the distance L c = 0.5L for three values of the amplitude P 0 of the exciting force (Fig. 6).

Fig. 6
figure 6

Dependence of the ratio of the maximum amplitudes of displacement harmonics at sub- (a) and superharmonic (b) resonances on the application point of the exciting force on the neutral line (dashed lines) and at the nodes of the lower face of the beam (solid lines) for P 0 = 200 (■), 1000 (●), and 1500 N (▲).

Full size image

The derived dependences of the ratio of the maximum amplitudes of displacement harmonics at superharmonic resonance on the point of application of the exciting force allow the following conclusion to be drawn: at subharmonic resonance, the increase in the amplitude P 0 applied at the nodes of the lower face of the beam results in the increase in the ratio of the maximum amplitudes of displacement harmonics, whereas at superharmonic resonance, it results in its decrease with a practically constant qualitative nature of this ratio dependence on the exciting force application point.

To get a more detailed analysis of the results shown in Fig. 6, consider the time dependence of the relative displacement of the neutral line in the cross section of the beam free end for the steady-state vibration mode. Figure 7 illustrates one vibration period at sub- and superharmonic resonances in case of the application of the harmonic exciting force of the amplitude P 0 = 1000 N for L P = 0.728L . As seen, during the force application at the nodes of the beam lower face, the nature of the time dependence of the neutral line displacement clearly reflects the increase in the amplitude of the first (resonant) harmonic at subharmonic resonance and the decrease in the second (resonant) harmonic at superharmonic resonance, which results in the observed increase in the ratio A 1/A 2 and decrease in the A 2/A 1. This change in the displacement amplitude will be the more significant, the greater the amplitude of the exciting force.

Fig. 7
figure 7

Dependence of the relative displacement of the neutral line in the cross section of the free edge of the beam at sub- (a) and superharmonic (b) resonances in the case of the application of the harmonic exciting force of the amplitude P 0 = 1000 N for L P =0.728L, \( \overline{y}=y/{A}_{cont}, \) A cont is the displacement amplitude of the free end of the uncracked beam for the given load (Solid lines – for the neutral line, dashed lines – for the nodes of the beam lower face.)

Full size image

Conclusions

  1. 1.

    A three-dimensional model of the beam with a breathing crack has been developed assuming the contact interaction of its faces, which allows the consideration of the beam stress state for all excited vibration modes and their change at the crack opening.

  2. 2.

    The dependences of the amplitude ratio of the fundamental displacement harmonics at sub- and superharmonic resonances on the point of the exciting force application have been derived, which agree qualitatively with the known calculation results obtained by the analytical and numerical methods, although their quantitative difference exists.

  3. 3.

    The regularities have been established in the influence of the point of the exciting force application along the length and height of the beam cross section on the value of the ratio of the amplitudes of the fundamental displacement harmonics.