Introduction. It was mentioned earlier in [1, 2] that researchers’ attention was still focused on clarifying an interrelation between vibration parameters of beam-like structures and their damages in the form of a closing fatigue crack under super- and subharmonic resonances. However, the currently available solutions – both analytical and numerical ones – are limited to addressing vibration of an elastic system taking into account the linear viscous friction only. In [2] we provided the results of analytical determination of vibrodiagnostic parameters of the presence of a closing mode I edge crack in beams of rectangular cross section under the conditions of excitation of subharmonic resonance allowing for the amplitude-dependent damping.

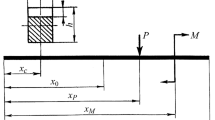
In further elaboration on the work [2, 3], we will consider here, for the case of a cantilever beam of the same cross section and with the same crack (Fig. 1), the results of calculation of the influence of the above-mentioned damping on the vibrodiagnostic parameters of the crack presence under the second-order superharmonic resonance in any jth bending mode, i.e., at an excitation frequency ν equal to half the natural frequency of the jth mode of the damaged beam ω0j .

Fig. 1
figure 1

Schematic representation of a cantilever beam of rectangular cross section with an edge crack under conditions of forced harmonic excitation of bending vibrations.

Full size image

Type of Inelastic Resistance. Consider characteristic types of inelastic resistance as a function of the amplitude A j of displacement (deflection) of the beam free end during the beam deformation by the resonance-inducing jth bending mode (see Table 1).

Table 1 Types of Inelastic Resistance
Full size table

Table 1 gives also the respective expressions for the beam logarithmic decrement δ n (ω0j , A j ), 0 which are easily represented by a single relationship

$$ {\delta}_n={k}_n{A}_j^{n-1}, $$
(1)

subject to the condition

$$ {k}_n=4{h}_n{\upomega}_{0j}^{n-2}\upphi (n)=\frac{2^{n+1}\left(n-1\right){\upeta}_n}{n\left(n+1\right)} $$
(2)

Procedure of Calculation of Vibrodiagnostic Parameters of a Damaged Beam. According to the findings [3], in the case of tuned subharmonic resonance in the jth mode, for the main vibrodiagnostic parameter of the presence of a closing crack in a beam section x = x c we can take the ratio between the maximum amplitude of the second (resonant) harmonic A 2j with a frequency ω0j and the amplitude of the beam fundamental forced vibration with a frequency (1/2)ω0j , i.e., the amplitude of the full first harmonic A 1Σ:Ā 2/1(j)=A 2j /A 1Σ. In the formulas [3] for the parameter Ā 2 =A 2/ A 1, which correspond to the solution of the differential equation of vibration of a single-mass system, the exciting load q can be expressed in terms of the first harmonic amplitude A 1j \( \left(q=\frac{3}{4}{\upomega}_{0j}^2{A}_{1j}\right) \), and thus, these formulas can be written in the following form for a distributed parameters system:

$$ {\overline{A}}_{2/1(j)}=\sqrt[n]{\frac{0.58\alpha {\lambda}_j}{k_n{A}_{1\varSigma}^{n-1}}} $$
(3)

for a weak resonance (Ā 2< 0.9), and

$$ {\overline{A}}_{2/1(j)}=\sqrt[n+1]{\frac{0.5256\alpha {\lambda^2}_j}{k_n{A}_{1\varSigma}^{n-1}}} $$
(4)

for a strong resonance (Ā 2 > 0.9), where γ j is equal to the ratio between the amplitudes of the first harmonic of the fundamental forced vibration in a single resonant jth mode (A 1j ) and in a finite number of modes to be considered (A 1Σ),i.e., λ j = A ij / A 1Σ.

In this case, the formula for a weak resonance should be used when

$$ \frac{\alpha }{k_n}<1.7241\cdot {0.9062}^n{A}_1^{n-1} $$
(5)

In formulas (3)–(5), α is the parameter that represents the initial (i.e., prior to the resonance occurrence) nonlinearity of the vibrating system during its deformation by the fundamental forced vibration in the resonant jth mode among other modes [1].

According to [1], α is determined in terms of the energy characteristic of beam damage κ [ α = κ/ (1 + κ)], which is computed using the values of the normal stress intensity factor K 1 for the crack located in the specified section x = x c with a given crack relative depth γ = a / h, and the amplitude functions of the deflection line of the intact beam y i (x) = A 1i (x) in a limited number N of its bending modes (1 ≤ i ≤ N) by the formula

$$ \upkappa =6\uppi h{H}_1\left(\upgamma \right)\frac{{\left(\frac{d^2{y}_j}{d{x}^2}\right)}_{x={x}_c}{\displaystyle \sum_{i=1}^N{\left(\frac{d^2{y}_i}{d{x}^2}\right)}_{x={x}_c}}}{{\displaystyle \underset{0}{\overset{1}{\int }}\left(\frac{d^2{y}_i}{d{x}^2}\right)dx}}, $$
(6)

where

$$ {H}_1\left(\upgamma \right)=0.078{\uptheta}^2\left[{\left(1-\upgamma \right)}^{-2}{\left(1-\upgamma \right)}^4-1.5\right], $$
(7)

θ = 1.15 − 60γ 2 at 0< γ < 0.05 and θ = 1 пpи γ > 0.05.

For the case of the cantilever beam at hand, the amplitude function of of the deflection line is given by the formulas

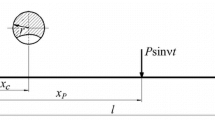
$$ {y}_i(x)=\frac{P{l}^3}{EI{\left({k}_jl\right)}^4}{X}_i\left({x}_P\right){X}_i(x){\beta}_i $$

for the vibration excited by a concentrated force P sin vt applied in section x = x P ,

$$ {y}_i(x)=\frac{M{l}^3}{EI{\left({k}_jl\right)}^4}{X}_i^{\prime}\left({x}_M\right){X}_i(x){\beta}_i $$

for the vibration excited by a concentrated moment M sin vt applied in section x = x M , and

$$ {y}_i(x)=\frac{Bm{v}^2{l}^3}{EI{\left({k}_jl\right)}^4}{X}_i(x){\displaystyle \underset{0}{\overset{1}{\int }}{X}_i(x){\beta}_i} $$

for the vibration excited by displacement of restraint (x = 0) B sin vt, where

$$ {X}_i(x)=\left( \cosh {k}_ix- \cos {k}_ix\right)-\frac{ \cosh {k}_il+ \cos {k}_il}{ \sinh {k}_il+ \sin {k}_il}\left( \sinh {k}_ix- \sin {k}_ix\right) $$
$$ {\beta}_i={\left[{\left(\frac{k_il}{k_jl}\right)}^4-{\left(\frac{v}{\upomega_j}\right)}^2\right]}^{-1} $$

v = ω j /2, k i l is the ith root of the frequency equation, EI is the bending stiffness of the beam section, m is the unit mass of the beam length, and ω j is the natural frequency of the jth mode.

For one more diagnostic parameter we can consider the ratio of the amplitude A 2 j to the maximum amplitude A 0 j of the fundamental harmonic under the principal resonance (v = ω0j ) in the jth mode (A 2 j / 0 j = Ā 2/0(j)). This ratio is given by

$$ {\overline{A}}_{2/0(j)}=\sqrt[n]{0.24616\alpha \frac{Q_s}{Q_0}} $$
(8)

under the weak superharmonic resonance, and

$$ {\overline{A}}_{2/0(j)}={\sqrt[n+1]{0.24616\alpha \left(\frac{Q_s}{Q_0}\right)}}^2{A}_{0j}^{n-1} $$
(9)

under the strong superharmonic resonance, where Q s and Q 0 are the amplitudes of the forcing load (P, M, Bmv 2) under the superharmonic and principal resonances, respectively.

It is evident that with n ≠1, in the case of a strong superharmonic resonance, the values of Ā 2/0(j), as well as those of the parameters A 2/1( j ) (3) and (4), are not relative characteristics for they depend on absolute values of the amplitude A 0 j or A 1Σ and thus on the exciting load level Q 0 or Q s , and on the choice of the place where the deflection is to be recorded. Also, formulas (3), (4), and (9) include the coefficient k n whose value generally differs for different exponents n of the amplitude dependence of the decrement δ n .

In this context, let us consider the parameter A 2/1( j ) when selecting the k n value from the condition that the maximum deflection amplitude at any section x *under the principal resonance for the specified jth mode and exciting load amplitude Q 0 should be equal to that in the linear viscous friction (n =1) with a specified decrement value δ1 = k 1:

$$ {k}_n=\frac{\delta_1^n}{\uppi^{n-1}{Q}_0^{n-1}{\varDelta}_j^{n-1}}, $$
(10)

where the constant Δ j is given by

$$ \frac{l^3{X}_j\left({x}_P\right){X}_j\left({x}^{*}\right)}{EI{\left({k}_jl\right)}^4},\frac{l^3{X}_j^{\prime}\left({x}_M\right){X}_j\left({x}^{*}\right)}{EI{\left({k}_jl\right)}^4}\mathrm{or}\frac{l^3{X}_j\left({x}^{*}\right){\displaystyle \underset{0}{\overset{1}{\int }}{X}_j(x)}dx}{EI{\left({k}_jl\right)}^4}, $$
(11)

for the vibrations excited by a concentrated force, moment, or displacement of restraint, respectively.

In this case, with the same method of excitation of the superharmonic resonance with a load amplitude Qs whereby \( {A}_{1\varSigma }=\frac{4}{3}\frac{Q_s}{\lambda_j}{\varDelta}_j \), we will find from (3) and (4) the parameters

$$ {\overline{A}}_{2/1(j)}=2.3562\frac{\lambda_j}{\delta_1}\sqrt[n]{0.24616\alpha {\left(\frac{Q_0}{Q_s}\right)}^{n-1}}, $$
(12)

and

$$ {\overline{A}}_{2/1(j)}=2.3562\frac{\lambda_j}{\delta_1}\sqrt[n+1]{0.09467\alpha \delta {\left(\frac{Q_0}{Q_s}\right)}^{n-1}}, $$
(13)

whose values are independent of the absolute level of Q 0 and Q s .

Assessment of the Fit between the Results of the Analytical and Numerical Solutions. Before proceeding to a study of the influence of the amplitude-dependent damping parameters, we will compare the results of calculation by the procedure outlined above and the data of numerical solution for the beam vibration excited by a concentrated force under the linear viscous friction conditions (n =1, k n =δ1), where the vibrodiagnostic parameters (3), (4) and (8), (9) depend neither on the absolute value of the loads Q 0 and Q s , nor on their ratio.

For the purpose of comparison, we considered the available data obtained through the use of the beam finite-element model, where the variation of stiffness of the element with a crack during the crack opening was determined in terms of the stress intensity factor [4], and the results of the solution run by means of ANSYS software package [5] using a linear eight-node finite element (Solid45), where a breathing crack was represented in the form of a mathematical cut with appropriate contact problem conditions. The resulting nonlinear system of differential equations is solved by time integration followed by the Fourier transform.

Figures 2 and 3 compare, for the case of the first resonant mode (j =1), the respective functions of the parameters Ā 2/1 and Ā 2/0 vs. the location of the exciting force application (x P / l) for a beam with a ratio h/ l ≈ 0.085 and relative crack depth γ = 0.2, the crack being located in sections x c = 01l and 0.5l, with δ1 = 0.01, which were plotted by calculation and by the data of numerical solutions. For the parameter Ā 2/0 the ratio between the exciting force amplitudes under the superharmonic resonance P s and principal resonance P 0 is 100. It is obvious that the results are in good agreement.

Fig. 2
figure 2

The vibrodiagnostic parameter Ā 2/1 vs. the point of application of the exciting force (x P / l ) for a beam containing a crack of relative depth γ = 0.2 in the sections x c = 0.1l and 0.5l. (Here and in Fig. 3: solid lines are the calculated results, dash lines are data of numerical solutions, and dash-and-dot lines are data provided in [4].)

Full size image
Fig. 3
figure 3

The vibrodiagnostic parameter Ā 2/0 vs. the point of application of the exciting force (x P / l) for a beam containing a crack of relative depth γ = 0.2 in sections x c = 0.1l and 0.5l.

Full size image

Noteworthy is the characteristic feature that makes the difference between the weak superharmonic resonance and strong one. For instance, the results of the numerical solution for the single-mass model whose forced vibration is described by the equation

$$ \ddot{y}+2{h}_1+\overset{.}{y}+{\upomega}^2\left[1-5\alpha \left(1+\mathrm{sign}\ y\right)\right]y= \sin \nu t, $$

demonstrate that under the weak superharmonic resonance the amplitude-frequency response of the second harmonic almost corresponds to the principal resonance, with the maximum amplitudes being equal (A 2 = A 0 ), while in the case of the strong superharmonic resonance the resonance peak is much narrower (Fig. 4). This certainly makes difficult finding the resonance.

Fig. 4
figure 4

The amplitude-frequency response of a vibrating system under the weak (α =0.014, Ā 2/1 = 0.776) and strong (α =0.2, Ā 2/1 = 3.20) second-order superharmonic resonances.

Full size image

The Influence of the Trend of the Amplitude Dependence of Vibration Decrement on Vibrodiagnostic Parameters. As in the above discussion, we will restrict our consideration to the case of excitation of the first resonant mode (j =1).

When using formulas (3), (4), and (9), e.g., for the vibration excited by a concentrated force applied to the section x P = l, and measuring the deflection in the section x *= l, we should know, in addition to the parameter α = κ/(1 + κ), where κ is given by (5), the absolute value of A 1Σ or A 01 for a given amplitude of the exciting force P s or P 0:

$$ {A}_{1\varSigma }=\frac{4}{3}{P}_s\frac{\varDelta_1}{\lambda_1},{A}_{01}=\sqrt[n]{P_0}\frac{\uppi}{k\uppi}{\varDelta}_1, $$
(14)

where

$$ {\varDelta}_1=\frac{l^3{X}_1^2(l)}{EI{\left({K}_1l\right)}^4},{\lambda}_1=\frac{4}{3}{X}_1^2(l){\left[{\displaystyle \sum_{i=1}^N\frac{X_i^2(l)}{{\left(\frac{k_il}{k_1l}\right)}^4-\frac{1}{4}}}\right]}^{-1} $$
(15)

Then, (3) and (4) will become respectively

$$ {\overline{A}}_{2/1}={\lambda}_1\sqrt[n]{\frac{0.435\alpha }{k_n\left({P}_s{\varDelta_1}^{n-1}\right)}} $$
(16)

and

$$ {\overline{A}}_{2/1}={\lambda}_1\sqrt[n+1]{\frac{0.3942\alpha }{k_n{\left({P}_s{\varDelta}_1\right)}^{n-1}}} $$
(17)

while (9) will take the form

$$ {\overline{A}}_{2/0}=\sqrt[n+1]{0.09467\alpha {k}_n^{1/n}{\left(\frac{P_s}{P_0}\right)}^2{\left(\uppi {P}_0{\varDelta}_1\right)}^{\left(n-1\right)/n}} $$
(18)

It follows from (16)–(18) that the variation of the beam damage assessed by the parameters Ā 2/1 and Ā 2/0 is advisable to be determined with the same value of the exciting load amplitude for the chosen method of excitation and place of vibration recording, or an adjustment should be made for a difference in these values.

The influence of the exponent n on the vibrodiagnostic parameters is clearly seen from the function Ā 2/1(n ) (Fig. 5) calculated by formula (17) for different values of the coefficient k n [1/m n-1] for a beam with a crack of relative depth γ= 0.2 located in the root section, for the following beam dimensions: b = 0.004 m, h = 0.02 m, and l = 0.23 m; the elastic modulus of the material E = 2∙1011 N/m2 , the exciting force amplitude P s =100 N.

Fig. 5
figure 5

The vibrodiagnostic parameter Ā 2/1 as a function of the exponent n for different values of the coefficient k n in the case of vibration excited by a concentrated force applied to the section x P = l.

Full size image

Figure 6 shows a similar function of the parameter Ā 2/0 (18) for the same beam with the ratio P s / P 0 = 50, P0 = 2 N.

Fig. 6
figure 6

The vibrodiagnostic parameter Ā 2/0 as a function of the exponent n for different values of the coefficient k n for vibration excited by a concentrated force applied to the section x P = l

Full size image

Finally, let us look at the influence of the trend of the amplitude dependence of vibration decrement on the vibrodiagnostic parameter Ā 2/1 (12), (13), which is independent of absolute values of the exciting load amplitudes Q 0 and Q s , but the chosen value of Q 0 dictates the value of the vibration amplitude \( {A}_{01}=\frac{\pi }{\delta_1}{\varDelta}_1{Q}_0 \) , whereby the damping capacity of a beam with the nonlinear resistance (n≠1) is equal to that with the amplitude-independent resistance (n=1) as represented by a decrement value of δ1.

By way of illustration of the use of formulas (12) and (13), Fig. 7 shows the dependence of Ā 2/1 on the location of the exciting concentrated force P application for a beam with a ratio h / l = 0.85 and with a crack of relative depth γ = 0.2 located in the sections x c = 0 and x c = 0.25l, for different ratios P s / P 0 and different trends of the amplitude dependence of vibration decrement with δ1 = 0.01. Figure 8 gives Ā 2/1 vs. the relative crack depth γ, the crack being located in the root section, for different values of the exponent n in the case of vibration excited by a concentrated force and moment applied to the section x P = x M = 1 and by displacement of support at P s / P 0 = M s / M 0 = B s / B 0 = 1.

Fig. 7
figure 7

The parameter Ā 2/1 as a function of the point of application of the exciting force in the case of a crack of relative depth γ = 0.2 located in the sections x c = 0 (a) and 0.25l (b), with different values of the exponent n of the amplitude dependence of inelastic resistance for different values of the ratio P s / P 0. (Solid lines – Ps / P 0 = 1, dash lines – P s / P 0 =10, dash-and-dot lines – P s / P 0 =50.)

Full size image
Fig. 8
figure 8

The vibrodiagnostic parameter Ā 2/1 vs. the relative crack depth γ, the crack being located in the beam root section, for different values of the exponent n in the case of vibration excited by a concentrated force (solid lines) and moment (dash-and-dot lines) and by displacement of support (dash lines).

Full size image

Through the example of a beam with a relative depth γ = 0.2 of the crack located in the root section, Fig. 9 illustrates the influence of the ratio of amplitudes of the forcing loads Q s / Q 0 on Ā 2/1 values for the vibration excited by a concentrated force applied to the section x P = l for different values of n and δ1

Fig. 9
figure 9

The vibrodiagnostic parameter Ā 2/1 as a function of the ratio of exciting load amplitudes Q s / Q 0 for different values of the logarithmic decrement δ1 and exponent n. (Solid lines – n = 2, dash lines – n = 1.5, and horizontal lines – n = 1.)

Full size image

Conclusions. We have considered here the methods (based on the calculation of vibrations of an intact system) for the determination of the influence of nonlinearity of damping capacity of a beam under the second-order superharmonic resonance in the lowest natural mode of bending vibration on the vibrodiagnostic parameters of the presence of an edge closing crack in the beam. For vibrodiagnostic parameters we used the ratio of the maximum amplitude of the second resonant harmonic to the total amplitude of the first harmonic (Ā 2/1) and to the maximum amplitude of the principal resonance (Ā 2/0). For the power-law dependence of decrement on amplitude (δ n = k n A n−1) we have determined the possible dependences of the parameters Ā 2/1 and Ā 2/0 on the exponent n at different values of the coefficient k n , on the crack relative depth γ, and location x c as well as on special features of vibration excitation. Damping capacity of a vibrating system is shown to have an essential effect on the values of the vibrodiagnostic parameters of the amplitude dependence. However, the trend of their dependence on the crack relative depth and location and on the method of vibration excitation remains unchanged.