1 Introduction

The core problem of algorithms in machine learning is how to find a suitable model from limited training data so that it can make accurate predictions or decisions on unknown data. To address this problem, machine learning researchers have proposed different learning criteria and optimization methods to guide the model selection and training process. The learning criterion of empirical risk minimization (ERM), which is applied to the recently popular GPT (Generative Pretrained Transformer) model. GPT is an autoregressive language model based on the Transformer structure. It can achieve excellent performance in a variety of natural language processing tasks through large-scale unsupervised pretraining and supervised fine-tuning. The training process of GPT involves the idea of empirical risk minimization Ouyang et al. (2022), that is, to improve the generalization ability of the model on the test set by minimizing the loss function of the model on the training set. Taking general linear regression as an example, assuming that the loss function is the mean square error, plus \(l_2\) regularization, the minimization of the objective function can be written as

$$\begin{aligned} \mathop {min}_{\omega , b} \ \frac{1}{2m}\displaystyle \sum _{i=1}^m(y_i-\omega ^Tx_i-b)^2+\lambda \Vert \omega \Vert ^2_2 \end{aligned}$$

where \(w\in \Re ^L\) is the weight vector of the model, b is the intercept, \(y_i\) is the observed value of sample i, and \(x_i\) is the feature vector of sample i. n is the total number of samples and \(\lambda \) is the regularization hyperparameter. We use \(F_i:\Re ^L\rightarrow \Re \) to denote the objective function for the i-th sample, and then the above can be written in a more general form:

$$\begin{aligned} \mathop {min}_{\omega } F(\omega )=\frac{\displaystyle \sum _{i=1}^m F_i(\omega )}{m} \end{aligned}$$
(1.1)

The full gradient descent algorithm Cauchy (1847) is a classic algorithm to solve the above problems. The basic idea is that each time the parameters are updated, the gradient information on the entire training set is used to advance a certain step in the opposite direction of the gradient, thereby gradually reducing the value of the loss function until it converges to a local minimum or global min. However, when the training set is large, calculating the gradient will be very time-consuming, and the same gradient must be calculated repeatedly every time the parameters are updated, resulting in inefficiency. In addition, the full gradient descent algorithm is also sensitive to the choice of learning rate. If the learning rate is too large or too small, it will affect the convergence speed and effect. In order to overcome the shortcomings of the full gradient descent algorithm, many improved methods have appeared: Bottou (2010); Bottou et al. (2018); Robbins and Monro (1951); Goodfellow et al. (2016). At the same time, in order to increase the convergence rate of SGD algorithms, Le Roux Schmidt et al. (2017) proposed an SGD method with variance technology, and based on this work, more gradient methods with variance technology such as CGVR (Jin et al. (2018)), SCGN (Yuan et al. (2021a)), SCGA (Kou and Yang (2022)), and their common feature is that they all use the stochastic conjugate gradient method. Among them, CGVR and SCGA are both hybrid conjugate gradient methods, and both achieve linear convergence rates under strong convex conditions. In addition to this, there are also adaptive methods that are popular in machine learning such as: AdaGrad (Lydia and Francis (2019)), AdaDelta (Zeiler (2012)), Adam (Kingma and Ba (2014)). Due to their adaptive step size and relatively robust selection of hyper-parameters, they perform well on many problems even without fine-tuning hyper-parameters. With the increasing size of data in machine learning problems, and the good performance of traditional conjugate gradient methods in dealing with large-scale equations, we have reason to believe that the stochastic conjugate gradient method can be better applied in machine learning.

1.1 Conjugate gradient method

Considering the traditional unconstrained optimization problem:

$$\begin{aligned} \min \{ f(x) \ \mid \ x \in \Re ^L \}, \end{aligned}$$
(1.2)

where \(f:\Re ^L\rightarrow \Re \). The conjugate gradient method is a important algorithm to solve the problem (1.2), which is a method between the steepest descent method and the Newton method. It overcomes the slow convergence of the steepest descent method and avoids the disadvantage of the Newton method that needs to calculate the Hesse matrix. The CG method, which is defined by

$$\begin{aligned} d_{s+1}=\left\{ \begin{array}{ll} -g_{s+1}+\beta _{s}d_{s}, &{} \text{ if }\,\,\,\, s\ge 0,\\ -g_{s+1},&{} \text{ if }\,\,\,\,s=0, \end{array} \right. \end{aligned}$$
(1.3)

where \(g_{s+1}=\nabla f(x_{s+1})\) is the gradient of f(x) at \(x_{s+1},\) and \(\beta _s \in \Re \) is a scalar which has four classic CG formulas with

$$\begin{aligned} \begin{aligned}&\beta _s^{PRP}=\frac{g_{s+1}^Ty_{s+1}}{\Vert g_s\Vert ^2},\,\, [22, 23, 27]\\&\beta _s^{FR}=\frac{g_{s+1}^Tg_{s+1}}{\Vert g_{s}\Vert ^2},\,\, [20] \\&\beta _s^{HZ}=\frac{g_{s+1}^Ty_{s+1}(d_s^Ty_{s+1}-2\Vert y_{s+1}\Vert ^2(g_{s+1}^Td_{s}))}{y_{s+1}^Td_{s}},\,\, [21] \\&\beta _s^{DY}=\frac{g_{s+1}^Tg_{s+1}}{y_{s+1}^Td_{s}},\,\, [25], \end{aligned} \end{aligned}$$

where \(\Vert \cdot \Vert \) denote the Euclidean norm and \(y_{k+1}=g_{s+1}-g_s\). For better theoretical or numerical results, many scholars have revised these classical directions Yuan et al. (2022a, 2021b, 2021a, 2022b, 2019); Wang et al. (2022). Among them, Yuan et al. (2019) obtained the global convergence of PRP through a modified wolf line search. Recently, the adaptive conjugate gradient method proposed by Wang and Ye (2023) has a better performance in training neural networks for image processing. CGVR is a hybrid of FR and PRP methods on the basis of SVRG (Johnson and Zhang (2013)), and SCGA is a similar work on SAGA (Defazio and Bach (2014)). Although both of them exhibit faster convergence rates experimentally, both require strong theoretical assumptions in convergence analysis, which is worthy of our further study. Jiang et al. (2023) weakens the hypothesis by restarting the coefficients. In order to weaken the condition of the assumption, it prompts us to think about the direction of descent and the step size. Inspired by Yuan, we consider using line search to get some better theoretical properties. As we all know, when we require the step size to satisfy the strong wolf step size condition Wolfe (1969), we can avoid the case where the direction is not the descending direction,

$$\begin{aligned} \begin{aligned}&f(x_s+\alpha _{s}d_s)\le f(x_s)+\eta \alpha _s\nabla f(x_s)^Td_s,\\&|\nabla f(x_s+\alpha _sd_s)^Td_s|\le -\sigma \nabla f(x_s)^Td_s \end{aligned} \end{aligned}$$
(1.4)

where \(0<\eta<\sigma <1\). Due to its strong properties and numerical effects, some scholars use the strong wolfe condition in stochastic optimization problems (Kou and Yang (2022); Jin et al. (2018)).

2 Inspiration and algorithm

Inspired by many scholars and the conjugate gradient and line search for continuous optimization in the introduction, we want to apply the new conjugate gradient method and line search to stochastic optimization problems. Here we first review two different gradient estimates in stochastic methods. In stochastic optimization algorithms, using the mini-batch sampling method can improve computational speed, avoid redundant samples, and accelerate convergence. This method achieves acceleration by processing only a small portion of the data per iteration, while ensuring accuracy of results. It significantly reduces computational costs and is more easily applicable to large-scale datasets. The gradient estimation expression of the mini-batch SAGA algorithm is as follows::

$$\begin{aligned} G_s=\nabla F_{C_s}(\omega _s)-\frac{\displaystyle \sum _{i\in C_s }\nabla F_i(\omega _{[s-1]})}{|C_s|}+\frac{\displaystyle \sum _{i=1}^m\nabla F_i(\omega _{[s-1]})}{m} \nonumber \\ \end{aligned}$$
(2.1)

where \(\omega _{[s]}\) represents the latest iterate at which \(\nabla F_i\) was evaluated, \(C_s\) represents the s-th small batch and \(|C_s|\) represents the size of the batch. \(\nabla F_i(\omega _{[s]})\) is the gradient of the i-th sample at iterate \(\omega _{[i]}\). Taking the expectation from the above equation can be seen that it is an unbiased estimate. The first three-term CG formula is presented by Zhang et al. (2007) for continuous optimization problems (1.2):

$$\begin{aligned} d_{s+1}=\left\{ \begin{array}{ll} -g_{s+1}+\frac{g_{s+1}^Ty_{s+1} d_{s}-g_{s+1}^Td_{s}y_{s+1}}{\Vert g_{s}\Vert ^2}, &{} \text{ if }\,\,\,\, s\ge 1\\ -g_{s+1},&{} \text{ if }\,\,\,\,s=0, \end{array} \right. \end{aligned}$$
(2.2)

we write in a more general form:

$$\begin{aligned} d_{s+1}=-g_{s+1}+\beta _{s+1}d_s-\theta _{s+1}y_{s+1} \end{aligned}$$

where \(y_{s+1}=g_{s+1}-g_s\), \(\beta _{s+1}\) is a parameter of the standard PRP conjugate gradient method, \(\theta _{s+1}\) is a parameter of the three-term CG method. \(\beta _{s+1}\) and \(\theta _{s+1}\) are calculated as follows:

$$\begin{aligned} \beta _{s+1}=\frac{g^T_{s+1}y_{s+1}}{\Vert g_s\Vert ^2}, \ \theta _{s+1}=\frac{g^T_{s+1}d_s}{\Vert g_s\Vert ^2} \end{aligned}$$
(2.3)

Some studies on the three-term conjugate gradient method have shown that it has the good property. In Kim et al. (2023), he applied the three-term conjugate gradient method to the artificial neural network, which is comprehensively compared with SGD, Adam, AMSGrad Reddi et al. (2019) and AdaBelief Zhuang et al. (2020) methods and is competitive, but it doesn’t do much theoretical analysis. Kou and Yang (2022) tried to add the conjugate gradient method to SAGA and got SCGA. Yang (2022) combining mini-batch SARAH (Nguyen et al. (2017)) with FR conjugate gradient methods named CG-SARAH-SO. Huang et al. (2023) combined the modified PRP with SARAH to propose BSCG. Inspired by Yang, Kou and Kim, can we take advantage of the property of the three-term conjugate gradient to obtain the convergence rate estimated in other gradients? we try to use the excellent properties of conjugate gradient directions, remove some assumptions, and adopt a new direction inspired:

$$\begin{aligned} d_{s+1}=\left\{ \begin{array}{ll} -g_{s+1}+\frac{y_{s+1}^Tg_{s+1} d_{s}-d_{s}^Tg_{s+1}y_{s+1}}{\mu _1\Vert y_{s+1}\Vert \Vert d_{s}\Vert +\mu _2\Vert y_{s+1}\Vert \Vert g_{s+1}\Vert +\Vert g_{s}\Vert ^2}, &{} \text{ if }\,\,\,\, s\ge 1\\ -g_{s+1},&{} \text{ if }\,\,\,\,s=0, \end{array} \right. \nonumber \\ \end{aligned}$$
(2.4)

we try to apply direction (2.4) to the stochastic optimization problem:

$$\begin{aligned} P_{s+1}=\left\{ \begin{array}{ll} -G_{s+1}+B_{s+1}P_s-O_{s+1}Y_{s+1}, &{} \text{ if }\,\,\,\, s\ge 1\\ -G_{s+1},&{} \text{ if }\,\,\,\,s=0, \end{array} \right. \end{aligned}$$
(2.5)

where \(P_{s+1}\) represents the descending direction of the sample iteration and \(Y_{s+1}=G_{s+1}-G_s\). \(B_{s+1}\) and \(O_{s+1}\) are calculated as follows:

$$\begin{aligned} B_{s+1}= & {} \frac{G^T_{s+1}Y_{s+1}}{\mu _1\Vert Y_{s+1}\Vert \Vert P_{s}\Vert +\mu _2\Vert Y_{s+1}\Vert \Vert G_{s+1}\Vert +\Vert G_{s}\Vert ^2},\nonumber \\ \end{aligned}$$
(2.6)
$$\begin{aligned} O_{s+1}= & {} \frac{G^T_{s+1}P_s}{\mu _1\Vert Y_{s+1}\Vert \Vert P_{s}\Vert +\mu _2\Vert Y_{s+1}\Vert \Vert G_{s+1}\Vert +\Vert G_{s}\Vert ^2}\nonumber \\ \end{aligned}$$
(2.7)

Dai (2002) proposes two Armjio-style line search methods, one of which is as follows:

$$\begin{aligned} \begin{aligned} f(x_{s+1})&\le f(x_s)+\eta \alpha _s g_s^Td_s,\\ g_{s+1}^Td_{s+1}&\le -\sigma _2\Vert g_{s+1}\Vert ^2\\ \end{aligned} \end{aligned}$$
(2.8)

given constants \(t \in (0,1),\eta >0\),\(\sigma _2\in (0,1]\), \(\alpha _s=max\{t,t^2,...\}\). In fact, the second search line of this line includes sufficient descent, but because it uses the direction when \(s=s+1\), it leads to a large amount of calculation when looking for the step size. In order to make the step size more acceptable, we are in a correction item has also been added to the Armjio condition. Inspired by Yuan et al. (2019) of modifying Wolfe’s line search criterion, we modify Dai’s line search. In order to get an appropriate step size \(\alpha _k \), we design a modifed inexact line search:

$$\begin{aligned} \begin{aligned} f(x_{s+1})\le f(x_s)+&max\{\eta _1\alpha _s g_s^Td_s,-\eta _2\alpha _s^2\Vert g_s\Vert ^2\},\\ g_{s+1}^Td_{s+1}+&\sigma _1\Vert d_{s+1}\Vert ^2\le -\sigma _2\Vert g_{s+1}\Vert ^2\\ \end{aligned} \end{aligned}$$
(2.9)

where \(\eta _1\) and \(\eta _2\) are constants in (0,1) and \( \sigma _2+\sigma _1>1, \sigma _1\le 1, \sigma _2>0\), when \(\sigma _1\) is small enough, it approximates the second criterion of (2.8). It can lead to some useful conclusions with the nature of the direction when discussing the convergence of the algorithm later. We write (2.9) in the form of a random line search and apply it to a stochastic optimization problem to find the step size:

$$\begin{aligned}{} & {} F_C(x_{s+1})\le F_C(x_s)+max\{\eta _1\alpha _s G_s^TP_s,-\eta _2\alpha _s^2\Vert G_s\Vert ^2\},\nonumber \\{} & {} G_{s+1}^TP_{s+1}+\sigma _1\Vert P_{s+1}\Vert ^2\le -\sigma _2\Vert G_{s+1}\Vert ^2 \end{aligned}$$
(2.10)

Direction (2.1) calculated by the conjugate gradient method and modified line search (2.10), we give the algorithm SATCG. Due to the properties of sufficient descent and trust region, we have reasons to believe that SATCG possesses better theoretical properties compared to SCGA and CGVR.

The remainder of this paper is organized as follows. In Section 1, we review the SGD algorithm, gradient estimation methods with variance reduction techniques, and conjugate gradient methods. In Section 2, inspired by the SCGA and three conjugate gradient methods, we propose the SATCG algorithm. In Section 3, we provide a theoretical analysis of SATCG. In Section 4, we analyze the experimental performance of SATCG in two machine learning models.

Algorithm 1
figure a

SATCG

Full size image

2.1 Contribution

\(\diamondsuit \) We provide a convergence analysis of SATCG in the non-convex condition, and compared to SCGA and CGVR, SATCG exhibits superior theoretical properties, achieving linear convergence rate with fewer assumptions.

\(\diamondsuit \) We analyze the performance of SATCG in two machine learning models and find that it exhibits better numerical performance than traditional SGD methods on large-scale datasets. We also compare it to adaptive algorithms. Additionally, we investigate the performance of SATCG and SCGA on small-sized datasets. Overall, SATCG demonstrates superior convergence properties compared to traditional SGD algorithms and remains competitive with SCGA, while providing more stable numerical performance.

3 Features and convergence of SATCG

Assumption 3.1

For all of the individual function \(\nabla F_i(\omega )\) is Lipschitz smooth. From the properties of Lipschitz, we can obtain the following conclusion:

$$\begin{aligned} F(\omega )\le F(v)+<\nabla F(v),\omega -v>+\frac{L}{2} \Vert \omega -v\Vert ^2 \end{aligned}$$
(3.1)

Assumption 3.2

The Polyak-ojasiewicz (PL) condition holds for some \(\Omega \) > 0.

$$\begin{aligned} F(\omega ) - F(\omega _*) \le 2\Omega \Vert \nabla F(\omega )\Vert ^2 \end{aligned}$$

where \(F(\omega _*)\) is the lower bound on the function F. The PL condition does not contain any convexity, an example in the article in Karimi et al. (2016): \(f(x)=x^2+3sin^2x\), when \(\Omega =8\), the PL condition is satisfied, but the function is non-convex.

Theorem 3.1

We can derive the following two properties based on Direction 1:

$$\begin{aligned} G_s^TP_s=-\Vert G_s\Vert ^2 \end{aligned}$$
(3.2)

and

$$\begin{aligned} \Vert P_s\Vert \le (1+\frac{2}{\mu _1})\Vert G_s\Vert \end{aligned}$$
(3.3)

Proof

When s=1, (3.2) and (3.3) obviously hold. For \(s>2\), by (2.4) we have

$$\begin{aligned} \begin{aligned} G_s^TP_s&=G_s^T[-G_s+\frac{Y_s^TG_s P_{s-1}-P_{s-1}^TG_sY_s}{\mu _1\Vert Y_s\Vert \Vert P_{s-1}\Vert +\mu _2\Vert Y_s\Vert \Vert G_s\Vert +\Vert G_{s-1}\Vert ^2}]\\&=-\Vert G_s\Vert ^2+\frac{Y_s^TG_s P_{s-1}^TG_s-P_{s-1}^TG_sY_s^TG_s}{\mu _1\Vert Y_s\Vert \Vert P_{s-1}\Vert +\mu _2\Vert Y_s\Vert \Vert G_s\Vert +\Vert G_{s-1}\Vert ^2}\\&=-\Vert G_s\Vert ^2 \end{aligned} \end{aligned}$$

We can get: \( G_s^TP_s=-\Vert G_s\Vert ^2\ge -\Vert G_s\Vert \Vert P_s\Vert \), then \(\Vert P_s\Vert \ge \Vert G_s\Vert \). By (2.4) we have

$$\begin{aligned} \begin{aligned} \Vert P_s\Vert&=\Vert -G_s+\frac{Y_s^TG_s P_{s-1}-P_{s-1}^TG_sY_s}{\mu _1\Vert Y_s\Vert \Vert P_{s-1}\Vert +\mu _2\Vert Y_s\Vert \Vert G_s\Vert +\Vert G_{s-1}\Vert ^2}\Vert \\&\le \Vert G_s\Vert +\frac{2\Vert Y_s\Vert \Vert G_s\Vert \Vert P_{s-1}\Vert }{\mu _1\Vert Y_s\Vert \Vert P_{s-1}\Vert +\mu _2\Vert Y_s\Vert \Vert G_s\Vert +\Vert G_{s-1}\Vert ^2}\\&\le \Vert G_s\Vert +\frac{2\Vert Y_s\Vert \Vert G_s\Vert \Vert P_{s-1}\Vert }{\mu _1\Vert Y_s\Vert \Vert P_{s-1}\Vert +\mu _2\Vert Y_s\Vert \Vert G_s\Vert +\Vert G_{s-1}\Vert ^2}\\&\le (1+\frac{2}{\mu _1})\Vert G_s\Vert \end{aligned} \end{aligned}$$

In summary, (3.2) and (3.3) are established. The theorem is still satisfied when the direction is (2.4) and the line search is (2.9).

Lemma 3.1

Suppose that \(x_1\) is a starting point that satisfies satisfy the gradient L-smooth. Consider the descending direction to satisfy (2.4), where the stepsize \(\alpha _s\) is determined through line search (2.9). In this case, for every \(s\), line search will compute a positive stepsize \(\alpha _s\) > 0 and generate a descent direction \(d_{s+1}\). Furthermore, it can be shown that:

$$\begin{aligned}\alpha _s\ge min\{1,c_1\},c_1=\frac{2t(1-\eta _1)}{L} \end{aligned}$$

So we can say that there will be an upper and lower bound on the step size \(\alpha _s\) that satisfies \(\alpha _s \in [\alpha _1,1]\), 0\(<\alpha _1<\)1.

Proof

Since \(d_1=-g_1\), \(d_1\) is a descent direaction.

For any \(\bar{\alpha _s}\), define \(x_{s+1}=x_s+\bar{\alpha _s}d_s\), similar to proofs in Dai (2002). As theorem 3.1 shows \(g_s^Td_s=-\Vert g_s\Vert ^2\), then

$$\begin{aligned}&{} -\Vert g_{s+1}\Vert ^2+\sigma _1 \Vert d_{s+1}\Vert ^2\le -\sigma _2\Vert g_{s+1}\Vert ^2 \le - \frac{\sigma _2}{(1+\frac{2}{\mu _1})^2}\Vert d_{s+1}\Vert ^2\\ {}&{} \quad (\sigma _1+\frac{\sigma _2}{(1+\frac{2}{\mu _1})^2})\Vert d_{s+1}\Vert ^2\le \Vert g_{s+1}\Vert ^2 \end{aligned}$$

Because \(\sigma _2+\sigma _1>1\) and \(\Vert P_s\Vert \le (1+\frac{2}{\mu _1})\Vert G_s\Vert \) holds. The above equation clearly exists. From the properties of Lipschitz, then we have that

$$\begin{aligned}{} & {} f(x_{s+1})-f(x_s)\le \eta _1\bar{\alpha _s}g_s^Td_s\\ {}{} & {} \quad \le max\{\eta _1\bar{\alpha _s}g_s^Td_s,-\eta _2\bar{\alpha _s}\Vert g_s\Vert ^2\},\\ {}{} & {} \qquad for\ all \ \bar{\alpha _s} \in (0,\frac{2t(1-\eta _1)}{L}\frac{|g_s^Td_s|}{\Vert d_s\Vert ^2}) \end{aligned}$$

Because the \(g^T_sd_s=-\Vert g_s\Vert ^2\), by theorem 3.1, we can derive the \(\bar{\alpha _s} \in (0,\frac{2(1-\eta _1)}{L}) \). There due to line search determines a positive stepsize \(\bar{\alpha _s}>0\) and further, above holds with constant \(c_1=\frac{2t(1-\eta _1)}{L}\).

Theorem 3.2

Assuming that the step size satisfies condition 1 and is in the direction of 2.5, then the gradient \(G_s\) satisfy

$$\begin{aligned}\frac{\Vert G_{s+1}\Vert }{\Vert G_s\Vert }\le \frac{2\mu _1+4}{\mu _1\mu _2(1-\frac{1-\sigma _1}{\sigma _2})}=\beta \end{aligned}$$

It is evident that when \(\frac{2\mu _1+4}{\mu _1\mu _2} \)< \(\frac{\sigma _2-\sigma _1-1}{\sigma _2}\), the inequality \(\beta =\frac{\Vert g_{s+1}\Vert }{\Vert g_s\Vert }\)< 1 holds true.

Proof

Multiply \(P_{s+1}\) at both ends of the direction (2.4)

$$\begin{aligned} \begin{aligned} \Vert P_{s+1}\Vert ^2&=-P_{s+1}^TG_{s+1}\\ {}&\quad +\frac{Y_{s+1}^TG_{s+1} P_{s+1}^TP_{s}-P_{s}^TG_{s+1}P_{s+1}^TY_{s+1}}{\mu _1\Vert Y_{s+1}\Vert \Vert P_{s}\Vert +\mu _2\Vert Y_{s+1}\Vert \Vert G_{s+1}\Vert +\Vert G_{s}\Vert ^2}\\&\le \Vert G_{s+1}\Vert ^2+\frac{2\Vert Y_{s+1}\Vert \Vert G_{s+1}\Vert \Vert P_{s+1}\Vert \Vert P_{s}\Vert }{\mu _1\Vert Y_{s+1}\Vert \Vert P_{s}\Vert +\mu _2\Vert Y_{s+1}\Vert \Vert G_{s+1}\Vert +\Vert G_{s}\Vert ^2}\\&\le \frac{1-\sigma _1}{\sigma _2}\Vert P_{s+1}\Vert ^2+\frac{2}{\mu _2}\Vert P_{s+1}\Vert \Vert P_{s}\Vert \\ \end{aligned} \end{aligned}$$

The inequality in the last line is due to the second line of the search (2.10):

$$\begin{aligned} -\Vert P_{s+1}\Vert ^2+\sigma _1\Vert P_{s+1}\Vert ^2\le & {} G_{s+1}^TP_{s+1}+\sigma _1\Vert P_{s+1}\Vert ^2\\ {}\le & {} -\sigma _2\Vert G_{s+1}\Vert ^2 \end{aligned}$$

By (3.2) and (3.3), when the \(\Vert P_{s+1}\Vert \ne 0\), we get

$$\begin{aligned} (1-\frac{1-\sigma _1}{\sigma _2})\Vert G_{s+1}\Vert\le & {} (1-\frac{1-\sigma _1}{\sigma _2})\Vert P_{s+1}\Vert \\ {}\le & {} \frac{2}{\mu _{2}}(1+\frac{2}{\mu _1})\Vert G_s\Vert \end{aligned}$$

then we have

$$\begin{aligned} \frac{\Vert G_{s+1}\Vert }{\Vert G_s\Vert }\le \frac{2\mu _1+4}{\mu _1\mu _2(1-\frac{1-\sigma _1}{\sigma _2})}\\ \end{aligned}$$

Lemma 3.2

Let \(\omega ^*\) be the unique minimizer of \(F\). Taking expectation with respect to \(C_s\) of \(\Vert G_0\Vert ^2\), we obtain

$$\begin{aligned}E[\Vert G_0\Vert ^2]\le 2L[F(\omega _0)-F(\omega _*)]\end{aligned}$$

For details, see Lemma 4 of the Kou and Yang (2022).

Theorem 3.3

Suppose that Assumptions 3.1, and Theorem 3.2 hold. Let \(\omega _*\) be the unique minimizer of \(F\). Then, for all \(s\ge 0\), we have taking expectation in this relation conditioned on \(C_s\). From Lemma 3, it can be known that the step size searched by line search (2.9) has upper and lower bounds, so the step size of (2.10) also has upper and lower bounds. Assuming that we choose \(\alpha _1<2\Omega (1-\beta ^2)\), we can get the linear convergence rate of the algorithm.

Proof

By \(\omega _{s+1}=\omega _{s}+\alpha _s P_s\), the inequality (3.1) can be written as

$$\begin{aligned} \begin{aligned} F_{C_s}(\omega _{s+1})-F_{C_s}(\omega _s)\le \alpha _sG_s^Td_s+\frac{1}{2}\alpha _s^2L\Vert P_s\Vert ^2\\ \end{aligned} \end{aligned}$$

On \(C_s\) taking expectations on both sides of inequality,

$$\begin{aligned} \begin{aligned}&E[F(\omega _{s+1})]-E[F(\omega _s)]\\&\quad \le E[\alpha _sG_s^TP_s]+\frac{1}{2}\alpha _s^2LE[\Vert P_s\Vert ^2]\\&\quad \le -\alpha _sE[\Vert G_s\Vert ^2]+\frac{1}{2}\alpha _s^2L(1+\frac{2}{\mu _1})^2E[\Vert G_s\Vert ^2]\\&\quad \le -\alpha _1E[\Vert G_s\Vert ^2]\\&\quad +[\frac{L\alpha _s^2}{2} (1+\frac{2}{\mu _1})^2]E[\Vert G_s\Vert ^2]\\&\quad \le -\alpha _1\Vert E[G_s]\Vert ^2+[\frac{L\alpha _s^2}{2} (1+\frac{2}{\mu _1})^2]\beta ^{2s}E[\Vert G_0\Vert ^2]\\&\quad \le -\alpha _1\Vert \nabla F(\omega _s)\Vert ^2\\&\quad +[\frac{L}{2} (1+\frac{2}{\mu _1})^2]\beta ^{2s}2LE[F(\omega _0)-F(\omega _*)] \end{aligned} \end{aligned}$$

The second inequality uses (3.3), the third inequality can be obtained from Lemma 3.1, and the fourth inequality uses Theorem 3.2. The last line can be obtained by Lemma 3.2 and Lemma 3.3. Adding the expectation of \(F(\omega _*)\) to both sides of the inequality, we get

$$\begin{aligned} \begin{aligned}&E[F(\omega _{s+1})]-E[F(\omega _*)]\\ {}&\quad \le (1-\frac{\alpha _1}{2\Omega })(E[F(\omega _s)]-E[F(\omega _*)])\\&\qquad +[L^2 (1+\frac{2}{\mu _1})^2]\beta ^{2s}E[F(\omega _0)-F(\omega _*)]\\ \end{aligned} \end{aligned}$$

Then, we define

$$\begin{aligned} \begin{aligned} \xi&=1-\frac{\alpha _1}{2\Omega } \\ T(i)&=L^2 (1+\frac{2}{\mu _1})^2\beta ^{2i}\\ T&=1+L^2(1+\frac{2}{\mu _1})^2\frac{1}{\xi -\beta ^2}\\ X_{s+1}&=E[F(\omega _{s+1})]-E[F(\omega _*)]\\ \end{aligned} \end{aligned}$$

The above formula can be expressed as:

$$\begin{aligned} \begin{aligned} X_{s+1}&\le (1-\frac{\alpha _1}{2\Omega })X_s+T(s)X_0 \\&\le (1-\frac{\alpha _1}{2\Omega })^2X_{s-1}+T(s-1)X_0+T(s)X_0 \end{aligned} \end{aligned}$$
(3.4)

We scale the right side of (3.4) to \(s=0\) has the following formula:

$$\begin{aligned} \begin{aligned} X_{s+1}&\le [\xi ^{s+1}+\displaystyle \sum _{i=0}^s\xi ^{s-i}T(i)]X_0\\&\quad \displaystyle \sum _{i=0}^s\xi ^{s-i}T(i)=\xi ^sL^2(1+\frac{2}{\mu _1})^2\sum _{i=0}^s(\frac{\beta ^2}{\xi })^i\\&=\xi ^sL^2(1+\frac{2}{\mu _1})^2\frac{1-(\frac{\beta ^2}{\xi })^{s+1}}{1-\frac{\beta ^2}{\xi }}\\ \end{aligned} \end{aligned}$$

Through the above conclusions, we can get the linear convergence rate of the algorithm 1

$$\begin{aligned} \begin{aligned}&E[F(\omega _{s+1})]-E[F(\omega _*)]\le [\xi ^{s+1}\\&\quad +\xi ^sL^2(1+\frac{2}{\mu _1})^2 \frac{1}{1-\frac{\beta ^2}{\xi }}]E[F(\omega _0)-F(\omega _*)]\\&\quad \le \xi ^{s+1}[1+L^2(1+\frac{2}{\mu _1})^2\frac{1}{\xi -\beta ^2}]E[F(\omega _0)-F(\omega _*)]\\&\quad \le \xi ^{s+1}TE[F(\omega _0)-F(\omega _*)] \end{aligned} \end{aligned}$$

4 Applications of algorithm in machine learning models

We used the following two models to evaluate our algorithm, mainly for the following two reasons:

1. These two models are machine learning models using non-convex sigmoid loss function, which can better adapt to the distribution of data and Noise, improve the robustness and generalization ability of the model. All the codes are written in MATLAB 2018a on a PC with a 12th Gen Intel(R) Core(TM) i7-12650 H 2.30 GHz and 16 GB of memory.

2. These two models represent two different regularization strategies: Nonconvex regularized ERM model uses non-convex regularization terms, such as \(\ell _0\) norm or \(\ell _p\) norm (0 < p < 1), To enhance the sparsity of the model; the Nonconvex SVM model uses the \(\ell _2\) norm as a regularization term to control the complexity of the model. Both strategies have their own advantages and disadvantages, and we hope to analyze the performance of our algorithm under different regularization settings by comparing their performance (Tables 1, 2).

Table 1 Dataset
Full size table
Table 2 Parmeter value
Full size table

All of the above datasets have been scaled to the [−1, 1] range via max-min through the preprocessing phase.

5 Test model 1

Nonconvex SVM model with a sigmoid loss function

$$\begin{aligned} min \ \frac{1}{n} \sum _{i=1}^n F_i(\omega )+\sigma \Vert \omega \Vert ^2 \end{aligned}$$

where \(F_i(\omega )=1-tanh(v_i\) < \(\omega ,u_i\)>\(), u\in \Re \) and \(v \in \{-1,1\}\) represent the feature vector and corresponding label respectively.

6 Test model 2

Nonconvex regularized ERM model with a nonconvex sigmoid loss function

$$\begin{aligned} min \ \frac{1}{n} \sum _{i=1}^n F_i(\omega )+\frac{\sigma }{2}\Vert \omega \Vert ^2 \end{aligned}$$

where \(F_i(\omega )=\frac{1}{[1+exp(b_ia_i^T\omega )]}\). Binary classification problem is a common type of problem in machine learning, which requires us to divide the data into two categories, such as distinguishing spam and normal emails, or distinguishing whether a sonar signal is a rock or a metal.

Fig. 1
figure 1

Comparison of SATCG with several classes of algorithms on 12 datasets adult, covtype, ijcnn, mnist, a9a, w8a, diabetes, fourclass, german.number, inosphere, snoar, splice for Model 1.(The x-axis represents numbers of iterations. The y-axis represents loss function values.)

Full size image
Fig. 2
figure 2

Comparison of SATCG with several classes of algorithms on 12 datasets adult, covtype, ijcnn, mnist, a9a, w8a, diabetes, fourclass, german.number, inosphere, snoar, splice for Model 2.(The x-axis represents numbers of iterations. The y-axis represents loss function values.)

Full size image
Fig. 3
figure 3

Comparison of SATCG and SCGA on 6 datasets diabetes, fourclass, german.number, inosphere, snoar, splice for Model 1. (The x-axis represents numbers of iterations. The y-axis represents loss function values.)

Full size image
Fig. 4
figure 4

Comparison of SATCG and SCGA on 6 datasets diabetes, fourclass, german.number, inosphere, snoar, splice for Model 2. (The x-axis represents numbers of iterations. The y-axis represents loss function values.)

Full size image
Fig. 5
figure 5

Compare the performance of SATCG with different regularization coefficients (0.001,0.0001,0.00001) on Model 1. (The x-axis represents numbers of iterations. The y-axis represents loss function values.)

Full size image
Fig. 6
figure 6

Compare the performance of SATCG with different regularization coefficients (0.001,0.0001,0.00001) on Model 2. (The x-axis represents numbers of iterations. The y-axis represents loss function values.)

Full size image

7 Algorithm comparison

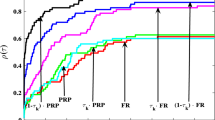
In both model tests, SGD, SAGA, SARAH, Adam, and Rmsprop all use an initial step size of 0.1, while Adam has momentum parameters of 0.9 and 0.999, and Rmsprop has a momentum parameter of 0.99, which are commonly used settings. The results are presented in Figs. 1 and 2, where we compare the convergence of SATCG and SGD class algorithms with adaptive algorithms on 8 different datasets. It is evident that SATCG generally achieves faster convergence on all datasets and models.

In Figs. 3 and 4, we compare a stochastic conjugate gradient method known as SCGA. Kou’s study also compares SCGA with CGVR in several small-scale datasets. In addition, we compare the convergence of SATCG and SCGA in six smaller datasets. From the experimental results of Comparative Model 1, we observe that SATCG and SCGA perform similarly in the diabetes and fourclass datasets, but SATCG exhibits better descent and stability in the remaining four datasets. But in Model 2, SCGA has a better performance.

Figures 5 and 6 show the performance of SATCG with different regularization coefficients on six small-scale data sets. It can be seen that SATCG has better experimental results and faster decline when the regularization coefficient is smaller.

In summary, SATCG offers more advantages compared to SGD algorithms, and it exhibits greater stability and competitiveness than SCGA, Adam, and Rmsprop.

8 Conclusion

In this paper, we present an extension of the modified traditional three-conjugate gradient method and line search technique for immediate optimization. We achieve a linear convergence rate with weaker conditional assumptions in our theoretical analysis. Additionally, we test the convergence of our algorithm across 16 datasets using machine learning models. We compare the results of our algorithm SATCG with several other mainstream algorithms and find that SATCG demonstrates faster and more stable convergence.