High-dimensional sparse single–index regression via Hilbert–Schmidt independence criterion

Abstract

Hilbert-Schmidt Independence Criterion (HSIC) has recently been introduced to the field of single-index models to estimate the directions. Compared with other well-established methods, the HSIC based method requires relatively weak conditions. However, its performance has not yet been studied in the prevalent high-dimensional scenarios, where the number of covariates can be much larger than the sample size. In this article, based on HSIC, we propose to estimate the possibly sparse directions in the high-dimensional single-index models through a parameter reformulation. Our approach estimates the subspace of the direction directly and performs variable selection simultaneously. Due to the non-convexity of the objective function and the complexity of the constraints, a majorize-minimize algorithm together with the linearized alternating direction method of multipliers is developed to solve the optimization problem. Since it does not involve the inverse of the covariance matrix, the algorithm can naturally handle large p small n scenarios. Through extensive simulation studies and a real data analysis, we show that our proposal is efficient and effective in the high-dimensional settings. The $\texttt {Matlab}$ codes for this method are available online.

1 Introduction

Let $Y\in \mathbb {R}$ be an univariate response and $\textbf{X}\in \mathbb {R}^p$ be a $p\times 1$ predictor. The single-index model, as a practically useful generalization of the classical linear regression model, considers the following problem

$$\begin{aligned} Y=g({\varvec{\beta }}^{\top }\textbf{X},\epsilon ), \end{aligned}$$

(1.1)

where ${\varvec{\beta }}$ is a $p\times 1$ vector, $\epsilon$ is an unknown random error independent of $\textbf{X}$, and g is a link function. Letting $\text{ span }({\varvec{\beta }})$ denote the column subspace spanned by ${\varvec{\beta }}$, then the goal of the single-index model is to estimate $\text{ span }({\varvec{\beta }})$ without specifying or estimating the link function g. To our best knowledge, Li and Duan (1989) firstly studied this problem and proposed to estimate $\text{ span }({\varvec{\beta }})$ under the linearity condition that $E(\textbf{X}|{\varvec{\beta }}^{\top }\textbf{X})$ is a linear function of ${\varvec{\beta }}^{\top }\textbf{X}$. This linearity condition applies to the marginal distribution of $\textbf{X}$ and is common in the regression modelling.

Later, Cook (1994, 1998) introduced Sufficient Dimension Reduction (SDR), which expands the concept of the single-index model. SDR aims to find the minimal subspace $\mathcal{S}\subseteq \mathbb {R}^p$ such that , where stands for independence and $P_{\mathcal{S}}$ denotes the projection operator to the subspace $\mathcal{S}$. Under mild conditions (Cook 1996; Yin et al. 2008), such a subspace exists and is unique. We call it the central subspace and denote it by $\mathcal{S}_{Y|\textbf{X}}$ and its dimension by $d=\text{ dim }(\mathcal{S}_{Y|\textbf{X}})$, which is often far less than p. When the central subspace is one dimensional (in other words, $d=1$), the corresponding regression problem is just the single-index model (1.1). Many methods have been proposed to estimate the central subspace (Li 1991; Cook and Weisberg 1991; Xia et al. 2002; Cook and Ni 2005; Zhu and Zeng 2006; Li and Wang 2007; Wang and Xia 2008; Cook and Forzani 2009; Zeng and Zhu 2010; Yin and Li 2011; Ma and Zhu 2012). For a comprehensive list of references on SDR methods, please refer to Ma and Zhu (2013).

Unfortunately, one drawback of the SDR methods mentioned above is that the estimated linear combinations contain all the original predictors, which often makes it difficult to interpret the extracted components. To improve interpretability, numerous attempts have been made to perform variable selection and dimension reduction simultaneously, including Cook (2004); Ni et al. (2005); Li et al. (2005); Li (2007); Li and Yin (2008) and Chen et al. (2010). It is known that these methods perform well when the number of covariates p is less than the sample size n, but do not work under the scenario $p>n$. To tackle the difficulty, Yin and Hilafu (2015) suggested sequential procedures for SDR, and Lin et al. (2018) proposed the high-dimensional sparse Sliced Inverse Regression (SIR). Moreover, Wang et al. (2018) introduced a reduced-rank regression method for estimating the sparse directions, and Tan et al. (2018) proposed a convex formulation for fitting sparse SIR in high dimensions. Additional recent approaches to high-dimensional SDR can be found in Qian et al. (2019); Tan et al. (2020) and Zeng et al. (2022).

In this article, motivated by the work of Zhang and Yin (2015) and Tan et al. (2018), we develop a new approach for high-dimensional single-index models via Hilbert-Schmidt Independence Criterion (HSIC). The proposed method can perform variable selection and can handle the large p small n scenarios simultaneously. In comparison to existing high-dimensional sparse SDR methods, it requires relatively weak conditions. The key idea is to reformulate the HSIC based single-index model by estimating the orthogonal projection ${\varvec{\beta }}{\varvec{\beta }}^{\top }$ onto the subspace span(${\varvec{\beta }}$) rather than span(${\varvec{\beta }}$) itself, with the constraints of the nuclear norm relaxing the normalization constraint. Based on the reformulation, a lasso penalty on the orthogonal projection ${\varvec{\beta }}{\varvec{\beta }}^{\top }$ is then introduced to encourage the estimated solution to be sparse. The numerical studies indicate the superiority of the proposed method.

The main contributions of our work are summarized as the follows. First, our method extends the HSIC-based single-index regression (Zhang and Yin 2015) to adapt to sufficient variable selection in large p small n situations via a smart parameter reformulation. Second, motivated by the majorization-minimization principle, we design a computationally fast and efficient algorithm, called MM-LADMM, to solve the non-convex constrained optimization problem. Third, a cross-validation procedure is developed to select the sparsity tuning parameter. Last but not least, our method can be naturally extended to multivariate response regression models where few methods work.

Although the proposed algorithm draws some inspiration from Tan et al. (2018), it is significantly more complicated and tricky due to the fact that the objective function in our method is inherently non-convex while theirs is simply linear. Moreover, the cross-validation scheme for selecting the sparsity tuning parameter in Tan et al. (2018) relies on the assumption that the distribution of $\textbf{X}|Y$ follows a multivariate normal distribution, while our method utilizes a kernel method to estimate the link function which perfectly avoids this assumption.

The rest of the article is organized as follows. Section 2 reviews the background of the HSIC-based single-index method and then introduces the sparse single-index regression via HSIC. Section 3 details our proposed algorithm. In Sect. 4, we conduct extensive simulation studies and a real data analysis. A short conclusion and some technical proofs are provided in Sect. 5 and Appendix, respectively.

The following notations will be used in our exposition. Let $\Vert \cdot \Vert$ denote the $\ell _2$ norm of a vector and $\Vert \cdot \Vert _\textrm{F}$ denote the Frobenius norm of a matrix, respectively. Let $P_{{\varvec{\eta }}({\varvec{\Sigma }})}={\varvec{\eta }}({\varvec{\eta }}^{\top } {\varvec{\Sigma }}{\varvec{\eta }})^{-1}{\varvec{\eta }}^{\top }{\varvec{\Sigma }}$ denote the projection operator which projects onto span(${\varvec{\eta }}$) relative to the inner product $\langle \textbf{a},\textbf{b}\rangle = \textbf{a}^{\top } {\varvec{\Sigma }}\textbf{b}$, and $Q_{{\varvec{\eta }}({\varvec{\Sigma }})}=\textbf{I}-P_{{\varvec{\eta }}({\varvec{\Sigma }})}$, where $\textbf{I}$ denotes the identity matrix. The trace of a matrix $\textbf{A}$ is denoted by $\textrm{tr}(\textbf{A})$, and the Euclidean inner product of two matrices $\textbf{A}, \textbf{B}$ is denoted by $\langle \textbf{A},\textbf{B} \rangle =\textrm{tr}(\textbf{A}^{\top }{} \textbf{B})$. We use ${\mathbb I} _{(a>0)}$ to denote the indicator function, and $\lambda _{\max }( \cdot )$ the largest eigenvalue of a matrix.

2 Methodology

2.1 Review of single–index regression via HSIC

Gretton et al. (2005a, 2007, 2009) proposed an independence criterion, called the Hilbert-Schmidt independence criterion, to detect statistically significant dependence between two random variables. HSIC for univariate X and Y, denoted by H(X, Y), has the population expression

$$\begin{aligned} \begin{aligned} H(X,Y)=&E\left[ K(X-X')L(Y-Y')\right] \\&+E\left[ K(X-X')\right] E\left[ L(Y-Y')\right] \\&-2E\left\{ E\left[ K(X{-}X')|X \right] E\left[ L(Y{-}Y')|Y\right] \right\} , \end{aligned}\nonumber \\ \end{aligned}$$

(2.1)

where $X'$ and $Y'$ denote independent copies of X and Y, and $K(\cdot )$ and $L(\cdot )$ are certain positive definite kernel functions. From (2.1), H(X, Y) exists when the various expectations over the kernels are finite, which is true as long as the kernels $K(\cdot )$ and $L(\cdot )$ are bounded.

Remark 1

A commonly used kernel is the Gaussian kernel (see Kankainen 1995), i.e.,

$$\begin{aligned}&K(X-X'):=\exp \left( \frac{-(X-X')^2}{2\sigma _X^2} \right) \text{ and }\\&L(Y-Y'):= \exp \left( \frac{-(Y-Y')^2}{2\sigma _Y^2} \right) . \end{aligned}$$

To facilitate computation, we present and implement our method using the Gaussian kernel throughout the article.

According to Gretton et al. (2005b), for certain kernels, H(X, Y) defined in (2.1) characterizes the distance between the joint distribution of X, Y and the product of their marginal distributions. Hence, H(X, Y) equals 0 if and only if the two random variables are independent, which makes possible its application in the field of SDR. Indeed, under mild conditions, Zhang and Yin (2015) showed that solving (2.2) with respect to a general $p\times 1$ vector ${\varvec{\beta }}$ would yield a basis of $\mathcal{S}_{Y|\textbf{X}}$, or in other words, the single-index direction:

$$\begin{aligned} {\varvec{\beta }}=\underset{{\varvec{\beta }}^{\top }{\varvec{\Sigma }}{\varvec{\beta }}=1}{\arg \max }\, H({\varvec{\beta }}^{\top }\textbf{X},Y), \end{aligned}$$

(2.2)

where ${{\varvec{\Sigma }}}$ denotes the covariance matrix of $\textbf{X}$. Since the HSIC index $H({\varvec{\beta }}^{T}\textbf{X},Y)=H(-{\varvec{\beta }}^{\top }\textbf{X},Y)$, the constraint ${\varvec{\beta }}^{\top }{\varvec{\Sigma }}{\varvec{\beta }}=1$ can not give a unique solution of the parameter ${\varvec{\beta }}$. However, both solutions ${\varvec{\beta }}$ and $-{\varvec{\beta }}$ span the same space, which is unique and of our interest.

Let $\left\{ (\textbf{X}_i,Y_i): i=1,\ldots ,n \right\}$ be an i.i.d sample of random vectors $(\textbf{X},Y)$, and $\hat{{\varvec{\Sigma }}}$ and $\hat{\sigma }_Y$ be the sample covariance matrix and sample variance of $\textbf{X}$ and Y, respectively. The sample estimate of $H({\varvec{\beta }}^{\top }\textbf{X},Y)$, denoted by $H_n({\varvec{\beta }}^{\top }\textbf{X},Y)$, is the sum of three U-statistics (see Serfling 1980; Gretton et al. 2007):

$$\begin{aligned}{} & {} H_n({\varvec{\beta }}^{\top }\textbf{X},Y){=}\frac{1}{n^2}\sum _{i,j=1}^{n} K_{ij}({\varvec{\beta }})L_{ij}-\frac{2}{n^3} \sum _{i,j,k=1}^{n}K_{ij}({\varvec{\beta }})L_{ik}\nonumber \\{} & {} \qquad \qquad \qquad \qquad \,+\frac{1}{n^4}\sum _{i,j,k,l=1}^{n} K_{ij}({\varvec{\beta }})L_{kl}, \end{aligned}$$

(2.3)

where

$$\begin{aligned}&K_{ij}({\varvec{\beta }}):=\exp \left( \frac{-({\varvec{\beta }}^{\top }(\textbf{X}_i-\textbf{X}_j) )^2}{2{\varvec{\beta }}^{\top }\hat{{\varvec{\Sigma }}}{\varvec{\beta }}} \right) \text{ and } \nonumber \\&L_{ij}:=\exp \left( \frac{-(Y_i-Y_j)^2}{2\hat{\sigma }_{Y}^2} \right) \end{aligned}$$

(2.4)

for $i,j\in \{1,\ldots ,n\}$. Hence, the estimator of a basis for the central subspace $\mathcal{S}_{Y|\textbf{X}}$ is

$$\begin{aligned} {{\varvec{\beta }}}_{n}=\underset{ {\varvec{\beta }}^{\top }\hat{{\varvec{\Sigma }}}{\varvec{\beta }}=1}{\arg \max }\, H_{n}({\varvec{\beta }}^{\top }\textbf{X},Y). \end{aligned}$$

(2.5)

Then, the central subspace is estimated as span(${{\varvec{\beta }}}_{n}$), and the estimated index is ${{\varvec{\beta }}}_{n}^{\top }\textbf{X}$. Zhang and Yin (2015) established the consistency and asymptotic normality of the above estimator.

2.2 Sparse single–index regression via HSIC

To reduce model complexity and thus to improve interpretation, especially in high-dimensional scenarios, a common assumption is that only a few number of the covariates are active in the single-index regression. Therefore, by (2.2), the single-index direction can be solved by

$$\begin{aligned} {\varvec{\beta }}=\arg \max \, H({\varvec{\beta }}^{\top }\textbf{X},Y),\\ \mathrm{s.t.}~ {\varvec{\beta }}^{\top }{\varvec{\Sigma }}{\varvec{\beta }}=1, ~\Vert {\varvec{\beta }}\Vert _0 \le s, \end{aligned}$$

where $\Vert {\varvec{\beta }}\Vert _0$ denotes the number of the non-zero elements in ${\varvec{\beta }}$ and s indicates the number of the active predictors.

A natural estimator of ${\varvec{\beta }}$ is then

$$\begin{aligned} {\varvec{\beta }}_n=\arg \max \, H_n({\varvec{\beta }}^{\top }\textbf{X},Y),\nonumber \\ \mathrm{s.t.}~ {\varvec{\beta }}^{\top }{\hat{\varvec{\Sigma }}}{\varvec{\beta }}=1, ~\Vert {\varvec{\beta }}\Vert _0 \le s,\nonumber \\ \end{aligned}$$

(2.6)

where $H_n({\varvec{\beta }}^{\top }\textbf{X},Y)$ is defined in (2.3). Thus, the central subspace is estimated as span(${{\varvec{\beta }}}_{n}$), and the estimated index is ${{\varvec{\beta }}}_{n}^{\top }\textbf{X}$. In addition, the estimated active predictors are those associated with non-zero coefficients.

However, solving (2.6) directly is absolutely not trivial. Indeed, the optimization (2.6) with $\ell _0$ norm is known to be an ‘NP hard’ problem, since it would require searching through all $\left( {\begin{array}{c}p\\ s\end{array}}\right)$ sub-vectors of ${\varvec{\beta }}$ satisfying the equality constraints, which takes exponential time in s. Moreover, the objective function of ${\varvec{\beta }}$ in (2.6) may not be convex, and the equality constraint function is not an affine transformation, which together make the optimization problem much trickier.

3 Algorithm

3.1 Problem reformulation

To solve the sparse single-index regression via HSIC (2.6) efficiently, we reform the optimization as the follows. Firstly, instead of using (2.3), we utilize an equivalent form (see Gretton et al. 2007; Wu and Chen 2021) of $H_n({\varvec{\beta }}^{\top }\textbf{X},Y)$, obtained by replacing the U-statistics with V-statistics

$$\begin{aligned} H_n({\varvec{\beta }}^{\top }\textbf{X},Y)=\frac{1}{n^2}\text{ tr }(\textbf{K}\textbf{J}\textbf{L}\textbf{J})=\frac{1}{n^2}\sum _{i,j=1}^{n} K_{ij}({\varvec{\beta }}) \tilde{L}_{ij} \end{aligned}$$

(3.1)

to facilitate optimization, where $\textbf{K}$ and $\textbf{L}$ are the $n\times n$ matrices with entries $K_{ij}({\varvec{\beta }})$ and $L_{ij}$ defined in (2.4), and $\displaystyle \textbf{J}=\textbf{I}-n^{-1}\textbf{1}\textbf{1}^{\top }$ with $\textbf{1}$ denoting a $n\times 1$ vector of ones. Here, $\tilde{L}_{ij}$ denotes the (i, j)-th entry of the product matrix $\tilde{\textbf{L}}=\textbf{J}\textbf{L}\textbf{J}$.

Given (3.1) and letting ${\varvec{\Pi }}={\varvec{\beta }}{\varvec{\beta }}^{\top }$, the HSIC-based single-index regression procedure (2.5) can then be reformulated as the following minimization problem:

$$\begin{aligned} \begin{aligned}&\underset{ {\varvec{\Pi }}\in \mathcal{M}}{\textrm{min}}\, -\frac{1}{n^2}\sum _{i,j=1}^{n} \exp \left( -\frac{ \langle {\varvec{\Pi }},\textbf{Z}_{ij} \rangle }{2} \right) \tilde{L}_{ij}, \\&\text{ s.t. } \quad \hat{{\varvec{\Sigma }}}^{1/2} {\varvec{\Pi }}{\hat{{\varvec{\Sigma }}}}^{1/2} \in \mathcal{B}, \end{aligned} \end{aligned}$$

(3.2)

where $\textbf{Z}_{ij}=(\textbf{X}_i-\textbf{X}_j)(\textbf{X}_i-\textbf{X}_j)^{\top }$, $\mathcal{B}=\{ \hat{{\varvec{\Sigma }}}^{1/2} {\varvec{\Pi }}\hat{{\varvec{\Sigma }}}^{1/2}: {\varvec{\beta }}^{\top }\hat{{\varvec{\Sigma }}}{\varvec{\beta }}=1 \}$, and $\mathcal{M}$ is the set of $p \times p$ symmetric positive semi-definite matrices. In this new formulation, our focus is changed to directly estimate the orthogonal projection ${\varvec{\Pi }}$ onto the subspace spanned by ${\varvec{\beta }}$ instead of estimating the basis ${\varvec{\beta }}$ directly.

To further achieve variable selection, we add an $\ell _1$ penalty term on ${\varvec{\Pi }}$ to (3.2) to encourage a sparse estimate:

$$\begin{aligned} \begin{aligned}&\underset{ {\varvec{\Pi }}\in \mathcal{M}}{\textrm{min}}\, -\frac{1}{n^2}\sum _{i,j=1}^{n} \exp \left( -\frac{ \langle {\varvec{\Pi }},\textbf{Z}_{ij} \rangle }{2} \right) \tilde{L}_{ij} +\lambda \Vert {\varvec{\Pi }}\Vert _{1}, \\&\text{ s.t. } \quad {\textrm{tr}}(\hat{{\varvec{\Sigma }}}^{1/2} {\varvec{\Pi }}\hat{{\varvec{\Sigma }}}^{1/2} )\le 1, \end{aligned} \end{aligned}$$

(3.3)

where $\Vert {\varvec{\Pi }}\Vert _1 = \sum _{i,j}|{\varvec{\Pi }}_{ij}|$ and $\lambda >0$ is a tuning parameter. The $\ell _1$ penalty on ${\varvec{\Pi }}$ encourages a sparse estimate for ${\varvec{\beta }}$, and a convex relation with the nuclear norm on $\hat{{\varvec{\Sigma }}}^{1/2} {\varvec{\Pi }}\hat{{\varvec{\Sigma }}}^{1/2}$ is implemented on the equality constraint to facilitate computation. Similar work can be found in sparse principal component analysis, canonical correlation analysis, and sliced inverse regression (Vu et al. 2013; Gao et al. 2017; Tan et al. 2018, 2018, 2020). We note that (3.3) may still not be a canonical convex optimization problem, since the objective function of ${\varvec{\Pi }}$ may not be convex, which inspires us to further explore the properties of the objective function and then turn to the majorization-minimization principle (Lange et al. 2000; Hunter and Lange 2004) to obtain a good optimizer; see the following subsection for algorithmic details.

Remark 2

If the kernel is chosen as the product kernel, we can naturally extend the above method to settings where the response is multivariate. That is, for a q-dimensional response $\textbf{Y}=(Y_1,\ldots ,Y_q)^{\top }$, we use the product kernel to compute $\tilde{L}_{ij}$ in (3.3):

$$\begin{aligned} L(\textbf{Y}-\textbf{Y}'):=\prod _{i=1}^{q}\exp \left( \frac{-|Y_i-Y_i^{'}|^2}{2\sigma _{Y_i}^2} \right) , \end{aligned}$$

where $\textbf{Y}'=(Y_1^{'},\ldots ,Y_q^{'})^{\top }$ is an independent copy of $\textbf{Y}$. Our simulation shows that this extension works quite well. See Studies 5 and 6 in the following numerical study.

3.2 The MM-LADMM algorithm

In this subsection, we propose an efficient optimization algorithm for solving the problem (3.3). Let $f({\varvec{\Pi }})$ denote the objective function of the problems (3.2). Although $f({\varvec{\Pi }})$ may not be convex, it is differentiable and has Lipschitz continuous gradient over a bounded convex set. We state properties of the objective function $f({\varvec{\Pi }})$ in the following proposition, whose proof is given in the Appendix.

Proposition 3.1

$f({\varvec{\Pi }})$ is differentiable, and its derivative function is

$$\begin{aligned} \nabla f({\varvec{\Pi }})=\frac{1}{2n^2} \sum _{i,j=1}^{n} \exp \left( -\frac{ \langle {\varvec{\Pi }}, \textbf{Z}_{ij} \rangle }{2} \right) \tilde{L}_{ij}\textbf{Z}_{ij}, \end{aligned}$$

(3.4)

or equivalently,

$$\begin{aligned} \nabla f({\varvec{\Pi }})=\frac{1}{n^2} \mathbb {X}^{\top }\left( {\textrm{diag}}(\textbf{C}{\varvec{1}}_{n})- \textbf{C}\right) \mathbb {X}, \end{aligned}$$

(3.5)

where $\textbf{C}$ is a $n\times n$ matrix with the entry $\displaystyle c_{ij}{=}\exp (-{ \langle {\varvec{\Pi }}, \textbf{Z}_{ij} \rangle }/{2} )\tilde{L}_{ij}$, ${\varvec{1}}_{n}$ is a $n\times n$ matrix with the entry 1, and $\mathbb {X}=[\textbf{X}_1,\ldots ,\textbf{X}_n]^{\top }$. Moreover, $\nabla f({\varvec{\Pi }})$ is Lipschitz over the set $\mathcal{D}=\{ {\varvec{\Pi }}\in \mathcal{M}: \textrm{tr}(\hat{{\varvec{\Sigma }}}^{1/2} {\varvec{\Pi }}\hat{{\varvec{\Sigma }}}^{1/2} )\le 1 \}$.

It is worth noting that we would like to use the expression form (3.5) instead of (3.4) to calculate the derivative function $\nabla f({\varvec{\Pi }})$. Plus, the Lipschitz continuity property of $f({\varvec{\Pi }})$ motivates us to design a method to performe the optimization from the viewpoint of the majorization-minimization principle (Lange et al. 2000; Hunter and Lange 2004).

Since the objective function $f({\varvec{\Pi }})$ has a Lipschitz continuous gradient over the bounded set $\mathcal{D}$, there exists a positive constant $L < \infty$ such that

$$\begin{aligned} f({\varvec{\Pi }})\le f(\tilde{{\varvec{\Pi }}})+\langle {\varvec{\Pi }}-\tilde{{\varvec{\Pi }}}, \nabla f(\tilde{{\varvec{\Pi }}}) \rangle +\frac{L}{2} \Vert {\varvec{\Pi }}-\tilde{{\varvec{\Pi }}}\Vert _{\textrm{F}}^2, \end{aligned}$$

(3.6)

for all ${\varvec{\Pi }}\in \mathcal{D}$ and $\tilde{{\varvec{\Pi }}}\in \mathcal{D}$. Thus, the right hand side of (3.6) is a majorizing function of $f({\varvec{\Pi }})$ at ${\varvec{\Pi }}$ (i.e., the right hand side of (3.6) is greater than or equal to $f({\varvec{\Pi }})$ for all ${\varvec{\Pi }}\in \mathcal{D}$ with equality at ${\varvec{\Pi }}=\tilde{{\varvec{\Pi }}}$). This suggests the following Majorize-Minimize (MM) iteration to solve the problem (3.3):

$$\begin{aligned} {\varvec{\Pi }}^{(r+1)}= & {} \underset{{\varvec{\Pi }}\in \mathcal{D}}{\arg \min }\, \left\{ f({\varvec{\Pi }}^{(r)})+\langle {\varvec{\Pi }}-{\varvec{\Pi }}^{(r)}, \nabla f({\varvec{\Pi }}^{(r)}) \rangle \right. \nonumber \\{} & {} \quad +\left. \frac{L}{2} \Vert {\varvec{\Pi }}-{\varvec{\Pi }}^{(r)}\Vert _{\textrm{F}}^2+\lambda \Vert {\varvec{\Pi }}\Vert _1 \right\} ,\nonumber \\= & {} \underset{{\varvec{\Pi }}\in \mathcal{D}}{\arg \min }\ \, \frac{L}{2}\left\| {\varvec{\Pi }}-\left[ {\varvec{\Pi }}^{(r)}-\frac{1}{L} \nabla f({\varvec{\Pi }}^{(r)}) \right] \right\| _{\textrm{F}}^2 \nonumber \\{} & {} \quad + \lambda \Vert {\varvec{\Pi }}\Vert _1, \end{aligned}$$

(3.7)

where ${\varvec{\Pi }}^{(r+1)}$ and ${\varvec{\Pi }}^{(r)}$ are the $(r+1)$-th and r-th iterates of the optimization variable ${\varvec{\Pi }}$, respectively. By the property (3.6), we can easily obtain

$$\begin{aligned} f({\varvec{\Pi }}^{(r+1)})+ \lambda \Vert {\varvec{\Pi }}^{(r+1)}\Vert _{1} \le f({\varvec{\Pi }}^{(r)})+\lambda \Vert {\varvec{\Pi }}^{(r)}\Vert _{1} \text{ for } \text{ all } r, \end{aligned}$$

which means that iterates generated from the algorithm are guaranteed to monotonically decrease the objective function value. Hunter and Lange (2004) showed that the sequence $\{ {\varvec{\Pi }}^{(r)} \}_{r\ge 0}$ obtained by the iterative formula (3.7) converges to a critical point of the problem (3.3). The MM algorithm is a simple and well-applicable algorithmic framework for solving such problems. The key challenge in making the proposed algorithm numerically efficient lies in solving the subproblem (3.7).

The subproblem (3.7) is a quadratic problem with a convex constraint, so any local minimum can be guaranteed to be a global minimum. We employ the Linearized Alternating Direction Method of Multipliers algorithm (LADMM, Zhang et al. 2011; Wang and Yuan 2012; Yang and Yuan 2013) to solve it. This algorithm can allow us to tackle the difficulty caused by the interaction between the penalty term and the constraints. We give the derivation details of solving the subproblem (3.7) via the LADMM algorithm in the Appendix. In practice, we find that this algorithm can solve the subproblem quite efficiently.

Algorithm 1 presents the entire algorithm flow to solve the problem (3.3). It has two loops: an outer loop in which the MM algorithm approximates the original problem (3.3) iteratively by a series of convex relaxations, and an inner loop in which the LADMM algorithm is used to solve each convex relaxation (3.7). In the inner loop, the update of ${\varvec{\Pi }}$ performs soft-thresholding, and the update of $\textbf{H}$ is via a projection operator which needs to compute a singular value decomposition and modify the obtained singular values with a monotone piecewise linear function. For specific details about the projection operator, please refer to Proposition 6.1 in the Appendix. Matlab codes for implementing the algorithm are available at https://github.com/CalvinWu-ai/sHSIC.

Algorithm 1

MM-LADMM Algorithm for Solving (3.3)

Remark 3

Since the optimization problem (3.3) may not be convex, different initial values ${\varvec{\Pi }}^{(0)}$ would produce different local optimizers. To alleviate this problem, the routine procedure is to try multiple initial values and then choose the best one. However, for ease of calculation, we selected the initial values ${\varvec{\Pi }}^{(0)}$ crudely as zero matrices, inspired by a similar algorithm in Zeng et al. (2022). Despite the possible non-convexity of the problem (3.3), this crude selection of initial values works fine throughout all our numerical experiments, and we suggest this selection for the proposed algorithm.

3.3 Tuning parameter selection

The tuning parameter $\lambda$ in the proposed method determines the sparsity level of the estimate. Motivated by Tan et al. (2018), we use an M-fold cross-validation procedure to select $\lambda$. Let $C_1,\ldots ,C_M$ denote M equally sized and mutually disjoint subsamples of the whole dataset. The cross-validation procedure utilizes each single subsample as the test data and the remaining $M-1$ subsamples as the training data to compute the prediction error for each $\lambda$. Specifically, given a fixed $\lambda$, the corresponding overall prediction error is computed as

$$\begin{aligned} \frac{1}{M|C_m|}\sum _{m=1}^{M} \sum _{i\in C_m} \left\{ Y_i- \hat{E}(Y|\textbf{X}=\textbf{X}_i)\right\} ^2, \end{aligned}$$

where $|C_m|$ denotes the cardinality of the set $C_m$ and $\hat{E}(Y|\textbf{X}=\textbf{X}_i)$ is an estimate of $E(Y|\textbf{X}=\textbf{X}_i)$ from the training data. The working tuning parameter is the one which minimizes the prediction error.

We use the Nadaraya-Watson kernel method to estimate the conditional expectation $E(Y|\textbf{X})$. Recall that $\hat{{\varvec{\beta }}}$ is estimated by the top eigenvector of $\hat{{\varvec{\Pi }}}$. Given a new data $\textbf{X}^*$, the Nadaraya-Watson kernel estimator of the conditional mean $E(Y|\textbf{X}=\textbf{X}^*)$ is

$$\begin{aligned} \hat{E}(Y|\textbf{X}=\textbf{X}^*)=\sum _{i=1}^{n} \frac{ K_h(\hat{{\varvec{\beta }}}^{\top }(\textbf{X}^*-\textbf{X}_i)) }{ \sum _{j=1}^{n} K_h(\hat{{\varvec{\beta }}}^{\top }(\textbf{X}^*-\textbf{X}_j)) } Y_i, \end{aligned}$$

(3.8)

where $K_h(t)=K(t/h)/h$ is a kernel function with a bandwidth h. To facilitate computation, we use a Gaussian kernel and take the cross-validation with the leave-one-out estimate of the residual sum of squares to select the bandwidth. Notice that there is a trick to compute the cross-validation function of h with a single fit. This trick vastly reduces the computational complexity at the price of the increasing memory consumption. For specific details, please refer to Fan and Gijbels (1996).

We note that Tan et al. (2018) proposed a similar cross-validation procedure to select the sparsity tuning parameter. However, their approach is based on the framework of principal fitted components (Cook and Forzani 2008), which requires the distribution of $\textbf{X}| Y$ to be normally distributed. Clearly, this assumption is not suitable to our settings and to various real applications. The proposed procedure, which includes the Nadaraya-Watson kernel estimate of the conditional mean, does not depend on the distribution of $\textbf{X}|Y$ and thus avoids the assumption.

4 Numerical study

4.1 Simulations

In this section, we conduct simulations to compare our method with 3 state-of-the-art high-dimensional sparse SDR methods: Lasso-SIR (Lin et al. 2019), convex-SIR (Tan et al. 2018) and SEAS (Zeng et al. 2022). Specifically, within the SEAS framework, we consider 3 SEAS estimators: SEAS-SIR, SEAS-Intra and SEAS-PFC, all elucidated in Zeng et al. (2022). For a fair comparison, we use the publicly available codes and default parameter settings of the above 3 methods. We use two measures: the True Positive Rate (TPR) and the False Positive Rate (FPR), to assess how well the methods select variables. In particular, TPR is defined as the proportion of active predictors that are correctly identified while FPR is defined as the proportion of irrelevant predictors that are falsely identified. Hence, an estimator with a bigger TPR and a smaller FPR is better. Furthermore, we calculate the absolute correlation coefficient (corr) between the true single index and its estimator to evaluate accuracy of the methods. Clearly, a higher absolute correlation coefficient indicates a better estimator.

Recall that $\hat{{\varvec{\Pi }}}$ is an estimator of the orthogonal projection ${\varvec{\Pi }}$, and the estimated vector of coefficients $\hat{{\varvec{\beta }}}$ is obtained by computing the top eigenvector of $\hat{{\varvec{\Pi }}}$. When computing TPR and FPR in practice, we truncated $\hat{{\varvec{\beta }}}$ by zeroing out its entries whose magnitude is smaller than $10^{-4}$. In all our simulations, the initial point $\Pi ^{(0)}$ of our algorithm started as the zero matrix. To assess these methods fairly, the following 6 data generating schemes are considered.

Table 1 Summary of Studies 1–4. The mean, averaged over 200 datasets, are reported. All entries are multiplied by 100. The bold numbers in each row highlight the best methods

Study 1.:

This model is a classic linear regression model from Tan et al. (2018):

$$\begin{aligned} Y=\sqrt{3}{\varvec{\beta }}^{\top }\textbf{X}+2\epsilon , \end{aligned}$$

where $\epsilon \sim N(0,1)$, $\textbf{X}=(X_1,\ldots ,X_p)^{\top }\sim N_{p}(\textbf{0},\mathbf{\Sigma })$ with $\mathbf{\Sigma }_{ij}=0.5^{|i-j|}$ for $1\le i,j\le p$, and $\textbf{X}$ and $\epsilon$ are independent. In this study, the central subspace is spanned by the vector ${\varvec{\beta }}=(1,1,1,0,\ldots ,0)^{\top }/\sqrt{3}$ with $p-3$ zero coefficients.

Study 2.:

This model is a nonlinear regression model from Yin and Hilafu (2015):

$$\begin{aligned} Y=1+\exp ({\varvec{\beta }}^{\top }\textbf{X})+\epsilon , \end{aligned}$$

where $\epsilon$, $\textbf{X}$ and ${\varvec{\beta }}$ are specified as those in Study 1.

Study 3.:

This model is from Chen et al. (2018):

$$\begin{aligned} Y=({\varvec{\beta }}^{\top }\textbf{X}+0.5)^2+0.5\epsilon , \end{aligned}$$

where $\epsilon$ and $\textbf{X}$ are generated as those in Study 1. In this study, the central subspace is spanned by the vector ${\varvec{\beta }}=(1,1,1,1,0,\ldots ,0)^{\top }/2$ with $p-4$ zero coefficients.

Study 4.:

This model is a mean function model similar to Zhang and Yin (2015):

$$\begin{aligned} Y=\sin ({\varvec{\beta }}^{\top }\textbf{X})+0.2\epsilon , \end{aligned}$$

where $\epsilon \sim N(0,1)$. The predictor $\textbf{X}=(X_1,\ldots ,X_p)^{\top }$ is independent of $\epsilon$ and defined as follows: the last $p-1$ components $(X_2,\ldots ,X_p)^{\top } \sim N_{p-1}(\textbf{0},\mathbf{\Sigma })$ with $\mathbf{\Sigma }_{ij}=0.5^{|i-j|}$ for $2\le i,j\le p$ and the first component $X_1=|X_2+X_3|+0.1 \xi$, where $\xi$ is an independent standard normal random variable. In this study, the central subspace is spanned by the vector ${\varvec{\beta }}=(1,1,1,0,\ldots ,0)^{\top }/\sqrt{3}$ with $p-3$ zero coefficients.

Study 5.:

This model is a multivariate response model combining Study 1 and Study 3:

$$\begin{aligned} \left\{ \begin{aligned} Y_1&={\varvec{\beta }}^{\top }\textbf{X}+2\epsilon , \\ Y_2&=({\varvec{\beta }}^{\top }\textbf{X}+0.5)^2+0.5\epsilon , \end{aligned} \right. \end{aligned}$$

where $\epsilon \sim N(0,1)$. The predictor $\textbf{X}=(X_1,\ldots ,X_p)^{\top }$ is independent of $\epsilon$ and defined as those in Study 1 or 3. In this study, ${\varvec{\beta }}=(1,1,1,1,0,\ldots ,0)^{\top }/2$ with $p-4$ zero coefficients.

Study 6.:

This model is a multivariate response model combining Study 3 and Study 4:

$$\begin{aligned} \left\{ \begin{aligned} Y_1&=({\varvec{\beta }}^{\top }\textbf{X}+0.5)^2+0.5\epsilon , \\ Y_2&=\sin ({\varvec{\beta }}^{\top }\textbf{X})+0.2\epsilon , \end{aligned} \right. \end{aligned}$$

where $\epsilon \sim N(0,1)$. The predictor $\textbf{X}=(X_1,\ldots ,X_p)^{\top }$ is independent of $\epsilon$ and defined as those in Study 4. ${\varvec{\beta }}=(1,1,1,1,0,\ldots ,0)^{\top }/2$ with $p-4$ zero coefficients.

Table 2 Summary of Study 3. The mean, averaged over 200 datasets, are reported. All entries are multiplied by 100

Table 3 Summary of Studies 5 and 6. The mean, averaged over 200 datasets, are reported. All entries are multiplied by 100

The first four studies mainly focus on univariate response SDR, while the next two studies explore multivariate response SDR. Since the methods for comparison can not be applied to the multivariate response cases, the comparison are only conducted in Studies 1–4. The simulation results are summarized in Table 1. In Study 1, although our method exhibits a slight advantage over the other methods in terms of FPR, it generally performs less favorably in comparison to these methods. This phenomenon can be well explained by that the SIR-type methods should have the best performance in the classic linear model. In Study 2, the four methods demonstrate similar performance. In Study 3, the mean function is nearly symmetric about 0, which causes serious problems to the SIR-type methods. Nevertheless, our method is still valid in this setting and significantly outperforms the other methods. In Study 4, the linearity condition is destroyed. Hence, in such a case it is not surprising that our proposed method performs much better than the methods for comparison. To summarize, compared with existing approaches, our proposed method performs quite well across all the 4 studies in the high-dimensional setting.

In the first 4 studies, we go futher to examine the influence of covariate correlation on estimation. Specifically, we generate $\textbf{X}$ from a multivariate normal distribution $N_p(\textbf{0},\mathbf{\Sigma })$, where ${\varvec{\Sigma }}_{ij}=\rho ^{|i-j|}$, and then we explore different values of $\rho$ within the set $\left\{ 0.1,0.3,0.5,0.7,0.9\right\}$. It is evident that a larger $\rho$ corresponds to a higher level of covariate correlation. The simulation results show that both the performance of variable selection and estimation accuracy of the proposed method remain quite stable as the correlation among the covariates increases from $\rho =0.1$ to $\rho =0.7$, and are only slightly affected at the high correlation level of $\rho =0.9$. Similar phenomena also occurs in the 3 sparse SDR methods for comparison, except that FPR of the convex-SIR estimator jumps to an extremely high level at $\rho =0.9$ in Studies 3–4. Since the results of Studies 1–4 are similar, we only report the results for Study 3 in Table 2 as an illustration.

Studies 5 and 6 investigate the performance of the proposed method in multivariate response models. As far as we know, there seems to be no apparent competitor in such scenarios. The results are summarized in Table 3, and we can see that our proposed method works fine even if the response is multivariate.

To better understand the computational efficiency of the proposed algorithm relative to competing approaches, we record the computation time of each method in Study 3 as an illustrative example. For a fair comparison, we record the total computation time for each method, including a 5-fold cross-validation to select from 50 tuning parameters in a proper range. The results are displayed in Fig. 1. Subfigures (a) and (b) plot the log computation time and the absolute correlation coefficient of each method against the sample size, respectively. The figures together show that the speed of our method is comparable to convex-SIR and SEAS-PFC with significantly high estimation accuracy. Although Lasso-SIR enjoys the fastest speed, its accuracy seems quite poor in comparison to the other methods. Furthermore, our method presents scalability to sample size in the sense that its computation time does not significantly increase as the sample size increases, while the computation times of other methods rise with the sample size.

Fig. 1

Box plots of a natural log computation time (seconds) and b absolute correlation coefficient for each SDR method for Study 3 with $\rho =0.5$

Table 4 Summary of the regression results in the real data. The bold numbers in each row highlight the best two methods

4.2 Real data analysis

In this part, we evaluate the performance of our proposed method in a real dataset about riboflavin (vitamin $\text{ B}_2$) production with Bacillus subtilis, which is publicly available in the R package hdi. This dataset was analyzed by Dezeure et al. (2015); Hilafu and Yin (2017), and Serfling (1980) for high-dimensional analysis. It consists of a single real-valued response variable which is the logarithm of the riboflavin production rate and $p=4088$ predictors measuring the logarithm of the expression level of 4088 genes. The purpose is to systematically search genomic features that contain sufficient information for the riboflavin production rate prediction. We center the response and standardize all the covariates before analysis.

The sample size $n=71$ is small compared with the covariate dimension $p=4088$. To handle the ultrahigh dimensionality, we preselect the most significant 100 genes via the sure independence screening procedure based on the distance correlation (Li et al. 2012). Following the work of Hilafu and Yin (2017), we split the data into a training set of 50 samples and a test set of 21 samples. The training set is used to select features and estimate the central subspace. To evaluate the performance in the test data, we fit a linear model with the estimated single index as the predictor, rather than building a complex model.

Fig. 2

Panel a are the scattterplots of y against the estimated index ${\hat{{\varvec{\beta }}}}^{\top }\textbf{X}$ in the training set; Panel b are the scatterplots of the actual and predicted values for the testing samples

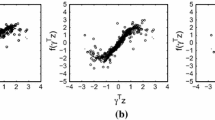
We compare the proposed method with convex-SIR, Lasso-SIR and SEAS, as done in the simulation. Table 4 reports the adjusted-$R^2$ in the training data and Root Mean Squared Error (RMSE) for the test samples. Specifically, our method obtained an adjusted $R^2$ 73.6% in the training data with a significantly small RMSE 0.409 for the test data. Lasso-SIR obtained the largest adjusted $R^2$ 83.3% with a bigger RMSE 0.538, indicating possible overfitting for this real data set. Convex-SIR and SEAS performed less favorably than the aforementioned two methods. The scatterplots in Figs. 2 give a clear picture of the performance of the 4 methods in the training data and the test data.

5 Conclusion

In this article, we develop an MM-LADMM algorithm to handle large p and small n scenarios for single index regression, extending the HSIC based method of Zhang and Yin (2015) to adapt to high-dimensional settings. The proposed approach estimates the basis of the central subspace and performs sufficient variable selection simultaneously. Compared with other high-dimensional sparse SDR methods, our method requires much weaker conditions. To be specific, it requires very mild conditions on $\textbf{X}$ and no particular assumptions on $Y|\textbf{X}$ or $\textbf{X}| Y$ while retaining the model free property. The simulation studies showed that our method is highly efficient and stable in both $n>p$ and $n<p$ scenarios.

There are several possible prospects for future research. It may be of interest to extend the proposed method to multiple-index models, which is absolutely not trivial since it may need a completely new algorithm design. Moreover, the current computational bottleneck of our method is on solving the majorization step, which bears a computational complexity of $O(p^3)$ per iteration. Thus, it will be also interesting to redesign a highly efficient algorithm such that the proposed method is scalable to accommodate large-scale data. Finally, the asymptotic properties of the proposed estimator, which are not covered in the current article, are deserved to investigate in the future.

Technical derivations

1.1 Proof of proposition 3.1

Proof. We first compute the gradient function $\nabla f({\varvec{\Pi }})$. Recalling the definition of $f({\varvec{\Pi }})$, we directly have

$$\begin{aligned} \nabla f({\varvec{\Pi }})=\frac{1}{2n^2} \sum _{i,j=1}^{n} \exp \left( -\frac{ \langle {\varvec{\Pi }}, \textbf{Z}_{ij} \rangle }{2} \right) \tilde{L}_{ij}\textbf{Z}_{ij}. \end{aligned}$$

Noting that $\textbf{C}\in \mathbb {R}^{n\times n}$ with $\displaystyle c_{ij}=\exp (-{ \langle {\varvec{\Pi }}, \textbf{Z}_{ij} \rangle }/{2} )\tilde{L}_{ij}$ and $\mathbb {X}=[\textbf{X}_1,\ldots ,\textbf{X}_n]^{\top }$, we have

$$\begin{aligned} \nabla f({\varvec{\Pi }})= & {} \frac{1}{2n^2} \sum _{i,j=1}^{n} c_{ij}\textbf{Z}_{ij}\\= & {} \frac{1}{2n^2} \sum _{i,j=1}^{n} c_{ij}(\textbf{X}_i-\textbf{X}_j)(\textbf{X}_i-\textbf{X}_j)^{\top } \\= & {} \frac{1}{2n^2} \sum _{i,j=1}^{n} c_{ij}\left( \textbf{X}_i\textbf{X}_i^{\top } + \textbf{X}_j\textbf{X}_j^{\top }-\textbf{X}_i\textbf{X}_j^{\top }{-}\textbf{X}_j\textbf{X}_i^{\top } \right) \\= & {} \frac{1}{n^2} \sum _{i,j=1}^{n} c_{ij}\left( \textbf{X}_i\textbf{X}_i^{\top } -\textbf{X}_i\textbf{X}_j^{\top } \right) \\= & {} \frac{1}{n^2} \mathbb {X}^{\top }\left( \text{ diag }(\textbf{C}{\varvec{1}}_{n})- \textbf{C}\right) \mathbb {X}, \end{aligned}$$

which establishes the first part of Proposition 3.1. Next, we prove the Lipschitz continuity of $\nabla f({\varvec{\Pi }})$ over the bounded set $\mathcal{D}=\{ {\varvec{\Pi }}\in \mathcal{M}: \textrm{tr}(\hat{{\varvec{\Sigma }}}^{1/2} {\varvec{\Pi }}\hat{{\varvec{\Sigma }}}^{1/2} )\le 1 \}$. For any ${\varvec{\Pi }}\in \mathcal{D}$ and $\tilde{{\varvec{\Pi }}}\in \mathcal{D}$, by the triangle inequality, we obtain

$$\begin{aligned}{} & {} \Vert \nabla f({\varvec{\Pi }})-\nabla f(\tilde{{\varvec{\Pi }}}) \Vert _\textrm{F} \\ {}= & {} \left\| \frac{1}{2n^2} \sum _{i,j=1}^{n} \exp \left( -\frac{ \langle {\varvec{\Pi }}, \textbf{Z}_{ij} \rangle }{2} \right) \tilde{L}_{ij}\textbf{Z}_{ij} \right. \\{} & {} \quad \left. -\frac{1}{2n^2}\sum _{i,j=1}^{n} \exp \left( -\frac{ \langle \tilde{{\varvec{\Pi }}}, \textbf{Z}_{ij} \rangle }{2} \right) \tilde{L}_{ij}\textbf{Z}_{ij} \right\| _\textrm{F} \\\le & {} \frac{1}{2n^2} \sum _{i,j=1}^{n} |\tilde{L}_{ij}|\Vert \textbf{Z}_{ij}\Vert _\textrm{F} \left| \exp \left( -\frac{ \langle {\varvec{\Pi }}, \textbf{Z}_{ij} \rangle }{2} \right) \right. \\{} & {} \quad \left. - \exp \left( -\frac{ \langle \tilde{{\varvec{\Pi }}}, \textbf{Z}_{ij} \rangle }{2} \right) \right| \\\le & {} \frac{1}{2n^2} \sum _{i,j=1}^{n} |\tilde{L}_{ij}|\Vert \textbf{Z}_{ij}\Vert _\textrm{F} \left| \frac{ \langle {\varvec{\Pi }}-\tilde{{\varvec{\Pi }}}, \textbf{Z}_{ij} \rangle }{2} \right| , \end{aligned}$$

where the last inequality holds since $|e^x-e^y|\le |x-y|$, for any $y\le x\le 0$. Further, by the Cauchy-Schwartz inequality, we know $| \langle {\varvec{\Pi }}-\tilde{{\varvec{\Pi }}}, \textbf{Z}_{ij} \rangle |\le \Vert {\varvec{\Pi }}-\tilde{{\varvec{\Pi }}}\Vert _\textrm{F}\Vert \textbf{Z}_{ij}\Vert _\textrm{F}$. Thus, we finally get

$$\begin{aligned} \Vert \nabla f({\varvec{\Pi }})-\nabla f(\tilde{{\varvec{\Pi }}}) \Vert _\textrm{F}\le & {} \frac{1}{4n^2} \sum _{i,j=1}^{n} |\tilde{L}_{ij}|\Vert \textbf{Z}_{ij}\Vert _\textrm{F}^2 \Vert {\varvec{\Pi }}-\tilde{{\varvec{\Pi }}}\Vert _\textrm{F}\\= & {} \frac{\sum _{i,j=1}^{n} |\tilde{L}_{ij}|\Vert \textbf{Z}_{ij}\Vert _\textrm{F}^2}{4n^2} \Vert {\varvec{\Pi }}-\tilde{{\varvec{\Pi }}}\Vert _\textrm{F}, \end{aligned}$$

where ${\sum _{i,j=1}^{n} |\tilde{L}_{ij}|\Vert \textbf{Z}_{ij}\Vert _\textrm{F}^2}/(4n^2)$ is a constant, which verifies the claim. $\Box$

1.2 Linearized alternating direction method of multipliers algorithm for solving (3.7)

To implement the LADMM algorithm, we rewrite the subproblem in formula (3.7) as

$$\begin{aligned} \begin{aligned} \underset{{\varvec{\Pi }}, \textbf{H}\in \mathcal{M}}{\min }\;&\frac{L}{2}\left\| {\varvec{\Pi }}-\left[ {\varvec{\Pi }}^{(r)}-\frac{1}{L} \nabla f({\varvec{\Pi }}^{(r)}) \right] \right\| _\textrm{F}^2 +\lambda \Vert {\varvec{\Pi }}\Vert _1\\&\quad +\infty \cdot {\mathbb I} _{(\textrm{tr}(\textbf{H})>1)}, \\&\text{ s.t. } \quad \hat{{\varvec{\Sigma }}}^{1/2} {\varvec{\Pi }}\hat{{\varvec{\Sigma }}}^{1/2} = \textbf{H}. \end{aligned} \end{aligned}$$

This is equivalent to minimizing the following scaled augmented Lagrangian function,

$$\begin{aligned} \begin{aligned} \mathcal{L}_{\rho }({\varvec{\Pi }},\textbf{H},{\varvec{\Gamma }})=&\frac{L}{2}\left\| {\varvec{\Pi }}-\left[ {\varvec{\Pi }}^{(r)}-\frac{1}{L} \nabla f({\varvec{\Pi }}^{(r)}) \right] \right\| _\textrm{F}^2\\&+ \lambda \Vert {\varvec{\Pi }}\Vert _1+\infty \cdot {\mathbb I} _{(\textrm{tr}(\textbf{H})>1)}\\&+\frac{\rho }{2}\Vert \hat{{\varvec{\Sigma }}}^{1/2} {\varvec{\Pi }}\hat{{\varvec{\Sigma }}}^{1/2} - \textbf{H}+{\varvec{\Gamma }}\Vert _\textrm{F}^2, \end{aligned} \end{aligned}$$

where $\rho$ is a small constant and ${\varvec{\Gamma }}$ is the dual variable. The LADMM algorithm minimizes the augmented Lagrangian function by alternatively solving one block of variables at a time. In particular, to update ${\varvec{\Pi }}$ at the j-th iteration, we need to minimize

$$\begin{aligned}{} & {} \frac{L}{2}\left\| {\varvec{\Pi }}-\left[ {\varvec{\Pi }}^{(r)}-\frac{1}{L} \nabla f({\varvec{\Pi }}^{(r)}) \right] \right\| _\textrm{F}^2 +\lambda \Vert {\varvec{\Pi }}\Vert _1\\{} & {} \quad +\frac{\rho }{2}\Vert \hat{{\varvec{\Sigma }}}^{1/2} {\varvec{\Pi }}\hat{{\varvec{\Sigma }}}^{1/2} - \textbf{H}_j+{\varvec{\Gamma }}_j \Vert _\textrm{F}^2, \end{aligned}$$

where $\textbf{H}_j$ and ${\varvec{\Gamma }}_j$ are the j-th estimates of $\textbf{H}$ and ${\varvec{\Gamma }}$, respectively. However, there is no closed-form solution for the above minimization problem. To tackle the difficulty, Fang et al. (2015) proposed to linearize the quadratic term in the above problem by applying a second-order Taylor expansion. Following their work, we obtain the update for ${\varvec{\Pi }}$:

$$\begin{aligned} \begin{aligned} {\varvec{\Pi }}_{j+1}&{=}\underset{{\varvec{\Pi }}\in \mathcal{M}}{\arg \min }\; \frac{L}{2}\left\| {\varvec{\Pi }}-\left[ {\varvec{\Pi }}^{(r)}{-}\frac{1}{L} \nabla f({\varvec{\Pi }}^{(r)}) \right] \right\| _\textrm{F}^2 +\lambda \Vert {\varvec{\Pi }}\Vert _1 \\&\quad +\rho \langle {\varvec{\Pi }}-{\varvec{\Pi }}_j, \hat{{\varvec{\Sigma }}}{\varvec{\Pi }}_j \hat{{\varvec{\Sigma }}}-\hat{{\varvec{\Sigma }}}^{1/2} (\textbf{H}_j-{\varvec{\Gamma }}_j)\hat{{\varvec{\Sigma }}}^{1/2} \rangle \\&\quad +\frac{\tau }{2} \Vert {\varvec{\Pi }}-{\varvec{\Pi }}_j\Vert _\textrm{F}^2. \end{aligned} \end{aligned}$$

As suggested by Fang et al. (2015), we pick $\tau \ge 4\rho \lambda _\textrm{max}^2(\hat{{\varvec{\Sigma }}})$ to ensure the convergence of the LADMM algorithm. The above iterate can be written in the more familiar notation:

$$\begin{aligned} \begin{aligned} {\varvec{\Pi }}_{j+1}&=\underset{{\varvec{\Pi }}\in \mathcal{M}}{\arg \min }\; \frac{L+\tau }{2} \Big \Vert {\varvec{\Pi }}\\&\quad {-}\Big \{ \frac{\tau }{L+\tau } \Big [ {\varvec{\Pi }}_{j}{-}\frac{\rho }{\tau }\hat{{\varvec{\Sigma }}}{\varvec{\Pi }}_{j}\hat{{\varvec{\Sigma }}}{+}\frac{\rho }{\tau }\hat{{\varvec{\Sigma }}}^{1/2}(\textbf{H}_j{-}{\varvec{\Gamma }}_{j})\hat{{\varvec{\Sigma }}}^{1/2} \Big ] \\&\quad +\frac{L}{L+\tau } \Big [ {\varvec{\Pi }}^{(r)}-\frac{\nabla f({\varvec{\Pi }}^{(r)})}{L}\Big ] \Big \} \Big \Vert _\textrm{F}^2 +\lambda \Vert {\varvec{\Pi }}\Vert _1 \end{aligned} \end{aligned}$$

which has the closed-form solution

$$\begin{aligned}&{\varvec{\Pi }}_{j+1} =\\&~~ \textrm{Soft}\left( \frac{\tau }{L+\tau } \left[ {\varvec{\Pi }}_{j}-\frac{\rho }{\tau }\hat{{\varvec{\Sigma }}}{\varvec{\Pi }}_{j}\hat{{\varvec{\Sigma }}}+\frac{\rho }{\tau }\hat{{\varvec{\Sigma }}}^{1/2}(\textbf{H}_j-{\varvec{\Gamma }}_{j})\hat{{\varvec{\Sigma }}}^{1/2} \right] \right. \\&\quad \left. +\frac{L}{L+\tau } \left[ {\varvec{\Pi }}^{(r)}-\frac{\nabla f({\varvec{\Pi }}^{(r)})}{L}\right] ,\frac{\lambda }{L+\tau } \right) , \end{aligned}$$

where $\textrm{Soft}(\cdot ,\cdot )$ implements the element-wise soft-thresholding on a matrix $\textbf{A}=(A_{ij})$: $\textrm{Soft}(\textbf{A},b)=\{\textrm{Soft}(A_{ij},b)\}=\{\textrm{sign}(A_{ij})\max (|A_{ij}|-b,0)\}$. Next, the update of $\textbf{H}$ can be obtained as

$$\begin{aligned} \textbf{H}_{j+1} =\underset{ \textbf{H}\in \mathcal{M}, \textrm{tr}(\textbf{H})\le 1 }{\arg \min }\; \frac{1}{2}\Vert \textbf{H}-(\hat{{\varvec{\Sigma }}}^{1/2}{\varvec{\Pi }}_{j+1}\hat{{\varvec{\Sigma }}}^{1/2}+{\varvec{\Gamma }}_{j}) \Vert _\textrm{F}^2, \end{aligned}$$

which has a closed-form solution according to the following proposition.

Proposition 6.1

Let $\mathcal{F}=\{ \textbf{H}\in \mathcal{M}: \textrm{tr}(\textbf{H})\le 1 \}$ and $P_{\mathcal{F}}(\textbf{W})={\arg \min }_{ \textbf{H}\in \mathcal{F}}\; \Vert \textbf{H}-\textbf{W}\Vert _\textrm{F}^2/2$. If $\textbf{W}$ has the singular value decomposition $\textbf{W}=\sum _{i=1}^{p}\omega _{i}\varvec{u}_{i}\varvec{u}_{i}^{\top }$, then $P_{\mathcal{F}}(\textbf{W})=\sum _{i=1}^{p}(\omega _{i}-\theta ^{*})_{+}\varvec{u}_{i}\varvec{u}_{i}^{\top }$, where $(\omega _{i}-\theta ^*)_{+}=\max (\omega _i-\theta ^*,0)$ and $\theta ^{*}$ is the minimum value satisfying $\sum _{i=1}^{p}(\omega _{i}-\theta )_{+}\le 1.$

The above proposition follows directly from Lemma 4.1 in Vu et al. (2013), Proposition 10.2 in Gao et al. (2017), and Proposition 1 in the Appendix of Tan et al. (2018). Thus, by Proposition 6.1, we have

$$\begin{aligned} \textbf{H}_{j+1}=P_{\mathcal{F}}(\hat{{\varvec{\Sigma }}}^{1/2}{\varvec{\Pi }}_{j+1}\hat{{\varvec{\Sigma }}}^{1/2}+{\varvec{\Gamma }}_{j}). \end{aligned}$$

Finally, we update the dual variable by

$$\begin{aligned} {\varvec{\Gamma }}_{j+1} = {\varvec{\Gamma }}_{j}+ \hat{{\varvec{\Sigma }}}^{1/2}{\varvec{\Pi }}_{j+1}\hat{{\varvec{\Sigma }}}^{1/2}-\textbf{H}_{j+1}. \end{aligned}$$