1 Introduction

Magnetic helicity is a geometrical quantity that describes the twist, writhe, and linkage of magnetic-field lines. It is invariant in ideal magnetohydrodynamics (MHD; Woltjer, 1958) and is approximatelly conserved even in nonideal MHD conditions (Taylor, 1974; Pariat et al., 2015). These properties make helicity an important quantity in plasma physics studies (e.g. Ji, Prager, and Sarff, 1995; Brown et al., 1999; Dasgupta et al., 2002).

Magnetic helicity of a magnetic field [\(\boldsymbol {B}\)] in a volume [\(V\)] is defined as \(H_{m}(\boldsymbol {B})=\int_{V} \mathrm{d}V \boldsymbol {A} \cdot\boldsymbol {B}\), where \(\boldsymbol {A}\) is the vector potential such that \(\boldsymbol {B}=\nabla\times\boldsymbol {A}\). This quantity is gauge-invariant as long as the surface enclosing \(V\) is a flux surface, i.e. when the normal component of the magnetic field vanishes there. This is obviously not the case for arbitrarily shaped volumes, but an appropriate helicity with respect to a reference field can still be defined (Berger and Field, 1984; Finn and Antonsen, 1985). This is the relative magnetic helicity, which is given by

$$ H= \int_{V} \mathrm{d}V (\boldsymbol {A}+\boldsymbol {A}_{\mathrm{p}}) \cdot(\boldsymbol {B}-\boldsymbol {B}_{\mathrm{p}}), $$
(1)

with \(\boldsymbol {B}_{\mathrm{p}}=\nabla\times\boldsymbol {A}_{ \mathrm{p}}\) the reference field, usually taken to be a potential field, and \(\boldsymbol {A}_{\mathrm{p}}\) its vector potential. The important condition allowing gauge independence is that the studied field and the potential field must have the same normal component on the whole boundary of the system.

The application range of relative magnetic helicity (hereafter simply helicity) in the Sun is quite broad, extending from the solar dynamo (e.g. Brandenburg and Subramanian, 2005) to the triggering of coronal mass ejections: according to Rust (1994), the existence of solar eruptions might be attributed to the need to shed the coronal magnetic helicity, constantly accumulating from a continuous injection through the photosphere.

In the solar context, different methods and approaches can be used to evaluate magnetic helicity. A review and comparison of several of these methods is presented by Valori et al. (2016). The focus of this article is on the finite-volume methods (e.g. Thalmann, Inhester, and Wiegelmann, 2011; Valori, Démoulin, and Pariat, 2012; Yang et al., 2013), that is methods that employ the definition of helicity as a volume integral and thus require the three-dimensional (3D) magnetic field in the entire volume as input.

In all of these methods, the relative magnetic helicity is computed in Cartesian geometry. The natural coordinate system for the Sun, however, is the spherical one, and so it is necessary to be able to calculate helicity in spherical coordinates. Possible applications of such a calculation include MHD simulations in spherical geometry (e.g. Masson, Antiochos, and DeVore, 2013; Fan, 2016; Karpen et al., 2017), as well as nonlinear force-free (NLFF) field extrapolations (e.g. Gilchrist and Wheatland, 2014; Savcheva et al., 2016).

Although there are studies that compute magnetic helicity in spherical coordinates (e.g. Bobra, van Ballegooijen, and DeLuca, 2008; Fan, 2010; Savcheva et al., 2015; Karpen et al., 2017), they used various assumptions and/or simplifications. The respective helicity computations are then problem dependent, and the methods used cannot be generalized to other datasets. In the MHD simulations of Fan (2010), for example, no magnetic flux penetrates the lateral boundaries of the volume, which results in the simplification of the helicity calculations. In another example, Karpen et al. (2017) drove a coronal-hole jet with a rotational photospheric plasma motion that left the initially prescribed potential magnetic field (and corresponding vector potential) approximately unchanged, thus simplifying the helicity calculations.

In other cases, such as Bobra, van Ballegooijen, and DeLuca (2008), a different helicity formula was used. In spherical coordinates, this reads

$$ H_{R}= \int_{V} \mathrm{d}V (\boldsymbol {A}\cdot\boldsymbol {B} - \boldsymbol {A}_{\mathrm{p}}\cdot\boldsymbol {B}_{\mathrm{p}})+ \int_{S} \mathrm{d}S \chi B_{r}. $$
(2)

This relation stems from the original definition of relative helicity (Berger and Field, 1984) where space is divided into two regions; the volume of interest [\(V\)] and a complementary volume [\(V'\)], where \(\boldsymbol {B}'=\boldsymbol {B}_{\mathrm{p}}'\), and thus \(\boldsymbol {A}'- \boldsymbol {A}'_{\mathrm{p}}=\nabla\chi\) for some scalar function \(\chi\) (the primed quantities refer to \(V'\)). The interface of the two volumes is denoted as \(S\), while \(B_{r}\) is the radial field component. Additionally, the boundary of \(V\cup V'\) is considered as a flux surface, or extending to infinity.

In the particular case examined by Bobra, van Ballegooijen, and DeLuca (2008), \(V\) is the coronal wedge-shaped volume of interest, and \(V'\) its sub-photospheric extension to the center of the Sun, and so neither of them is in general bounded by a flux surface. Following Bobra, van Ballegooijen, and DeLuca (2008), however, \(V'\) is a bounded volume, and since \(V\cup V'\) is bounded by a flux surface, it follows that \(V'\) should be bounded by a flux surface below the photosphere. This necessarily implies that the photospheric boundary \(S\) has to be flux balanced, i.e. without net magnetic flux. These restrictions could be lifted by considering \(V'\) as the whole volume outside \(V\), but this was not the choice made in the original derivation of Equation 2, as the limitation of the surface integral to the photosphere demonstrates. The first term in Equation 2 indeed represents the contribution to helicity from \(V\), while the same quantity in \(V'\) reduces to the surface integral of the second term because of the assumption \(\boldsymbol {B}'=\boldsymbol {B}_{\mathrm{p}}'\) there. Had a different geometry of \(V'\) been adopted, an additional contribution to Equation 2 should be considered.

To determine whether, and under which conditions, Equation 1 is equivalent to Equation 2, we apply the latter to the same volume as the former \(V\cup V'\). The contribution to relative magnetic helicity from \(V'\) is exactly zero, however, since \(\boldsymbol {B}'= \boldsymbol {B}_{\mathrm{p}}'\) there. In the volume of interest [\(V\)] we can expand the terms in Equation 1 as

$$ H= \int_{V} \mathrm{d}V (\boldsymbol {A}\cdot\boldsymbol {B} - \boldsymbol {A}_{\mathrm{p}}\cdot\boldsymbol {B}_{\mathrm{p}})+ \int_{V} \mathrm{d}V (\boldsymbol {A}_{\mathrm{p}}\cdot \boldsymbol {B} - \boldsymbol {A}\cdot\boldsymbol {B}_{\mathrm {p}}). $$
(3)

The first term coincides with the respective term in Equation 2, while the second is a mixed term that can also be written as the surface integral

$$ H_{\mathrm{mix}}= \oint_{\partial V}\mathrm{d}S \hat{\boldsymbol {n}} \cdot (\boldsymbol {A} \times\boldsymbol {A_{\mathrm{p}}}), $$
(4)

after using standard vector identities (Valori, Démoulin, and Pariat, 2012). Here \(\hat{\boldsymbol {n}}\) stands for the outward-pointing unit vector on the boundary of the volume of interest \(\partial V\).

To better compare the surface terms of the two helicity equations, we reverse the steps in the derivation of the second term of Equation 2 and obtain

$$ \int_{S}\mathrm{d}S \chi B_{r}= \int_{\partial V'}\mathrm{d}S \chi\bigl(\hat{\boldsymbol {n}}' \cdot\boldsymbol {B}'\bigr)= \int_{V'}\mathrm{d}V \nabla\chi\cdot\boldsymbol {B}'. $$
(5)

In the first equality, the surface integral is extended to the whole boundary of the sub-photospheric volume [\(\partial V'\)] by the assumption that \(\partial V'-S\) is a flux surface [\(\hat{\boldsymbol {n}}'\cdot\boldsymbol {B}'=0\)] with \(\hat {\boldsymbol {n}}'\) denoting the outward-pointing unit vector on \(\partial V'\). The second equality follows directly from Gauss’ theorem and an integration by parts. Now, since \(\nabla\chi\cdot\boldsymbol {B}'=(\boldsymbol {A}'- \boldsymbol {A}'_{\mathrm{p}})\cdot\boldsymbol {B}'=-\nabla\cdot( \boldsymbol {A}'\times\boldsymbol {A'_{\mathrm{p}}})\) in \(V'\), we derive

$$ \int_{S}\mathrm{d}S \chi B_{r}=- \int_{\partial V'}\mathrm{d}S \hat{\boldsymbol {n}}'\cdot \bigl(\boldsymbol {A}'\times\boldsymbol {A'_{\mathrm{p}}} \bigr)=- \int_{S}\mathrm{d}S \hat{\boldsymbol {n}}' \cdot \bigl(\boldsymbol {A}'\times\boldsymbol {A'_{\mathrm{p}}} \bigr). $$
(6)

Again, only the photospheric part survives in the surface integral since the remaining boundaries are flux surfaces. Moreover, as noted by Finn and Antonsen (1985), Equation 2 is gauge invariant if additionally the tangential components of the two vector potentials are continuous across \(S\), a condition that leads to \(\boldsymbol {A}'\times \boldsymbol {A'_{\mathrm{p}}}=\boldsymbol {A}\times \boldsymbol {A_{\mathrm{p}}}\) on \(S\). Replacing in Equation 6 also that \(\hat{\boldsymbol {n}}'=-\hat{\boldsymbol {n}}\) on \(S\), we finally obtain

$$ \int_{S}\mathrm{d}S \chi B_{r}= \int_{S}\mathrm{d}S \hat{\boldsymbol {n}}\cdot(\boldsymbol {A} \times\boldsymbol {A_{\mathrm{p}}}). $$
(7)

The surface term in the Bobra, van Ballegooijen, and DeLuca (2008) formulation thus corresponds to the photospheric part of the \(H_{\mathrm{mix}}\) term.

The comparison of the surface terms of the two helicity formulations, given by Equations 7 and 4, shows that they coincide if the condition \(\hat{\boldsymbol {n}}\cdot(\boldsymbol {A} \times\boldsymbol {A_{\mathrm{p}}}) =0\) holds on the coronal part of the boundary of the volume of interest: \(\partial V-S\). The conditions for Equations 1 and 2 to be equivalent are thus that \(\hat{\boldsymbol {n}}\cdot(\boldsymbol {A}\times \boldsymbol {A_{\mathrm{p}}}) | _{\partial V-S}=0\) on the coronal part of \(\partial V\) and \(\hat{\boldsymbol {n}}'\cdot \boldsymbol {B}' | _{\partial V'-S}=0\) on the sub-photospheric part of \(\partial V'\), also implying magnetic-flux balance on \(S\). The first condition is obviously gauge dependent, unless \(V\) extents to infinity (where the vector potentials presumably vanish), or \(\partial V\) is a flux surface (so that the tangential components of \(\boldsymbol {A}\) vanish there). If additionally the sub-photospheric part of \(\partial V'\) is treated as by Bobra, van Ballegooijen, and DeLuca (2008), i.e. it is assumed as generic and not bounded by a flux surface, with \(S\) not flux balanced, then the condition \(\hat{\boldsymbol {n}}\cdot(\boldsymbol {A}\times \boldsymbol {A_{\mathrm{p}}})=0\) must be valid there as well, and then \(H_{\mathrm{mix}}=0\) holds throughout the boundary of \(V\cup V'\).

In deriving Equation 2, the gauge-dependent assumption \(H_{\mathrm{mix}}=0\) is therefore made implicitly. This should be taken into account when applying this equation to finite volumes, since it is a gauge-dependent condition that is not valid in general.

In this article we extend the computationally most efficient and robust of the finite-volume methods in Cartesian coordinates (Valori, Démoulin, and Pariat, 2012; Moraitis et al., 2014) to the spherical geometry. The equations that we derive are applicable to both spherical-shell and spherical-wedge geometries. However, we focus on the latter because it is of more common use. We also compare the results produced by this method with helicity values computed with an approximate method based on Equation 2, and we determine the applicability of the latter. In Section 2 we describe the implementation details of the method, and in Section 3 we perform its validation against semi-analytic force-free magnetic-field models. In Section 4 we apply it to a set of NLFF fields that are also described there, and finally in Section 5 we summarize and discuss the results of the article.

2 Relative Magnetic Helicity in Spherical Coordinates

Relative magnetic helicity is computed directly from its definition by Finn and Antonsen (1985), Equation 1. From a given 3D magnetic field [\(\boldsymbol {B}\)], we have to estimate the other three vector fields appearing in Equation 1, namely the potential magnetic field [\(\boldsymbol {B}_{\mathrm{p}}\)] and the corresponding vector potentials [\(\boldsymbol {A}\) and \(\boldsymbol {A}_{\mathrm{p}}\)] of the two magnetic fields. Note that helicity as given in Equation 1 is independent of the gauges used in the vector potentials as long as the normal components of the original and potential fields match along the whole boundary of the volume, i.e.

$$ \hat{\boldsymbol {n}}\cdot\boldsymbol {B}| _{\partial V}= \hat{\boldsymbol {n}}\cdot\boldsymbol {B}_{\mathrm{p}} | _{\partial V} . $$
(8)

The relative magnetic helicity can then be calculated in two steps, similarly to the Cartesian case (Valori, Démoulin, and Pariat, 2012; Moraitis et al., 2014), as detailed in this section.

2.1 Calculation of the Potential Field

The potential field can always be expressed through a scalar potential \(\Phi\) as \(\boldsymbol {B}_{\mathrm{p}}=\nabla\Phi\). The potential then satisfies Laplace’s equation \(\nabla^{2}\Phi=0\) in \(V\). In spherical coordinates, this reads

$$ \frac{1}{r^{2}} \frac{\partial}{\partial r} \biggl( r^{2} \frac{ \partial\Phi}{\partial r} \biggr) +\frac{1}{r^{2}\sin\theta} \frac{ \partial}{\partial\theta} \biggl( \sin\theta\frac{\partial \Phi}{\partial\theta} \biggr) +\frac{1}{r^{2}\sin\theta^{2}} \frac{ \partial^{2} \Phi}{\partial\phi^{2}}=0. $$
(9)

The requirement of Equation 8, ensuring gauge invariance, leads to the following Neumann boundary conditions for the scalar potential:

$$ \frac{\partial\Phi}{\partial\hat{\boldsymbol {n}}} \bigg| _{\partial V}= \hat{\boldsymbol {n}} \cdot\boldsymbol {B} | _{\partial V}. $$
(10)

We note that the solution of Laplace’s equation under Neumann boundary conditions exists (up to an additive constant) only for flux-balanced fields, \(\int_{\partial V}\boldsymbol {B}\cdot\mathrm {d}\boldsymbol {S}=0\), a condition that is never fully satisfied with numerical data.

Laplace’s equation is solved with the use of a FORTRAN routine contained in the MUDPACK library (Adams, 1989). The routine uses a multigrid iteration method to obtain the solution and is therefore efficient, quick, and computationally not demanding. The multigrid method requires a uniform computational grid that has dimensions of the special form \(m 2^{n} +1\), for \(n\) some positive integer and \(m\) a small prime number, like 2, 3, or 5. In the case that either of these conditions is not fulfilled by the input magnetic field data, we linearly interpolate them to an appropriate grid, and we inevitably introduce numerical errors to the following helicity calculations.

2.2 Calculation of the Vector Potentials

2.2.1 Analytical Derivation

For the calculation of the vector potential of a given 3D magnetic field, we follow the conceptual method initially developed by DeVore (2000), and subsequently adapted to finite volumes by Valori, Démoulin, and Pariat (2012). We start from the defining relation of the vector potential [\(\boldsymbol {B}=\nabla\times\boldsymbol {A}\)] written in spherical coordinates,

$$\begin{aligned} (B_{r},B_{\theta},B_{\phi})= \biggl(& \frac{1}{r\sin\theta} \frac{ \partial}{\partial\theta} ( \sin\theta A_{\phi} ) -\frac{1}{r \sin\theta} \frac{\partial A_{\theta}}{\partial\phi}, \\ &\frac{1}{r\sin\theta} \frac{\partial A_{r}}{\partial\phi} - \frac{1}{r} \frac{\partial}{\partial r} (r A_{\phi}), \\ &\frac{1}{r} \frac{\partial}{\partial r} (r A_{\theta})- \frac{1}{r} \frac{\partial A_{r}}{\partial\theta} \biggr) . \end{aligned}$$
(11)

We then employ the DeVore gauge (DeVore, 2000) in which the radial component of the vector potential is identically zero: \(A_{r}=0\). This same gauge has also been used by Valori, Démoulin, and Pariat (2012), Amari et al. (2013), Moraitis et al. (2014), and Yeates and Hornig (2016).

The \(\theta\)- and \(\phi\)-components of Equation 11 can then be immediately integrated with the results

$$ A_{\phi}(r,\theta,\phi)=\frac{r_{0}}{r}A_{\phi}(r_{0}, \theta, \phi)-\frac{1}{r} \int_{r_{0}}^{r}\mathrm{d}r' r'B_{\theta}\bigl(r', \theta,\phi\bigr) $$
(12)

and

$$ A_{\theta}(r,\theta,\phi)=\frac{r_{0}}{r}A_{\theta}(r_{0}, \theta,\phi)+\frac{1}{r} \int_{r_{0}}^{r}\mathrm{d}r' r'B_{\phi}\bigl(r', \theta,\phi\bigr) , $$
(13)

respectively, and \(r_{0}\) is an arbitrary radius inside the volume. These can be written more compactly as

$$ \boldsymbol {A}(r,\theta,\phi)=\frac{1}{r} \biggl( r_{0} \boldsymbol {a}( \theta,\phi)+\hat{\boldsymbol {r}}\times \int_{r_{0}}^{r}\mathrm{d}r' r'\boldsymbol {B}\bigl(r',\theta,\phi\bigr) \biggr) , $$
(14)

where \(\boldsymbol {a}(\theta,\phi)= ( A_{\theta}(r_{0},\theta, \phi),A_{\phi}(r_{0},\theta,\phi) ) \) is a 2D integration vector that represents the vector potential on the surface \(r=r_{0}\).

Substituting Equation 14 in the radial component of Equation 11, and using the divergence-freeness of the field, we obtain

$$ \nabla_{\perp}\times\boldsymbol {a}= \frac{1}{r_{0}\sin\theta} \biggl( \frac{\partial}{\partial\theta} ( \sin\theta\alpha_{\phi} ) -\frac{\partial\alpha_{\theta}}{ \partial\phi} \biggr) =B_{r}(r_{0},\theta,\phi), $$
(15)

where the symbol “⊥” stands for the direction normal to the radial one. This relation can be thought of as a restriction on the possible choices for the remaining freedom in the gauge of \(\boldsymbol {A}\).

2.2.2 DeVore Simple Gauge

A first simple solution to Equation 15, which corresponds to a first family of gauges, is given by the relations

$$ \alpha_{\phi}(\theta,\phi)= \frac{cr_{0}}{\sin\theta} \int_{\theta_{0}}^{\theta}\mathrm{d}\theta'\sin \theta' B_{r}\bigl(r _{0},\theta ',\phi\bigr) $$
(16)

and

$$ \alpha_{\theta}(\theta,\phi)= -(1-c)r_{0}\sin\theta \int_{\phi _{0}}^{\phi}\mathrm{d}\phi' B_{r}\bigl(r_{0},\theta,\phi'\bigr), $$
(17)

where \(\theta_{0}\) and \(\phi_{0}\) are arbitrary angles, and \(c\in[0,1]\) is a constant, typically \(c=1/2\). The vector potential in this gauge is given by Equations 14, 16, and 17, and its calculation requires the computation of four 1D integrals. In our implementation here, the integrations are treated with the simple trapezoidal method, although more sophisticated methods can be envisioned. In the following we refer to this gauge family as the DeVore simple gauge (DVS).

2.2.3 DeVore Coulomb Gauge

An alternative family of gauges can be obtained when \(\boldsymbol {a}\), the vector potential on the surface \(r=r_{0}\), satisfies the Coulomb gauge: \(\nabla_{\perp}\cdot\boldsymbol {a}=0\). This is automatically fulfilled if \(\boldsymbol {a}\) is expressed through a 2D scalar function [\(u\)], as given by

$$ \boldsymbol {a}=\hat{\boldsymbol {r}}\times\nabla_{\perp}u= \frac{1}{r_{0}} \biggl( -\frac{1}{\sin\theta}\frac{\partial u}{ \partial\phi}, \frac{\partial u}{\partial\theta} \biggr) . $$
(18)

By substituting Equation 18 in Equation 15, we find that the function \(u\) satisfies the 2D Poisson equation \(\nabla_{ \perp}^{2}u=B_{r}(r_{0},\theta,\phi)\). This equation can be solved easily with the additional assumption of the Dirichlet boundary condition, \(u=0\), along the boundary of the \(r=r_{0}\) plane. The use of this boundary condition allows for a more generic \(B_{r}\)-distribution, such as a non-flux-balanced one, compared to the corresponding Neumann boundary condition, as follows from the uniqueness condition of the Poisson equation. In our particular implementation, we solved the Poisson equation with the aid of a FORTRAN routine from the FISHPACK library (Swarztrauber and Sweet, 1979).

The vector potential in this gauge family is given by Equations 14 and 18, and its calculation requires the computation of two 1D integrals and of a 2D Poisson equation. While Amari et al. (2013) called this gauge the restricted DeVore gauge, we denote it the DeVore Coulomb gauge (DVC), because, when applied to the potential field, this satisfies the Coulomb gauge in the whole volume (see Section 2.2 in Valori, Démoulin, and Pariat, 2012).

2.2.4 Reference Boundary Choice

In addition to the two gauges for the integration vector (DVS and DVC), there is also the choice of the location of the reference surface in the vector-potential calculation. We consider here only the two interesting cases, the bottom and the top surfaces of the volume, similarly to Equations 10 and 11 of Valori, Démoulin, and Pariat (2012), although other choices exist as well (see Section 2.2.3 of Valori et al., 2016). These cases are denoted by the letters “b” and “t”, respectively, and they follow the symbol of the gauge. A given vector potential can thus be in any of the four different gauges: DVSb, DVSt, DVCb, or DVCt.

The vector potential for the potential field can be obtained with the same method by just replacing \(\boldsymbol {B}\) with \(\boldsymbol {B}_{ \mathrm{p}}\) in the above relations. It can thus also be in four different gauges, and since in general the gauges of the two vector potentials are independent, there are 16 possible combinations in the calculation of helicity.

3 Validation

3.1 Test Datasets

The performance of the helicity calculation method was checked against the semi-analytical, force-free field solutions of Low and Lou (1990, hereafter LL fields). We simulated an active region (AR) with linear dimensions \({\approx}\, 200\,\mbox{--}\,250~\mbox{Mm}\) at a solar latitude of \({\pm}\, 30^{\circ}\), which translates into the angular dimensions \({\approx}\, 15\,\mbox{--}\,20^{\circ}\) on the Sun. The particular location of the synthetic AR is of course irrelevant in the computation of helicity. The precision of our method is only very marginally affected by the particular values of the domain. Nonetheless, we wish to work with a synthetic AR domain as close as possible to a realistic case. For this, we assumed the spherical wedge volume \(V=\{(r,\theta,\phi): r\in [700~\mbox{Mm}, 900~\mbox{Mm}],\theta\in[50^{\circ},70^{\circ}], \phi\in[10^{\circ},30^{\circ}]\}\) with height \({\approx}\, 200~\mbox{Mm}\) and the AR at the small side of the wedge. The volume was discretized by a uniform grid of size \(129\times129\times129\) grid points.

The usual parameters of the LL fields were also assumed, \(n=m=1\), while the source was placed at a depth of \({\approx}\, 30~\mbox{Mm}\) below the AR (or \(l=0.3\) in LL notation), and was rotated by the angle \(\phi=\pi/4\) with respect to the radial direction. A plot of the LL field, denoted hereafter as \(\boldsymbol {B}_{\mathrm{LL}}\), with some representative field lines is shown in Figure 1. In order to check the effect of resolution, we also used the same volume, but discretized by \(257\times257\times257\) grid points.

Figure 1
figure 1

Plot of the 1293-grid LL magnetic field that was used in the tests. Shown are the image of the radial component of the LL field on the photosphere with the designated gray scale and angular dimensions \(20^{\circ}\times20^{\circ}\), and a set of representative field lines up to the height of 200 Mm from the solar surface.

Full size image

The first step in estimating the helicity of \(\boldsymbol {B}_{ \mathrm{LL}}\) was to calculate its scalar potential \(\Phi_{ \mathrm{LL}}\), as described in Section 2. The corresponding potential field was obtained from the relation \(\boldsymbol {B}_{\mathrm{p},\mathrm{LL}}=\nabla\Phi_{\mathrm{LL}}\), where the numerical derivatives used are of second order inside \(V\), and on the boundary are given by Equation 8. The solenoidality of these magnetic fields is verified below.

3.2 Solenoidality Verification

The divergence-freeness of a magnetic field is quantified in three ways. The first is by the average fractional flux increase [\(\langle |f _{i}| \rangle \)] defined by Wheatland, Sturrock, and Roumeliotis (2000).

The second verification metric is the flux imbalance ratio [\(\epsilon_{\mathrm{flux}}\)]. This is defined by

$$ \epsilon_{\mathrm{flux}}= \frac{|\Phi^{+}-\Phi^{-}|}{\Phi ^{+}+\Phi^{-}} , $$
(19)

where \(\Phi^{+}\) and \(\Phi^{-}\) are the positively defined fluxes entering and leaving the volume through all of its boundaries, respectively. A highly flux-balanced field, indicating also a solenoidal field, corresponds to the limit \(\epsilon_{\mathrm{flux}}=0\), while the opposite holds for \(\epsilon_{\mathrm{flux}}=1\).

The third metric that we used relates to the magnetic energies. For each \(\boldsymbol {B}_{\mathrm{LL}}\) and \(\boldsymbol {B}_{\mathrm {p,LL}}\) at each resolution, we calculated its magnetic energy (in arbitrary units) as \(E=\int B^{2}\,\mathrm{d}V\) (cf. Table 1). By subtracting the magnetic energy of the potential field from the magnetic energy of the LL field, we obtained the free energy: \(E_{\mathrm{c}}\). Table 1 indicates that the free energy corresponds to \({\approx}\,26\)% of the total energy of the LL field, a value typical for LL fields, independently of the resolution. The solenoidality can finally be estimated thanks to the energy ratio \(E_{\mathrm{div}}/E\), with \(E_{\mathrm{div}}\) a pseudo-energy given by

$$ E_{\mathrm{div}}= \biggl\vert 2 \int_{V} \boldsymbol {B}_{\mathrm{p},\mathrm{LL}} \cdot( \boldsymbol {B}_{\mathrm{LL}}-\boldsymbol {B}_{\mathrm{p},\mathrm{LL}})\, \mathrm{d}V \biggr\vert . $$
(20)

This energy vanishes for perfectly solenoidal fields and quantifies the violation of Thompson’s theorem by non-purely solenoidal fields (Valori et al., 2013). This quantity is more widely used to estimate non-solenoidality (Pariat et al., 2015; Valori et al., 2016; Pariat et al., 2017; Polito et al., 2017). Table 1 shows that the low values of \(E_{\mathrm{div}}/E\) are again an indication of the good level of solenoidality and another proof of the validity of the LL field as a test field, since non-solenoidality was shown to be the strongest source of errors in helicity estimations (see Valori et al., 2016).

Table 1 Parameters for the input LL fields, and their corresponding potential fields.
Full size table

3.3 Vector-Potential Verification

The second main step in the volume-helicity calculation is computing the vector potentials. It is important to check the quality of the reconstruction of the vector potential, i.e. that the curl of the computed vector potential indeed corresponds to its source magnetic field. For this, we used two methods.

First, we directly compared the \(r\)-, \(\theta\)-, and \(\phi\)-components of the original fields [\(\boldsymbol {B}_{\mathrm{LL}}\) and \(\boldsymbol {B}_{\mathrm{p},\mathrm{LL}}\)] with their respective vector-potential-reconstructed magnetic fields: \(\nabla\times \boldsymbol {A}_{\mathrm{LL}}\) and \(\nabla\times\boldsymbol {A}_{ \mathrm{p,LL}}\). To compare the components, we computed their linear (Pearson) correlation coefficients, which are presented in Table 2.

Table 2 Metrics for the reconstruction of the magnetic field from the respective vector potential.
Full size table

In addition, we computed the vector-field comparison metrics given by Schrijver et al. (2006): the vector correlation [\(C_{\mathrm{vec}}\)], the Cauchy–Schwarz metric [\(C_{\mathrm{CS}}\)], the complement of the normalized vector error [\(E_{\mathrm{n}}'\)], the complement of the mean vector error [\(E_{\mathrm{m}}'\)] and the total energy normalized to that of the input field [\(\epsilon\)]. For two arbitrary vector fields, original [\(\boldsymbol {X}\)] and reconstructed [\(\boldsymbol {Y}\)], consisting of \(N\) points, these read

$$\begin{aligned} C_{\mathrm{vec}} = &\frac{{ \sum_{i} \boldsymbol {X_{i}}\cdot\boldsymbol {Y_{i}}}}{ ( { \sum_{i} |\boldsymbol {X_{i}}|^{2}}{ \sum_{i} |\boldsymbol {Y_{i}}|^{2}} ) ^{1/2}}, \end{aligned}$$
(21)
$$\begin{aligned} C_{\mathrm{CS}} = &\frac{1}{N}{ \sum _{i} \frac{\boldsymbol {X_{i}}\cdot\boldsymbol {Y_{i}}}{| \boldsymbol {X_{i}}| |\boldsymbol {Y_{i}}|}}, \end{aligned}$$
(22)
$$\begin{aligned} E_{\mathrm{n}}' = &1-\frac{{ \sum_{i} |\boldsymbol {X_{i}}-\boldsymbol {Y_{i}}|}}{{ \sum_{i} |\boldsymbol {X_{i}}|}}, \end{aligned}$$
(23)
$$\begin{aligned} E_{\mathrm{m}}' = &1-\frac{1}{N}{ \sum _{i} \frac{|\boldsymbol {X_{i}}-\boldsymbol {Y_{i}}|}{|\boldsymbol {X_{i}}|}}, \end{aligned}$$
(24)
$$\begin{aligned} \epsilon = &\frac{{ \sum_{i} |\boldsymbol {Y_{i}}|^{2}}}{{ \sum_{i} |\boldsymbol {X_{i}}|^{2}}} . \end{aligned}$$
(25)

All metrics indicate the good agreement of the two fields by values close to unity.

In Table 2 we present the values of these parameters for a few example reconstructions of the LL field, and separately, of the potential field. We performed different tests using the two different gauges discussed in Section 2.2, DVS and DVC; the two different spatial resolutions, 1293 and 2573; and/or the two different reference surfaces: bottom and top. As an example, consider the first row in Table 2, where the values correspond to the reconstruction of the LL field of \(129^{3}\) grid points with a vector potential in the simple DeVore gauge, and with the top surface as the reference surface for the integration.

Table 2 demonstrates that the correlation coefficients are all very close to one. The value for the \(r\)-component presents the weakest correlation since this component involves the greatest number of numerical operations. The values for Schrijver’s metrics also indicate that the reconstruction is excellent in all of the cases. We further note that the reconstruction in spherical coordinates has comparable accuracy to the corresponding one for the Cartesian case (Table 8 in Valori et al., 2016).

From the values of Table 2, we can draw a few conclusions. First, the differences for the two different spatial resolutions are very small for both \(\boldsymbol {B}_{\mathrm{LL}}\) and \(\boldsymbol {B} _{\mathrm{p},\mathrm{LL}}\), with the latter exhibiting slightly better metrics in the lower-resolution field. Second, the differences between the reconstructions performed with the DVS or the DVC gauges are practically nonexistent for \(\boldsymbol {B}_{\mathrm{LL}}\) and \(\boldsymbol {B}_{ \mathrm{p,LL}}\). We note here that the vector potentials in the DVC gauge satisfy the Coulomb gauge on the surface \(r=r_{0}\) to a high degree. This can be seen by taking the \(129^{3}\)-grid potential field as an example, where the absolute fractional flux increase of its vector potential in the DVCt gauge is \(\langle |f_{i}| \rangle =1.4 \times 10^{-7}\), a value comparable to the best-performing methods of Valori et al. (2016, Figure 7f).

The most important differences in the reconstruction metrics are found, however, between the top and bottom reference surfaces, mostly in the parameters \(E_{\mathrm{n}}'\) and \(E_{\mathrm{m}}'\), which are the most sensitive ones. We note that using the top boundary yields more precise results. This is a general characteristic of the helicity-computation methods based on the DeVore gauge and the properties of the data tested, as has been noted by Moraitis et al. (2014), Pariat et al. (2015), Valori et al. (2016). In solar-like datasets, the magnetic field at the top surface is weaker and smoother than the field at the bottom, and, as a result, the integrations involved in the vector-potential computation that start from the top surface are also smoother.

Additionally, the values of the metrics for the potential fields [\(\boldsymbol {B}_{\mathrm{p},\mathrm{LL}}\)] are, in general, slightly inferior to the respective values for \(\boldsymbol {B}_{\mathrm{LL}}\). This is to be expected since the potential field is derived from the LL field and thus carries any numerical errors in it.

As a final check, we computed the relative helicity as given by Equation 1 using all of the possible different gauge combinations for the vector potentials of \(\boldsymbol {B}_{\mathrm{LL}}\) and its potential fields. The helicity values produced for the \(129^{3}\)-grid fields are all very similar, ranging in \(-145.2\pm0.4\) (in arbitrary units), indicating that helicity is indeed independent of the chosen gauge up to a factor \(2\times10^{-3}\).

As a conclusion of this section, we can say that the developed helicity computation method in spherical coordinates performs extremely well. This is deduced from the high solenoidality of the constructed potential magnetic fields and also from the level of reproduction of the magnetic fields from the respective vector potentials. In addition, the method is computationally very efficient, as it requires only a few minutes to compute the helicity for the \(257^{3}\)-grid field on a commercial laptop.

4 Application to Solar Active Region 3D Extrapolated Magnetic Fields

After establishing that our method performs as expected on a semi-analytical magnetic field, we now apply it to typical magnetic-field data from a reconstructed solar active region. This will show the performance of our method in a more solar-like case, and it will also provide an opportunity of comparing our results with more approximate helicity calculations methods.

4.1 NLFF Field Model

We used a set of data-constrained nonlinear force-free field models of NOAA AR 11060 (SOL2010-04-08T02:35:00L110C176). They were constructed in order to topologically study this specific AR (Savcheva et al., 2016). All computations were performed in spherical coordinates.

The fields were produced by the flux-rope-insertion method (van Ballegooijen, 2004), which involves various intermediate steps that we briefly summarize here. First, a global potential magnetic field is computed from a low-resolution synoptic magnetogram. Then, a modified potential-field extrapolation is performed starting from a high-resolution magnetogram centered on the AR, and with lateral boundary conditions given by the global field. The relevant calculations are made directly with the vector potential [\(\boldsymbol {A}_{ \mathrm{p,MF}}\)] to ensure solenoidality of the respective magnetic field. This potential field [\(\boldsymbol {B}_{\mathrm{p,MF}}=\nabla \times\boldsymbol {A}_{\mathrm{p,MF}}\)] is then modified with two sources in the photosphere where the inserted flux rope is to be anchored.

The flux rope is inserted by modifying the initial vector potential with a combination of axial and poloidal flux. The model is then relaxed toward a force-free state using the magnetofrictional (MF) method. In the MF code, the vector potential [\(\boldsymbol {A}_{ \mathrm{MF}}\)] is again relaxed and not the magnetic field [\(\boldsymbol {B}_{\mathrm{MF}}= \nabla\times\boldsymbol {A}_{\mathrm{MF}}\)]. During the MF relaxation, \(\hat{\boldsymbol {n}}\cdot\boldsymbol {B}_{\mathrm{MF}}\) is held constant at the photospheric boundary; the other five boundaries are very far away from the AR core so that the field there is very well approximated by the potential field. The potential magnetic field and its respective vector potential remain constant and equal to their value at the initial instant during the MF process, as this is not a temporal evolution. The full details of the method used to produce the NLFF fields are described by Savcheva et al. (2016) and references therein.

A magnetic-field model is considered as stable if, after the relaxation, it has reached a force-free equilibrium where no residual Lorentz force is present, otherwise it is considered to be marginally stable or unstable. An unstable model is obtained from a stable model by adding slightly more axial flux to the stable inserted-flux-rope parameters. The parameters that we used here are the same as those used by Savcheva et al. (2016).

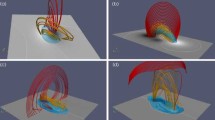
This marginally unstable NLFF model also leads to an “eruption” resembling a coronal mass ejection during the MF evolution of the field, as was demonstrated by Savcheva et al. (2016). The gradual expansion and elevation of the flux rope can also be inferred from the evolution of the field-line connectivity and of the flux-rope height that are shown in Figure 2. A data-constrained MHD simulation starting from a similar initial condition and proving that an unstable model obtained with the flux-rope insertion method is unstable as well in the MHD sense was performed by Kliem et al. (2013) and demonstrated a good correspondence with the observations.

Figure 2
figure 2

Evolution of the flux-rope morphology with iteration number. For the snapshots at 25,000 (top), 90,000 (middle), and 155,000 (bottom) iterations, the plots show a number of characteristic field lines overplotted on the horizontal cut of the current density at \(z=10~\mbox{Mm}\) (left), and the vertical cut of the current density along the blue line of the left plot (right). Spatial scales are in units of Mm.

Full size image

We used 38 snapshots of the magnetic-field evolution: three at very early stages at 0, 100, and 1000 iterations, and the remaining from 5000 to 175,000 iterations with a step of 5000 iterations. The magnetic field covered an area of \({\approx}\,40^{\circ}\times 40^{\circ}\) in the \(\theta\) – \(\phi\) plane, and it extended 805 Mm in the radial direction. The magnetic-field datacubes had the dimensions of \(385 \times 385 \times 385\) grid points. The grid in the \(\phi\)-direction was uniform with a step size of \(0.11^{\circ}\), while along the \(r\)- and \(\theta\)-directions, it was nonuniform. In the \(\theta\)-direction, the step size increased from \(0.08^{\circ}\) to \(0.11^{\circ}\) toward the Equator, while along \(r\), the step size increased from 1.4 Mm in the photosphere to 3 Mm in the uppermost level. The grid that we used here was structured in this way.

4.2 Results

In this section we compute the instantaneous value of helicity during the relaxation of the magnetic field with the MF method, using the method of this article, and also the approximate method based on Equation 2. The method of this article is denoted as the exact method since it makes no assumptions, it treats all boundaries appropriately, and it performs very well with the LL field, as we showed in the previous section.

4.2.1 Exact Method

To compute the magnetic helicity with the method of this article, we started from the magnetic field [\(\boldsymbol {B}_{\mathrm{MF}}\)], which is defined on a nonuniform grid, and we interpolated it to a uniform grid on the same volume. This is not a necessary step in general, but the current implementation of the method is more accurate with a uniform grid. A simple trilinear interpolation is sufficient to obtain similar levels of accuracy as in the LL case, as we show below.

From the interpolated magnetic field [\(\boldsymbol {B}_{\mathrm {DV}}\)] we computed the vector fields, \(\boldsymbol {B}_{\mathrm{p,DV}}\), \(\boldsymbol {A}_{\mathrm{DV}}\), and \(\boldsymbol {A}_{\mathrm {p,DV}}\), using the method described in Section 2. Note that the potential field was computed at each snapshot in order to take into account possible changes of \(\hat{\boldsymbol {n}}\cdot\boldsymbol {B}_{ \mathrm{DV}}\) caused by the interpolation from \(\boldsymbol {B}_{ \mathrm{MF}}\). The helicity computation that uses the method of this article is thus based on the relation

$$ H= \int_{V}\,\mathrm{d}V (\boldsymbol {A}_{\mathrm{DV}}+ \boldsymbol {A}_{ \mathrm{p,DV}})\cdot(\boldsymbol {B}_{\mathrm{DV}}- \boldsymbol {B}_{ \mathrm{p,DV}}). $$
(26)

The evolution of the magnetic helicity as computed with the exact method is shown in Figure 3. The helicity that we obtained is an increasing function of iteration number, after the first few snapshots of the flux-rope insertion, and it seems to saturate at a value a little above \({\approx}\,1.76\times10^{42}~\mbox{Mx}^{2}\). The increasing helicity evolution pattern is in contrast to the respective free-energy pattern, which decreases, as shown in Figure 8 of Savcheva et al. (2016), and it also contradicts the general trend between free energy and helicity (Tziotziou et al., 2014). Nevertheless, it is in line with the removal of negative helicity as the flux rope expands and subsequently erupts during the MF evolution.

Figure 3
figure 3

Evolution of relative magnetic helicity [\(H\)] during the MF relaxation as computed with the method of this article, Equation 26. Computations are made with three different gauge combinations for the vector potentials of the original and potential magnetic fields, shown in that order in the label.

Full size image

The level of gauge invariance is quite high, as can be deduced from the values of helicity computed with three different combinations of the DVSt and DVCt gauges for the vector potentials of the original and of the potential magnetic fields. The three different helicity curves of Figure 3 practically coincide, exhibiting differences \({\lesssim}\,0.2\)%.

The computed potential magnetic field is sufficiently solenoidal, as the average (over all snapshots) values for the metrics \(\langle |f_{i}| \rangle =3.0\times10^{-4}\) and \(\epsilon_{\mathrm{flux}} =3.5\times10^{-4}\) indicate. The average values of the reconstruction metrics for the vector potential \(\boldsymbol {A}_{\mathrm{DV}}\) (as in Table 2) for this case are all \({>}\,0.99\), except for \(E_{\mathrm{n}}'=0.97\), \(E_{\mathrm{m}}'=0.97\), and \(\epsilon=0.97\). Similarly, for \(\boldsymbol {A}_{\mathrm {p,DV}}\), they are \({>}\,0.98\), except for \(E_{\mathrm{n}}'=0.93\), \(E_{\mathrm{m}}'=0.90\), and \(\epsilon=1.03\). The vector-potential reconstructions are thus slightly inferior to those of the LL case, but they are still very good. Combined with the fact that the computed helicity is also gauge independent to a high degree, as Figure 3 shows, this leads to the conclusion that this can be considered as the actual AR helicity, and it further justifies the characterization of the method as exact.

4.2.2 Approximate Method

The second method that we used to compute helicity follows the reasoning of Bobra, van Ballegooijen, and DeLuca (2008), that is, it employs the definition of Equation 2. Furthermore, we used two different sets of vector fields in the computations. The first is the direct outcome of the MF code. The relation that we used in this case is

$$ H_{R}= \int_{V}\,\mathrm{d}V (\boldsymbol {A}_{\mathrm{MF}}\cdot \boldsymbol {B}_{\mathrm{MF}} - \boldsymbol {A}_{\mathrm {p,MF}}\cdot \boldsymbol {B}_{\mathrm{p,MF}})+ \int_{S}\,\mathrm{d}S \chi_{\mathrm{MF}} B_{\mathrm{MF},r}, $$
(27)

where all MF-related quantities are explicitly stated. The scalar quantity \(\chi_{\mathrm{MF}}\) at a point \(\mathcal{P}\) of the photospheric plane \(S\) is given by the line integral \(\chi_{ \mathrm{MF}}(\mathcal{P})=\int_{\mathcal{O}}^{\mathcal{P}} \mathrm{d} \boldsymbol {l}\cdot(\boldsymbol {A}_{\mathrm{MF}}-\boldsymbol {A}_{ \mathrm{p,MF}})\), where \(\mathcal{O}\) is a reference point on the same plane. We also note that the vector fields involved in Equation 27 are the original, uninterpolated ones, and that the potential field and its respective vector potential do not change during the relaxation. The MF code evolves \(\boldsymbol {A}_{\mathrm{MF}}\), but on the (coronal) boundary the condition \(\boldsymbol {A}_{\mathrm{MF}} \times\boldsymbol {A}_{\mathrm{p,MF}}=0\) is maintained valid at all times so that Equation 27 is as accurate as possible.

The second set of vector fields that we used in this approximate method is the set from the exact method. We used again the same relation, namely

$$ H_{R}'= \int_{V}\,\mathrm{d}V (\boldsymbol {A}_{\mathrm{DV}}\cdot \boldsymbol {B}_{\mathrm{DV}} - \boldsymbol {A}_{\mathrm {p,DV}}\cdot \boldsymbol {B}_{\mathrm{p,DV}})+ \int_{S}\,\mathrm{d}S \chi_{\mathrm{DV}} B_{\mathrm{DV},r}, $$
(28)

with \(\chi_{\mathrm{DV}}(\mathcal{P})=\int_{\mathcal{O}}^{\mathcal{P}} \mathrm{d}\boldsymbol {l}\cdot(\boldsymbol {A}_{\mathrm {DV}}-\boldsymbol {A} _{\mathrm{p,DV}})\). The evolution of helicity obtained with these two approximate methods is plotted in Figure 4, along with the result of the exact method in the DVSt–DVSt gauge combination.

Figure 4
figure 4

Evolution of relative magnetic helicity as computed with the method of this article [\(H\)] using Equation 26, and with the approximate ones \(H_{R}\) using Equation 27 and \(H_{R}'\) using Equation 28.

Full size image

We note that the pattern of the \(H_{R}\)-method is very similar to that of the exact method. The helicity values are on average 15% higher than those of the exact method, however. This difference is due to the limitations of the formulation of Equation 2 with respect to the finite-volume geometry used, as was pointed out in the Introduction. We see therefore that our helicity computation method improves, by the above designated percent, on the approximate method of Equation 2.

For the \(H_{R}'\)-method, we note that the general pattern of helicity evolution is similar to the other two methods. However, the helicity values obtained are (on average) higher by 55% than the exact ones, and by 35% than those of the \(H_{R}\)-method. This large difference is expected since the vector potentials of Equation 28 are in the DeVore gauge and they do not assume the condition \(H_{ \mathrm{mix}}=0\) that Equation 2 implies, since \(\boldsymbol {A}_{\mathrm{DV}}\times\boldsymbol {A}_{\mathrm {p},\mathrm{DV}}\neq0\) on the boundary. According also to the discussion in the Introduction, the relation of Equation 2 depends on the gauges chosen for the vector potentials, unless the bounding surface is a flux surface. The use of Equation 2 with vector potentials that do not respect its validity conditions can thus lead to differences in helicity on the order of 30 – 40%, at least in the case examined here.

We conclude that helicity calculations based on Equation 2 are problematic when using finite volumes (regardless of the coordinate system). The conditions of validity of Equation 2 are rarely true in practice, and so its use with finite-volume data should be avoided. Situations where it is safer to use this relation include, for example, the infinite-plane geometry originally used by Berger and Field (1984).

5 Discussion

A method for computing relative magnetic helicity in spherical geometry was presented in this article. The necessity for such a method stems from the fact that magnetic helicity is an important quantity with many applications in the solar context, and that the natural coordinate system for the Sun is the spherical one. The method developed treats the generic problem of computing helicity in a spherical volume, and it is thus superior to previous methods that either employed simplified conditions on the boundary for the magnetic fields and/or the vector potentials, or used approximations in the computations.

Testing of the developed method with semi-analytic NLFF field models showed that it works very well and has an accuracy that is similar to corresponding calculations in the Cartesian case. More specifically, the potential magnetic field produced by the method is highly divergence free, and the computed vector potentials also reproduce the respective magnetic fields to a high degree.

Additionally, from the application on a data-driven NLFF field model of a solar AR, we already see an improvement in the helicity values compared to approximate methods used in the past. The specific approximate method that we examined here has an important limitation. It assumes a certain choice for the gauge of the vector potentials, which is hard to enforce in finite volumes. As a result, the helicity values obtained with the different gauge choices can be quite different from each other and also from the method developed in this article.

In all cases where the magnetic field is represented in spherical geometry and it is known in the whole volume, such as in MHD simulations or NLFF field reconstructions, the method presented here is expected to give the most accurate estimation of the structure’s magnetic helicity, and it does this with minimal computational effort and resources.