1 Introduction

Magnetic helicity can be used to characterize complex, three-dimensional magnetic fields that are the result of, e.g., numerical simulations or nonlinear force-free field (NLFFF) extrapolations (see review of Berger 2003 and Démoulin, 2007, and references therein). Coronal magnetic helicity in particular is also derived by integrating in time the photospheric flux (see Démoulin and Pariat 2009 for a review).

Magnetic helicity must be carefully defined in order to be unequivocally employed. This is related to the available gauge freedom in the choice of the vector potential involved in its definition, which yields different helicity values unless the volume considered is bounded by flux surfaces. To overcome this limitation, Berger and Field (1984) and Finn and Antonsen (1985) introduced a magnetic helicity that is defined relative to a reference field with the same normal component on the boundaries of the volume considered: the relative magnetic helicity. Applying this concept to extrapolated photospheric magnetograms yields an estimation of the relative magnetic helicity in the semi-infinite half-volume above vector magnetograms that is derived by DeVore (2000).

However, in both numerical simulations and non-global photospheric magnetic-field extrapolations, the discretized volumes are always finite. The usual assumption that lateral and top boundaries do not influence the computation of the magnetic helicity is violated if, for instance, a significant amount of magnetic flux goes through lateral and top boundaries. This happens typically when important flux contributions exist close to the edge of the vector magnetograms or close to the boundaries in numerical simulations.

Progress in the generalization of helicity computations has been recently made by developing new methods that compute the relative magnetic helicity in finite volumes (Rudenko and Myshyakov 2011; Thalmann, Inhester, and Wiegelmann 2011; Seehafer and Kliem 2012). These methods are all based on the Coulomb gauge. Although the choice of the gauge is irrelevant for the relative magnetic-helicity value, it may heavily influence the practical computation. Indeed, all the preceding works, sharing the same choice for the gauge, offer solutions that are analytically complicated and/or computationally heavy.

In this article we present a fast, accurate, and easy-to-implement method of computing the relative magnetic helicity in a finite volume. In contrast to previous works, we exploit the gauge freedom by choosing one which, among other advantages, greatly simplifies the algebra and is trivial to implement exactly in numerical codes. The selected gauge – or, more exactly, family of gauges – only requires that one component of the vector potential vanishes. Therefore, as we demonstrate, our method is a direct extension of the work by DeVore (2000) to finite volumes. An application of this method has already been given by Valori et al. (2011).

The formalism that we develop also allows us to answer an important question: Can we meaningfully compare relative magnetic helicities of different magnetic fields, e.g. the relative magnetic helicity of a given dataset at different times? The basis of such a question is that, even if the discretization volume is the same, a different distribution of magnetic field on the boundaries will lead to different reference fields, and it is therefore not obvious that the values of helicities relative to these different reference fields are comparable with each other. A first example where this question is relevant is the comparison of the helicity content of the field of an active region before and after a major eruptive event, as was studied in Schrijver et al. (2008). A second example is the fast-changing magnetic field at small scales observed in forming active regions. Our study proves that the magnetic helicity values of two different active regions can be directly compared with each other.

Before proceeding with the exposition of our method, let us briefly recapitulate the definition and the main properties of the relative magnetic helicity needed in the rest of this article. The relative magnetic helicity of a field B=∇×A with respect to that of a reference field B p=∇×A p, in a volume \(\mathcal{V}\), is defined as (Finn and Antonsen 1985)

$$H = \int_{\mathcal{V}} ( {\mathbf{A}} + {\mathbf{A}} _{\mathrm {p}}) \cdot( {\mathbf{B}} - {\mathbf{B}} _{\mathrm {p}}) \, \mathrm {d}\mathcal{V} . $$
(1)

For general gauge transformations \(\tilde{ {\mathbf{A}} } = {\mathbf{A}} - {\mathbf{\nabla}} \Theta\) and \(\tilde{ {\mathbf{A}} }_{\mathrm{p}} = {\mathbf{A}} _{\mathrm {p}}- {\mathbf{\nabla}} \Psi\), the relative magnetic helicity becomes

$$\tilde{H} = H-\int_{\partial\mathcal{V}} \hat { {\mathbf{n}} }\cdot( {\mathbf{B}} - {\mathbf{B}} _{\mathrm {p}}) (\Theta+\Psi) \, \mathrm {d}\sigma\, +\int_{\mathcal{V}} (\Theta+\Psi ) {\mathbf{\nabla}} \cdot( {\mathbf{B}} - {\mathbf{B}} _{\mathrm {p}}) \, \mathrm {d}\mathcal{V} , $$
(2)

where \(\hat { {\mathbf{n}} }\) is the external normal to the surface \(\partial\mathcal {V}\) bounding the volume \(\mathcal{V}\), and dσ is the infinitesimal surface on \(\partial\mathcal{V}\). Since B and B p are solenoidal, the value of H is gauge-invariant for any pair of scalar fields (Θ, Ψ) if

$$(\hat { {\mathbf{n}} }\cdot {\mathbf{B}} )|_{\partial\mathcal{V}} = (\hat { {\mathbf{n}} }\cdot {\mathbf{B}} _{\mathrm {p}})|_{\partial\mathcal{V}}, $$
(3)

i.e., provided that B and B p have the same distribution of normal field on the boundaries of the volume \(\mathcal{V}\). Note that the invariance of the gauge under the above conditions does not require the gauges to be the same. In the following we employ the term helicity to refer to the relative magnetic helicity [H] defined in Equation (1).

The integral in Equation (1) can be divided into a contribution due only to B, one only to B p, and a mixed term

$$H=H_{\mathrm {B}}-H_{\mathrm {p}}+ H_{\mathrm {mix}}, $$
(4)

where

(5)

Simple vector transformations show that

$$H_{\mathrm {mix}}= \int_{\partial\mathcal{V}} \hat { {\mathbf{n}} }\cdot( {\mathbf{A}} {\mathbf{\times}} {\mathbf{A}} _{\mathrm {p}}) \,\mathrm {d}\sigma, $$
(6)

and, in the particular case that the reference field is potential [B p=∇ ϕ],

$$H_{\mathrm {p}}= \int_{\partial\mathcal{V}} \phi(\hat { {\mathbf{n}} }\cdot {\mathbf{A}} _{\mathrm {p}}) \, \mathrm {d}\sigma - \int_{\mathcal{V}} \phi( {\mathbf{\nabla}} \cdot {\mathbf{A}} _{\mathrm {p}}) \, \mathrm {d}\mathcal{V} . $$
(7)

For specific combinations of gauge and boundary conditions for A and A p, both H mix and H p vanish, and the helicity reduces to H=H B (see Sections 3.5 and 5).

H is gauge-invariant by definition as long as Equation (3) is satisfied. However, in order to practically compute the vector potentials we must specify their gauges. Analytical and numerical considerations often guide the choice of a particular pair of gauges to simplify the derivation of the vector potentials. Moreover, as we will show in Section 5, the choice of pertinent gauges can also clarify some physical properties of H. Therefore, the derivation of the vector potential [A] for a magnetic field [B] in a given volume \([\mathcal{V}]\) is the critical step for a proper computation of H. We split this task into different steps. In Section 2 we introduce the gauge that allows for a simple computation of vector potentials in a finite volume. Section 3 is devoted to the derivation of the formula for the computation of the helicity in a finite volume. In Section 4 our method and the method by DeVore (2000) are applied to an analytical solution of the force-free equation. Finally, the problem of comparing H of different magnetic fields is addressed in Section 5. Further applications and conclusions are discussed in Section 6.

2 Vector Potentials in the A z =0 Family of Gauges

For the computation of vector potentials we follow the method of DeVore (2000), but we apply it to a finite rectangular volume \(\mathcal{V}=[x_{1},x_{2}]\times[y_{1},y_{2}]\times [z_{1},z_{2}]\), rather than to the semi-infinite space z≥0. In the following we will focus the derivation along a privileged direction \([\hat { {\mathbf{z}} }]\). Note that our results are valid for every direction, and that the following derivations can be generalized by permutation of the axis of the Cartesian domain. The following derivation is also not restricted to Cartesian domains and can easily be generalized to other coordinate systems, e.g. to spherical coordinates.

2.1 General Derivation

Using the freedom in the choice of the gauge, let us consider a vector potential [A] such that

$$\hat { {\mathbf{z}} }\cdot {\mathbf{A}} =0 $$
(8)

everywhere in \(\mathcal{V}\). A direct integration of the x- and y-components of ∇×A=B in the interval [z 1;z] leads to

while the z-component of ∇×A=B gives a condition on the integration vector a≡(A x (x,y,z=z 1),A y (x,y,z=z 1),0), i.e.

$$0 = \partial_x a_{{y}}-\partial_ya_{{x}}-B_{z}(x,y,z=z_1) . $$
(9)

Any solution of Equation (9) can be used to write

$$ {\mathbf{A}} = {\mathbf{a}} -\hat { {\mathbf{z}} }\, {\mathbf{\times}} \int_{z_1}^{z} {\mathbf{B}} \, \mathrm {d}z' , $$
(10)

which is the desired expression for the vector potential [A] such that ∇×A=B in \(\mathcal{V}\).

An alternative expression for A can be obtained by integrating the x- and y-components of ∇×A=B in the interval [z;z 2], namely,

$$ {\mathbf{A}} = {\mathbf{b}} +\hat { {\mathbf{z}} }\, {\mathbf{\times}} \int_{z}^{z_2} {\mathbf{B}} \, \mathrm {d}z' , $$
(11)

where b≡(A x (x,y,z=z 2),A y (x,y,z=z 2),0) is any solution of

$$0=\partial_x b_{{y}}-\partial_yb_{{x}}-B_{z}(x,y,z=z_2) . $$
(12)

Equation (12) has the same form as Equation (9), but it is computed at z=z 2 rather than at z=z 1.

The relation between the two integration functions a and b is obtained imposing that Equations (10) and (11) represent the same vector potential, which leads to

$$ {\mathbf{a}} = {\mathbf{b}} + \hat { {\mathbf{z}} }\, {\mathbf{\times}} \int_{z_1}^{z_2} {\mathbf{B}} \, \mathrm {d}z' , $$
(13)

or equivalently,

$$ {\mathbf{A}} (x,y,z=z_1) = {\mathbf{A}} (x,y,z=z_2)+ \hat { {\mathbf{z}} }\, {\mathbf{\times}} \int_{z_1}^{z_2} {\mathbf{B}} \, \mathrm {d}z' . $$
(14)

This relation between the values of A at the opposite sides of \(\mathcal{V}\) in the z-direction is a consequence of the gauge employed and of the solenoidal property of B. It states that if, e.g., b is a solution of Equation (12), then a, as defined in Equation (13), is a solution of Equation (9). We can choose between the two equivalent representations of A, Equations (10) and (11), provided that we use Equation (13) to fix a in terms of b if we want to compare them.

2.2 Relation to the Coulomb Gauge

A gauge commonly used for helicity computation (cf. Section 1) is the Coulomb gauge

$$ {\mathbf{\nabla}} \cdot {\mathbf{A}} _{\mathrm{coulomb}} = 0 , $$
(15)

since it often simplifies analytical calculations (Berger 1988), although it may require considerable effort to be satisfied in numerical applications. The relation of Equation (8) to the Coulomb gauge is obtained by taking the divergence of Equation (10), yielding

$$ {\mathbf{\nabla}} \cdot {\mathbf{A}} = \partial_x a_{{x}}+\partial_ya_{{y}} + \int_{z_1}^{z} (\partial_x B_{y}-\partial_y B_{x})\, \mathrm {d}z' . $$
(16)

Hence, the gauge equation (8) reduces to the Coulomb gauge under two conditions: first, that a subset of solutions of Equation (9) satisfying the solenoidal condition in the horizontal plane is chosen, and, second, that the magnetic field has no electric current in the z-direction. An example of such a case is given in Section 5.

2.3 Gauge Freedom

The gauge equation (8) does not determine A entirely, since a solution of Equation (9) (or of Equation (12), depending on which form of A is used) must still be provided. We give an example of such a solution in Section 3.3. Even when a solution of Equation (9) is adopted, the gradient of an arbitrary function of x and y can be added to A, or equivalently to a (respectively, b). This does not change the formulations of A, as long as Equation (13) is satisfied, i.e. as long as the same gradient is added to b (respectively, a).

All of the previous relations are valid for any vector potential that satisfies Equation (8). In particular, if we use the same gauge condition for A p and for A, i.e. \(\hat { {\mathbf{z}} }\cdot {\mathbf{A}} _{\mathrm {p}}=0\), then Equations (9) – (14) can be equivalently written for A p and B p.

3 Computation of Helicity in a Finite Rectangular Volume

We consider practical cases where the solenoidal magnetic field [B] is given in a finite, three-dimensional rectangular grid discretizing \(\mathcal{V}\). To compute the gauge-invariant helicity using Equation (1) we must, first, fix a reference field [B p] such that Equation (3) is satisfied, and, second, compute the vector potentials A and A p that correspond to B and B p, respectively.

3.1 The Potential Field as Reference Field

Choosing the potential field as the reference one, Equation (3) can be satisfied by B p=∇ ϕ if the scalar potential ϕ(x,y,z) is the solution of the Laplace equation

$$\left \{ \begin{array}{l} \Delta\phi=0; \\({\partial\phi}/{\partial\hat{n}}) |_{\partial\mathcal{V}} =(\hat { {\mathbf{n}} }\cdot {\mathbf{B}} )|_{\partial\mathcal{V}},\end{array} \right . $$
(17)

where \(\partial\mathcal{V}\) represents all boundaries, not just the bottom one.

Our main purpose is to compute the helicity value in practical cases. Therefore, we simply assume a numerical solution of Equation (17). Since we ensure numerically that B and B p have the same distribution of normal field at the boundaries, the helicity defined in Equation (1) will lead to the same value for whatever gauges are used to compute A and A p; i.e. it will be gauge-invariant (provided that B and B p are solenoidal). Since Equation (17) can be solved numerically using standard methods (e.g. Press et al., 1992), we do not investigate this step any further.

3.2 Vector Potentials

In order to construct the vector potentials required for the computation of H, we proceed using the results of Section 2.1. First, we identify with the subscript “p” all quantities referring to the reference field B p (now chosen to be the potential-field solution of Equation (17)), and without subscript those referring to B. Second, although the gauge for A can be different from the one for A p, we choose the gauge introduced in Section 2.1 for both fields, i.e.

$$\hat { {\mathbf{z}} }\cdot {\mathbf{A}} =\hat { {\mathbf{z}} }\cdot {\mathbf{A}} _{\mathrm {p}}=0 . $$
(18)

Third, we need to choose one particular combination of Equation (10) and Equation (11) for A and A p among those allowed by the gauge invariance. As an example, let us choose both vector potentials in the form of Equation (11), i.e.

$$ {\mathbf{A}} _{\mathrm {p}}= {\mathbf{b}} _{\mathrm{p}}+\hat { {\mathbf{z}} }\, {\mathbf{\times}} \int_{z}^{z_2} {\mathbf{B}} _{\mathrm {p}}\, \mathrm {d}z' $$
(19)

for the potential field, where the integration vector b p≡(A p,x (x,y,z=z 2),A p,y (x,y,z=z 2),0) must satisfy

$$0 = \partial_x b_{\mathrm {p},y}- \partial_y b_{\mathrm {p},x}-B_{z}(x,y,z=z_2) ; $$
(20)

and

$$ {\mathbf{A}} = {\mathbf{b}} +\hat { {\mathbf{z}} }\, {\mathbf{\times}} \int_{z}^{z_2} {\mathbf{B}} \, \mathrm {d}z', $$
(21)

where b≡(A x (x,y,z=z 2),A y (x,y,z=z 2),0) obeys

$$0 = \partial_x b_{{y}} -\partial_yb_{{x}} -B_{z}(x,y,z=z_2) . $$
(22)

Note that b satisfies exactly the same Equation (20) as b p, since by construction B z (z=z 2)=B p,z (z=z 2) from Equation (3), but they need not be the same: the two differ in general for a solution of the associated homogenous problem (i.e. by a gradient of a function of x and y).

As mentioned above, A p (respectively A) could also be written equivalently in terms of a p (respectively a) from Equation (10), as in Equation (33) in Section 3.5.

3.3 Example of a Practical Gauge

To proceed further in the calculation of H, we must specify solutions to Equations (20) and (22), which is equivalent to saying that we must specify our gauge further. For simplicity, we consider a particular case where b and b p are chosen to be equal. The consequence of this choice is that writing Equation (14) for both a and a p and imposing A(x,y,z=z 2)=A p(x,y,z=z 2) yields

$$ {\mathbf{a}} - {\mathbf{a}} _{\mathrm{p}}= {\mathbf{A}} (x,y,z=z_1)- {\mathbf{A}} _{\mathrm {p}}(x,y,z=z_1) = \hat { {\mathbf{z}} }\, {\mathbf{\times}} \int_{z_1}^{z_2}( {\mathbf{B}} - {\mathbf{B}} _{\mathrm {p}}) \, \mathrm {d}z' , $$
(23)

i.e. fixing the relation of the constant at the top boundary also imposes a relation between the values of the two vector fields at the bottom boundary.

Next, we need to specify a particular solution for \({\mathbf{b}} = {\mathbf{b}} _{\mathrm{p}}\equiv \bar { {\mathbf{b}} }\), where we introduced the symbol \(\bar { {\mathbf{b}} }\) to distinguish the particular gauge defined here from the more general case of Section 3.2. A simple choice for \(\bar { {\mathbf{b}} }\) that satisfies Equations (20) and (22) is

(24)
(25)

which completely determines A p and A from Equations (19) and (21). All required fields are then specified, and the helicity can be computed directly from Equation (1).

3.4 Contributions to the Helicity Integral

In this section we illustrate the properties of the helicity integral equation (1) for the gauge of Equation (18), in the general case of finite volumes. Let us consider the decomposition of the helicity integral as given by Equations (6) and (7). Using Equation (16) for the potential field, one obtains ∇⋅A p=∇⋅a p, which can be used to write Equation (7) as

$$H_{\mathrm {p}}= \int_{\partial_{\mathrm{lat}} \mathcal{V}} \phi (\hat { {\mathbf{n}} }\cdot {\mathbf{A}} _{\mathrm {p}}) \, \mathrm {d}\sigma -\int_{\mathcal{V}} \phi ( {\mathbf{\nabla}} \cdot {\mathbf{a}} _{\mathrm{p}}) \,\mathrm {d}\mathcal{V} , $$
(26)

where the first term on the right-hand side is computed on the lateral boundaries \(\partial_{\mathrm{lat}} \mathcal{V}\) of \(\partial\mathcal {V}\), while the second one involves the horizontal divergence ∇⋅a p=∂ x a p,x +∂ y a p,y . Within the freedom of gauge, the integration function a p satisfying Equation (9) can be chosen to be solenoidal so that the second integral vanishes (see Section 5 for an example of such a case). However,

$$H_{\mathrm {p}}=\int_{\partial_{\mathrm{lat}} \mathcal{V}} \phi (\hat { {\mathbf{n}} }\cdot {\mathbf{A}} _{\mathrm {p}})\, \mathrm {d}\sigma $$
(27)

will generally be non-null because of the finiteness of ϕ and A p at the lateral boundaries.

Due to the gauge equation (18), H mix in Equation (6) has contributions only at the bottom and top boundaries. At the bottom (respectively, top) boundary, A and A p are equal to a and a p (respectively, b and b p), respectively, and we can write Equation (6) directly as

$$H_{\mathrm {mix}}= \int_{x_1}^{x_2} \int _{y_1}^{y_2} \ \hat{ {\mathbf{z}} } \cdot\bigl[( {\mathbf{b}} {\mathbf{\times}} {\mathbf{b}} _{\mathrm{p}})-( {\mathbf{a}} {\mathbf{\times}} {\mathbf{a}} _{\mathrm{p}}) \bigr] \, \mathrm {d}x\,\mathrm {d}y , $$
(28)

where we used the fact that \(\hat { {\mathbf{n}} }=-\hat{ {\mathbf{z}} }\) at the bottom boundary (z=z 1) and \(\hat { {\mathbf{n}} }=\hat{ {\mathbf{z}} }\) at the top one (z=z 2).

As discussed in Section 2.3, Equation (18) does not fully prescribe A and A p. Therefore, we are free to add additional conditions in order to link the boundary values of A and A p and simplify the expression of H mix. A possible additional constraint is

$$ {\mathbf{a}} = {\mathbf{a}} _{\mathrm{p}}\quad\Longleftrightarrow\quad {\mathbf{A}} (x,y,z=z_1)= {\mathbf{A}} _{\mathrm {p}}(x,y,z=z_1) , $$
(29)

which is the complementary case of Equation (23) considered in Section 3.3. Similarly as in that case, from Equation (13) the condition of Equation (29) implies a specific link between b and b p, namely

$$ {\mathbf{b}} - {\mathbf{b}} _{\mathrm{p}}= - \hat { {\mathbf{z}} }\, {\mathbf{\times}} \int _{z_1}^{z_2} ( {\mathbf{B}} - {\mathbf{B}} _{\mathrm {p}}) \, \mathrm {d}z' , $$
(30)

from which we have

$$H_{\mathrm {mix}}= \int_{x_1}^{x_2} \int _{y_1}^{y_2} {\mathbf{b}} _{\mathrm{p}}\cdot \biggl( \int _{z_1}^{z_2} ( {\mathbf{B}} - {\mathbf{B}} _{\mathrm {p}}) \, \mathrm {d}z' \biggr)\, \mathrm {d}x'\,\mathrm {d}y' . $$
(31)

The latter expression clearly shows that H mix is, in general, nonzero.

In conclusion, our computation of the helicity requires the use of the complete helicity integral, Equation (1), since H mix and H p are not, in general, vanishing. It is only in specific cases, such as in a half-space (see Section 3.5) or with a very specific selection of the gauge (see Section 5), that H can be reduced to the simplified form \(H_{\mathrm {B}}=\int {\mathbf{A}} \cdot {\mathbf{B}} \, \mathrm {d}\mathcal{V}\).

3.5 The DeVore Limit

In this section we show that the solution in DeVore (2000) is a particular case of the preceding derivation. The computation of helicity by DeVore (2000) differs from our derivations in three aspects:

  1. i)

    \(\mathcal{V}\) is the half-space \(\tilde{\mathcal{V}}=\{z \geq z_{1}\}\), with z 1=0 in DeVore (while we consider a finite domain);

  2. ii)

    in DeVore the scalar potential ϕ is given by the Green function solution of the Laplace equation in \(\tilde{\mathcal{V}}\). In practice, this means assuming that the vertical magnetic field at z=z 1 is negligible outside the effective domain of computation (we relax this constraint by solving the Laplace equation with \(\hat { {\mathbf{n}} }\cdot {\mathbf{B}} _{\mathrm {p}}=\hat { {\mathbf{n}} }\cdot {\mathbf{B}} \) at all boundaries, Equation (17));

  3. iii)

    the vector potentials A and A p are equal at z=z 1 in DeVore (this is not necessary in our formulation).

Let us start by choosing for A and A p the same forms as employed by DeVore (2000), i.e.

(32)
(33)

By taking the limit z 2→∞ we have B p(z 2→∞)=0, so Equation (12) has no source term and b p=0 can be taken as its solution. Therefore, we obtain

$$ {\mathbf{A}} _{\mathrm {p}}=\hat { {\mathbf{z}} }\, {\mathbf{\times}} \int_{z}^{\infty} {\mathbf{B}} _{\mathrm {p}}\, \mathrm {d}z' , $$
(34)

which is equivalent to Equation (4) of DeVore (2000). In this limit, the gauge for the potential field reduces to the Coulomb gauge (see Section 2.2).

Let us now consider A: the assumption iii) translates in our formalism into a=a p. Using Equation (13) in the limit b p→0, we have

$$ {\mathbf{a}} = {\mathbf{a}} _{\mathrm{p}}= \hat { {\mathbf{z}} }\, {\mathbf{\times}} \int_{z_1}^{\infty} {\mathbf{B}} _{\mathrm {p}}\, \mathrm {d}z' = {\mathbf{A}} _{\mathrm {p}}(x,y,z=z_1) , $$
(35)

and, therefore,

$$ {\mathbf{A}} = {\mathbf{A}} _{\mathrm {p}}(x,y,z=z_1) -\hat { {\mathbf{z}} }\, {\mathbf{\times}} \int_{z_1}^{z} {\mathbf{B}} \, \mathrm {d}z' , $$
(36)

which is the same as Equation (6) in DeVore (2000). Note that for A the gauge \(\hat { {\mathbf{z}} }\cdot {\mathbf{A}} =0\) is not equivalent to the Coulomb gauge.

Let us now show how assumptions i) and iii) also simplify two of the helicity integrals of Equation (5). First, iii), i.e. a=a p, implies that the helicity of the mixed term [H mix] is given by Equation (31). Since b p(z 2→∞)=0, H mix vanishes in this limit. Second, Equation (35) implies that a p is solenoidal; then the helicity of the potential field H p is given by Equation (27). Since by iii) the lateral contributions are computed at infinity where ϕ→0, then H p also vanishes, and the helicity integral reduces to H=H B as in DeVore (2000).

Note that in practical applications of the method of DeVore (2000) summarized in this section, the grid will not cover the whole half-space \(\tilde{\mathcal{V}}=\{z \geq z_{1}\}\). The field must then be sufficiently weak at the top and lateral boundaries for a correct computation of the helicity. The effect of the violation of this implicit requirement in the method of DeVore (2000) is analyzed in Section 4.3.

4 Numerical Tests

In this section we apply our helicity computation to the model of an active region magnetic field derived by Titov and Démoulin (1999; hereafter TD).

4.1 The Test Field

The TD equilibrium is an approximate solution of the force-free equations that represents an arched, line-tied flux rope embedded in a sheared potential field of arcade topology. This equilibrium was employed in several CME- and topology-related studies (e.g. Roussev et al. 2003; Török and Kliem 2005; Kliem and Török 2006; Titov 2007; Török et al. 2011; Kliem, Rust, and Seehafer 2011).

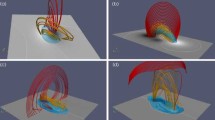
The particular configuration employed here (hereafter B TD) is defined by the same parameters of the “Low_HFT” case discussed by Valori et al. (2010), except that signs were changed so as to have a mirror image of that equilibrium with positive helicity. Unlike the original formulation by Titov and Démoulin (1999), the magnetic field decreases in all directions moving away from the flux rope. Representative field lines depicting the flux rope and the surrounding potential field are shown in the left panels of Figure 1.

Figure 1
figure 1

Left: Selected field lines of the B TD field belonging to the flux rope (red) and to the surrounding potential field (green), in projection (top) and perspective (bottom) views. Right: Iso-contours of \(B^{\mathrm{TD}}_{z}(z=0)\). The full discretized volume in x and y is shown. In the z-direction the volume reaches z=16. In all panels the white continuous line is the polarity-inversion line.

Full size image

The discretized volume is \(\mathcal{V}_{\mathrm{d}}=[-12, 12] \times[-20, 20]\times[0, 16]\) with uniform resolution Δ=0.12 in all directions. Lengths and magnetic field are normalized such that the field strength is unity at the apex of the torus axis, located at z=1. (This is actually only approximately correct; a more precise explanation of the normalization can be found in Valori et al. (2010).) Note that the distribution of the magnetic field at the bottom boundary (z=z 1, see right panel in Figure 1) is perfectly flux balanced (as it is at the top boundary, z=z 2), while there is a significant net flux going through the left (x=x 1) and right (x=x 2) lateral boundaries of \(\mathcal{V}_{\mathrm{d}}\). The relatively strong field in the x-direction can be understood in terms of the far-field approximation of the current ring: at large distances, the field is approximately that of a magnetic dipole oriented along the positive x-axis.

4.2 Computation of Integrals

The computation of vector potentials as described in Section 2 requires evaluating integrals of the type \(F(z)=\int_{z_{1}}^{z} \ f(t) \, \mathrm {d}t\), as in Equation (10). F(z) must satisfy ∂ z F(z)=f(z) numerically; i.e. it must satisfy the numerical formulation of the Fundamental Theorem of Integral Calculus. Assuming that second-order central differences are used for taking derivatives, this can be obtained by using the recurrence formulae

(37)

where F(z)=F(z 1+kΔ)≡F(k) with k=0,1,2,…,(n z −1), and Δ is the uniform spatial resolution in z. The value F(1) is fixed assuming that the first-order forward derivative is used when ∂ z F(0) is taken.

A similar expression can be derived for \(G(z)=\int_{z}^{z_{2}} \ f(t) \,\mathrm {d}t\) used in Equation (11), and the relations F(k)=G(0)−G(k) and G(k)=F(n z −1)−F(k) allow us to write one as a function of the other. Practically, it is advisable to choose the formulation of the integral with F or G according to where f is smoother, since this will minimize the inaccuracies in the one-sided formula employed in the computation of F(1) (respectively, G(n z −2)). Still, using a second- or a third-order forward formula rather than the first-order one suggested above typically changes the results reported below by less than 1 %.

Such a recursive formula ensures that the theorem is fulfilled in a numerical sense up to roundoff errors, e.g. that B=∇×A in the second-order central difference discretization (if ∇⋅B=0 numerically in the same discretization).

4.3 Dependence of Helicity Values on the Volume, and Comparison with DeVore’s Method

In order to study the dependence of the helicity on the considered volume, and in particular the differences between the half-space and the finite-volume computations, we now consider several examples of subvolumes of \(\mathcal{V}_{\mathrm{d}}\).

The finite-volume formulae of Section 3 are defined for the computation in \(\mathcal{V}_{\mathrm{d}}\), as well as in any of its subvolumes. Therefore, we simply refer to the value of helicity computed as described in Sections 3.1 – 3.3 as the finite-volume helicity [H FV]. In particular, the gauge obtained by specifying \(\bar { {\mathbf{b}} }\) as in Equations (24) and (25) is employed in this section.

On the other hand, the half-space formulae of Section 3.5, i.e. the method of DeVore (2000), can be applied only to the entire half-space. Of course, this is not possible in practical cases, since numerical domains are always finite. Therefore, we compute the required potential field [B p] restricting the input vertical field to the considered subdomain of \(\mathcal{V}_{\mathrm{d}}\), and we refer to the value of helicity computed using Equations (34), (36) as the DeVore helicity [H D].

We emphasize that DeVore’s method is not questioned here. What is tested and compared with our method is its application to practical cases that unavoidably violate the assumptions under which DeVore’s method is derived.

Changing the integration volume has different consequences for the finite-volume method and for the DeVore method. In the first case, the effective values of the field at the boundaries are used to recalculate the potential field. Therefore, the potential field is as close as possible to B, in the sense that it will reflect to some extent the scaling properties of B with distance. However, in DeVore’s method, the potential field is determined only by the sources at z=z 1 and does not depend on the value of B on the five other boundaries of the domain.

4.3.1 Subvolumes of Different Heights

Let us first consider volumes that have the same extension in x and y but differ in height. We take the largest extension in the horizontal directions, so that the flux concentrations are far away from the edges at z=z 1. The left panel in Figure 2 shows that H FV becomes constant as soon as the top boundary moves out of the volume occupied by the flux rope, i.e. as soon as it moves into a volume where the field is potential. Since the reference potential field scales “by construction” approximately as B with height, and since the nonlinear field is concentrated in the neighborhood of the center of the bottom boundary, it is not surprising that the helicity stops increasing in the upper part of the volume.

Figure 2
figure 2

Comparison of helicity values for B TD, as a function of the z-position of the top boundary of the computational volume \(\mathcal{V}_{\mathrm{d}}\), using DeVore’s (dashes) and the finite-volume (black solid line) methods, and their ratio (red solid line). The two panels refer to symmetric (left) and nonsymmetric (right) domains in x and y. The location of the twisted flux rope is indicated in orange.

Full size image

In contrast, H D increases with height for the whole explored range of altitudes of the top boundary. In the proximity of the flux rope the difference in the helicity computed with the two methods is larger than 40 %, and it is still 4 % at a height that is about ten times the height of the flux rope. This residual difference at large heights is due to the fact that the lateral boundaries are at a large but finite distance: there is still significant flux through them. However, there is an unmistakable trend for the two methods to give the same value in the limit of \(\mathcal{V}_{\mathrm{d}}\) going to the half-space, in agreement with our results in Section 3.5.

When the DeVore method is used, changing the height of the top boundary does not change the potential field that is used for the computation of H D, but only the volume of it that is considered in Equation (34). Thus, it is not sufficient that the field is merely potential at the lateral boundaries for the DeVore’s method to give an approximately correct value of the helicity when applied to finite volumes.

The behavior illustrated in the left panel of Figure 2 is not a consequence of the symmetry of the employed equilibrium. Indeed, a very similar one is found if subdomains that are nonsymmetric in the x- and y-directions are considered, as the right panel of Figure 2 shows. In this case both curves show a slightly smaller helicity content due to the smaller volume, but are otherwise very similar to the case in the left panel.

4.3.2 Subvolumes of Different Widths

We consider here subvolumes that differ for the position of the lateral boundaries. The main difference from the cases in Section 4.3.1 is that here, by also restricting the domain at z=z 1, we also modify the sources of the potential fields for DeVore’s method.

We first consider subvolumes differing for the position of the right lateral boundary (at x=x 2, see left panel in Figure 3). The relative difference between the two methods stays at 4 % as long as the right boundary does not reach a distance that is about three times the minor radius of the flux rope, although it does not significantly increase until it touches the flux rope itself.

Figure 3
figure 3

Left: Comparison of helicity values for B TD, as a function of the position of the right boundary of the computational volume \(\mathcal{V}_{\mathrm{d}}\), using DeVore’s (dashes) and the finite-volume (black solid line) methods, and their ratio (red solid line). Right: Same as in left panel but for different positions of the back boundary.

Full size image

A similar behavior is found for subvolumes differing in the location of the back boundary (at y=y 2), as can be seen in the right panel of Figure 3. Also, in this case, the relative difference between the two methods starts to increase from the 4 % value for a position of the back boundary that is about twice the size of the flux rope in the y-direction.

We finally consider two cases that are more likely to occur in applications: in the first case the volume of the field is changed symmetrically on all lateral sides; in the second case the volume is changed by progressively shifting toward the center only the back and the right boundaries (nonsymmetric case). The resulting helicity values for the symmetric and nonsymmetric cases are shown in the left and right panels, respectively, of Figure 4. In both cases, the subvolumes have the same aspect ratio L x /L y as \(\mathcal{V}_{\mathrm{d}}\), whereas the top boundary is kept at a fixed position (z 2=12).

Figure 4
figure 4

Comparison of helicity values for B TD, as a function of the position of the back boundary of the computational volume \(\mathcal {V}_{\mathrm{d}}\), using DeVore’s (dashes) and the finite-volume (black solid line) methods, and their ratio (red solid line). For each subvolume, only the position of the back boundary is given as reference, while the other boundaries are placed as follows. Left: the front boundary is placed symmetrically at −y; the right and left boundaries are placed at ± yL x /L y (symmetric case). Right: the front and left boundaries are kept at the fixed position at y=−19 and x=−12, respectively, and the right boundary is placed at x=yL x /L y (asymmetric case).

Full size image

Figure 4 shows that in the symmetric case the effect of closer boundaries is stronger than in the asymmetric one, and it also starts at larger distances. This happens because the volumes in the two cases are very different: in the symmetric case the flux rope is always at the center between the four lateral boundaries, while in the asymmetric case only one of the two boundaries may get very close to it.

In conclusion, we verified that the helicity computation can be heavily affected by the considered volume. The finite-volume method, while agreeing with DeVore’s method if the boundaries of the computational volume are placed far away from the non-potential field, yields values of helicity that are typically higher (respectively, smaller) than DeVore’s method at large (respectively, short) distances from the flux rope (but see Figure 2 for counter-examples).

The difference in the computed helicity values between the two methods rises very sharply close to the flux rope once the boundaries are within a distance between two and three times the flux rope size. However, this is different from the dependence on the top boundary, which seems to be more sensitive for the computation of helicity: the two methods provide a similar value only when the top boundary is at an altitude larger than ten times the flux rope’s height. Obviously, such scaling considerations depend on the scaling properties of the TD equilibrium that we have adopted as a test field.

4.3.3 Contributions to the Helicity Integral

Let us now consider the different contributions, H B, H mix, and H P, to the helicity integral of the finite-volume case, defined by Equation (5) (see also Section 3.4). The left panel in Figure 5 shows that the main contribution to the helicity comes from the mixed term [H mix] and in second place from H B, whereas the contribution of the potential field is entirely negligible. The importance of the H mix term results from the approximate orthogonality of the potential field and the field generated by the current ring, and hence of their vector potentials, at the left and right boundaries (see Equation (6)).

Figure 5
figure 5

Contributions to the helicity integral in H FV as a function of the z-position of the top boundary (left, cf. with the left panel of Figure 2), and of the back boundary in the symmetric case (right, cf. the left panel of Figure 4) of the computational volume \(\mathcal{V}_{\mathrm{d}}\).

Full size image

The relative contributions to the helicity integrals are largely independent of the particular subvolume of \(\mathcal{V}_{\mathrm{d}}\) that is employed, as the right panel of Figure 5 shows in a second example.

4.3.4 Large Field-of-View Potential Field for H D

There are situations where it is possible to compute the potential field in a much wider volume than is available for the helicity computation. This typically occurs when the vertical magnetic field (required for the computation of the potential field) is available for the entire solar disk, while the nonlinear coronal magnetic field, computed using nonlinear extrapolation, is available only above an active region. In this situation, the general wisdom is to compute the potential field in the largest available volume, and to use that field for the calculation of H D in the smaller subvolume.

Figure 6 shows how the results of Section 4.3.2 (plotted in red solid line) are modified when the potential field (as described in Section 3.5) is computed using the largest available volume [\(\mathcal{V}_{\mathrm{d}}\)] whereas the required integrations for H D extend only to the considered subdomain of \(\mathcal{V}_{\mathrm{d}}\).

Figure 6
figure 6

Comparison of H D/H FV for B TD, as a function of the position of the back boundary of the computational volume \(\mathcal {V}_{\mathrm{d}}\), for two different ways of computing the potential field entering H D: using the entire available field of view (blue dashes) or only the subvolume fraction (solid red line). Red lines are the same as in Figure 4. For each subvolume, only the position of the back boundary is given as reference, while the other boundaries are placed as follows. Left: the front boundary is placed symmetrically at − y; the right and left boundaries are placed at ± yL x /L y (symmetric case). Right: the front and left boundaries are kept at the fixed position at y=− 19 and x=− 12, respectively, and the right boundary is placed at x=yL x /L y (asymmetric case).

Full size image

Unexpectedly, for small volumes (i.e. when the boundaries are in the proximity of the flux rope), the relative difference between H FV and H D is larger if the whole available domain \(\mathcal {V}_{\mathrm{d}}\) is used to compute B p in the H D formula, rather than if only the subvolume is considered to compute B p (Section 3.1). For instance, close to the flux rope in the symmetric case (left panel of Figure 6), the ratio H D/H FV for sources from the entire domain \(\mathcal{V}_{\mathrm{d}}\) (blue dashes) has a value that is almost twice that for the subdomain sources (red curve). A similar behavior, although less marked, is also clearly visible in the asymmetric case (right panel). The different ways of computing the potential field for H D are relevant only if the considered subvolume is smaller than the source distribution at z=z 1. In Figure 6 this is clearly indicated by the overlap of the curves for larger volumes.

5 Comparison of the Helicity of Different Magnetic Fields

Let us consider two magnetic fields that have a different distribution of normal field at the boundaries. According to Equation (1), the helicity values of such fields are defined with respect to distinct potential fields. A question naturally arises: Is it meaningful to compare such helicity values, even if they are not defined with respect to the same reference field?

In order to answer that question, let us consider the expression for the vector potential of the potential field written in the form of Equation (10). As we have shown in Section 2.3, we are free to modify the solution a satisfying Equation (9) by the gradient of a scalar function of x and y. Moreover, as we already pointed out, we are allowed to fix independently the gauges of A and A p as long as Equation (3) is satisfied. In this section we use these freedoms to impose an additional constraint on A p such that the corresponding helicity [H p] vanishes. If this is possible, then the helicity of different fields can be computed with respect to potential fields that are indeed different, but that all have the same value of magnetic helicity (i.e. zero). Consequently, different helicity values can be meaningfully compared with each other, in much the same way as values of the free energy of different fields can be compared with each other.

In order to fix such constraints, we require that the helicity of the potential field [B p=∇ ϕ] as defined by Equation (5) and computed by Equation (26)

(38)

vanishes. The last term on the right-hand side of Equation (38) vanishes if the vector function a p, in addition to the corresponding Equation (9) for the potential field, also satisfies the condition

$$ {\mathbf{\nabla}} \cdot {\mathbf{a}} _{\mathrm{p}}= \partial_x a_{\mathrm{p},x}+\partial_y a_{\mathrm{p},y}=0 . $$
(39)

Incidentally, we note that, since the field is potential, this condition implies that the gauge of A p reduces in this case to the Coulomb gauge (as discussed in Section 2.2).

Both conditions of Equations (9) and (39) can be satisfied by introducing an auxiliary function u(x,y) and a constant (i.e., space-independent) vector \((\tilde {a}_{\mathrm {p},x}; \tilde {a}_{\mathrm {p},y})\) such that

$$a_{\mathrm{p},x}=\tilde {a}_{\mathrm {p},x}-\partial_y u, \qquad a_{\mathrm{p},y}=\tilde {a}_{\mathrm {p},y}+\partial_x u, $$
(40)

from which Equation (9) is transformed into

$$\bigl(\partial_x^2 +\partial_y^2\bigr)u = B_{\mathrm {p},z}(x,y,z=z_1) . $$
(41)

The two-dimensional Poisson problem in Equation (41) can be solved numerically with, for instance, Dirichlet boundary conditions, u=0, on \(\partial\mathcal{V}|_{z=z_{1}}\). Substituting Equation (40) into Equation (10) (written for the potential field), then A p into Equation (38), we obtain

$$H_{\mathrm {p}}= \alpha \tilde {a}_{\mathrm {p},x}+ \beta \tilde {a}_{\mathrm {p},y}+ \gamma , $$
(42)

with

(43)

i.e. where α, β, and γ are combinations of surface terms computed at the lateral boundaries of \(\mathcal{V}\).

If the magnetic configuration is antisymmetric, e.g. in the x-direction, then α=0, and to require that H p=0 implies that \(\tilde {a}_{\mathrm {p},y}=-\,\gamma/\beta\). However, in general, H p=0 implies an under-determined linear equation. A possible choice for the solution is

$$\tilde {a}_{\mathrm {p},x}=-\frac{\gamma}{2\alpha}; \qquad \tilde {a}_{\mathrm {p},y}=-\frac{\gamma }{2\beta} . $$
(44)

Equation (44) provides the desired gauge transformation such that H p=0, for any field B p.

As an additional consideration, note that with a similar derivation one can write H mix, defined by Equation (5), as a linear function of \(\tilde {a}_{\mathrm {p},x}\) and \(\tilde {a}_{\mathrm {p},y}\):

$$H_{\mathrm {mix}}= \epsilon \tilde {a}_{\mathrm {p},x}+ \zeta \tilde {a}_{\mathrm {p},y}+ \eta . $$
(45)

The coefficients ϵ, ζ, and η can also be expressed as combinations of surface terms computed at the lateral boundaries as in Equations (43). Thus, in general, Equations (42) and (45) define a linear system that determines \(\tilde {a}_{\mathrm {p},x}\) and \(\tilde {a}_{\mathrm {p},y}\) such that H p=0 and H mix=0.

In summary, we prove above that it is possible to define the helicity relative to a reference potential field that has zero helicity. Therefore, values of H computed for different fields can be directly compared with each other. Moreover, we have indicated how a particular choice of the gauge can also cancel the term H mix, which implies that H can be computed simply as H=H B. While the formal expression of H B is simpler than that of H, its practical use requires the computation of several integrals (Equation (43) and equivalent ones to cancel H mix); hence, this approach is not recommended for practical computations. Of course, since the helicity defined by Equation (1) is gauge-invariant, the same value is obtained in both cases.

6 Conclusions

In this article we present a fast, accurate, and easy-to-implement algorithm for the computation of the relative magnetic helicity in a finite rectangular domain. The derivation can easily be generalized to other coordinate systems, e.g. spherical coordinates. Unlike other work in the literature, but similarly to the well-known method for the half-space by DeVore (2000), we adopt a gauge that greatly simplifies the expressions for the vector potentials; we impose the vanishing of their vertical component: \(\hat { {\mathbf{z}} }\cdot {\mathbf{A}} =0\). The method reproduces the formula in DeVore (2000) if the whole half-space is considered.

This type of gauge, unlike the Coulomb gauge, is of trivial enforcement in numerical setups and is numerically exact. Because of its possible applications, in Section 2 we derive and discuss the properties of this gauge \([\hat { {\mathbf{z}} }\cdot {\mathbf{A}} =0]\) in a finite volume. We show how the computation of the vector potential reduces to the computation of a one-dimensional integral, which is very efficient and accurate, provided that some numerical details are correctly incorporated (Section 4.2).

The gauge-invariant helicity [H] in the finite rectangular volume \(\mathcal{V}\) can then be directly computed from its defining formula, Equation (1), using

  1. i)

    the x- and y-components of the potential field B p, derived from the numerical solution of the three-dimensional Laplace equation, Equation (17);

  2. ii)

    the relevant two-dimensional integration functions defining a=a p (or b=b p) as one-dimensional integrals (as, e.g., in Equations (24) and (25));

  3. iii)

    the x- and y-components of the vector potentials A and A p, as one-dimensional direct integrations according to Equations (19), (21).

The main numerical effort required by these steps is the solution of a single three-dimensional Laplace equation. By comparison with similar lists in Rudenko and Myshyakov (2011) and Thalmann, Inhester, and Wiegelmann (2011), it becomes evident how the method that we propose here is far more efficient computationally. The typical running time for the computation of the finite-volume helicity for a grid of ≈ 2003 nodes (equivalent to the one used in this article) is just a few seconds on a standard laptop.

To address the relevance of the helicity computation in finite volumes, we compare our results with the standard DeVore computation using the TD field as a test. It is confirmed that the two methods agree for volumes that are large enough, but differences become increasingly greater the closer the boundaries are to the flux rope. With respect to the size of the flux rope, a factor three in the horizontal directions and even a factor ten in the vertical one are required in order to reduce the difference between the two methods below a few percent.

In the practical computation of the magnetic helicity, two basic approaches are possible. The first is to employ H in its general form as given by Equation (1), and to use the gauge freedom to derive the vector potentials in a way that is simple for the application considered. This is the approach that we adopt in Sections 3 and 4. The second possibility is to use the simplified form H B, which is obtained using very specific gauges for A and A p. Such an approach is used in Section 5 to prove that, using the residual freedom in the gauge \(\hat { {\mathbf{z}} }\cdot {\mathbf{A}} =0\), the relative helicity of the reference potential field can be set equal to zero. This defines a reference value, zero, for the helicity of magnetic fields with different normal field components \([\hat { {\mathbf{n}} }\cdot {\mathbf{B}} ]\) at the boundaries. Therefore, the value of helicity obtained for distinct magnetic fields having different distributions of \(\hat { {\mathbf{n}} }\cdot {\mathbf{B}} \) at the boundaries can be directly compared with each other, very much as their free energies can. In particular, it is meaningful to follow the coronal helicity of an active region as its photospheric field evolves.

The study of helicity and energy evolution of an active region provides complementary information. Unlike the magnetic energy, helicity is also well conserved by resistive magnetic reconnection. Therefore, H is useful to relate, for instance, the source active region of a CME to its interplanetary counterpart (magnetic cloud, e.g., Nakwacki et al., 2011).