1 Introduction

According to economic theory, insurance markets emerge in response to the willingness of risk-averse consumers to pay a premium to be protected from costly random events. Low voluntary demand for insurance covering flood (Dixon et al. 2006; Browne & Hoyt 2000) and earthquake (Palm & Hodgson 1992) damages, often in the presence of discounted premiums, however, brings to question whether households are insensitive to rare events.

Increasing numbers of homeowners moving to high-risk areas (Kunreuther & Michel-Kerjan 2009) and a greater frequency of extreme weather events (Pielke & Downton 2000) have led to increased damages resulting from natural disasters over the past few decades. This happens as federal and state exposure to disaster risks rises through subsidized insurance programs and a growing market share of state-run residual insurance markets in high-risk states such as Florida (Kunreuther & Michel-Kerjan 2009; Kunreuther & Pauly 2006). A better understanding of how consumers react to repeated low probability risks can contribute to important policy discussions about the proper level of government subsidy and relief funding (Shavell 2014), and the optimal structure of insurance contracts (Michel-Kerjan & Kunreuther 2011).

Whether market behavior such as low insurance takeup results from households’ perceptions of risks is difficult to judge using only observational data from the field. Some of the reasons for this include the difficulty in estimating the actual risk faced by individual households, the confounding effect that regulatory institutions have on market outcomes, and the difficulty in determining the causal relationships between risk perceptions and risk mitigation. This paper avoids some of these obstacles by studying risk-taking behavior in a controlled laboratory experiment that uses real monetary risks to motivate thoughtful decision-making.

Subjects in the experiment owned multiple digital “properties” for one or more “decision periods” and were told that the value of one of these properties at the end of a given decision period would determine their final payment for participating. Each property had a chance of experiencing a “disaster” that could eliminate either half or all of a property’s value, resulting in the subject earning a significantly lower final payment. Given the information they received about each property, subjects chose whether to purchase insurance coverage by paying a premium that was deducted from their final payment. Subjects in the experiment chose whether to purchase insurance while facing a “one-shot” risk and made a sequence of insurance decisions while facing a repeated risk. In both settings, subjects learned about the risk through experience. However, in the repeated choice setting, subjects learned directly from experience because each experienced outcome had a potential impact on one’s final income; in the one-shot setting subjects learned indirectly by observing a set of past outcomes generated by the risk. I use several different modeling approaches to understand how subjects learned about and respond to risks across different choice environments.

Economists traditionally use models of rational belief learning in conjunction with expected utility theory (EUT) to understand consumer behavior in the presence of uncertainty. An EUT decision-maker responds to hazards by first forming beliefs about the probability that the hazard will occur and then weighing the expected benefits of reducing hazard exposure against the cost of taking protective measures. EUT combines naturally with models of belief formation that fall under headings such as rational expectations, adaptive expectations, or Bayesian updating. These common approaches share the assumption that individuals rationally integrate all available information and act on beliefs that minimize expected prediction error.

Although this is often a reasonable and parsimonious approach to understanding market behavior, its predictions are sometimes at odds with empirical studies of insurance demand. Browne et al. (2015), for instance, compare the demand for flood insurance and bicycle theft insurance using data from a German insurer and find that there is an unexplained preference toward insuring against the higher-frequency, lower-consequence bike thefts even after conditioning on the expected loss of both hazards. The preference to insure against higher-frequency hazards runs counter to EUT, which typically assumes that individuals are risk-averse and therefore should have greater aversion to low-probability, high-consequence hazards.

There is also evidence that housing markets fail to capitalize flood risks into prices of properties that reside in 500-year floodplains and that 100-year floodplains respond disproportionately to recent floods that occurred within the preceding decade (Atreya et al. 2015; Bin & Landry 2013). Insensitivity to low-probability flood risks may be a consequence of households being uninformed about the hazard probabilities and other details that are required to properly identify the costs and benefits of risk mitigation (Palm & Hodgson 1992; Kunreuther & Slovic 1978). These are just some of the reasons one might expect households to fail to live up to the predictions of a rational theory of decision-making.

Prospect theory (PT) is a competing model for decision-making under risk that has in many cases proven to be more robust than EUT in explaining decisions made by subjects in laboratory environments. PT emerged out of commonly observed patterns documented in a series of choice experiments (Kahneman & Tversky 1979; Tversky & Kahneman 1992). One important finding supported by PT is that subjects in laboratory experiments tend to overweight low-probability risks. If these findings generalize, then we would expect insurance takeup for low-probability risks to exceed insurance takeup for high-probability ones.

More recent laboratory studies, however, show that the pattern of overweighting low probabilities observed in the original PT choice experiments occurs only if subjects learn about risky prospects from description. In Kahneman & Tversky (1979) subjects made a series of choices between two risky prospects, prospect A and prospect B. For every one of these decisions, subjects received a complete description of the risk associated with each prospect (example: “Choose between A: $6,000 with 0.45 probability or B: $3,000 with 0.90 probability). While decisions made in this setting (from description) produced evidence that subjects overweight low-probability risks, Hertwig et al. (2004), Barron & Erev (2003), and Hertwig & Erev (2009) show that this pattern reverses when subjects instead learn about risks from experience.

These experiments studied decisions made from experience by observing how subjects behaved as they learned about risk by sampling random outcomes from unknown prospects— prospects for which subjects had no prior knowledge of the underlying probabilities. Subjects in Barron and Erev’s experiment made repeated decisions about whether to be paid from one of two unknown prospects. After each choice, subjects observed the random payment generated by each prospect and used that information to inform their next choice. Hertwig et al.’s experiment allowed subjects to randomly sample outcomes from each prospect before deciding which one to select to count for payment. While Barron and Erev’s experiment studied learning in a repeated choice setting, Hertwig et al. studied learning by observing one-shot decisions. In both settings, subjects underweighted low-probability risks compared with high-probability ones. The contrast between these findings and the overweighting of low probabilities observed in the PT experiments is commonly referred to as the “experience-description gap.”

The experiment reported in this paper documents only decisions made from experience: subjects made insurance choices based on an observed sequence of disasters. Because subjects did not make comparable decisions from description and they faced only relatively low-probability risks, the experiment is not a proper test of the experience-description gap. It instead focuses on identifying specific features of the learning process that uniquely influence decisions from experience and, perhaps, explain why individuals underweight low probability risks in this setting. The features I examine most closely are (1) attention to the recency of outcomes, (2) differences in interpretation of direct versus indirect experience, (3) misinterpretation of random outcomes using the representative heuristic, and (4) the tendency to repeat prior choices.

Table 1 classifies three environments in which researchers typically study decision-making under risk; it also shows which of these are included in the current study and the responses to low-probability risks observed in prior studies pertaining to each environment. The experiment reported here does include some element of description (in addition to experience) in that subjects received some information about the risk before observing a random sample of outcomes. This feature is shared by an experiment reported by Jessup et al. (2008), who find that presenting prior information to subjects makes them more sensitive to low-probability risks in early decision periods, though underweighting nevertheless persists in later decision periods.

Table 1 How people respond to low-probability (LP) risk in different environments
Full size table

There are some existing studies that draw a similar comparison between one-shot and repeated choices. Erev et al. (2010) and Hertwig & Erev (2009) both document consistent underweighting of low-probability risks across one-shot and repeated choice environments. Erev et al. (2010) present results from a competition to determine which model offers the best out of sample predictions of behavior in an experiment where subjects chose among risky prospects in all three of the environments outlined in Table 1. They discover that a stochastic version of PT offers the best predictions for decisions made from description and a weighted combination of several different heuristic decision rules gives the best predictions for decisions made from experience. In a similar study, Hau et al. (2008) compare model predictions for decisions made from experience, giving special attention to heuristics subjects may use for responding to repeated risks. They find that the most successful predictions come from a two-stage version of PT and a maximax decision heuristic in which the decision-maker simply selects the risky prospect with the most favorable experienced outcome.

The current study focuses primarily on models that fit into the Bayesian expected utility framework because these sorts of models serve as the foundation for the majority of economic analysis used to inform policy. I combine Bayesian learning models with a constant-relative-risk-aversion (CRRA) utility function to predict subjects’ choices. I propose several modifications of the Bayesian model that are motivated by either empirical regularities or potentially fruitful theoretical hypotheses. Each modification nests the standard Bayesian model as a special case. Beyond simply determining which decision model provides the best statistical fit to subjects’ behavior, I use the models to interpret how decisions and risk preferences are affected by the choice environment.

The focus on modeling risk taking in a repeated exposure setting is what distinguishes this study from most previous experiments on insurance takeup. Examples of studies that examine insurance choice in descriptive settings are Slovic et al. (1977) and Laury et al. (2009). Interestingly, Laury et al. (2009) find that subjects in their experiment preferred to insure against low-probability risks. This is perhaps a manifestation of the experience-description gap, as participants in an experienced risk insurance experiment reported in Ganderton et al. (2000) did the opposite by insuring more against high-probability risks. Other experiments that examine insurance choices in an experienced risk setting include Shafran (2011) and Meyer (2012). The study by Meyer finds that recent losses are responsible for reductions in risk taking, particularly if losses were unprotected. Subjects in Shafran’s experiment engaged in greater risk taking for low-probability, high-consequence hazards than for high-probability, low-consequence hazards with the same expected outcome. Shafran also finds that recent losses were negatively correlated with subjects’ risk taking in subsequent periods even though prior losses did not convey any information about the underlying risk.

Subjects in the current study reduced their risk taking by purchasing insurance more often following disasters, though model estimates show that subjects weighted observed outcomes proportionately whether or not they occurred recently. There is no evidence that subjects exhibited recency bias, holding an irrational belief that more recent events were more informative; increases in insurance takeup immediately following a loss were proportional to the increase one would expect from a Bayesian expected utility maximizer. There is some evidence, however, that subjects weighted directly experienced outcomes more heavily than those experienced indirectly. Unexplained autocorrelation in subjects’ choices, called inertia, also predicted decisions in the repeated choice environment. Subjects were risk-averse on average, though they appear to have been less risk-averse in the repeated choice environment than in the one-shot setting. In Section 3.2.7 I discuss how the lower revealed risk aversion in the repeated choice portion of the experiment could be a consequence of inertia across choices. I conclude by discussing insights for public policy in Section 6.

2 Experiment design

The experiment took place in a computer lab, where subjects interacted with a web-based interface that was designed using Qualtrics. Subjects made a total of 39 decisions about whether to buy insurance, reported their beliefs about the probability of a disaster before each decision, and also made a series of choices used to determine their individual risk preferences. At the start of the experiment, subjects learned that their final payment would be calculated based on one of three tasks: the Decision Task, the Guess Task, or the Lottery Task. The Decision Task payment was based on a randomly generated disaster outcome for a randomly selected decision period and the subject’s choice of insurance coverage. The Guess Task rewarded subjects for the accuracy of their reported beliefs that a disaster would occur during a given decision period. The Lottery Task generated a random or fixed payment based on a subject’s stated preference for a risky payment versus fixed payment.

The experiment was divided into three segments. The first two segments, the One-shot round and the Repeat round, each contained a series of decision periods in which subjects decided whether to buy insurance and predicted the likelihood of a disaster occurring. The insurance premium varied across subjects: subjects faced either a low premium of $2.25 (actuarially fair), a medium premium of $4.50, or a high premium of $7.50. In the One-shot round, subjects made decisions and predictions without receiving feedback so that there was no possibility of learning from past choices. In the Repeat round, subjects received feedback about past outcomes associated with each choice. The third segment of the experiment, the Lottery round, had subjects make a series of decisions about whether to accept a lottery or a fixed payment. The results from the Lottery round do not apply directly to research questions posed in this article and will instead be discussed in a companion paper.

2.1 One-shot round

At the start of the One-shot round, subjects received instruction that they would own eight different “digital properties,” each of which was worth $30. Each property had either a high (15%) or a low (5%) risk of experiencing a disaster each year. Each year was equivalent to a single decision period. Subjects owned each property for only one year, so they made a total of eight decisions in the One-shot round. Subjects knew that each property could either be high-risk or low-risk, but did not know for certain the risk associated with each. If a disaster occurred, subjects were told that the value of the property would be reduced to either $15 or $0 with equal probability. For each of the eight properties, subjects viewed a 19-year disaster history generated by the risk associated with that property. These histories were randomly determined prior to the experiment (see Table 5 in the Appendix for a complete list).

Given the uncertainty about risk, subjects could use the information conveyed by the disaster history to infer the probability of a disaster in the current year—year 20. They used a slider bar to indicate their approximation of the probability that a disaster would occur in year 20 and could receive as much as $4 and as little as $0 reward depending on the accuracy of their approximation. Instructions for guessing rewards are available in the Online Appendix and were adopted from the quadratic scoring rule described in Offerman & Sonnemans (2001). These guesses served as a measure of subjects’ risk perceptions.

Each period’s Decision Task income was calculated as the value of the property at the end of the current year, subject to a randomly generated disaster outcome based on the property’s risk. Subjects had the option to buy insurance that would fully refund any losses incurred from a potential disaster. The premium payment for insurance would be deducted from the $30 income generated by the property. Figure 3 in the Appendix shows an example of the decision screen displayed in the One-shot round.

Subjects received no immediate feedback about outcomes associated with their properties during the One-shot round. If one of the properties of this round was selected to count for final payment, subjects would learn the outcome only at the very end of the session, prior to receiving payment.

2.2 Repeat round

During the Repeat round, subjects owned a single property, labeled their “Matched Property,” for a total of 50 years.Footnote 1 Subjects earned $30 in rental income each year from their Matched Property. A disaster had the same effect, insurance had the same price, and correct risk approximations were rewarded the same as in the One-shot round. Each year corresponded to a decision period; however, subjects could not purchase insurance until after year 19. The first 19 years followed one of the predetermined sequences listed in Table 5.Footnote 2 The outcome for each subsequent year was determined immediately following the subject’s decision, generated randomly according to the Matched Property’s underlying risk. The Matched Property had the same risk for all 50 years, and as in the One-shot round, this risk was either high (15%) or low (5%).

The reason for removing the option to insure for the first 19 periods was to generate a direct comparison of period 20 decisions between rounds. While in the One-shot round the first 19 outcomes were merely observed as a sampled history, subjects directly experienced these 19 outcomes during the Repeat round as each disaster affected the income generated by their Matched Properties. This comparison is important for identifying differences in the effect of direct versus indirect experience, which I discuss in Section 3.2.3.

Figure 4 in the Appendix gives an example of a decision screen subjects encountered in the Repeat round. Each year the history table updated to include a log of past disaster outcomes and income earned. There was also a dynamic bar chart indicating the cumulative losses from past disasters and insurance payments. A key feature of the Repeat round is that it provided subjects feedback regarding their past decisions and random disaster outcomes. Subjects were instructed that each of these experienced outcomes had a chance to be selected to count for their final payment and that the probability of their property experiencing a disaster in a given year was independent from outcomes in previous years. From a Bayesian perspective, the frequency of previous disasters conveyed information about the future expected value of buying insurance.

2.3 Subject comprehension

At the start of each session, subjects completed a series of tasks to ensure that they each had a concrete understanding of the experimental environment. First, the experiment began by asking three separate comprehension questions designed to test the participant’s understanding of probabilities (questions are listed in the Online Appendix). The experiment platform prevented subjects from starting the experiment until they answered all three comprehension questions correctly. All subjects successfully completed the test without issue. Subjects also received two handouts, each containing tables and charts illustrating how their payments would be calculated for the Decision Task and Guess Task. This information was also displayed on the web-based platform at the beginning of the experiment; the handouts served as a supplemental reference. Before beginning the One-shot round, subjects completed a practice round where the relationship among their insurance choices, their approximations, and their final payment was explained in detail.

2.4 Survey

At the end of the experiment subjects answered a three-question cognitive reflection test (CRT), a measure found to be correlated with IQ and intertemporal preferences (Toplak et al. 2011). They also reported sex and college major.

3 Theory

3.1 Insurance choice

Each period in the experiment a participant earns income of size W and faces a chance of experiencing a wealth-destroying disaster with probability p. A participant’s future income is defined over a two-state vector (W, W − L), where L denotes the losses incurred by a disaster. The subject can insure by paying a premium r to fully indemnify against any losses caused by a disaster. An insured subject’s future income is W − r in both states.

According to EUT, people make insurance choices that maximize their expected utility U—a value representing one’s level of satisfaction. People receive positive utility from income so that d U/d W > 0; and they are risk-averse under the assumption that d 2 U/d W 2 < 0. The expected utility from choosing not to insure is \(E[U(W;\theta )|c=0]=(1-\hat {p})U(W;\theta )+\hat {p} U(W-L;\theta )\), where \(\hat {p}\) denotes one’s belief about the probability a disaster will occur, 𝜃 denotes one’s risk preferences, and c : c ∈ {0, 1} represents the decision of whether or not to insure. Expected utility from choosing to insure is E[U(W; 𝜃)|c = 1] = U(W − r; 𝜃). A subject in the experiment maximizes utility by choosing to insure whenever

$$U(W - r;\theta) \ge E[U(W;\theta)|c=0].$$

To allow for some unobserved variation in subjects’ preferences, this model can be modified by applying an i.i.d. error term ε to each decision, so that the probability that a subject insures is q : q = P r(U(W − r; 𝜃) − E[U(W; 𝜃|c = 0] ≥ ε). The probability that a subject i insures at time t is then expressed by

$$q_{it} = \int I\left[U(W-r;\theta) - E_{it}\left[U(W;\theta)|c_{it}=0\right] \ge \varepsilon \right] dG(\varepsilon),$$

where I[⋅] is an indicator equaling 1 when its argument is true and G(⋅) is the random distribution of unobserved utility.

Subjects who are risk-averse buy insurance to reduce their exposure to negative income shocks L, and may choose to do so even if premiums exceed the expected payout of the policy. However, the fact that U is increasing in income implies that subjects are less likely to insure when it is priced with a higher premium. EUT also predicts that subjects insure more frequently as \(\hat {p}\) increases because this (1) increases the variance of income when uninsured and (2) raises the expected payout of the insurance. The effect of increased income variance applies only to persons who are risk-averse, though the increase in expected payout acts as an incentive to buy insurance regardless of risk preferences.

3.2 Dynamics in risk taking

Choosing whether to insure is essentially making a choice between a risky prospect and a safe one. When subjects make insurance decisions from description, they possess full information about the distribution of the risk, implying that \(\hat {p}=p\).Footnote 3 By assuming an EUT framework, one can therefore infer subjects’ underlying risk preferences by observing the insurance choices they make from description. Insurance choices made from experience, however, may be influenced by incomplete knowledge of the probabilities associated with a risky prospect: \(\hat {p} \neq p\). When epistemological concerns arise, choices are likely to reflect variation in the interpretation of experiences as well as variation in risk-preferences.

3.2.1 Bayesian beliefs - \(\hat {p}_{B}\)

If subjects are perfectly rational then they consider the set of experienced outcomes and calculate \(\hat {p}\) using Bayes’ rule. Bayes’ rule states that for two random events A and B, P r(A) ⋅ P r(A|B) = P r(B) ⋅ P r(B|A). The Bayesian posterior probability of a disaster D occurring at period t is \(\hat {p}_{B}(t) = \hat {p}_{B}^{H}(t) \cdot H_{p} + (1-\hat {p}_{B}^{H}(t))\cdot L_{p}\), where H p and L p represent the high and low probability risks of disaster. These probabilities are weighted by the Bayesian belief at period t that one is either high-risk \(\hat {p}_{B}^{H}(t)\) or low-risk \(1-\hat {p}_{B}^{H}(t)\). Each period these beliefs update by applying Bayes’ rule to calculate the probability of existing in the high-risk state conditional on the observed history of experienced outcomes. After some simplification, this yields the following rule for calculating the probability of disaster:

$$ \hat{p}_{B}(t) = L_{p} + \frac{(H_{p} - L_{p})}{1 + (L_{p}/H_{p})^{y_{1t}}((1-L_{p})/(1-H_{p}))^{y_{0t}}}. $$
(1)

The observed or experienced outcomes in period t are represented by a variable D t , which equals one if a disaster occurs at period t and zero otherwise. These outcomes enter into the Bayesian updating function through the variables y 1t and y 0t , which are calculated as follows:

$$ y_{1t} = \sum\limits_{\tau=1}^{t-1} D_{\tau}, $$
(2)
$$ y_{0t} = t - 1 - y_{1t}. $$
(3)

In the experiment the values for L p and H p are 0.05 and 0.15 and both states are equally likely prior to any experience. The Bayesian probability therefore begins at \(\hat {p}_{B}(0)=0.1\) and subsequently updates for each of the 50 periods of the Repeat round, or it is applied to the 19 sampled outcomes revealed prior to decisions during the One-shot round. Though this particular updating rule is tailored to the simple environment encountered by subjects in the experiment where one may be either high-risk or low-risk, the Bayesian framework applies analogously under more realistic conditions in which risk types are more numerous or even continuous.

It is optimal for subjects to apply Bayes’ rule when updating beliefs based on experienced outcomes because \(\hat {p}_{B}\) minimizes the expected squared error between one’s perceived risk and one’s true risk: \(\hat {p}_{B} \in \min _{\hat {p}} E[(\hat {p} - p)^{2}]\). Subjects may, however, make systematic errors when applying Bayes’ rule to update beliefs based on experience. In the remainder of this section I consider three different modifications of the Bayesian updating function that account for possible errors in belief updating. I also discuss a modification to the utility function that yields novel predictions for decisions made from experience.

3.2.2 Memory - \(\hat {p}_{M}\)

Individuals evaluating risky prospects from experience may choose to interpret an event differently depending on how recently it occurred. One possibility is that people place a greater weight on more recent events. The effect of biased attention toward recent events on risk mitigation is explored by Volkman-Wise (2015), who presents a model of demand for catastrophe insurance in which buyers overweight posterior probabilities that are representative of recent catastrophic outcomes. Buyers in the model tend to overvalue insurance immediately following a rare catastrophic event but tend to undervalue it before the event occurs. For rarely occurring events such as severe floods or earthquakes, disproportionately weighting more recent outcomes therefore has the overall effect of diminishing risk mitigation efforts and insurance takeup.

There is some empirical evidence that households overweight recent events when deciding whether to buy flood insurance. Using annual market data from the National Flood Insurance Program (NFIP), Gallagher (2014) reports that flood insurance penetration within a given county increases 8 to 9% in response to a recent Presidential Disaster Declaration for a flood affecting that county. The impact of these floods on demand, however, quickly diminishes over time and disappears completely after about 10 years. By comparing this observed behavior with predictions from a Bayesian learning model, Gallagher concludes that the transient nature of these demand shocks makes sense only if homeowners disproportionately place a greater weight on more recent events. Lack of hazard experience over a prolonged period may conversely reduce insurance coverage. NFIP records from Florida show that of the 985,000 flood insurance policies-in-force in the year 2000, only about 370,000 were still in force by 2005, as homeowners allowed their policies to lapse (Michel-Kerjan & Kousky 2010). These empirical findings lend some credence to the idea that recency bias is responsible for an underweighting of low-probability risks.

To accommodate the possibility that subjects weight a disaster event differently depending on its recency, I modify the Bayesian learning function to include a behavioral parameter ϕ, representing a subject’s memory of past events. The memory parameter ϕ enters into the calculation of y 1t and y 0t to generate the belief \(\hat {p}_{M}(t)\). Let the modified values of y be denoted \(\tilde {y}_{t1}\) and \(\tilde {y}_{t0}\), such that

$$ \tilde{y}_{1t} = \sum\limits_{\tau=1}^{t-1} \phi^{t-\tau-1}D_{\tau}, $$
(4)
$$ \tilde{y}_{0t} = \sum\limits_{\tau=1}^{t-1} \phi^{t-\tau-1} - \tilde{y}_{1t}. $$
(5)

If ϕ = 1, subjects weight all periods equally so that \(\hat {p}_{M}=\hat {p}_{B}\). A value of ϕ less than one means that subjects apply disproportionately more weight to recent events, whereas a value greater than one means they apply less weight to recent events.Footnote 4

3.2.3 Direct experience - \(\hat {p}_{X}\)

Proximity or degree of direct exposure may also affect how one interprets one’s past experience with a risk. In contrast with the 8 to 9% takeup in flood insurance Gallagher observes for counties directly affected by a major flood, neighboring counties experienced only a 2 to 3% increase. The disparity in takeup for those not directly hit by floods is consistent with results from surveys in which households report higher perceptions of flood risks given closer proximity to recent flooding events (Kellens et al. 2013). The gap in perceptions may reflect a tendency for people to place a higher weight on information gathered through personal experience (Anderson & Holt 1997) or to simply pay less attention to events that only affect others (Van Boven & Loewenstein 2005). In a similar vein, Viscusi & Zeckhauser (2015) find that perception of morbidity risks associated with tap water is influenced more by contracting an illness oneself than it is by learning about illnesses contracted by one’s friends. They conclude that direct experience has a greater impact on risk perception than indirect experience.

Motivated by these empirical findings, I estimate the following modification on the Bayesian model to identify potential differences in the effects of disasters observed from direct versus indirect experience:

$$ \tilde{y}_{1t} = \sum\limits_{\tau=1}^{t-1} \phi^{t-\tau-1}D_{\tau} + \alpha\sum\limits_{\tau=1}^{t-1}\phi^{t-\tau-1}D_{\tau}^{X}, $$
(6)
$$ \tilde{y}_{0t} = \sum\limits_{\tau=1}^{t-1} \phi^{t-\tau-1} + \alpha \sum\limits_{\tau=1}^{t-1} \phi^{t-\tau-1}x_{t} - \tilde{y}_{1t}. $$
(7)

The variables x t and \( {D}_{\tau}^{X} \) take on values 1 when outcomes and disasters are experienced directly and 0 when they are not. In the experiment, direct experience happens whenever the outcome of a period has a potential impact on a subject’s final income, as is the case in the Repeat round. Outcomes observed in the One-shot round, in contrast, do not affect subjects’ earnings and are therefore classified as indirect experiences. The parameter α is the additional weight applied to direct experience. If α equals zero, then direct and indirect experiences are perceived equally; if α is greater (less) than zero, direct experiences are weighted more (less) than indirect ones. The model also includes the ϕ parameter so that it nests the memory model discussed in the previous section.

3.2.4 Representative heuristic - \(\hat {p}_{N}\)

A person using the representative heuristic may overestimate the extent to which the distribution of a small sample of outcomes should be representative of the underlying distribution. For example, upon observing the outcome of six consecutive coin flips returning either heads (H) or tails (T), people regard the sequence H-T-H-T-T-H to be more likely than the sequence H-H-H-T-T-T (Tversky & Kahneman 1974). The presence of streaks in outcomes violates people’s notion that small sets of outcomes should “locally” represent the 50–50 chance of either heads or tails. The gambler’s fallacy is one important manifestation of this type of thinking. Using the coin-flip example, the gambler’s fallacy is defined as the tendency to falsely believe an H outcome is more likely after observing a streak of T outcomes even though all flips are statistically independent. The hot-hand fallacy can also emerge from the flawed perception of local representativeness. The hot-hand fallacy, deriving its name from its prevalence in perceptions of basketball free throws (Gilovich et al. 1985), refers to the overreliance on small samples to draw conclusions about future outcomes. Because streaks are deemed unlikely to result from random chance from the locally representative point of view, the hot-hand fallacy can lead people to make improper inferences about the underlying distribution of outcomes, such as concluding that the coin producing a streak of T outcomes is unfairly weighted to favor the T side.

To account for the influence of local representativeness and its associated heuristics on subjects’ decisions in the experiment, I adopt a model of such behavior outlined in Rabin (2002). Rabin’s model simulates local representativeness by assuming decision-makers perceive random outcomes as though they were drawn without replacement from a finite urn of size N. For example, in the experiment subjects who perceived themselves to be high risk would view disasters as if they were drawn from an urn containing 0.15N disaster outcomes and 0.85N safe outcomes. The urn periodically “refreshes” its finite set of outcomes after a certain number of periods. In the experiment, I denote the last refresh period at period t as t 0. The representative heuristic therefore implies the following modification to the updating rule:

$$ \tilde{y}_{1t} = \sum\limits_{\tau=t_{0}}^{t-1} D_{\tau}, $$
(8)
$$ \tilde{y}_{0t} = t - t_{0} - \tilde{y}_{1t}. $$
(9)

I assume that the size of the urn is 20 and that it refreshes once every 9 periods. These parameters correspond to estimates of Rabin’s model using experimental data reported in Asparouhova et al. (2009). The model applies in a straightforward manner to the experiment reported here. For instance, at periods t = 21 and t = 30, the values for t 0 are 18 and 27.

3.2.5 Beta-Bernoulli - \(\hat {p}_{E}\)

In the experiment p is distributed according to a simple binomial distribution so that it takes on the values 0.05 or 0.15 with equal chance. However, for decisions made in more complex natural hazard environments, the distribution of p is not always so straightforward to discern and, even if it is, people may ignore or fail to properly integrate descriptive information about the distribution of p into their beliefs. Often in empirical applications where the distribution of a hazard probability p is unknown, researchers assume that risk perceptions follow a Beta-Bernoulli process. One can find examples of this modeling approach applied in research on perceptions of flood risks (Gallagher 2014), health risks (Viscusi & O’Connor 1984; Davis 2004), environmental risks (Viscusi & Zeckhauser 2015), and driving risks (Andersson 2011), to name a few.

In a Beta-Bernoulli model, the posterior of p is governed by a Beta distribution and the expected value of p given this distribution is

$$ \hat{p}_{E}= \frac{y_{1t} + a}{t + a + b}. $$
(10)

The parameters a and b represent the prior belief about the risk before subjects observe any outcomes. Because subjects are told that the prior risk is 0.1, it must be true that a/(a + b) = 0.1, implying b = 9a. Therefore, a is the only free parameter in the model. It represents the strength of the prior: a greater (lower) value of a implies that beliefs update with lower (greater) magnitude following observation of outcomes generated by p. The purpose of estimating the Beta-Bernoulli model is to determine how well it fits the choice data compared with the properly specified Bayesian model, \(\hat {p}_{B}\). The results of this comparison could be relevant to field research that assumes the adequacy of the Beta-Bernoulli model in describing risk perceptions, although the “true” Bayesian specification remains unknown.

3.2.6 Inertia - I

Nevo & Erev (2012) propose a model of behavior in which decision-makers facing a repeated choice among unknown risky prospects engage in three activities: exploration, exploitation, and inertia. In exploration mode a decision-maker selects alternatives randomly and in exploitation mode one selects the alternative with the highest subjectively estimated payout. Inertia describes the tendency for decision-makers to simply repeat previous decisions without considering changes in the expected payoffs. Whereas exploration and exploitation describe a process compatible with belief updating and utility maximization, inertia seems to represent more of an anomaly.

The tendency to repeat recent choices may arise from several different behavioral motivations. Subjects may fail to update beliefs properly in repeated risk environments and thereby fail to update choices accordingly. If this is the case, then inertia may be understood through modifications to the belief-updating process, such as those discussed in the previous sections. Inertia may also result from a decision-maker simply choosing not to revise decisions based on newly acquired information. This may happen if the cognitive costs of revising the decision outweigh the expected benefits, or it may also reflect a bias toward the status quo (Kahneman et al. 1991). In either case, these behaviors motivate an extension of the EUT framework.

I determine the effect of inertia on choices made by subjects in the experiment by estimating the following model:

$$ U(W_{it},c_{it}) = u(W_{it}) + \delta \sum\limits_{\tau=1}^{t-1} \phi^{t-\tau-1}c_{i\tau}. $$
(11)

The function u(⋅) represents the CRRA consumption utility the subject receives from income W. The introduction of the second term means that the subject’s decision utility also depends on choices made in previous periods. If δ = 0 then past choices have no effect on current choices and there is no inertia. If δ is greater (less) than zero, then there is positive (negative) inertia across repeated choices. That is, a positive δ means that (not) insuring in the previous period makes one more (less) likely to insure in the subsequent period regardless of risk preferences or possible changes in risk perceptions. The inertia effect of previous choices decays according to the parameter ϕ.

3.2.7 Inertia and underweighting of low-probability risks

Although commonly observed in studies of repeated choice under risk (Erev & Haruvy 2013), inertia has received little attention as a possible explanation for underweighting low-probability risks. In theory, however, inertia can indeed bias decision-makers toward selecting low-probability risky prospects in repeated risk environments.

To understand the connection between inertia and underweighting of low-probability risks, consider the following illustration. A representative agent encounters a hazard that occurs with fixed probability p at times t = 0, 1 and 2 and decides whether to purchase insurance to protect against the hazard at times t = 1 and 2. Suppose the agent uses a simple decision rule for buying insurance such that if the hazard occurred at time t − 1 the agent insures at time t with probability q : q ∈ (0, 1], and if no hazard occurred at t − 1 the agent never insures at t. Therefore, the probability that the agent insures at each time t = 1 and 2 is given by pq. Now suppose that at time t = 2 the agent experiences inertia from his previous choice such that the probability he insures at time 2 is given by p q − δ(1 − c 1), where c t : c t ∈ {0, 1} represents the agent’s choice to insure at time t and δ : δ > 0 represents the degree of inertia, assuming that choices are positively autocorrelated. The expected probability that the agent insures at time 2 is therefore given by

$$pq - \delta(1-pq).$$

Notice that the term in the expression representing the influence of inertia, − δ(1 − p q), is both negative and increasing in the value of p. This implies that inertia reduces the agent’s likelihood to insure at time 2 and its negative impact is greater for low-probability risks. A low-probability risk implies a greater likelihood that the agent will experience a negative inertia effect from choosing not to insure at t = 1.Footnote 5 In a repeated risk environment, therefore, inertia is more likely to increase risk taking for low-probability risks than it is for more frequent ones.

4 Data

UC Irvine’s Experimental Social Science Laboratory (ESSL) and Claremont’s Center for Neuroeconomics Studies (CNS) both served as locations for the experiment. Participants were recruited from email databases of volunteers who expressed interest in participating in experiments. All participants were students at UC Irvine and the Claremont Colleges. Subjects received a $7 minimum payment for participation and additional earnings ranging from $0 to $30. The total sample consisted of 156 subjects who participated over eight different sessions. Subjects took 35 to 45 minutes to complete the experiment and on average earned $17.25.

A total of 23 subjects participated in the low premium treatment, 9 in the medium premium treatment, and 124 in the high premium treatment.Footnote 6 I sampled the high premium at a disproportionate rate because preliminary pilot results suggested that this treatment induced the greatest within-subject variation in choices. Sufficient within-subject variation in insurance choices is needed to identify which factors influence changes in risk taking in a repeated choice setting.

5 Results

Insurance takeup rates were 46%, 50% and 78% among the high, medium, and low premium groups. Takeup among subjects was positively affected by the number of disasters they experienced or observed. Columns (1), (2), (4) and (5) of Table 2 report marginal effect estimates for a logit regression with insurance choice as the dependent variable. The estimates show the effect of an increased Bayesian posterior belief (\(\hat {p}_{B}\)) in the likelihood of a disaster, which is calculated by applying Bayes’ rule to the experienced outcomes for a given subject in a given period. A one percentage point increase in the Bayesian posterior corresponded to a two to four percent increase in probability of insuring (p < .01). An increase in the premium between subjects reduces takeup by about 4.6 percentage points for each dollar increase (p < .01), implying that subjects had a negatively sloped demand curve for insurance.

Table 2 Determinants of insurance purchase
Full size table

The choice environment appears to have influenced subjects’ risk-taking behavior. Insurance takeup conditional on experience was 8 to 10 percentage points higher in the One-shot round than in the Repeat round (p < .05). Column (3) uses a linear probability model to estimate the effect of lagged choices on the current insurance choice during the Repeat round while controlling for subject fixed effects and experience as measured by \(\hat {p}_{B}\). Choices were indeed positively autocorrelated even after controlling for experience (p < .01), suggesting that inertia predicted risk taking in the Repeat round.

Columns (4) to (6) of Table 2 repeat the regressions reported in the first three columns, replacing the Bayesian posterior with subjects’ stated beliefs, or guesses, represented by the symbol \(\hat {p}_{SB}\). On average, a 1 percentage point increase in stated belief corresponded with a 1% increased likelihood of insuring (p < .01). Coefficients on other covariates remain roughly the same when using \(\hat {p}_{SB}\) rather than \(\hat {p}_{B}\). This is because \(\hat {p}_{SB}\) is significantly correlated with \(\hat {p}_{B}\) (p < .01), as is reported in Table 3. Table 3 shows the estimates of a linear regression with \(\hat {p}_{SB}\) as the dependent variable. Subjects stated higher perceived risk in the One-shot round than in the Repeat round (p < .01). Interestingly, subjects also stated higher perceived risk in the higher-premium treatments (p < .01), suggesting that they may have understood the premium as a signal for the underlying risk. Subjects nevertheless purchased insurance less frequently at higher premiums, implying that price sensitivity dominated any potential signaling effects.

Table 3 Determinants of stated belief
Full size table

Incorporating survey results shows that female participants were more risk-averse: takeup among females was 8 to 12 percentage points higher conditional on experience (p < .05).Footnote 7 Females also reported higher risk perceptions on average than males (p < .1). Scores on the cognitive reflection test were not correlated with insuring behavior or risk perceptions.

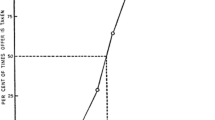
Figure 1 depicts the evolution of insurance takeup rates and perceived risk for both the high- and low-risk groups during the Repeat round. At period 20 the high-risk group started at 57% takeup while the low-risk group started at 44%. As one would expect, takeup between groups diverged as each group learned more about their true risk: by period 50 the high-risk group had 64% takeup while the low-risk group takeup was only 27%.

Fig. 1
figure 1

Changes in insurance takeup and perceived risk across the repeated choice round. The gray dots represent individual subjects’ stated beliefs for a given period and are jittered to improve visualization. The black dotted lines show the true probability for the group represented, while the gray dotted lines show the risk for the other group as a reference

Full size image

It is also noteworthy that the median perceived risk typically stayed within the correct bounds for rational Bayesian inference and even approached the true risk (0.05 and 0.15) in later rounds for both the low- and high-risk groups. In contrast, mean stated beliefs for the low- and high-risk groups were 0.18 and 0.22, well above the rational boundary of 0.15. This apparent overestimation in large part owes to the fact that guessing “0.50” was the modal response among subjects, an observation that is visually detectable in panels (b) and (c) of Fig. 1. It is unclear why “0.50” was such a popular response; it is perhaps a default selection for subjects who chose not to dedicate cognitive effort toward correctly guessing their risk. As a result, the median stated belief among subjects performs much better at approximating the true risk or rational Bayesian beliefs than does the mean stated belief.

5.1 Structural estimates

To gain a deeper understanding of the learning process underlying subjects’ insurance decisions, I estimate the parameters of the models described in Section 3.2. I assume that the unobserved utility affecting subjects’ decisions is extreme value distributed so that G(ε) is a logistic distribution and the probability of subject i insuring in period t is

$$q_{it} = \frac{e^{\lambda U(W-r;\theta)}}{e^{\lambda U(W-r;\theta)}+e^{\lambda E_{it}[U(W;\theta)|c_{it}=0]}}. $$

The predicted choice probabilities therefore depend on the values assigned to each alternative by the utility function, the perceived disaster probability \(\hat {p}\) used to form expectations, and a weighting parameter, λ. The weighting parameter is inversely proportional to the variance of ε and is estimated simultaneously with the risk aversion parameter from the utility function and whichever parameters generate \(\hat {p}\). I retrieve parameter values using a Nelder and Mead maximum likelihood algorithm that finds the parameters that maximize the joint log likelihood function implied by the model and subjects’ insurance choices. Standard errors were calculated by taking the square root of the diagonal elements of the Hessian matrix used in the algorithm.Footnote 8 The algorithm is scripted in the mle2 package for R.

The assumed CRRA utility function has a parameter of relative risk aversion 𝜃 and takes income W as its argument. CRRA utility is expressed by the power function U = u(W) = W 1−𝜃/(1 − 𝜃) for 𝜃 ≠ 1, and u(W) = ln(W) for 𝜃 = 1. The parameter 𝜃 is the Arrow-Pratt measure of relative risk aversion, where 𝜃 = 0 indicates risk neutrality, 𝜃 > 0 risk aversion, and 𝜃 < 0 risk seeking.

The perceived probability of disaster enters into q i t by determining the expected utility given that one is uninsured: \(E_{it}[U(W)|c_{it}=0] = \hat {p}(i,t)U(W-L) + (1-\hat {p}(i,t))U(W).\) The values for W and L are 30 and 22.5 in the experiment (L is calculated as the expected loss given that a disaster occurs). The parameters and data used for calculating \(\hat {p}\) are outlined in Section 3.2 and vary depending on the learning model that one assumes. Table 4 reports the parameter estimates for each model.

Table 4 Learning parameter estimates with 95% confidence intervals
Full size table

Estimates of the CRRA coefficient 𝜃 range from 0.7 to 0.89 under various specifications of the risk learning model. Using stated beliefs as the basis for decisions during the Repeat round, however, implies a much lower estimate of 0.27, likely owing to frequent overestimation in stated risk perceptions. All estimates are significantly greater than zero, demonstrating that subjects were risk-averse on average. Estimates of 𝜃 for the standard Bayesian (\(\hat {p}_{B}\)) and memory (\(\hat {p}_{M}\)) models were both 0.86 in the One-shot round and were 0.76 and 0.77 in the Repeat round. The lower values of 𝜃 in the Repeat round show that subjects revealed lower risk aversion in the repeated choice setting. This result is consistent with the regression analysis finding that subjects insured more in the One-shot round conditional on experienced outcomes.

The memory model gives identical predictions to those of the standard Bayesian model; the estimate for ϕ is statistically indistinguishable from one in both the One-shot and Repeat rounds. The result of a log-likelihood test verifies this claim: adding the ϕ parameter does not generate a statistically significant increase in the value of the joint log-likelihood associated with the Bayesian model. Subjects appear to have acted rationally in this regard, weighting outcomes equally whether or not they occurred recently.

There is also no evidence that the representative heuristic (\(\hat {p}_{N}\)) offers a better explanation of subjects’ choices than the standard Bayesian model. The log-likelihood ratios (LL-Ratios) for the Bayesian model are 0.16 and 0.07 for the One-shot and Repeat rounds, whereas the representative heuristic model produces ratios of 0.09 and 0.02. The LL-Ratio is calculated as one minus the log-likelihood of the model divided by the log-likelihood implied by random choice in which q is the unconditional probability of insuring. A higher LL-Ratio results from the model providing a better statistical fit to the choice data.

Each of the learning models predicted choices better in the One-shot round than in the Repeat round. Models that appeared in both rounds achieved LL-Ratios ranging from 0.09 to 0.3 in the One-shot round while having ratios between 0.02 to 0.14 in the Repeat round. Bayesian risk estimates and subjects’ stated beliefs, therefore, were better at explaining One-shot insurance choices than repeated choices with the same risk.

The poorer performance of the risk learning models in the Repeat round may be a consequence of unexplained autocorrelation in subjects’ insurance choices. Indeed, the estimated inertia model (I) has a value of δ significantly above zero, indicating that choices were positively autocorrelated. More recent choices had a greater influence: the estimate of ϕ is less than one at standard significance levels. There is also reason to believe that inertia may explain the gap in revealed risk aversion between the One-shot and Repeat rounds. The risk coefficient 𝜃 implied by the inertia model is 0.85, which is statistically indistinguishable from the estimate of 0.86 implied by the Bayesian model using One-shot choices but greater than the estimate of 0.76 using the Repeat choices. This result supports the hypothesis that inertia leads to lower revealed risk aversion: only controlling for inertia closes the estimated risk-aversion gap between rounds (see Fig. 2).

Fig. 2
figure 2

Estimates of risk aversion - 𝜃. The whiskers represent 95% confidence intervals for each estimate. The dark horizontal black line serves as a reference for the estimated value for the Bayesian model using One-shot choices. RH is an abbreviation for representative heuristic

Full size image

Estimates from the direct experience model (\(\hat {p}_{X}\)) provide additional evidence that subjects’ insurance decisions were influenced by factors not accounted for in the standard Bayesian model. I estimate the effect of experience by pooling decisions made at period 20 in both the One-shot and Repeat rounds. I limit the analysis to period 20 decisions because outcomes after period 19 in the Repeat round are endogenous, thereby weakening the direct comparison of the effect of random outcomes across environments. The estimated value of α is 2.88, implying that experienced outcomes weighed about three to four times more heavily on subjects’ risk perceptions. The results of a log-likelihood test confirm that the addition of a parameter accounting for direct experience significantly increases the fit of the Bayesian expected utility model.

The Beta-Bernoulli model performs similarly to the properly specified Bayesian model, achieving LL-Ratios of 0.16 and 0.07 in the One-shot and Repeat rounds. The estimate of a is roughly the same across rounds, suggesting that prior beliefs had equal strength in each choice environment.

6 Discussion

It is noteworthy that subjects’ decisions did not reflect a biased attention toward more recent outcomes. Experiments reported in Shafran (2011) and Meyer (2012) suggest the contrary, though these papers provide only reduced form evidence of so-called recency bias, whereas this study provides more concrete structural estimation of the influence of recency.Footnote 9 The results also add additional perspective to the observed tendency of flood insurance takeup and property prices to respond primarily to recent floods (Gallagher 2014; Atreya et al. 2015; Bin & Landry 2013). Clearly there are important differences in decisions made in a laboratory environment versus the decisions faced by actual market participants. However, if the findings from this experiment do generalize across settings, the priority that markets assign to recent disasters is perhaps best understood as a consequence of highly diffuse priors over environmental risks rather than an indication of recency bias.

Alternatively, disproportionate attention to recent events could persist among property owners directly impacted by disasters. Indeed, survey research suggests that “affect” based communication of flood risk, which often uses imagery to simulate direct experience with a disaster, is the most effective way to encourage disaster preparedness (Kellens et al. 2013). In the experiment, the importance of salience and affect is evidenced by the fact that subjects weighted directly experienced outcomes more heavily than those that they merely observed. Similarly, property owners are likely to weight statistical evidence of local flood risks less than personal experiences with floods. There is, however, little evidence supporting the hypothesis that the behavior of directly impacted individuals drives changes in aggregate demand for goods such as flood insurance. Kousky (2016) and Gallagher (2014) find that, conditional on the issuing of a disaster declaration, variation in the damages attributed to a recent disaster has little to no effect on subsequent changes in county-level flood insurance takeup. To the extent that damages are a proxy of direct experience, it appears that the effects of direct experience may be insignificant compared to changes in flood insurance demand caused by standard belief updating. The degree to which the direct experiences of a subset of market participants influences changes in aggregate demand would be an interesting topic for future research.

The role of inertia in predicting individuals’ willingness to take risks is another finding that seems worthy of further investigation. The reasons behind the observed inertia in subjects’ choices could, admittedly, be quite trivial. For example, subjects may have experienced fatigue and simply repeated previous decisions to save effort. One would not expect such fatigue to have the same influence on decisions made in more natural settings, where risk taking involves higher stakes and decisions are more spread out over time. Nevertheless, there are still other reasons to suspect inertia to take place outside the laboratory. A household may delay purchase of insurance for reasons related to status quo bias (Johnson et al. 1993; Cai et al. 2016). If homeowners are present-biased, then the initial costs of engaging risk mitigation or preparedness could deter them from taking such measures even if they accurately perceive the benefits of risk reduction as outweighing the associated costs (O’Donoghue & Rabin 1999). Present bias could therefore lead to procrastination in risk-reducing efforts, which would manifest as inertia in risk-taking behavior.

What policy insights can be gathered from these results? The absence of recency bias suggests that communication of flood risk should be focused more on conveying to property owners the devastating consequences of flooding rather than trying to correct perceptions about the probability of experiencing a flood. An example of this approach is discussed in Kousky & Michel-Kerjan (2015), who suggest improving flood risk communication by placing a greater emphasis on historical claims data that illustrate how disastrous floods can be. There are at least two ways to mitigate possible market distortions caused by inertia. If inertia results from procrastination, or present bias, then engagement in risk preparedness measures could be increased by lowering upfront costs households must bear to adopt these measures. Substituting upfront costs for future costs has, for example, been shown to effectively reduce procrastination in household savings contributions (Thaler & Benartzi 2004) and increase charitable giving (Breman 2011). Alternatively, inertia can be exploited by making enrollment in risk mitigation programs a default option for households. Michel-Kerjan & Kunreuther (2011) offer a suggestion along these lines, proposing that annual flood insurance policies offered by the NFIP be substituted for multi-year contracts so that homeowners are more likely to stay insured year-to-year.