Self-protection against repeated low probability risks

Abstract

This paper reports the results of experiments designed to test the effect of experience on preferences for self-protection against low and high probability losses. Subjects gained experience by repeatedly making choices about whether or not to invest in a protective activity and then observing the result of their choice. Half of the subjects faced a low probability risk while the other half faced a higher probability risk with the severity of loss scaled down to hold expected value constant. Protection was more common against the high probability risk. Despite receiving full information about the risks in advance, most subjects made choices in response to prior outcomes. This led to a great deal of experimentation when losses were common (the high probability risk) but very little experimentation when losses were infrequent (the low probability risk).

Individuals regularly make decisions to invest in self-protection, expenditures which reduce the probability of a loss without affecting the severity of the loss. For example, getting immunizations, buying a car with anti-lock brakes, or installing a burglar alarm are all examples of self-protection. The goals of this paper are to analyze individual preferences for self-protection with particular attention to how demand for protection changes as the probability of a loss gets very small and how experience with a risk affects preferences for protection. We develop theoretical predictions and test these predictions using experiments.

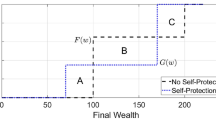
Expected utility theory stands as the benchmark model of individual choice (Von Neumann and Morgenstern 1947) when individuals face risky outcomes with known probabilities. Unlike insurance, self-protection is not always attractive to a risk averse expected utility maximizer, even if its expected benefits exceed its cost (Ehrlich and Becker 1972). This is true because self-protection exposes individuals to the possibility of incurring both the cost of protection and the bad outcome, thus increasing the maximum possible loss.

Expected utility theory models choice in one-shot decisions with a full description of the possible outcomes and associated probabilities. We denote these kinds of decisions as the descriptive paradigm. In many real-world situations, individuals make repeated choices when faced with risk, observing outcomes between each choice. Thus, individuals have the opportunity to learn from experience and change their choices over time. We denote these kinds of decisions as the feedback paradigm. If individuals initially have limited information (or possibly no information) about the possible outcomes and/or probabilities, then expected utility theory offers little insight regarding how individuals will behave.

Instead, theories of learning are necessary to model choice in the feedback paradigm. When individuals are unsure of the true probabilities of each outcome in a risky choice situation, expected utility theory can be extended to allow for a Bayesian learning process regarding the probabilities of each outcome (Viscusi 1979b). Viscusi (1979a), in a paper closely related to this one, takes this approach in developing a theoretical model of self-protection in a dynamic setting with insurance. He shows that strong priors on the probability of a loss will lead to a decrease in self-protection and an increase in insurance. Unlike Viscusi (1979a), however, subjects in the experiments from this paper are given full information about the gambles and so adaptation is not necessary to make optimal decisions.

Years of research have shown numerous situations in which individuals do not behave as expected utility maximizers. As a result, new models have been developed that attempt to explain observed behavior, even if departing from the normative prescriptions of expected utility maximization and Bayesian learning. Prospect theory (Kahneman and Tversky 1979) is one such model, developed to address systematic deviations from expected utility theory for one-shot descriptive-based decisions. In prospect theory, individuals have a value function which depends on gains or losses from a reference point rather than on absolute outcomes. The value function is assumed to be concave for gains and convex for losses. Prospect theory also incorporates a probability weighting function to explain the observation that individuals overweight low probability events and underweight high probability events.

In the feedback paradigm, models have also been developed that explain observed behavior which conflicts with rational learning (see Busemeyer and Townsend 1993 or Erev and Barron 2005). Erev and Barron (2005) propose a model of individual behavior based on three empirical regularities observed in the pure feedback paradigm, experiments in which individuals initially have no information at all about possible outcomes or probabilities. Two of these empirical regularities are particularly relevant to the experiments in this paper. First, the payoff variability effect refers to the observation that greater variability in payoffs leads subjects toward random choice. Second, individuals underweight low probability events when making decisions purely from experience.¹ This observation contrasts with the overweighting of low probability events noted in the descriptive paradigm, leading to what has been termed an experience description gap (see Hertwig and Erev 2009). One explanation for this observation is termed recency effects, in which individuals weight recent outcomes more heavily than older outcomes when learning from experience. Since low probability events are unlikely to have occurred recently, this behavior leads to the underweighting of low probability events (see Hertwig et al. 2004).

Many experiments have been conducted in both the descriptive and feedback paradigms to test the predictions of expected utility theory, prospect theory, and various theories of learning. These studies have mostly involved experiments which more closely resemble insurance than protection. Usually, subjects make choices between a risky gamble and a safe gamble where the safe gamble reduces the range of possible outcomes in return for a loss in expected value.

In the descriptive paradigm, Keren and Wagenaar (1987) and Keren (1991) show that subjects behave differently when faced with a one-shot gamble and a repeated gamble, choosing the safe gamble in the one-shot setting and the risky gamble in the repeated setting. Chen and Corter (2006) show that individuals may actually prefer a mixed option for the repeated gambles, making one choice for some repetitions and the other choice for other repetitions. Barron and Erev (2003) show that subjects underweight low probability events in the pure feedback paradigm compared to the same gambles in the descriptive paradigm. In the descriptive paradigm, they also find that many subjects reverse their choices in the one-shot gamble compared to the repeated gamble, although this effect is not always statistically significant.

These studies use experiments which fall exclusively in either the descriptive paradigm, in which there is no opportunity for learning, or the feedback paradigm, in which learning is required to overcome missing information. If choice in the real world always fell into one category or the other, then this would be enough. In truth, there are many examples where individuals have a full description of the problem and where they make repeated choices with feedback. When sitting at a roulette or craps table, individuals get feedback after each bet. Yet, careful thought prior to sitting down could determine the exact probabilities associated with each bet. Similarly, individuals make repeated choices to protect or insure their house against natural disasters, and they have the option of combining past experience with expert opinion about the likelihood of adverse events and the effectiveness of various protective activities. Thus, it is useful to understand not just the differences between the two paradigms, but also how individuals behave when both paradigms apply.

Some of the first experimental papers to include both feedback and a full description of the gambles tried to explain the equity premium puzzle based on the idea that risky gambles are more desirable when repeated. Hypothesizing that feedback causes subjects to consider each gamble on its own, Gneezy and Potters (1997) show that providing more frequent feedback causes subjects to prefer safer gambles while less frequent feedback leads to riskier choices.²

More recently, several papers have investigated the effect of feedback in the presence of a full description of the gambles for gambles exclusively in the loss or gain domain. Yechiam and Busemeyer (2006) show that individuals are less likely to insure against a low probability loss when experiencing feedback after each round. Jessup et al. (2008) show that individuals underweight rare events when provided feedback even when provided a full description of the gamble.

The results of these studies and others confirm that subjects behave differently when facing a single gamble and a repeated gamble and when facing repeated gambles with and without feedback. Self-protection offers a distinct type of choice, which is different from most of the gambles studied in the preceding experiments but highly relevant to the real world. It is not immediately clear that prior results will extend to self-protection experiments. For example, consider the observation that feedback promotes underweighting of rare events. In self-protection experiments, a rare event is possible both with and without protection, so preferences for self-protection will not depend on whether rare events are underweighted but on the relative underweighting of the rare event with and without protection.

Several previous studies have estimated the value of protection against low probability losses in experimental or survey settings (Kunreuther et al. 1998; Kunreuther et al. 2001; Kruse and Thompson 2003). All of these studies ask only descriptive questions about the value of protection without providing feedback about the outcomes that result from subjects’ choices.

Shogren (1990) has subjects repeatedly bid on how much they will pay for self-protection with feedback between bids. He finds that subjects initially pay a higher risk premium for protection against low probability losses than high probability losses but feedback reduces this phenomenon. One important difference from the experiments in this paper is that self-protection completely eliminates the risk in Shogren (1990) so that the certainty effect noted by Kahneman and Tversky (1979) may influence results.

Kunreuther et al. (2004) conduct laboratory experiments with repeated decisions about self-protection against earthquake damages. As in this paper, subjects make repeated choices with feedback although they are not provided full information about the effectiveness of self-protection. They find under-investment when self-protection is effective and over-investment when it is ineffective. In this paper, we provide more information to subjects in a simpler decision making framework and similarly find that subjects are not very sensitive to the cost effectiveness of self-protection.

This paper advances the self-protection literature by examining how the probability of loss affects preferences for protection as well as investigating the effect of feedback. Each round of the experiments in this paper exposes subjects to a possible loss. Subjects face a choice of whether or not to incur a cost to reduce the probability of the loss. The probabilities of a loss, both with and without self-protection, are provided to the subjects. We present theory and experimental results on the effect of varying four treatment variables. A between-subjects design tests the effect of varying the probability of a loss and the cost of self-protection. A within-subjects design tests the effect of increasing the number of repetitions without feedback and the effect of providing feedback.

First, decisions regarding a low probability high consequence (LPHC) loss are compared to a high probability low consequence (HPLC) loss, holding the expected loss constant. We show that a risk averse expected utility maximizer should be more likely to invest in self-protection for the LPHC risk while prospect theory, due to convexity of the value function over losses, allows for the opposite, that individuals are more likely to invest in self-protection for the HPLC risk. The experiments are consistent with prospect theory, showing that individuals are more likely to protect against the HPLC risk.

Second, decisions in which the cost of self-protection equals expected benefits are compared to decisions where the expected benefits exceed the cost of self-protection. Clearly, individuals should be more likely to protect when the cost of protection is lower, holding all else constant. The experiments, however, find that levels of protection are about the same with either cost in the purely descriptive choice setting.

Third, decisions in a one-shot and repeated framework are compared in the absence of any feedback. Expected utility theory predicts that individuals should make the same choice in both frameworks, assuming that changes in wealth are small enough (Samuelson 1963). The same result holds under similar assumptions for prospect theory. The experiments confirm the theory for most subjects. This result is in contrast to prior results such as those in Keren and Wagenaar (1987), although the type of gambles in the prior experiments more closely resemble insurance, not self-protection.

Finally, repeated decisions are compared with and without feedback. Since subjects receive full information about the gambles, expected utility theory and prospect theory offer clear predictions regardless of whether feedback is provided. Nonetheless, subjects may still use the feedback to guide future choices. For example, subjects may use the provided information to form priors and update their subjective probabilities based on past outcomes (Viscusi 1989). In the experiments, there is strong evidence that subjects react to prior outcomes when making choices in the feedback paradigm. Subjects more closely resemble Bayesian learners than descriptive expected utility maximizers though other adaptive processes based on reactions to prior losses explain the data equally well.

Two effects noted in previous studies of the feedback paradigm are also tested. First, recency effects imply that protection is less likely against LPHC events when feedback is provided. This is partially confirmed. Subjects in the LPHC treatments who chose not to protect in the descriptive paradigm were significantly less likely to protect in the feedback paradigm than their HPLC counterparts, although no differences were observed among those who did protect in the descriptive paradigm. Second, the payoff variability effect implies that an individual’s choice will be more random in the LPHC treatments which exhibit greater variability in payoffs. The experiments find the opposite, that subjects play more randomly in the HPLC treatments. Although this conflicts with previous findings, one explanation is that subjects play more randomly when they get feedback that varies frequently, even if the variance in payoffs is smaller.

The following section explains the experimental design and provides theoretical predictions for risk averse expected utility maximizers. Section 2 presents the results, and Section 3 concludes.

1 Theory and experimental design

Each subject began the session with $30.00 in earnings. In each round, subjects faced a risk of a loss $\frac{L}{s}$ with probability sp ₀. For a cost c, subjects could reduce the probability to sp ₁. This gamble was repeated n times, with each outcome independent of all other outcomes. The parameters L, p ₀, and p ₁ were fixed at $3.00, 0.02, and 0.01, respectively.

There were two between-subjects treatment variables. The first was c, the cost of protection. The cost of protection was either set so that expected payoffs were equivalent with or without protection ($0.03) or so that protection resulted in higher expected payoffs ($0.02). The second treatment variable was s. Subjects either faced a high probability of a small loss (s = 20) or a low probability of a large loss (s = 1), with expected payoffs held constant. This design yielded four possible scenarios which are summarized in Table 1. Each subject played only one of the four scenarios.

Table 1 Summary of experiments

Sessions were divided into four parts which differed in the value of n and in the feedback presented. All other parameters (L, s, p ₀, p ₁, and c) remained constant throughout the session. In the first part, denoted the one-shot gamble, subjects indicated whether or not they wanted protection when facing the gamble once. In the second part, denoted the repeated gamble without feedback, subjects indicated whether or not they wanted protection if the gamble was to be repeated 100 times. In the third part, denoted the repeated gamble with feedback, subjects made a sequence of 100 choices about whether or not to protect, receiving feedback after each round about whether they incurred a loss in the previous round. In the fourth part, which replicated the repeated gamble without feedback, subjects again indicated whether or not they wanted protection if the gamble was to be repeated 100 times.³

Subjects were students at California Polytechnic State University. The sessions lasted approximately thirty minutes, and average earnings were $14.78.

This design allows tests of the effect of four treatment variables: the effect of increasing s, the effect of increasing n, the effect of increasing c, and the effect of providing feedback between rounds. To examine the effect of increasing s, n, and c in the descriptive paradigm, we state propositions based on expected utility theory with risk aversion. Given the already large body of literature showing deviations from expected utility maximization, we do not necessarily expect subjects to play as perfect expected utility maximizers. Rather, the theory of expected utility maximization acts as a starting point to be tested based on observed behavior in the experiments. Following each proposition, a discussion of how predictions would change under prospect theory is included. Lastly, five hypotheses for behavior in the treatments with feedback are presented, based on the theory and past empirical observations of decision making in the feedback paradigm.

A risk averse expected utility maximizer maximizes the expected value of his or her utility function. The utility function is a function of total wealth Y which satisfies

Assumption 1

u′(Y) > 0

and

Assumption 2

u′′(Y) < 0.

Assumption 1 reflects a preference for more wealth and Assumption 2 imposes risk aversion.

Kahneman and Tversky (1979) highlight several systematic deviations from expected utility maximization and propose a new theory of decision making called prospect theory. For the experiments in this paper, there are three important distinctions between prospect theory and expected utility. First, gambles are expressed as gains or losses relative to a reference point rather than in terms of final outcomes. In this paper, all gambles are exclusively in the loss domain relative to their initial wealth at the beginning of the experiment. Second, the value function which translates dollar values to utility is convex for losses. Third, subjects weight the value function for each possible loss according to a subjective probability of that loss occurring rather than the objective probability. These subjective probabilities overweight unlikely events and underweight high probability events. Furthermore, the probability weighting function starts out concave and then becomes convex (see Tversky and Kahneman 1992; Prelec 1998).

1.1 The effect of increasing s

The parameter s allows for changes in the magnitude of the loss and the probability of loss, holding the expected loss constant. Risk averse expected utility maximizers are more likely to invest in protection against LPHC risks (small s) than HPLC risks (high s) with the same expected loss. This fact is stated formally in the following proposition:

Proposition 1

(Increasing s) A risk averse expected utility maximizer who dislikes protection for some s ₀ also dislikes protection for all s > s ₀.

Proof

Let c ^* denote the highest cost that an individual will pay for protection. c ^* is defined so that the following equality holds:

$$ sp_0u\left(Y_0\!-\frac{L}{s}\right)\!+(1\!-sp_0)u\left(Y_0\right) \!= sp_1u\left(Y_0\!-c^{*}\!-\frac{L}{s}\right)\!+(1\!-sp_1)u\left(Y_0\!-c^{*}\right). $$

Totally differentiating yields the following expression for $\frac{\partial c^{*}}{\partial s}$:

$$ \frac{\partial c^{*}}{\partial s}\!=\! \frac{p_1\left[u\left(Y_0\!-c^{*}\!-\frac{L}{s}\right)\!+\frac{L}{s}u'\left(Y_0\!-c^{*}\!-\frac{L}{s}\right)-u\left(Y_0-c^{*}\right)\right]-p_0\left[u\left(Y_0-\frac{L}{s}\right)+\frac{L}{s}u'\left(Y_0-\frac{L}{s}\right)-u\left(Y_0\right)\right]}{sp_1u'\left(Y_0-c^{*}-\frac{L}{s}\right)+(1-sp_1)u'\left(Y_0-c^{*}\right)}. $$

The denominator is positive as a result of Assumption 1. Since, by the definition of protection,

$$ 0<p_1<p_0, $$

and, by Assumption 2,

$$ \begin{array}{rll} 0&<&u\left(Y_0-c^{*}-\frac{L}{s}\right)+\frac{L}{s}u^{\prime}\left(Y_0-c^{*}-\frac{L}{s}\right)-u\left(Y_0-c^{*}\right)\\ &<& u\left(Y_0-\frac{L}{s}\right)+\frac{L}{s}u^{\prime}\left(Y_0-\frac{L}{s}\right)-u\left(Y_0\right), \end{array} $$

the numerator is negative. Thus, $\frac{\partial c^{*}}{\partial s} < 0$.

Let c denote the actual cost of protection. An individual who dislikes protection for an arbitrary s ₀ has $c^{*}(s_0)<c$. Since $\frac{\partial c^{*}}{\partial s} < 0$, c ^*(s) < c for all s > s ₀, and thus the individual dislikes protection for all s > s ₀.□

Under prospect theory, the value function is convex in the loss domain which leads to the reverse prediction with linear probability weights, that individuals are more likely to protect against the HPLC risk. However, under the range of probabilities in these experiments, the probability weighting function is concave which makes protection against the LPHC risks more desirable than under linear probability weighting. Combining the convexity of the value function with the concavity of the weighting function, prospect theory offers no clear prediction in either direction. It is still noteworthy that a preference for protection against the HPLC risk is consistent with prospect theory while inconsistent with expected utility theory under risk aversion.

1.2 The effect of increasing n

In a famous article, Samuelson (1963) proved that if an expected utility maximizing agent prefers a single gamble over another at all relevant income levels, then he or she must also prefer that gamble repeated n times over the other repeated gamble (for all n). A key assumption is that the single gamble is preferred at all relevant income levels. We restate that assumption below in the context of this paper:

Assumption 3

An agent prefers to self-protect when facing a one-shot risk with wealth Y = Y₀ if and only if he also prefers to self-protect when facing a one-shot risk for all Y such that $Y_0 \ge Y \ge Y_0-\frac{nL}{s}-nc$.

We now show that individuals should make the same choice when facing a single gamble, a repeated gamble without feedback, and a repeated gamble with feedback.

Proposition 2

(Increasing n) An individual prefers protection when facing a gamble repeated n times (with or without feedback between rounds) if and only if the individual also prefers protection when facing the gamble once.

Proof

Denote $Y_{n-1} \in [Y_0-\frac{(n-1)L}{s}-(n-1)c,Y_0]$ as an individual’s income after n − 1 repetitions of the gamble, with n > 1. Conditional on outcome Y _n − 1, an individual’s expected utility from the final repetition is

$$ sp_0u\left(Y_{n-1}-\frac{L}{s}\right)+(1-sp_0)u\left(Y_{n-1}\right) $$

if he does not invest in protection, and

$$ sp_1u\left(Y_{n-1}-\frac{L}{s}-c\right)+(1-sp_1)u\left(Y_{n-1}-c\right) $$

if he does invest in protection. If Assumption 3 holds, the individual will make the same choice in the final round as for the one-shot gamble, for any possible Y _n − 1.

Assume that an individual, in round i < n, plans to make the one-shot gamble choice for sure in all rounds (i + 1,...,n). In round i, conditional on outcome Y _i − 1, an individual’s expected utility for the remaining rounds is

$$ \begin{array}{rll} \sum\limits_{k=0}^{n-i} &\left[sp_0u\left(Y_{i-1}-\frac{L}{s}-(n-i)cI-k\frac{L}{s}\right)\right.\\ &+\left.\left(1-sp_0\right)u\left(Y_{i-1}-(n-i)cI-k\frac{L}{s}\right)\right] p(k) \end{array} $$

if he does not invest in protection, and

$$ \begin{array}{rll} \sum\limits_{k=0}^{n-i} &\left[sp_1u\left(Y_{i-1}-\frac{L}{s}-c-(n-i)cI-k\frac{L}{s}\right)\right.\\ &+\left.\left(1-sp_1\right)u\left(Y_{i-1}-c-(n-i)cI-k\frac{L}{s}\right)\right] p(k) \end{array} $$

if he does invest in protection, where I is an indicator equal to 1 if the individual prefers protection for the one-shot gamble and 0 otherwise, and

$$ p(k) =\left\{ \begin{array}{@{}l@{\quad}l} {n-i \choose k} (sp_0)^k (1-sp_0)^{n-i-k} & \text{if $I=0$}\\ {n-i \choose k} (sp_1)^k (1-sp_1)^{n-i-k}& \text{if $I=1$}\\ \end{array} \right. $$

p(k) is the probability of k losses in the last n − i rounds, given that the individual is making choice I. With the assumption that the individual plans to make the one-shot gamble choice for sure in all rounds (i + 1,...,n), p(k) is the same regardless of the choices the individual makes in round i. By Assumption 3, each element of the first sum is larger than each corresponding element of the second sum if the individual prefers not to protect for the one-shot gamble (for all possible Y_i − 1) and each element of the second sum is larger than each corresponding element of the first sum if the individual prefers to protect for the one-shot gamble (for all possible Y_i − 1). Thus, expected utility is maximized over the remaining rounds by making the same choice in round i as for the one-shot gamble.

We have now shown that the individual makes the same choice in round n as for the one-shot gamble, and that, if the individual is making the same choice in all rounds (i + 1,...,n), he will make that choice in round i as well. Combining these two results, it must be the case that the individual makes the same choice in all n rounds as for the one-shot gamble.

Because the previous analysis is valid for any possible outcome of the previous rounds (Y _i − 1), this result applies to a sequence of gambles with or without feedback between rounds.□

Under prospect theory, subjects make decisions about each gamble in terms of the loss or gain relative to their initial wealth. Each choice in a repeated gamble is framed identically to a single gamble, regardless of previous losses or gains. Thus, prospect theory also predicts that individuals make the same choice for single and repeated gambles.

1.3 The effect of increasing c

Individuals are less likely to protect when the cost of protection goes up. Although this result should be readily apparent, we provide the proposition and proof below in the interest of completeness. This proof relies only on the assumption of a preference for money and thus easily extends to prospect theory.

Proposition 3

(Increasing c) An individual who dislikes protection for some c ₀ also dislikes protection for all c > c ₀.

Proof

By Assumption 1,

$$ \begin{array}{rll} p_1u\left(Y_0-c_0-\frac{L}{s}\right)&+&(1-p_1)u\left(Y_0-c_0\right)>p_1u\left(Y_0-c-\frac{L}{s}\right)\\ &+&\,(1-p_1)u\left(Y_0-c\right) \end{array} $$

for all c > c ₀. From that, it follows that, if

$$ p_0u\left(Y_0-\frac{L}{s}\right)+(1-p_0)u\left(Y_0\right)>p_1u\left(Y_0-c_0-\frac{L}{s}\right)+(1-p_1)u\left(Y_0-c_0\right), $$

then

$$ p_0u\left(Y_0-\frac{L}{s}\right)+(1-p_0)u\left(Y_0\right)>p_1u\left(Y_0-c-\frac{L}{s}\right)+(1-p_1)u\left(Y_0-c\right) $$

for all c > c ₀.□

1.4 The effect of feedback

After making a single choice about a single gamble and a single choice about a gamble repeated 100 times, subjects made 100 repeated choices about a gamble with feedback between choices. We present five hypotheses to test regarding the effect of feedback across treatments.

Proposition 2 predicts that subjects should make the same choice in each of the 100 repeated rounds. Nonetheless, prior study results indicate that, even in the absence of feedback, subjects may have preferences for a mixed option of some rounds with protection and some rounds without (Chen and Corter 2006). Other studies with feedback indicate that subjects may follow an adaptive process in which prior outcomes affect future choices. For example, subjects may act as Bayesian learners, placing some weight on the provided probabilities and forming subjective probabilities based on observed outcomes (Viscusi 1989). Alternatively, subjects may act as reinforcement learners, a less sophisticated learning process in which subjects make choices which have led to high payoffs in the past. Both kinds of adaptation lead to our first hypothesis:

Hypothesis 1

(Adaptation) Prior outcomes have a significant effect on subjects’ choices.

The experimentation and adaptation noted above may reflect a Bayesian process where subjects update their subjective probabilities of incurring a loss based on prior outcomes. We now formalize this process and present a plan to test this hypothesis. Denote subjects’ perceived probability of a loss in round t without protection as $p^t_0$ and with protection as $p^t_1$. Denote the priors as $p^1_0$ and $p^1_1$. After observing the outcome of each round, subjects update their perceived probability of a loss for the chosen option. At any point in time,

$$ p^t_i=\frac{p^1_i+\sum_{j=1}^{t-1}l^j_i}{n^0+\sum_{j=1}^{t-1}n^j_i} $$

(1)

where i ∈ {0, 1} and $l^j_i$ is 1 if the subject chose i and incurred a loss in round j, $n^j_i$ is 1 if the subject chose i in round j, and n ⁰ is the weight placed on the prior probability. This implies that subjects update their perceived probability each round as follows:

$$ p^t_i=\frac{p^{t-1}_i\left(n^0+\sum_{j=1}^{t-2}n^j_i\right)+l^{t-1}_i}{n^0+\sum_{j=1}^{t-1}n^j_i}. $$

(2)

The perceived expected value from each choice in round t is:

$$ EV^t_i=\frac{EV^{t-1}_i\left(n^0+\sum_{j=1}^{t-2}n^j_i\right)+n^{t-1}_i\pi^{t-1}_i}{n^0+\sum_{j=1}^{t-1}n^j_i} $$

(3)

where $\pi^t_i \in [0,1]$ is the actual payoff from choosing i in round t, normalized so that the worst possible payoff is 0 and the best payoff is 1. Note that $EV^t_i=EV^{t-1}_i$ when choice i is not chosen in round t − 1 since subjects do not observe what would have happened had they chosen i. We assume that the probability of making choice i in round t depends on the perceived expected value associated with that choice:

$$ Pr^t(i)=\frac{e^{\lambda EV^t_i}}{\sum_{j=0}^1 e^{\lambda EV^t_j}} $$

(4)

where λ is a parameter which captures the importance of perceived expected values in determining the choice (smaller values imply more random choices). The parameters λ, n ⁰, and $EV^1_0$ will be estimated by maximum likelihood with $EV^1_1$ normalized to 0 so that $EV^1_0$ represents the increase in expected value from choosing not to protect.

In running our estimations, Eq. 3 will be further modified to include two additional parameters to incorporate recency effects.

$$ EV^t_i=\frac{\delta \left(n^0+\sum_{j=1}^{t-2}\left(\gamma + (1-\gamma)n^j_i\right)\right)EV^{t-1}_i+\left(\gamma + (1-\gamma)n^{t-1}_i\right)\pi^{t-1}_i}{\delta\left(n^0+\sum_{j=1}^{t-2}\left(\gamma + (1-\gamma)n^j_i\right)\right)+\left(\gamma + (1-\gamma)n^{t-1}_i\right)}. $$

(5)

The parameter δ ∈ [0, 1] allows for recency effects in which recent outcomes with a given strategy count more heavily than older outcomes with the same strategy. Values less than 1 imply that older outcomes are weighted less heavily than more recent outcomes in forming subjective probabilities. The parameter δ ∈ [0, 1] allows for recency effects in which strategies played more often in recent rounds are preferred to strategies which have not been played recently. When the parameter γ = 0, subjects only update the probabilities associated with choice i following rounds in which they actually choose i. When γ = 1, subjects update the probabilities associated with i as if they incurred a loss in rounds in which they do not actually choose i ($\pi^{t-1}_i$ is set equal to the payoff when a loss occurs if choice i was not chosen in round t − 1). Values between 0 and 1 imply that subjects treat all foregone payoffs as losses but weight them less heavily than actual payoffs.

The results of maximum likelihood estimations based on Eqs. 3 and 5 will be used to test the following hypothesis:

Hypothesis 2

(Bayesian updating) Subjects’ choices depend on the average payoff earned for each option over all prior rounds.

Following our analysis of the adaptive process used by subjects over the course of the 100 rounds with feedback, three additional hypotheses regarding treatment effects in the rounds with feedback will be considered. First, some authors have found evidence that subjects making decisions with feedback depreciate past payoffs so that more recent payoffs are weighted more heavily than older payoffs in the decision making process (i.e. δ < 1). In the experiments in this paper, in the LPHC treatments, subjects are unlikely to have incurred a loss in the recent past, regardless of whether they have invested in protection. Thus, higher depreciation rates make protection less desirable since recent rounds with protection will have incurred the fixed cost of protection while typically providing no benefit. In the HPLC treatments, losses will occur at least every five rounds on average and almost every other round without protection. Thus, the benefits of protection will be more apparent even with depreciation of past payoffs. These “recency effects” lead to the prediction that feedback makes self-protection less desirable in the LPHC treatments.

Hypothesis 3

(Recency effects) Feedback leads to lower levels of self-protection in the LPHC treatments relative to the HPLC treatments.

Second, the adaptive processes described above may allow subjects to learn their true preferences for self-protection. This leads to the prediction that when protection is a better deal in expected value terms, feedback will lead to more protection than when it is not.

Hypothesis 4

(Maximization) Feedback leads to higher levels of protection in the low cost treatments relative to the high cost treatments.

Third, a commonly observed effect in decisions with feedback is the payoff variability effect. The payoff variability effect predicts that choice becomes random as the variability in possible payoffs increases. The payoff variability effect leads to the prediction that choice will be more random in the LPHC treatments than in the HPLC treatments since there is greater variability in payoffs in the LPHC treatments.

Hypothesis 5

(Payoff variability effect) In the LPHC treatments, subjects choose protection closer to 50% of the time than in the HPLC treatments.

2 Results

The last three columns of Table 1 show the percentage choosing to protect in the one-shot gamble, the repeated gamble without feedback, and the repeated gamble with feedback, respectively. The remainder of this section is divided into four parts, one for each of the four treatment effects discussed in the previous section.

2.1 The effect of changing s

Subjects were more likely to protect themselves against a HPLC event than a LPHC event, a contradiction of Proposition 1 but consistent with prospect theory. This result was persistent across the descriptive and feedback paradigms and for one-shot and repeated gambles.

Table 2 shows the difference between the percentage choosing to protect against the HPLC risk and the percentage choosing to protect against the LPHC risk. For example, when faced with a one-shot HPLC gamble, 20 out of 30 subjects (or 67%) chose to protect themselves while only nine out of 28 (or 32%) chose to protect when faced with a one-shot LPHC gamble, a difference of 35%. The difference is always positive, indicating higher frequencies of protection against HPLC risks. The effect is fairly consistent as the cost of protection changes, although for the one-shot gamble, the effect is stronger in the low cost sessions than in the high cost sessions.

Table 2 The effect of changing s

Table 2 also shows p-values for Fisher exact tests for whether the frequency of self-protection choices is the same in the HPLC and LPHC treatments. These tests demonstrate that the observed differences are statistically significant when the data from both cost treatments are aggregated. Looking only at the high cost treatment, the effect is still present, but the null hypothesis that s has no effect cannot be rejected due to the small sample size.

2.2 The effect of changing n (no feedback)

Most subjects made the same choice for a one-shot gamble and a repeated gamble without feedback. Overall, 43 out of 58 subjects (or 74%) made the same choice when faced with a one-shot gamble and when faced with the same gamble repeated 100 times. This percentage is roughly equivalent in the low cost (77%) and high cost (70%) versions of the game and in the low probability (71%) and high probability (77%) versions of the game. A Wilcoxon signed rank test fails to reject the null hypothesis that the median player makes the same choice for the one-shot and repeated gambles (p-value: 0.439). Among those who did switch, there is no apparent trend in the direction of the switch, with six switching from no protection to protection and nine making the opposite switch.

This observation is in contrast to several other studies where most subjects respond differently to the one-shot gamble and the repeated gamble (for example, Keren and Wagenaar 1987; Gneezy and Potters 1997). One important difference between this study and previous studies is that previous work has involved gambles which more closely resemble insurance in that the safe gamble has a tighter range of outcomes but a lower expected value. This is the first study to address this question for self-protection gambles. In this setting, repetition no longer makes the high expected value gamble (i.e. self-protection in the low cost treatments) more desirable.

2.3 The effect of changing c

Table 3 shows the difference in the percentage choosing to protect in the low cost and high cost treatments as well as p-values for Fisher exact tests of the effect of the cost treatment variable. In a purely descriptive framework, subjects were no more likely to protect themselves when protection was a better value. Despite the fact that subjects could earn more money by choosing to protect themselves when the cost of protection was low, there was very little difference in subjects’ choices in the first two parts of the experiment when the cost was altered.

Table 3 The effect of changing c

In the two descriptive parts of the session before the rounds with feedback, 23 out of 46 (50%) chose to protect themselves in the high cost version while 38 out of 70 (54%) chose to protect themselves in the low cost version. While slightly more chose to protect in the low cost version, the difference is not statistically significant. Fisher exact tests using the data from the first two parts of the session both fail to reject the null hypothesis that subjects are equally likely to protect regardless of the cost of protection. In fact, in the case of the one-shot gamble with a LPHC risk, a higher percentage chose to protect themselves in the high cost version than in the low cost version.

In contrast, when faced with the repeated gamble with feedback, subjects in the low cost version were significantly more likely to protect themselves than those in the high cost version. In the low cost treatments, subjects chose to protect in 2,103 out of 3,500 (60%) rounds while subjects chose to protect in only 774 out of 2,300 (34%) rounds in the high cost treatments. A Fisher exact test rejects the null hypothesis, indicating that subjects are more likely to protect when protection is cheaper. This change in behavior in the rounds with feedback can mostly be explained by the fact that subjects in the high cost version were less likely to protect themselves in the rounds with feedback than in the other parts.

2.4 The effect of feedback

In contrast to the prediction of Proposition 2, most subjects did not make the same choice in each of the 100 rounds with feedback. When facing the repeated gamble with feedback, only 19 out of 58 subjects (33%) made the same choice 100 times. The remaining 39 subjects changed their response at least once over the course of the 100 rounds. It is clear that many subjects used the feedback about the outcomes of previous rounds when making their decisions. Table 4 shows the results of a fixed effects logit estimation with the choice to protect as the dependent variable (1 = protection, 0 = no protection). The variable AandLoss is defined as 1 if the individual chose not to protect and lost in the previous round and 0 otherwise. The variable BandLoss is defined as 1 if the individual chose to protect and lost in the previous round and 0 otherwise. The variable BandNoLoss is defined as 1 if the individual chose to protect and did not lose in the previous round and 0 otherwise. The reported values indicate the change in the probability of choosing protection when a given variable is 1 instead of 0. Following a loss, subjects who were choosing not to protect were 24% more likely to protect. Subjects who were choosing to protect were 28% less likely to protect following a loss. These results confirm Hypothesis 1.

Table 4 Fixed-effects logit

To further analyze the effect of feedback, an autoregressive conditional hazard (ACH) model is used to explain the decision to switch choices (Hamilton and Jorda 2002). This approach models the duration between rounds in which an individual switches choices, allowing the results of previous rounds to impact the duration. Since the gambles remain constant over the course of the session, the only new information to come to light each round is whether or not a loss occurred. Three estimations are reported in Table 5. The first includes dummies for both treatment variables (c and s) and their interaction, omitting information about prior losses. The second adds a dummy for whether a loss occurred in the previous round (the only new information since the previous choice was made). The third adds interactions with this variable and each of the treatment dummies (although only one of these additional terms is significant).

Table 5 Autoregressive conditional hazard estimates

Table 6 uses the results of the third estimation from Table 5 to explain the probability of switching choices in each of the four treatments. In both HPLC treatments, subjects switch choices relatively frequently (about one out of every five rounds), with a loss in the prior round boosting the odds of switching by about 5%. In contrast, subjects switch relatively infrequently in the LPHC treatments (about one out of every 20 rounds). Following a loss, however, subjects in the LPHC treatments are much more likely to switch, with the odds going up to 9% or as high as 25%.

Table 6 Autoregressive conditional hazard results interpreted

To test Hypothesis 2, we estimate the learning model described by Eqs. 4 and 5 and test whether δ = 1 and γ = 0. Table 7 summarizes the results. Only the 39 subjects who changed their choice at least once are included in the estimations. The table shows results for all such subjects as well as separate estimations for the HPLC and LPHC treatments. The mean squared deviation (MSD) is shown along with the MSD if we impose δ = 1 and γ = 0, the MSD from random choice, and the MSD from the ACH model in column 3 of Table 5.

Table 7 Adaptation estimations

From the MSD results in Table 7, it is clear that the adaptive models outperform random choice. In the HPLC treatments, there is very little difference between the MSD of the general adaptive model and the model which imposes δ = 1 and γ = 0. However, in the LPHC treatments, there are significant recency effects and subjects also appear to discount the payoffs of strategies they have not chosen recently. The MSD in the general adaptive model shows a much better fit than when δ = 1 and γ = 0.

The MSD for the ACH model described above is also shown, and it explains the observed behavior slightly better than the general learning model for the high probability treatments although not quite as well for the low probability treatments. It is interesting to note that the ACH model predicts choice based only on the frequency with which losses occur and not on the actual payoffs received. It is therefore distinctly different from a Bayesian updating process.

Subjects behave more like Bayesian learners than like pure expected utility maximizers or random players. Nonetheless, subjects in the LPHC treatments weight recent rounds more heavily than older rounds and are also biased against strategies they have not chosen recently. As a result, the more general learning process described by Eq. 5 explains the data best. Additionally, the ACH model, a competing non-Bayesian adaptive process which also predicts reactions to prior losses, performs as well as the learning models.

Hypothesis 3 states that feedback should reduce protection in the LPHC treatments relative to the HPLC treatments. In the LPHC treatments, subjects chose to protect 11 out of 28 times (39%) when facing the repeated gamble without feedback. With feedback, 845 out of 2,800 (30%) choices were to protect. However, this decline in protection with feedback shows up only in the high cost treatments where protection rates fall from 36 to 14%. In the low cost treatments, protection rates are about 41% with and without feedback.

Among the 26 subjects who chose not to protect when facing the repeated gamble without feedback, protection rates with feedback were significantly higher in the HPLC treatment than in the LPHC treatment (Fisher exact test p-value: 0.000). This difference was still statistically significant when looking exclusively at either the low cost or the high cost treatments. However, among the 32 subjects who chose to protect when facing the repeated gambles without feedback, protection rates were about the same in both the HPLC and LPHC treatments.

Hypothesis 4 states that feedback should increase protection in the low cost treatments relative to the high cost treatments. In the high cost treatments, in which expected payoffs were the same with or without protection, feedback led subjects to choose protection significantly less often. When facing the repeated gamble without feedback, 12 out of 23 (52%) chose to protect. When facing the repeated gamble with feedback, 774 out of 2,300 (34%) choices were to protect. This decline in protection in the rounds with feedback occurred in both the HPLC and LPHC treatments.

In the low cost treatments, in which higher payoffs could be earned with protection, feedback led subjects to protect slightly more often. With feedback, subjects chose to protect in 2,103 out of 3,500 (60%) rounds compared to 20 out of 35 (57%) choices without feedback. Not only was this effect small in magnitude, but it is entirely a result of increased protection in the HPLC treatment; there was virtually no change in protection in the LPHC, low cost treatment.

Among the 26 subjects who chose not to protect when facing the repeated gamble without feedback, protection rates were about the same in both the low cost and high cost treatments. However, among the 32 subjects who chose to protect when facing the repeated gambles without feedback, protection rates with feedback were significantly higher in the low cost treatment than in the high cost treatment (Fisher exact test p-value: 0.066).

Hypothesis 5 states that subjects will play more randomly in the LPHC treatments, switching frequently between protection and no protection. The data show the opposite, that subjects experiment more often in the HPLC treatments. Figure 1 shows the number of times subjects switched their choice in the LPHC and HPLC treatments. Of the 19 subjects who did not change their choice at all in the 100 rounds with feedback, 13 were in the LPHC treatment (68%). Furthermore, 19 out of 28 subjects (68%) in the LPHC treatment switched their choice three times or less. In the HPLC treatment, 19 out of 30 subjects (63%) switched their choice 10 or more times and half of the subjects switched their choice at least 20 times.

Fig. 1

Experimentation in repeated gamble with feedback

One explanation for this observation is that subjects respond to feedback which occurs more frequently in the HPLC treatments, even if the variability in payoffs in smaller. In the LPHC treatments, the vast majority of rounds will end without a loss regardless of the individual’s choice. In the experiments, only 47 out of 2,800 (1.7%) rounds ended in a loss. Thus, subjects receive very little feedback when probabilities are low. In contrast, losses are more common in the HPLC treatment, where 755 out of 3,000 (25%) rounds ended in a loss. Thus, increased experimentation in the HPLC treatment may be driven by the frequency with which losses occur, not the increased variability in payoffs.

After completing the rounds with feedback, subjects in the low cost treatments faced one more decision about the repeated gamble without feedback. This question was included to test for learning from the experience gained in the rounds with feedback. The vast majority of subjects (31 out of 35) made the same choice both times they faced the repeated gamble without feedback. This indicates that subjects’ tendency to experiment when provided with feedback did not alter their preference for the gamble without feedback.

3 Conclusions

Subjects were significantly more likely to protect against a high probability low consequence risk than against a low probability high consequence risk with the same expected loss, violating the prediction for risk averse expected utility maximizers. Furthermore, subjects facing a HPLC risk with a high cost of protection were twice as likely to protect as those facing a LPHC with a low cost of protection, even though the latter would have earned more money from choosing to protect. This is consistent with prospect theory if the probability weighting function is convex, linear, or not too concave.

Subjects are not very sensitive to changes in the price of self-protection in the descriptive paradigm. However, providing feedback led to significantly less self-protection when the cost of protection was just equal to its expected value while no such effect was observed when protection costs less than its expected value.

The provision of feedback resulted in a great deal of experimentation among subjects, as expected based on prior experiments but in contrast to the predictions of expected utility theory. Subjects did not act as pure Bayesian learners, weighting recent outcomes more heavily than older outcomes and showing bias against strategies not chosen recently.

Part of subjects’ experimentation is a result of sensitivity to the outcomes of prior rounds. Subjects were more likely to switch choices immediately following a loss regardless of whether they had chosen to buy protection or not. This result is consistent with empirical data on decisions about risk in the context of earthquake and flood insurance, where individuals buy more insurance immediately following adverse events (Kunreuther 1978; Browne and Hoyt 2000).

It is also noteworthy that more experimentation occurred in the high probability low consequence treatments, a reversal of the payoff variability effect. Subjects play more randomly when facing the gambles with less payoff variability. Intuitively, this can be explained by subjects’ tendency to react to prior outcomes since, although there is more variance in the payoffs in the low probability treatments, most rounds in those treatments will result in the same payoff.

These experiments demonstrate some limitations of existing theories at explaining individual behavior with respect to self-protection with feedback. While there have been many experimental studies of decision making regarding gambles which closely resemble insurance, few studies have investigated self-protection. This paper has shown that some previously noted effects, such as the tendency to reverse choices for a one-shot gamble and a repeated gamble, may not extend to decisions about self-protection.

From a policy perspective, if experts believe that protection against a low probability risk is warranted, the results presented here suggest that frequent monitoring combined with small fines for individuals who fail to protect may lead to much higher levels of protection. Such a policy will create a high probability low consequence loss in addition to the low probability high consequence loss.