Introduction

Vermiculite is a valuable multifaceted product from which over 100 types of different products and materials are manufactured. Firing of vermiculite in order to swell up the material is an energy-intensive process, hence the electric furnaces designed for this purpose are being constantly improved.

Due to the high cost of electric power in many regions of Russia, modular trigger electric furnaces for heat treatment of vermiculite base and other friable materials [1,2,3] were not competitive with reverberatory furnaces until recently despite the low energy capacity of the process: 150 – 160 mJ/m3 as opposed to 235 – 260 mJ/m3 [4]. New furnaces with movable (vibrating) platform [5] are able to fundamentally alter this situation, since analytic calculations [6, 7] and experimental results [8] show that a specific energy capacity of 45 – 65 mJ/m3 can be achieved using concentrates from the Kovdorsk deposit. This has been conclusively proved.

But no analysis of the relationships between the energy capacity of the process of firing of vermiculite using concentrates from different size groups both in modular-trigger furnaces and in furnaces with movable floors has yet to be carried out.

The objective of the present study is to establish a relationship between the specific energy capacity of the process of firing of vermiculite and the size of the grains of base concentrates and to identify efficient operating regimes of new furnaces based on their productive capacity.

Productive Capacity of Furnace

The hourly volumetric productive capacity Π V , m3/h, of a three-module furnace is determined from the formula

$$ {\Pi}_V=V\cdot 3600/t, $$

where V is the volume of a block of swollen grains occupying the surface of the bottom plate of the platform, m3, and t, the average time it takes the grains to travel across the surface of the bottom platform (for the fifth size group of Medium concentrate from the Koksharov deposit [9]).

This same volume V, m3, may be expressed as the total volume of the grains, assuming a conditional diameter of the grains based on the coefficient of porosity of a block k equal to the ~0.365 for swollen vermiculite [10]:

$$ V={V}_{\Sigma \mathrm{v}}/\left(1-k\right), $$
(1)

where V Σv is the total volume of grains relative to their conditional diameter.

The number of swollen grains on the three bottom plates of the platform n with weighted-mean conditional diameter D = 0.0047 m [7] (Medium vermiculite concentrate) with width of the floor B = 0.9 m and length L = 0.4 m (based on the section of poured base product from the feeder, its working section L w = 0.37 m) and assuming an ordinal structure of the arrangement of the grains, is determined by the formula

$$ n=3\left(B/D\right)\left(L/D\right)=3\left( BL/{D}^2\right) $$

Recalling the formula for the volume of a sphere, an expression for calculating the productive capacity Π v , m3/h, of a three-module furnace with movable bottom platform assumes the following form:

$$ {\Pi}_V=a\cdot \frac{0.1667\uppi {D}^3\cdot 3600\cdot n}{t\left(1-k\right)}=a\cdot \frac{3\cdot 0.1667\uppi DLB\cdot 3600}{t\left(1-k\right)}, $$
(2)

where a is a coefficient that takes into account the proportion of material (vermiculite) capable of optimum swelling in the process of firing, disregarding any inert material present which, according to the data of [9], is present in Medium concentrate at a rate of 10% (whence a = 0.9).

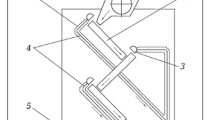
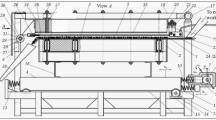
In experiments performed on a physical model of the furnace, i.e., the single-phase self-contained module shown in Fig. 1 a Medium concentrate of the fifth size group with weighted-mean conditional diameter D = 4.7 mm was used. For this model the time t it takes a grain to travel across the vibrating bottom platform was 3.31 sec. The time was determined by injecting markers into the total flow of swollen vermiculite and found as the arithmetic mean of five measurements.

Fig. 1.
figure 1

Physical model: 1) heat cover; 2) panel; 3) mounting; 4) springs; 5) frame; 6) cable.

Full size image

The experimental value of the productive capacity of a module amounted to 1.186 m3/h, which, scaled on the basis of a three-module furnace, yields a values of 3.56 m3/h.

The productive capacity of a three-module furnace determined by means of (1) for this size group was found to be 3.78 m3/h. If a value of 3.56 m3/h is adopted as the base value, the design productive capacity (Eq. (2)) yields a result which is overstated by 6.2%.

We next introduce a coefficient k 0 determined by the ratio 3.56/3.78. Then the formula for the productive capacity Π v , m3/h, assumes the final form

$$ {\Pi}_V=a\cdot \frac{3\cdot 0.1667\uppi DLB\cdot 3600}{t\left(1-k\right)}\cdot {k}_0. $$
(3)

Thermal Power of Furnace and Energy Capacity of Firing Process

The thermal power N T may be determined on the basis of the Stefan – Boltzmann equation [11]:

$$ {N}_T=\upsigma {T}^4{f}_{\mathrm{h}}, $$
(4)

where σ is the Stefan – Boltzmann constant, σ = 5.67 × 10−8W/(m2 ⋅ K4) [11]; \( {T}_{\mathrm{h}}^4 \), absolute temperature of the heating elements of module, K; f h, total area of all radiating surfaces of the heaters of a single module; for the physical module f h = 0.282 m2.

Recalling that a furnace creates an active electric load in the network, losses of energy may be ignored, whence the electric input will be given as

$$ IU={N}_T=\upsigma {T}^4{f}_{\mathrm{h}}, $$

where I is the current intensity and U the voltage.

The specific energy intensity of the firing process e s, J/m3, may be calculated in terms of the temperature of the heaters:

$$ {e}_{\mathrm{s}}=\frac{3\upsigma {T}^4{f}_{\mathrm{h}}}{\Pi_V}\cdot 3600. $$
(5)

But it is first necessary to derive temperature-time relationships that express the possible regimes for firing of vermiculite from different size groups.

The flux power of the radiant energy incident on a vermiculite monolayer traveling on the bottom platform, the energy Q r, W, which it absorbs, and the specific energy of heat assimilation θΣ, J/kg, are related to the mass productive capacity of the furnace ΠG, kg/s, by the relationship

$$ {\uptheta}_{\Sigma}{\Pi}_G={Q}_{\mathrm{r}}, $$
(6)

where Q r is determined by an expression found in [12]. Recalling that in the new design of the furnace the heaters are raised above the floor tile, the expression for the absorbed power assumes the form

$$ {\displaystyle \begin{array}{l}\kern5em {Q}_{\mathrm{r}}={\upalpha}_{\mathrm{v}} IU{\upvarepsilon}_{\mathrm{f}}\left(2{\upvarphi}_{\mathrm{h}.\mathrm{v}}\right.\\ {}+{\upvarphi}_{\mathrm{c}.\mathrm{v}}\left.\left[2\frac{\upvarphi_{14}+{\upvarphi}_{34}{\upvarphi}_{13}{\uprho}_4}{1-{\uprho}_{\mathrm{v}}{\uprho}_4{\upvarphi}_{34}^2}+\left(2{\upvarphi}_{Ak}2{\upvarphi}_{Bk}+2{\upvarphi}_{Ck}\right)\right]\right),\end{array}} $$
(7)

αv is the absorptivity of a monolayer vermiculite flow [13], αv = 0.768; I and U, effective values of the current force, A, and voltage, V, in the electric network of the heaters of the furnace; εh, degree of blackness of Nichrome heaters of furnace, εh = 0.96; φh. v and φc. v, angular coefficients of flows from heaters to vermiculite (φh. v = φ13 = 0.43) and from cover to vermiculite (φc. v = φ43 = φ34 = 0.333); φ14, φ34, and φ13, angular coefficients that determine the geometrico-optical characteristics of the conditional work chambers of the firing modules, φ14 = 0.116, φ34 = 0.333, and φ13 = 0.43; ρv, reflecting power of monolayer vermiculite flow; ρ4, reflecting power of thermal insulating coating of cover made of mullite-silicaceous felt, ρ4 = 0.65; φ Ak , φ Bk , and φ Ck , average angular coefficients of flows from heaters of adjacent chambers of a firing module [12] (a conditional working chamber comprises the space between the adjacent cavities of the heating elements), with φ Ak  = 0.128, φ Bk  = 0.078, and φ Ck  = 0.04.

Let us next define the mass productive capacity, kg/sec:

$$ {\Pi}_G={m}_{\mathrm{v}}/t, $$

where m v is the mass of vermiculite concentrate found on the three bottom plates, kg.

Since the mass of dehydrated vermiculite is reduced due to the yield of chemically bound and interlayer water by 20 – 24% [10], a correction factor of 0.78 must be introduced into the left-hand side of Eq. (7). Then 0.78m is the mass of the moving monolayer flow, scaled on the basis of the swollen material; based on formula (1) it may be defined in terms of the total volume of grains found simultaneously on the three bottom plates of the furnace.

The true density ρ, kg/m3 of swollen vermiculite grain

$$ \uprho ={\uprho}_{\mathrm{b}}/\left(1-k\right), $$
(8)

where ρb is the bulk density of vermiculite, kg/m3.

In the case of a bulk density of swollen vermiculite made of Medium concentrate ρb ≈ 90kg/m3 (found experimentally), the true density ρ = 141.7 kg/m3 is determined by a calculation using formula (8).

An expression that determines the mass m v of the monolayer vermiculite flow on the three bottom plates of the furnace will have the form

$$ {m}_{\mathrm{v}}=0.78\cdot 0.1667\uppi {D}^3\cdot n\uprho =0.249\kern0.5em \mathrm{kg}. $$
(9)

In light of (4), Eq. (7) may be reduced to the form

$$ {\displaystyle \begin{array}{l}\kern4em {\uptheta}_{\Sigma}\frac{m_{\mathrm{v}}}{t}={\upalpha}_{\mathrm{v}}\upsigma {T}^4{\upvarepsilon}_{\mathrm{f}}\left(2{\upsigma}_{\mathrm{h}.\mathrm{v}}\right.\\ {}+{\upsigma}_{\mathrm{c},\mathrm{v}}\left.\left[2\frac{\upvarphi_{14}+{\upvarphi}_{34}{\upvarphi}_{13}{\uprho}_{14}}{1-{\uprho}_{\mathrm{v}}{\uprho}_4{\upvarphi}_{34}^2}+\left(2{\upvarphi}_{Ak}+2{\upvarphi}_{Bk}+2{\upvarphi}_{Ck}\right)\right]\right),\end{array}} $$
(10)

and a temperature-time relationship that determines the operating regime of a furnace with vibrating bottom platform may be obtained from the latter:

$$ T=\sqrt{\begin{array}{l}\frac{\uptheta_{\Sigma}{m}_{\mathrm{v}}}{t\cdot {\upalpha}_{\mathrm{v}}{\upsigma \upvarepsilon}_{\mathrm{f}}f\left(2{\upsigma}_{\mathrm{h}.\mathrm{v}}+{\upsigma}_{\mathrm{c}.\mathrm{v}}\left[2\frac{\upvarphi_{14}+{\upvarphi}_{34}{\upvarphi}_{13}{\uprho}_{14}}{1-{\uprho}_{\mathrm{v}}{\uprho}_4{\upvarphi}_{34}^2}\right.\right.}.\\ {}\kern3em +\left.\left.\left(2{\upvarphi}_{Ak}+2{\upvarphi}_{Bk}+2{\upvarphi}_{Ck}\right)\right]\right)\end{array}} $$
(11)

The specific energy of heat assimilation θΣ, J/kg, for Koksharov vermiculite of 921.8 kJ/kg was established in recent experiments on a physical model and is shown in [1, 7].

The above value corresponds to pure vermiculite concentrate, hence it must be taken into account that roughly 10 wt.% inert material is presented in Medium concentrate and that inert material also “consumes” energy:

$$ {\uptheta}_{\mathrm{v}}=0.1{c}_{\mathrm{v}}m\Delta T=0.1\cdot 942.5\cdot \left(512-100\right)=38.8\mathrm{kJ}/\mathrm{kg}, $$

where 0.1 is the mass fraction of the inert material in 1 kg of concentrate; c in, specific heat capacity of inert material, for sand in the temperature range 20 – 600°C equal on average to 942.5 J/(kg·°C) [14]; m, mass of initial concentrate, m = 1 kg; and ∆T, variation of temperature in the course of heating.

Then Eq. (11) assumes the final form

$$ T=\sqrt{\begin{array}{l}\frac{\left[0.9\cdot \left({\uptheta}_{\mathrm{x}}+{\uptheta}_{\mathrm{c}}+{\uptheta}_{\mathrm{b}}+{\uptheta}_{\mathrm{i}}\right.\right]\cdot {m}_{\mathrm{v}}}{t\cdot {\upalpha}_{\mathrm{v}}{\upsigma \upvarepsilon}_{\mathrm{f}}f\left(2{\upsigma}_{\mathrm{h}.\mathrm{v}}+{\upsigma}_{\mathrm{c}.\mathrm{v}}\left[2\frac{\upvarphi_{14}+{\upvarphi}_{34}{\upvarphi}_{13}{\uprho}_{14}}{1-{\uprho}_{\mathrm{v}}{\uprho}_4{\upvarphi}_{34}^2}\right.\right.}.\\ {}\kern1em +\left.\left.\left(2{\upvarphi}_{Ak}+2{\upvarphi}_{Bk}+2{\upvarphi}_{Ck}\right)\right]\right)\end{array}} $$
(12)

The temperature-time relationships may now be obtained.

If an annealing time t corresponding to the experimental value of 3.31 sec is adopted, we obtain from (12) a temperature on the heaters of 1151 K, or 878°C. A calculation using Kelvin temperatures by comparison with the experimentally obtained temperature of 926°C = 1199 K yields a 4.1% divergence. This level of precision of the final formula (12) may be satisfied, since this degree of insignificant divergence is negligible.

Let us specify several values of the annealing time t and construct a temperature-time relationship for Medium concentrate in the fifth size group (Fig. 2, curve D c = 4.7 mm). The working point a corresponds to a temperature-time regime close to the steady-state thermal regime in the furnace attained in the experiment [15] with average density of swollen vermiculite 90 – 92 kg/m3. Point b indicates the upper temperature threshold ~940°C beyond which the finely dispersed particles adhere to the surface of the heaters. The other graphs, which correspond to different conditional diameters D c, were also constructed from Eq. (12).

Fig. 2.
figure 2

Temperature-time relationship for different sizes of the average conditional diameters of swollen grains of Medium concentrate; t, sec, at points 1) 3.68; 2) 3.12; 3) 2.67; 4) 2.26.

Full size image

Using formulas (3) – (5), we calculated the volumetric productive capacity and thermal power of a three-module furnace along with the specific energy capacity in annealing of vermiculite concentrates of different size groups with annealing time 3.31 sec. The results of the calculations are presented in Table 1.

Table 1. Results of Calculations of Productive Capacity, Thermal Power, and Specific Energy Capacity
Full size table

The data show that thermal power grows with increasing productive capacity caused by an increase in size of the swollen grains and that this larger thermal power produces optimum swelling of the material. In addition, the specific energy capacity does not exhibit any tendency to vary in the course of annealing of concentrates belonging to different size groups. But this study was performed for an annealing time of 3.31 sec, which was the same for all the concentrates.

Determination of Efficient Operating Regimes

The second problem of the study was to find and evaluate efficient operating regimes of electric furnaces provided with movable bottom platforms in the case of concentrates of different size groups.

Let us now turn to Fig. 2. Point b on curve D c = 4.7 mm establishes a boundary for the limiting temperatures (~940°C) beyond which is found a region of elevated probability for the formation of hard carbon on the surface of Nichrome, its local overheating, burn-through, and failure of the furnace apparatus. For size groups of the concentrates in the range from 4 to 6.5 mm, therefore, the temperature-time regime will be determined at working points 1 – 4.

We next calculate the productive capacity and thermal power of the furnace and the specific energy capacity of the annealing process for concentrates belonging to these size groups, bearing in mind the time it takes for the vermiculite to travel across the bottom plates to points 1 – 4 (cf. Fig. 2). Results of the calculations are presented in Table 2.

Table 2. Productive capacity, Thermal Power, and Energy Capacity for Concentrates with Conditional Diameter 4 – 6.5 mm
Full size table

The fact that the thermal power of the radiation does not change is due to the identical temperatures on the surface of the electric heaters: T 1 = T 2 = T 3 = T 4 = 940°C. Nor does the productive capacity vary, since it is determined by two factors, on the one hand, it falls with decreasing size from D c = 6.5 mm to D c = 4.7 mm, while on the other hand, it grows due to the decrease in the time it takes vermiculite to travel across the floor plates from 3.68 to 2.26 sec.

The travel time t i and conditional diameter D c vary synchronously, leaving the ratio D c / t i unchanged. Therefore, the specific energy capacity of the process remains the same in these temperature-time regimes.

If a criterion that limits the heat processing procedure by temperature is adopted for concentrates with sizes D c from 4.0 to 6.5 mm, selection of the temperature-time regimes for concentrates with conditional diameter from 1 to 3 mm will be carried out based on the need to maintain a maximally high productive capacity of the furnace. Recall, for example, the three points denoted in Fig. 2 by the small squares A, B, and C with temperatures of 888, 995, and 1053 K, respectively.

Using formulas (3) – (5), we calculate the productive capacity, thermal power, and specific energy capacity for these size groups of the concentrates, bearing in mind the time it takes vermiculite to travel across the bottom plates to points A, B, and C: t A = 3.0 sec; t B =2.5 sec; and t C = 2.0 sec. The results of the calculations are presented in Table 3.

Table 3. Productive capacity, Thermal Power, and Energy Capacity for Concentrates with Conditional Diameter 1, 2, and 3 mm
Full size table

Here the thermal power increases, since the temperature grows from point C to point A. In addition, though the annealing time is now less, the productive capacity nevertheless grows due to the increase in the size of the grains of swollen vermiculite.

A calculation of the specific energy capacity by means of (5) shows that it remains unchanged at these points. Moreover, we obtain the same result if we select any other points on the temperature-time curves (cf. Fig. 2); that is, the energy capacity does not change. This is a law that follows from the balance between the power of a flow of radiant energy and the product of the mass productive capacity times the specific energy of heat assimilation (formula (6)).

Thus, the objective posed at the start of the study, to establish a relationship between the specific energy capacity of the process of annealing of vermiculite and the size of the grains of raw concentrates, has been achieved. That is, it has been established that the specific energy capacity is independent of the size groups of one and the same concentrate.

In the course of the experiments performed on the physical model, tests were carried out to measure the productive capacity, density, and temperature of Medium vermiculite in order to understand the influence of the bulk density of swollen vermiculite on the productive capacity of a furnace. Samples of vermiculite were selected every 80 – 90 sec and in each case three values of the temperature of vermiculite and two values of the density were determined, after which the productive capacity was calculated.

The dependence of the volumetric productive capacity Π v , on the density of swollen vermiculite in the interval 92 – 126 kg/m3 with significant variation in the temperature, from 452 to 382°C and less, is shown in Fig. 3. The productive capacity falls only 0.03 m3/hr, i.e., it remains practically constant.

Fig. 3.
figure 3

Productive capacity of physical model of furnace as a function of the final packed density of swollen vermiculite: U= 168.6W, I = 84.7 A.

Full size image

Let us consider the ratio of the capacity of thermal radiation of vermiculite N 1/N 2 at a density of 92 kg/m3 and, for example, at 100 kg/m3, since along this segment there is practically no variation in the density. According to the Stefan – Boltzmann law, at these temperatures, expressed in degrees Kelvin (725 and 665 K), the ratio will be given as follows:

$$ \frac{N_1}{N_2}=\frac{T_{92}^4}{T_{100}^4}=\frac{725^4}{665^4}=1.41 $$
(13)

The ratio (13) shows that, from the point of view of energy, consumption of 41% of the thermal energy in order to maintain the density of vermiculite near the minimum limit of 90 kg/m3 set by the manufacturer is not useful, and, in fact, the difference in densities amounts to only 8 kg/m3. Therefore, adjustment of the furnace to a thermal regime should be performed so that the least possible density is not attained. The graph in Fig. 3 persuasively demonstrates that oscillations in the density near the least possible value do not have any effect on the volume of material produced.

If, based on the data of Tables 1 – 3 , the average design specific energy capacity of the process of firing of vermiculite is around 80 mJ/m3, then, taking into account this saving, a significantly lesser value (46 – 48 mJ/m3) may be attained for Medium concentrate and even less, around 30 mJ/m3 for Kovdorsk concentrate.

A horizontal arrangement of the bottom platform plants is yet another method of achieving further savings in energy. The angle of inclination in the physical model of the furnace is now around 19° to the horizontal, but with this inclination a strong air draft that cools the heating elements is created due to the difference in temperatures and the density of the air in the firing space of the module. The eccentric drive is not able to achieve clearly expressed frequency- and amplitude-controlled asymmetric oscillations that assure a one-sided vibratory transport effect. The volumetric hydraulic vibration exciter which is described in [16, 17] may be used to implement such a regime.

Conclusion

A high energy efficiency of electric furnaces with movable bottom platforms designed for firing of vermiculite concentrates of different size groups has been demonstrated as a result of the investigations.

It was established that the thermal power of the heaters (and the consumed electric power) grows with increasing productive capacity due to the increase in the size of the swollen grains and that this assures optimum swelling of the material. In addition, the specific energy capacity of the process of firing of vermiculite does not exhibit any tendency to vary in the course of processing concentrates of any size. This result is regular and is obtained here for the first time.

The problem of determining efficient temperature-time operating regimes of electric furnaces with movable bottom platforms was solved.

Still another new result is that an additional 40% decrease in the specific energy capacity of the annealing process is achieved by adjusting the furnace to a slightly reduced temperature regime, which leads to a barely significant reduction in the packed density of the swollen product. The lowest possible specific energy capacity of the firing process attained on the physical model of the furnace (46 – 48 mJ/m3) shows that electric furnaces with movable bottom platforms will be competitive on the market of equipment used in the production of vermiculite and vermiculite products.

Research on improving the new furnace design has not been completed. Modernization of a single-phase separate module is continuing. The new construction will be provided with an arrangement of heaters underneath the bottom board, and a nonlinear “hydraulic” spring of a volumetric hydraulic vibration exciter of oscillations of the bottom platform will be installed.