1 Introduction

Information processing is a well-developed and growing discipline, theoretically and for applications [1,2,3,4]. Through technological progress such as miniaturization and other advances, information processing devices are being driven to their ultimate physical limits, where we meet the quantum level. At this level, it then becomes necessary to explicitly consider the quantum nature of the effects involved when processing information. Nevertheless, at this quantum level, we also reach new properties inaccessible in classical, which bring new and specific means exploitable for the treatment of information with increased performances. Among the most significant properties, specifically quantum superposition plays a significant role in information processing and quantum entanglement [5]. Indeed, quantum superposition, for example, makes it possible to envisage parallel information processing. At the same time, quantum entanglement offers correlation or remote coupling possibilities that can be exploited for unexpected information processing benefits. However, the field of quantum information has thus developed for several decades [6,7,8,9]. In fact, we can illustrate its progression and contributions through various emblematic processes. Non-local quantum correlations arising from entanglement and the appearance of a violation of the laws of relativistic causality allowed physicists to make detailed theoretical studies [10, 11] and also in practice [12,13,14]. These investigations gave rise to informational effects such as superdense coding [15, 16], which allowed unattainable communication speeds in conventional, or like the teleportation of a quantum state that is destroyed during its measurement and is reconstructed remotely in an exact manner [17,18,19].

Low-dimensional quantum spin systems have recently enticed significant attention in characterizing quantum information systems due to their magnetic properties arising from quantum fluctuations and low dimensionality. Quantum impacts are specifically appropriate in the spin\(-1/2\) quantum systems. The quasi-one-dimensional antiferromagnetic spin\(-1/2\) has been theoretically and experimentally explored [20]. Regarding this, numerous experimentations on higher-dimensional compounds [21,22,23,24,25] demonstrate that the isotropic exchange coupling in various systems is inadequate to explain magnetic effects such as weak ferromagnetism.

Theoretically, the Dzyaloshinskii–Moriya (DM) term was first put up by Dzyaloshinskii [26] as a spin vector product to explain the low ferromagnetism of antiferromagnetic materials and was based on symmetry reasons. The spin–orbit coupling in perturbation was considered when Moriya obtained the formula for this term, and he demonstrated that it is first order in the fine structure constant [27]. Moriya’s calculus revealed that a symmetric anisotropy term was detected in addition to the DM component, but it was deemed negligible by Moriya concerning the anti-symmetric part. However, investigations [28, 29] have shown this assumption needs to be corrected if the underlying microscopic pattern from which the spin–spin couplings arise possesses SU(2) spin symmetry. Since the DM term alone breaks SU(2) symmetry, the symmetric term can compensate for the destruction of SU(2) generated by the DM interaction. For this class of systems, the symmetric anisotropy term is called the Kaplan–Shekhtman–Entin–Wohlman–Aharony (KSEA) interaction which is tuned so that SU(2) symmetry is retrieved [28,29,30]. On the other hand, the two-qubit Heisenberg model with the DM and KSEA interactions received much attention from physicists to explain quantum entanglement and correlation [31, 32]. Furthermore, magnetism systems, such as the Heisenberg spin chains, have been the subject of intensive study in recent years and are considered natural candidates for exploiting quantum resources. In fact, many important works were produced, considering the isotropic Heisenberg XXX chain [31,32,33], the anisotropic Heisenberg XY chain [34, 35] and the anisotropic Heisenberg XYZ chain [36].

Recently, the entanglement counted by concurrence in a two-qubit Heisenberg XXX model with KSEA and DM couplings has been explored in work [33]. The authors determined the concurrence expression by using the physical quantities related to the selected system; their findings indicated that temperature, spin coupling constant and x-components of KSEA and DM couplings could all play a role in determining the degree of intricacy between states. Moreover, these results implied that state separabilities are achieved in high-temperature regions or by switching spin coupling. On the other hand, the state entanglement was obtained at low temperatures by operating increased values of the x-components of the parameters KSEA and DM couplings. Moreover, the authors demonstrated that the KSEA and DM couplings similarly affect high-temperature concurrence behaviors.

We noticed that the entanglement for an XYZ spin model with the DM coupling along the x-axis had yet to be discussed. Although, the study made by [33] did not exploit the different types of anisotropic interactions. They are focused only on the models of magnetism in low-dimensional materials based on the homogeneous Heisenberg XXX model. We think it is very interesting and should be included in studies of spin chain entanglement by considering a two-qubit in the anisotropic Heisenberg XYZ model under the x-direction of KSEA and DM couplings. Solving the Hamiltonian system, we derive the corresponding eigenvalues as well as eigenstates, which will be used to determine the density matrix, which is considered a key to studying the system’s entanglement by concurrence. Indeed, for \(J_x=J_y=J_z=J\), one can easily find the different quantities obtained in [33]. Moreover, the Ising model will only investigate by replacing \(J_x=J_y=0\) and \(J_z\ne 0\) and switching the KSEA and DM couplings.

The structure of this paper is as follows. In section 2, we introduce the Hamiltonian of the system with the x-component parameters of the KSEA and DM couplings. Afterward, by varying the parameters of the \(\Gamma _x\) and the coupling constant \(J_x\), we study the ground-state entanglement of the system at zero temperature. Moreover, phase diagrams are given to study the system’s dominance states. In section 3, we determine the thermal density matrix \(\rho (T)\) in order to analyze the expression of concurrence C, which will be used to investigate the system’s entanglement. In addition, by exploring the analytical results, we examine the critical temperature \(T_c\) above which the thermal entanglement completely vanishes. In section 4, we study two special cases, such as the Ising and the Heisenberg XXX models with the x-components KSEA and DM couplings. In section 5, numerical studies will be performed to highlight the system behavior. Finally, the paper will be closed with a findings overview and perspectives of the studied system.

2 The model and the ground-state entanglement

For a two-qubit anisotropic Heisenberg XYZ chain with DM and KSEA interactions, the Hamiltonian of spin \(\frac{1}{2}\) is written by

$$\begin{aligned} \mathcal {H}_N=\sum _{i=1}^{N-1} \left( J_x\sigma _i^x\sigma _{i+1}^x+J_y\sigma _i^y\sigma _{i+1}^y+J_z\sigma _i^z\sigma _{i+1}^z +\overrightarrow{D}\cdot (\overrightarrow{\sigma }_{i}\times \overrightarrow{\sigma }_{i+1})\right) +\mathcal {H}_{KSEA},\nonumber \\ \end{aligned}$$
(1)

where \(J_x\), \(J_y\) and \(J_z\) are the coupling constants, the \(\sigma _i^{x,y,z}\) are the Pauli matrices, and \(\overrightarrow{D}\) is the DM vector coupling. The anisotropic anti-symmetric interaction DM results from the spin–orbit coupling [26, 27, 35]. What comes next, we restrict ourselves our study to the case where the DM interaction exists only along the x-axis, i.e., (\(\overrightarrow{D}=D_x.\overrightarrow{x}\)). For simplicity, we set \(\hbar =1\).

In general, the KSEA anisotropic symmetric interaction can be written as [37]

$$\begin{aligned} \mathcal {H}_{KSEA}=\sum _{i=1}^{N-1}\left( \begin{array}{cccc} \sigma _i^x &{} \sigma _i^y &{}\sigma _i^z \\ \end{array} \right) \left( \begin{array}{cccc} 0 &{} a_{12} &{} a_{13} \\ a_{12} &{} 0 &{} a_{23} \\ a_{13} &{} a_{23} &{} 0 \\ \end{array} \right) \left( \begin{array}{cccc} \sigma _{i+1}^x \\ \sigma _{i+1}^y \\ \sigma _{i+1}^z \\ \end{array} \right) . \end{aligned}$$
(2)

We consider a special kind of KSEA interaction: \(a_{12} = 0\), \(a_{13} = 0\) and \(a_{23} = \Gamma _ x\), we restrict to chains of only two spins N = 2, and the Hamiltonian equation (1) may be expressed in the standard computing base \(\mathbb {B}=\{ \left| 00\right\rangle , \left| 01\right\rangle , \left| 10\right\rangle , \left| 11\right\rangle \}\) using its matrix form which is defined by

$$\begin{aligned} \mathcal {H}=\left( \begin{array}{cccc} J_z &{} G_2 &{} G_3 &{} J_x-J_y \\ G_2^* &{} -J_z &{} J_x+J_y &{} G_3^* \\ G_3^* &{} J_x+J_y &{} -J_z &{} G_2^* \\ J_x-J_y &{} G_3 &{}G_2 &{} J_z \\ \end{array} \right) , \end{aligned}$$
(3)

where \(G_{2,3}=\pm i D_x-i \Gamma _x\). The spectrum of \(\mathcal {H}\) is easily obtained as

$$\begin{aligned} \mathcal {H}|\psi _{1,2}\rangle =\varepsilon _{1,2}|\psi _{1,2}\rangle \\ \nonumber \mathcal {H}|\psi _{3,4}\rangle =\varepsilon _{3,4}|\psi _{3,4}\rangle . \end{aligned}$$
(4)

Here, the eigenstates are written by

$$\begin{aligned} |\psi _{1,2}\rangle= & {} \frac{1}{\sqrt{2}}(-\sin (\varphi _{1,2})|00\rangle \mp i\cos (\varphi _{1,2})|01\rangle \pm i\cos (\varphi _{1,2})|10\rangle + \sin (\varphi _{1,2})|11\rangle ) \nonumber \\ |\psi _{3,4}\rangle= & {} \frac{1}{\sqrt{2}}( \sin (\varphi _{3,4})|00\rangle \mp i\cos (\varphi _{3,4})|01\rangle \mp i\cos (\varphi _{3,4})|10\rangle + \sin (\varphi _{3,4})|11\rangle ),\nonumber \\ \end{aligned}$$
(5)

where \(\varphi _{1,2}\) and \(\varphi _{3,4}\) are defined by

$$\begin{aligned} \varphi _{1,2}= & {} \arctan \left( \frac{2D_x}{\Omega _1\pm \Sigma }\right) \nonumber \\ \varphi _{3,4}= & {} \arctan \left( \frac{2 \Gamma _x }{\Omega _2\mp \Delta }\right) , \end{aligned}$$
(6)

as well as the quantities \(\Omega _1\), \(\Omega _2\), \(\Delta \) and \(\Sigma \) are given by

$$\begin{aligned} \Omega _1= & {} \sqrt{4 D_x^2+\Sigma ^2} \nonumber \\ \Omega _2= & {} \sqrt{4 \Gamma _x^2+\Delta ^2} \nonumber \\ \Delta= & {} J_y-J_z\nonumber \\ \Sigma= & {} J_y+J_z. \end{aligned}$$
(7)

The energies of the system are expressed by

$$\begin{aligned} \varepsilon _{1,2}= & {} -J_x\mp \Omega _1 \end{aligned}$$
(8)
$$\begin{aligned} \varepsilon _{3,4}= & {} J_x\mp \Omega _2. \end{aligned}$$
(9)

At this stage, we have determined the spectrum of our system, and it is important to address the ground-state entanglement of the system at absolute zero temperature \(T = 0\), which is necessary before exploring thermal quantum entanglement. In order to highlight the dependence of the ground-state energy on the coupling \(J_x\), we use Eqs. (8) and (9), and the ground-state energies can be written as

$$\begin{aligned} \left\{ \begin{array}{lll} \epsilon _1 &{}=&{}-J_x-\Omega _1 \quad \quad \quad if\,\,\,\,J_x>\frac{\Omega _2-\Omega _1}{2}\\ \epsilon _3 &{}=&{}J_x-\Omega _2 \quad \quad \quad \,\, if\,\,\,\,\,J_x<\frac{\Omega _2-\Omega _1}{2}\\ \epsilon _1 &{}=&{}\epsilon _3=-\frac{\Omega _1+\Omega _2}{2}\quad \quad if \,\,\,J_x=\frac{\Omega _2-\Omega _1}{2}. \end{array} \right. \end{aligned}$$
(10)

For the two first cases, the fundamental states are, respectively, the maximally entangled states \(\left| \psi _1\right\rangle \) and \(\left| \psi _3\right\rangle \), which implies that \(C = 1\). However, at the critical point \(J_x=\frac{1}{2}(\Omega _2-\Omega _1)\) (the lines delimiting distinct ground states in Fig. 1), the fundamental state is \(\frac{1}{\sqrt{2}}\)(\(|\psi _1\rangle \)+\(|\psi _3\rangle \)), which is an equal mixture of the doublet states \(|\psi _1\rangle \) and \(|\psi _3\rangle \), leading to the minimal concurrence \(C=0\).

To obtain the phase diagram of the system studied, we plot the function \( \Gamma _x=\pm {\sqrt{(2J_x+\Omega _1 )^2-\Delta ^2}\over 2}\) extracted from the condition of the previous equation in terms of \(J_x\).

Fig. 1
figure 1

The phase diagram of a two-qubit XYZ Heisenberg model. Here, \(\Sigma =0\) and \(\Delta =2\)

Full size image

3 Thermal density matrix and concurrence

After determining the spectrum of a system, even though this system is in a mixed state, it is simple to determine its density matrix. When a system is in thermal equilibrium, its state at a given temperature T can be represented by the density matrix \(\rho _{AB}(T)\). That will be succeeded by using the spectral decomposition of the Hamiltonian (2), which allows the thermal density matrix \(\rho _{AB}(T)\) to be represented as

$$\begin{aligned} \rho _{AB}(T)={1\over \mathbb {Z}}\sum _{l=1}^{4}e^{-\beta \epsilon _l}|\psi _l\rangle \langle \psi _l|, \end{aligned}$$
(11)

where \(\beta ={1\over k_BT}\), in which T is the temperature and \(k_B\) is the Boltzmann constant. For simplicity, we take \(k_B=1\), and the partition function of the system is defined by

$$\begin{aligned} \mathbb {Z}=\textrm{Tr}e^{-\beta \mathcal {H}}=2 e^{\beta J_x} \cosh \left( \beta \Omega _1\right) +2 e^{-\beta J_x} \cosh \left( \beta \Omega _2\right) . \end{aligned}$$
(12)

The system density matrix, as discussed previously in thermal equilibrium, can be represented in the normal calculation basis by inserting (5) and (4) into Equation (11) and obtaining

$$\begin{aligned} \rho _{AB}(T)={1\over \mathbb {Z}}\left( \begin{array}{cccc} r &{} \nu &{} \mu &{}s \\ \nu ^* &{} \gamma &{} \eta &{} \mu ^* \\ \mu ^* &{} \eta &{} \gamma &{} \nu ^* \\ s &{} \mu &{} \nu &{} r \\ \end{array} \right) . \end{aligned}$$
(13)

The elements of this density matrix, after a cumbersome algebraic manipulation, are given by

$$\begin{aligned} r,\gamma= & {} e^{\beta J_x}\frac{\Omega _1\cosh \left( \beta \Omega _1\right) \mp \Sigma \sinh \left( \beta \Omega _1\right) }{2\Omega _1}+e^{-\beta J_x}\frac{\Omega _2\cosh \left( \beta \Omega _2\right) \pm \Delta \sinh \left( \beta \Omega _2\right) }{2\Omega _2} \nonumber \\ \eta ,s= & {} -e^{\beta J_x}\frac{\Omega _1\cosh \left( \beta \Omega _1\right) \pm \Sigma \sinh \left( \beta \Omega _1\right) }{2\Omega _1}+e^{-\beta J_x}\frac{\Omega _2\cosh \left( \beta \Omega _2\right) \mp \Delta \sinh \left( \beta \Omega _2\right) }{2\Omega _2} \nonumber \\ \nu ,\mu= & {} \mp i e^{\beta J_x}\frac{Dx\sinh \left( \beta \Omega _1\right) }{\Omega _1} +i e^{-\beta J_x}\frac{\Gamma _x\sinh \left( \beta \Omega _2\right) }{\Omega _2}. \end{aligned}$$
(14)

For the density matrix \(\rho _{AB}\), the concurrence of the state is given by

$$\begin{aligned} C(\rho _{AB})=\max \left[ 0,2\max \left( \lambda _1,\lambda _2,\lambda _3,\lambda _4\right) -\sum _{i=1}^4\lambda _{i}\right] , \end{aligned}$$
(15)

where \(\lambda _i(i=1,2,3,4)\) are the square roots of the eigenvalues of the matrix

$$\begin{aligned} \mathbb {R}= \rho _{AB} \sigma _{1}^y\otimes \sigma _{2}^y \rho _{AB}^* \sigma _{1}^y\otimes \sigma _{2}^y. \end{aligned}$$
(16)

A simple calculation can be used to obtain the following \(\mathbb {R}\) matrix

$$\begin{aligned} \mathbb {R}={1\over \mathbb {Z}^2}\left( \begin{array}{cccc} U_1 &{} Q_1 &{} Q_2 &{} U_2 \\ Q_1^* &{} V_1 &{} V_2 &{} Q_2^* \\ Q_2^* &{} V_2 &{}V_1 &{} Q_1^* \\ U_2 &{} Q_2 &{} Q_1 &{} U_1\\ \end{array} \right) , \end{aligned}$$
(17)

where the components of the matrix \(\mathbb {R}\) are represented by

$$\begin{aligned} U_{1,2}= & {} \pm e^{2\beta J_x}\frac{\Omega _1\cosh \left( 2\beta \Omega _1\right) -\Sigma \sinh \left( 2\beta \Omega _1\right) }{2\Omega _1} +e^{-2\beta J_x}\frac{\Omega _2\cosh \left( 2\beta \Omega _2\right) +\Delta \sinh \left( 2\beta \Omega _2\right) }{2\Omega _2} \nonumber \\ V_{1,2}= & {} \pm e^{2\beta J_x}\frac{\Omega _1\cosh \left( 2\beta \Omega _1\right) +\Sigma \sinh \left( 2\beta \Omega _1\right) }{2\Omega _1}+e^{-2\beta J_x}\frac{\Omega _2\cosh \left( 2\beta \Omega _2\right) -\Delta \sinh \left( 2\beta \Omega _2\right) }{2\Omega _2}\nonumber \\ Q_{1,2}= & {} \mp ie^{2\beta J_x}\frac{D_x \sinh \left( 2\beta \Omega _1\right) }{\Omega _1}+ie^{-2\beta J_x}\frac{\Gamma _x \sinh \left( 2\beta \Omega _2\right) }{\Omega _2}. \end{aligned}$$
(18)

After some straightforward calculation, we get

$$\begin{aligned} \lambda _{1,2}= & {} \frac{e^{\beta J_x}\cosh \left( \beta \Omega _1\right) \mp e^{\beta J_x} \sinh \left( \beta \Omega _1\right) }{2e^{\beta J_x}\cosh \left( \beta \Omega _1\right) +2e^{-\beta J_x} \cosh \left( \beta \Omega _2\right) } \nonumber \\ \lambda _{3,4}= & {} \frac{e^{-\beta J_x}\cosh \left( \beta \Omega _2\right) \mp e^{-\beta J_x} \sinh \left( \beta \Omega _2\right) }{2e^{\beta J_x}\cosh \left( \beta \Omega _1\right) +2e^{-\beta J_x} \cosh \left( \beta \Omega _2\right) }. \end{aligned}$$
(19)

Thus, the corresponding concurrence can be expressed as

$$\begin{aligned} C(\rho _{AB}(T))= & {} max[|\lambda _{2}-\lambda _{4}|-\lambda _{1}-\lambda _{3},0], \end{aligned}$$
(20)
$$\begin{aligned} C(\rho _{AB}(T))= & {} \left\{ \begin{array}{lll} max[0, \frac{e^{\beta J_x}\sinh \left( \beta \Omega _1\right) -e^{-\beta J_x} \cosh \left( \beta \Omega _2\right) }{e^{\beta J_x}\cosh \left( \beta \Omega _1\right) +e^{-\beta J_x} \cosh \left( \beta \Omega _2\right) }];&{}\hbox {if }J_x\ge \frac{1}{2}(\Omega _2-\Omega _1)\\ \\ max[0,\frac{-e^{\beta J_x}\cosh \left( \beta \Omega _1\right) +e^{-\beta J_x} \sinh \left( \beta \Omega _2\right) }{e^{\beta J_x}\cosh \left( \beta \Omega _1\right) +e^{-\beta J_x} \cosh \left( \beta \Omega _2\right) }];&{}\hbox {if }J_x<\frac{1}{2}(\Omega _2-\Omega _1).\\ \end{array} \right. \end{aligned}$$
(21)

The XYZ model presents a quantum phase transition with the critical temperature \(T_c\). When the temperature increases, the thermal variation will be introduced in the system; thus, the entanglement will be modified due to the mixing of the fundamental and excited states. When the temperature is higher than a critical temperature, the entanglement is null, and this means that the entanglement disappears completely at \(T \ge T_c\). The quantum phase transition occurs at the critical temperature \(T_c\). However, from Eq. (21), the critical temperature \(T_c\) is determined by two different equations as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} e^{ 2 J_x/T_c}\frac{\sinh \left( \Omega _1/T_c\right) }{ \cosh \left( \Omega _2/T_c\right) }=1;&{}\hbox {if }J_x\ge \frac{1}{2}(\Omega _2-\Omega _1)\\ \\ e^{ -2 J_x/T_c}\frac{\sinh \left( \Omega _2/T_c\right) }{ \cosh \left( \Omega _1/T_c\right) }=1;&{}\hbox {if }J_x<\frac{1}{2}(\Omega _2-\Omega _1).\\ \end{array} \right. \end{aligned}$$
(22)

When \(\Omega _2=0\), the first equation reduces to equation \(e^{ 2 J_x/T_c}\sinh \left( \Omega _1/T_c\right) =1\) and the second equation has no solution. On the other hand, when \(\Omega _1=0\), the first equation a does not admit any solution and the second equation reduces to equation \(e^{ -2 J_x/T_c}\sinh \left( \Omega _2/T_c\right) =1 \).

From the above two equations, we know that when the temperature is larger than the critical temperature, when \(\Omega _1=2J_x\) it is found that \(T_c=\frac{4J_x}{ln3}\) for the coupling constant according to x-component \(J_x>\frac{-\Omega _1}{2} \)and when \(\Omega _2=-2J_x\) it is found that \(T_c=\frac{-4J_x}{ln3}\) for the coupling constant according to x-component \(J_x<\frac{\Omega _2}{2} \).

For the antiferromagnetic case we observe that the critical temperature \(T_c\) increases as the parameter \(J_x\) increases. Oppositely \(T_c\) decreases as \(J_x\) increases for the ferromagnetic case. Of course, the critical temperatures are same when \(J_x=0\).

The first limiting case concerns the high-temperature regime. The eigenvalues of the matrix R are represented in the following manner

$$\begin{aligned} \lambda _{1,2}\simeq & {} \frac{1}{4} +\frac{1}{4}(J_x\mp \Omega _1) \beta \nonumber \\\lambda _{3,4}\simeq & {} t\frac{1}{4} +\frac{1}{4}(J_x\mp \Omega _2), \beta \end{aligned}$$
(23)

Following a comparison of the eigenvalues of R at high temperature, the expression of concurrence, in this case, may be expressed by the relationship

$$\begin{aligned} C(T)\simeq \left\{ \begin{array}{lll} max[0,\frac{1}{2} \left( \left( J_x+\Omega _1\right) \beta -1\right) ];&{}\hbox {if }J_x\ge \frac{1}{2}(\Omega _2-\Omega _1)\\ \\ max[0,\frac{1}{2} \left( \left( -J_x+\Omega _2\right) \beta -1\right) ];&{}\hbox {if }J_x<\frac{1}{2}(\Omega _2-\Omega _1).\\ \end{array} \right. \end{aligned}$$
(24)

When the temperature T approaches a certain value, the expression of concurrence reveals that \(\mathcal {C}\rightarrow 0\) makes the system states separable and not entangled at high temperature.

The last limiting case is studying strong DM and KSEA interactions. In this perspective, we assume that \(D_x \gg \Sigma \), \(\Gamma _x \gg \Delta \) and \(J_x\rightarrow 0\); as a result, the eigenvalues of the matrix R are expressed in the following form

$$\begin{aligned} \lambda _{1,2}\simeq & {} \frac{\cosh \left( 2\beta D_x\right) \mp \sinh \left( 2\beta D_x\right) }{2\cosh \left( 2\beta D_x\right) +2 \cosh \left( 2\beta \Gamma _x\right) } \nonumber \\ \lambda _{3,4}\simeq & {} \frac{\cosh \left( 2\beta \Gamma _x\right) \mp \sinh \left( 2\beta \Gamma _x\right) }{2\cosh \left( 2\beta D_x\right) +2 \cosh \left( 2\beta \Gamma _x\right) }. \end{aligned}$$
(25)

It is clear that (25) depends on \(\Gamma _x\) and \(D_x\). Therefore, the expression of concurrence is also dependent on the \(\Gamma _x\) and \(D_x\). The concurrence is expressed by

$$\begin{aligned} C(T)\simeq \left\{ \begin{array}{lll} max[0,\frac{\sinh (2 \beta \Gamma _x)-\cosh (2 \beta \Gamma _x)+\sinh (2 \beta D_x)}{\cosh (2 \beta \Gamma _x)+\cosh (2 \beta D_x)} ];&{}\hbox {if }\Gamma _x\ge D_x\\ \\ max[0,\frac{-\cosh (2 \beta D_x)}{\cosh (2 \beta \Gamma _x)+\cosh (2 \beta Dx)} ];&{}\hbox {if }\Gamma _x<D_x.\\ \end{array} \right. \end{aligned}$$
(26)

For the large values of \(\Gamma _x\) and \(D_x\), if \(\Gamma _x< D_x\), the concurrence takes the value \(C =0\), and this condition indicates that the states become separable. Inversely, when \(\Gamma _x\ge D_x\), the concurrence approaches 1, which indicates that the states are entangled.

4 Special cases

Before starting the numerical study, two special cases are discussed. Using the analytical formula in equation (21) and by adjusting some quantities, such as the spin couplings \(J_x\), \(J_y\) and \(J_z\), we give a detailed study for the general XYZ Heisenberg model. Then, we shall consider the Ising model \((J_x = J_y = 0 \) with \(J_z\ne 0\)) and the XXX model (\(J_x=J_y=J_z=J\)). Now, we arrive to analyze the amount of quantum entanglement via the concurrence C in spin systems in the presence of the DM and KSEA interactions.

4.1 Ising model

To start, we consider the Ising model corresponding to the case (\(J_x = J_y = 0 \) and \(J_z\ne 0\)), which implies that \(\Delta = -J_z\) and \(\Sigma =J_z\) with \(D_x=\Gamma _x=0\), which indicates that \(\Omega _1=\Omega _2=|J_z|\). Replacing in Eq. (21), we obtain

$$\begin{aligned} C(T)=max[0,-\frac{e^{-\frac{|J_z|}{T}}}{e^{-\frac{|J_z|}{T}}+e^{\frac{|J_z|}{T}}}]=0. \end{aligned}$$
(27)

We can see from the density matrix of eq. (13) why the Ising thermal system does not entangle any temperature T, and it is diagonal in the standard basis involving no quantum entanglement. This is not surprising given that the maximum four entangled states as eigenvectors \(|\psi _{1,2}\rangle \) and \(|\psi _{3,4}\rangle \) are degenerate, implying that the Ising thermal state lacks entanglement.

4.2 XXX model

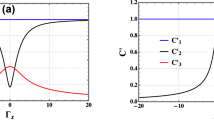
Let us now to analyze the concurrence C in Heisenberg XXX model corresponding to the case, where \(J_x = J_y = J_z = J\) and \(D_x=\Gamma _x=1\). In this situation, the expression of C is written by

$$\begin{aligned} {C(T)= \left\{ \begin{array}{lll} max[0,\frac{-\cosh (\frac{2}{T}) +e^{ \frac{2J}{T}}\sinh (\frac{2 \sqrt{1 + J^2}}{T}}{\cosh (\frac{2}{T}) +e^{ \frac{2J}{T}}\cosh (\frac{2\sqrt{1 + J^2}}{T}}];&{}\hbox {if }J\ge 0\\ \\ max[0,\frac{\sinh (\frac{2}{T}) -e^{ \frac{2J}{T}}\cosh (\frac{2 \sqrt{1 + J^2}}{T}}{\cosh (\frac{2}{T}) +e^{ \frac{2J}{T}}\cosh (\frac{2\sqrt{1 + J^2}}{T}}];&{}\hbox {if }J<0.\\ \end{array} \right. } \end{aligned}$$
(28)

Conversely to the Ising model, the concurrence for the XXX model is different to zero at low temperature. For \(T\rightarrow 0\), the ground state of the system is a single state \(|\psi _2\rangle \) or \(|\psi _4\rangle \), which is maximally entangled states. And by increasing the temperature, the singlet mixes with the triplets in an intricate state until the critical temperature in this case the concurrence is null, which is clearly noted in figure (2). Now, to investigate the behaviors of the system we plots the thermal concurrence in terms of temperature for different values of parameter J with \(D_x=\Gamma _x=1\).

Fig. 2
figure 2

The concurrence C in terms of temperature T for three values of the coupling constant J

Full size image

5 Results and discussion

This section of the paper will focus on numerical analysis based on the preceding parts. To accomplish this, we will investigate numerous aspects of entanglement in a two-qubit Heisenberg XYZ chain with x-directions of the DM and KSEA interactions. By varying the x-components of the DM and KSEA interactions, we will investigate concurrence in terms of temperature T and the coupling parameters for the spin interactions \(J_x\), \(J_y\) and \(J_z\). Also, we illustrate the concurrence C in connection to numerous system-influencing parameters.

Fig. 3
figure 3

The concurrence C(\(\rho \)) as a function of T and \(\Gamma _x\) for different values of DM interaction. Here, \(J_x = 1\), \(\Sigma =2\) and \(\Delta =0\)

Full size image

Figure 3 shows the behavior of the concurrence \(C(\rho )\) as function of the temperature T and \(\Gamma _x\) for different values of the parameter \(D_x\) (i.e., the DM interaction strength). In Fig. 3a, the blue area represents non-entangled or separable states in the system. In Fig. 3b–d, we analyze the concurrency of the system taking into account the DM interaction. It is evident that as the parameter D rises, the area of the entangled states grows.

Fig. 4
figure 4

The dependence of the concurrence C for the XYZ model with the absolute temperature T for different parameters ( \(D_x=3\), \(\Delta = 2\) and \(\Sigma = 0\))

Full size image

In Fig. 4, we plot the concurrence C as a function of temperature T. We observe that while the temperature rises, the concurrence reduces, and we can clearly find that for a certain temperature, increasing \(\Gamma _x\) can reduce concurrency if \(\Gamma _x\) is less than \(\Gamma _{xc}=\frac{1}{2}\sqrt{(2 J_x + \Omega _1)^2 - \Delta ^2} \rightarrow \sqrt{15}\) and can increase concurrence if \(\Gamma _x\) is higher than \(\Gamma _{xc}\) and the concurrence is always null even if temperature varies for the case \(\Gamma _x=\Gamma _{xc}\).

Fig. 5
figure 5

The dependence of the concurrence C for the XYZ model with the \(\Gamma _x\) for \(J_x=-1\), \(\Delta = 1\) and \(\Sigma = 0\)

Full size image
Fig. 6
figure 6

The concurrence C is a function of \(J_x\) for different values of T. We get \(C \approx 1\) only for \(T \approx 0\); we have set \( \Delta = 2\), \(\Sigma = 0\) and \(\Gamma _x=3\) for Fig. (a)

Full size image

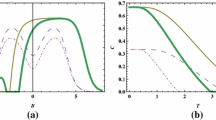
Figure 5 shows the concurrence depending on \(D_x\) at a fixed temperature and spin coupling coefficients for two values of positive \(\Gamma _x\). In Fig. 4a, for \(T=0.5\) at \(D_x=0\) the concurrency is zero for \(\Gamma _x=0\) and takes maximum value for \(\Gamma _x=2\), and when we increase the value of \(|D_x|\), the concurrence will be decreased to zero after the concurrence will be increased to a maximum value. In Fig. 5b, for \(T=3\) when we increase the value of \(|D_x|\), the concurrence will be increased to a peak value, and Dx has a smaller critical value and more entanglement for \(\Gamma _x=0\) compared to \(\Gamma _x=2\). In Fig. 6, by fixing \(\Sigma \), \( \Delta \), \(D_x\), \(\Gamma _x\) and varying \(J_x\) for different values of temperature T we see that the concurrence increases if we pick values of \(J_x\) greater or lower than \(\frac{\Omega _2-\Omega _1}{2}\), noting that the concurrence is null for \(J_{xc}=1.44\). However, there is a value of \(J_x\) beyond which C does not rise. This behavior is more drastic if we are in the region where \(J_x\ge \frac{\Omega _2-\Omega _1}{2}\). There, only for \(T \approx 0\) we obtain \(C \approx 1\). For any other value of T, increasing \(J_x\) makes \(C\rightarrow C_{max}\), where \(C_{max} < 1\). And more, the higher the T, the lower the value of \(C_{max}\). We are in the region where \(J_x<\frac{\Omega _2-\Omega _1}{2}\), which is in agreement with the results in Fig. (1).

Fig. 7
figure 7

The \(D_x\)-dependence of the critical temperature \(T_c\) for antiferromagnetic and ferromagnetic with choosing \(\Delta = 2\) and \(\Sigma =0\)

Full size image

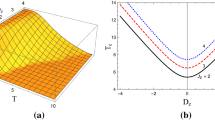
Figure 7 depicts the behavior of critical temperature versus the parameters of the \(D_x\) for different values of \(\Gamma _x\). In Fig. 7a, we plot \(T_c\) as a function of \(D_x\) with choosing \(J_x=1\); as this figure shows, \(T_c\) increases monotonically with rising \(|D_x|\) in the region \(|D_x|\ge D_{xc}\). When the value of the parameter \(D_x\) is constant, we find that \(T_c\) reduces with an increase in \(\Gamma _x\). However, it behaves differently in the region \(|D_x|< D_{xc}\). In Fig. 7b, we plot \(T_c\) as a function of \(D_x\) by choosing \(J_x = -1\); we see that we have the same behavior with the lower critical temperature compared to the case of \(J_x=1\), which is in conformity with the findings correspond to the XXX model investigated in Fig. 2.

6 Conclusion and perspectives

In this work, we have investigated the thermal entanglement in a two-qubit Heisenberg XYZ chain with the x-components of the DM and KSEA interactions. The Hamiltonian model was introduced, and the eigensystems of the studied system have been found through mathematical calculations. However, the eigenstates allow us to describe the phase diagram of the ground state at absolute zero temperature. Afterward, we have established the expression of concurrence in terms of the spin’s coupling constant \(J_i(i=x, y, z)\), the x-components of DM and KSEA interactions, and the temperature T. Next, we analyzed the numerical behavior of the measured entanglements of our model. Additionally, we have studied various limits and also special cases, such as Ising and XXX Heisenberg models, by fixing some quantities involved in our study. On the other hand, we have shown that the degree of entanglement of the system states has affected by the spin’s coupling constant J, the temperature T and the x-components of DM or KSEA interactions. Indeed, when the spin coupling \(J_x\) is increased, and for small values of \(\Gamma _x\), the critical temperature is more elevated, the state system is maximally entangled. Additionally, with the great values of \(\Gamma _x\), the critical temperature will be lower, and the system becomes less entangled. Finally, we have deduced that the separability of the states has been obtained at high temperatures or critical value of \(\Gamma _{xc}\). Besides, the entanglement of the states can be obtained for large values of \(D_x\) or low temperatures.

Still, some fascinating queries have to be managed. Can we utilize the studied system to examine entanglement’s dynamic behaviors and illustrate the fundamental characteristics of quantum entanglement at a finite time? A connected question arose, what about other correlation measurements to study? These points and associated queries are under consideration.