1 Introduction

The reversible logic is one of the most applied issues in novel technologies, i.e., quantum computations, optical computations, QCA, etc. [1,2,3,4]. In the processing circuits, there are computational components, such as adder and multiplier, and other computational circuits. Since all components should be reversible in a reversible system, the different parts of such a processing system are implemented by the reversible technologies [1, 5], i.e., the constituent parts of the processor such as registers and arithmetic and logic unit, memory, multiplexers, etc. One of the important parts of the processing systems is the arithmetic and logic unit, responsible for the implementation of the different operations on the data. In most conducted research so far, some efforts have been made to design the different computational circuits, e.g., adder, multiplier, and also the computation and logic units in reversible form. Such being a case will decrease the different costs of these circuits as much as possible [6,7,8]. One of the interesting fields in this issue is designing the reversible multiplier. Multipliers are the most practical circuits in the processing systems, and making them reversible increases the costs. As mentioned earlier, the desired cost criteria can be the quantum cost, the number of gates, delay, or the circuit size in terms of the number of inputs and outputs. Designing a reversible multiplier with a lower cost has captured many reversible system designers. The cost criteria include many different items, i.e., quantum cost, the number of gates, the number of ancilla inputs, and garbage outputs [5].

In most works done in this field so far, some efforts have been made to design a quantum reversible multiplier with a lower quantum cost [9,10,11,12,13,14,15,16]. However, regularly, the reversible circuits suffer from a higher number of ancilla inputs and garbage outputs. This is due to the fact that in order to make a digital circuit reversible, it is required to add a number of garbage outputs, and followed by that, the number of ancilla inputs [17, 18]. In most synthesis methods of reversible circuits, there is a restriction on the circuit size, meaning that if the number of inputs and outputs are high, the circuit design will be problematic. Accordingly, one of the methods proposed for such circuits is hierarchical design. As an illustration, in order to implement the multiplier in [9,10,11,12,13,14,15,16, 19], a number of reversible circuits have been designed for the generation of partial products. Afterward, another reversible circuit is provided for the summation of these partial products. Because each circuit requires the addition of ancilla inputs and garbage output, the number of these inputs and outputs is numerous in the overall circuit.

In quantum circuits, the processing operations are carried out on the elements transmitting the data of these systems [1]. The great number of circuit inputs and outputs in the reversible technologies, e.g., quantum circuits, means that the number of constituent elements of the desired system’s data (like Qubits) should be high. Creating these elements is regularly costly. For instance, one of the qubit creation methods in quantum technology is the Ion-trap method, where an atom is loaded electrically, becoming an ion. The production of each ion calls for costly instrumentations [20, 21]. Therefore, one of the interesting fields among researchers is to find a way to reduce the number of qubits and, in other words, diminish the size of reversible circuits [22,23,24,25].

Decreasing the number of constituent blocks of a reversible circuit can reduce the circuit size. This study aims to provide a method for designing an n\(\times \)n quantum multiplier, substantially reducing the number of ancilla inputs and garbage outputs. Despite the most works taken care of in the multiplier design field so far, which is done in two steps of designing the partial product generation and the partial product summation circuit design, this method is implemented based on the reduction of the multiplier constituent blocks. The main idea of this method is to design a multiplier in the form of blocks, where each one constitutes one of the multiplier columns and generates one qubit of the final multiplication result. Each block receives the pertinent qubit to itself from the main inputs and also the carry inputs from the previous columns. Compared to the previous studies, the number of ancilla inputs and garbage outputs of the multiplier by this method is improved between 14–66%. Also, the total number of inputs and outputs of the multiplier is declined by 9–55% using the provided method. The reduction of inputs and outputs in the reversible circuits can invariably increase the number of gates and the quantum costs of the circuit. That is because a reversible function requires constant inputs used as auxiliary signals, the fewer these signals, the more costly gates are required for building the functions. In the proposed method, the criteria, e.g., quantum costs and the number of gates rise, are addressed in the evaluation and comparison section.

In addition to the aforementioned points, there is another issue that should be taken into consideration: the reliability of the system. The fault is inevitable in a quantum system due to the quantum decoherence, fault in information, and quantum operations. Accordingly, in the implementation of gates and reversible quantum circuits, employing fault correction methods, is of significant importance for raising the circuits’ reliability.

The fault tolerance means the capability of the system for proceeding with a defined operation even under the breakdown condition. Generally, the fault tolerance is correlated with the reliability, the correct performance, and the lack of failure of the system. A fault-tolerant system should be able to take care of the software and hardware breakdowns, power consumption, or other unpredicted breakdowns, maintaining its initial performance despite the mentioned problems [26].

Quantum fault correction in reliable quantum systems is unavoidable. When a qubit is placed in a certain superposition, it gradually encounters deviation due to the connection it forms with its surrounding environment. Accordingly, after measurement, the probability of observing different basic cases with their considered initial values will be different. This phenomenon is called quantum decoherence. We want the ratio of quantum gate run time to the quantum coherence loss time of qubits to be extremely small. Decoherence does not solely lead to fault. However, if different qubits in series encounter successive decoherence, this value can bring about a fault in final cases [1]. Quantum fault correction codes must be employed to overcome this phenomenon. These codes are the result of applying algorithms on correct qubits, which can be employed to track the fault location and correct them.

The article is arranged as follows. In Sect. 2, reversible logic will briefly be explained. Section 3 examines the previous works in reversible and fault-tolerant multiplies. Section 4 describes the proposed method of this article for the design of reversible multiplies and making them fault-tolerant. In this section, the multiplication operation and design method of a multiplier in a column-wise manner are explained. Ultimately, the results obtained by this evaluation method are compared with previous works in Sect. 5.

2 Literature review

In this section, an introduction to reversible logic and quantum circuits is presented, which is required to better understand the concepts covered in this article. First, the concepts pertinent to reversibility are examined, and then fault tolerance in the quantum circuit will be studied.

2.1 Reversibility

Reversible circuits are made up of reversible gates. These gates have special properties that most classic gates lack. One of these properties is that the expressing function of them is one-to-one. Accordingly, the numbers of inputs and outputs of these gates are equal. Besides, the input value of these gates can be obtained by having their output values. Figure 1 demonstrates several known reversible gates and their quantum function description matrix. These reversible gates are known as primitive quantum gates and can be employed in the quantum implementation of each reversible gate. The description matrix of each quantum gate is necessarily unitary.

Fig. 1
figure 1

Symbol of basic quantum gates and their matrices [5]

Full size image

Quantum circuits can be evaluated by different criteria. One of these criteria is quantum cost. Due to the fact that the reversible gates of the NCT set were used in this research, the quantum cost of the gates of this set is defined as follows.

Definition 1

Quantum cost of one- and two- input gates in NCT set equals 1. To calculate the quantum cost of each gate with more than two inputs, it is decomposed into a circuit including basic gates and its quantum cost is calculated based on the previous rule.

Two methods can be employed to calculate the quantum cost of the reversible quantum gate. First, a gate can be implemented by using a quantum gate 1\(\times \)1 or 2\(\times \)2 and then counting their number. Second, new gates can be synthesized using known gates whose quantum costs are known and add them up to calculate quantum cost [5].

Other quantum gates can be built using primitive gates; For instance, the Toffoli gate is one of them. Toffoli gate is indeed the developed version of C-NOT gate [27,28,29], whose control input number is greater than 1. \(TOF_n\) represents a Toffoli gate with n number of inputs. Toffoli gate with two inputs is demonstrated in Fig. 2a. In this gate, if the value of all control inputs equals 1, the output value of the target line will be complement of the value of the target input. Otherwise, the value of the target output will equal the value of the target input [30]. Quantum implementation of this gate is indicated in Fig. 2b using quantum basic gates. According to definition 1, the quantum cost of the Toffoli gate with three inputs equals 5.

Fig. 2
figure 2

a Toffoli gate with two control inputs. b quantum implementation of Toffoli gate [30]

Full size image

A set including Toffoli gates with any number of inputs is a universal set, and every reversible circuit can be implemented using that set of gates [31].

Another evaluation criteria employed in some other works is the number of quantum gates used in a circuit. The number of inputs and outputs in quantum circuits is also of paramount importance. Inputs of a quantum circuit include main and ancilla inputs. Ancilla inputs are usually produced to make the number of circuit inputs and outputs equal. Circuit outputs also include main and garbage outputs. Garbage outputs are usually added to the circuit to create a one-to-one relationship between input combinations and output combinations.

2.2 The fault tolerance

Fault tolerance is practically crucial since it is impossible to create a perfect system. The main problem is that as the system complexity increases, the reliability level declines substantially. As an illustration, if the reliability of the singular components is 99.99%, the reliability of a system with 100 components without redundancy will be 99.01%, and the reliability of a system with 10,000 components without redundancy will be 36.79%; in this case, these are not acceptable in most applications. If we expect the reliability of 99% for a system containing 10,000 components, the reliability of the singular components should be at least 99.999%, meaning an intense cost enhancement [26].

The other problem is that although the designers make drastic efforts to solve entire hardware and software issues before providing products to the market, it has been shown that this objective is unachievable. Some unexpected environmental factors are inevitably not taken into consideration, and some individual mistakes are not predictable. Accordingly, even in the case of a complete and perfect system design and creation, the out-of-control conditions of the designer could bring about some issues. A system incapable of performing the desired performance has encountered failure [26].

One of the fault causes in the quantum systems was the decoherence phenomenon. This phenomenon in [32] is defined as follows.

Definition 2

Decoherence means the change of state of the quantum system as a result of interaction with the surrounding environment.

This phenomenon is a strong challenge in the quantum world and should be studied as a fault source. In the entire definition of quantum systems, it is implicitly assumed that they are apart from their surrounding environment. However, they could connect with the outside world. Accordingly, the state of a quantum system could be changed following this connection. This change can be interpreted as the change of the quantum system components and fault occurrence. Since these changes are inevitable, a group of research is done in the realm of identifying such faults and making the system tolerant against them.

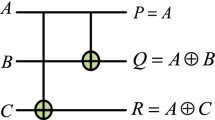
One of the methods used for making a quantum circuit fault-tolerant is using a balance between the input and output parities. Indeed, in this method, in order to create a fault-tolerant circuit, some gates are used, which are fault-tolerant themselves. A group of these gates is recognized as conservative gates [33]. Their performance is such that the number of qubit with the value of ’1’ in each input combination is equal to its corresponding counterpart in the output combination. As an illustration, the Fredkin reversible gate, which was introduced before and whose truth table and symbol are indicated in Fig. 3, is considered a conservative gate.

Fig. 3
figure 3

a Fredkin gate symbol. b a Fredkin gate truth table [33]

Full size image

The circuit that is completely consisted of the conservative gates is also conservative. Accordingly, the existence of single and some of the multiple faults could be identified concerning the existence or the absence of equivalence between the number of “1”s in the input and output values.

The conservative gates do not have a variety of types. Therefore, merely making use of these circuits in the reversible ones can lead them to a limit. The other gates used in the implementation of tolerant reversible circuits are the parity preserving gates [34]. As it could be interpreted from its name, these gates maintain the equality between the input and output parities in the entire state. Thereby, in the case of one or plenty of faults, we can identify them. In Figs. 4 and 5, two samples of the parity preserving gates could be observed.

Fig. 4
figure 4

a NFT gate symbol. b The quantum implementation of NFT gate. c The truth table of an NFT gate [34]

Full size image
Fig. 5
figure 5

a F2G gate symbol. b The quantum implementation of F2G gate. c The truth table of a F2G gate [34]

Full size image

Each reversible circuit constituted by the parity preserving gates is the parity preserving. In the next section, we will investigate the efforts where the fault-tolerant arithmetic and logic unit is designed using the parity preserving gates.

The other method used for the tolerant implementation of the reversible circuits is using the quantum gates of Clifford+T set. Such circuits are used in approximate computing applications. This set includes a number of basic quantum gates that have low latency. Therefore, before changing their values due to quantum decoherence, they complete the operation on the input values [35]. Accordingly, it is expected that the faults caused by decoherence do not occur in them. The set above is a universal set [36]. Therefore, each quantum circuit could be implemented using them and other gates created by them.

3 The previous works

A multiplier is one of the important components of the computational systems since it plays in most processing operations [31, 37, 38]. In [39], an improved design is provided for the implementation of the reversible multiplier. For this purpose, it introduces a reversible gate called BVF, which duplicates the multiplier inputs. Next, by using this gate, they have designed a multiplier where the number of Fan-out gates has declined by 50%, compared to the previous works introduced in [40,41,42]. All in all, the total cost of implementation and circuit size is declined. [43] has provided a fault-tolerant reversible multiplier by the Booth-based algorithm called K-Algorithm, which has improved by 33% in the costs like the number of quantum gates, ancilla inputs, and garbage outputs, compared to the previous works.

In [44], a 4\(\times \)4 quantum multiplier scalable to n\(\times \)n is proposed. In this article, the cost criteria of a multiplier are reduced compared to similar works by improving multiplier components and proposing new implementations for them. These criteria include the number of quantum gates, the number of ancilla inputs, the number of garbage outputs, and quantum cost.

One of the common methods of reversible multiplier implementation is a partition of a multiplier into two sections: Generation circuit of partial products and summer circuit for adding these partial products and producing final multiplication product [9,10,11,12,13,14,15,16, 37, 38]. In the following, this method will be examined for different articles.

In [11], Pouraliakbar et al. proposed a new reversible multiplier with a lower quantum cost, lesser number of gates, a constant number of inputs, and lesser number of additional outputs, compared to previous works. In this article, the circuit is divided into two sections. The first section consists of AND and NAND operations for producing partial products, and TG and PG reversible gates are employed to implement them. The second section consists of storage and reversible adder circuits. Besides, Zomorrodi Moghaddam et al. in [45] introduced a new structure for an n\(\times \)n multiplier. This article focuses on reducing quantum costs. For this purpose, the adder circuit is integrated with the multiplier to increase the efficiency of circuit hardware.

In [10], Peres gates are employed to produce partial products. In addition, since there is not fan-out in reversible circuits, RAM gates that comprise three CNOT gates are employed to produce several copies of a signal. In order to add partial products, a known adder structure is employed. In [11], a multiplier structure of signed magnitude of Wallace is implemented. In this structure also partial products are implemented by Toffoli gates. Moreover, Feynman gates are employed to produce fan-out. Afterward, the sum operation is carried out by using HNG and Peres gates as full adder and half adder. This work attempts to reduce circuit depth as much as possible using a structure considered for sum operation.

When partial products are produced by Peres gates, the adder that is proposed in [12] employs known Carry Save Adder to sum these partial products. Besides, [13, 14] employs an improved reversible adder with a fewer number of ancilla inputs and garbage outputs. However, the circuits producing partial products are reversible gates like Tofolli, similar to other works.

In designs proposed in [15, 16], first, the partial products are generated by the reversible gates introduced by previous works. Then, adder structures such as Ripple Carry Adder are built by gates such as ZPLG, HNG, and PPTG and produce a final multiplication product. Despite works carried out so far, blocks are designed in [46] that simultaneously carry out production steps of partial products and adding them. Besides, given that the gates proposed in this work are parity preserving, the proposed multiplier is fault-tolerant. In this work also the number of ancilla inputs and garbage outputs is increased since the number of constituent blocks of the final circuit is high.

In [22], the value of garbage output onto which partial products are put is reset to zero using a Toffoli gate and is used as a new ancilla input. Thereby, the number of ancilla inputs is reduced. In [23], the shift and sum algorithms are employed to implement the multiplication operation. In order to carry out shift operations, few replacement operators are consecutively employed. Afterward, the multiplied value is added to the multiplication product if necessary using a controlled adder circuit. This article significantly reduced the number of ancilla inputs and garbage outputs. It is worth mentioning that in most of the other works, the outputs that follow the input value without change are not considered garbage output to count the number of garbage outputs. However, these outputs must be accounted for as garbage outputs since they are not main outputs. Accordingly, the number of ancilla inputs is a better criterion for comparison.

4 The structure of fault-tolerant quantum multiplier

This section proposes a method to implement an n\(\times \)n fault-tolerant reversible multiplier with a reduced number of constant inputs and garbage outputs.

4.1 The column-wise architecture for quantum multiplier

The proposed method is based on dividing the multiplication operation of two n-qubit quantities into subsections that are responsible for producing one qubit of the final multiplication product. Indeed, the multiplication operation is column-wise. In each column, the required qubits from input values multiplied by each other, and the product qubit pertinent to that column and also the carry qubits that must be added to the next columns generated.

First, the way multiplication operation is carried out on two n-qubit quantities is explained. To be more specific, a multiplication function between two 8-qubit digits is indicated in Fig. 6 as an example. In the first three rows, there are a few carry qubits produced in previous columns that are added to each column. The \(C_{i,j}\) indicates the carry digit that is produced in column i and added to column j. Rows four and five indicate two 8-qubit quantities that are supposed to be multiplied by each other. \(a_i\) and \(b_j\) are digits with place value i of quantity a and place value j of quantity b, respectively. In these values, the less significant digit is on the right and the most significant digit is on the left. In the next eight rows, there are partial products indicated by \(a_ib_j\). For simplicity, each one of them is indicated by \(P_{i,j}\). The final multiplication is indicated in the last row. The digit pertinent to column i of the ultimate product is indicated by \(S_i\).

Fig. 6
figure 6

Multiplication operation of two 8-qubit quantities

Full size image
Fig. 7
figure 7

Quantum multiplier production pseudo-code

Full size image
Fig. 8
figure 8

Quantum multiplier production pseudo-code(Cont.)

Full size image

The method of product generation is described in the form of pseudo-code indicated in Figs. 7, 8. In the following, different parts of this pseudo-code and the way multiplication products are generated and carry outputs in each column will elaborately be explained. The number of columns required for the desired multiplier equals the number of multiplication product’s qubits. Given that the multiplication product of two n-qubit quantities will be a 2n-qubit quantity, the column number of an n-qubit multiplier will be 2\(\times \)n as can be seen in Fig. 6.

$$\begin{aligned} \#Col =\ 2 \times n \end{aligned}$$
(1)

Afterward, the number of partial products in each column and also the number of carry inputs inserted from previous columns to each column must be determined to be able to produce these partial products using suitable reversible gates, add them to each other, and add carry inputs to them. As indicated in Fig. 6, the number of partial products in columns increases from the first column to the middle column and then decreases until the last column (rows 2 to 7). For example, in Fig. 6 the partial product of column 10 of an 8-bit reversible multiplier is shown. The number of partial products for column i in an n-qubit quantum multiplier is given by Eq. 2. As it is clear from this equation, column number starts from 0 and goes up to 2n-1.

$$\begin{aligned} \#PP_i\ = {\left\{ \begin{array}{ll} i+1 \quad \quad \quad \ if\ 0\le i<n\\ 2n-i-1 \quad if \ n\le i<2n\\ \end{array}\right. } \end{aligned}$$
(2)

In order to find the number of carry inputs of each column, by starting from the first column, we should specify the carry outputs and the columns where these outputs enter to. As an illustration, consider column 9 in Fig. 6. When the previous columns are explored, it is specified that in column 6, the number of partial products and carry inputs is equal to 9. Then, the sum of this column could be at most 9, which needs 4 qubits in binary format for being displayed. Therefore, three carry outputs will be entered into columns 7, 8, and 9. Also, columns 7 and 8 have the carry outputs to column 9. Accordingly, column 9 has three carry inputs. In Fig. 6 the carries entered to column 9 of an 8-bit reversible multiplier are shown.

As indicated in lines 12 to 19 of the pseudo-code of Figs. 7, 8 in order to determine the number of input and output signals of each column, we should take some notes into consideration. The main inputs of each column, containing the values of qubits A and B, are propagated without being changed to the outputs to the same column. These inputs are used in the next columns, and since there is no fan-out in the reversible gates, these signals should pass through the columns without change. In addition, other signals are required for the multiplication and carry outputs. If the desired column does not have any carry input, these signals are recognized as the ancilla input and obtain a constant value of ’0’. As an instance, in Fig. 9a, we can see the relevant block to column 1. This column has four main inputs and six main outputs. Thereby, two ancilla inputs with a constant value of ’0’ are added to them so that the number of inputs and outputs of the circuit are equal. If the desired column has a carry input, the sum of that column on the relevant signal to this input is generated. Therefore, for the sum output signal, instead of ancilla input, the carry input is used. In Fig. 9b, the relevant block to column 3 is demonstrated, which is an instance of the mentioned state. If the desired column has more than one carry input, based on each, an ancilla input is added to the column with a constant value of ’0’. The example of this state is observed in Fig. 9c, which indicates column 9 with three carry inputs. Since a number of the signals of this column is not used in the next one, it is displayed as a garbage output.

Fig. 9
figure 9

Some of the constituent blocks of the 8-qubit quantum multiplier

Full size image

Now, we should specify the reversible gates required for the summation of these partial products and the addition of input carries in each column. In each column, in order to produce each partial multiplier and its addition to the previous product, we need a reversible gate set. In this article, each of these sets is called a "Group". Therefore, in each column, based on each partial product, a group is required. As an illustration, for column 1 of the 8-qubit multiplier, the required circuit diagram is observed in Fig. 10a. If the desired column has a carry input, partial products are added to that signal. Thereby, there is no need for the addition of a group based on the carry input. An example of this state is column 3 of the 8-qubit multiplier, which is indicated in Fig. 10b. However, if more than one carry input exists in a column, an additional group is required to add each of them to the carry summations. Column 9 of the 8-qubit multiplier is indicated as an instance in Fig. 10c. In this figure, the signals on which no action is performed in each block have crossed that block with a bold line. Therefore, the number of the column i groups is determined using Eq. 3.

Fig. 10
figure 10

The diagram block of the existing groups in some of the 8-qubit quantum multiplier columns. a column 1. b column 3. c column 9

Full size image
$$\begin{aligned} \#\text {Group}_i\ = {\left\{ \begin{array}{ll} \#PP_i\\ \quad \quad \quad \quad \text {if}\ \text {column}\ i\ \text {has}\ \text {not}\ \text {carry}\ \text {input}\\ \\ \#PP_i+\#\text {Carry}\_in_i-1\\ \quad \quad \quad \quad \text {if}\ \text {column}\ i\ \text {has}\ \text {carry}\ \text {input(s)}\\ \end{array}\right. } \end{aligned}$$
(3)

In the next step, the gates of each group will be determined. The number of gates of each group is obtained concerning the maximum summation that the group creates, and it is equal to the number of required qubits for the display of this maximum value (lines 27 to 35). If there is no carry input in a column, the maximum summation of the first group is 1, the next 2, and so forth. As an illustration, in Fig. 10a, a value that the first group creates is equal to a partial product that can be 1 at maximum. Also, the next group adds the next partial product, and the generated value could be at most 2, requiring 2 qubits for display. Figure 11 demonstrates the designed reversible circuit for column 1.

Fig. 11
figure 11

The reversible circuit of column 1 of the 8-qubit multiplication

Full size image

If there is a carry input in a column, the maximum summation of the first group equals 2, the next 3, and so forth, since it adds the first partial product group to the carry one. As an illustration, the first group in Fig. 10b and c can generate the maximum value of 2, the next 3 and so on. Figure 12 demonstrates the summation of the partial products and the addition of the previous carry qubit to them in column 3. In this column, 5 qubits are summed with each other, including four partial product and a carry qubit. Therefore, the multiplication of this column calls for 3 qubits. The low-value summation qubit appears on the signal \(C_{2,3}\) and the high-value qubits on the constant inputs. As mentioned before, in order to generate each partial product, a Toffoli gate with two control inputs, \(TOF_3\), is used. Since these multiplications are added to the carry qubit, a Toffoli gate is placed with three control inputs before each of them. In order to generate the third partial product and its addition to the previous summation, three gates have been used since the generated summation can have a value of 4, and its display requires 3 qubits.

Fig. 12
figure 12

The reversible circuit of column 3 of the 8-qubit multiplier

Full size image

According to what is mentioned before, the number of the group j gates from column i is determined using Eq. 4. Group number starts from 0 like column number.

$$\begin{aligned} \#\text {Gate}_{i,j}\ = {\left\{ \begin{array}{ll} \lfloor \log _2(1+j)\rfloor +1\ \text {if}\ \text {column}\ i\ \text {does't}\ \text {have}\ \text {carry}\ \text {input}\\ \lfloor \log _2(2+j)\rfloor +1\ \text {if}\ \text {column}\ i\ \text {has}\ \text {carry}\ \text {input(s)}\\ \end{array}\right. } \end{aligned}$$
(4)

In the next step, the number of the inputs of the used gates is determined in each group (Lines 36 to 46). The responsibility of each group is that if the relevant partial product or the carry input to that group has a value of 1, it adds 1 unit to the desired column’s summation. As indicated before, the last gate of each group that is pertinent to a partial product, one gate is 3-input Toffoli and the previous ones 4-input, 5-input, and so forth, respectively. This state can be observed in the six first group of Fig. 13, which is related to column 9 of the 8-qubit multiplier. Also, the last gate of a group is related to a carry input, a 2-input Toffoli gate, and the previous gates 3-input, 4-input, and so forth, respectively. An example of this state could be observed in the last two groups in Fig. 13.

Fig. 13
figure 13

The reversible circuit of column 9 of the 8-qubit multiplier

Full size image

Accordingly, the number of the inputs of gate number k in group j from column i is determined using Eq. 5. Gate number and input number of the gates start from 0.

$$\begin{aligned} \#\text {Gate}\_in_{i,j,k}\ = {\left\{ \begin{array}{ll} \#\text {Gate}_{i,j}+2-k\\ \quad \text {if}\ \text {the}\ \text {group}\ \text {is}\ \text {related}\ \text {to}\ \text {a}\ \text {partial}\ \text {product}\\ \\ \#\text {Gate}_{i,j}+1-k\\ \quad \text {if}\ \text {the}\ \text {group}\ \text {is}\ \text {related}\ \text {to}\ \text {a}\ \text {carry}\ \text {input}\\ \end{array}\right. } \end{aligned}$$
(5)

In the last step, it must be determined that the desired gates will be placed on which one of the signals (rows 47 to 58). In the groups pertinent to partial products, two first input of each gate is connected to the counterpart signals of that partial product. For instance, in Fig. 13, the group 0 is pertinent to the partial product \(P_{2,7}\). Thereby, the two first inputs of this group’s gates will be connected to \(a_2\) and \(b_7\) signals. The next input of each gate connects to the relevant column’s sum-product signal. In group 0, the next input will connect to \(s_9\) signal. Its following inputs will also be connected to ancilla signals with a constant value or carry outputs. In the groups pertinent to carry inputs, the first gate input will connect to the desired carry input, the next input of the gate will connect to multiplication product output, and other inputs will connect to carry outputs of the relevant column. Take group 7 in Fig. 13 as an example. The first input of each gate is placed in the \(c_{6,9}\) signal. The next input is connected to signal \(s_9\), and the next inputs are connected to output carry signals of, \(c_{9,10}\), \(c_{9,11}\) and \(c_{9,12}\).

So far, the multiplier circuit is designed with two n-qubit inputs. For instance, the 4-qubit multiplier with all mentioned steps will be created, as indicated in Fig. 14. In this figure, the sections related to different columns are separated from each other with dashed lines.

Fig. 14
figure 14

Reversible circuit of 4-qubit multiplier

Full size image

For the quantum implementation of each \(TOF_n\) gate with \(n>3\), it is necessary to add an ancilla input. But in each of the proposed multiplier blocks, there are signals that are useless for some gates. It is also proved in [47] that the initial value of the added ancilla input is trivial for the quantum implementation of the \(TOF_n\) gate. So the existing unused signal with any initial value can be used as an ancilla signal to implement this particular gate. As a result, no ancilla input and garbage output have been added to these circuits in order to implement quantum gates. For example, Fig. 15 shows the implementation of block 1 of the presented 4-bit multiplier, including well-known quantum gates, namely CNOT, Controlled-V, and \(Controlled-V^+\). As can be seen, in the implementation of the 4-input Toffoli gate (\(TOF_4\)), the \(a_0\) signal has been used as an ancilla signal, and therefore, no ancilla input has been added to this circuit. It should be noted that the quantum implementation of other blocks is the same.

Fig. 15
figure 15

Quantum implementation of block 1 of multiplier

Full size image

4.2 Add fault-tolerance property to the multiplier

The next objective is to add the fault-tolerance capability to this circuit (rows 59 to 64). For this purpose, a p signal is added to the circuit such that the value of this signal always keeps a balance between input values and output values of the circuit. Multiplier signals are categorized into three categories:

  1. 1.

    There are main signals of the circuit that produce garbage outputs (such as \(b_0\)...\(b_{n-1}\), \(a_0\)...\(a_{n-1}\)). There are target signals that none of the gates are placed onto them. Thereby, the value of these signals will not change from input to output. Thereby, these signals will not change the parity between the input and output.

  2. 2.

    The constant inputs have a value of ’0’ that are signals for propagation between two non-consecutive columns and produce garbage outputs. The target signals of some gates are placed on these. Thus, they might bring about some changes in the parity.

  3. 3.

    The constant inputs have a value of ’0’ and produce main multiplier outputs. These inputs can also change the parity between input and output values.

The only thing that must be done is to pay attention to the parity between input and output in the signals of the two last categories. These signals have a constant value of ’0’ in input, and this their parity in the input is even. In order to strike a parity between the values of these signals in the output, the value of all these signals must be XOR to each other. Thereby, a Feynman (\(TOF_2\)) gate whose target signal is placed on signal p must be added to each one of these signals. This method is implemented on a 4-qubit quantum multiplier, and its result is indicated in Fig. 16.

Fig. 16
figure 16

4-qubit multiplier of the reversible circuit with the fault-tolerance capability

Full size image

5 Evaluation and comparison

Given that in most of the works carried out in reversible multiplier design, the magnitude of the proposed multipliers is 4. Thereby, in this section, different comparison criteria for the proposed multiplier are considered with the size of 4 to be able to compare it with other works and provide a remarkable evaluation of the proposed design. But in order to be able to compare the results of this work with the scalable multipliers that will be presented in the future, in Table 1, a report of the value of different multiplier criteria for different sizes is provided. Also, Table 2 provides the same report for the fault-tolerant multiplier. Various criteria are employed to evaluate reversible circuits. Some of the most important ones include the number of gates, quantum cost, the constant (ancilla) inputs, and the garbage outputs [5]. In the method proposed by this article, the main objective is to reduce the number of ancilla inputs and the number of garbage outputs. Hence, as explained in [5], the quantum cost and the number of circuit gates increase by reducing ancilla inputs and garbage outputs.

Table 1 Evaluation of reversible multiplier with different sizes
Full size table
Table 2 Evaluation of reversible fault-tolerant multiplier with different sizes
Full size table

To obtain the ratio of the growth rate of the number of gates of the multiplier to the size of the circuit, the following analysis is used. As explained earlier, the number of columns of the multiplier with size n is equal to \(2\times n\). Also, the number of groups in each column is equal to the number of partial products in it plus the number of carry inputs in that column. This number in the worst case (in the middle column) is equal to n+k. n is the size of the multiplier and k is the number of carry inputs of the column. Also, the number of gates forming each group is equal to the number of bits forming the sum produced by that group. Considering that the total number of groups forming the multiplier in the first column is 1 and it increases until the middle column and decreases again, it is of the order of \(n^2\). The number of bits required to display the sum of each column is equal to \(log_2n\) in the maximum case. As a result, the number of gates forming the reversible multiplier with size n is of the order of \(O(n^2log_2n)\). This can be seen in Tables 1, 2.

To better understand the meaning of the values in Tables 1, 2, the diagram in Fig. 17 shows the ratio of the number of gates as well as the quantum cost of the multiplier to its size. These values are presented in order to compare with subsequent works and evaluate them.

Fig. 17
figure 17

The plot of the ratio of quantum cost and number of gates to the size of the reversible multiplier

Full size image
Table 3 Comparison between different reversible multipliers
Full size table

In most of the previous works, an attempt is made to reduce quantum cost criteria and the number of gates as much as possible. However, no significant reduction in the number of ancilla inputs and garbage outputs has been taken place in those works. The present article aimed to simultaneously reduce the production cost of several qubits by reducing the number of ancilla input and garbage output criteria, and as it is evident, this is one of the essential objectives of quantum circuit designs. In Table 3, a comparison is made between the number of garbage outputs, ancilla inputs, quantum cost, and the number of circuit gates proposed by different references and those of the proposed circuit. It must be noted that some works, including [13, 14, 22], aimed to reduce the number of inputs and outputs, while no report has been made regarding other criteria, such as quantum cost and the number of gates. The values of the criteria mentioned in Table 3 are produced by RCViewer+ analyzer software. As can be seen, the quantum cost that is the analysis tool for the reported proposed circuit equals 405.

Table 4 Comparison between different fault-tolerant reversible multipliers
Full size table

As indicated in Table 3, the method proposed in this article generally improved the number of ancilla inputs and garbage outputs of multiplier from 14% and 66% compared to previous works. As explained earlier, this issue can be attributed to the reduction in the constituent blocks to the final circuit, and similarly, the reduction in the number of ancilla inputs and garbage outputs. Indeed, the multiplier’s total number of inputs and outputs is reduced between 9% and 55%. This reduction must be significant due to the high cost of qubit production in quantum technologies. It should be noted that in this work, all outputs that transfer values other than the product are considered garbage outputs. While some of these outputs show exactly the input value. For example, in Fig. 14, all signals \(a_0\) to \(a_3\) and \(b_0\) to \(b_3\) directly transfer the input value to the output and therefore have a valid value. In many works, such outputs are not considered garbage outputs and in this case, the number of garbage outputs can be reported as less than the stated value.

In the following, a similar comparison is also made in fault-tolerant reversible multipliers. Table 4 demonstrates the result of this comparison. As can be seen, the works carried out in this field have not focused on reducing the number of inputs and outputs of circuits. Therefore, the size of the designed circuits is usually great. The minimum number of ancilla inputs in one of the latest works is 44. The high value of this number is attributed to the hierarchical nature of these circuit designs. The circuit size is significantly increased because of the great number of blocks, inputs, and outputs in each block. On the contrary, compared to the best work carried out so far, the design proposed by this research has had a 70% reduction in the criterion pertinent to the number of ancilla inputs and garbage outputs, and its quantum cost increased by 2.2 times. The importance of reducing the circuit’s size criterion and the main reason this article focuses on these criteria are explained in previous sections.

6 Conclusion

This study proposes a column-wise structure for the reversible quantum multiplier. In this structure, contrary to most other works carried out on the implementation of quantum multipliers that have considered separate blocks for the production of partial products and adding them, calculation operations for multiplication of two quantities are implemented in the form of constituent columns of the multiplication operation. This issue has significantly reduced the number of constituent blocks of the multiplier, and thus, the number of ancilla inputs and garbage outputs has been remarkably decreased. Besides, the mentioned blocks are designed in a way that the main inputs of multipliers pass through them without experiencing a change. This advantage eliminates the need to use a separate circuit to produce a fan-out.

In order to evaluate this method, the studies conducted in the implementation of a quantum multiplier are examined. A similar method is employed in these works listed in Table 3. In most of them, some blocks are designed to produce partial products and some blocks to add them. The number of ancilla inputs in the mentioned previous works is between 23 and 36. Besides, the number of garbage outputs employed in these works varied from 22 to 32. The number of ancilla inputs and garbage outputs was reduced to 12 by using the method proposed in this article and by reducing the number of multiplier blocks. Compared to previous works, the number of ancilla inputs and garbage outputs of the multiplier in this method has reduced between 14 to 66%. Indeed, the size of the multiplier circuit that is the main focus of this article has reduced between 9 and 55%, compared to the previous works. Circuit size is the total number of inputs and outputs of the circuit, including main and ancilla inputs and main and garbage outputs. Besides, the fault-tolerant multiplier of the proposed design is compared with that of previous, similar works, as indicated in Sect. 5. As shown, the number of ancilla inputs and garbage outputs has been reduced up to 70% in this method.

Future works may study the implementation of other calculation and processing circuits and focus on reducing the number of inputs and outputs by reducing constituent blocks of those circuits. In addition, with the method discussed in this article, the cost of adding fault tolerance to these circuits can be greatly reduced.