Novel parity-preserving reversible logic array multipliers

Abstract

Reversible logic as a new promising design domain can be used for DNA computations, nanocomputing, and especially constructing quantum computers. However, the vulnerability to different external effects may lead to deviation from producing correct results. The multiplication is one of the most important operations because of its huge usage in different computing systems. Thus, in this paper, some novel reversible logic array multipliers are proposed with error detection capability through the usage of parity-preserving gates. By utilizing the new arrangements of existing reversible gates, some new circuits are presented for partial product generation and multi-operand addition required in array multipliers which results in two unsigned and three signed parity-preserving array multipliers. The experimental results show that the best of signed and unsigned proposed multipliers have the lowest values among the existing designs regarding the main reversible logic criteria including quantum cost, gate count, constant inputs, and garbage outputs. For $4\times 4$ multipliers, the proposed designs achieve up to 28 and 46% reduction in the quantum cost and gate count, respectively, compared to the existing designs. Moreover, the proposed unsigned multipliers can reach up to 58% gate count reduction in $16\times 16$ multipliers.

1 Introduction

In recent years, the high power consumption of VLSI circuits has decelerated feature size reduction of nanometer-scale technologies as was expected from the Moore’s law. Therefore, some researches have been conducted to examine novel design areas in order to resolve the new challenges. The reversible logic design paradigm is one of the candidates to overcome the high power dissipation due to the fact that there is no information loss in these circuits. This is based on the fact that one bit information loss results in kTln2 joules of energy dissipation in which k is the Boltzmann’s constant and T is the absolute temperature at which the computation is performed [1]. Therefore, opposed to ordinary or irreversible logic circuits in which information loss is common, the circuits comprising only reversible logic gates do not dissipate this type of energy [2] as the internal power consumption. As a result, reversible logic circuits are worthy to be investigated despite having some physical and implementation difficulties.

Each gate or circuit requires having a one-to-one mapping between its input vector and output vector to be accounted as reversible. In this manner, the number of outputs is equal to the number of inputs. In addition, the input vector can be recovered from the output vector, which means no information is lost in these gates or circuits. Regarding the main characteristic of reversible logic circuits, these circuits can be thought for using in different applications such as DNA computations, nanocomputing, optical computing, quantum computing, and low-power circuits.

Different external noises and environmental effects can result in a fault and cause a reversible circuit to deviate from producing intended outputs. This way, the information is also lost because the input vector will not be recovered from the output vector, anymore. Therefore, similar to irreversible circuits, the fault-tolerance capability at least in the form of fault or error detection should be considered in reversible circuits. A cost-effective approach to detect errors in reversible circuits is the use of parity-preserving gates. This approach is based on the parity-based coding which is a well-known and low-cost method to detect errors in irreversible circuits. A gate having this characteristic is called a parity-preserving reversible gate. In this paper, this characteristic is the main property which will be focused on. However, it should be considered that the implementation of reversible circuits is more complicated in comparison with irreversible circuits because two simple concepts including fan-out and feedback are not allowed in reversible logic [3].

One of the most important arithmetic operations in different computing systems is the multiplication. Among different types of multipliers, the array multipliers have received more attention as the fast multipliers. Therefore, in reversible logic design paradigm, array multipliers should be considered especially respecting fault-tolerance and error detection capabilities. Until now, different types of reversible multipliers have been designed such as [4,5,6,7,8,9,10,11,12,13]. Even though many of these designs such as [4, 6,7,8, 10, 12] are related to array multipliers, in most of them the parity-preserving gates required for error detection capability have not been used. Therefore, in this paper, some novel parity-preserving reversible logic array multipliers are proposed with the emphasis on requiring lower costs especially the quantum cost compared to the few existing parity-preserving designs. In this manner, respecting the main parts of array multipliers, the new designs for partial product generation (PPG) and multi-operand addition (MOA) are presented by exploiting better and newer parity-preserving gates as well as some new arrangements of the existing gates. The proposed multipliers comprise both signed and unsigned multipliers to be used in different applications. Based on the results analysis, the proposed array multipliers contain more optimized design criteria compared to previous parity-preserving reversible array multipliers especially regarding gate count and quantum cost.

The rest of the paper is organized as follows. In Sect. 2, some basic concepts and definitions as well as the parity-preserving reversible gates are described. In Sect. 3 the related works are discussed. In Sect. 4 the new designs for the PPG part, and in Sect. 5 the new designs for the MOA part are proposed. Constructing the new signed and unsigned parity-preserving array multipliers by combining the proposed PPGs and MOAs are shown and evaluated in Sect. 6. Finally, some conclusions are drawn in Sect. 7.

2 Preliminaries

2.1 Basic concepts and definitions

A reversible gate or circuit is an $n \times n$ circuit so that for any n-tuple input vector, a unique n-tuple output vector will appear at the circuit’s output. Due to the fact that the input vector can be retrieved by the output vector, as well, we can write $I_{v} \leftrightarrow O_{v}$ in which $I_{v} = (I_{0},I_{1}, {\ldots },I_{n-1})$ and $O_{v} = (O_{0},O_{1}, {\ldots },O_{n-1})$ are the input and output vectors, respectively.

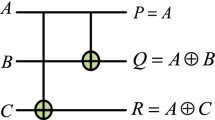
A parity-preserving reversible gate is a gate in which the parity of the inputs is equal to the parity of the outputs according to the following equation in which represents for the XOR operation:

$$\begin{aligned} I_{0}\bigoplus I_{1}\bigoplus \cdots \bigoplus I_{n-1}=O_{0}\bigoplus O_{1}\bigoplus \cdots \bigoplus O_{n-1} \end{aligned}$$

(1)

The parity-preserving characteristic for a gate makes possible all single-error detection and some of multiple-error detection at its outputs. It is worth mentioning that a reversible circuit containing only the parity-preserving gates has itself the parity-preserving property. Therefore, if a reversible circuit with error detection capability is intended, it should only include the parity-preserving gates.

In a reversible gate or circuit, the constant inputs are the inputs whose values do not change in a gate and are maintained at either 0 or 1 in order to perform the intended functions. These inputs are also added to a gate to make it reversible [14]. In addition, the outputs that would not be used in the subsequent computations are called the garbage outputs. In other words, the garbage outputs are needed just to maintain the circuit’s reversibility or to make it parity-preserving [15, 16]. Another parameter considered in reversible circuits is the hardware complexity or total logical calculation which is the number of AND, XOR, and NOT operations, separately, appeared in the output expressions. In other words, the hardware complexity shows the computational complexity of a reversible circuit that can be important in some types of implementations. This way, if $\alpha$, $\beta$, and $\gamma$ are the representatives for XOR, AND, and NOT operations in the outputs, respectively, then the hardware complexity can be computed according to the following equation:

$$\begin{aligned} \hbox {Hardware}\, \hbox {complexity} = N(\alpha ).\alpha +N(\beta ).\beta +N(\gamma ). \gamma \end{aligned}$$

(2)

In the equation above, $N({}^{*})$ is the number of *-type operations in the output expressions.

As stated in [17], in calculating the hardware complexity, it will be better and more precise if the common operations in the output expressions would be accounted once. Therefore, in this paper, the calculation approach presented in [17] is used.

The quantum cost (QC) is the most important parameter in designing the reversible circuits. This criterion is defined as the number of $1\times 1$ and $2\times 2$ quantum primitives required for implementing a reversible circuit. The NOT gate is the only $1\times 1$ quantum primitive which has the quantum cost of one unit. However, for constructing the reversible gates bigger than $2\times 2$, different quantum primitives should be used. In a point of view, the reversible gates can be classified in two general groups, parity-preserving reversible gates and non-parity-preserving reversible gates. As in this paper we are only dealing with the parity-preserving circuits, the main parity-preserving gates are introduced in the following.

2.2 Parity-preserving reversible gates

Many of the basic reversible gates such Feynman gate (FG) [18], Toffoli gate (TG) [19], and Peres gate (PG) [20] are not parity-preserving. However, in the parity-preserving reversible gates that will be described in the following, the parity of the input vector is equal to the parity of the output vector.

• 1. Double Feynman gate (F2G) [21] as a parity-preserving $3\times 3$ reversible gate with the quantum cost of two is shown in Fig. 1a. The hardware complexity of this gate is equal to $2\alpha$. This gate can be used as a fan-out generator in reversible circuit synthesis.

• 2. Fredkin gate (FRG) [22] (Fig. 1b) as the oldest parity-preserving reversible gate with the quantum cost of five has the hardware complexity equal to $2\alpha +4\beta +1\gamma$ due to the fact that there exist two distinct XOR operations, four distinct AND operations, and only a distinct NOT operation in its output expressions. This gate is a universal gate that means all logic operations or reversible logic circuits can be implemented only by using this type of gates.

Fig. 1

Block diagrams of a double Feynman gate, and b Fredkin gate

Fig. 2

Block diagrams of a new fault-tolerant gate, and b modified Islam gate

Fig. 3

Block diagram of a LMH gate, and b F2PG

• 3. New fault-tolerant gate (NFT) [23] as another parity-preserving reversible gate with the quantum cost of five has the hardware complexity equal to $3\alpha +3\beta +2\gamma$ according to its outputs shown in Fig. 2a. Similar to FRG, this gate is a universal gate.

• 4. Modified Islam gate (MIG) [24] (Fig. 2b) is a $4\times 4$ parity-preserving reversible gate with the quantum cost of 7 and the hardware complexity equal to $3\alpha +2\beta +1\gamma$. This gate is a universal gate, as well. In addition, this gate can be used as a parity-preserving half adder when its C and D inputs are set to zero. In this case, the output sum and carry are produced on Q and R outputs, respectively.

• 5. LMH (Lafifa–Mushfiq–Hafiz) [25] shown in Fig. 3a is a $4\times 4$ parity-preserving reversible gate with the quantum cost of six and the hardware complexity equal to $3\alpha +2\beta +1\gamma$. The obtained hardware complexity is based on the fact that the common or the same operations in the outputs are accounted once according to the approach presented in [17]. Thus, since two XOR operations in the output expressions operate on the same operands (in R and S outputs shown in Fig. 3a), this gate includes three distinct XOR operations which results in $3\alpha$ instead of $4\alpha$. In addition, two same operations ${\bar{\hbox {A}}}\hbox {C}$ and two same AB operations exist in the output expressions which result in a simpler term $2\beta$ instead of $4\beta$. Finally, a distinct NOT operation $({\bar{\hbox {A}}})$ results in $1\gamma$.

• 6. F2PG [8] shown in Fig. 3b is a $5\times 5$ parity-preserving reversible gate which has the quantum cost of 14. The hardware complexity of this gate is equals to $6\alpha +5\beta +2\gamma$. This gate can be used as a parity-preserving full adder when the D and E inputs are set to zero. In this case, the output sum and carry will be equal to $Sum = A\bigoplus B\bigoplus C$ and $Cout = (A \bigoplus B)C \bigoplus AB$ that are produced on the R and S outputs, respectively.

• 7. ZPLG [26] shown in Fig. 4a is another $5\times 5$ parity-preserving reversible gate with the quantum cost of eight and its hardware complexity is equal to $8\alpha +3\beta +1\gamma$. Similar to F2PG, this gate can be used as a parity-preserving full adder when the D and E inputs are set to zero. In this case, the output sum and carry are produced on the R and S outputs, respectively. In addition, this gate produces the full adder with minimum quantum cost.

• 8. ZCG [26] shown in Fig. 4b is a $4\times 4$ parity-preserving reversible gate with the quantum cost of six. The hardware complexity of this gate is equal to $5\alpha +2\beta +1\gamma$. Similar to MIG, this gate can be used as a parity-preserving half adder when its C and D inputs are set to zero. In addition, this gate produces the minimum cost half adder.

Fig. 4

Block diagrams of a ZPLG, and b ZCG

3 Related works

3.1 Parity-preserving reversible full adders

All types of multipliers, i.e., serial, parallel, and array multipliers, in some manner require the addition operation. This operation is usually performed by using full adders and half adders. Although there are many designs for non-parity-preserving adders such as [15, 27, 28], only the parity-preserving adders can be helpful for the parity-preserving multipliers. There exist some parity-preserving gates that can perform the operation of a parity-preserving full adder (such as F2PG [8], LCG [17] and ZPLG [26]) or half adder (MIG [24] and ZCG [26]) after setting some of their inputs to zero as the constant inputs. However, a full adder can be constructed by connecting two half adders, as well. In addition, a parity-preserving full adder may be constructed by using a few parity-preserving gates similar to SNFA (single NFT full adder) [29] which includes three F2Gs and a NFT gate. This gate has the quantum cost of 11 more than that of LCG and ZPLG but less than that of F2PG, and its hardware complexity is equal to $9\alpha +3\beta +2\gamma$.

3.2 Parity-preserving reversible multipliers

Due to the fact that the multiplication is a vital operation in most of processing system, many studies have been performed to design optimal multipliers including reversible designs. The multipliers are designed in two manners, serial or parallel in which the array multipliers can be considered as the most important subgroup of parallel multipliers. These different types of multipliers can be utilized according to different requirements of the variety of applications. Therefore, when a low-cost design is very important, serial multipliers are better because of having a lower cost. On the other hand, if a high-speed design is intended, array or parallel multipliers are better because they have more speed.

The first parity-preserving serial multipliers are proposed in [9] based on the well-known Booth’s algorithm and its modified version called Keshuv or K-algorithm for multiplying signed numbers. Even though these multipliers require low costs, their delay is high because of their nature and base algorithms. One of the popular parallel multiplier architectures is array multiplier. As stated before, the array multipliers include two parts, partial product generation (PPG) and multi-operand addition (MOA) as shown in Fig. 5. In the PPG part only partial products are produced by a simple parallel circuit, and in the MOA part the produced partial products will be added together. Despite the fact that various reversible array multipliers exist in the literature, few designs are also parity-preserving. The first parity-preserving signed array multiplier is proposed in [8] based on the Baugh–Wooley method [30]. In this design, the Wallace tree structure is used for the MOA part. According to [8], a $5\times 5$ signed multiplier requires 57 reversible gates with the total quantum cost of 401 in which the parity-preserving gates including F2G, FRG, MIG, NFT, and F2PG are utilized. The undesirable property of this design is that it cannot simply be extended for larger designs. In fact, the MOA part should be designed and optimized for each multiplier size.

In [7] a parity-preserving unsigned array multiplier is proposed utilizing F2Gs and FRGs to implement the PPG part, and only MIGs to construct half adders and full adders of MOA part. This multiplier requires a quantum cost of 244 for a $4\times 4$ multiplier. In [25] another unsigned parity-preserving array multiplier is presented that in comparison with [7] reduces the required quantum cost of a $4\times 4$ multiplier to 205. This design utilizes FRG and LMH to implement the PPG part according to Fig. 6, and incorporates MIG and SNFA to construct half adders and full adders, respectively, for the MOA part. In Fig. 6, vectors x and y are 4-bit input operands, and G at the output of the gates stands for garbage outputs.

Fig. 5

A $4\times 4$ unsigned multiplier that can be implemented as an array multiplier with two parts

Fig. 6

Partial product generation for the $4\times 4$ unsigned array multiplier [25]

4 Proposed partial product generation circuits

The first part or stage of an array multiplier is the PPG. Normally, after finishing the PPG, the next stage (MOA) in which the partial products should be added can be started. In an irreversible $n\times n$ array multiplier, $n^{2}$ AND gates are required to produce all $P_{ij}$s that are equal to $x_{j}y_{i}$ in which x and y are n-bit input operands, and i and j are the indices from 0 to $n-1$. Therefore, in the $4\times 4$ reversible counterpart, reversible gates should produce all $P_{ij}{s}$ according to Fig. 5 despite the fact that there is not any separate AND gate in reversible logic. Thus, in the first proposed parity-preserving partial product generation circuit depicted in Fig. 7, FRGs are adjusted for AND operations. In this figure, F2Gs are only utilized for fan-out production required in this circuit. This circuit, in spite of having simple structure, had not been proposed in the literature. This PPG which includes 16 FRGs and 8 F2Gs for a $4\times 4$ array multiplier has the quantum cost of 96.

Fig. 7

First proposed partial product generation for the $4\times 4$ array multiplier

One of the benefits of array multipliers is that they can simply be extended for larger designs based on the smaller designs. Thus, the number of different required gates and the quantum cost of the first proposed PPG can be computed by using Eqs. (3) and (4), respectively, for n-bit operands $(n\ge 2)$ to be used in $n\times n$ array multipliers.

$$\begin{aligned} \hbox {Required}\, \hbox {gates}\, \hbox {of}\, \hbox {1st}\, \left( {n\times n} \right) \, \hbox {PPG}= & {} n^{2}\times \hbox {FRG} + n\times \lfloor n/2\rfloor \times \hbox {F2G} \end{aligned}$$

(3)

$$\begin{aligned} \hbox {QC}\, \hbox {of}\, \hbox {1st}\, \left( {n\times n} \right) \, \hbox {PPG}= & {} n^{2}\times \hbox {QC}_\mathrm{FRG} +n\times \lfloor n/2\rfloor \times \hbox {QC}_\mathrm{F2G} \nonumber \\= & {} 5n^{2}+2n\times \lfloor n/2\rfloor \end{aligned}$$

(4)

Signed array multipliers may require different partial products. The best signed array multipliers are based on the Baugh–Wooley method [30]. In fact, based on the Baugh–Wooley method, two different partial product arrangements can be used according to Figs. 8 and 9. In this paper, we call them BW1 and BW2, respectively, in which the second arrangement (Fig. 9) has lower costs. On the other hand, the first PPG proposed in Fig. 7 cannot be used for BW1 even though it can be used for BW2. Therefore, proposing the PPGs in which all the items shown in Figs. 8 and 9 required for the MOA part are produced can be very advantageous because otherwise more gates should be used to produce the inverted operands, separately.

Fig. 8

$4\times 4$ signed multiplication based on the first Baugh–Wooley method

Fig. 9

$4\times 4$ signed multiplication based on the second Baugh–Wooley method

In Fig. 8, some terms include an inverted operand. These terms can be produced by properly adjusting the inputs of FRGs and changing the bit locations of both input operands compared to Fig. 7. This way, the second proposed parity-preserving PPG circuit for a $4\times 4$ array multiplier is shown in Fig. 10. This circuit which is useful for the BW1 method utilizes two more F2Gs compared to Fig. 7 to produce ${x}_{3},\, {y}_{3}$, and the inverted ${x}_{3}$ and ${y}_{3}$ (bold items in Fig. 10) required in Fig. 8. As a result, the second proposed PPG circuit has the quantum cost of 100 which is only four units higher than that of the first proposed PPG circuit, and on the other hand, it can be used in a signed array multiplier without any modification.

By more investigation, it is obtained that the LMH gate introduced in [25] can be used instead of an FRG and an F2G, while it can produce the terms required in the BW1 method. In fact, an LMH gate with the quantum cost of six which is one unit more than that of FRG, can be used to propagate two input signals compared to one input in the FRG, and thus helps to eliminate some F2Gs by this fan-out production. Therefore, the third proposed parity-preserving PPG circuit for a $4\times 4$ array multiplier is obtained according to Fig. 11 and can be used in the BW1 method-based signed multiplier with the quantum cost lower than that of the first and second proposed PPG circuits. In Fig. 11, some FRGs are used in the locations in which only one signal propagation is required, and thus there is no need to LMH gates. In fact, three FRGs in the right-most locations (except the lower-right FRG) propagate ${y}_{0}$ input signal, and three other FRGs in the last row propagate ${x}_{0}$ input signal to their right-hand gates. In addition, two F2Gs are required similar to Fig. 10 to produce ${x}_{3},\, {y}_{3}$, and the inverted ${x}_{3}$ and ${y}_{3}$ (bold items in Fig. 11) required for the BW1 method.

Fig. 10

Second proposed partial product generation for $4\times 4$ array multiplier based on the first Baugh–Wooley method

To extend the size of second and third proposed PPG circuits to be used in larger signed multipliers, the following equations can be used to predict the number of different gates and total quantum cost for n-bit operands:

$$\begin{aligned} \hbox {Required}\, \hbox {gates}\, \hbox {of}\, \hbox {2nd}\, \left( {n\times n} \right) \, \hbox {PPG}= & {} n^{2}\times \hbox {FRG}+\left( n\times \lfloor n/2\rfloor \right. \nonumber \\&\left. +\,n\hbox { mod }2+2 \right) \times \hbox {F2G} \end{aligned}$$

(5)

$$\begin{aligned} \hbox {QC}\, \hbox {of}\, \hbox {2nd}\, \left( {n\times n} \right) \, \hbox {PPG}= & {} n^{2}\times \hbox {QC}_\mathrm{FRG} +\left( n\times \lfloor n/2\rfloor +\,n\hbox { mod }2+2 \right) \nonumber \\&\times \, \hbox {QC}_\mathrm{F2G} =5n^{2}+2\left( n\times \lfloor n/2\rfloor \right. \nonumber \\&\left. +\,n \hbox { mod }2 \right) +4 \end{aligned}$$

(6)

$$\begin{aligned} \hbox {Required}\, \hbox {gates}\, \hbox {of}\, \hbox {3rd}\, \left( {n\times n} \right) \hbox {PPG}= & {} \left( {n-1} \right) ^{2}\times \hbox {LMH}\nonumber \\&+\left( {2n-1} \right) \times \hbox {FRG}+2\times \hbox {F2G} \end{aligned}$$

(7)

$$\begin{aligned} \hbox {QC}\, \hbox {of}\, \hbox {3rd}\, \left( {n\times n} \right) \, \hbox {PPG}= & {} \left( {n-1} \right) ^{2}\times \hbox {QC}_\mathrm{LMH} +\left( {2n-1}\right) \times \hbox {QC}_\mathrm{FRG}\nonumber \\&+2\times \hbox {QC}_\mathrm{F2G} =6n^{2}-2n+5 \end{aligned}$$

(8)

Fig. 11

Third proposed partial product generation for $4\times 4$ array multiplier based on the first Baugh–Wooley method

Fig. 12

Fourth proposed partial product generation for $4\times 4$ array multiplier based on the second Baugh–Wooley method

According to Fig. 9, some terms of partial products should be inverted to be used in a signed array multiplier based on the BW2 method. The gate with the lowest cost that can produce an inverted product term is LMH. Thus, to produce the required terms shown in Fig. 9, a new arrangement of LMH gates and FRGs with appropriate input adjustments is suggested as the forth proposed parity-preserving PPG circuit for a $4\times 4$ array multiplier as shown in Fig. 12. In this figure, some LMH gates are adjusted with the constant inputs of zero and one for their third and fourth inputs to produce the inverted product terms, and other LMH gates are adjusted with two zero constant inputs to produce normal product terms. Moreover, FRGs are used as far as possible to produce the remaining product terms in the locations that there is no need to LMH gates. The quantum cost of this PPG circuit is equal to 91 and is the lowest among four proposed PPG circuits.

To extend the size of fourth proposed PPG circuit to be used in larger signed multipliers, Eqs. (9) and (10) are used to predict the number of different required gates and total quantum cost for n-bit operands. In addition, to demonstrate the generalized structure of the PPG circuits for n-bit operands, it is shown in Fig. 13 for the best proposed PPG in this paper to be used in $n\times n$ signed array multipliers.

$$\begin{aligned} \hbox {Required}\, \hbox {gates}\, \hbox {of}\, \hbox {4th}\, \left( {n\times n} \right) \, \hbox {PPG}= & {} (\left( {n-1} \right) ^{2}+2)\times \hbox {LMH}\nonumber \\&+\left( {2n-3} \right) \times \hbox {FRG} \end{aligned}$$

(9)

$$\begin{aligned} \hbox {QC}\, \hbox {of}\, \hbox {4th}\, \left( {n\times n} \right) \, \hbox {PPG}= & {} (\left( {n-1} \right) ^{2}+2)\times \hbox {QC}_\mathrm{LMH} +\left( {2n-3} \right) \nonumber \\&\times \, \hbox {QC}_\mathrm{FRG}=6n^{2}-2n+3 \end{aligned}$$

(10)

Fig. 13

Generalized structure of fourth proposed partial product generation for $n\times n$ array multiplier

To compare the proposed PPG circuits in this paper with the previous designs, Table 1 illustrates different characteristics and reversible logic criteria for all PPG designs. It is worth mentioning that the calculation of values for the criteria in each circuit is straightforward. In fact, the number of required gates, constant inputs and garbage outputs are obtained based on the figure drawn for each proposed circuit. The number of constant inputs in each figure is the number of gates’ inputs whose values are either ’0’ or ’1’. In addition, the number of garbage outputs is the number of gates’ outputs that are not connected to the other gates or are not used as the outputs of the circuit. The values for other criteria are obtained by summing the values for all the gates. In Table 1, the first three rows are mainly for unsigned multipliers, and the remaining rows are the designs based on the first or second Baugh–Wooley method for signed multiplication. In addition, the bold items show the best values in each column, separately for signed and unsigned PPG circuits. According to this table, the fourth proposed PPG is the best for the signed multiplication in all criteria except the number of garbage outputs. Moreover, this PPG can be assumed as the best in general because its criteria are very close to that of the unsigned design in [25] while a signed multiplier can be used for unsigned operands and it is not true, reversely.

Table 1 Comparison of PPG parts of different parity-preserving array multipliers

Fig. 14

First proposed multi-operand addition for $4\times 4$ unsigned array multiplier

5 Proposed multi-operand addition circuits

The second part of an array multiplier is the multi-operand addition or MOA. Because of the nature of this part which is the addition operation, the main building blocks will be full adders and half adders. As stated before, the full adder and half adder with the lowest quantum cost as the main criterion are ZPLG and ZCG both introduced in [26] with the quantum cost of 8 and 6, respectively. Regarding other criteria, the number of constant inputs and garbage outputs are almost the same in different full adder and half adder designs. In this section similar to previous section, the designs for signed and unsigned multiplications are separately proposed. Thus, the first proposed parity-preserving MOA circuit for a $4\times 4$ unsigned array multiplier is shown in Fig. 14. In this figure, all the terms of partial products produced in the PPG part are added based on their weight in the addition process to produce the result of multiplication which is an eight-bit output P. In Fig. 14, when two operands should be added together ZCG is used as the half adder. Moreover, in Fig. 14 the output carries of full adders and half adders are passed to the next column diagonally as much as possible to reduce the overall delay. This circuit has the quantum cost of 88 because of having eight ZPLGs and four ZCGs. To extend the size of first proposed MOA circuit to be used in larger multipliers, Eqs. (11) and (12) can be used to predict the number of different required gates and total quantum cost for n-bit operands.

$$\begin{aligned} \hbox {Required}\, \hbox {gates}\, \hbox {of}\, \hbox {1st}\, \left( {n\times n} \right) \, \hbox {MOA}= & {} n\left( {n-2} \right) \times \hbox {ZPLG} \nonumber \\&+\,n\times \hbox {ZCG} \end{aligned}$$

(11)

$$\begin{aligned} \hbox {QC}\, \hbox {of}\, \hbox {1st}\, \left( {n\times n} \right) \, \hbox {MOA}= & {} n\left( {n-2} \right) \times \hbox {QC}_\mathrm{ZPLG} \nonumber \\&+\,n\times \hbox {QC}_\mathrm{ZCG} =8n^{2}-10n \end{aligned}$$

(12)

For signed multipliers based on the Baugh–Wooley method, different MOAs should be designed for BW1 and BW2 because of different structures of Figs. 8 and 9. In fact, the new MOA circuits should add the partial products produced by the PPG circuits for BW1 and BW2. Therefore, the second parity-preserving MOA circuit for a $4\times 4$ signed array multiplier is proposed in Fig. 15 which is beneficial for the BW1 method. In addition, the third proposed parity-preserving MOA circuit for a $4\times 4$ signed array multiplier is depicted in Fig. 16 which is useful for the BW2 method. In Fig. 16, the only F2G is used to perform an operation equivalent to the addition by one based on the lower-left ’1’ shown in Fig. 9. In fact, in Fig. 16 a ZCG as a half adder should add the output carry of lower-left ZPLG by one which requires six units more quantum cost. In this special case, this addition operation is equivalent to inverting the output carry of lower-left ZPLG that can be performed by using a F2G after an appropriate adjustment of its inputs which results in a reduction of quantum cost by four.

Fig. 15

Second proposed multi-operand addition for $4\times 4$ signed array multiplier

Fig. 16

Third proposed multi-operand addition for $4\times 4$ signed array multiplier

To extend the size of third proposed MOA circuit to be used in larger signed multipliers, Eqs. (13) and (14) can be used to predict the number of different required gates and total quantum cost for n-bit operands. Moreover, Fig. 17 demonstrates the generalized structure of this MOA as the best proposed MOA in this paper respecting the quantum cost for signed multiplication of n-bit operands.

$$\begin{aligned} \hbox {Required}\, \hbox {gates}\, \hbox {of}\, \hbox {3rd}\, \left( {n\times n} \right) \, \hbox {MOA}= & {} \left( {n-1} \right) ^{2}\times \hbox {ZPLG} \nonumber \\&+\left( {n-1} \right) \times \hbox {ZCG}+1\times \hbox {F2G} \end{aligned}$$

(13)

$$\begin{aligned} \hbox {QC}\, \hbox {of}\, \hbox {3rd}\, \left( {n\times n} \right) \, \hbox {MOA}= & {} \left( {n-1} \right) ^{2}\times \hbox {QC}_\mathrm{ZPLG} +\left( {n-1} \right) \times \hbox {QC}_\mathrm{ZCG}\nonumber \\&+1\times \hbox {QC}_\mathrm{F2G} =8n^{2}-10n+4 \end{aligned}$$

(14)

Fig. 17

Generalized structure of third proposed multi-operand addition for $n\times n$ signed array multiplier

To compare the proposed MOA circuits in this paper with the previous designs, Table 2 illustrates different characteristics and reversible logic criteria for all MOA designs. In this table, the first three rows are only applicable to unsigned multipliers, and the remaining three rows are the designs dedicated for signed multiplications based on the first or second Baugh–Wooley method. In addition, the bold items show the best values in each column, separately for signed and unsigned MOA circuits. However, the best values have not been bold in some cases where all the appropriate designs have the same value or the best value cannot be selected. According to this table, the first proposed MOA has the lowest quantum cost among the designs applicable to unsigned multiplication, and the third proposed MOA has the lowest quantum cost among the designs beneficial for signed multiplication.

Table 2 Comparison of MOA parts of different parity-preserving array multipliers

6 Results and discussion

In this section, the proposed parity-preserving signed and unsigned array multipliers will be illustrated by combining the appropriate proposed PPG circuits and MOA circuits. After constructing different multipliers, some comparisons will be performed between the proposed multipliers and their previous signed or unsigned counterparts. In the comparisons, similar to Tables 1 and 2, five main criterions are used including gate count, number of constant inputs, number of garbage outputs, quantum cost, and hardware complexity even though the quantum cost is the most important criterion. In the following, at first unsigned array multipliers and then, signed array multipliers are characterized and evaluated.

6.1 Unsigned array multipliers

Based on the previously proposed PPG and MOA circuits in this paper for unsigned array multiplication, we propose two parity-preserving unsigned array multipliers. For the $4\times 4$ multiplication, the first proposed multiplier is constructed by combining the first PPG and the first MOA proposed before depicted in Figs. 7 and 14, respectively. This multiplier has the quantum cost of 184 that is the sum of 96 and 88. The second proposed multiplier is constructed by combining the PPG shown in Fig. 6 from [25] as the best unsigned PPG and the first proposed MOA depicted in Fig. 14. This combination leads to the best unsigned multiplier with the quantum cost of 177 which is the minimum value among all designs. Therefore, two proposed parity-preserving unsigned array multipliers are characterized in Table 3 along with all previous designs that are from [7] and [25]. In this table, the bold items show the best values in each column. According to this table, the second proposed multiplier is the best with respect to all design criteria except the hardware complexity where one of two designs, the design in [7] or the second proposed multiplier in this paper, can be judged as the best. Moreover, to illustrate the precise amounts of improvements attained by two proposed unsigned multipliers, Fig. 18 depicts the percentages of reduction in four criterions for the first and second 4-bit designs compared to the designs proposed in [7] and [25]. Based on this figure, the improvements of the second proposed multiplier in this paper compared to [7] is 41.7, 23.4, 23.4, and 27.5% for the gate count, constant inputs, garbage outputs, and quantum cost, respectively. Moreover, the improvements of the second proposed multiplier compared to [25] as the best of previous designs is 46.2 and 13.7% for the gate count and quantum cost, respectively, while their constant inputs and garbage outputs are equal.

Table 3 Comparison of different parity-preserving unsigned array multipliers

Fig. 18

Improvements of the first and second proposed 4-bit unsigned array multipliers compared to previous designs

To figure out the proposed multipliers for larger input operands, Table 4 demonstrates the number of different required gates and quantum cost for $n\times n$ multipliers as the functions of operands’ size n together with the results for two samples $8\times 8$ and $16\times 16$ multipliers. In this table, two proposed unsigned array multipliers are only compared to [25] as the best of previous designs. Furthermore, Fig. 19 depicts the percentages of reduction in the gate count and quantum cost of the proposed unsigned array multipliers compared to [25], for $8\times 8$ and $16\times 16$ multipliers. The important result based on this figure is that the amounts of improvements attained by both proposed multipliers for $16\times 16$ size is higher than that of $8\times 8$ size which itself has a higher improvement compared to the $4\times 4$ multiplier. Therefore, larger multipliers such as $32\times 32$ size benefit more from the proposed designs.

Table 4 Comparison of larger unsigned array multipliers and their general formulae

In addition to the possibility for calculating the gate count and quantum cost of larger multipliers according to Table 4, other criteria can be estimated for $n\times n$ multipliers, as well. In other words, it is possible to estimate the number of constant inputs and the number of garbage outputs for $n\times n$ multipliers by considering the number of constant inputs or garbage outputs in each gate type of the PPG and MOA parts of the proposed multipliers, and considering the main formula for the required gates of PPG and MOA circuits, as well. For example, Eqs. (15) to (18) can be used to estimate these criteria for the first and second proposed array multipliers. In addition, the design proposed in [25] follows Eqs. (17) and (18) for its constant inputs and garbage outputs, respectively, which are compatible with the results presented in Table 3.

$$\begin{aligned} \hbox {Constant}\, \hbox {inputs}\, \hbox {of}\, \hbox {1st}\, \left( {n\times n} \right) \, \hbox {multiplier}= & {} 3n^{2} +2n\times \left( \lfloor n/2 \rfloor -1 \right) \end{aligned}$$

(15)

$$\begin{aligned} \hbox {Garbage}\, \hbox {outputs}\, \hbox {of}\, \hbox {1st}\, \left( {n\times n} \right) \, \hbox {multiplier}= & {} 4n^{2}-3n\nonumber \\&+\,n\times \left( {\left( {{n}+1} \right) \hbox { mod }2} \right) \end{aligned}$$

(16)

$$\begin{aligned} \hbox {Constant}\, \hbox {inputs}\, \hbox {of}\, \hbox {2nd}\, \left( {n\times n} \right) \, \hbox {multiplier}= & {} 4n^{2}-4n+1 \end{aligned}$$

(17)

$$\begin{aligned} \hbox {Garbage}\, \hbox {outputs}\, \hbox {of}\, \hbox {2nd}\, \left( {n\times n} \right) \, \hbox {multiplier}= & {} 4n^{2}-4n+1 \end{aligned}$$

(18)

Fig. 19

Improvements of the first and second proposed unsigned array multipliers with different sizes compared to the design in [25]

6.2 Signed array multipliers

The proposed signed array multipliers are based on the previously proposed PPG and MOA circuits in this paper for signed array multiplication. This way, we propose three new parity-preserving signed array multipliers. For the $4\times 4$ multiplication, the first proposed signed multiplier as the third proposed multiplier in this paper is constructed by combining the second PPG (Fig. 10) and the second MOA (Fig. 15) proposed before based on the BW1 method. This multiplier has the quantum cost of 214 that is the sum of 100 and 114. The second proposed signed multiplier (the fourth proposed multiplier in this paper) is constructed by combining the third PPG (Fig. 11) and the second MOA (Fig. 15) based on the BW1 method. This multiplier with the quantum cost of 207 is totally better that the first proposed signed multiplier regarding different criteria. The third proposed signed multiplier (the fifth proposed multiplier in this paper) is constructed by combining the fourth PPG (Fig. 12) and the third MOA (Fig. 16) based on the BW2 method. This combination leads to the best signed array multiplier with the quantum cost of 183 which is the minimum value among all signed designs.

Three proposed parity-preserving signed array multipliers are characterized in Table 5 along with the only existing design in [8]. In this table, the bold items show the best values in each column. According to this table, the fifth proposed multiplier is the best with respect to all design criteria except the hardware complexity where one of two designs, the design in [8] or the fifth proposed multiplier in this paper, can be judged as the best. Moreover, Table 6 depicts the best proposed signed array multiplier in this paper compared to the only existing $5\times 5$ design from [8] that its MOA part is based on the Wallace tree structure. This table reveals the superiority of the proposed design that uses a simple array for its MOA, in comparison with the design in [8].

Table 5 Comparison of different parity-preserving signed array multipliers

Table 6 Best proposed signed array multiplier compared to the only existing $5\times 5$ Baugh–Wooley multiplier

To illustrate the precise amounts of improvements attained by the best proposed signed multiplier, Fig. 20 depicts the percentages of reduction in four criterions for the fifth proposed design compared to the design in [8] for $4\times 4$ and $5\times 5$ multiplier sizes. Based on this figure, all criteria have some enhancements in the fifth proposed multiplier. The best improvements are obtained for the quantum cost as the most important criterion, that are equal to 25.9 and 25% for $4\times 4$ and $5\times 5$ multipliers, respectively. Moreover, the improvements in the gate count are equal to 23.7 and 14% for $4\times 4$ and $5\times 5$ multipliers, respectively.

To figure out the performance of fifth proposed multiplier for larger input operands, Table 7 demonstrates the formulae for the major reversible logic criteria for $n\times n$ multipliers as the functions of operands’ size n together with the results for two samples $8\times 8$ and $16\times 16$ multipliers. Based on this table, the number of constant inputs and the number of garbage outputs will be equal in each specific multiplier size.

Fig. 20

Improvements in the fifth proposed array multiplier compared to the design in [8] for different sizes

Table 7 Evaluation of the best proposed signed array multiplier with different sizes based on its general formulae

7 Conclusion

In this paper, five novel parity-preserving reversible array multipliers were proposed by designing some new partial product generation and multi-operand addition circuits required in array multipliers, for both signed and unsigned multiplications. To attain better designs, the new arrangements of existing parity-preserving reversible gates were utilized as well as exploiting newer gates. Therefore, the proposed signed and unsigned array multipliers can be used in different reversible logic applications especially in the speed-critical applications. The proposed signed array multipliers are based on the first and second Baugh–Wooley method. The last proposed signed array multiplier in this paper as the best design has achieved 26% improvement in the quantum cost compared to the best existing design. In addition to the basic $4\times 4$ multipliers, the proposed multipliers have been generalized to $n\times n$ multipliers, and some general formulae were exploited to investigate larger multipliers such as $8\times 8$ and $16\times 16$ designs. The experimental results have shown the superiority of the proposed designs with different sizes compared to the existing designs respecting the main reversible logic criteria especially the quantum cost and gate count.