1 Introduction

Based on quantum mechanics principles, quantum key agreement (QKA) [1, 2] can realize unconditional secure communication by providing encryption and decryption keys for “one-time-one pad” cryptosystem. It is new and different information protection technology from quantum key distribution (QKD) [3,4,5,6]. Unlike QKD, which allows one party to decide the key independently and sends it to the other party, QKA requires all participants to jointly and fairly establish a shared key. Therefore, QKA is more suitable for practical needs.

At present, QKA are widely concerned [7,8,9,10] since the first QKA protocol [7] was given in 2004. The first QKA protocol mainly uses the idea of quantum teleportation. Subsequently, several new QKA protocols were proposed. Most of them cannot resist the participant attack [9] or the controlled-Not attack [10]. One successful two-party QKA protocol was proposed by Chong and Hwang in 2010 [11]. Now, there have been many new successful QKA protocols including two-party QKA [11,12,13] and multi-party QKA [13,14,15,16,17,18]. These QKA protocols mainly use single particles or Bell states as quantum sources. Subsequently, researchers also put forward some QKA protocols based on four-particle cluster states [1, 19, 20]. Since the security of QKA protocols will also be adversely affected by channel noise, researchers have spent more energy on the study of the QKA protocols [2, 21, 22] against collective noise. In order to adapt to different application environments, researchers also proposed controlled quantum key agreement protocols [23] and semi-quantum key agreement protocols [24]. On the other hand, in practical application, the attackers often want to disguise themselves as participants to obtain shared keys, that is, to implement man-in-the-middle attacks on QKA protocols. Thus, the QKA protocols should first authenticate the identities of the participants before key negotiation. This is very important for the QKA protocols to be applied safely. Unlike the classical mutual authentication key agreement protocols, which have been studied more, the research on mutual authentication quantum key agreement (MAQKA) is still less. In 2021, Zhu et al.[25] and Ma et al.[26] proposed a MAQKA protocol, respectively. Since then, such MAQKA protocols have also attracted more attention from researchers.

In this paper, we propose a new MAQKA protocol based on Bell states. It can not only generate shared keys fairly, but also authenticate participants’ identities before negotiating keys. The participants can authenticate each other’s identity according to whether they can choose the correct measurement bases with their shared secret identity information. They generate shared secret keys by using the entanglement swapping property of Bell states. The security analysis shows that the authentication process of the MAQKA protocol can resist forgery attacks and is unconditionally secure, and the key agreement process of the MAQKA protocol can resist external attacks and participant attacks. Compared with the two existing MAQKA protocols, the new MAQKA protocol has higher quantum bit efficiency, and it can realize identity authentication and key negotiation without the participation of trusted or semi-trusted third party, thus reducing the communication complexity.

The rest of this paper is organized as follows. In Sect. 3, we present a new MAQKA protocol. Section 3 gives its security analysis and performance analysis. Finally, a conclusion is given in Sect. 4.

2 The mutual authentication quantum key agreement protocol

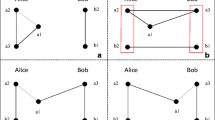
A hash function H(x) outputting an n-bit value is used in our MAQKA protocol. Moreover, the mutual identity authentication needs a secret identity information \(K_{AB}\), which is shared by Alice and Bob in advance. If Alice and Bob want to negotiate a session key, they must first authenticate each other’s identity and then negotiate the key after passing the identity authentication. See Fig. 1 and the following specific steps for details of the MAQKA protocol. In Fig 1(c), the square symbol denotes the measurement with Z-base, the diamond symbol denotes the measurement with X-base, and BM denotes Bell measurement here.

Fig. 1
figure 1

The process of MAQKA protocol without considering decoy states. a Bell states preparation. b Bell states transmission. c Bob’s identity authentication. d Alice’s identity authentication. e Key negotiation

Full size image

Step 1. Bell states preparation and transmission: Alice and Bob prepare \(n+m\) Bell states \(|\phi ^{+}\rangle =\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )=\frac{1}{\sqrt{2}}(|++\rangle +|--\rangle )\), respectively. Alice records the first-particle sequence of \(n+m\) Bell states as \(L_{A}=L_{A}^{(1)}L_{A}^{(2)}\cdots L_{A}^{(n+m)}\) and the second-particle sequence as \(S_{A}=S_{A}^{(1)}S_{A}^{(2)}\cdots S_{A}^{(n+m)}\). Similarly, Bob gets the sequences \(L_{B}=L_{B}^{(1)}L_{B}^{(2)}\cdots L_{B}^{(n+m)}\) and \(S_{B}=S_{B}^{(1)}S_{B}^{(2)}\) \(\cdots S_{B}^{(n+m)}\). From the set \(\{|0\rangle , |1\rangle ,\) \( |+\rangle , |-\rangle \}\), Alice and Bob randomly select some decoy states and insert their sequences \(S_{A}\) and \(S_{B}\) at random. Alice sends the new sequence \(S'_{A}\) to Bob, and Bob sends the new sequence \(S'_{B}\) to Alice. Moreover, they all keep the sequences \(L_{A}\) and \(L_{B}\) themselves.

Step 2. Eavesdropping detection: For the sequence \(S'_{A}\), Alice announces the positions and measurement bases of the decoy states. With the correct bases, Bob measures the decoy photons and sends the measurement results to Alice. Then Alice computes the error rate and determines whether the channel is safe or not. For the sequence \(S'_{B}\), similar work is required. If the channels are safe, they continue to execute the protocol. Otherwise, they terminate the protocol and restart.

Step 3. Mutual authentication: After eavesdropping detection, the sequences \(S'_{A}\) and \(S'_{B}\) have been restored to the sequences \(S_{A}\) and \(S_{B}\). Since the methods of authenticating Alice and Bob are completely similar, we only take Bob’s identity authentication as an example. It is carried out in the following three steps.

(a) Alice randomly selects a number r and makes it public. Then she computes \(\overline{K}_{AB}=H(K_{AB}||r)\), which is expressed as \(\overline{K}_{AB}=\overline{K}_{AB}^{(1)}\overline{K}_{AB}^{(2)}\cdots \overline{K}_{AB}^{(n)}\). According to the value of \(\overline{K}_{AB}^{(i)}\), she chooses the measurement bases to measure the particle \(L^{(i)}_{A}\) in the sequence \(L_{A}\), where \(i=1,2, \cdots , n\). If \(\overline{K}_{AB}^{(i)}=0\), Alice chooses Z-basis \(\{|0\rangle , |1\rangle \}\) as the measurement base; if \(\overline{K}_{AB}^{(i)}=1\), Alice chooses X-basis \(\{|+\rangle , |-\rangle \}\) as the measurement base. When Alice finishes measuring all the first n particles in the sequence \(L_{A}\), she codes the measurement results as \(R_{A}=R^{(1)}_{A}R^{(2)}_{A}\cdots R^{(n)}_{A}\). The coding rule she uses is: If the quantum state is \(|0\rangle \) or \(|+\rangle \), then \(R^{(i)}_{A}=0\); if the quantum state is \(|1\rangle \) or \(|-\rangle \), then \(R^{(i)}_{A}=1\).

For example, Alice prepares six Bell states in Step 1, that is, the Bell state sequence is \(|\phi ^{+}\rangle |\phi ^{+}\rangle |\phi ^{+}\rangle |\phi ^{+}\rangle |\phi ^{+}\rangle |\phi ^{+}\rangle \) . If the hash value \(\overline{K}_{AB}\) she calculates in this step is 0101, the measurement bases she chooses are ZXZX. However, there may be 16 different measurement results for the first four particles of the sequence \(L_{A}\), corresponding to 16 different coding sequences \(R_{A}\). See Table 1 for details. Moreover, the probability of each result is 1/16. However, when Alice completes the measurement in this step, the first four quantum states of her sequence \(L_{A}\) will inevitably collapse to one of these 16 kinds.

Table 1 The relationship among the hash value \(\overline{K}_{AB}\), the measurement results of the sequence \(L_{A}\) and the coding sequence \(R_{A}\)
Full size table

(b) According to the key \(K_{AB}\) and the random number r, Bob computes the hash value \(\overline{K}'_{AB}=H(K_{AB}||r)\), which is recorded as \(\overline{K}'_{AB}=\overline{K}_{AB}'^{(1)}\overline{K}_{AB}'^{(2)}\) \(\cdots \overline{K}_{AB}'^{(n)}\). After that, Bob selects his measurement bases in terms of the value \(\overline{K}'_{AB}\). If \(\overline{K}_{AB}'^{(i)}=0\), his measurement base is \(\{|0\rangle , |1\rangle \}\) . If \(\overline{K}_{AB}'^{(i)}=1\), his measurement base is \(\{|+\rangle , |-\rangle \}\). After Bob has measured all the first n particles in the sequence \(S_{A}\), his measurement results are coded as the sequence \(R'_{A}=R'^{(1)}_{A}R'^{(2)}_{A}\cdots R'^{(n)}_{A}\). Bob’s coding rule is exactly the same as Alice’s coding rule for the sequence \(L_{A}\). Then the sequence \(R'_{A}\) is announced by Bob.

(c) By comparing the values of \(R_{A}\) and \(R'_{A}\), Alice judges whether Bob’s identity is correct. Continue with the above example of Step 3(a). When \(\overline{K}_{AB}=0101\), since there are 16 different measurement results for the sequence \(L_{A}\), then the sequence \(S_{A}\) will collapse to 16 different state sequences. However, according to the measurement correlation property of Bell states, the quantum states of the sequence \(L_{A}\) and the sequence \(S_{A}\) correspond to the same. That is, if the measurement results of the sequence \(L_{A}\) are \(|1\rangle |+\rangle |0\rangle |+\rangle \), then the quantum states of the sequence \(S_{A}\) after collapsing in Step 3(a) are also \(|1\rangle |+\rangle |0\rangle |+\rangle \). Therefore, when the measurement bases of Bob and Alice are consistent, the measurement results of the sequence \(S_{A}\) are consistent with those of the sequence \(L_{A}\).

It is worth noting that the first n particles of \(L_{B}\) and \(S_{B}\) are also used to detect the identity of Alice. Therefore, only the last m particles are left in the four sequences \(L_{A}\), \(S_{A}\), \(L_{B}\) and \(S_{B}\), which are re-marked as \(L^{*}_{A}=L_{A}^{(n+1)}L_{A}^{(n+2)}\cdots L_{A}^{(n+m)}\), \(S^{*}_{A}=S_{A}^{(n+1)}S_{A}^{(n+2)}\cdots S_{A}^{(n+m)}\), \(L^{*}_{B}=L_{B}^{(n+1)}L_{B}^{(n+2)}\) \(\cdots L_{B}^{(n+m)}\) and \(S^{*}_{B}=S_{B}^{(n+1)}S_{B}^{(n+2)}\cdots S_{B}^{(n+m)}\). Moreover, the two sequences \(L^{*}_{A}\) and \(S^{*}_{B}\) are in Alice’s hands, the other two sequences \(L^{*}_{B}\) and \(S^{*}_{A}\) are in Bob’s hands.

Step 4. Key negotiation: After the mutual authentication between Alice and Bob is successful, they negotiate the session key together. Alice performs Bell measurements on the corresponding m pairs of particles in the sequences \(L^{*}_{A}\) and \(S^{*}_{B}\). At the same time, Bob performs Bell measurements on the corresponding m pairs of particles in the sequences \(L^{*}_{B}\) and \(S^{*}_{A}\). According to the entanglement exchange relation of Bell states \(|\phi ^{+}\rangle \), that is,

$$\begin{aligned} |\phi ^{+}\rangle _{12}|\phi ^{+}\rangle _{34}= & {} \frac{1}{2}(|\phi ^{+}\rangle _{14}|\phi ^{+}\rangle _{23} +|\phi ^{-}\rangle _{14}|\phi ^{-}\rangle _{23}\\&+|\psi ^{+}\rangle _{14}|\psi ^{+}\rangle _{23} +|\psi ^{-}\rangle _{14}|\psi ^{-}\rangle _{23}), \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1) \end{aligned}$$

we know that the measurement results of Alice and Bob are equal. And, for each Bell measurement, they will get the states \(|\phi ^{+}\rangle \), \(|\phi ^{-}\rangle \), \(|\psi ^{+}\rangle \), or \(|\psi ^{-}\rangle \) with a 1/4 probability. Alice and Bob negotiate a session key encoding rule, that is, \(|\phi ^{+}\rangle \) corresponds to 00, \(|\phi ^{-}\rangle \) corresponds to 01, \(|\psi ^{+}\rangle \) corresponds to 10, and \(|\psi ^{-}\rangle \) corresponds to 11. Therefore, after encoding their m measurement results, they can get a binary sequence K with a length of 2m. The sequence K is the session key negotiated by both parties.

3 Security analysis and performance analysis

3.1 Security analysis of mutual authentication

In the following, let us analyze the security of mutual authentication from three aspects.

Correctness: According to the description and examples of the mutual authentication, it judges whether Bob’s identity is correct or not by comparing the gap between \(R_{A}\) and \(R'_{A}\). If Bob’s identity is correct, he must own \(K_{AB}\) and can calculate the correct value \(\overline{K}'_{AB}=H(K_{AB}||r)\). Moreover, he has \(\overline{K}'_{AB}=\overline{K}_{AB}\). Therefore, Alice and Bob choose the same measurement bases. According to the measurement correlation property of Bell states, the measurement results of the sequence \(S_{A}\) are consistent with those of the sequence \(L_{A}\). That is, there is \(R_{A}=R'_{A}\) when Bob’s identity is correct.

For example: When \(\overline{K}_{AB}=0101\), Alice chooses the measurement bases ZXZX. According to Table 1, we easily know that Alice’s measurement results are one of 16 cases. If Alice’s measurement results are \(L_{A}=L^{(1)}_{A}L^{(2)}_{A}L^{(3)}_{A}L^{(4)}_{A}=|1\rangle |+\rangle |0\rangle |+\rangle \), then her coding sequence is \(R_{A}=R^{(1)}_{A}R^{(2)}_{A}R^{(3)}_{A}R^{(4)}_{A}=1000\). Since there is \(\overline{K}'_{AB}=\overline{K}_{AB}\) for correct Bob’s identity, the measurement bases chosen by Bob are exactly the same as those chosen by Alice. For the sequence \(S_{A}\), Bob’s measurement results are also \(|1\rangle |+\rangle |0\rangle |+\rangle \). So his coding sequence is also \(R'_{A}=1000\), that is, \(R_{A}=R'_{A}\). Therefore, Bob can pass the identity authentication by using his correct identity information.

Forgery attack: If Charlie wants to authenticate herself as Bob, she must not know \(K_{AB}\). So she cannot get the right \(\overline{K}'_{AB}\) and cannot choose the right measurement bases. For every particle of the sequence \(S_{A}\), she can only choose one randomly between two measurement bases Z and X. Moreover, the corresponding probability is 1/2. If the measurement bases of Charlie and Alice are consistent, then Charlie’s measurement results must be correct. Continue to use the previous example, if Alice’s measurement results are \(L_{A}=L^{(1)}_{A}L^{(2)}_{A}L^{(3)}_{A}L^{(4)}_{A}=|1\rangle |+\rangle |0\rangle |+\rangle \), then the sequence \(S_{A}\) must collapse to \(S_{A}=S^{(1)}_{A}S^{(2)}_{A}S^{(3)}_{A}S^{(4)}_{A}=|1\rangle |+\rangle |0\rangle |+\rangle \). For \(S^{(1)}_{A}=|1\rangle \), Charlie can choose two possible measurement bases Z and X with a probability of 1/2. If Charlie chooses Z base for measuring the particle \(S^{(1)}_{A}\), then her measurement result must be \(|1\rangle \). However, if Charlie chooses X base for her measurement, she must obtain one of two measurement results \(|+\rangle \) or \(|-\rangle \). Since \(|1\rangle =\frac{1}{\sqrt{2}}(|+\rangle -|-\rangle )\), the probability of each result is 1/2. When Charlie’s measurement result is \(|-\rangle \), her code is \(R'^{(1)}_{A}=1\) and \(R'^{(1)}_{A}=R^{(1)}_{A}\). When Charlie’s measurement result is \(|+\rangle \), her code is \(R'^{(1)}_{A}=0\) and \(R'^{(1)}_{A}\ne R^{(1)}_{A}\). Therefore, Charlie’s probability of getting \(R'^{(i)}_{A}=R^{(i)}_{A}\) is \(\frac{1}{2}+\frac{1}{2}\times \frac{1}{2}=\frac{3}{4}\). For n long sequence \(S_{A}=S_{A}^{(1)}S_{A}^{(2)}\cdots S_{A}^{(n)}\), the successful probability of her forgery attack is \((\frac{3}{4})^{n}\). If n approaches \(\infty \), the value \((\frac{3}{4})^{n}\) approaches 0. Therefore, her identity forgery attack fails.

Unconditional security: The mutual authentication has used the hash function H(x). The hash values are used to determine the measurement bases of Alice and Bob. In Step.3(c), Bob publishes the corresponding coding sequence \(R'_{A}\) after measuring the sequence \(S_{A}\). However, an attacker cannot get Bob’s measurement bases from the value \(R'_{A}\). Because the coding rules stipulate that both \(|0\rangle \) and \(|+\rangle \) are coded as “0,” both \(|1\rangle \) and \(|-\rangle \) are coded as “1.” For the value \(R'_{A}=0000\), the sequence \(S_{A}\) is one of 16 cases. See Table 2 for details. Therefore, there are 16 kinds of possible measurement base sequences, which correspond to 16 kinds of different hash value sequences \(\overline{K}'_{AB}\). Thus, the attacker does not know the hash values \(\overline{K}'_{AB}\) (\(\overline{K}'_{AB}=H(K_{AB}||r)=\overline{K}_{AB}\)). So he can’t compute the secret identity information \(K_{AB}\). In fact, our mutual authentication does not use the computational complexity security of hash function H(x), such as one-way property and anti-collision property. For each identity authentication, we only use the information compression ability of hash function H(x). Moreover, the hash value \(\overline{K}'_{AB}\) (\(\overline{K}_{AB}\)) is different for each different r. Thus, our mutual authentication is still unconditionally secure.

Table 2 The relationship among the hash value \(\overline{K}'_{AB}\), the sequence \(S_{A}\) and the coding sequence \(R'_{A}\)
Full size table

3.2 Security analysis of key negotiation

Now, we show that the key negotiation is secure against both participant and external attacks.

First, we consider participant attacks. The secret key negotiation of this MAQKA protocol is realized by the entanglement exchange of Bell states. The entanglement exchange relations of Bell states ensure that the key negotiated by both parties are equal and random. Neither Alice nor Bob can change this randomness, so neither can control the shared key independently. That is, neither Alice nor Bob can successfully carry out the participant attack.

Second, we consider external attacks. The key agreement here also faces four types of attacks, including Trojan horse attacks, intercept-resend attack, measure-resend attack and entangle-measure attack [1, 2]. Since all the sequences in the channel are transmitted only once, this MAQKA protocol is naturally immune to two kinds of Trojan horse attacks [27, 28]. Moreover, there are decoy particles inserted in all transmission sequences. All the decoy particles are chosen from the set \(\{|0\rangle , |1\rangle ,\) \( |+\rangle , |-\rangle \}\) which form two different orthogonal bases. These decoy states are used to detect channel security, which ensures the security of both the transmitted sequences \(S'_{A}\) and \(S'_{B}\). That is, the security detection of Step.2 can find all the attacks such as intercept-resend attack, measure-resend attack and entangle-measure attack. The security detection probability can be referred to the references [1, 2]. On the other hand, the entanglement exchange of Bell states makes key negotiation free of information leakage [29].

Thus, the key negotiation of our MAQKA protocol is also unconditionally secure since it is also based on quantum mechanics principles [3, 30, 31].

3.3 Performance analysis

Then we discuss the performance of new MAQKA protocol which is mainly characterized by quantum bit efficiency \(\eta =\frac{c}{q+b}\)[32]. For the parameters c, q and b, they represent the shared key bits, the qubits and the classical bits for decoding the partial secret keys, respectively. If we only want to calculate the quantum bit efficiency of key negotiation phase, we may not consider the consumption of quantum states for identity mutual authentication. In our MAQKA protocol, the length of the shared key is 2m, the number of Bell states used to negotiate the shared key is also 2m and the number of the classical bits is 0. When calculating the specific value of quantum bit efficiency, it can be assumed that the number of decoy states and transmitted particles is equal. Thus, there are also 2m decoy states and the qubit efficiency of our MAQKA protocol is \(\eta =\frac{2m}{4m+2m}=\frac{1}{3}\approx 33.33\%\). When we want to calculate the quantum bit efficiency of the whole MAQKA protocol, the consumption of quantum states for identity mutual authentication is considered. There are 2n Bell states needed for identity mutual authentication in our MAQKA protocol. Similarly, we also assume that we need the same number of decoy states for the mutual authentication phase. Then the number of decoy states is also 2n. So the qubit efficiency of our whole protocol is \(\eta '=\frac{2m}{4(n+m)+2(n+m)}\). When n is equal to m, the qubit efficiency \(\eta '\) is equal to 1/6, which is approximately \(16.67\%\). In a similar way, we calculate the overall efficiency of the existing two MAQKA protocols. Compared with the existing MAQKA protocols (see Table 3), our MAQKA protocol has great advantages in qubit efficiency.

Table 3 Comparison between our MAQKA protocol and the existed MAQKA protocols
Full size table

In the new MAQKA protocol, Bell states are used as quantum resource, which are easier to realize with the existing technology than three-particle entangled states [25] and five-particle entangled states [26]. For the measurement basis, our protocol uses the single-particle measurement basis and Bell basis to measure the corresponding quantum states. So its realizing difficulty of particle measurement is very close to that of the existing two protocols. Because ZWL protocol [25] only uses single-particle measurements, MHLZ protocol [26] uses single-particle measurements and Bell measurements. Further, the implementation of this MAQKA protocol can be completed without the help of a trusted or semi-trusted third party, which makes its steps relatively simpler and it less communication traffic. Moreover, two participants of the MAQKA protocol only needs once quantum communication and fewer classical communication. However, both ZWL [25] and MHLZ [26] protocols require the participation of the third party to achieve mutual authentication and key negotiation. And MHLZ protocol [26] requires more quantum communication and classical communication.

4 Conclusion

Based on Bell states, we design a two-party MAQKA protocol which can realize mutual authentication and key negotiation without the participation of trusted or semi-trusted third party. Compared with the existing MAQKA protocols, the new MAQKA protocol not only reduces the complexity of its steps, but also reduces the communication between participants. It uses the secret identity information and the measurement correlation property of Bell states to realize mutual identity authentication. It uses the entanglement swapping property of Bell states to realize key negotiation. We also show that the new MAQKA protocol is unconditionally secure. More specifically, its identity authentication can resist forgery attacks; its key negotiation resist external attacks and participant attacks. Moreover, it has higher quantum bit efficiency. Therefore, it is more suitable for practical application.