Quantum multiparty cryptosystems based on a homomorphic random basis encryption

Abstract

Quantum information processing protocols have great advantages over their classical counterparts, especially on cryptography. Homomorphic encryption (HE) schemes enable processing encrypted data without decrypting them. In this paper, we study a quantum version of the HE scheme (iacr-ePrint/2019/1023) and improve it with flexible parties. Furthermore, we propose a threshold quantum secret scheme since multiparty cryptosystem is more practical due to its flexibility. These two schemes only require sequential decryption of quantum states. As a result, both schemes are information theoretically secure, perfectly correct and support homomorphism in a fully compact and non-interactive way. Finally, they are tested and verified on the IBM Q Experience platform.

1 Introduction

It is well known that a fully quantum theory of information and information processing offers, among other benefits, a brand of cryptography with security based on fundamental physics, and a reasonable hope of implementing quantum computers that could speed up the solution of certain mathematical problems [1]. These benefits come from distinctive quantum properties such as superposition, entanglement, and nonlocality [2, 3] which do not exist in classical mechanics. In the last four decades, many important quantum information processing protocols have been proposed, including quantum key distribution (QKD) [4], quantum teleportation [5], quantum factoring algorithm [6] and Grover search algorithm [7].

Quantum cryptography is one of the most successful applications in quantum information processing since physical laws ensure its inherent security. Contrarily, classical cryptography usually relies on the assumptions of computational complexity. The first quantum cryptosystem is quantum key distribution which is used to generate random secret keys that are only shared by two parties [4]. Later, quantum cryptography has been extensively studied and many protocols are proposed [8,9,10,11,12,13,14,15].

The homomorphic encryption (HE) scheme enables processing of encrypted data without decrypting them in advance. This useful feature was known for over 30 years. In 2009, Craig Gentry [16] introduced the first plausible and achievable fully homomorphic encryption (FHE) scheme , which supports processing of any function over the encrypted data (see the surveys [17, 18]). But the scheme can only achieve computational security. It is natural to ask whether the physical principle of quantum mechanics can be applied to construct HE schemes so that better security/performance can be achieved. The answer is certain, and various quantum homomorphic encryption (QHE) schemes have been proposed. In summary, these schemes can be classified into two categories. One is efficient with information-theoretical security (ITS) that can only evaluate a subset of all possible functions [19,20,21,22,23,24]; the other can only achieve computational security [25,26,27,28,29]. Besides, it has been shown that it is impossible to construct an efficient quantum FHE with ITS [30, 31]. Recently, Dor Bitan et al. proposed a quantum homomorphic encryption scheme [32] using a specific family of random bases. It can encrypt and outsource the storage of classical data while enabling quantum gate computations over the encrypted data with ITS.

In this work, we improve Dor Bitan’s scheme with multiparty structure to achieve flexibility. After that, the scheme will be more practical in multiparty situation. Because after the dealer encrypts the data, more than one participant can cooperate to decrypt it sequentially with an appointed key. Furthermore, a (t, n) threshold quantum secret sharing scheme (QSS) (see basic definitions in  [33]) is proposed so that no less than t participants can cooperate to recover the secret. In fact, the QSS scheme can be seen as a derivative of the QHE scheme [32]. Also, there is a QSS scheme [34] derived from the QHE scheme [22]. These two QSS schemes can evaluate the encoded quantum states without the need to decode the secret while having some differences, such as threshold ((t, n) or (n, n)), shared secrets (classical bits or quantum states), particle transmission mode (straight line type or tree type). As a result, both proposed schemes in this paper keep the same properties as the basic one [32] after analysis. Specifically, both schemes are information theoretically secure, perfectly correct and also support homomorphic operations in a fully compact and non-interactive way. Finally, we carry out experiments on the IBM Q Experience platform and the statistical results confirm the feasibility of our schemes.

2 Preliminaries

2.1 The homomorphic random basis encryption scheme

Homomorphic encryption (HE) schemes can be described in a collection of four algorithms, which are key generation (Gen), encryption (Enc), evaluation (Eval), decryption (Dec). We give a brief review of the homomorphic random basis encryption scheme in the following.

• Gen Output a key that is a uniformly random pair ($\theta ,\phi$) from [0,2$\pi$]$\times \{\frac{{\pi }}{{2}},-\frac{{\pi }}{{2}}\}$.

• Enc Output a qubit $|q \rangle$ which is achieved from $|q \rangle =K |b \rangle$ with input message $b \in \{0,1\}$ and a key $k=(\theta ,\phi )$. Here the K is the encrypting operator in the form

  $$\begin{aligned} K = \left[ {\begin{array}{*{20}{c}} {\cos ({\theta /2})}&{}{\sin ({\theta /2})}\\ {e^{i\phi }\sin ({\theta /2})}&{}{ - e^{i\phi }\cos ({\theta /2})} \end{array}} \right] . \end{aligned}$$

• Dec Output the plaintext of the input $|q \rangle$ with the key $k=(\theta ,\phi )$. It can be achieved by applying $K^\dag$ to $|q \rangle$ and outputting the measurement of $K^\dag |q \rangle$ in the computational basis.

It supports homomorphic evaluation of the X gate, CNOT gate and D gate (used to create Bell state), where the control qubit is in the computational basis. Here, we focus on the X gate and CNOT gate, which appear in our paper. For the X gate, we can set $\left| {{\psi _\mathrm{{0}}}} \right\rangle \mathrm{{ = }}K\left| 0 \right\rangle ,\left| {{\psi _1}} \right\rangle \mathrm{{ = }}K\left| 1 \right\rangle$ and get

$$\begin{aligned} X\left| {{\psi _\mathrm{{0}}}} \right\rangle = \pm i\left| {{\psi _1}} \right\rangle ,X\left| {{\psi _1}} \right\rangle = {\mp } i\left| {{\psi _0}} \right\rangle . \end{aligned}$$

(1)

For the CNOT gate with control qubit in the computational basis, we can verify that

$$\begin{aligned} {\mathrm{CNOT}}| {1\rangle \otimes |{\psi _\mathrm{{0}}}} \rangle = \pm i\left| {1\rangle \otimes | {\psi _1}} \right\rangle ,\mathrm{{CNOT}}\left| {1\rangle \otimes |{\psi _1}} \right\rangle = {\mp } i\left| {1\rangle \otimes |{\psi _0}} \right\rangle . \end{aligned}$$

(2)

Since $\pm i$ (${\mp } i$) is an overall phase, we can drop it when measuring the quantum states.

2.2 The secret sharing scheme of Shamir

Here, we introduce the secret sharing scheme proposed by Shamir with (t, n) threshold [35]. In the scheme, it shows how to divide the secret s into n pieces in such a way that any t pieces can recover s easily, but never reveals any information about s even with complete knowledge of $t-1$ pieces. The scheme consists of two algorithms:

• 1. Share generation the dealer D picks a random polynomial f(x) of degree $t-1$: $f(x)=a_0+a_1x+\cdots +a_{t-1}x^{t-1}\hbox {mod} p$ with secret $s=a_0$ and all coefficients $a_0,a_1,\ldots ,a_{t-1}$ are in a finite field ${\mathbb {F}}_p$, p is a prime. Then D computes: $s_j=f(x_j),j=1,2,\ldots ,n$ with that $x_j$ is the public information of party $P_j$. At last, the algorithm outputs a list of n shares ($s_1,s_2,\ldots ,s_n$) and allocates each share $s_j$ to party $P_j$ securely.

• 2. Secret reconstruction it takes any m ($m \ge t$) shares $s_{j}, j \in {\mathcal {U}}=\{i_1,i_2,\ldots ,i_m\},$${\mathcal {U}} \subseteq \{1,2,\ldots ,n\}$ as inputs and outputs the secret s, which can be achieved from

  $$\begin{aligned} s = \sum \limits _{j \in {\mathcal {U}}} c_j = \sum \limits _{j \in {\mathcal {U}}} {f({x_{{j}}})} \prod \limits _{r \in {\mathcal {U}},r \ne j} {\frac{{{x_{{r}}}}}{{{x_{{r}}} - {x_{{j}}}}}} \hbox {mod} p. \end{aligned}$$

  (3)

3 Multiparty decryption over the classical bit

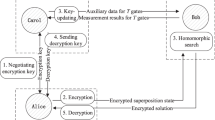
Suppose the dealer Alice uses the random basis encryption scheme ($\left| 0 \right\rangle ,\left| 1 \right\rangle$ represent classical bit 0,1 respectively) to encrypt her message among n participants Bob$_j,j=1,2\ldots ,n$. After receiving the encrypted quantum state, n participants Bob$_j$ can collaborate to decrypt the message of Alice. The multiparty decryption (MD) scheme can be described as follows with a flowchart in Fig. 1a.

• 1: Alice generates n decryption keys ${\theta _j}, j = 1,2, \ldots ,n$ from her key $\theta _0 \in [0,2\pi ]$ and sends each $\theta _j$ to the participant Bob$_j$ using QKD, where the keys satisfy the condition $\theta _0 = \sum \nolimits _{j = 1}^n {{\theta _j} \bmod 2\pi }.$

• 2: Alice uses the random basis encryption scheme to encrypt her message b yielding the encrypted qubit in the form $\left| q \right\rangle =K_0 |b\rangle$. Later, it is shared among n participants, here $K_0$ is the encrypting operator K with a key ($\theta _0, \phi =\frac{\pi }{2}$).

• 3: Participants Bob$_j,j=1,2\ldots ,n-1$, each performs $UK_j^\dag$ on the received qubit sequentially and passes it to the next with $U = \left[ {\begin{array}{*{20}{c}}0&{}1\\ i&{}0\end{array}}\right]$.

• 4: Finally, the last participant Bob$_n$ receives the resulted qubit and performs $V_nK_n^\dag$ on it. The operators $K_j^\dag , j=1,2\ldots ,n$ are the conjugate transpose of the encrypting operator K with a key ($\theta _j, \phi =\frac{\pi }{2}$), which are in the form

  $K_j^\dag = \left[ {\begin{array}{*{20}{c}} {\cos ({{{\theta _j}} /2})}&{}{ - i\sin ({{{\theta _j}}/2})}\\ {\sin ({{{\theta _j}} /2})}&{}{i\cos ({{{\theta _j}} /2})} \end{array}}\right] ,$ and

  $$\begin{aligned} {V_n} = \left\{ {\begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{c}} -1&{}0\\ 0&{}-1 \end{array}} \right] =-I,n = 1\bmod 4,}\\ {\left[ {\begin{array}{*{20}{c}} 0&{}{ 1}\\ -1&{}0 \end{array}} \right] =-XZ,n = 2\bmod 4,}\\ {\left[ {\begin{array}{*{20}{c}} { 1}&{}0\\ 0&{}{ 1} \end{array}} \right] =I,n = 3\bmod 4,}\\ {\left[ {\begin{array}{*{20}{c}} 0&{}-1\\ { 1}&{}0 \end{array}} \right] =XZ,n = 0\bmod 4.} \end{array}} \right. \end{aligned}$$

  After that, he measures the qubit in the computational basis and outputs the measurement result b as the message of Alice.

Fig. 1

The flow chart of the MD scheme (a) and QSS scheme (b)

4 Threshold quantum secret sharing scheme

Recently, a verifiable framework for quantum secret sharing was proposed [36]. Here, we propose a QSS under this framework which includes four algorithms (see the flowchart in Fig. 1b).

• 1. Classical private share distribution in this algorithm, the dealer Alice uses Shamir’s scheme to produce n shares $s_j, j=1,2,\ldots ,n$ from the private value s with threshold $t (t \le n)$ and prime p. She sends these shares $s_j$ to each participants Bob$_j$ using QKD.

• 2. Secret encoding assume Alice’s secret is a classical bit b, then she uses the random basis encryption scheme to encrypt it with a key ($\theta _0 = \frac{{2\pi s}}{p}, \phi =\frac{\pi }{2}$) and the resulted qubit is $\left| q \right\rangle =K_0|b\rangle$. After that, the qubit is shared among participants.

• 3. Sequential operation on single quantum system after receiving the qubit, arbitrary m participants can recover the secret of Alice, here we assume these m participants are Bob$_j,j=1,2\ldots ,m$. To recover the secret, each except Bob$_m$ first prepares a random bit $b_j \in \{0,1\}, j=1,2,\ldots ,m-1$ as the control qubit, then performs the CNOT gate with the received qubit as the target qubit. Later, each continues to perform $UK_j^\dag$ on the received qubit sequentially with ${\theta _j} = \frac{{2\pi {c_j}}}{p}$ ($c_j$ can be computed in Eq. 3).

• 4. Secret reconstruction the last participant Bob$_m$ also prepares the random bit $b_m$ and performs the CNOT gate, however, followed with the decryption $V_mK_m^\dag$. Finally, he measures the qubit in the computational basis and outputs the measurement result $b + \sum \nolimits _{j = 1}^m {{b_m}} \bmod 2$. By exchanging the random numbers $b_j$, each of m participants can recover the value b as Alice’s secret.

5 Analysis of the two schemes

5.1 Correctness

We will prove that both schemes generate expected outputs in the following.

In both schemes, if all the operations on the qubit do not transform the state (or with an overall phase), then the measurement result of the qubit equals to the original classical bit. Here, we first prove the following Theorem 1, which can show the correctness of the MD scheme.

Theorem 1

If ${V_1}K_1^\dag K_0=I$ and ${V_n}K_n^\dag \left[ {\prod \limits _{j = n - 1}^1 {(UK_j^\dag )} } \right] K_0 = I, n \ge 2$ hold with the condition $\theta _0 = \sum \limits _{j = 1}^n {{\theta _j}} \hbox {mod} 2\pi$, then the MD scheme can achieve the perfect correctness.

Proof

For the first case, it has the form

$$\begin{aligned} \begin{aligned} {V_1}K_1^\dag K_0&= \begin{bmatrix} -1&{}0\\ 0&{}-1 \end{bmatrix} {\begin{bmatrix} {\cos \frac{{{\theta _1}}}{2}}&{}{ - i\sin \frac{{{\theta _1}}}{2}}\\ {\sin \frac{{{\theta _1}}}{2}}&{}{i\cos \frac{{{\theta _1}}}{2}} \end{bmatrix}} {\begin{bmatrix} {\cos \frac{{{\theta _0 }}}{2}}&{}{\sin \frac{{{\theta _0 }}}{2}}\\ {i\sin \frac{{{\theta _0 }}}{2}}&{}{ - i\cos \frac{{{\theta _0 }}}{2}} \end{bmatrix}} \\&=\begin{bmatrix} -{\cos \frac{{{\sigma _1}}}{2}}&{}-{ \sin \frac{{{\sigma _1}}}{2}}\\ {\sin \frac{{{\sigma _1}}}{2}}&{}-{\cos \frac{{{\sigma _1}}}{2}} \end{bmatrix}=I,(\sigma _1=\theta _0 -\theta _1 ). \end{aligned} \end{aligned}$$

(4)

Then, it is the same for $n=2,3,4$,

$$\begin{aligned} \begin{aligned} {V_2}K_2^\dag U K_1^\dag K_0&= {V_2}K_2^\dag \begin{bmatrix} 0&{}1\\ i&{}0 \end{bmatrix} \begin{bmatrix} {\cos \frac{{{\sigma _1}}}{2}}&{}{ \sin \frac{{{\sigma _1}}}{2}}\\ {-\sin \frac{{{\sigma _1}}}{2}}&{}{\cos \frac{{{\sigma _1}}}{2}} \end{bmatrix}\\&=\begin{bmatrix} 0&{}1\\ -1&{}0 \end{bmatrix} {\begin{bmatrix} {\cos \frac{{{\theta _2}}}{2}}&{}{ - i\sin \frac{{{\theta _2}}}{2}}\\ {\sin \frac{{{\theta _2}}}{2}}&{}{i\cos \frac{{{\theta _2}}}{2}} \end{bmatrix}} {\begin{bmatrix} {-\sin \frac{{{\sigma _1 }}}{2}}&{}{\cos \frac{{{\sigma _1 }}}{2}}\\ {i\cos \frac{{{\sigma _1 }}}{2}}&{}{ i\sin \frac{{{\sigma _1 }}}{2}} \end{bmatrix}} \\&=\begin{bmatrix} -{\cos \frac{{{\sigma _2}}}{2}}&{}-{ \sin \frac{{{\sigma _2}}}{2}}\\ {\sin \frac{{{\sigma _2}}}{2}}&{}-{\cos \frac{{{\sigma _2}}}{2}} \end{bmatrix}=I,(\sigma _2=\theta _0 -\theta _1-\theta _2 ). \end{aligned} \end{aligned}$$

(5)

$$\begin{aligned} \begin{aligned} {V_3}K_3^\dag \prod \limits _{j = 2}^1 {(UK_j^\dag )} K_0&= {V_3}K_3^\dag \begin{bmatrix} 0&{}1\\ i&{}0 \end{bmatrix} \begin{bmatrix} {-\sin \frac{{{\sigma _2}}}{2}}&{}{ \cos \frac{{{\sigma _2}}}{2}}\\ {-\cos \frac{{{\sigma _2}}}{2}}&{}{-\sin \frac{{{\sigma _2}}}{2}} \end{bmatrix}\\&=\begin{bmatrix} 1&{}0\\ 0&{}1 \end{bmatrix} {\begin{bmatrix} {\cos \frac{{{\theta _3}}}{2}}&{}{ - i\sin \frac{{{\theta _3}}}{2}}\\ {\sin \frac{{{\theta _3}}}{2}}&{}{i\cos \frac{{{\theta _3}}}{2}} \end{bmatrix}} {\begin{bmatrix} {-\cos \frac{{{\sigma _2 }}}{2}}&{}{-\sin \frac{{{\sigma _2 }}}{2}}\\ {-i\sin \frac{{{\sigma _2 }}}{2}}&{}{ i\cos \frac{{{\sigma _2 }}}{2}} \end{bmatrix}} \\&=\begin{bmatrix} -{\cos \frac{{{\sigma _3}}}{2}}&{}-{ \sin \frac{{{\sigma _3}}}{2}}\\ {\sin \frac{{{\sigma _3}}}{2}}&{}-{\cos \frac{{{\sigma _3}}}{2}} \end{bmatrix}=I,(\sigma _3=\theta _0 -\sum \nolimits _{j = 1}^3 {{\theta _j}} ). \end{aligned} \end{aligned}$$

(6)

$$\begin{aligned} \begin{aligned} {V_4}K_4^\dag \prod \limits _{j = 3}^1 {(UK_j^\dag )} K_0&= {V_4}K_4^\dag \begin{bmatrix} 0&{}1\\ i&{}0 \end{bmatrix} \begin{bmatrix} {-\cos \frac{{{\sigma _2}}}{2}}&{}{ -\sin \frac{{{\sigma _2}}}{2}}\\ {\sin \frac{{{\sigma _2}}}{2}}&{}{-\cos \frac{{{\sigma _2}}}{2}} \end{bmatrix}\\&=\begin{bmatrix} 0&{}-1\\ 1&{}0 \end{bmatrix} {\begin{bmatrix} {\cos \frac{{{\theta _4}}}{2}}&{}{ - i\sin \frac{{{\theta _4}}}{2}}\\ {\sin \frac{{{\theta _4}}}{2}}&{}{i\cos \frac{{{\theta _4}}}{2}} \end{bmatrix}} {\begin{bmatrix} {\sin \frac{{{\sigma _3 }}}{2}}&{}{-\cos \frac{{{\sigma _3 }}}{2}}\\ {-i\cos \frac{{{\sigma _3 }}}{2}}&{}{ -i\sin \frac{{{\sigma _3 }}}{2}} \end{bmatrix}} \\&=\begin{bmatrix} -{\cos \frac{{{\sigma _4}}}{2}}&{}-{ \sin \frac{{{\sigma _4}}}{2}}\\ {\sin \frac{{{\sigma _4}}}{2}}&{}-{\cos \frac{{{\sigma _4}}}{2}} \end{bmatrix}=I,(\sigma _4=\theta _0 -\sum \nolimits _{j = 1}^4 {{\theta _j}} ). \end{aligned} \end{aligned}$$

(7)

Until now, we can summarize it for the general case $n=4m+1, 4m+2, 4m+3, 4m+4, m\in \{1,2,\ldots \}$. For $n=4m+1$, it has the form

$$\begin{aligned} \begin{aligned} {V_{n}}K_{n}^\dag&\left[ {\prod \limits _{j = m - 1}^0 {\left( {\prod \limits _{l = 4}^1 {UK_{4j + l}^\dag }} \right) }} \right] K_0 \\&= {V_{n}}K_{n}^\dag \left[ {\prod \limits _{j = m - 1}^1 {\left( {\prod \limits _{l = 4}^1 {UK_{4j + l}^\dag } } \right) } } \right] \begin{bmatrix} {\cos \frac{{{\sigma _4}}}{2}}&{}{ \sin \frac{{{\sigma _4}}}{2}}\\ {i\sin \frac{{{\sigma _4}}}{2}}&{}{-i\cos \frac{{{\sigma _4}}}{2}} \end{bmatrix}\\&={V_{n}}K_{n}^\dag \left[ {\prod \limits _{j = m - 1}^2 {\left( {\prod \limits _{l = 4}^1 {UK_{4j + l}^\dag } } \right) } } \right] \begin{bmatrix} {\cos \frac{{{\sigma _8}}}{2}}&{}{ \sin \frac{{{\sigma _8}}}{2}}\\ {i\sin \frac{{{\sigma _8}}}{2}}&{}{-i\cos \frac{{{\sigma _8}}}{2}} \end{bmatrix}\\&={V_{n}}K_{n}^\dag \begin{bmatrix} {\cos \frac{{{\sigma _4m}}}{2}}&{}{ \sin \frac{{{\sigma _4m}}}{2}}\\ {i\sin \frac{{{\sigma _4m}}}{2}}&{}{-i\cos \frac{{{\sigma _4m}}}{2}} \end{bmatrix}\\&=I,(\sigma _{4m+1}=\theta _0 -\sum \nolimits _{j = 1}^{4m+1} {{\theta _j}} ). \end{aligned} \end{aligned}$$

(8)

Later, it is easy to verify the equation when $n=4m+2,4m+3,4m+4$ just like the method to verify $n=2,3,4$. At last, we can get ${V_1}K_1^\dag K_0=I$ and ${V_n}K_n^\dag \left[ {\prod \limits _{j = n- 1}^1 {(UK_j^\dag )} } \right] K_0 = I, n \ge 2$, and this completes the proof. $\square$

Since the QSS scheme is derived from the MD scheme and we use Theorem 1 to show the correctness of the MD scheme; thus, we can use a new theorem derived from Theorem 1 to show the correctness of the QSS scheme. In the QSS scheme, we can easily verify that $\theta _0 = \frac{{2\pi s}}{p}, {\theta _j} = \frac{{2\pi {c_j}}}{p}, j=1,2,\ldots ,m$ satisfy $\theta _0 = \sum \nolimits _{j = 1}^m {{\theta _j}} \hbox {mod} 2\pi$ using Eq. 3. Therefore proving Theorem 2 is enough to show the correctness.

Theorem 2

If the following equation

$$\begin{aligned} {V_m}K_m^\dag \left[ {\prod \limits _{j = m - 1}^1 {(UK_j^\dag X^{b_j})} } \right] K_0 = \left\{ {\begin{array}{*{20}{c}} {I,{ \oplus _{j = 1}^m{b_j} = 0,} }\\ {Y,{ \oplus _{j = 1}^m{b_j} = 1,} } \end{array}} \right. \end{aligned}$$

(9)

$m\ge 2$, holds for the condition $\theta _0 = \sum \limits _{j = 1}^m{{\theta _j}} \hbox {mod} 2\pi$, it can be concluded that the QSS scheme is perfectly correct.

Proof

Using Theorem 1, we can know that sequential operations can complete the decryption successfully. So Eq. 9 can be rewritten as

$$\begin{aligned} {V_m}K_m^\dag \left[ {\prod \limits _{j = m - 1}^1 {(UK_j^\dag )} } \right] X^{\oplus _{j = 1}^m{b_j} } K_0 = \left\{ {\begin{array}{*{20}{c}} {I,{ \oplus _{j = 1}^m{b_j} = 0,} }\\ {Y,{ \oplus _{j = 1}^m{b_j} = 1.} } \end{array}} \right. \end{aligned}$$

(10)

If ${ \oplus _{j = 1}^m{b_j} = 0}$, it is the same as Theorem 1 and if ${ \oplus _{j = 1}^m{b_j} = 1}$, we can simplify it as ${K_0^\dag }XK_0 = Y$.

In conclusion, Eq. 9 holds for $\theta _0 = \sum \limits _{j =1}^m {{\theta _j}} \hbox {mod} 2\pi$ yielding the correctness of the Theorem 2. $\square$

5.2 Security

In the paper [37], the authors first sketch a scenario for private quantum channels. Assume Alice wants to send a pure state $|\phi \rangle$ to Bob from the set ${\mathcal {S}}$, she appends ancilla qubits $\rho _a$ to $|\phi \rangle \langle \phi |$ and then applies unitary transformation $U_i$ to $|\phi \rangle \langle \phi | \otimes \rho _a$, where i is the key with probability $p_i$. Bob (shares the key i with Alice) receives the resulted state and performs $U_i^{-1}$ to get $|\phi \rangle \langle \phi | \otimes \rho _a$. After that, he removes the ancilla $\rho _a$ and achieves Alice’s information $|\phi \rangle \langle \phi |$. Then they formalize this scenario so that Bob can recover the state perfectly with security against an eavesdropper in their definition. Following this idea, we adapt the definition to continuous setting for random basis encryption [32] and multiparty decryption.

Definition 1

Let ${\mathcal {S}} \subseteq {\mathcal {H}}_2$ be a set of qubits, $Q=\{U_i,i \in I \}$ be a superoperator where each $U_i$ is a unitary mapping on ${\mathcal {H}}_2$, and $\rho _0$ be some density matrix. Then $[ {\mathcal {S}}, {\mathcal {E}}, \rho _0]$ is called perfect masking of a given element $|\phi \rangle$ if and only if for all $|\phi \rangle \in {\mathcal {S}}$ we have

$$\begin{aligned} \int _I {{U_i}\left| \phi \right\rangle } \left\langle \phi \right| U_i^\dag = {\rho _{0.}} \end{aligned}$$

(11)

In the proposed MD scheme, for the dealer’s encryption, we have ${\mathcal {S}}=\{|0\rangle ,|1\rangle \}$, $Q=\{K_0, \theta _0 \in I\}$ and $I=[0,2\pi ]$ is a set of real numbers. According to Definition 1, the dealer’s encryption is perfectly secure if and only if for all $| \phi \rangle \in {\mathcal {S}}$,

$$\begin{aligned} \int _I {{K_0}\left| 0 \right\rangle } \left\langle 0 \right| K_0^\dag =\int _I {{K_0}\left| 1 \right\rangle } \left\langle 1 \right| K_0^\dag , \end{aligned}$$

(12)

is satisfied. A routine computation in the following can show the left and right sides of Eq. 12 are equal.

Proof

$$\begin{aligned} \int _I {K_0}| 0 \rangle \left\langle 0 \right| K_0^{\dag }= & {} \int _{\theta _0=0}^{2\pi } \begin{bmatrix} {\frac{1+\cos \theta _0}{2} }&{}{ -\frac{i\sin \theta _0}{2}}\\ {\frac{i\sin \theta _0}{2}}&{}{\frac{1-\cos \theta _0}{2}} \end{bmatrix}=\begin{bmatrix} {\pi }&{}{ 0}\\ {0}&{}{\pi } \end{bmatrix},\\ \int _I {K_0}|1\rangle \langle 1 |)K_0^{\dag }= & {} \int _{\theta _0=0}^{2\pi }\begin{bmatrix} {\frac{1-\cos \theta _0}{2} }&{}{\frac{ i\sin \theta _0}{2}}\\ {-\frac{i\sin \theta _0}{2}}&{}{\frac{1+\cos \theta _0}{2}} \end{bmatrix}=\begin{bmatrix} {\pi }&{}{ 0}\\ {0}&{}{\pi } \end{bmatrix}. \end{aligned}$$

$\square$

So for other participants’ local operations $Q=\{UK_j^\dag ,\theta _j \in I\}$, $j=1,2,\ldots ,n-1$, ${\mathcal {S}}=\left\{ {\left| {{\varphi _{j-1}}} \right\rangle _b = \left[ {\prod \limits _{r = j-1}^1 {(UK_r^\dag )} } \right] {K_0}\left| b \right\rangle ,b = 0,1} \right\}$ for $j=2,3,\ldots ,n-1$ and ${\mathcal {S}}=\left\{ {\left| {{\varphi _{0}}} \right\rangle _b ={K_0}\left| b \right\rangle ,b = 0,1} \right\}$ for $j=1$, we need to show

$$\begin{aligned} \int _I {UK_j^\dag \left| \varphi _{j-1} \right\rangle }_{0 \,0} \left\langle \varphi _{j-1}\right| K_j U^\dag =\int _I {UK_j^\dag \left| \varphi _{j-1} \right\rangle }_{1 \,1} \left\langle \varphi _{j-1} \right| K_j U^\dag . \end{aligned}$$

(13)

Fortunately, after computation, we can achieve that the both sides of Eq. 13 are equal as well. To conclude, after the dealer’s encryption, the density matrix that an adversary sees is equal and it is the same for participants’ partial decryption, regardless of the input. Therefore, the adversary cannot gain any information about the encrypted message and our MD scheme is secure.

To show the security of the QSS, the method of proof is the same as the MD scheme. After the dealer’s operation, we have $Q=\{K_0,\theta _0 \in I\}$, here $I=[0,2\pi ]$ is a set of real numbers, so the condition is Eq. 12. For other participants’s operations, we have $Q=\{UK_j^\dag X^{b_j},\theta _j \in I\}$, $b_j\in \{0,1\}, j=1,2,\ldots ,m-1$, ${\mathcal {S}}=\left\{ {\left| {{\varphi _{j-1}}} \right\rangle _b = \left[ {\prod \limits _{r = j-1}^1 {(UK_r^\dag X^{b_r} )} } \right] {K_0}\left| b \right\rangle ,b = 0,1} \right\}$ for $j=2,3,\ldots ,m-1$ and ${\mathcal {S}}=\left\{ {\left| {{\varphi _{0}}} \right\rangle _b ={K_0}\left| b \right\rangle ,b = 0,1} \right\}$ for $j=1$, so the condition is

$$\begin{aligned} \int _I {UK_j^\dag X^{b_j}\left| \varphi _{j-1} \right\rangle }_{0\,0} \left\langle \varphi _{j-1} \right| X^{b_j}K_j U^\dag =\int _I {UK_j^\dag X^{b_j}\left| \varphi _{j-1} \right\rangle }_{1\,1} \left\langle \varphi _{j-1} \right| X^{b_j}K_j U^\dag , \end{aligned}$$

(14)

with $X^\dag =X$. The correctness of Eq. 14 can also be verified after computation. Finally, we can conclude the QSS scheme is also secure.

6 Experiments on IBM Q experience

In the paper, the used unitary operations are most single-qubit operations. Therefore, to show the feasibility of our schemes, we run them in a superconducting qubit platform, provided by the IBM Q Experience.

In Sect. 5.1, we have shown the correctness of our schemes in theory. Here, we first design four cases for the MD scheme with

$$\begin{aligned} \begin{aligned}&n=2, \theta _0=\frac{{\pi }}{{2}}, \theta _1=\frac{{\pi }}{{3}}, \theta _2=\frac{{\pi }}{{6}},\\&n=3, \theta _0=\frac{{3\pi }}{{5}}, \theta _1=\frac{{\pi }}{{5}}, \theta _2=\frac{{\pi }}{{10}}, \theta _3=\frac{{3\pi }}{{10}}, \\&n=4, \theta _0=\frac{{5\pi }}{{9}}, \theta _1=\frac{{5\pi }}{{3}}, \theta _2=\frac{{17\pi }}{{9}}, \theta _3=\frac{{-\pi }}{{2}},\theta _4=\frac{{3\pi }}{{2}},\\&n=5, \theta _0=\frac{{\pi }}{{4}}, \theta _1=\frac{{5\pi }}{{4}}, \theta _2=\frac{{3\pi }}{{4}}, \theta _3=\frac{{7\pi }}{{4}},\theta _4=\frac{{\pi }}{{4}},\theta _5=\frac{{\pi }}{{4}}. \end{aligned} \end{aligned}$$

(15)

In each case, the dealer first uses $\theta _0$ to encrypt her bit b ($b=n \hbox {mod}2$), then n participants sequentially decrypt the resulted qubit using $\theta _j$. At last, they can get dealer’s bit by measuring in the computational basis.

To perform the experiments, we can design the corresponding quantum circuit following Fig. 1a and it is illustrated in Fig. 2. Thanks to the $U_3$ operation offered by IBM Q Experience, which is in the form

$$\begin{aligned} {U_3}(\theta ,\phi ,\lambda ) = \left[ {\begin{array}{*{20}{c}} {\cos ({\theta / 2})}&{}{ - {e^{i\lambda }}\sin ({\theta /2})}\\ {{e^{i\phi }}\sin ({\theta /2})}&{}{{e^{i\lambda + i\phi }}\cos ({\theta /2})} \end{array}} \right] . \end{aligned}$$

(16)

Therefore, the operations used in the MD scheme can be represented as

$$\begin{aligned} \begin{aligned}&{K_0} = {U_3}({\theta _0},{\pi /2},0)Z,U = {U_3}(\pi ,{\pi /2},0)Z,\\&K_j^\dag = {U_3}({\theta _j},{{0,\pi } /2}),j = 1,2, \ldots ,n. \end{aligned} \end{aligned}$$

(17)

Fig. 2

The designed quantum circuit for testing the MD scheme. Here, “Z”,“X”,“U3” and panel gates represent the Pauli Z gate, Pauli X gate, ${U_3}(\theta ,\phi ,\lambda )$ gate and measurement in the computational basis, respectively

Fig. 3

The designed quantum circuit for QSS scheme with “+” represents the CNOT gate and others are the same in Fig. 2

At last, we first run the circuit for three rounds with each round containing 8192 shots for simulation. However, for experiment, we run each line in the circuit independently. We show the statistical results for both simulation and experiment in Fig. 4.

It is the same for testing the QSS scheme. Assume the following (4,5)-QSS case, the selected random function is $f(x)=2x^3+4x^2+9x+12 \bmod 13$ ($s=12$, $p=13$), the public information of participants $P_j$ are $x_j=1,2,3,4,5$, respectively. Considering Bob$_j,j \in {\mathcal {U}}=\{1,2,3,5\}$ want to cooperate to recover the secret $S=b \in \{0,1\}$, they each can compute the $\theta _j$:

$$\begin{aligned} \theta _0=\frac{{24\pi }}{{13}},\theta _1=\frac{{14\pi }}{{13}},\theta _2= \frac{{4\pi }}{{13}},\theta _3=\frac{{8\pi }}{{13}},\theta _5=\frac{{24\pi }}{{13}}. \end{aligned}$$

(18)

Besides, the random selected numbers $b_j$ are 1, 0, 1, 1.

Following Fig. 1b, a corresponding quantum circuit for this QSS case is designed as Fig. 3.

We also run the circuit for three rounds with each round containing 8192 shots for simulation and experiment, and we show the results in Fig. 5.

Fig. 4

Measurement results of quantum circuit in Fig. 2. The simulation results (a) and experimental results (b) are performed on the “ibmq_qasm_simulator” simulator and “ibmqx2” superconducting quantum systems. The error bar denotes the standard deviation

Fig. 5

Measurement results of quantum circuit in Fig. 3 with the same setup in Fig. 4. Here, b is the secret with the measurement result r satisfying $r=b+\sum \nolimits _{j \in {\mathcal {U}}} {b_j} \hbox {mod}2$

In Figs. 4a and 5a, we can see the results of simulation are 100% correct, which confirm the correctness of our schemes. However, when it comes to the experimental implementations, the MD scheme can achieve the correctness with 98% on average and the QSS scheme can only get the correct answer with 91% on average (see Figs. 4b and 5b). We would like to remark the wrong results come from the gate errors, which could be complemented by error corrections. Moreover, the error rate of the two qubits gate CNOT is larger than a single-qubit gate, which results the lower accuracy of the QSS scheme.

7 Conclusion

The homomorphic encryption scheme enables processing of encrypted data without decrypting them in advance which will be a useful solution for the delegation of computation [38]. In this paper, we first study a QHE scheme using a random base. It can encrypt and outsource the storage of classical data while enabling quantum gate computations over the encrypted data with ITS. Then, we improve it to achieve the multiparty structure which is flexible with the number of parties and further propose a threshold QSS scheme. As a result, we analyze the correctness and security of both schemes yielding they still keep the same properties as the basic one. Also, we test and verify them on the IBM Q Experience and the statistical results confirm their feasibility successfully.