Keywords

1 Background

Cloud services have become very common in recent years. Many computer companies offer information storage and processing services for individuals, companies, and organizations. These services allow customers to enjoy an enormous storage space, massive processing power, and cheap, convenient and efficient management facilities. Many customers all over the world enjoy such services. However, in many cases, the information that the customer wants to export to the cloud is confidential. In such cases, there is a concern that the confidentiality of the information will be compromised due to hacking or even by the cloud company’s employees. One possible way of maintaining privacy is to encrypt the information by the user before sending it to the cloud (and keep the encryption keys secretly). This way is suitable in cases where the customer is only interested in storing the information. However, in many cases, the customer is also interested in processing the data by the cloud servers. In such cases, a question arises – how (if at all) can we enjoy the cloud’s processing services while keeping the confidentiality of the data? This problem is hereafter referred to as the secure delegation problem. The works reviewed in this manuscript seek solutions for this problem.

The secure delegation problem was first raised in 1978 by Rivest, Adelman, and Dertouzos. In their seminal paper [34], they suggested to use ‘privacy homomorphisms,’ nowadays known as homomorphic encryption schemes, to encrypt the data and enable oblivious processing of it by (honest-but-curious) remote servers (possibly in the cloud). The data is typically represented by finite field elements. Encryption schemes are composed of algorithms for encryption, decryption, and key generation (typically denoted Enc, Dec, and Gen). To phrase the problem mathematically, let \(m_1, m_2\) be elements of a finite field (or a ring), and \(c_1,c_2\) their encryptions generated by an encryption system denoted \(\pi \). Can \(c_1,c_2\) be used to publicly generate \(c_{\text {add}}=\) Enc\(_{\pi }\big (m_1+m_2\big )\) or \(c_{\text {mult}}=\) Enc\(_{\pi }\big (m_1\cdot m_2\big )\)? If it is possible to use \(c_1,c_2\) to publicly generate \(c_{\text {add}}=\) Enc\(_{\pi }\big (m_1+m_2\big )\) (respectively, \(c_{\text {mult}}=\) Enc\(_{\pi }\big (m_1\cdot m_2\big )\)), then \(\pi \) is additively homomorphic (respectively, multiplicatively homomorphic). If both tasks can be carried out, then \(\pi \) is a fully homomorphic encryption (FHE) system.

The search for fully homomorphic encryption schemes has been going on for many years and was tagged as ‘the holy grail of cryptography’. The first significant breakthrough in the field occurred in 2009, when Craig Gentry proposed the first (computationally secure) fully homomorphic encryption scheme [23]. Gentry’s scheme has been refined and additional FHE schemes have been proposed [2, 13, 24, 25, 37,38,39]. Unfortunately, the time complexity of the currently known FHE schemes is too high to make them practical [1, 31].

While FHE schemes can provide solutions to the secure delegation problem, they can achieve at most computational security, but not information-theoretical (IT-) security. In IT-secure schemes, the security of the scheme is derived purely from information theory and depends neither on the computing power of the adversary nor on any computational hardness assumptions. The security of cryptographic schemes that have computational security is based on unproven assumptions regarding the non existence of efficient algorithms for solving specific mathematical problems and the computing power of the possible adversary. FHE schemes cannot achieve IT-security since existences of an IT-secure FHE scheme would contradict known theorems regarding private information retrieval.

Solutions for the secure delegation problem can be divided into two categories according to their overall approach. FHE schemes suggest solutions for the secure delegation problem based on the centralized approach. This approach assumes that the user delegates the data to be stored and processed by a single server. The second approach to the secure delegation problem is the distributed approach, in which the user distributes the secret information between several clouds. In the distributed approach, the user typically uses a secret sharing scheme to distribute shares of the data among the servers. In this case, the users’ privacy is kept as long as no more than a predefined threshold of the servers collude in an adversarial attempt to reveal the data. Unlike FHE scheme, distributed solutions to the secure delegation problem often achieve IT-security. The first work reviewed in this manuscript [8] presents a distributed approach solution to the secure delegation problem that suggests an IT-secure delegation scheme. This scheme supports homomorphic evaluation of quadratic functions and 2-CNF circuits over a dynamic database of secrets with no communication between the servers.

The distributed approach to the secure delegation problem is related to secure multiparty computation (MPC). MPC is an active field of research in cryptography [6, 19,20,21,22, 27, 33, 40]. This field discusses the following problem. Several participants are holding secret inputs and wish to evaluate a multivariate function over their secret inputs while not revealing to each other any information regarding their secret inputs (except for what may be deduced from the output). MPC schemes differ in their security and efficiency levels and their assumptions regarding the behavior of the parties and the communication setting. One of the typically used ideas is to secret share inputs. Then, adding two secret shared values can implement logical OR gate, multiplication of two secret-shared values (and reducing the degree of the obtained polynomial) can implement a logical AND gate. Using these two gates, a general logical circuit can be blindly computed.

More often than not, MPC schemes provide distributed solutions to the secure delegation problem. In several cases, it also works the other way around. Namely, some distributed solutions to the secure delegation problem can be used to construct MPC schemes. The second work reviewed in this manuscript considers a specific secret sharing scheme – the distributed random matrix (DRM) scheme [10]. That secret sharing scheme is used to construct an efficient and IT-secure preprocessing-MPC protocol and a distributed solution for the secure delegation problem. These schemes support homomorphic evaluation of polynomials over non-zero inputs with optimal round complexity. We present the one-time secrets (OTS) protocols that enable the evaluation of multivariate polynomials over shares of non-zero secrets without requiring a secret sharing phase invoked in an offline preprocessing phase. In addition, [10] deals with the problem of handling possibly zero secrets in several ways. By enabling the servers to communicate with each other, we manage to enable the homomorphic evaluation of polynomials of an arbitrary degree. Recall that in [8], we were able to support evaluation of polynomials of degree at most two with no communication between the servers.

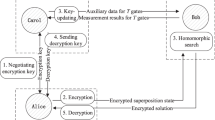
So far, we have described the secure delegation problem and possible solutions for it assuming all participants are classic computers. An equally exciting problem arises when it is assumed that some (or all) of the participants are quantum computers. In the third work reviewed in this manuscript, [11], we take the centralized approach, assume that the user and server are quantum computers, and seek efficient and IT-secure solutions to the secure delegation problem. In that paper, the homomorphic encryption system presented is used to construct a quantum key distribution (QKD) protocol that is resistant to attacks based on weak measurements (WM). We present new proposed WM-based attacks against existing QKD schemes that cannot be applied against our system (Table 1).

Table 1. A comparison of the solutions presented here.
Full size table

In the rest of the paper, we review the works [8, 10, 11] in more detail– for each work, we provide some additional background, examine the overall concept and methods, and the main contributions.

2 Communication-Less Evaluation

In 1979, Adi Shamir [35] presented one of the two first (N, t)-secret sharing schemes (see [12] for the other suggestion). Such a scheme allows a user to split a piece of information (hereafter a secret) among a set of N participants in such a way that only subsets of size at least t are able to recover the secret, while smaller subsets will not be able to learn any information about the secret. Secret sharing is a vital building block in MPC schemes and distributed solutions to the secure delegation problem. In Shamir’s secret sharing scheme, the secret s is an element of a finite field of order p, denoted by \(\mathbb {F}_p\), and is shared by a user among a set of N parties (where \(p > N\)) in the following way. Each party \(P_i\), \(1 \le i \le N\), is assigned by the user with an arbitrary element \(\alpha _i\) of \(\mathbb {F}_p^\times \), where the \(\alpha _i\)’s are distinct. Random elements \(a_j\) of \(\mathbb {F}_p\), \(1 \le j \le t-1\), are picked by the user. Let f be the polynomial defined by \(f(x)= s +\sum _{j=1}^{t-1} a_j x^j\) in the field \(\mathbb {F}_p\). Each party \(P_i\) gets the value \(f(\alpha _i)\). Shamir proved that, in this way, every group of t parties is able to reconstruct s, but no group of \(t-1\) parties gains any information about s [35].

One prominent property of Shamir’s scheme is that it is additively homomorphic. This property is based on the fact that the sum of polynomials of degree \(\le t-1\) is again a polynomial of degree \(\le t-1\). Unfortunately, since the product of two polynomials of degree \(\le t-1\) is in general of a higher degree, Shamir’s scheme is not multiplicatively homomorphic. As the degree of the polynomial gets larger, a larger coalition is required in order to extract the secret. One of the main results obtained in [8] is a method for making Shamir’s scheme support one homomorphic multiplication of secrets while, in some sense, not increasing the degree of the polynomial that represents the secrets. This is our novel function sieving method. This method provides a way of choosing the non-free coefficients for two \(N-1\) degree polynomials, \(f_1\) and \(f_2\), such that, if \(f_1(0)=s_1\) and \(f_2(0)=s_2\), then interpolating the N points \(\bigl (\alpha _i,f_1(\alpha _i)\cdot f_2(\alpha _i)\bigr )\) (for \(1\le i \le N\)) one obtains a polynomial whose value at zero is \(s_1\cdot s_2\). Our method enables to find the specific cases in which the polynomials \(f_1\) and \(f_2\) are such that, multiplying the shares of the corresponding secrets, one obtains N products of shares that represent a polynomial of degree \(\le N-1\) that has the right value at 0. We define a set of \(2(N-1)\)-tuples. Each tuple contains suitable non-free coefficients for a pair of polynomials for which homorphic multiplication in Shamir’s scheme works.

The Algorithm in a Nutshell. We now briefly sketch the outline of our constructions in more detail. Assume that the field \(\mathbb {F}_p\), in which the secrets \(s_1\) and \(s_2\) reside, is such that \(p \equiv 1 \pmod {N}\). In that case, since \(\mathbb {F}_p^\times \) is cyclic, it contains a primitive root of unity of order N. Let \(\alpha \) be such a root. For \(1 \le j \le N\) denote \(\alpha _j := \alpha ^j\), and assign to each party \(P_j\) the value \(\alpha _j\). Let \(a_i,b_i \in \mathbb {F}_p\), \(1 \le i \le N-1\), and consider the polynomials \(f_1(x) = s_1 + \sum _{i=1}^{N-1} a_i x^i\) and \(f_2(x) = s_2 + \sum _{i=1}^{N-1} b_i x^i\), in \(\mathbb {F}_p[x]\). Share the secrets \(s_1,s_2\) among the parties using \(f_1,f_2\). Let \(y_j = f_1(\alpha _j) \cdot f_2(\alpha _j)\), \(1\le j \le N.\) The pairs \((\alpha _j,y_j)\in \mathbb {F}_p^2\) are N distinct points through which the polynomial \((f_1 \cdot f_2)(x)\) passes.

Since \(f:=f_1 \cdot f_2\) is of degree \(\le 2N-2\), it is uniquely determined by \(2N-1\) points. Since there are only N points \((\alpha _j,y_j)\), interpolation of them will certainly not yield \((f_1 \cdot f_2)(x)\). Nevertheless, let g(x) be the interpolation polynomial for the N points, \((\alpha _j,y_j)\). Obviously, g is of degree \( \le N-1\). Since f and g agree on the roots of \(\psi \), we have \(g(x) \equiv f(x) \pmod {\psi (x)}\), where \(\psi (x) = \prod _{j=1}^{N} (x-\alpha _j)\). Since the \(\alpha _j\)’s are all the roots of unity of order N, we have \(\psi (x) = x^{n+1} -1.\) Hence, it is easy to compute g.

In fact, denote \(f(x) = s_1s_2 + \sum _{i=1}^{2N-2} c_i x^i.\) We have \(x^{N} \equiv 1 \pmod {\psi (x)}\), and therefore \(g(x) \equiv f(x) \equiv s_1s_2 + c_{N} + \sum _{i=1}^{N-1} (c_i + c_{N+i}) x^i \pmod {\psi (x)}.\) This in turn implies that \(g(0) = s_1s_2 + c_{N}\). Thus, if we take \(f_1\) and \(f_2\) such that \(c_{N}=0\), we get \(g(0) = f(0)\). Now, \(c_{N}= \sum _{i=1}^{N-1} a_i b_{N-i}\). Hence, instead of picking the coefficients of \(f_1\) and \(f_2\) uniformly at random, we pick them in such a way that \(c_{N}=0\).

This is, in essence, the function sieving method. Instead of using Shamir’s secret sharing scheme with random polynomials from \(\mathbb {F}_p [x]\), we use it with polynomials \(f_1,f_2\), for which \(c_{N}=0\), which compels \(g(0)=f(0)\). Such a pair \((f_1,f_2)\) is a 1-homomorphic multiplicative pair of polynomials.

This method enables a user to securely distribute a confidential database of m elements to a set of N semi-trusted servers while enabling homomorphic evaluation of quadratic functions and 2-CNF circuits over the secrets efficiently, with no communication between servers, IT-secure against coalitions of up to \(N-2\) semi-honest servers, with \(O(m^2)\) ciphertext, and dynamically. A secure outsourcing scheme is dynamic if it enables the user to add (or remove) new records to the database with no need for storing and re-sharing existing secrets by the dealer. The dynamic property is vital for a secure outsourcing scheme and may have significant benefits in many practical applications. Whenever one wishes to outsource the storage of a database to a set of semi-trusted servers, some pieces of data may not be known at the moment of construction of the database and are expected to be known in the future. A dynamic scheme resolves the need for storing a copy of the entire database on the user’s computer. In [8], we review existing communication-less schemes that enable similar homomorphic properties (e.g., Beaver’s multiplication technique [4], or other variants of Shamir’s scheme) and show that these schemes are either non-dynamic or less secure.

3 Optimal-Round P-MPC

The search for solutions for the secure delegation problem often gives rise to MPC protocols, as exemplified in [10]. MPC is an extensively studied field in cryptography rooted in Yao’s millionaire problem from the early 80’s [40]. In their seminal work from 1988, Ben-Or et al. [6] showed that, in the plain model, every function of N inputs can be efficiently computed with perfect passive security by N parties if and only if one assumes that the majority of the participant are honest. One may enable multiparty computation of functions in the presence of a dishonest majority by switching to the preprocessing model, first suggested in [5]. The preprocessing model enables achieving perfect passive security against dishonest majority by enabling the parties to engage in an offline preprocessing phase before the secret inputs are known. At the end of that offline phase, the parties obtain correlated randomness (CR) – random coins to be used in the online phase of the protocol. Given a preprocessing MPC protocol (hereafter P-MPC), the space complexity of the scheme indicates how the amount of CR required for the scheme grows with respect to other parameters.

An important measure of efficiency of MPC schemes is their round complexity. Two rounds of communication are now known to be optimal for MPC – in the plain or preprocessing model [15, 32]. Ishai et al. suggested in [30] two-round P-MPC protocols with perfect passive security against dishonest majority, followed by several improvements [14, 16]. There already exist MPC schemes with optimal round complexity and dishonest majority. Nevertheless, all these schemes require amounts of either time, memory or communication exponential in some of the parameters: depth or size of the circuit, size of the domain, or number of parties. The space complexity of known solutions is (believed to be inherently) exponential in the size of the input and N.

In [10], we construct efficient N-party P-MPC schemes for polynomials over non-zero inputs. There already exist schemes for efficient evaluation of polynomials over non-zero inputs [26]. However, our schemes are the first not to require an additional secret sharing round during the preprocessing stage. We also suggest several ways of handling possibly-zero inputs. Each of these ways best suits different families of functions. These schemes are based on the DRM secret sharing scheme, a novel homomorphic secret sharing scheme established in [10]. These results were established based on our work [9], where we constructed efficient schemes for secure outsourcing of stream computations.

The DRM secret sharing scheme, presented in [10], supports homomorphic multiplications of secrets and, after a single round of communication, supports homomorphic additions of secrets. We use the DRM secret sharing scheme to construct the one-time secrets (OTS) protocols. These protocols enable the evaluation of multivariate polynomials over shares of non-zero secrets with the following properties: communication and space complexities linear in the number of monomials, optimal round complexity, perfect security against dishonest majority. The main advantage of our scheme is that we achieve all these properties without requiring a secret sharing phase invoked in an offline preprocessing phase. In addition, our paper suggests new techniques for handling possibly-zero secrets in several ways.

The Algorithm in a Nutshell. We now review the main ideas behind our method. First, we construct the Distributed Random Matrix (DRM) secret-sharing scheme. In this scheme, a secret is randomly split to a sum of field elements, and each of the addends is randomly split to a product of field elements. The factors of these products are put in the rows of a matrix, and each column of that matrix is considered a share of the secret. Namely, given an element x of a finite field \(\mathbb {F}_p\), we split x to a sum of N random \(\mathbb {F}_p\) elements \(\gamma _i\), \(1 \le i \le N\). Then, each of the \(\gamma _i\)’s is split to a random product of \(\mathbb {F}_p\) elements \(m_{i,j}\), \(1\le j \le N\). Denote by C the square matrix of order N whose entries are the multiplicative shares \(m_{i,j}\) of the additive shares \(\gamma _i\). The \(m_{i,j}\) are randomly picked under the condition that C contains zeroes only on its main diagonal, if any. The N columns of C are N DRM-shares of x. The double splitting of each secret (additively splitting the secret and multiplicatively splitting each addend) enables supporting both homomorphic multiplications and additions. In [10] we prove that, the DRM secret sharing scheme supports homomorphic multiplications with multiplicatively secret-shared \(\mathbb {F}_p^\times \) elements. Furthermore, a single round of communication enables the parties to switch to additive shares of x.

Next, the DRM secret sharing scheme is used to construct a P-MPC scheme. The outline of the scheme is as follows. In the preprocessing phase, each party is supplied with a sufficient amount of CR in the form of DRM shares of \(1 \in \mathbb {F}_p\) – one share for each monomial in the target polynomial. Recall that these DRM shares support homomorphic multiplications. To evaluate the polynomial over the secret inputs, for each monomial, each party multiplies the corresponding DRM-share (a column vector) with a power of the secret as required by that monomial, and obtains a new column vector. In the first communication round, the entries of this column are split among the other servers. Next, each server computes the products of the values obtained in the previous round (one product for each monomial) and adds these products to obtain an additive share of the output. Lastly, the parties distribute the additive shares of the output to each other, and each party locally adds them to obtain the output. The main advantage of our scheme is that it requires no secret sharing round in the preprocessing phase.

Our results are also extended to the client-server model, providing an IT-secure solution to the secure delegation problem. The DRM single-round client-server scheme enables a set of users to securely outsource the storage of their private inputs to a set of servers and have the servers evaluate polynomials over the entire collection of users-inputs (non-zero). The users obtain the result after a single round of communication between the servers.

To securely delegate non-zero secrets to the servers, the user distributes multiplicative shares of each secret among the servers. Then, to enable homomorphic evaluation of polynomials of arbitrary degree over the secrets, the user sends a query to the server containing a description of the polynomial and DRM-shares of \(1 \in \mathbb {F}_p\), one for each monomial, to be used as CR. Next, the servers use the CR to evaluate the polynomial in a single round of communication and send the shares of the result to the user.

The DRM client-server scheme is perfectly secure against coalitions of up to \(N-1\) honest-but-curious servers. The users do not communicate with each other during the execution of the scheme. Each user distributes secret-shares of the inputs to the servers and receives the output from the servers.

The innovative approach of the scheme enables handling high degree polynomials without being concerned with the depth of the arithmetic circuit, which is one of the main complexity bottlenecks in MPC. The communication and space complexities of our schemes are independent of the degree of the polynomial, and the required CR is independent of the function.

To emphasize the importance of round-efficiency, we note that, while processing information becomes faster as technology improves, the time it takes to transmit information between two distant places is strictly limited by the speed of light. One may consider a future need to perform MPC over inputs held by parties residing in distant places, perhaps in different continents or even in space. Denote by T the time it takes to process the computations needed for the evaluation of some function f using our schemes. If sending a message between parties takes more than T, then optimal-round schemes outperform any scheme with non-optimal round complexity.

4 Quantum HE and Applications

Quantum computers may allow feasible solutions to problems that are currently considered impractical to solve [7, 18, 28, 36]. In view of this fact, it is natural to wonder if quantum computers can be used to achieve an IT-secure FHE scheme. In 2014, [41] showed that it is impossible to construct an efficient IT-secure quantum FHE (QFHE) scheme. Efficient IT-secure (quantum or classical) encryption schemes can support homomorphic evaluation of only a subset of all possible functions.

In a search for a quantum encryption scheme of classical data, [11] suggested the random basis encryption scheme – an efficient, IT-secure, perfectly correct, non-interactive, and fully compact encryption scheme that supports homomorphic evaluation of several quantum gates. The scheme presented in [11] shares some resemblance with the quantum one-time pad (QOTP) based encryption scheme. In QOTP based schemes, Pauli gates are randomly applied to plaintext qubits to obtain IT-secure encryption, while supporting homomorphic evaluation of Pauli gates. QOTP was suggested by Ambainis et al. in [3].

The main difference between the random basis encryption scheme and the QOTP-based schemes is that in [11], a plaintext bit is encrypted by a rotation of the corresponding qubit in an angle chosen from an immense number of possibilities, while in [3] there are only four possible different encodings for a plaintext qubit. The random basis encryption scheme essentially implements a continuous version of the (discrete) QOTP scheme. The difference between the continuous and discrete versions becomes significant in several scenarios when considering attacks based on weak measurements (WM).

Another advantage of our random basis encryption scheme over QOTP-based schemes is that in contrast to the legacy quantum one-time pad based HE scheme, that requires modifications of the keys by the user, our scheme is computation agnostic. Namely, when delegating computations, the user is not required to carry out such computations and key-adjustments and can remain utterly oblivious to the implementation method chosen by the server/cloud.

Weak measurements enable accumulating information regarding the state of a qubit while not collapsing the state, but only biasing it a little. In [11], it is shown how WM can be used to attack quantum key distribution (QKD) schemes that are based on QOTP. Namely, we demonstrate a WM attack on the [7] and [17] schemes that enables an adversary to obtain a non-negligible advantage at guessing a key-bit while reducing the risk of being caught.

Our WM attack works as follows. First, we weakly interact the subject qubit with an ancillary qubit. Then, we (strongly) measure the ancillary qubit. The outcome of the (strong) measurement of the ancillary qubit is the outcome of the weak measurement of the subject qubit. This process enables imprecisely measuring quantum states, outsmarting the uncertainty principle.

To this end, we construct a two-qubit quantum gate that is very close to the identity operator (not doing anything), but slightly tends towards the CNOT quantum gate. The CNOT quantum gate enables copying computational basis qubits () without disturbing them. If the qubits are not in the computational basis, the CNOT gate disturbs themFootnote 1. Our two-qubit quantum gate can be taken to be arbitrarily close to the identity operator, hence enabling a tradeoff between information gain and state disturbance.

Explicitly, given \(\varepsilon >0\), let \(W_\varepsilon =\sqrt{\varepsilon }\cdot i \cdot CNOT + \sqrt{1-\varepsilon } \cdot I\) a two-qubit gate (I is the identity operator and i is the square root of \(-1\)). In our WM attacks, \(W_\varepsilon \) is used to weakly interact a target qubit with an ancillary qubit. If the target qubit is in the computational basis, then measuring the ancillary qubit provides some information regarding the target qubit. If the target qubit is in the Hadamard basis, we obtain no information, but only slightly disturb the state.

In addition, [11] presents the random basis CNOT QKD scheme – an IT-secure QKD scheme that is resilient against weak measurement based attacks. Another advantage of our QKD scheme compared to other schemes is that only one side measures, and the other side can decide to blindly negate the state without knowing the chosen random base.

The random basis encryption scheme is shown to be useful in another setting – securing entanglement. Entanglement is an essential resource in many quantum settings – teleportation, private communication, and distinguishing quantum states [29]. The utilization of entanglement in communication, computation, and other scenarios is a very active area of research. In practice, entanglement is typically generated by direct interactions between subatomic particles. The generation of entangled systems requires efforts and expenditures. In [11] it is suggested that, once entanglement was generated, it should be secured in the sense that only its rightful owners will be able to use it. We demonstrate a process of securing entanglement using the random basis encryption scheme. Moreover, we show that our method of securing entanglement provides safer implications in the face of weak measurements compared to possible straightforward QOTP based methods for the same task.

5 Conclusions

We believe that distributed computing can benefit much from using the techniques reviewed above and in particular secure multiparty computation. The classical methods of secure multiparty computation imply high communication overhead. The reviewed works’ scope is to advance the research for reducing the communication overhead in the scope of dynamic database, streaming computation, and quantum computers.