1 Introduction

Quantum entanglement is an important physical resource in quantum information theory, which distinguishes between quantum and classical worlds [1]. The most significant property of the quantum entanglement is a monogamous behavior. This monogamy property shows the shareability of entanglement in multipartite systems. For example, it plays a significant role in the quantum cryptography which restricts the information gain by an eavesdropper [2], and in quantum channel discrimination [3].

The monogamy of quantum entanglement has a long history. Monogamy relations were first established by Coffman–Kundu–Wootters (CKW) in [4], where a three-qubit system consisted of the subsystems A, B, and C was considered. It was shown that the entanglement between the subsystems A and B and entanglement between the subsystems A and C cannot be greater than the entanglement between the subsystems A and BC. The concept of monogamy property has been extended to the general N-qubit system [5]. Monogamy inequalities for various entanglement measures such as concurrence [4], entanglement of formation [6], negativity [7, 8], Tsallis-q entanglement [9, 10], Rényi-\(\alpha \) entanglement [11], and unified-(q, s) entanglement [12] have been further studied.

As a dual to the monogamy property, the polygamy property in multipartite systems has been introduced using the concurrence of assistance to quantify the distributed bipartite entanglement in multi-qubit systems [13]. Polygamy relations are also established using various entanglement measures such as entanglement of formation [14], Tsallis-q entanglement [9], and convex-roof extended negativity [8].

In this paper, we study the monogamy relation based on the xth power of entanglement measures. Simultaneously, we also work on the polygamy relations.

  • We first find the generalized tighter monogamy relation related to the Tsallis-q entanglement, which gives us better bounds than the previous relations [10]. The polygamy relation related to the Tsallis-q entanglement for any tripartite mixed state is obtained, which is generalized to multi-qubit systems.

  • We propose the comparatively tighter monogamy relations for the class of multi-qubit generalized W-class states and the class of partially coherent superposition (PCS) of a generalized W-class state and the vacuum. We have investigated the monogamy relations of the concurrence of assistance and the negativity of assistance for these two classes. Previously, the monogamy of entanglement for these two classes has been investigated in [15,16,17]. They have proved the monogamy relations for the squared concurrence and the squared negativity. The general monogamy relation for the xth power of concurrence of assistance for generalized multi-qubit W-class states has been proved in [18], and this result is further explored for the negativity of assistance [19]. The bounds in our work are tighter than the previously proposed bounds [18, 19], which are proved only for W-class states.

  • Previously, polygamy relation was based on the bipartite Tsallis-q entanglement of assistance [9]. We present polygamy relation using the Tsallis-q entanglement, which are established for pure and mixed generalized W-class states. These relations are used to find entanglement \(|{\psi }\rangle _{AB|C_1 \ldots C_{N-2}}\) between AB and rest of the parties.

This paper is organized as follows: In Sect. 2, we define entanglement measures and their monogamy relations. In Sect. 3, we provide a tighter monogamy relation in terms of the Tsallis-q entanglement for multi-qubit systems. Dual monogamy relations for generalized W-class states are also provided. In Sects. 4 and 5, we establish the lower bound of the negativity of assistance and the concurrence of assistance, respectively. Numerical examples are provided in Sect. 6. In Sect. 7, we conclude our results.

2 Preliminaries

For any bipartite pure state \(|{\psi }\rangle _{AB}\) in a \(d \otimes d^{'} (d \le d^{'} )\) quantum system, the Schmidt decomposition is represented as

$$\begin{aligned} |{\psi }\rangle _{AB}= \sum _{i=0}^{d-1} \sqrt{\lambda _{i}}|{ii}\rangle , \quad \lambda _{i} \ge 0, \quad \sum _{i=0}^{d-1} \lambda _{i}=1. \end{aligned}$$
(1)

The concurrence \(\mathcal {C}(|{\psi }\rangle _{AB})\) for a bipartite pure state is defined by [20]

$$\begin{aligned} \mathcal {C}(|{\psi }\rangle _{AB}) =\sqrt{2\left( 1-\text {tr}\left( \rho ^{2}_{A}\right) \right) }, \end{aligned}$$
(2)

where \(\rho _{A} =\text {tr}_{B}(|{\psi }\rangle _{AB}\langle {\psi }|)\). For any bipartite mixed state \(\rho _{AB}\), the concurrence \(\mathcal {C}(\rho _{AB})\) and the concurrence of assistance (COA) \(\mathcal {C}_{\alpha }(\rho _{AB})\) are given by

$$\begin{aligned} \mathcal {C}(\rho _{AB})&= \min _{\{p_i, |{\psi _i}\rangle _{AB} \}} \sum _{i} p_i \mathcal {C}(|{\psi _i}\rangle _{AB}), \end{aligned}$$
(3)
$$\begin{aligned} \mathcal {C}_{\alpha }(\rho _{AB})&= \max _{\{p_i, |{\psi _i}\rangle _{AB} \}} \sum _{i} p_i \mathcal {C}(|{\psi _i}\rangle _{AB}), \end{aligned}$$
(4)

where the minimum and maximum are taken over all possible pure state decompositions \(\{p_i, |{\psi _i}\rangle _{AB} \}\) of \(\rho _{AB}\), respectively.

For N-qubit pure state \(|{\psi }\rangle _{AB_1, B_2, \ldots , B_{N-1}}\), the multipartite monogamy relation of the concurrence is given by [5]

$$\begin{aligned} \mathcal {C}^2 \left( |{\psi }\rangle _{A|B_1, \ldots , B_{N-1}} \right) \ge \sum _{i=1}^{N-1} \mathcal {C}^2 \left( \rho _{AB_i} \right) , \end{aligned}$$
(5)

where \(\mathcal {C}\left( |{\psi }\rangle _{A|B_{1},\ldots ,B_{N-1}}\right) \) of the state \(|{\psi }\rangle _{A|B_{1},\ldots ,B_{N-1}}\) is the bipartite concurrence under the partition A and \(B_{1}, B_{2},\ldots , B_{N-1}\), and \(\mathcal {C}\left( \rho _{AB_i} \right) \) denotes the entanglement between A and \(B_i\).

Dual to the monogamy inequality, the generalized polygamy relation based on the COA has been proved as [13]

$$\begin{aligned} \mathcal {C}^2 \left( |{\psi }\rangle _{A|B_1, \ldots , B_{N-1}} \right) \le \sum _{i=1}^{N-1} \mathcal {C}^2_{\alpha } \left( \rho _{AB_i} \right) . \end{aligned}$$
(6)

Another well-known technique used to quantify the bipartite entanglement is the negativity. For any bipartite pure state \(|{\psi }\rangle _{AB}\), the negativity \(\mathcal {N}(|{\psi }\rangle _{AB})\) is given by [21]

$$\begin{aligned} \mathcal {N}(|{\psi }\rangle _{AB}) = 2\sum _{i<j} \sqrt{\lambda _i \lambda _{j}} = \left( \text {tr}\sqrt{\rho _A}\right) ^2 -1. \end{aligned}$$
(7)

The convex-roof extended negativity (CREN) gives a perfect discrimination of the positive partial transposition bound between the entangled state and separable state in any bipartite quantum system [22, 23]. The CREN \(\mathcal {N}(\rho _{AB})\) and CREN of assistance (CRENOA) \(\mathcal {N}_{\alpha }(\rho _{AB})\) for any bipartite mixed state \(\rho _{AB}\) are defined as

$$\begin{aligned} \mathcal {N}(\rho _{AB})&= \min _{\{p_i, |{\psi _i}\rangle _{AB} \}} \sum _{i} p_i \mathcal {N}(|{\psi _i}\rangle _{AB}), \end{aligned}$$
(8)
$$\begin{aligned} \mathcal {N}_{\alpha }(\rho _{AB})&= \max _{\{p_i, |{\psi _i}\rangle _{AB} \}} \sum _{i} p_i \mathcal {N}(|{\psi _i}\rangle _{AB}). \end{aligned}$$
(9)

The monogamy inequality of the negativity for the N-qubit system is defined by [8]

$$\begin{aligned} \mathcal {N}^2\left( |{\psi }\rangle _{A|B_1 \ldots B_N-1}\right) \ge \sum _{i=1}^{N-1} \mathcal {N}^2\left( \rho _{AB_{i}}\right) . \end{aligned}$$
(10)

The Tsallis-q entanglement is a well-known entropic measure, and its analytical formula and the monogamy relation were first introduced in [9]. This relation has been further explored for the analytic formula with the arbitrary q such that [10]:

$$\begin{aligned} \mathcal {T}_q \left( |{\psi }\rangle _{AB} \right) = f_q \left( \mathcal {C}^2\left( |{\psi }\rangle _{AB} \right) \right) , \end{aligned}$$
(11)

where the function \(f_q \left( x \right) \) is defined as

$$\begin{aligned} f_q \left( x \right) = \dfrac{1}{q-1} \left[ 1 - \left( \dfrac{1 + \sqrt{1 -x}}{2} \right) ^q - \left( \dfrac{1 - \sqrt{1 - x}}{2} \right) ^q \right] . \end{aligned}$$
(12)

There exists a relationship between the Tsallis-q entanglement of assistance and COA which is given by [9]

$$\begin{aligned} \mathcal {T}_{\alpha (q)} \left( \rho _{AB} \right) \ge f_q \left( \mathcal {C}^2_{\alpha }\left( \rho _{AB} \right) \right) . \end{aligned}$$
(13)

Monogamy inequality of the squared Tsallis-q entanglement for the N-qubit system is defined by [10]

$$\begin{aligned} \mathcal {T}_{q}^2 \left( \rho _{A|B_1 \ldots B_{N-1}} \right) \ge \sum _{i=1}^{N-1} \mathcal {T}_{ q}^2 \left( \rho _{AB_i } \right) , \end{aligned}$$
(14)

where \(\dfrac{5 - \sqrt{13 }}{2} \le q \le \dfrac{5 + \sqrt{13 }}{2}\).

3 Distribution of entanglement with Tsallis-q entanglement

In this section, we establish the monogamy and polygamy inequalities of the Tsallis-q entanglement to characterize the distribution of entanglement in multi-qubit systems. A numerical evidence of these relations is investigated in Sect. 6.

3.1 Monogamy relation of the Tsallis-q entanglement

The lower bounds are established using the xth power of the Tsallis-q entanglement. The following bounds are proved for the arbitrary N-qubit mixed states.

Theorem 1

For the N-qubit mixed state \(\rho _{A|B_1 \ldots B_{N-1}}\), if \(\mathcal {T}_{q}(\rho _{AB_i}) \ge \mathcal {T}_{q}(\rho _{AB_{i+1} \ldots B_{N-1}}) \) for \(i=1,2, \ldots ,m,\) and \(\mathcal {T}_{q}(\rho _{AB_j}) \le \mathcal {T}_{q}(\rho _{AB_{j+1} \ldots B_{N-1}}) \) for \(j=m+1, \ldots ,N-2\), \(\forall \) \(1 \le m \le N-3\), \(N \ge 4\), we have

$$\begin{aligned} \mathcal {T}_{q}^x (\rho _{A|B_1 \ldots B_{N-1}})&\ge \mathcal {T}_{q}^x(\rho _{AB_1}) + \sum _{i=2}^{m} \mathcal {K}^{i-1} \mathcal {T}_{q}^x(\rho _{AB_i}) + \mathcal {K}^{m+1} \left( \sum _{i=m+1}^{N-2} \mathcal {T}_{q}^x(\rho _{AB_i}) \right) \nonumber \\&\quad + \mathcal {K}^m \mathcal {T}_{q}^x(\rho _{AB_{N-1}}), \end{aligned}$$
(15)

where \(\dfrac{5 - \sqrt{13 }}{2} \le q \le \dfrac{5 + \sqrt{13 }}{2}\) , \(\mathcal {K}= 2^{x/2} - 1\) and \(x \ge 2\).

Proof

From (14), we get

$$\begin{aligned} \mathcal {T}_q^2(\rho _{A|B_1B_{2}}) \ge \mathcal {T}_q^2(\rho _{A|B_1}) + \mathcal {T}_q^2(\rho _{A|B_{2}}). \end{aligned}$$

Without loss of generality, we assume that \(\mathcal {T}_q(\rho _{A|B_1}) \ge \mathcal {T}_q(\rho _{A|B_{2}})\). Then, we have

$$\begin{aligned} \mathcal {T}_q^x(\rho _{A|B_1B_{2}})&\ge \left( \mathcal {T}_q^2(\rho _{A|B_1}) + \mathcal {T}_q^2(\rho _{A|B_{2}}) \right) ^{x/2} \nonumber \\&= \mathcal {T}_q^x(\rho _{A|B_1}) \left( 1 + \dfrac{\mathcal {T}_q^2(\rho _{A|B_{2}})}{\mathcal {T}_q^2(\rho _{A|B_1})} \right) ^{x/2} \nonumber \\&\mathop \ge \limits ^{\mathrm {(a)}} \mathcal {T}_q^x(\rho _{A|B_1}) \left[ 1 + \mathcal {K}\left( \dfrac{\mathcal {T}_q(\rho _{A|B_{2}})}{\mathcal {T}_q(\rho _{A|B_1})} \right) ^x \right] \nonumber \\&= \mathcal {T}_q^x(\rho _{A|B_1}) + \mathcal {K}\mathcal {T}_q^x(\rho _{A|B_{2}}), \end{aligned}$$
(16)

where (a) is due to the inequality \( (1 + t)^x \ge 1 + \left( 2^{x}-1\right) t^x\), for \(x \ge 1\), \(0 \le t \le 1\), and \(\mathcal {K}= 2^{x /2} -1\). Assuming that \(\mathcal {T}_{q}(\rho _{AB_i}) \ge \mathcal {T}_{q}(\rho _{AB_{i+1}\ldots B_{N-1}}) \) for \(i=1,2,\ldots ,m\), for the N-qubit state. Then, by using (16), we get

$$\begin{aligned} \mathcal {T}_q^x(\rho _{A|B_1 \ldots B_{N-1}})&\ge \mathcal {T}_q^x(\rho _{A|B_1}) + \mathcal {K}\mathcal {T}_q^x(\rho _{A|B_2 \ldots B_{N-1}}) \nonumber \\&\ge \mathcal {T}_q^x(\rho _{A|B_1}) + \mathcal {K}\mathcal {T}_q^x(\rho _{A|B_2}) + \mathcal {K}^2 \mathcal {T}_q^x(\rho _{A|B_3\ldots B_{N-1}}) \nonumber \\&\ge \cdots \ge \mathcal {T}_q^x(\rho _{A|B_1}) + \mathcal {K}\mathcal {T}_q^x(\rho _{A|B_2}) + \cdots \nonumber \\&\quad + \mathcal {K}^{m-1} \mathcal {T}_q^x(\rho _{A|B_m}) + \mathcal {K}^m \mathcal {T}_q^x(\rho _{A|B_{m+1} \ldots B_{N-1}}) . \end{aligned}$$
(17)

As \(\mathcal {T}_q(\rho _{AB_j}) \le \mathcal {T}_q(\rho _{AB_{j+1} \ldots B_{N-1}}) \) for \(j = m+1,\ldots ,N-2\), we get

$$\begin{aligned} \mathcal {T}_q^x(\rho _{AB_{m+1} \ldots B_{N-1}})&\ge \mathcal {K}\mathcal {T}_q^x(\rho _{AB_{m+1}}) + \mathcal {T}_q^x(\rho _{AB_{m+2} \ldots B_{N-1}}) \nonumber \\&\ge \mathcal {K}\left( \sum _{k=m+1}^{N-2} \mathcal {T}_q^x(\rho _{AB_{k}}) \right) + \mathcal {T}_q^x(\rho _{AB_{N-1}}). \end{aligned}$$
(18)

Combining (17) and (18), we complete the proof. \(\square \)

Remark 1

Theorem 1 gives us the tighter monogamy relation of any N-qubit mixed state for the Tsallis-q entanglement with an arbitrary range. If \(\mathcal {T}_{q}(\rho _{AB_i}) \ge \mathcal {T}_{q}(\rho _{AB_{i+1} \ldots B_{N-1}}) \) for all \(i=1,2, \ldots ,N-2\), then we have

$$\begin{aligned} {\mathcal {T}}_{q}^x(\rho _{A|B_1B_2 \ldots B_{N-1}})&\ge {\mathcal {T}}_{q}^x(\rho _{AB_1}) + \mathcal {K}{\mathcal {T}}_{q}^x(\rho _{AB_2}) + \cdots \nonumber \\&\quad + \mathcal {K}^{N-3} {\mathcal {T}}_{q}^x(\rho _{AB_{N-2}}) + \mathcal {K}^{N-2} {\mathcal {T}}_{q}^x(\rho _{AB_{N-1}}), \end{aligned}$$
(19)

where \(\mathcal {K}= 2^{x/2} - 1\) and \(x \ge 2\).

3.2 Polygamy relation of the Tsallis-q entanglement

This subsection explains the polygamy property of the Tsallis-q entanglement. The following theorem shows the polygamy property of the Tsallis-q entanglement for tripartite mixed states.

Theorem 2

For any tripartite quantum state \(\rho _{ABC}\) with \(q \in \left[ 1,2 \right] \bigcup \left[ 3, \dfrac{5 + \sqrt{13}}{2} \right] \), we have

$$\begin{aligned} \mathcal {T}_{q} \left( \rho _{A|BC} \right) \le \mathcal {T}_{q}\left( \rho _{B|AC} \right) + \mathcal {T}_q\left( \rho _{C|AB} \right) . \end{aligned}$$
(20)

Proof

For any bipartite quantum state \(\rho _{AB}\) with \(\rho _{A} = \text {tr}_B \left( \rho _{AB} \right) \), \(\rho _{B} = \text {tr}_A \left( \rho _{AB}\right) \), and \(q \ge 1\), we have

$$\begin{aligned} S_{q}\left( \rho _{AB} \right) \le S_{q}\left( \rho _{A} \right) + S_{q}\left( \rho _{B} \right) , \end{aligned}$$
(21)

by using the subadditivity of the Tsallis-q entropy [24]. Let

$$\begin{aligned} \rho _{A|BC} = \sum _{i} p_i |{\psi _{i}}\rangle _{ABC}\langle {\psi _{i}}|, \end{aligned}$$

be the optimal decomposition of \(\mathcal {T}_q \left( \rho _{A|BC} \right) \), i.e.,

$$\begin{aligned} \mathcal {T}_q \left( \rho _{A|BC} \right) = \sum _{i} p_{i} \mathcal {T}_q \left( |{\psi _i}\rangle _{A|BC} \right) . \end{aligned}$$
(22)

For each pure state \(|{\psi _{i}}\rangle _{ABC}\) decomposition with its reduced density matrices \(\rho _{BC}^i = \text{ tr }_A |{\psi _i}\rangle _{ABC} \langle {\psi _i }|, \rho _{B}^i = \text{ tr }_{AC}|{\psi _i}\rangle _{ABC} \langle {\psi _i}|\) and \(\rho _{C}^i = \text{ tr }_{AB}|{\psi _i}\rangle _{ABC} \langle {\psi _i}|\), we have

$$\begin{aligned} \mathcal {T}_{q} \left( |{\psi _i}\rangle _{A|BC} \right)&= S_{q}\left( \rho _{BC}^i \right) \nonumber \\&\mathop \le \limits ^{\mathrm {(a)}} S_{q}\left( \rho _{B}^i \right) + S_{q}\left( \rho _{C}^i \right) \nonumber \\&= \mathcal {T}_{q} \left( |{\psi _i}\rangle _{B|AC} \right) + \mathcal {T}_{q} \left( |{\psi _i}\rangle _{C|AB} \right) , \end{aligned}$$
(23)

where (a) is due to the subadditivity of the Tsallis-q entropy. Using (22), we have

$$\begin{aligned} \mathcal {T}_q \left( \rho _{A|BC} \right)&= \sum _{i} p_{i} \mathcal {T}_q \left( |{\psi _i}\rangle _{A|BC} \right) \nonumber \\&\mathop \le \limits ^{\mathrm {(a)}}\sum _{i} p_{i}\mathcal {T}_q \left( |{\psi _i}\rangle _{B|AC} \right) + \sum _{i} p_{i}\mathcal {T}_q \left( |{\psi _i}\rangle _{C|AB} \right) \nonumber \\&\mathop \le \limits ^{\mathrm {(b)}} \mathcal {T}_{q}\left( \rho _{B|AC} \right) + \mathcal {T}_{q}\left( \rho _{C|AB} \right) , \end{aligned}$$
(24)

where (a) comes from (23); and (b) is due to the definition of the Tsallis-q entanglement. \(\square \)

Corollary 1

(Multi-Party System) For any multi-party quantum state \(\rho _{AB_1 \ldots B_{N-1}}\) with \(q \in \left[ 1,2 \right] \bigcup \left[ 3, \dfrac{5 + \sqrt{13}}{2} \right] \), we have

$$\begin{aligned} \mathcal {T}_{q} \left( \rho _{A|B_1 \ldots B_{N-1}} \right) \le \sum _{i=1}^{N-1} \mathcal {T}_{q} \left( \rho _{B_i|A \ldots \hat{B_{i}} \ldots B_{N-1}} \right) , \end{aligned}$$
(25)

where \(\mathcal {T}_{q} \left( \rho _{B_i|A \ldots \hat{B_{i}} \ldots B_{N-1}} \right) = \mathcal {T}_{q} \left( \rho _{B_i|A \ldots B_{i-1} B_{i+1} \ldots B_{N-1}} \right) \).

Remark 2

Theorem 2 gives the upper bound of the Tsallis-q entanglement for the tripartite mixed state \(\rho _{ABC}\). The iterative use of Theorem 2 leads us to the generalization of the multipartite quantum system which is presented in Corollary 1.

W-class states are used in quantum information processing task such as quantum channel discrimination, quantum teleportation and quantum superdense coding [3, 25]. The knowledge regarding the distribution of entanglement in multi-qubit W-class states is extremely important. In order to understand its behavior in multipartite systems, we analyze its polygamy properties.

Generalized W-class states for N-qubit systems are defined as

$$\begin{aligned} |{W}\rangle = a|{00 \ldots }\rangle +b_1 |{1 0\ldots 0}\rangle + \cdots + b_n |{0 \ldots 01}\rangle , \end{aligned}$$
(26)

where \(|a|^2 + \sum _{i=1}^N |b_i|^2 = 1\). For these states, it has been proved that [18]:

$$\begin{aligned} \mathcal {C}(\rho _{AB_i})&= \mathcal {C}_{\alpha }(\rho _{AB_i}) , \end{aligned}$$
(27)

where \(\rho _{AB_i} = \text {Tr}_{B_1 \ldots B_{i-1}B_{i+1} \ldots B_{N-1}}\) and \(i= 1,2, \ldots ,N-1\).

The following theorems explain the polygamous behavior of the Tsallis-q entanglement for the generalized W-class states. Previously, the Tsallis-q entanglement polygamy relations were based on the bipartite Tsallis-q entanglement of assistance [9]. Now, we prove that these polygamy relations are based on the Tsallis-q entanglement for W-class states.

Theorem 3

For the N-qubit pure W-class states \(|{\psi }\rangle _{A|B_1 \ldots B_{N-1}}\), the Tsallis-q entanglement satisfies

$$\begin{aligned} \mathcal {T}_{q} \left( |{\psi }\rangle _{A|BC_1 \ldots C_{N-2}} \right) \le \mathcal {T}_{\alpha (q)} \left( \rho _{AB} \right) + \sum _{i=1}^{N-2} \mathcal {T}_{q} \left( \rho _{AC_i} \right) , \end{aligned}$$
(28)

where \(q \in \left[ \dfrac{5 - \sqrt{13}}{2},2 \right] \bigcup \left[ 3, \dfrac{5 + \sqrt{13}}{2} \right] \).

Proof

We have

$$\begin{aligned} \mathcal {T}_q \left( |{\psi }\rangle _{A|BC_1 \ldots C_{N-2}} \right)&\mathop =\limits ^{\mathrm {(a)}} f_{q} \left[ \mathcal {C}^2 \left( |{\psi }\rangle _{A|BC_1 \ldots C_{N-2}} \right) \right] \\&\mathop = \limits ^{\mathrm {(b)}} f_{q} \left( \mathcal {C}^2_{\alpha } \left( \rho _{AB} \right) + \mathcal {C}^2 \left( \rho _{AC_1 \ldots C_{N-2}} \right) \right) \\&\mathop \le \limits ^{\mathrm {(c)}} f_{q} \left( \mathcal {C}^2_{\alpha } \left( \rho _{AB} \right) \right) + f_{q} \left( \mathcal {C}^2 \left( \rho _{AC_1 \ldots C_{N-2}} \right) \right) \\&\mathop \le \limits ^{\mathrm {(d)}}\mathcal {T}_{\alpha (q)} \left( \rho _{AB} \right) + f_{q} \left( \mathcal {C}^2 \left( \rho _{AC_1 \ldots C_{N-2}} \right) \right) \\&\mathop =\limits ^{\mathrm {(e)}} \mathcal {T}_{\alpha (q)} \left( \rho _{AB} \right) + f_{q} \left( \mathcal {C}^2 \left( \rho _{AC_1} \right) + \cdots + \mathcal {C}^2 \left( \rho _{AC_{N-2}} \right) \right) \\&\mathop \le \limits ^{\mathrm {(f)}} \mathcal {T}_{\alpha (q)} \left( \rho _{AB} \right) + f_{q} \left( \mathcal {C}^2 \left( \rho _{AC_1} \right) \right) + \cdots +f_{q} \left( \mathcal {C}^2 \left( \rho _{AC_{N-2}} \right) \right) \\&\mathop = \limits ^{\mathrm {(g)}} \mathcal {T}_{\alpha (q)} \left( \rho _{AB} \right) + \mathcal {T}_{q} \left( \rho _{AC_1} \right) + \cdots + \mathcal {T}_{q} \left( \rho _{AC_{N-2}} \right) . \end{aligned}$$

where (a) follows from the definition of the analytic relationship between the Tsallis-q entanglement and the concurrence; (b) is due to the fact that \(\mathcal {C}^2(|{\psi }\rangle _{A|BC}) = \mathcal {C}^2_{\alpha } (\rho _{AB}) + \mathcal {C}^2(\rho _{AC})\) [26]; (c) is due to the concavity property of the Tsallis-q entanglement; (d) is due to the definition of the Tsallis-q entanglement of assistance; (e) is due to the fact that \(\mathcal {C}^2(\rho _{AC_1 \ldots C_{N-2}}) = \sum _{i=1}^{N-2} \mathcal {C}^2(\rho _{AC_i})\), which is equal only for W-class states [15]; (f) is due to the concavity property; and (g) comes from [10, Theorem 1]. \(\square \)

Theorem 4

For the N-qubit W-class states \(\rho _{AB_1 \ldots B_{N-1}}\), the Tsallis-q entanglement satisfies

$$\begin{aligned} \mathcal {T}_q \left( \rho _{A|B_{1}B_2 \ldots B_{N-1}} \right) \le \sum _{i=1}^{N-1} \mathcal {T}_{q} \left( \rho _{AB_i} \right) , \end{aligned}$$
(29)

where \(q \in \left[ \dfrac{5 - \sqrt{13}}{2},2 \right] \bigcup \left[ 3, \dfrac{5 + \sqrt{13}}{2} \right] \).

Proof

The Tsallis-q entanglement as a function of the concurrence is

$$\begin{aligned} \mathcal {T}_q \left( \rho _{A|B_{1}B_2 \ldots B_{N-1}} \right)&= f_{q} \left[ \mathcal {C}^2 \left( \rho _{A|B_{1}B_2 \ldots B_{N-1}} \right) \right] \\&\mathop \le \limits ^{\mathrm {(a)}} f_{q} \left( \sum _{i=1}^{N-1} \mathcal {C}_{\alpha }^2 \left( \rho _{AB_{N-1}} \right) \right) \mathop \le \limits ^{\mathrm {(b)}} \sum _{i=1}^{N-1}f_{q} \left( \mathcal {C}_{\alpha }^2 \left( \rho _{AB_i} \right) \right) \\&\mathop = \limits ^{\mathrm {(c)}} \sum _{i=1}^{N-1}f_{q} \left( \mathcal {C}^2 \left( \rho _{AB_i} \right) \right) \mathop = \limits ^{\mathrm {(d)}} \sum _{i=1}^{N-1} \mathcal {T}_{q} \left( \rho _{AB_i} \right) , \end{aligned}$$

where (a) and (b) are due to the monotonicity and concavity properties given in [10]; (c) follows from the generalized W-class states, in which \(\mathcal {C}_{\alpha } \left( \rho _{AB} \right) = \mathcal {C}\left( \rho _{AB} \right) \); and (d) comes from [10, Theorem 1]. \(\square \)

Remark 3

Theorems 3 and  4 give the upper bound of the Tsallis-q entanglement for pure and mixed generalized W-class states, respectively. Moreover, these bounds are analytically obtainable due to the relationship between the concurrence and the Tsallis-q entanglement.

According to the result in [9, 10], the Tsallis-q entanglement of N-qubit mixed state satisfies a monogamy inequality of entanglement. This paper provides a polygamy relation with respect to the Tsallis-q entanglement for the generalized W-class states. The following corollaries can be used to calculate the upper bound on \(\rho _{AB|C_1 \ldots C_{N-2}}\).

Corollary 2

(Pure State) For the N-qubit W-class states, the Tsallis-q entanglement satisfies

$$\begin{aligned} \mathcal {T}_{q} \left( |{\psi }\rangle _{AB|C_1 \ldots C_{N-2}} \right) \le 2 \mathcal {T}_{\alpha (q)} \left( \rho _{AB} \right) + \sum _{i=1}^{N-2} \left[ \mathcal {T}_q \left( \rho _{AC_{i}} \right) + \mathcal {T}_q \left( \rho _{BC_{i}} \right) \right] , \end{aligned}$$
(30)

where \(q \in \left[ 1,2 \right] \bigcup \left[ 3, \dfrac{5 + \sqrt{13}}{2} \right] .\)

Proof

By considering \(|{\psi }\rangle _{ABC_1 \ldots C_{N-2}}\) as the tripartite quantum state \(|{\psi }\rangle _{A|B\mathbf C }\) with \(\mathbf C = C_1C_2 \ldots C_{N-2}\), (23) can be rewritten as

$$\begin{aligned} \mathcal {T}_{q} \left( |{\psi }\rangle _{AB|\mathbf C } \right) \le \mathcal {T}_{q} \left( |{\psi }\rangle _{A|B\mathbf C } \right) + \mathcal {T}_{q} \left( |{\psi }\rangle _{B|A\mathbf C } \right) . \end{aligned}$$
(31)

From the multi-qubit Tsallis-q entanglement polygamy inequality in (28), we have

$$\begin{aligned}&\mathcal {T}_{q} \left( |{\psi }\rangle _{A|BC_1 \ldots C_{N-2}} \right) \le \mathcal {T}_{\alpha (q)} \left( \rho _{AB} \right) + \sum _{i=1}^{N-2} \mathcal {T}_{q} \left( \rho _{AC_i} \right) , \nonumber \\&\mathcal {T}_{q} \left( |{\psi }\rangle _{B|AC_1 \ldots C_{N-2}} \right) \le \mathcal {T}_{\alpha (q)} \left( \rho _{BA} \right) + \sum _{i=1}^{N-2} \mathcal {T}_{q} \left( \rho _{BC_i} \right) . \end{aligned}$$
(32)

Combining (31) and (32), we arrive at the desired result. \(\square \)

Corollary 3

(Mixed State) For the N-qubit W-class states, the Tsallis-q entanglement satisfies

$$\begin{aligned} \mathcal {T}_{q} \left( \rho _{AB|C_1 \ldots C_{N-2}} \right) \le 2 \mathcal {T}_{q} \left( \rho _{AB} \right) + \sum _{i=1}^{N-2} \left[ \mathcal {T}_q \left( \rho _{AC_{i}} \right) + \mathcal {T}_q \left( \rho _{BC_{i}} \right) \right] , \end{aligned}$$
(33)

where \(q \in \left[ 1,2 \right] \bigcup \left[ 3, \dfrac{5 + \sqrt{13}}{2} \right] \).

Corollaries 2 and 3 are used to calculate entanglement between AB and rest of the parties. Corollary 2 is used for pure multi-qubit generalized W-class states, while Corollary 3 is used for the mixed states.

4 Monogamy relation of negativity of assistance

In the following, we study the monogamy property of the CRENOA for the class of partially coherent superposition (PCS) of multi-qudit generalized W-class states and the vacuum [8]. The multi-qudit generalized W-class state \(W_{N}^{d}\) is defined as

$$\begin{aligned} |{W_{N}^{d}}\rangle _{A_{1}A_{2} \ldots A_{N}} = \sum _{i=1}^{d-1} \left( a_{1i}|{i0 \ldots 0}\rangle + a_{2i}|{0i \ldots 0}\rangle + \cdots + a_{Ni}|{00 \ldots 0i}\rangle \right) , \end{aligned}$$
(34)

where \(\sum _{j}^{N} \sum _{i}^{d-1} |a_{ji}|^2 =1\). A partially coherent superposition of a generalized W-class state and the vacuum \(|{0^{\otimes N}}\rangle \) is given as

$$\begin{aligned} \rho _{A_{1}A_{2} \ldots A_{N}}&= p |{W_{N}^{d}}\rangle \langle {W_{N}^{d}}| + \left( 1 - p \right) |{0^{\otimes N}}\rangle \langle {0^{\otimes N}}| \nonumber \\&\quad + \lambda \sqrt{p \left( 1 - p \right) } \left( |{W_{N}^{d}}\rangle \langle {0^{\otimes N}}| + |{0^{\otimes N}}\rangle \langle {W_{N}^{d}}| \right) , \end{aligned}$$
(35)

where \(\lambda \) is the degree of coherence with \(0 \le \lambda \le 1 \). For \(\lambda = 1\), (35) becomes the coherent superposition of a generalized W-class state and \(|{0^{\otimes N}}\rangle \), while it is an incoherent or mixture when \(\lambda = 0\). For the PCS state, CREN and CRENOA saturate to the bipartite entanglement between A and \(B_{i}\), i.e.,

$$\begin{aligned} \mathcal {N}\left( \rho _{AB_i} \right) = \mathcal {N}_{\alpha } \left( \rho _{AB_i} \right) , \end{aligned}$$
(36)

where \(i= 1 \ldots N-1\) [8].

The following theorem is established to give a tighter lower bound on CRENOA.

Theorem 5

For the N-qudit PCS state, if \(\mathcal {N}(\rho _{AB_i}) \ge \mathcal {N}\left( \rho _{A|B_{i+1} \ldots B_{N-1}}\right) \) for \(i=1,2, \ldots ,m\), and \(\mathcal {N}(\rho _{AB_j}) \le \mathcal {N}\left( \rho _{A|B_{j+1} \ldots B_{N-1}}\right) \) for \(j=m+1,\ldots ,N-2\), \(\forall 1 \le m \le N-3,\) \(N \ge 4\), then we have

$$\begin{aligned} \mathcal {N}^x_{\alpha }(\rho _{A|B_1B_2 \ldots B_{N-1}})&\ge \mathcal {N}^x_{\alpha }(\rho _{AB_1}) + \mathcal {K}\mathcal {N}^x_{\alpha }(\rho _{AB_2}) + \cdots + \mathcal {K}^{m-1} \mathcal {N}^x_{\alpha }(\rho _{AB_m}) \nonumber \\&\quad + \mathcal {K}^{m+1} \left( \sum ^{N-2}_{l=m+1} \mathcal {N}^x_{\alpha }(\rho _{AB_l}) \right) + \mathcal {K}^m \mathcal {N}^x_{\alpha }(\rho _{AB_{N-1}}), \end{aligned}$$
(37)

where \(\mathcal {K}= 2^{x/2} -1 \) and \(x \ge 2 \).

Proof

For the N-qudit PCS state, according to the definition \(\mathcal {N}(\rho )\) and \(\mathcal {N}_{\alpha }(\rho )\), we have \(\mathcal {N}_{\alpha }(\rho _{A|B_1 \ldots B_{N-1}}) \ge \mathcal {N}(\rho _{A|B_1 \ldots B_{N-1}})\) when \(x \ge 2\), we have

$$\begin{aligned} \mathcal {N}^x_{\alpha }(\rho _{A|B_1 \ldots B_{N-1}})&\mathop \ge \limits ^{\mathrm {(a)}} \mathcal {N}^x(\rho _{A|B_1 \ldots B_{N-1}}) \\&\mathop \ge \limits ^{\mathrm {(b)}} \mathcal {N}^x(\rho _{AB_1}) + \mathcal {K}\mathcal {N}^x(\rho _{AB_2}) + \cdots + \mathcal {K}^{m-1} \mathcal {N}^x(\rho _{AB_m}) \\&\quad + \mathcal {K}^{m+1} \left( \sum ^{N-2}_{l=m+1} \mathcal {N}^x(\rho _{AB_l}) \right) + \mathcal {K}^m \mathcal {N}^x(\rho _{AB_{N-1}}) \\&\mathop = \limits ^{\mathrm {(c)}} \mathcal {N}^x_{\alpha }(\rho _{AB_1}) + \mathcal {K}\mathcal {N}^x_{\alpha }(\rho _{AB_2}) + \cdots + \mathcal {K}^{m-1} \mathcal {N}^x_{\alpha }(\rho _{AB_m}) \\&\quad + \mathcal {K}^{m+1} \left( \sum ^{N-2}_{l=m+1} \mathcal {N}^x_{\alpha }(\rho _{AB_l}) \right) + \mathcal {K}^m \mathcal {N}^x_{\alpha }(\rho _{AB_{N-1}}), \end{aligned}$$

\(\square \)

where (a) is due to the relation \(a^x \ge b^x\) for \(a \ge b \ge 0\), \(x \ge 2\); (b) is due to Eq. (20) from [27]; and (c) follows from (36).

Remark 4

: Theorem 5 gives the tighter lower bound of CRENOA. This theorem gives the distribution of entanglement for the PCS states. The following relation is a special case of Theorem 5, when \(\mathcal {N}(\rho _{AB_i}) \ge \mathcal {N}(\rho _{AB_{i+1} \ldots B_{N-1}}) \) for all \(i=1,2, \ldots ,N-2\):

$$\begin{aligned} \mathcal {N}^x_{\alpha }(\rho _{A|B_1B_2 \ldots B_{N-1}})&\ge \mathcal {N}^x_{\alpha }(\rho _{AB_1}) + \mathcal {K}\mathcal {N}^x_{\alpha }(\rho _{AB_2}) + \cdots \nonumber \\&\quad + \mathcal {K}^{N-3} \mathcal {N}^x_{\alpha }(\rho _{AB_{N-2}}) + \mathcal {K}^{N-2} \mathcal {N}^x_{\alpha }(\rho _{AB_{N-1}}), \end{aligned}$$
(38)

where \(\mathcal {K}= 2^{x /2} -1\) and \(x \ge 2\).

5 Monogamy relation of concurrence of assistance

In the following, we examine the monogamy relation of COA for the PCS state when \(d = 2\). Let us consider relations between the concurrence and the negativity. For any bipartite pure state \(|{\psi }\rangle _{AB} = \sqrt{\lambda _1 } |{00}\rangle + \sqrt{\lambda _2 } |{11}\rangle \) in a \(d \otimes d\) quantum system with the Schmidt rank two, we have

$$\begin{aligned} \mathcal {N}(\rho _{AB}) = ||{\psi }\rangle \langle {\psi }|^{T_B} || - 1 = 2\sqrt{\lambda _1 \lambda _2} = \sqrt{2 \left( 1 - \text {tr} \rho ^2_A \right) }. \end{aligned}$$

In other words, the negativity and the concurrence are equal for any pure state with the Schmidt rank two. It follows from the fact that for any two-qubit mixed state \(\rho _{AB} = \sum _{i} p_i |{\psi _i}\rangle _{AB} \langle {\psi _i}|\):

$$\begin{aligned} \mathcal {N}\left( \rho _{AB} \right)&= \min _{\{p_i, |{\psi _i}\rangle _{AB} \}} \sum _i p_i \mathcal {N}\left( |{\psi _{i}}\rangle _{AB} \right) \nonumber \\&= \min _{\{p_i, |{\psi _i}\rangle _{AB} \}} \sum _i p_i \mathcal {C}\left( |{\psi _{i}}\rangle _{AB} \right) \nonumber \\&= \mathcal {C}\left( \rho _{AB} \right) , \end{aligned}$$
(39)

and the relation between COA and CRENOA is

$$\begin{aligned} \mathcal {N}_{\alpha } \left( \rho _{AB} \right)&= \max _{\{p_i, |{\psi _i}\rangle _{AB} \}} \sum _i p_i \mathcal {N}\left( |{\psi _i }\rangle _{AB} \right) \nonumber \\ {}&= \max _{\{p_i, |{\psi _i}\rangle _{AB} \}} \sum _i p_i \mathcal {C}\left( |{\psi _i }\rangle _{AB} \right) \nonumber \\ {}&= \mathcal {C}_{\alpha } \left( \rho _{AB} \right) , \end{aligned}$$
(40)

Lemma 1

For the N-qubit PCS state, we have

$$\begin{aligned} \mathcal {C}\left( \rho _{AB} \right) = \mathcal {C}_{\alpha } \left( \rho _{AB} \right) , \end{aligned}$$
(41)

by combining (36), (39) and (40).

The following theorem gives the finer characterization of entanglement distribution for multi-qubit PCS states.

Theorem 6

If \(\mathcal {C}\left( \rho _{AB_i}\right) \ge \mathcal {C}\left( \rho _{A|B_{i+1} \ldots B_{N-1}}\right) \), \(i=1,2, \ldots ,m\) and \(\mathcal {C}\left( \rho _{AB_j}\right) \le \mathcal {C}\left( \rho _{A|B_{j+1} \ldots B_{N-1}}\right) \), \(j=m+1, \ldots ,N-2\), \(\forall 1 \le m \le N-3,\) \(N \ge 4\) for any N-qubit PCS states, we have

$$\begin{aligned} \mathcal {C}^x_{\alpha }(\rho _{A|B_1B_2 \ldots B_{N-1}})&\ge \mathcal {C}^x_{\alpha }(\rho _{AB_1}) + \mathcal {K}\mathcal {C}^x_{\alpha }(\rho _{AB_2}) + \cdots + \mathcal {K}^{m-1} \mathcal {C}^x_{\alpha }(\rho _{AB_m}) \nonumber \\&\quad +\mathcal {K}^{m+1} \left( \sum ^{N-2}_{l=m+1} \mathcal {C}^x_{\alpha }(\rho _{AB_l}) \right) + \mathcal {K}^m \mathcal {C}^x_{\alpha }(\rho _{AB_{N-1}}), \end{aligned}$$
(42)

where \(\mathcal {K}= 2^{x/2} -1 \) and \(x \ge 2 \).

Proof

For the N-qubit PCS state, according to the definitions \(\mathcal {C}(\rho )\) and \(\mathcal {C}_{\alpha }(\rho )\), we have \(\mathcal {C}_{\alpha }(\rho _{A|B_1 \ldots B_{N-1}}) \ge \mathcal {C}(\rho _{A|B_1 \ldots B_{N-1}})\) and for \(x \ge 2\),

$$\begin{aligned} C^x_{\alpha }(\rho _{A|B_1 \ldots B_{N-1}})&\mathop \ge \limits ^{\mathrm {(a)}} C^x(\rho _{A|B_1 \ldots B_{N-1}}) \\&\mathop \ge \limits ^{\mathrm {(b)}} \mathcal {C}^x(\rho _{AB_1}) + \mathcal {K}\mathcal {C}^x(\rho _{AB_2}) + \cdots + \mathcal {K}^{m-1} \mathcal {C}^x(\rho _{AB_m}) \\&\quad +\mathcal {K}^{m+1} \left( \sum ^{N-2}_{l=m+1} \mathcal {C}^x(\rho _{AB_l}) \right) + \mathcal {K}^m \mathcal {C}^x(\rho _{AB_{N-1}}) \\&\mathop = \limits ^{\mathrm {(c)}} \mathcal {C}^x_{\alpha }(\rho _{AB_1}) + \mathcal {K}\mathcal {C}^x_{\alpha }(\rho _{AB_2}) + \cdots + \mathcal {K}^{m-1} \mathcal {C}^x_{\alpha }(\rho _{AB_m}) \\&\quad + \mathcal {K}^{m+1} \left( \sum ^{N-2}_{l=m+1} \mathcal {C}^x_{\alpha }(\rho _{AB_l}) \right) + \mathcal {K}^m \mathcal {C}^x_{\alpha }(\rho _{AB_{N-1}}), \end{aligned}$$

\(\square \)

where (a) is due to the relation \(a^x \ge b^x\) for \(a \ge b \ge 0\), \(x \ge 2\); (b) comes from [27, Theorem 1]; and (c) is due to Lemma 1.

Remark 5

Theorem 6 gives the tighter lower bound of COA. Theorem 6 is the more generalized form of the following relation. If \(\mathcal {C}\left( \rho _{AB_i} \right) \ge \mathcal {C}\left( \rho _{AB_{i+1} \ldots B_{N-1}} \right) \) for all \(i=1,2, \ldots ,N-2\), then we have

$$\begin{aligned} \mathcal {C}^x_{\alpha }(\rho _{A|B_1B_2 \ldots B_{N-1}})&\ge \mathcal {C}^x_{\alpha }(\rho _{AB_1}) + \mathcal {K}\mathcal {C}^x_{\alpha }(\rho _{AB_2}) + \cdots \nonumber \\&\quad + \mathcal {K}^{N-3} \mathcal {C}^x_{\alpha }(\rho _{AB_{N-2}}) + \mathcal {K}^{N-2} \mathcal {C}^x_{\alpha }(\rho _{AB_{N-1}}), \end{aligned}$$
(43)

where \(\mathcal {K}= 2^{x /2} -1\) and \(x \ge 2\).

Note that the CRENOA and COA satisfy dual monogamy relations of entanglement [8, 13]. We present a monogamy relation with respect to CRENOA and COA for PCS states. These relations give rise to the restriction of entanglement distribution in PCS states.

Remark 6

The dual monogamy bounds for multi-qubit generalized W-class states given in Sect. 3.2 also hold for PCS states due to relation (41) between the concurrence and the concurrence of assistance. Similarly, the bounds proved in Sects. 4 and 5 are also true for generalized W-class states.

6 Examples

In this section, we present the numerical evidence of the proved theorems. In the following, numerical examples are given to fortify our results.

Example 1

Let us consider 4-qubit entangled state

$$\begin{aligned} |{\psi }\rangle _{ABCD} = \lambda _{0} |{0000}\rangle + \lambda _{1} |{1001}\rangle + \lambda _{2} |{1010 }\rangle + \lambda _{3} |{1100}\rangle , \end{aligned}$$
(44)

where \(\sum _{i=0}^{3}|\lambda _{i}|^2 = 1\). We choose the parameter value \(\lambda _{i} = 1/\sqrt{4}\). We have a lower bound of the Tsallis-q entanglement \(\mathcal {T}_{q}\left( \rho _{A|BCD} \right) \):

  • From (15), we have

    $$\begin{aligned} \mathcal {T}_{q}\left( \rho _{A|BCD} \right) \ge \left( 0.125^{x} + 2 \mathcal {K}\times 0.125^{x} \right) ^{1/x}. \end{aligned}$$

  • From [10], we have

    $$\begin{aligned} \mathcal {T}_{q}\left( \rho _{A|BCD} \right) \ge \left( 3 \times 0.125^{x}\right) ^{1/x}, \end{aligned}$$

where \(q = 2, {\mathcal {K}}= \left( 2^{x/2} - 1 \right) \), and \(x \ge 2\). Figure 1 shows that our results are better than previous results.

Fig. 1
figure 1

Lower bound of the Tsallis-q entanglement \(\mathcal {T}_{q}\left( \rho _{A|BCD} \right) \) as a function of x when \(q = 2\). Dashed dotted black line shows the exact value of \(\mathcal {T}_{q}(\rho _{A|BCD})\), solid blue line shows the lower bound of \(\mathcal {T}_{q}(\rho _{A|BCD})\) from (15), and dashed red line shows lower bound from [10] (Color figure online)

Full size image

Example 2

We consider an arbitrary pure GHZ state

$$\begin{aligned} |{GHZ}\rangle = a |{0}\rangle ^{\otimes N} + b |{1}\rangle ^{\otimes N}, \end{aligned}$$
(45)

in the N-qubit system where \(|a|^{2} + |b|^{2} = 1 \). The generalized GHZ state is satisfied by Theorem 2. We have \(\rho _{1} = \rho _{2} = \cdots = \rho _{N} = a^{2} |{0}\rangle \langle {0}| + b^{2} |{1}\rangle \langle {1}|\). It is a straightforward calculation: \(\mathcal {C}^2_{A_{1}|A_{2} \ldots A_{N}} = \mathcal {C}^2_{A_{2}|A_{1} \ldots A_{N}} = \cdots = \mathcal {C}^2_{A_{i}|A_{1} \ldots A_{i-1} A_{i+1} \ldots A_{N}} = 4|\left( ab \right) ^2|\). According to Theorem 2, we have

$$\begin{aligned}&0 \le \sum _{i=1}^{N-1} \mathcal {T}_{q} \left( \rho _{B_i|A \ldots \hat{B_{i}} \ldots B_{N-1}} \right) - \mathcal {T}_{q} \left( \rho _{A|B_1 \ldots B_{N-1}} \right) , \\&0 \le \dfrac{N - 2}{q - 1}\left[ 1 - \left( \dfrac{ \left( 1 + \sqrt{1 - 4|\left( ab \right) ^2|}\right) ^q + \left( 1 - \sqrt{1 - 4|\left( ab \right) ^2|} \right) ^q }{2^q} \right) \right] . \end{aligned}$$

which is nonnegative for \(q \in \left[ 1,2 \right] \bigcup \left[ 3, \dfrac{5 + \sqrt{13}}{2} \right] \).

Example 3

Let us consider a four qubit cluster state, which is highly entangled state \(|{C_{4}}\rangle = 1/2 \left( |{0000}\rangle + |{0011}\rangle + |{1100}\rangle - |{1111}\rangle \right) \) [28]. The reduced states of \(|{C_4}\rangle \) are \(\rho _A = \rho _B =\rho _C =\rho _D = I/2\), thus applying Corollary 1

$$\begin{aligned} \sum _{i=1}^{3} \mathcal {T}_{q} \left( \rho _{B_i|A \ldots \hat{B_{i}} \ldots B_{3}} \right) - \mathcal {T}_{q} \left( \rho _{A|B_1B_2B_3} \right) = \dfrac{2}{q-1} \left[ 1 - \left( \dfrac{1}{2^{q-1}} \right) \right] , \end{aligned}$$
(46)

which is nonnegative for \(q \in \left[ 1,2 \right] \bigcup \left[ 3, \dfrac{5 + \sqrt{13}}{2} \right] \).

Example 4

Let us consider the 5-qubit W-state,

$$\begin{aligned} |{W}\rangle _{AB_1B_2B_3B_4} = \alpha |{00001}\rangle + \beta _{1} |{00010}\rangle + \beta _{2} |{00100}\rangle + \beta _{3} |{01000}\rangle +\beta _{4} |{10000}\rangle , \end{aligned}$$
(47)

where \(|\alpha |^{2} + \sum _{i = 1}^{4}|\beta _{i}|^{2} = 1 \). The parameter values are \(\alpha = \beta _{i} = 1/\sqrt{5}\). The lower bound of \(\mathcal {N}^x_{\alpha }(\rho _{A|B_1B_2B_3B_4})\) can be determined:

  • From (37), we have

    $$\begin{aligned} \mathcal {N}^x_{\alpha }(\rho _{A|B_1B_2B_3B_4}) \ge \left[ 3(2^{x/2}) - 2 \right] \left( \dfrac{2}{5}\right) ^x. \end{aligned}$$

  • From [19], for \(x \ge 2\), we have

    $$\begin{aligned} \mathcal {N}^x_{\alpha }(\rho _{A|B_1B_2B_3B_4}) \ge \left[ 1 + \dfrac{3x}{2} \right] \left( \dfrac{2}{5} \right) ^x. \end{aligned}$$

Figure 2 shows the lower bound of the negativity as a function of x. We can see that our bound is tighter.

Fig. 2
figure 2

Lower bound of the NOA as a function of x. Dashed dotted black line shows exact value of \(\mathcal {N}_{\alpha }(\rho _{A|B_1B_2B_3B_4})\) as a function of x, solid blue lines shows our result of (37), and dashed red line shows the result of [19] (Color figure online)

Full size image

Example 5

The class of states \(|{W_{n}}\rangle _{ABC}\) belongs to the category of W-states, which can be used for perfect teleportation and superdense coding [25]. This is given by

$$\begin{aligned} |{W_{n}}\rangle _{ABC } = \dfrac{1}{\sqrt{2 + 2n}}\left( |{100}\rangle _{ABC} + \sqrt{n}e^{i\gamma } |{010}\rangle _{ABC} + \sqrt{n + 1}e^{i\delta } |{100}\rangle _{ABC} \right) , \end{aligned}$$
(48)

where n is a real number, and \(\gamma \) and \(\delta \) are phase parameters. For simplicity, we take \(n =1\) and set phases to zero. For these parameters, the concurrence values are \(\mathcal {C}_{A|BC} = \sqrt{3}/2\), \(\mathcal {C}_{AB} = 1/2\) and \(\mathcal {C}_{AC} = 1/\sqrt{2}\). We will apply Theorem 6 to calculate the lower bound of COA. The lower bound of \(\mathcal {C}_{\alpha }^x\left( \rho _{ABC} \right) \) is given by:

  • From (42), we have

    $$\begin{aligned} \mathcal {C}_{\alpha }^x\left( \rho _{A|BC} \right) \ge \left( \dfrac{1}{\sqrt{2}}\right) ^x + \left[ 2^{x/2} - 1 \right] \left( \dfrac{1}{2}\right) ^x. \end{aligned}$$

  • From [19], we have

    $$\begin{aligned} \mathcal {C}^x_{\alpha }(\rho _{A|BC}) \ge \left( \dfrac{1}{\sqrt{2}}\right) ^x + \dfrac{x}{2 }\left( \dfrac{1}{2}\right) ^x. \end{aligned}$$

  • From [18], for \(x \ge 2\), we have

    $$\begin{aligned} \mathcal {C}^x_{\alpha }(\rho _{A|BC}) \ge \left( \dfrac{1}{\sqrt{2}}\right) ^x + \left( \dfrac{1}{2}\right) ^x . \end{aligned}$$

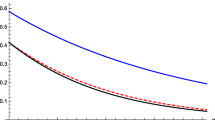
Figure 3 shows the lower bound of the concurrence as a function of x. We can see that our result has a tight bound as compared to [18, 19].

Fig. 3
figure 3

Lower bound of the concurrence as a function of x. Dashed dotted black line shows exact value of \(\mathcal {C}_{\alpha }(\rho _{A|BC})\) as a function of x, solid blue lines shows our result (42), dashed red line shows the result of [19], and dotted green line shows the result of [18] (Color figure online)

Full size image

7 Conclusion

Monogamy is a fundamental property of entanglement, which characterizes the entanglement distribution between the multipartite systems. In this paper, we provided the tighter monogamy relations to characterize the entanglement distribution. We have established the tighter monogamy relation for the Tsallis-q entanglement in multipartite systems. The Tsallis-q entanglement measure-based polygamy relation is investigated for tripartite mixed states. The dual monogamy relation based on the Tsallis-q entanglement is provided for the class of W-states and PCS states, and these results are analytically obtainable. The monogamy relation related to the xth power of CRENOA and COA has been examined for W-class states and PCS states. These relations are used for better classification of entanglement distribution for these two classes. In the future, these relations can be extended for generalized Noon states [29] and generalized entangled coherent states [30].