1 Introduction

Quantum entanglement is an essential feature of quantum mechanics which can enhance quantum technologies such as communication, cryptography and computing beyond classical limitations. A key property of multipartite entanglement is the monogamous relations [1, 2], which are important correlations with fundamental differences from the classical ones. They restrict the sharability of quantum correlations in multipartite quantum states. For example, for three qubit quantum systems, denoted by A, B and C, if A and B are in a maximally entangled state, then A cannot be entangled with C at all. This indicates that it should obey some trade-off relation on the amount of entanglement between the pairs AB and AC.

The monogamy relations give rise to the quantification and characterization of entanglement distribution among the multipartite systems. The first mathematical characterization of the monogamy of entanglement (MOE) was expressed as a form of inequality for three-qubit state [3]: the entanglement EA|BC between A and BC, the entanglement EAB (EAC) between A and B (C) satisfy EA|BC ≥ EAB + EAC. Further, Coffman, Kundu and Wootters (CKW) proposed that the squared concurrence also satisfies the monogamy relations for multiqubit states [2]. Osborne and Verstraete [4] proved the CKW monogamy inequality, which quantifies the frustration of entanglement between different parties. Later, the monogamy inequalities are generalized to other entanglement measures [5,6,7,8,9,10]. The monogamy property is of importance in many quantum information tasks, particularly, in quantum cryptography [11]. In the context of quantum cryptography, such monogamy property quantifies how much information an eavesdropper could potentially obtain about the secret key to be extracted. In the context of condensed-matter physics [12], the monogamy property gives rise to the frustration effects observed in, e.g., Heisenberg anti-ferromagnets. In addition to the monogamy of entanglement, the concept of monogamy has also appeared when discussing the violation of Bell’s inequalities [13]. They also play an important role in the security analysis of quantum key distribution [14], even in black-hole physics [15].

In Ref. [4, 6] the authors showed that the α th concurrence and the convex-roof extended negativity (CREN) satisfy the monogamy inequalities in multiqubit systems for α ≥ 2. It has also been shown that the α th entanglement of formation (EoF), the Tsallis-q entanglement and the Rényi-α entanglement satisfies the monogamy relations when \(\alpha \geq \sqrt {2}\), α ≥ 1, respectively [16,17,18,19,20].

In this paper, we establish some new monogamy relations of multipartite entanglement for arbitrary quantum states, based on the α-th power of the bipartite entanglement. We show that these new monogamy relations are tighter than the existing ones given in [16, 21,22,23,24,25,26,27,28].

2 Enhanced Monogamy Relations for Concurrence

We first consider the monogamy inequalities for concurrence. For a bipartite pure state |ψ〉AB in Hilbert space , the concurrence is defined as \({C}(|\psi \rangle _{AB})=\sqrt {2(1-\text {tr}({\rho _{A}^{2}}))}\) with ρA = trB(|ψ〉AB〈ψ|) [29, 30]. The concurrence for a bipartite mixed state ρAB is defined by the convex roof extension, \({C}(\rho _{AB})=\min \limits _{\{p_{i},|\psi _{i}\rangle \}}\sum \limits _{i}p_{i}{C}(|\psi _{i}\rangle )\), with the minimum taking over all possible pure state decompositions of \(\rho _{AB}=\sum \limits _{i}p_{i}|\psi _{i}\rangle \langle \psi _{i}|\), \(\sum p_{i}=1\) and pi ≥ 0. For an N-qubit state , the concurrence \({C}(\rho _{A|B_{1}{\cdots } B_{N-1}})\) of the state \(\rho _{A|B_{1}{\cdots } B_{N-1}}\) under bipartite partition A and B1⋯BN− 1 satisfies [17]

$$ {C}^{\alpha}(\rho_{A|B_{1}{\cdots} B_{N-1}})\geq{C}^{\alpha}(\rho_{AB_{1}})+{C}^{\alpha}(\rho_{AB_{2}})+\cdots+{C}^{\alpha}(\rho_{AB_{N-1}}), $$
(1)

for α ≥ 2, where \(\rho _{AB_{j}}\) denote the two-qubit reduced density matrices of subsystems ABj, j = 1,2,…,N − 1. The relation (1) is further improved, with the conditions of Theorem 1 in [16], as follows,

$$ \begin{array}{@{}rcl@{}} \!\!\!\!&&{C}^{\alpha}(\rho_{A|B_{1}{\cdots} B_{N-1}})\\ \!\!\!\!& \geq&{C}^{\alpha}(\rho_{AB_{1}})+\left( 2^{\frac{\alpha}{2}}-1\right){C}^{\alpha}(\rho_{AB_{2}})+\cdots+ \left( 2^{\frac{\alpha}{2}}-1\right)^{m-1}{C}^{\alpha}(\rho_{AB_{m}})\\ \!\!\!\!&&+\left( 2^{\frac{\alpha}{2}} - 1\right)^{m+1}[{C}^{\alpha}(\rho_{AB_{m+1}})+\cdots+{C}^{\alpha}(\rho_{AB_{N-2}})]+\left( 2^{\frac{\alpha}{2}} - 1\right)^{m}{C}^{\alpha}(\rho_{AB_{N-1}}), \end{array} $$
(2)

where α ≥ 2.

Generally, a bipartite entanglement measure E is said to be monogamous if

$$ E^{\alpha_{c}}(\rho_{A|B_{1}{\cdots} B_{N-1}})\geq \sum\limits_{i=1}^{N-1} E^{\alpha_{c}}(\rho_{AB_{i}}), $$
(3)

where \(\rho _{A|B_{i}}=\text {tr}_{B_{1}{\cdots } B_{i-1}B_{i+1}{\cdots } B_{N-1}}(\rho _{A|B_{1}{\cdots } B_{N-1}})\), αc is the minimum exponent for \(E^{\alpha _{c}}\) to be monogamous [31]. It has been shown in [31] that for 0 ≤ x ≤ 1 and t ≥ 1,

$$ (1+x)^{t}\geq 1+\displaystyle\frac{t}{2}(x-x^{t})+(2^{t}-1)x^{t}\geq 1+(2^{t}-1)x^{t}. $$
(4)

Lemma 1

For any 2 ⊗ 2 ⊗ 2N− 2 mixed state , assuming that CAB ≥ CAC, we have

$$ C^{\alpha}_{A|BC}\geq C^{\alpha}_{AB}+{\displaystyle\frac{\alpha}{4}}C^{2}_{AC}({C_{AB}^{\alpha-2}} -{C_{AC}^{\alpha-2}})+({\displaystyle2^{\frac{\alpha}{2}}-1})C^{\alpha}_{AC}, $$
(5)

for all α ≥ 2, where N stands for the number of qubit systems, A and B are qubit systems, C is a 2N− 2-dimensional qudit system, consisting of N − 2 qubit systems.

Proof

It has been shown that \(C^{2}_{A|BC}\geq C^{2}_{AB}+C^{2}_{AC}\) for arbitrary 2 ⊗ 2 ⊗ 2N− 2 tripartite state ρA|BC [4, 32]. In terms of CAB ≥ CAC, we have

$$ \begin{array}{@{}rcl@{}} C^{\alpha}_{A|BC} &&\geq (C^{2}_{AB}+C^{2}_{AC})^{\frac{\alpha}{2}}\\ &&=C^{\alpha}_{AB}\left( 1+\frac{C^{2}_{AC}}{C^{2}_{AB}}\right)^{\frac{\alpha}{2}} \\ &&\geq C^{\alpha}_{AB}\left[1+\frac{\alpha}{4}\frac{C^{2}_{AC}}{C^{2}_{AB}}+[2^{\frac{\alpha}{2}} -(1+{\frac{\frac{\alpha}{2}}{2}})]\left( \frac{C^{2}_{AC}}{C^{2}_{AB}}\right)^{\frac{\alpha}{2}}\right]\\ && =C^{\alpha}_{AB}+\frac{\alpha}{4}C^{2}_{AC}({C_{AB}^{\alpha-2}}-{C_{AC}^{\alpha-2}})+({\displaystyle2^{\frac{\alpha}{2}}-1})C^{\alpha}_{AC}, \end{array} $$

where the second inequality is due to (4). Moreover, if CAB = 0, then CAC = 0. That is to say the lower bound becomes trivially zero. □

From Lemma 1 we have the following proposition.

Proposition 1

For an N-qubit mixed state , if \({C_{AB_{i}}}\geq {C_{A|B_{i+1}{\cdots } B_{N-1}}}\) for i = 1,2,⋯ ,m, and \({C_{AB_{j}}}\leq {C_{A|B_{j+1}{\cdots } B_{N-1}}}\) for j = m + 1,⋯ ,N − 2 (1 ≤ m ≤ N − 3) , we have

$$ C^{\alpha}_{A|B_{1}B_{2}{\cdots} B_{N-1}}\geq \sum\limits^{m}_{i=1}h^{i-1}(C^{\alpha}_{AB_{i}}+J_{AB_{i}})+h^{m}\sum\limits^{N-2}_{j=m+1}(hC^{\alpha}_{AB_{j}}+\bar{J}_{AB_{j}}) +h^{m}C^{\alpha}_{AB_{N-1}}, $$
(6)

for N ≥ 4 and α ≥ 2, where \(h=2^{\frac {\alpha }{2}}-1\), \(J_{AB_{i}}={\frac {\alpha }{4}}C^{2}_{A|B_{i+1}{\cdots } B_{N-1}}(C^{\alpha -2}_{AB_{i}}-C^{\alpha -2}_{A|B_{i+1}{\cdots } B_{N-1}})\), \(\bar {J}_{AB_{j}}={\frac {\alpha }{4}}C^{2}_{AB_{j}}(C^{\alpha -2}_{A|B_{j+1}{\cdots } B_{N-1}}-C^{\alpha -2}_{AB_{j}})\).

Proof

From the inequality (5), we have

$$ \begin{array}{@{}rcl@{}} &&C^{\alpha}_{A|B_{1}B_{2}{\cdots} B_{N-1}}\\ &\geq& C^{\alpha}_{AB_{1}}+hC^{\alpha}_{A|B_{2}{\cdots} B_{N-1}}+{\frac{\alpha}{4}}C^{2}_{A|B_{2}{\cdots} B_{N-1}}(C^{\alpha-2}_{AB_{1}}-C^{\alpha-2}_{A|B_{2}{\cdots} B_{N-1}})\\ &\geq& C^{\alpha}_{AB_{1}}+h[C^{\alpha}_{AB_{2}}+hC^{\alpha}_{A|B_{3}{\cdots} B_{N-1}}+{\frac{\alpha}{4}}C^{2}_{A|B_{3}{\cdots} B_{N-1}}(C^{\alpha-2}_{AB_{2}}-C^{\alpha-2}_{A|B_{3}{\cdots} B_{N-1}})]\\ &&+{\frac{\alpha}{4}}C^{2}_{A|B_{2}{\cdots} B_{N-1}}(C^{\alpha-2}_{AB_{1}}-C^{\alpha-2}_{A|B_{2}{\cdots} B_{N-1}})\\ &\geq& \cdots\\ &\geq&\sum\limits^{m}_{i=1}h^{i-1}(C^{\alpha}_{AB_{i}}+J_{AB_{i}})+h^{m}C^{\alpha}_{A|B_{m+1}{\cdots} B_{N-1}}. \end{array} $$
(7)

Similarly, as \({C_{AB_{j}}}\leq {C_{A|B_{j+1}{\cdots } B_{N-1}}}\) for j = m + 1,⋯ ,N − 2, we get

$$ \begin{array}{@{}rcl@{}} &&C^{\alpha}_{A|B_{m+1}{\cdots} B_{N-1}} \\ &\geq& C^{\alpha}_{A|B_{m+2}{\cdots} B_{N-1}}+hC^{\alpha}_{AB_{m+1}}+{\frac{\alpha}{4}}C^{2}_{AB_{m+1}}(C^{\alpha-2}_{A|B_{m+2}{\cdots} B_{N-1}}-C^{\alpha-2}_{AB_{m+1}})\\ &\geq& \sum\limits^{N-2}_{j=m+1}(hC^{\alpha}_{AB_{j}}+{\bar J}_{AB_{j}})+C^{\alpha}_{AB_{N-1}}. \end{array} $$
(8)

By combining (7) and (8), we come to the conclusion. □

Remark 1

We have assumed \({C_{AB_{i}}}\geq {C_{A|B_{i+1}{\cdots } B_{N-1}}}\) and \({C_{AB_{j}}}\leq {C_{A|B_{j+1}{\cdots } B_{N-1}}}\) in Proposition 1. These constraints are most generally given by relabeling the subsystems. Due to the conditions of inequality (4), the second inequality of (7) and (8) hold, respectively. As \(J_{AB_{i}}\)s and \(\bar {J}_{AB_{j}}\)s are great than 0, we obtain the tighter lower bound than corresponding monogamy inequalities in [16]. Particularly, we have the following proposition.

Proposition 2

For any N-qubit mixed state, if \({C_{AB_{i}}}\geq {C_{A|B_{i+1}{\cdots } B_{N-1}}}\), for i = 1,2,⋯ ,N − 2, we have

$$ C^{\alpha}_{A|B_{1}B_{2}{\cdots} B_{N-1}}\geq \sum\limits^{N-2}_{i=1}h^{i-1}(C^{\alpha}_{AB_{i}}+J_{AB_{i}})+h^{N-2}C^{\alpha}_{AB_{N-1}}, $$
(9)

for α ≥ 2 and N ≥ 3, where \(h=2^{\frac {\alpha }{2}}-1\), \(J_{AB_{i}}={\frac {\alpha }{4}} C^{2}_{A|B_{i+1}{\cdots } B_{N-1}}(C^{\alpha -2}_{AB_{i}}-C^{\alpha -2}_{A|B_{i+1}{\cdots } B_{N-1}})\).

Proof

From the inequality (5), we have

$$ \begin{array}{@{}rcl@{}} &&C^{\alpha}_{A|B_{1}B_{2}{\cdots} B_{N-1}}\\ &\geq& C^{\alpha}_{AB_{1}}+hC^{\alpha}_{A|B_{2}{\cdots} B_{N-1}}+{\frac{\alpha}{4}}C^{2}_{A|B_{2}{\cdots} B_{N-1}}(C^{\alpha-2}_{AB_{1}}-C^{\alpha-2}_{A|B_{2}{\cdots} B_{N-1}})\\ &\geq& C^{\alpha}_{AB_{1}}+h[C^{\alpha}_{AB_{2}}+hC^{\alpha}_{A|B_{3}{\cdots} B_{N-1}}+{\frac{\alpha}{4}}C^{2}_{A|B_{3}{\cdots} B_{N-1}}(C^{\alpha-2}_{AB_{2}}-C^{\alpha-2}_{A|B_{3}{\cdots} B_{N-1}})]\\ &&+{\frac{\alpha}{4}}C^{2}_{A|B_{2}{\cdots} B_{N-1}}(C^{\alpha-2}_{AB_{1}}-C^{\alpha-2}_{A|B_{2}{\cdots} B_{N-1}})\\ &\geq& \cdots\\ &\geq& C^{\alpha}_{AB_{1}}+hC^{\alpha}_{AB_{2}}+\cdots+h^{N-2}C^{\alpha}_{AB_{N-1}}+h^{N-3}\cdot{\frac{\alpha}{4}}C^{2}_{AB_{N-1}} (C^{\alpha-2}_{AB_{N-2}}-C^{\alpha-2}_{AB_{N-1}})\\ &&+\cdots+h\cdot{\frac{\alpha}{4}}C^{2}_{A|B_{3}{\cdots} B_{N-1}}(C^{\alpha-2}_{AB_{2}} - C^{\alpha-2}_{A|B_{3}{\cdots} B_{N-1}}) + {\frac{\alpha}{4}}C^{2}_{A|B_{2}{\cdots} B_{N-1}}(C^{\alpha-2}_{AB_{1}}-C^{\alpha-2}_{A|B_{2}{\cdots} B_{N-1}}). \end{array} $$
(10)

According to the denotation of \(J_{AB_{i}}\), we obtain the result. □

Example 1

Let us consider the three-qubit state |ψ〉 in the generalized Schmidt decomposition form [33, 34],

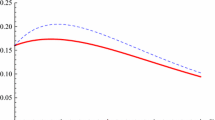
$$ |\psi\rangle=\lambda_{0}|000\rangle+\lambda_{1}e^{i{\varphi}}|100\rangle+\lambda_{2}|101\rangle+\lambda_{3}|110\rangle+\lambda_{4}|111\rangle, $$
(11)

where λi ≥ 0, i = 0,1,2,3,4, \(\sum \limits _{i=0}^{4}{\lambda _{i}^{2}}=1\). From the definition of concurrence, we have \(C_{A|BC}=2\lambda _{0}\sqrt {{{\lambda _{2}^{2}}+{\lambda _{3}^{2}}+{\lambda _{4}^{2}}}}\), CAB = 2λ0λ2 and CAC = 2λ0λ3. Set \(\lambda _{0}=\lambda _{2}=\frac {1}{2}\), \(\lambda _{1}=\lambda _{3}=\lambda _{4}=\frac {\sqrt {6}}{6}\), one has \(C_{A|BC}=\sqrt {\frac {7}{12}}\), \(C_{AB}=\frac {1}{2}, C_{AC}=\frac {\sqrt {6}}{6}\). Then \(C_{A|BC}^{\alpha }=({\frac {7}{12}})^{\frac {\alpha }{2}} \geq C_{AB}^{\alpha }+h C_{AC}^{\alpha }+\frac {\alpha }{4} C_{AC}^{2}(C_{AB}^{\alpha -2}-C_{AC}^{\alpha -2})=(\frac {1}{2})^{\alpha }+h\cdot (\frac {\sqrt {6}}{6})^{\alpha } +\frac {\alpha }{4}\cdot (\frac {\sqrt {6}}{6})^{2}[(\frac {1}{2})^{\alpha -2}-(\frac {\sqrt {6}}{6})^{\alpha -2}]\). While the result in [16] is \(C_{AB}^{\alpha }+h C_{AC}^{\alpha }= (\frac {1}{2})^{\alpha }+h\cdot (\frac {\sqrt {6}}{6})^{\alpha }\). One can see that our lower bound is tighter than theirs in [16], see Fig. 1.

Fig. 1
figure 1

The axis C represents the concurrence of |ψ〉, which is a function of α. The solid blue line represents the lower bound of concurrence of |ψ〉 in Example 1, the dashed red line represents the lower bound from our result, the solid black line represents lower bound from the result in [16]

Full size image

3 Enhanced Monogamy Relations for EoF

In quantifying quantum entanglement, the entanglement of formation (EoF) [35, 36] is a well defined important measure of entanglement for bipartite systems. Let and be m and n dimensional (m ≤ n) vector spaces, respectively. The EoF of a pure state is defined by

$$ E(|\psi\rangle)=S(\rho_{A}), $$
(12)

where ρA = trB(|ψ〉〈ψ|) and \(S(\rho )=-\text {tr}(\rho \log _{2}\rho )\). For a bipartite mixed state ρAB ∈ , the entanglement of formation is given by,

$$ E(\rho_{AB})=\underset{\{p_{i}, |\psi_{i}\rangle\}}{\min}\sum\limits_{i}p_{i}E(|\psi_{i}\rangle), $$
(13)

with the minimum taking over all possible pure state decompositions of ρAB.

Denote \(f(x)=H\left (\frac {1+\sqrt {1-x}}{2}\right )\), where \(H(x)=-x\log _{2}(x)-(1-x)\log _{2}(1-x)\). From (12) and (13), one has \(E(|\psi \rangle )=f\left (C^{2}(|\psi \rangle )\right )\) for 2 ⊗ m (m ≥ 2) pure state |ψ〉, and \(E(\rho )=f\left (C^{2}(\rho )\right )\) for two-qubit mixed state ρ [30]. It is obvious that f(x) is a monotonically increasing function for 0 ≤ x ≤ 1. The function f(x) satisfies the following relations:

$$ f^{\sqrt{2}}(x^{2}+y^{2})\geq f^{\sqrt{2}}(x^{2})+f^{\sqrt{2}}(y^{2}), $$
(14)

where \(f^{\sqrt {2}}(x^{2}+y^{2})=[f(x^{2}+y^{2})]^{\sqrt {2}}\).

From [2] one sees that EoF does not satisfy the inequality EA|BC ≥ EAB + EAC. In [37] the authors showed that EoF is a monotonic function satisfying \(E^{2}(C^{2}_{A|B_{1}B_{2}{\cdots } B_{N-1}})\geq E^{2}({\sum }_{i=1}^{N-1}C^{2}_{AB_{i}})\). For N-qubit systems, one has [17]

$$ E^{\alpha}_{A|B_{1}B_{2}{\cdots} B_{N-1}}\geq E^{\alpha}_{AB_{1}}+E^{\alpha}_{AB_{2}}+\cdots+E^{\alpha}_{AB_{N-1}}, $$
(15)

where \(E_{A|B_{1}B_{2}{\cdots } B_{N-1}}\) is the EoF of the state \(\rho _{A|B_{1}{\cdots } B_{N-1}}\), \(E_{AB_{i}}\) is the EoF of the mixed state \(\rho _{AB_{i}}=\text {tr}_{B_{1}B_{2}{\cdots } B_{i-1},B_{i+1}{\cdots } B_{N-1}}(\rho )\), i = 1,2,⋯ ,N − 1, \(\alpha \geq \sqrt {2}\). In particular, we have following relations.

Lemma 2

For any 2 ⊗ 2 ⊗ 2N− 2 mixed state , if CAB ≥ CAC, the following inequality holds for \(\alpha \geq \sqrt {2}\),

$$ E^{\alpha}_{A|BC}\geq E^{\alpha}_{AB}+(2^{t}-1)E^{\alpha}_{AC}+\displaystyle\frac{t}{2}E^{\sqrt{2}}_{AC}(E^{\alpha-\sqrt{2}}_{AB}-E^{\alpha-\sqrt{2}}_{AC}), $$
(16)

where \(t=\frac {\alpha }{\sqrt 2}\).

Proof

The proof is similar to the proof of Lemma 1. □

Note that, for any N-qubit mixed state , \(E^{\alpha }_{A|B_{1}B_{2}{\cdots } B_{N-1}}(\rho )\) no longer has similar relation like (6) in Proposition 1. However, the following proposition holds.

Proposition 3

For any N-qubit mixed state , if \({C_{AB_{i}}}\geq {C_{A|B_{i+1}{\cdots } B_{N-1}}}\) for all i = 1,2,⋯ ,N − 2 and \(\alpha \geq \sqrt {2}\), we have

$$ E^{\alpha}_{A|B_{1}B_{2}{\cdots} B_{N-1}}\geq \sum\limits^{N-2}_{i=1}h^{i-1}(E^{\alpha}_{AB_{i}}+R_{AB_{i}})+h^{N-2}E^{\alpha}_{AB_{N-1}}, $$
(17)

where h = 2t − 1, \(t=\frac {{\alpha }}{\sqrt {2}}\), and \(R_{AB_{i}} =\frac {t}{2}(E^{\sqrt {2}}_{AB_{i+1}}+\cdots +E^{\sqrt {2}}_{AB_{N-1}})(E^{\alpha -\sqrt {2}}_{AB_{i}}-E^{\alpha -{\sqrt {2}}}_{A|B_{i+1}{\cdots } B_{N-1}})\) with i = 1,2,⋯ ,N − 1.

Proof

For \(\alpha \geq \sqrt {2}\), we have

$$ \begin{array}{@{}rcl@{}} &&f^{{\alpha}}(x^{2}+y^{2})\\ &=&\left( f^{\sqrt{2}}(x^{2}+y^{2})\right)^{t} \\ &\geq& \left( f^{\sqrt{2}}(x^{2})+f^{\sqrt{2}}(y^{2})\right)^{t} \\ &\geq& f^{\alpha}(x^{2})+(2^{t}-1)f^{\alpha}(y^{2})\\ &&+\frac{t}{2}f^{\sqrt{2}}(y^{2})[f^{{\alpha}-\sqrt{2}}(x^{2})-f^{{\alpha}-\sqrt{2}}(y^{2})], \end{array} $$
(18)

where the first inequality is due to the inequality (14), and without loss of generality, we assume x2 ≥ y2, using the monotonicity of f(x) and inequality (4), the second inequality is obtained.

Let be the optimal decomposition of \(E_{A|B_{1}B_{2}{\cdots } B_{N-1}}(\rho )\) for the N-qubit mixed state ρ, we have

$$ \begin{array}{@{}rcl@{}} &&E_{A|B_{1}B_{2}{\cdots} B_{N-1}}(\rho)\\ &&={\sum}_{i}p_{i}E_{A|B_{1}B_{2}{\cdots} B_{N-1}}(|\psi_{i}\rangle)\\ &&={\sum}_{i}p_{i}f\left( C^{2}_{A|B_{1}B_{2}{\cdots} B_{N-1}}(|\psi_{i}\rangle)\right)\\ &&\geq f\left( {\sum}_{i}p_{i}C^{2}_{A|B_{1}B_{2}{\cdots} B_{N-1}}(|\psi_{i}\rangle)\right)\\ &&\geq f\left( \left[{\sum}_{i}p_{i}C_{A|B_{1}B_{2}{\cdots} B_{N-1}}(|\psi_{i}\rangle)\right]^{2}\right)\\ && \geq f\left( C^{2}_{A|B_{1}B_{2}{\cdots} B_{N-1}}(\rho)\right), \end{array} $$
(19)

where the first inequality is due to that f(x) is a convex function. The second inequality is due to the Cauchy-Schwarz inequality: \((\sum \limits _{i}{x_{i}^{2}})^{\frac {1}{2}}(\sum \limits _{i}{y_{i}^{2}})^{\frac {1}{2}}\geq \sum \limits _{i}x_{i}y_{i}\), with \(x_{i}=\sqrt {p_{i}}\) and \(y_{i}=\sqrt {p_{i}}C_{A|B_{1}B_{2}{\cdots } B_{N-1}}(|\psi _{i}\rangle )\). Due to the definition of concurrence and that f(x) is a monotonically increasing function, we obtain the third inequality. Therefore, we have

$$ \begin{array}{@{}rcl@{}} && E^{\alpha}_{A|B_{1}B_{2}{\cdots} B_{N-1}}(\rho)\\ & \geq& f^{\alpha}(C^{2}_{AB_{1}}+C^{2}_{AB_{2}}+\cdots+C^{2}_{AB_{N-1}})\\ & \geq& f^{\alpha}(C^{2}_{AB_{1}})+h\cdot f^{\alpha}(C^{2}_{AB_{2}}+\cdots+C^{2}_{AB_{N-1}})\\ &&+\frac{t}{2}f^{\sqrt2}(C^{2}_{AB_{2}}+\cdots+C^{2}_{AB_{N-1}})[f^{\alpha-\sqrt2}(C^{2}_{AB_{1}}) -f^{\alpha-\sqrt2}(C^{2}_{AB_{2}}+\cdots+C^{2}_{AB_{N-1}})]\\ & \geq& f^{\alpha}(C^{2}_{AB_{1}})+h\cdot f^{\alpha}(C^{2}_{AB_{2}}+\cdots+C^{2}_{AB_{N-1}})\\ &&+\frac{t}{2}[f^{\sqrt2}(C^{2}_{AB_{2}})+\cdots+f^{\sqrt2}(C^{2}_{AB_{N-1}})]\cdot[f^{\alpha-\sqrt2} (C^{2}_{AB_{1}})-f^{\alpha-\sqrt2}(C^{2}_{A|B_{2}{\cdots} B_{N-1}})]\\ & \geq& f^{\alpha}(C^{2}_{AB_{1}})+h\cdot f^{\alpha}(C^{2}_{AB_{2}})+\cdots+h^{N-2}\cdot f^{\alpha}(C^{2}_{AB_{N-1}})\\ &&+h^{(N-3)}\cdot \frac{t}{2}f^{\sqrt{2}}(C^{2}_{AB_{N-1}})[f^{\alpha-\sqrt{2}}(C^{2}_{AB_{N-2}})-f^{\alpha-{\sqrt{2}}} (C^{2}_{AB_{N-1}})]\\ &&+{\cdots} +\frac{t}{2}[f^{\sqrt2}(C^{2}_{AB_{2}})+\cdots+f^{\sqrt2}(C^{2}_{AB_{N-1}})] \cdot[f^{\alpha-\sqrt2}(C^{2}_{AB_{1}})-f^{\alpha-\sqrt2}(C^{2}_{A|B_{2}{\cdots} B_{N-1}})]\\ & \geq& E^{\alpha}_{AB_{1}}+h E^{\alpha}_{AB_{2}}+\cdots+h^{N-2}E^{\alpha}_{AB_{N}-1}+h^{N-3}\cdot \frac{t}{2}(E^{\sqrt2}_{AB_{N-1}})[E^{\alpha-\sqrt2}_{AB_{N-2}}-E^{\alpha-\sqrt2}_{AB_{N-1}}]+{\cdots} \\ &&+\frac{t}{2}(E^{\sqrt2}_{AB_{2}}+\cdots+E^{\sqrt2}_{AB_{N-1}})\cdot(E^{\alpha-\sqrt2}_{AB_{1}} -E^{\alpha-\sqrt2}_{A|B_{2}{\cdots} B_{N-1}}), \end{array} $$
(20)

where we have used the monogamy inequality (15) to obtain the first inequality. By using the relation (14) and the monotonicity of the function \(f^{\sqrt 2}(x)\), we get the third and the fourth inequalities. Since for any 2 ⊗ 2 quantum state \(\rho _{AB_{i}}\), \(E(\rho _{AB_{i}})=f\left [C^{2}(\rho _{AB_{i}})\right ]\), from (19) one gets the last inequality. □

Since \({C_{AB_{i}}}\geq {C_{A|B_{i+1}{\cdots } B_{N-1}}}\), (i = 1,2,⋯ ,N − 2), \(R_{AB_{i}}\geq 0\) holds, and our results are tighter than (8) in [16].

Example 2

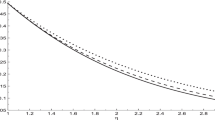
Let us consider the three-qubit state |ψ〉 in Example 1 again. Set \(\lambda _{0}=\lambda _{2}=\frac {1}{2}\) and \(\lambda _{1}=\lambda _{3}=\lambda _{4}=\frac {\sqrt {6}}{6}\) in (11). One has \(E_{A|BC}^{\alpha }=(0.674027)^{\alpha }\), \(E_{AB}^{\alpha }+hE_{AC}^{\alpha }+\frac {\alpha }{2\sqrt {2}}(E_{AC}^{\sqrt {2}}) (E_{AB}^{\alpha -\sqrt {2}}-E_{AC}^{\alpha -\sqrt {2}})=(0.354579)^{\alpha } +h\cdot (0.258403)^{\alpha }+\frac {\alpha }{2\sqrt 2} \cdot (0.258403)^{\sqrt 2}[(0.354579)^{\alpha -\sqrt 2}-(0.258403)^{\alpha -\sqrt 2}]\). While the result in [16] gives \(E_{AB}^{\alpha }+hE_{AC}^{\alpha }=(0.354579)^{\alpha }+h\cdot (0.258403)^{\alpha }\). We can verify that our result is better than the corresponding result in [16], see Fig. 2.

Fig. 2
figure 2

The axis E represents the EoF of the state |ψ〉, which is a function of α. The solid blue line represents the lower bounds of EoF of the state |ψ〉 in Example 2, the dashed red line represents the lower bound from our result, and the solid black line represents the lower bound from the result in [16]

Full size image

4 Enhanced Monogamy Relations for Negativity

Another well known quantifier of bipartite entanglement is the negativity, which is based on the positive partial transposition (PPT) criterion. Given a bipartite state ρAB in , the negativity is defined by [38] \(N(\rho _{AB})=(||\rho _{AB}^{T_{A}}||_{1}-1)/2\), where \(\rho _{AB}^{T_{A}}\) is the partial transposed matrix of ρAB with respect to the subsystem A, ||⋅||1 is the trace norm. The negativity is a convex function of ρAB. For convenience, we use \( N(\rho _{AB})=||\rho _{AB}^{T_{A}}||_{1}-1\) [6]. For any bipartite pure state |ψ〉AB, the negativity N(ρAB) is given by \(N(|\psi \rangle _{AB})=2\sum \limits _{i<j}\sqrt {\lambda _{i}\lambda _{j}}=(\text {tr}\sqrt {\rho _{A}})^{2}-1\), where λi are the eigenvalues of the reduced density matrix of |ψ〉AB. For a mixed state ρAB, the convex-roof extended negativity (CREN) is defined as

$$ N_{c}(\rho_{AB})=\min{\sum}_{i}p_{i}N(|\psi_{i}\rangle_{AB}), $$
(21)

where the minimum is taken over all possible pure state decompositions {pi, |ψi〉AB} of ρAB. CREN gives a perfect discrimination of positive partial transposed bound entangled states and separable states in any bipartite quantum systems [39, 40].

Notice that there exists a relationship between CREN and concurrence. For any bipartite pure state |ψ〉AB in a d ⊗ d quantum system with Schmidt rank 2, \(|\psi \rangle _{AB}=\sqrt {\lambda _{0}}|00\rangle +\sqrt {\lambda _{1}}|11\rangle \). One has \(N(|\psi \rangle _{AB})=\parallel |\psi \rangle \langle \psi |^{T_{B}}\parallel _{1}-1=2\sqrt {\lambda _{0}\lambda _{1}} =\sqrt {2(1-\text {tr}{\rho _{A}^{2}})}=C(|\psi \rangle _{AB})\). It follows that for any two-qubit mixed state \(\rho _{AB}=\sum p_{i}|\psi _{i}\rangle _{AB}\langle \psi _{i}|\),

$$ \begin{array}{@{}rcl@{}} N_{c}(\rho_{AB})&&=\min{\sum}_{i}p_{i}N(|\psi_{i}\rangle_{AB})\\ &&=\min{\sum}_{i}p_{i}C(|\psi_{i}\rangle_{AB})\\ &&=C(\rho_{AB}). \end{array} $$
(22)

Here NcAB = Nc(ρAB), then we have the following result.

Proposition 4

For an N-qubit mixed state, if \({N_{c}}_{AB_{i}}\geq {{N_{c}}_{{AB_{i}}{\cdots } B_{N-1}}}\) for i = 1,2,⋯ ,m, and \({N_{c}}_{AB_{j}}\leq {{N_{c}}_{{AB_{j}}{\cdots } B_{N-1}}}\) for j = m + 1,⋯ ,N − 2 (1 ≤ m ≤ N − 3, N ≥ 4), the following holds for all α ≥ 2,

$$ {N_{c}}^{\alpha}_{A|B_{1}B_{2}{\cdots} B_{N-1}}\geq \sum\limits^{m}_{i=1}h^{i-1}({N_{c}}^{\alpha}_{AB_{i}}+Q_{AB_{i}})+h^{m}\sum\limits^{N-2}_{j=m+1}(h{N_{c}}^{\alpha}_{AB_{j}}+\bar{Q}_{AB_{j}})+h^{m}{N_{c}}^{\alpha}_{AB_{N-1}}, $$
(23)

where \(h=2^{\frac {\alpha }{2}}-1\), \(Q_{AB_{i}}=\frac {\alpha }{4}{N_{c}}^{2}_{A|B_{i+1}{\cdots } B_{N-1}}\left ({{N_{c}}^{(\alpha -2)}_{AB_{i}}-{N_{c}}^{(\alpha -2)}_{A|B_{i+1}{\cdots } B_{N-1}}}\right )\), \(\bar {Q}_{AB_{j}}=\frac {\alpha }{4}{N_{c}}^{2}_{AB_{j}}\left ({N_{c}}^{(\alpha -2)}_{A|B_{j+1}{\cdots } B_{N-1}}-{N_{c}}^{(\alpha -2)}_{AB_{j}}\right )\).

Proof

From the inequality (5), we have

$$ \begin{array}{@{}rcl@{}} &&{N_{c}}^{\alpha}_{A|B_{1}B_{2}{\cdots} B_{N-1}}\\ &\geq& {N_{c}}^{\alpha}_{AB_{1}}+h{N_{c}}^{\alpha}_{A|B_{2}{\cdots} B_{N-1}}+{\frac{\alpha}{4}}{N_{c}}^{2}_{A|B_{2}{\cdots} B_{N-1}}({N_{c}}^{(\alpha-2)}_{AB_{1}}-{N_{c}}^{(\alpha-2)}_{A|B_{2}{\cdots} B_{N-1}})\\ &\geq& {N_{c}}^{\alpha}_{AB_{1}}+h[{N_{c}}^{\alpha}_{AB_{2}}+h{N_{c}}^{\alpha}_{A|B_{3}{\cdots} B_{N-1}}+{\frac{\alpha}{4}}{N_{c}}^{2}_{A|B_{3}{\cdots} B_{N-1}}({N_{c}}^{(\alpha-2)}_{AB_{2}}-{N_{c}}^{(\alpha-2)}_{A|B_{3}{\cdots} B_{N-1}})]\\ &&+{\frac{\alpha}{4}}{N_{c}}^{2}_{A|B_{2}{\cdots} B_{N-1}}({N_{c}}^{(\alpha-2)}_{AB_{1}}-{N_{c}}^{(\alpha-2)}_{A|B_{2}{\cdots} B_{N-1}})\\ & \geq& \cdots\\ &\geq&\sum\limits^{m}_{i=1}h^{i-1}({N_{c}}^{\alpha}_{AB_{i}}+Q_{AB_{i}})+h^{m}{N_{c}}^{\alpha}_{A|B_{m+1}{\cdots} B_{N-1}}. \end{array} $$
(24)

Similarly, as \({{N_{c}}_{AB_{j}}}\leq {{N_{c}}_{A|B_{j+1}{\cdots } B_{N-1}}}\) for j = m + 1,⋯ ,N − 2, we get

$$ \begin{array}{@{}rcl@{}} &&{N_{c}}^{\alpha}_{A|B_{m+1}{\cdots} B_{N-1}} \\ &\geq& {N_{c}}^{\alpha}_{A|B_{m+2}{\cdots} B_{N-1}}+h{N_{c}}^{\alpha}_{AB_{m+1}}+{\frac{\alpha}{4}}{N_{c}}^{2}_{AB_{m+1}}\left( {N_{c}}^{(\alpha-2)}_{A|B_{m+2}{\cdots} B_{N-1}}-{N_{c}}^{(\alpha-2)}_{AB_{m+1}}\right)\\ &\geq& \sum\limits^{N-2}_{j=m+1}(h{N_{c}}^{\alpha}_{AB_{j}}+{\bar Q}_{AB_{j}})+{N_{c}}^{\alpha}_{AB_{N-1}}. \end{array} $$
(25)

Combining (24) and (25), we complete the proof. □

In particular, if \({{N_{c}}_{AB_{i}}}\geq {{N_{c}}_{A|B_{i+1}{\cdots } B_{N-1}}}\) for all i = 1,2,⋯ ,N − 2, we have the following proposition.

Proposition 5

For any N-qubit state , if \({N_{c}}_{AB_{i}}\geq {N_{c}}_{A|B_{i+1}{\cdots } B_{N-1}}\) for all i = 1,2,⋯ ,N − 2, we have

$$ {N^{\alpha}_{c}}_{A|B_{1}B_{2}{\cdots} B_{N-1}}\geq \sum\limits^{N-2}_{i=1}h^{i-1}({N^{\alpha}_{c}}_{AB_{i}}+Q_{AB_{i}})+h^{N-2}{N^{\alpha}_{c}}_{AB_{N-1}}, $$
(26)

for α ≥ 2, where \(h=2^{\frac {\alpha }{2}}-1\), \(Q_{AB_{i}}=\frac {\alpha }{4}{N_{c}}^{2}_{A|B_{i+1}{\cdots } B_{N-1}}({{N_{c}}^{\alpha -2}_{AB_{i}}-{N_{c}}^{\alpha -2}_{A|B_{i+1}{\cdots } B_{N-1}}})\).

Example 3

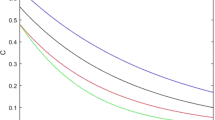
Let us consider the three-qubit state |ψ〉 (11) again. From the definition of CREN, we have \({N_{c}}_{A|BC}=2\lambda _{0}\sqrt {{\lambda _{2}^{2}}+{\lambda _{3}^{2}}+{\lambda _{4}^{2}}}\), NcAB = 2λ0λ2, and NcAC = 2λ0λ3. Set \(\lambda _{0}=\lambda _{2}=\frac {1}{2}\), \(\lambda _{1}=\lambda _{3}=\lambda _{4}=\frac {\sqrt {6}}{6}\), one has \({N_{c}}_{A|BC}^{\alpha }\geq {N_{c}}_{AB}^{\alpha }+h{N_{c}}_{AC}^{\alpha } +\frac {\alpha }{4}{N_{c}}_{AC}^{2}({N_{c}}_{AB}^{\alpha -2}-{N_{c}}_{AC}^{\alpha -2}) =(\frac {1}{2})^{\alpha }+h\cdot (\frac {\sqrt {6}}{6})^{\alpha } +\frac {\alpha }{4}\cdot (\frac {\sqrt {6}}{6})^{2}[(\frac {1}{2})^{\alpha -2}-(\frac {\sqrt {6}}{6})^{\alpha -2}]\). While from [16] one has \({N_{c}}_{AB}^{\alpha }+h{N_{c}}_{AC}^{\alpha }= (\frac {1}{2})^{\alpha }+h\cdot (\frac {\sqrt {6}}{6})^{\alpha }\). One can see that our lower bound is tighter than the results in [16] for α ≥ 2, see Fig. 3.

Fig. 3
figure 3

The axis Nc stands for the negativity of |ψ〉, which is a function of α. The solid blue line represents the lower bound of negativity of |ψ〉 in Example 3, the dashed red line represents the lower bound from our result, the solid black line represents lower bound from the result in [16]

Full size image

5 Enhanced Monogamy Relations for Tsallis-Q Entanglement

The Tsallis entropy is a generalization of the standard Boltzmann-Gibbs entropy. The Tsallis-q entropy [41, 42] with respect to a non-negative number q, can be used to characterize classical statistical correlations inherent in quantum states [43]. For a bipartite pure state |ψ〉AB, the Tsallis-q entanglement is defined by [20],

$$ T_{q}(|\psi\rangle_{AB})=S_{q}(\rho_{A})=\displaystyle\frac{1}{q-1}(1-tr({\rho_{A}^{q}})), $$
(27)

for any q > 0 and q≠ 1. If q tends to 1, Tq(ρ) converges to the von Neumann entropy, i.e., \(\lim _{q\to 1} T_{q}(\rho )=-tr(\rho \ln \rho )\). For a bipartite mixed state ρAB, the Tsallis-q entanglement is defined via the convex-roof extension, \(T_{q}(\rho _{AB})=\min \limits \displaystyle {\sum }_{i}p_{i}T_{q}(|\psi _{i}\rangle _{AB})\), with the minimum taken over all possible pure state decompositions of ρAB.

In [44], the authors proved an analytic relationship between the Tsallis-q entanglement and the concurrence for \(\frac {5-\sqrt {13}}{2}\leq q\leq \frac {5+\sqrt {13}}{2}\),

$$ T_{q}(|\psi\rangle_{AB})=g_{q}(C^{2}(|\psi\rangle_{AB})), $$
(28)

where the function gq(x) is defined by

$$ g_{q}(x)=\frac{1}{q-1}\left[1-\left( \frac{1+\sqrt{1-x}}{2}\right)^{q}-\left( \frac{1-\sqrt{1-x}}{2}\right)^{q}\right]. $$
(29)

It has been shown that \(T_{q}(|\psi \rangle )=g_{q}\left (C^{2}(|\psi \rangle )\right )\) for any 2 ⊗ m (m ≥ 2)-dimensional pure state |ψ〉, and \(T_{q}(\rho )=g_{q}\left (C^{2}(\rho )\right )\) for two-qubit mixed state ρ [20]. Hence (28) holds for any q such that gq(x) in (29) is monotonically increasing and convex. In particular, gq(x) satisfies the following relations for 2 ≤ q ≤ 3,

$$ g_{q}(x^{2}+y^{2})\geq g_{q}(x^{2})+{g_{q}^{2}}(y^{2}). $$
(30)

Lemma 3

For any 2 ⊗ 2 ⊗ 2N− 2 mixed state , if CAB ≥ CAC, the following inequality holds for α ≥ 1,

$$ {T_{q}}^{\alpha}_{A|BC}\geq {T_{q}}^{\alpha}_{AB}+(2^{\alpha}-1){T_{q}}^{\alpha}_{AC}+\frac{\alpha}{2}{T_{q}}_{AC}({T_{q}}^{\alpha-1}_{AB}-{T_{q}}^{\alpha-1}_{AC}), $$
(31)

where 2 ≤ q ≤ 3, N stands for the number of qubit systems, A and B are qubit systems, C is a 2N− 2-dimensional qudit system, consisting of N − 2 qubit systems.

Proof

The proof is similar to the proof of Lemma 1. □

The Tsallis-q entanglement satisfies \({T_{q}}_{A|B_{1}B_{2}{\cdots } B_{N-1}}\geq \displaystyle {\sum }_{i=1}^{N-1}{T_{q}}_{AB_{i}}\) [20], where i = 1,2,⋯N − 1, 2 ≤ q ≤ 3. It is further proved that \({{T_{q}^{2}}}_{A|B_{1}B_{2}{\cdots } B_{N-1}}\geq \displaystyle {\sum }_{i=1}^{N-1}{{T_{q}^{2}}}_{AB_{i}}\) for \(\frac {5-\sqrt {13}}{2}\leq q\leq \frac {5+\sqrt {13}}{2}\) in [44].

Note that, for any N-qubit mixed state , if \({C_{AB_{i}}}\geq {C_{A|B_{i+1}{\cdots } B_{N-1}}}\) for i = 1,2,⋯ ,m, and \({C_{AB_{j}}}\leq {C_{A|B_{j+1}{\cdots } B_{N-1}}}\) for j = m + 1,⋯ ,N − 2 (1 ≤ m ≤ N − 3, N ≥ 4), C(ρ) no longer satisfies the relation (6) in Proposition 1. Nevertheless, for the case that \({C_{AB_{i}}}\geq {C_{A|B_{i+1}{\cdots } B_{N-1}}}\) for i = 1,2,⋯ ,N − 2, we have an enhanced monogamy relation for the Tsallis-q entanglement.

Proposition 6

For an arbitrary N-qubit mixed state \(\rho _{A|B_{1}{\cdots } B_{N-1}}\), if \({C_{AB_{i}}}\geq {C_{A|B_{i+1}{\cdots } B_{N-1}}}\) for i = 1,2,⋯ ,N − 2 (N ≥ 3), the α th power of Tsallis-q entanglement satisfies the following monogamy relation,

$$ {T_{q}}^{\alpha}_{A|B_{1}B_{2}{\cdots} B_{N-1}}\geq \sum\limits^{N-2}_{i=1}h^{i-1}({T_{q}}^{\alpha}_{AB_{i}}+G_{AB_{i}})+h^{N-2}{T_{q}}^{\alpha}_{AB_{N-1}} $$
(32)

for α ≥ 1, where h = 2α − 1, and \(G_{AB_{i}}=\frac {\alpha }{2}({T_{q}}_{AB_{i+1}}+{\cdots } +{T_{q}}_{AB_{N-1}})({T_{q}}^{\alpha -1}_{AB_{i}}-{T_{q}}^{\alpha -1}_{A|B_{i+1}{\cdots } B_{N-1}})\).

Proof

For α ≥ 1, we have

$$ \begin{array}{@{}rcl@{}} &&g_{q}^{{\alpha}}(x^{2}+y^{2})\\ &&\geq \left( g_{q}(x^{2})+g_{q}(y^{2})\right)^{\alpha} \\ &&\geq {g_{q}}^{\alpha}(x^{2})+(2^{\alpha}-1){g_{q}}^{\alpha}(y^{2})+\frac{\alpha}{2}{g_{q}}(y^{2})({g_{q}}^{\alpha-1}(x^{2})-{g_{q}}^{\alpha-1}(y^{2})), \end{array} $$
(33)

where the first inequality is due to the inequality (30), and the second inequality is obtained analogously from the proof of the second inequality in (5).

Let be the optimal decomposition for the N-qubit mixed state ρ. We have

$$ \begin{array}{@{}rcl@{}} &&{T_{q}}_{A|B_{1}B_{2}{\cdots} B_{N-1}}(\rho)={\sum}_{i}p_{i}T_{q}(|\psi_{i}\rangle_{A|B_{1}B_{2}{\cdots} B_{N-1}})\\ &=&{\sum}_{i}p_{i}g_{q}\left[C^{2}_{A|B_{1}B_{2}{\cdots} B_{N-1}}(|\psi_{i}\rangle)\right]\\ &\geq& g_{q}\left[{\sum}_{i}p_{i}C^{2}_{A|B_{1}B_{2}{\cdots} B_{N-1}}(|\psi_{i}\rangle)\right] \geq g_{q}\left( \left[{\sum}_{i}p_{i}C_{A|B_{1}B_{2}{\cdots} B_{N-1}}(|\psi_{i}\rangle)\right]^{2}\right)\\ &=&g_{q}\left[C^{2}_{A|B_{1}B_{2}{\cdots} B_{N-1}}(\rho)\right],\\ \end{array} $$
(34)

where the first inequality is due to that gq(x) is a convex function. The second inequality is due to the Cauchy-Schwarz inequality: \((\sum \limits _{i}{x_{i}^{2}})^{\frac {1}{2}}(\sum \limits _{i}{y_{i}^{2}})^{\frac {1}{2}}\geq \sum \limits _{i}x_{i}y_{i}\), with \(x_{i}=\sqrt {p_{i}}\) and \(y_{i}=\sqrt {p_{i}}C_{A|B_{1}B_{2}{\cdots } B_{N-1}}(|\psi _{i}\rangle )\). Due to the definition of the Tsallis-q entanglement and that gq(x) is a monotonically increasing function, we obtain the third inequality. Therefore, we have

$$ \begin{array}{@{}rcl@{}} &&{T_{q}^{\alpha}}_{A|B_{1}B_{2}{\cdots} B_{N-1}}(\rho)\\ &\geq& g_{q}^{\alpha}\left[{\sum}_{i}C^{2}(\rho_{AB_{i}})\right]\\ &\geq& {g^{\alpha}_{q}}(C^{2}_{AB_{1}})+h\cdot{g^{\alpha}_{q}}(C^{2}_{AB_{2}})+{\cdots} +h^{(N-3)}\cdot{g^{\alpha}_{q}}(C^{2}_{AB_{N-2}})+h^{(N-2)}\cdot{g_{q}}^{\alpha}(C^{2}_{AB_{N-1}})\\ &&+h^{(N-3)}\cdot \frac{\alpha}{2}{g_{q}}^{\alpha}(C^{2}_{AB_{N-1}})[{g_{q}}^{\alpha-1}(C^{2}_{AB_{N-2}})-{g_{q}}^{\alpha-1}(C^{2}_{AB_{N-1}})]\\ &&+\cdots+\frac{\alpha}{2}[{g_{q}}^{\alpha}(C^{2}_{AB_{2}})+\cdots+{g_{q}}^{\alpha}(C^{2}_{AB_{N-1}})]\cdot[{g_{q}}^{\alpha-1}(C^{2}_{AB_{1}})-{g_{q}}^{\alpha-1}(C^{2}_{A|B_{2}{\cdots} B_{N-1}})]\\ & \geq& {T_{q}}_{AB_{1}}^{\alpha}+h{T_{q}}_{AB_{2}}^{\alpha}+\cdots+h^{N-3}{T_{q}}_{AB_(N-2)}^{\alpha}+h^{N-2}{T_{q}}_{AB_(N-1)}^{\alpha}\\ &&+h^{(N-3)}\cdot \frac{\alpha}{2}{T_{q}}_{AB_{N-1}}^{\alpha}({T_{q}}_{AB_{N-2}}^{\alpha-1}-{T_{q}}_{AB_{N-1}}^{\alpha-1})\\ &&+\cdots+\frac{\alpha}{2}({T_{q}}_{AB_{2}}^{\alpha}+{\cdots} {T_{q}}_{AB_{N-1}}^{\alpha})\cdot({T_{q}}_{AB_{1}}^{\alpha-1}-{T_{q}}_{A|B_{2}{\cdots} B_{N-1}}^{\alpha-1}), \end{array} $$

where we have used the monogamy inequality in (20) for N-qubit states ρ to obtain the first inequality. By using the fact that gq(x) is a monotonically increasing function and the inequality (4), we get the second inequality. Since for any 2 ⊗ 2 quantum state \(\rho _{AB_{i}}\), \(T_{q}(\rho _{AB_{i}})=g_{q}\left [C^{2}(\rho _{AB_{i}})\right ]\), from (34) one gets the last inequality. □

Example 4

Let us consider again the three-qubit state |ψ〉 (11). From the definition of Tsallis-q entanglement, we have \({T_{q}}_{A|BC}=g_{q}[(2\lambda _{0}\sqrt {{\lambda _{2}^{2}}+{\lambda _{3}^{2}}+{\lambda _{4}^{2}}})^{2}]\), \({T_{q}}_{AB}=g_{q}(4{\lambda _{0}^{2}}{\lambda _{2}^{2}})\) and \({T_{q}}_{AC}=g_{q}(4{\lambda _{0}^{2}}{\lambda _{3}^{2}})\). Set \(\lambda _{0}=\lambda _{2}=\frac {1}{2}\), \(\lambda _{1}=\lambda _{3}=\lambda _{4}=\frac {\sqrt {6}}{6}\) and q = 2, one has \({T_{2}}_{A|BC}^{\alpha }=(\frac {7}{24})^{\alpha }\geq {T_{2}}_{AB}^{\alpha } +(2^{\alpha }-1){T_{2}}_{AC}^{\alpha } +\frac {\alpha }{2}{T_{2}}_{AC}({T_{2}}_{AB}^{\alpha -1}-{T_{2}}_{AC}^{\alpha -1}) =(\frac {1}{8})^{\alpha }+(2^{\alpha }-1)(0.08333)^{\alpha }+\frac {0.08333\alpha }{2} [(\frac {1}{8})^{(\alpha -1)}-(0.08333)^{(\alpha -1)}]\). While the formula in [16] is \({T_{2}}_{AB}^{\alpha } +(2^{\alpha }-1){T_{2}}_{AC}^{\alpha }=(\frac {1}{8})^{\alpha }+(2^{\alpha }-1)(0.08333)^{\alpha }\). One can see that our result is better than that in [16] for α ≥ 1, see Fig. 4.

Fig. 4
figure 4

The axis T represents the Tsallis-q of |ψ〉, which is a function of α. The solid blue line represents the lower bounds of Tsallis-q of |ψ〉 (q = 2) in Example 4. The dashed red line represents the lower bound from our enhangced monogamy inequalities. The solid black line represents the lower bound from the result in [16]

Full size image

6 Conclusion

Entanglement monogamy is a fundamental property of quantum multipartite states. The extension of the monogamy relation for multipartite entanglement is far more from trivial. We have explored the multipartite entanglement based on the monogamy of the α th-power of concurrence Cα (α ≥ 2), entanglement of formation Eα (\(\alpha \geq \sqrt 2\)), negativity \(N^{\alpha }_{c}\) (α ≥ 2) and Tsallis-q entanglement \(T^{\alpha }_{q}\) (α ≥ 1). We have proposed a new class of monogamy relations of multipartite entanglement for arbitrary quantum states, and showed that these new monogamy relations have larger lower bounds and tighter than the existing monogamy relations presented in [21, 27, 28, 31]. These tighter monogamy relations give rise to finer characterization of the entanglement distributions among the subsystems of a multipartite system. Our approach may be also applied to the study of monogamy properties related to other quantum correlations.