1 Introduction

The idea of teleportation was advanced by Bennett et al. in 1993 in their work [1] where an arbitrary single qubit quantum state was transferred by an entangled quantum channel with the support of a classical communication. After that several teleportation protocols utilizing the idea of Bennett et al. in [1] were advanced for the purpose of the transferring of different types of quantum states. These protocols utilize different types of entangled quantum resources like W-states [2, 3], GHZ-states [4,5,6], cluster states [7, 8], Bell states [9, 10]. These protocols are broadly divided in two categories, one is the category of perfect teleportation while the other is the class of imperfect teleportation in which are included approximate teleportation [11,12,13] and probabilistic teleportation schemes [14, 15]. The basic difference between the above two types is that in the former the teleportation is performed with certainty and with fidelity one while in the latter it is either that the transferred state differs somewhat from the state intended to be transferred or that there is a chance of failure of the protocol. There is an extensive literature on several aspects of teleportation. We note some of these in [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]. Experimental realization of some quantum teleportation processes are reported in [32,33,34,35,36].

As mentioned earlier several types of quantum states have been teleported by using appropriate quantum resources. In particular two qubit entangled states are teleported by following a number of protocols which appear in works like [6, 21,22,23,24,25,26]. In reference [6] a protocol was described in which a pure EPR state \(\alpha |01\rangle +\beta |10\rangle \) could be perfectly teleported by using GHZ-like states. In 2005, Cola et al. [21] presented a teleportation scheme for bipartite states with the help of an entangled pair and an additional qubit. After that Nandi et al. [23] demonstrated that a two-qubit state \(\alpha (|00\rangle +|11\rangle )+\beta (|01\rangle +|10\rangle )\) can also be teleported by using GHZ-like states. In 2010, Liu et al. [26] described a protocol of controlled teleportation for the teleportation of an arbitrary two-particle state with the help of a five-qubit cluster state where the five-qubit channel is shared between the sender, the receiver and the supervisor.

More than one task of state transfer by a single teleportation protocol was first introduced by Zha et al. in 2012 in their work [8] in which two parties exchange states in their respective possessions. It is a bidirectional teleportation protocol by which two parties Alice and Bob can exchange single qubits in their respective possessions using a five-qubit entangled channel under the supervision of Charlie. After that several bidirectional teleportation protocols have appeared in the literature [8, 27,28,29,30,31, 37]. In the year 2015, Choudhury et al. [28] described a bidirectional controlled teleportation scheme for arbitrary two-qubit states where Alice and Bob can exchange arbitrary two-qubit states bilaterally under a controller Charlie by use of a ten-qubit entangled channel. In the year 2016 Yang et al. [30] demonstrated a new protocol of asymmetric bidirectional quantum controlled teleportation by using a seven-qubit cluster state as quantum channel where Alice transmits an arbitrary single qubit to Bob and Bob teleports an arbitrary two qubit state to Alice via the controller Charlie. Also in the same year, Li et al. [37] demonstrated a protocol where Alice transmits an arbitrary two-qubit entangled state to Bob and Bob transmits an arbitrary single qubit state to Alice under the supervision of a third-party Charlie.

In a recent paper, Li et al. [38] discussed another multi-task teleportation protocol in which three parties could send three different single qubits in their respective possessions to three desired receivers with the help of a single entangled channel under the supervision of a third party. Our intention here is to show that it is possible to teleport three 2-qubit entangled Bell-like states in the possessions of three senders to three respective receivers by utilizing a single entangled state of ten qubits as quantum channel. The protocol has a controller. The entangled resource is shared by the receivers, the senders and the supervisor. The purpose of the current work is to perform the task with fewer resources, with a drawback that it only works for a limited class of states.

2 Simultaneous teleportation protocol

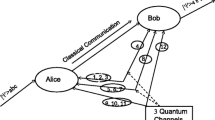
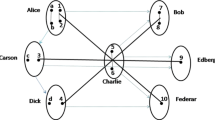
Our scheme is described as follows (Fig. 1). There are three parties Alice, Charlie and Edison who are in possessions of the two-qubit states \(|\psi \rangle _{p_{1}p_{2}} = a_{0}|00\rangle + a_{1}|11\rangle \), \(|\psi \rangle _{q_{1}q_{2}} = c_{0}|00\rangle + c_{1}|11\rangle \) and \(|\psi \rangle _{r_{1}r_{2}} = e_{0}|00\rangle + e_{1}|11\rangle \), respectively, where \(a_{0}\), \(a_{1}\), \(c_{0}\), \(c_{1}\), \(e_{0}\) and \(e_{1}\) are arbitrary complex numbers. These states need not be normalized. In abbreviation, we denote Alice’s, Charlie’s and Edison’s two-qubit particle \((p_{1}p_{2})\), \((q_{1}q_{2})\) and \((r_{1}r_{2})\) by p, q and r, respectively.

Fig. 1
figure 1

Schematic diagram of the simultaneous perfect teleportation protocol presented in this paper. Here a solid circles denote qubit, b bold black lines represent quantum sharing channel and c dotted lines with arrows stand for transferring classical information

Full size image

Alice wants to transmit her two-qubit state to Bob, Charlie wants to send his two-qubit state to David and Edison wants to send his two-qubit state to Ford. There is a supervisor Tom. For the purpose of teleportation a quantum channel consisting of ten qubits is shared between Alice, Charlie, Edison, Bob, David, Ford and Tom which is a cluster state having the form

$$\begin{aligned} |\psi \rangle _{AB_{1}B_{2}CD_{1}D_{2}TEF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}}[|0000000000\rangle + |1110001000\rangle + |0001111000\rangle \nonumber \\&+\, |1111110000\rangle +|0000001111\rangle \nonumber \\&+\, |1110000111\rangle + |0001110111\rangle + |1111111111\rangle ],\quad \end{aligned}$$
(1)

where the pairs of qubits \((B_{1},B_{2})\); \((D_{1},D_{2})\) and \((F_{1},F_{2})\) belong to Bob, David, and Ford, respectively, the qubits A, C and E belong, respectively, to Alice, Charlie and Edison and the qubit T belongs to the supervisor Tom.

The following composite state of sixteen qubits is expressed as

$$\begin{aligned} |\psi \rangle _{s}=|\psi \rangle _{p} \otimes |\psi \rangle _{q} \otimes |\psi \rangle _{r} \otimes |\psi \rangle _{AB_{1}B_{2}CD_{1}D_{2}TEF_{1}F_{2}}. \end{aligned}$$
(2)

To achieve the transfer of the states in the respective possessions of Alice, Charlie and Edison to the intended receivers Bob, David and Ford, respectively, Alice, Charlie and Edison perform measurements sequentially, each in the GHZ -states basis on the qubits in their possessions, that is, in the basis given by

$$\begin{aligned} |\phi ^\pm \rangle = \frac{|000\rangle \pm |111\rangle }{\sqrt{2}}~~~~~~~~~~|\eta ^\pm \rangle = \frac{|001\rangle \pm |110\rangle }{\sqrt{2}} \nonumber \\ \quad |\gamma ^\pm \rangle =\frac{|010\rangle \pm |101\rangle }{\sqrt{2}}~~~~~~~~~~|\delta ^\pm \rangle = \frac{|011\rangle \pm |100\rangle }{\sqrt{2}}. \end{aligned}$$
(3)

For that purpose Alice first performs her measurement and classically transmits to Charlie the information that her measurement is completed. Then Charlie performs his measurement and transmits classically to Edison the information that he has completed his measurement. Only the information that the measurement has been performed is sent, no measurement result is transmitted.

Then Alice, Charlie and Edison classically transmit their measurement results to the respective receivers Bob, David and Ford. Further Alice, Charlie and Edison also classically send their measurement results to the supervisor Tom. Tom then performs a von-Neumann measurement on his single qubit and transmits the result classically to each of the prospective receivers Bob, David and Ford. The corresponding measurement results of the senders Alice, Charlie and Edison and the supervisor Tom along with the outcome states after the measurements are displayed in the following Table 1. There are 128 possible combinations of the measurement results. To put them together in the single Table 1 we use the notation of [27] by which \(\pm _{p}\), \(\pm _{q}\) and \(\pm _{r}\) refer to measurements of Alice, Charlie and Edison, respectively, in the basis given by (3), \(\pm _{T}\) refer to the von-Neumann measurement of the supervisor Tom and they mean multiplications of ± signs. As illustrations, we write the cases included in the first row of the Table 1 explicitly in the following Table 2. Similar tabular breakups are applicable for each of the rest seven rows for more explicit expressions. Based on these classically transmitted information, Bob, David and Ford perform appropriate unitary operations on the states in their respective possessions to produce the states which were intended for sending. The protocol is thereby completed.

Some particular cases of the above protocol are illustrated below. We follow the symbols given in (3).

Table 1 Alice’s, Charlie’s, Edison’s and Tom’s measurement and the corresponding outcome states
Full size table
Table 2 Illustration of first row of Table 1
Full size table

If Alice’s measurement result is \(|\phi ^+\rangle \), then the other particles are collapsed into the state

$$\begin{aligned} |\Phi ^{1}\rangle _{qrB_{1}B_{2}CD_{1}D_{2}TEF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}} [~a_{0}|\psi \rangle _{q}\otimes |\psi \rangle _{r} \otimes (|000000000\rangle \nonumber \\&+\, |001111000\rangle + |000001111\rangle + |001110111\rangle )\nonumber \\&+\, ~a_{1}|\psi \rangle _{q}\otimes |\psi \rangle _{r} \otimes (|110001000\rangle \quad \nonumber \\&+\, |111110000\rangle + |110000111\rangle + |111111111\rangle )]. \end{aligned}$$
(4)

If Alice’s measurement result is \(|\phi ^-\rangle \), then the other particles are collapsed into the state

$$\begin{aligned} |\Phi ^{2}\rangle _{qrB_{1}B_{2}CD_{1}D_{2}TEF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}} [~a_{0}|\psi \rangle _{q}\otimes |\psi \rangle _{r} \otimes (|000000000\rangle \nonumber \\&+\, |001111000\rangle + |000001111\rangle + |001110111\rangle ) \nonumber \\&- ~a_{1}|\psi \rangle _{q}\otimes |\psi \rangle _{r} \otimes (|110001000\rangle \nonumber \\&+\, |111110000\rangle + |110000111\rangle + |111111111\rangle )].\qquad \end{aligned}$$
(5)

If Alice’s measurement result is \(|\eta ^+\rangle \), then the other particles are collapsed into the state

$$\begin{aligned} |\Phi ^{3}\rangle _{qrB_{1}B_{2}CD_{1}D_{2}TEF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}}[ ~a_{0}|\psi \rangle _{q}\otimes |\psi \rangle _{r} \otimes (|110001000\rangle + |111110000\rangle \nonumber \\&+\,|110000111\rangle + |111111111\rangle )\nonumber \\&+\,~a_{1}|\psi \rangle _{q}\otimes |\psi \rangle _{r} \otimes (|000000000\rangle \nonumber \\&+\, |001111000\rangle + |000001111\rangle + |001110111\rangle )]. \end{aligned}$$
(6)

If Alice’s measurement result is \(|\eta ^-\rangle \), then the other particles are collapsed into the state

$$\begin{aligned} |\Phi ^{4}\rangle _{qrB_{1}B_{2}CD_{1}D_{2}TEF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}}[~a_{0}|\psi \rangle _{q}\otimes |\psi \rangle _{r} \otimes (|110001000\rangle + |111110000\rangle \nonumber \\&+\,|110000111\rangle + |111111111\rangle )\nonumber \\&-~a_{1}|\psi \rangle _{q}\otimes |\psi \rangle _{r} \otimes (|000000000\rangle \nonumber \\&+\, |001111000\rangle + |000001111\rangle + |001110111\rangle )]. \end{aligned}$$
(7)

The other possibilities in the measurement of Alice do not appear in view of the fact that the combined state \(|\psi \rangle _{s}\) in (2) can be expressed as

$$\begin{aligned} |\psi \rangle _{s} = |\phi ^+\rangle ~|\Phi ^{1}\rangle ~ + ~ |\phi ^-\rangle ~|\Phi ^{2}\rangle ~ + ~ |\eta ^+\rangle ~|\Phi ^{3}\rangle ~ + ~ |\eta ^-\rangle ~|\Phi ^{4}\rangle , \end{aligned}$$

where \(|\phi ^\pm \rangle \) and \(|\eta ^\pm \rangle \) are given in (3) and \(|\Phi ^{1}\rangle \), \(|\Phi ^{2}\rangle \), \(|\Phi ^{3}\rangle \) and \(|\Phi ^{4}\rangle \) are given by the expressions in (4), (5), (6) and (7), respectively.

Let us assume that Alice’s measurement result is \(|\phi ^+\rangle \). Then Charlie has to perform Greenberger–Horne–Zeilinger (GHZ) state measurement on his three qubits.

If Charlie’s measurement result is \(|\phi ^+\rangle \), then the other particles are collapsed into the state

$$\begin{aligned} |\Psi ^{1}\rangle _{rB_{1}B_{2}D_{1}D_{2}TEF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}}[|\psi \rangle _{r}~a_{0}c_{0}(|00000000\rangle + |00001111\rangle )\nonumber \\&+\, |\psi \rangle _{r}~a_{0}c_{1}(|00111000\rangle + |00110111\rangle )\nonumber \\&+\, |\psi \rangle _{r}~ a_{1}c_{0}(|11001000\rangle + |11000111\rangle ) \nonumber \\&+\, |\psi \rangle _{r}~ a_{1}c_{1}(|11110000\rangle + |11111111\rangle )]. \end{aligned}$$
(8)

If Charlie’s measurement result is \(|\phi ^-\rangle \), then the other particles are collapsed into the state

$$\begin{aligned} |\Psi ^{2}\rangle _{rB_{1}B_{2}D_{1}D_{2}TEF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}}[|\psi \rangle _{r}~ a_{0}c_{0}(|00000000\rangle + |00001111\rangle )\nonumber \\&-\, |\psi \rangle _{r}~ a_{0}c_{1}(|00111000\rangle + |00110111\rangle )\nonumber \\&+\, |\psi \rangle _{r}~ a_{1}c_{0}(|11001000\rangle + |11000111\rangle )\nonumber \\&-\, |\psi \rangle _{r}~ a_{1}c_{1}(|11110000\rangle + |11111111\rangle )]. \end{aligned}$$
(9)

If Charlie’s measurement result is \(|\eta ^+\rangle \), then the other particles are collapsed into the state

$$\begin{aligned} |\Psi ^{3}\rangle _{rB_{1}B_{2}D_{1}D_{2}TEF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}}[|\psi \rangle _{r}~ a_{0}c_{0}(|00111000\rangle + |00110111\rangle )\nonumber \\&+\,|\psi \rangle _{r}~ a_{0}c_{1}(|00000000\rangle + |00001111\rangle )\nonumber \\&+\, |\psi \rangle _{r}~a_{1}c_{0}(|11110000\rangle + |11111111\rangle ) \nonumber \\&+\, |\psi \rangle _{r}~ a_{1}c_{1}(|11001000\rangle + |11000111\rangle )]. \end{aligned}$$
(10)

If Charlie’s measurement result is \(|\eta ^-\rangle \), then the other particles are collapsed into the state

$$\begin{aligned} |\Psi ^{4}\rangle _{rB_{1}B_{2}D_{1}D_{2}TEF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}}[|\psi \rangle _{r}~ a_{0}c_{0}(|00111000\rangle + |00110111\rangle )\nonumber \\&-\, |\psi \rangle _{r}~ a_{0}c_{1}(|00000000\rangle + |00001111\rangle )\nonumber \\&+\, |\psi \rangle _{r}~ a_{1}c_{0}(|11110000\rangle + |11111111\rangle ) \nonumber \\&-\, |\psi \rangle _{r}~ a_{1}c_{1}(|11001000\rangle + |11000111\rangle )]. \end{aligned}$$
(11)

The other possible measurement results of Charlie do not appear due to reasons similar to the case of Alice’s measurement, that is, since the combined state \(|\Phi ^{1}\rangle \) in (4) can be expressed as

$$\begin{aligned} |\Phi ^{1}\rangle = |\phi ^+\rangle ~|\Psi ^1\rangle ~ + ~ |\phi ^-\rangle ~|\Psi ^2\rangle ~ + ~ |\eta ^+\rangle ~|\Psi ^3\rangle ~ + ~ |\eta ^-\rangle ~|\Psi ^4\rangle , \end{aligned}$$

where \(|\phi ^\pm \rangle \) and \(|\eta ^\pm \rangle \) are given in (3) and \(|\Psi ^1\rangle \), \(|\Psi ^2\rangle \), \(|\Psi ^3\rangle \) and \(|\Psi ^4\rangle \) are given by the expressions in (8), (9), (10) and (11), respectively.

Now we assume that Charlie’s measurement result is \(|\phi ^+\rangle \). Then, Edison has to perform Greenberger–Horne–Zeilinger (GHZ) state measurement on his three qubits.

If Edison’s measurement result is \(|\phi ^+\rangle \), then the other particles are collapsed into the state

$$\begin{aligned} |\Omega ^{1}\rangle _{B_{1}B_{2}D_{1}D_{2}TF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}}[a_{0}c_{0}e_{0}|0000000\rangle +a_{0}c_{0}e_{1}|0000111\rangle \nonumber \\&+\, a_{0}c_{1}e_{0}|0011100\rangle + a_{0}c_{1}e_{1}|0011011\rangle \nonumber \\&+\, a_{1}c_{0}e_{0}|1100100\rangle +a_{1}c_{0}e_{1}|1100011\rangle \nonumber \\&+\, a_{1}c_{1}e_{0}|1111000\rangle + a_{1}c_{1}e_{1}|1111111\rangle ]. \end{aligned}$$
(12)

If Edison’s measurement result is \(|\phi ^-\rangle \), then the other particles are collapsed into the state

$$\begin{aligned} |\Omega ^{2}\rangle _{B_{1}B_{2}D_{1}D_{2}TF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}}[a_{0}c_{0}e_{0}|0000000\rangle -a_{0}c_{0}e_{1}|0000111\rangle \nonumber \\&+\, a_{0}c_{1}e_{0}|0011100\rangle - a_{0}c_{1}e_{1}|0011011\rangle \nonumber \\&+\, a_{1}c_{0}e_{0}|1100100\rangle -a_{1}c_{0}e_{1}|1100011\rangle \nonumber \\&+\,a_{1}c_{1}e_{0}|1111000\rangle - a_{1}c_{1}e_{1}|1111111\rangle ]. \end{aligned}$$
(13)

If Edison’s measurement result is \(|\eta ^+\rangle \), then the other particles are collapsed into the state

$$\begin{aligned} |\Omega ^{3}\rangle _{B_{1}B_{2}D_{1}D_{2}TF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}}[a_{0}c_{0}e_{0}|0000111\rangle +a_{0}c_{0}e_{1}|0000000\rangle \nonumber \\&+\, a_{0}c_{1}e_{0}|0011011\rangle + a_{0}c_{1}e_{1}|0011100\rangle \nonumber \\&+\, a_{1}c_{0}e_{0}|1100011\rangle +a_{1}c_{0}e_{1}|1100100\rangle \nonumber \\&+\, a_{1}c_{1}e_{0}|1111111\rangle + a_{1}c_{1}e_{1}|1111000\rangle ]. \end{aligned}$$
(14)

If Edison’s measurement result is \(|\eta ^-\rangle \), then the other particles are collapsed into the state

$$\begin{aligned} |\Omega ^{4}\rangle _{B_{1}B_{2}D_{1}D_{2}TF_{1}F_{2}}= & {} \frac{1}{2\sqrt{2}}[a_{0}c_{0}e_{0}|0000111\rangle -a_{0}c_{0}e_{1}|0000000\rangle \nonumber \\&+\, a_{0}c_{1}e_{0}|0011011\rangle - a_{0}c_{1}e_{1}|0011100\rangle \nonumber \\&+\, a_{1}c_{0}e_{0}|1100011\rangle - a_{1}c_{0}e_{1}|1100100\rangle \nonumber \\&+\, a_{1}c_{1}e_{0}|1111111\rangle -a_{1}c_{1}e_{1}|1111000\rangle ]. \end{aligned}$$
(15)

The other possible measurement results of Edison do not appear due to reasons similar to the case of Alice’s and Charlie’s measurement, that is,

$$\begin{aligned} |\Psi ^1\rangle = |\phi ^+\rangle ~|\Omega ^{1}\rangle ~ + ~ |\phi ^-\rangle ~|\Omega ^{2}\rangle ~ + ~ |\eta ^+\rangle ~|\Omega ^{3}\rangle ~ + ~ |\eta ^-\rangle ~|\Omega ^{4}\rangle , \end{aligned}$$

where \(|\phi ^\pm \rangle \) and \(|\eta ^\pm \rangle \) are given in (3) and \(|\Omega ^{1}\rangle \), \(|\Omega ^{2}\rangle \), \(|\Omega ^{3}\rangle \) and \(|\Omega ^{4}\rangle \) are given by the expressions in (12), (13), (14) and (15), respectively.

The senders Alice, Charlie and Edison transmit their measurement results to their intended receivers Bob, David and Ford, respectively, through classical channels. Further, Alice, Charlie and Edison individually send their results to Tom.

Finally, Tom performs von Neumann measurement on his qubit in the measurement basis

$$\begin{aligned} |\pm \rangle _{T} = \frac{1}{\sqrt{2}}(|0\rangle \pm |1\rangle )_{T}. \end{aligned}$$

Tom then sends his measurement result to Bob, David and Ford.

In Table 3 we describe the state obtained after Alice, Charlie and Edison perform their measurements sequentially on their respective three qubit states and after which the supervisor Tom measures on his single qubit state. In the last column of the Table 3 the corresponding unitary operations of Bob, David and Ford are specified. The above illustrates 8 out of 128 possible cases included in the protocol. These 8 cases are noted in Table 3 mentioned above. The rest of the possibilities can be similarly treated.

Table 3 Description of the protocol in 8 cases
Full size table

3 Discussion and conclusions

The creation of quantum entanglement is itself a challenging task. For that reason it may be that separate entangled resources are not readily available. So it is of interest to see whether multiple tasks of teleporting which would ordinarily require separate entangled resources can be performed through a single entangled channel. With this motivation we present a protocol whose main object is to establish that the multiple task of transferring three different Bell-like two-qubit states can be performed by three parties to three different receivers simultaneously through a quantum entangled channel of ten qubits. Particularly in a recent work by Wang et al. [39] it has been reported that ten-qubit entangled states can be prepared experimentally in a linear optical system. The efficiency of the protocol is given by the formula \(\eta = \frac{q_{s}}{q_{u} + b_{t}}\), where \(q_{s}\) is the number of qubits that consist of the quantum information to be shared, \(q_{u}\) is the number of the qubits that is used as the quantum channel (except for those chosen for security checking) and \(b_{t}\) is the number of classical bits transmitted [10, 40]. According to the above formula our efficiency is \(\eta = \frac{6}{27} =\frac{2}{9}\), while the efficiency \(\eta \) of the protocol Li et al. [38] is \(\frac{1}{14}\). There are also other ways of defining efficiencies of specific type protocols as, for instance, in the probabilistic teleportation processes, the chance of success, that is, the fraction of times the protocol is successful is a measure of efficiency of those protocols. In our present case, we use the definition of efficiency which is based on the requirement of resources. The more efficient is the protocol the more it can perform with less resources. Although the objectives of the present protocol and that of the multi-task protocol due to Li et al. [38] are different, from this point of view we can conclude that the present teleportation process performs with greater efficiency compared to the protocol of Li et al. [38]. The efficiency in our protocol is sufficiently increased due to the fact that only half of the states appearing in the basis are obtained in the measurements of all the three senders. Thus out of 1024 possible cases corresponding to the basis, 8 each in the measurements of the three senders and 2 in the measurement of the supervisor, only 128 appear as possible outcomes in our measurement. This is due to some symmetries involved in the problem itself. Consequently the requirement of classical bits for sending the measurement results are diminished leading to higher efficiency. There is no gain in terms of efficiency in restricting only to the teleportation of maximally entangled states. Further reduction in resources in the protocol is not possible. The protocol is symmetric in the arrangements of the senders and receivers. The same task of teleportation can be performed by arbitrarily fixing the orders of actions by the senders. But each order of measurements by the three senders will produce a separate protocol. This is why the preservation of the order of measurements by the senders is important for which they have to classically communicate between themselves appropriately. The protocol is performed in an integrated manner in which the three transfer of states cannot be separated nor any part of the ten-qubit channel can be utilized separately for the purpose of performing any one of these three tasks individually.