Dynamics of quantum correlation for a qubit–qutrit system in the presence of the dephasing environments

Abstract

We analytically study the dynamic behaviors of quantum correlation measured by three kinds of measures including quantum discord (QD), geometric quantum discord (GQD) and one-norm GQD for a qubit–qutrit system under the influence of dephasing environments with Ohmic-like spectral densities at nonzero temperature. It is shown that the similar evolution behaviors may be obtained for sub-Ohmic and Ohmic reservoirs. By properly choosing the system’s initial states and reservoir temperature, quantum correlation can take on some interesting results, such as the frozen and double sudden transition as well as the “revival” phenomenon, etc. Meanwhile, the remarkable similarities and differences among these correlation measures are also analyzed in detail and some significant results are presented. Our results provide some important information for the application of quantum correlation in hybrid qubit–qutrit systems in quantum information.

1 Introduction

To characterize and quantify quantum correlation is a basic and crucial problem in quantum information science, and lots of works have been carried out in this field [1, 2]. It has been shown that quantum correlation is more general and more fundamental than quantum entanglement because there exists other kind of nonclassical correlation other than entanglement that can speed up some computational tasks compared with classical computation even in some separable mixed states [3]. Such correlation may be quantified by a series of new measures of quantum correlation [4–9], among which QD [4] and GQD [5] have been proven to be the most popular measures. It has been discovered that QD is more robust against decoherence than entanglement [10] and takes zero for states with only classical correlation. In particular, QD exhibits the phenomena of sudden transition and sudden change for certain initial states in Markovian and non-Markovian environments [11–13]. This peculiar behavior has been investigated extensively from the point of view of theoretics and experiments for various systems [14–16]. QD is used to measure the quantum correlation between two subsystems. For a bipartite quantum system $\rho ^{AB}$, QD was originally defined as the difference between the quantum generalizations of two classically equivalent versions of the mutual information, namely [4]

$$\begin{aligned} D(\rho ^{AB})=I(\rho ^{AB})-C(\rho ^{AB}), \end{aligned}$$

(1)

where $I(\rho ^{AB})=S(\rho _{A})+S(\rho _{B})-S(\rho ^{AB})$ is the quantum mutual information and $C(\rho ^{AB})$ is the classical correlation, which can be expressed as $C(\rho ^{AB})=\max _{\{\pi ^B_i\}}[S(\rho _{A})-\sum _{i} p_iS(\rho _i)]$. Here, $S(\cdot )$ represents the von Neumann entropy, $\rho _{A}$ and $\rho _{B}$ are the reduced density operators of $\rho ^{AB}$, $\{\pi ^B_i\}$ is a set of von Neumann measurements performed on subsystem B and $\rho _i=\frac{\mathrm{Tr}_B\{(I_{A}\otimes \pi ^B_{i})\rho (I_{A}\otimes \pi ^B_{i})\}}{p_i}$ is the state of the subsystem A after obtaining the outcome i with the probability $p_i=\mathrm{Tr}[(I_{A}\otimes \pi ^B_{i})\rho (I_{A}\otimes \pi ^B_{i})].$

However, QD is difficult to calculate due to the complicated optimization involved. It has analytic expressions known only for certain classes of states [17, 18]. To overcome this difficulty, Dakić et al. [5] introduced the concept of GQD, which is defined as

$$\begin{aligned} D_{2}(\rho ^{AB})=\min _{\chi _{\in \varOmega _{0}}} \parallel \rho ^{AB}-\chi \parallel ^2, \end{aligned}$$

(2)

where $\Omega _{0}$ denotes the set of all zero discord states and $\parallel X\parallel ^2=\mathrm{tr}(X^{\dagger }X)$ is the usual Hilbert-Schmidt norm. GQD is analytical for general two-qubit states [19] as well as for arbitrary bipartite states [8, 20, 21].

For an arbitrary qutrit-qubit bipartite state, its Bloch form reads

$$\begin{aligned} \rho ^{AB}=\frac{1}{6}(I_6+\sum _{i=1}^3I_3\otimes x_i\sigma _i +\sum _{j=1}^8\lambda _j\otimes y_jI_2+\sum _{i=1}^3 \sum _{j=1}^8t_{ji}\lambda _j\otimes \sigma _i), \end{aligned}$$

(3)

where $\sigma _i$ and $\lambda _j$ are the traceless Hermitian generators of SU(2) and SU(3) group, respectively, satisfying $\mathrm{Tr}(\sigma _i\sigma _j)=\mathrm{Tr}(\lambda _i\lambda _j)=2\delta _{ij}$. The components of the local Bloch vectors $x_i=\mathrm{Tr}(\rho ^{AB}(I_3\otimes \sigma _i))$, $y_j=\mathrm{Tr}(\rho ^{AB}(\lambda _j\otimes I_2))$ and $t_{ji}=\mathrm{Tr}(\rho ^{AB}(\lambda _j\otimes \sigma _i))$. Then, the exact formula of GQD for qutrit-qubit states is given by [22]

$$\begin{aligned} D_{2}(\rho ^{AB})=\frac{1}{6}\parallel x\parallel ^2+\frac{1}{4}\parallel T\parallel ^2-k_\mathrm{max}, \end{aligned}$$

(4)

where $x=(x_1,x_2,x_3)^T$ and $T=(t_{ji})_{3\times 3}$ is the correlation matrix. $k_\mathrm{max}$ is the greatest eigenvalue of the matrix $\frac{xx^T}{6}+\frac{TT^T}{4}$. Here, the superscript T denotes transpose of vectors or matrices.

Just like QD, GQD has lately attracted wide attention too [23–27]. Unfortunately, it was recently pointed out that GQD cannot be regarded as a good measure for the quantumness of correlation, since it may increase under local operations on the unmeasured subsystem [28–30]. Nevertheless, this drawback can be completely overcome by the novel measurement of one-norm GQD [31, 32]. Interestingly, the similar freezing behavior in one-norm GQD was also found in [34]. While, another new phenomenon of environment-induced double sudden changes was first predicted in [34] and observed in recent experiment [35]. Similar to GQD, the one-norm GQD is defined as [32]

$$\begin{aligned} D_1(\rho )=\min _{\chi _{\in \Omega _{0}}}\parallel \rho ^{AB}-\chi \parallel _1, \end{aligned}$$

(5)

in the special case in which B is a qubit, which can be expressed as [33]

$$\begin{aligned} D_1(\rho )=\min _{\Pi _B}\parallel \rho ^{AB}-\Pi _B(\rho ^{AB})\parallel _1. \end{aligned}$$

(6)

Note that $\Vert F\Vert _{1}=\mathrm{Tr}{\sqrt{F^\dagger F}}$ is Schatten 1-norm, which can be rewritten as $\Vert F\Vert _1=\sum _{i}\sigma _{i}(F)$ where $\sigma _i(F)$ are the singular values of a matrix F. Here $\Pi _B(\rho ^{AB})=\sum _{i=0}^1{(I_A\otimes \Pi _i)\rho (I_A\otimes \Pi _i)}$ with $\Pi _i=U(\theta ,\varphi )|i> <i|U(\theta ,\varphi )^\dagger$ and $U(\theta ,\varphi )=\begin{pmatrix} \cos (\theta ) &{} -e^{-i\phi }\sin (\theta ) \\ e^{i\phi }\sin (\theta ) &{} \cos (\theta )\end{pmatrix}$, $\theta \in [0,\pi ], \varphi \in [0,2\pi ]$. $I_A$ denotes the identity operator for the subsystem A.

Most of the previous works consider only the two-qubit system. We know that the bipartite system with higher dimension can improve the efficiency of quantum information processing [36]. Hence, it is important to explore the behavior of quantum correlation in the systems with higher dimension. In Ref. [37], Girolami et al. discussed the ordering relationship between geometric discord and squared negativity in two qudit systems with arbitrary dimension. Under various dissipative channels, Wei et al. have studied the dynamics of GQD and found that all these dynamic evolutions do not lead to a sudden vanishing of GQD [27]. Recently, Guo et al. have investigated the dynamics and protection of quantum correlation of a qubit–qutrit system under local amplitude damping channels with finite temperature [38]. Motivated by these, in this paper we further study the dynamics of QD, GQD and one-norm GQD in a 2$\times$3 quantum system when dephasing noises with Ohmic-like spectral densities occur and some significant results are obtained.

The paper is organized as follows. In Sect. 2, we present the Hamiltonian of quantum system and give the general expression of GQD for qutrit-qubit in dephasing reservoirs. Then we discuss the dynamics behaviors of three correlation measures with Ohmic-like spectral densities in Sect. 3. Finally, in Sect. 4, a summary is given.

2 General expression of GQD for qutrit-qubit in bosonic reservoirs

Let us consider an open quantum system consisting of a qubit and a qutrit, each of which is coupled to its own bosonic thermal reservoir. The Hamiltonian of the system can be expressed as

$$\begin{aligned} H_\mathrm{total}=H_1+H_2, \end{aligned}$$

(7)

where $H_1$ and $H_2$ are the Hamiltonian of subsystem qubit and qutrit, respectively, which are given by

$$\begin{aligned} H_1= \omega _0\sigma _z+\sum _{k}\omega _{k_1}b^\dag _{k_1}b_{k_1}+2\sigma _z\sum _{k} (g^*_{k_1}b_{k_1}+g_{k_1}b^\dag _{k_1}), \end{aligned}$$

(8)

and

$$\begin{aligned} H_2=\frac{\omega _0}{2}\tau _z+\sum _{k}\omega _{k_2}b^\dag _{k_2}b_{k_2}+\tau _z\sum _{k} (g^*_{k_2}b_{k_2}+g_{k_2}b^\dag _{k_2}). \end{aligned}$$

(9)

Here $b^\dag _{k_i}$ and $b_{k_i}$ ($i=1, 2$) are the creation and annihilation operators of $k_i$th model for the two heat baths with frequencies $\omega _{k_i}$. $g_{k_i}$ is the coupling constant between the system and the $k_i$th harmonic oscillator of the heat bath. $\omega _0$ denotes the energy separation of qubit or qutrit. For simplicity, we assume that two heat baths are identical, the qubit-bath and qutrit-bath coupling constant are also equal, namely $\omega _{k_1}=\omega _{k_2}=\omega _{k}$, temperature $T_{A}=T_{B}=T$ and $g_{k_1}=g_{k_2}=g_{k}$. $\sigma _z$ and $\tau _z$ represent the operators of qubit and qutrit, their explicit forms are

$$\begin{aligned} \sigma _z={ \begin{pmatrix} 1 &{} 0\\ 0 &{} -1 \end{pmatrix},} \tau _z={ \begin{pmatrix} 1 &{}0 &{}0 \\ 0 &{}0 &{}0 \\ 0 &{}0 &{}-1 \\ \end{pmatrix}}. \end{aligned}$$

(10)

For studying the dynamics of quantum correlation for a qutrit-qubit system, here we consider one-parameter initial qutrit-qubit state described by

$$\begin{aligned} \rho _S(0)= & {} \frac{p}{2}(|00> <00|+|10> <10|+|21> <21|+|11> <11|+|10> <11|\nonumber \\&+\,|10> <10|) + \frac{1-2p}{2}(|20> <20|+|20> <01|\nonumber \\&+\,|01> <20|+|01> <01|),\nonumber \\ \end{aligned}$$

(11)

with $p\in [0,0.5]$ and $\rho _S(0)$ is separable only for $p=\frac{1}{3}$.

We assume that the system and the two heat baths are initially uncorrelated with the density operator i.e.,

$$\begin{aligned} \rho (0)=\rho _S(0)\otimes \rho ^1_B\otimes \rho ^2_B, \end{aligned}$$

(12)

where $\rho ^1_B=\exp [-\beta \sum _{k}\omega _{k_1}b^\dag _{k_1}b_{k_1}]/Z_{1}$ and $\rho ^2_B=\exp [-\beta \sum _{k}\omega _{k_2}b^\dag _{k_2}b_{k_2}]/Z_{2}$ are the density operators of the heat bath of qubit and qutrit with $Z_{i}=\prod _{k}(1-e^{-\beta \omega _{k}})^{-1}$ and $\beta =1/k_{B}T$ at the temperature T. Here, $k_{B}$ is the Boltzmann constant (for simplicity, we set $k_{B}=1$).

By making use of the unitary time evolution operator $U(t)=U_1(t)U_2(t)$ and tracing over the freedom of environment, the reduced density matrix of the qubit and qutrit at time t is governed by

$$\begin{aligned} \rho _S(t)=\mathrm{tr}_{B_1B_2}[U(t)\rho (0)U^\dag (t)], \end{aligned}$$

(13)

where $U_i(t)$ $(i=1,2)$ is the evolution operator of qubit (qutrit), which is given as follows (see the “Appendix” for detail derivations)

$$\begin{aligned} U_1(t)= & {} e^{-i\omega _0\sigma _zt}e^{-i\beta t\sum \limits _{k}\omega _{k}b^{\dag }_{k_{1}}b_{k_{1}}}e^{\sigma _z\sum \limits _{k} [b^{\dag }_{k_1}\alpha _{k_1}(t)-b_{k_1}\alpha _{k_1}^{*}(t)]-i\sigma ^2_zt\Delta (t)}, \end{aligned}$$

(14)

$$\begin{aligned} U_2(t)= & {} e^{-\frac{1}{2}i\omega _0\tau _zt}e^{-i\beta t\sum \limits _{k}\omega _{k_2}b^\dag _{k_2}b_{k_2}}e^{\frac{\tau _z}{2}\sum \limits _{k} [b^+_{k_2}\alpha _{k_2}(t)-b_{k_2}\alpha ^*_{k_2}(t)]-\frac{i}{4}\tau ^2_zt\Delta (t)}. \end{aligned}$$

(15)

In order to calculate GQD in what follows, it is useful to write the reduced density operator of the system in terms of basis $|mn\rangle$ ($m=-1, 0, 1$ and $n=0, 1$) as

$$\begin{aligned}{}[\rho _S(t)]_{mn,m'n'}=\langle mn|\mathrm{tr}_{B_1B_2}U(t)\rho (0)U^+(t)|m'n'\rangle , \end{aligned}$$

(16)

After straightforward calculations, above equation can be written as

$$\begin{aligned} \rho _S(t)=\left( \begin{array}{cccccc} \frac{p}{2}&{}0&{}0&{}0&{}0&{}0\\ 0 &{} \frac{1-2p}{2}&{}0 &{}0&{}\frac{1-2p}{2}e^{-it\Delta (t)}e^{-2\gamma (t)}&{}0\\ 0 &{} 0&{}\frac{p}{2}&{} \frac{p}{2}e^{i\omega _0t}e^{it\Delta (t)}e^{-\gamma (t)}&{}0&{}0\\ 0 &{} 0&{} \frac{p}{2}e^{-i\omega _0t}e^{-it\Delta (t)}e^{-\gamma (t)}&{} \frac{p}{2}&{}0&{}0\\ 0&{}\frac{1-2p}{2}e^{it\Delta (t)}e^{-2\gamma (t)}&{}0&{}0&{}\frac{1-2p}{2}&{}0\\ 0 &{} 0&{}0&{}0&{}0&{}\frac{p}{2}\\ \end{array} \right) , \end{aligned}$$

(17)

with

$$\begin{aligned} \Delta (t)= & {} \frac{1}{t}\sum \limits _k4|g_k|^2\frac{\sin (\omega _kt)-\omega _kt}{\omega ^2_k} \end{aligned}$$

(18)

$$\begin{aligned} \gamma (t)= & {} \sum \limits _k4|g_k|^2\frac{1-\cos (\omega _kt)}{\omega ^2_k}\coth \left( \frac{\beta \omega _k}{2}\right) . \end{aligned}$$

(19)

Thus, substituting Eq. (17) into Eqs. (3) and (4), we ultimately obtain the expression of GQD at time t

$$\begin{aligned} D[\rho _S(t)]=\frac{1}{4}[(1-3p)^2+2p^2e^{-2\gamma (t)}+(8p^2-8p+2)e^{-4\gamma (t)}-\eta _{\max }], \end{aligned}$$

(20)

where $\eta _{\max }=\max \{(1-2p)^2e^{-4\gamma (t)}+2p^2e^{-2\gamma (t)}, (1-2p)^2e^{-4\gamma (t)},(1-3p)^2\}$.

What is worth mentioning is that we will obtain the results about QD and one-norm GQD via numerical optimization of the von Neumann measurements. Taking one-norm GQD for example, the detail process of the computation about it can be obtained as follows. According to the definition of one-norm GQD, we have

$$\begin{aligned} \Pi _B(\rho _S(t))=\sum _{i=0}^1{(I_A\otimes \Pi _i)\rho _S(t) (I_A\otimes \Pi _i)}=\left( \begin{array}{cccccc} b_{11}&{}b_{12}&{}0&{}0&{}b_{15}&{}b_{16}\\ b_{21} &{} b_{22}&{}0 &{}0&{}b_{25}&{}b_{26}\\ 0 &{} 0&{}b_{33}&{} b_{34}&{}0&{}0\\ 0 &{} 0&{} b_{43}&{} b_{44}&{}0&{}0\\ b_{51}&{}b_{52}&{}0&{}0&{}b_{55}&{}b_{56}\\ b_{61} &{} b_{62}&{}0&{}0&{}b_{65}&{}b_{66}\\ \end{array} \right) , \end{aligned}$$

(21)

with $\Pi _0=\begin{pmatrix} \cos ^2(\theta ) &{} e^{-i\phi }\sin (\theta )\cos (\theta ) \\ e^{i\phi }\sin (\theta )\cos (\theta ) &{} \sin ^2(\theta )\end{pmatrix}$ and $\Pi _1=\begin{pmatrix} \sin ^2(\theta ) &{} -e^{-i\phi }\sin (\theta )\cos (\theta ) \\ -e^{i\phi }\sin (\theta )\cos (\theta ) &{} \cos ^2(\theta )\end{pmatrix}$. The diagonal elements of above equation are

$$\begin{aligned} b_{11}= & {} \frac{p}{2}+(1-3p)\sin ^2(\theta )\cos ^2(\theta ), b_{22}=\frac{1-2p}{2}-(1-3p)\sin ^2(\theta )\cos ^2(\theta ), \end{aligned}$$

(22)

$$\begin{aligned} b_{33}= & {} \frac{p}{2}+\frac{p}{8}e^{-i\phi }e^{-i\omega _0t}e^{-it\Delta (t)} e^{-\gamma (t)}\sin (4\theta )+\frac{p}{8}e^{i\phi }e^{i\omega _0t}e^{it\Delta (t)}e^{-\gamma (t)}\sin (4\theta ), \end{aligned}$$

(23)

$$\begin{aligned} b_{44}= & {} \frac{p}{2}-\frac{p}{8}e^{-i\phi }e^{-i\omega _0t}e^{-it\Delta (t)} e^{-\gamma (t)}\sin (4\theta )-\frac{p}{8}e^{i\phi }e^{i\omega _0t}e^{it\Delta (t)}e^{-\gamma (t)}\sin (4\theta ), \end{aligned}$$

(24)

$$\begin{aligned} b_{55}= & {} \frac{1-2p}{2}-(1-3p)\sin ^2(\theta )\cos ^2(\theta ), b_{66}=\frac{p}{2}+(1-3p)\sin ^2(\theta )\cos ^2(\theta ), \end{aligned}$$

(25)

and the non-diagonal elements

$$\begin{aligned} b_{12}= & {} -\frac{1-3p}{8}e^{-i\phi }\sin (4\theta ), b_{15}=\frac{1-2p}{8}e^{-i\phi }e^{-it\Delta (t)}e^{-2\gamma (t)}\sin (4\theta ), \end{aligned}$$

(26)

$$\begin{aligned} b_{16}= & {} (1-2p)e^{-2i\phi }e^{-it\Delta (t)}e^{-2\gamma (t)}\sin ^2(\theta )\cos ^2(\theta ),\nonumber \\ b_{25}= & {} (1-2p)e^{-it\Delta (t)}e^{-2\gamma (t)}\sin ^2(\theta )\cos ^2(\theta ), \end{aligned}$$

(27)

$$\begin{aligned} b_{26}= & {} -\frac{1-2p}{8}e^{-i\phi }e^{-it\Delta (t)}e^{-2\gamma (t)}\sin (4\theta ), b_{56}=\frac{1-3p}{8}e^{-i\phi }\sin (4\theta ), \end{aligned}$$

(28)

$$\begin{aligned} b_{34}= & {} pe^{-2i\phi }e^{-i\omega _0t}e^{-it\Delta (t)}e^{-\gamma (t)}\sin ^2(\theta )\cos ^2(\theta ) +pe^{i\omega _0t}e^{it\Delta (t)}e^{-\gamma (t)}\sin ^2(\theta )\cos ^2(\theta ), \end{aligned}$$

(29)

where $\rho _{ij}(t)=\rho _{ji}^{*}(t)$ for $i,j=1,\ldots ,6$.

If the initial parameters of quantum system and the phases $\theta \in [0,\pi ]$ and $\varphi \in [0,2\pi ]$ are given, we can evaluate the singular values of $\Vert \rho _S(t)-\Pi _B(\rho _S(t))\Vert _1$ using the expression of $\Pi _B(\rho _S(t))$ and the fact that $\Vert \rho _S(t)-\Pi _B(\rho _S(t))\Vert _1=\sum _{i}\sigma _{i}(\rho _S(t)-\Pi _B(\rho _S(t)))$ via singular value decomposition i.e. “svd” command of software Matlab. The optimal value of $\sum _{i}\sigma _{i}(\rho _S(t)-\Pi _B(\rho _S(t)))$ can be further obtained from the phases $\theta$ and $\varphi$ for given time. Thus, with these optimal values, the one-norm GQD can be achieved ultimately.

3 Quantum correlation for reservoirs with Ohmic-Like spectral densities

In this section, we will investigate correlation dynamics with the measures mentioned above by examining the effect of various parameters on them in the qutrit-qubit system. When the continuum limit of the bath modes is performed, $\sum \limits _k4|g_k|^2$ is replaced by $\int J(\omega )d\omega$ with $J(\omega )$ being the spectral density of the reservoir. In this situation, the decoherence function can be expressed as

$$\begin{aligned} \gamma (t)=\int \mathrm{d}\omega J(\omega )\omega ^{-2}\coth \left( \frac{\beta \omega }{2}\right) [1-\cos (\omega t)], \end{aligned}$$

(30)

We can consider any spectral density to characterize the environment. Without loss of generality, here we take the following Ohmic-like spectral density

$$\begin{aligned} J(\omega )=\lambda \Omega ^{1-s}\omega ^se^{-\frac{\omega }{\Omega }}, \end{aligned}$$

(31)

where $\lambda$ is a dimensionless coupling constant and $\Omega$ cuts off the spectral density at high frequencies. With the change of the bath parameter s, the environments vary from sub-Ohmic ones $(0<s<1)$ to Ohmic $(s=1)$ and super-Ohmic ones $(s>1)$ [26]. In the next section, we will employ the spectral density of Eq. (31) to discuss the time evolution of $D[\rho _S(t)]$ under reservoirs with different s.

Fig. 1

$D(\rho )$ as a function of $\Omega t$ with coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=0.5$ for various p

Fig. 2

$D_2(\rho )$ as a function of $\Omega t$ with coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=0.5$ for various p

3.1 Sub-ohmic reservoirs $(0<s<1)$

In this case, Eq. (30) can be calculated as

$$\begin{aligned} \gamma (t)= & {} \int \mathrm{d}\omega \lambda \Omega ^{1-s}\omega ^{s-2}e^{-\frac{\omega }{\Omega }} [1-\cos (\omega t)]\left[ 1+\frac{2e^{-\beta \omega }}{1-e^{-\beta \omega }}\right] \nonumber \\= & {} \frac{\lambda \Gamma (s)}{s-1}\left\{ 1-(1+\Omega ^2t^2)^{\frac{(1-s)}{2}} \cos \left[ (s-1)\arctan (\Omega t)\right] \right\} \nonumber \\&+\,\frac{2\lambda \Gamma (s)}{s-1}\sum \limits ^\infty _{m=1}(1+m\Omega \beta )^{1-s}\left\{ 1-\left[ 1+\left( \frac{\Omega t}{1+m\Omega \beta }\right) ^2\right] ^{\frac{(1-s)}{2}}\right. \nonumber \\&\left. \times \cos \left[ (s-1)\arctan \left( \frac{\Omega t}{1+m\Omega \beta }\right) \right] \right\} , \end{aligned}$$

(32)

and Eq. (18) can be calculated as

$$\begin{aligned} \Delta (t)= & {} -\frac{\lambda }{t}\Gamma (s-1)(1+\Omega ^2 t^2)^{-\frac{s}{2}}\left[ -\Omega t(1+\Omega ^2t^2)^{\frac{s}{2}}+s\Omega t(1+\Omega ^2t^2)^{\frac{s}{2}}\right. \nonumber \\&\left. +\,\Omega t\cos (s\arctan (\Omega t))-\sin (s\arctan (\Omega t))\right] , \end{aligned}$$

(33)

where $\Gamma (s)$ is the Gamma function. Bear in mind that the above expression of $\Delta (t)$ is suitable for the other cases of any $s\ne 1$. But $\Delta (t)=-\lambda \Omega t+\lambda \arctan (\Omega t)$ for ohmic reservoirs.

Fig. 3

$D_1(\rho )$ as a function of $\Omega t$ with coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=0.5$ for various p

Fig. 4

$D_2(\rho )$ as a function of $\Omega t$ with coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=1$ for various p

The effect of initial parameter p on the evolution of QD, GQD and one-norm GQD versus scalar time $\Omega t$ is plotted in Figs. 1, 2 and 3 with $s=0.5, \alpha =0.1$ and $\Omega \beta =1$. Figure 1a shows that quantum discord $D(\rho )$ decreases monotonously over time for $p=0$. However, with the increasing of p, we find that (1) there exists the phenomenon of sudden change (PSC) in quantum correlation $D(\rho )$; (2) the critical time corresponding to sudden change point (SCP) is prolonged gradually; (3) the amplitude of quantum correlation reduces by degrees and GQD decays more faster after SCP. Interestingly, when p is increased further, $D(\rho )$ will undergo an almost invariable process after decaying monotonously and before SCP, as seen in Fig. 1b. One should note that the behavior of $D(\rho )$ is similar to the case of $p=0$ when $p=1/3$, that is to say, $D(\rho )$ does not display the sudden change behavior (SCB) right now and the relevant figure of $D(\rho )$ is neglected for the sake of brevity. When p is more larger than 1 / 3, the SCB of quantum correlation reappears. The critical time is shorter and shorter with p. The maximal value of quantum correlation is increased piece by piece and the behavior as Fig. 1b disappears gradually over p. All these can be illustrated in Fig. 1c. When p is close to 0.5, Fig. 1d tells us that $D(\rho )$ will only decay monotonously to zero in the whole process.

Figure 2 depicts the performance of GQD based on the same parameters as Fig. 1 for various p. It is clear that the similar results can be found in Fig. 2a, b as Fig. 1a, b. However, Fig. 2c shows that the maximal value of quantum correlation is first decreased and then increased for larger p. Simultaneously, the same behavior as Fig. 2b is exhibited too and for comparatively large p such as $p=0.43$, quantum correlation owns more larger value before SCP. When p is close to 0.5, Fig. 2d shows that $D(\rho )$ remains nearly frozen for some time interval until the turning point time $t_{c}$ is reached, then it will decrease monotonously to zero as time goes on. $D(\rho )$ is frozen totally during the time interval $[0, t_{c}]$ for $p=0.5$. In addition, with the increase in p, the smaller freezing time and larger constant value of quantum correlation $D(\rho )$ will be obtained.

Fig. 5

$D(\rho )$ as a function of $\Omega t$ with coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=2$ for various p

Fig. 6

$D_2(\rho )$ versus $\Omega t$ with coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=2$ for various p

Fig. 7

$D_1(\rho )$ as a function of $\Omega t$ with coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=2$ for various p

Fig. 8

$D(\rho )$ as a function of $\Omega t$ with coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=3$ for various p

To see what happen for one-norm GQD, in Fig. 3, we plot its dynamics by employing the parameters used in both of previous figures for different p. As Figs. 1 and  2, provided $p=0$, $D_{1}(\rho )$ in Fig. 3a only behaves in a monotonously decreasing way. Interestingly, when p deviates from 0, $D_{1}(\rho )$ not only exhibits single SCB but also double sudden transition and freezing phenomenon during the time evolution for certain class of initial state (see Fig. 3a, b). One can see that, with the increase in p, the amplitude of $D_{1}(\rho )$ is reduced by degree and the freezing time is prolonged further. This can be very beneficial to quantum information and computation tasks that use discord as a physical resource due to its ability to withstand environmental decoherence and stay frozen for a period of time. Moreover, Fig. 3a, b show that the sudden transition points of one-norm GQD are dependent strongly on p. Nevertheless, once p exceeds 1 / 3, one-norm GQD presents single SCB, and the corresponding freezing time is cut down when p grows up, which is demonstrated in Fig. 3c. If $p=0.5$ is chosen, $D_{1}(\rho )$ ultimately ends up with zero in a monotonous way, which is exemplified by Fig. 3d and is consistent with QD of Fig. 1d for $p=0.5$.

At last, it is worth to stress that the outcomes of QD, GQD and one-norm GQD obtained above can be generalized to any other $0<s<1$ value.

3.2 Ohmic reservoir $(s=1)$

In this case, Eq. (30) is

$$\begin{aligned} \gamma (t)=\frac{1}{2}\lambda \left[ \ln (1+\Omega ^2t^2)+4\ln \Gamma \left( 1+\frac{1}{\Omega \beta }\right) -2\ln |\Gamma \left( 1+\frac{1}{\Omega \beta }+i\frac{t}{\beta }\right) |^2\right] , \end{aligned}$$

(34)

Since the dynamical behaviors of quantum correlation have high similarity with the case of sub-Ohmic reservoirs in this case, we here only consider the changes of GQD as a function of scalar time $\Omega t$ as described in Fig. 4 in which $\alpha =0.1$ and $\Omega \beta =1$. One can easily observe from Fig. 4 that the dynamics of $D_{2}(\rho )$ is highly similar with $0<s<1$, except that slower decrease and longer freezing time are presented in GQD than those of sub-Ohmic reservoirs.

3.3 Super-ohmic reservoirs $(s>1)$

In this case, the decoherence function can be worked out as

$$\begin{aligned} \gamma (t)= & {} \lambda \Gamma (s-1)\left\{ 1-(1+\Omega ^2t^2)^{\frac{1-s}{2}}\times \cos \left[ (s-1)\arctan (\Omega t)\right] \right\} \nonumber \\&+\,2\lambda \Gamma (s-1)\sum \limits ^\infty _{m=1}(1+m\Omega \beta )^{1-s} \nonumber \\&\times \left\{ 1-\left[ 1+\left( \frac{\Omega t}{1+m\Omega \beta }\right) ^2\right] ^{\frac{1-s}{2}}\times \cos \left[ (s-1)\arctan \left( \frac{\Omega t}{1+m\Omega \beta }\right) \right] \right\} ,\nonumber \\ \end{aligned}$$

(35)

Fig. 9

$D_2(\rho )$ as a function of $\Omega t$ with coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=3$ for various p

Fig. 10

$D_1(\rho )$ as a function of $\Omega t$ with coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=3$ for various p

Since both the reservoir temperature and parameter s play an important role in super-Ohmic case, the dynamics of GQD becomes much more complicated than above studied cases. Thus, it is difficult for us to give a general conclusion in the presence of super-Ohmic reservoirs. Here, we only reveal some interesting results at nonzero temperature $\Omega \beta =1$.

Figure 5 shows the plot of quantum discord $D(\rho )$ with parameter $s=2$, $\alpha =0.1$ for various p. What is the most important difference in Fig. 5 with Fig. 1 is $D(\rho )$ will exist in the form of a steady value in a long time instead of zero. Of course, the phenomena of sudden transition of $D(\rho )$ still can be observed in Fig. 5a for small p. But $D(\rho )$ shall decay monotonously to a steady value along with p being nearer to 1 / 3 as exhibited in Fig. 5b. In addition, we can find from Fig. 5c, d that $D(\rho )$ reveals the sudden transition behavior again in the regime $0.4<p<0.48$ and will keep a constant after the monotonous decay for $0.48\le p\le 0.5$.

Figure 6 indicates the change of GQD versus scalar time $\Omega t$ based on the parameters as Fig. 5 for various p. In fact, it is clear for us that the most of results in Fig. 6 are the same as Fig. 5 except that $D_{2}(\rho )$ possesses the freezed behavior in the initial time interval. However, in order to understand the difference of $D_{2}(\rho )$ between super-Ohmic reservoirs and Ohmic reservoirs better, a comparison is made. It is shown from Figs. 4 and 6 that the major difference between them is (1) $D_{2}(\rho )$ will eventually turn into a constant independent time t in Fig. 6. (2) When p is improved as indicated in Fig. 6b, $D_{2}(\rho )$ will decrease monotonously to a finite non-zero value instead of the behavior as Fig. 4b. (3) When p approaches to the value 0.5, $D(\rho )$ can be frozen with a longer time in Fig. 6d than in Fig. 4d.

One-norm GQD as a function of scalar time $\Omega t$ is displayed in Fig. 7 with different values of p. By comparing Figs. 7 with 3, one of the distinct features in Fig. 7 is disclosed that there is no the phenomena of double sudden transition of $D_{1}(\rho )$, although single DSC can still be observed for certain p. Moreover, $D_{1}(\rho )$ displays the longer-time-freezed behavior compared to $D_{2}(\rho )$ in Fig. 6d and can be maintained as a constant over time in the end.

Fig. 11

$D(\rho )$ versus $\Omega t$ for various p when coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=4.5$ are given

Fig. 12

$D_2(\rho )$ versus $\Omega t$ for various p when coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=4.5$ are given

In Figs. 8, 9 and 10, we examine the changes of three measures of quantum correlation in the super-Ohmic case of $s=3$ by taking parameter values $\Omega \beta =1$, $\alpha =0.1$ and different initial conditions into account. We can see from Fig. 8 that $D(\rho )$ will reach a stable value in a shorter time in comparison with Fig. 6 after going through a sudden change for small p. Nevertheless when $p=0.2$, PSC vanishes and $D(\rho )$ only decays asymptotically to a finite invariant value. It is interesting to note that once PSC dies away, it will be no longer appearance, which can be visualized from Fig. 8b, c. In addition, we find from Fig. 8b, c that $D(\rho )$ is of constant function in a short time, which is evidently different from Fig. 6. The plots of Figs. 9 and 10 correspond to the behavior of $D_{2}(\rho )$ and $D_{1}(\rho )$ versus $\Omega t$, respectively. It is noticed that the same results can be obtained in previous two figures of Figs. 9 and 10 as ones in Fig. 8. Howbeit, $D_{2}(\rho )$ and $D_{1}(\rho )$ can be kept constant permanently during the whole time evolution for p being close to 0.5 (see Figs. 9c, 10d). This is a rather surprising feature of non-classical correlation.

Fig. 13

$D_1(\rho )$ versus $\Omega t$ for various p when coupling constant $\alpha =0.1$, temperature $\beta \Omega =1$ and $s=4.5$ are given

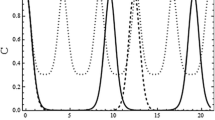
Figures 11, 12, 13 display some curious behaviors on the dynamics of quantum correlation as a function of the dimensionless parameter $\Omega t$ for $s=4.5$ and different initial states. In Fig. 11, we encounter a “revival” of $D(\rho )$ after it arrives at the minimal value $D_{\mathrm{min}}(\rho )$ for all p. As the time approaches infinity, a stable QD that bigger than $D_{\mathrm{min}}(\rho )$ can be obtained. Still, the PSC can be observed for some p in $D(\rho )$. Surprisingly, likewise there is “revival” phenomenon for quantum correlation $D_{2}(\rho )$ and $D_{1}(\rho )$ as showed in Figs. 12 and 13. In comparison with Fig. 11, some unique results are exhibited in Figs. 12 and 13. We notice from Figs. 12c and 13c that quantum correlation decays asymptotically to a stable value without the “revival” and sudden change phenomenon. Howbeit, Fig. 12d shows that GQD wins a constant after experiencing sudden change and “revival” behaviors. Figure 13d indicates that one-norm GQD shall keep a constant all the time when $p=0.5$. But, for p approaching 0.5, it changes in the way as Figs. 12c and 13c.

We would like to give a brief discussion on the Ohmic-like reservoirs. In the situation of super-Ohmic reservoirs with $\beta \Omega =1$ as well as $\alpha =0.1$, we find the performances of GQD are high similarity with the behavior of $s=1$ or $s=2$ for $1\le s<2$. It is also worth noting that for a great value of s, such as $s=6$, the time evolution of quantum correlation is similar to $s=1$ again. But GQD takes zero value very fast as the increase in s. Moreover, our result suggests that GQD is more robust at low temperature Ohmic-like environment. But, more complex dynamics behaviors on GQD will be involved by adjusting environment temperature in super-Ohmic cases. The details of the evolution for this case will be considered elsewhere. On the other hand, because of the numerical complex, a detail discussion on QD and one-norm GQD for any s ($s>1$) and environment temperature will also be considered elsewhere.

4 Summary

We have studied the dynamics of quantum correlation for two noninteracting qubit and qutrit system, each locally interacting with its own dephasing reservoir described by Ohmic-like spectral densities. To comprehend the quantum correlation preferably, three types of correlation measures have been adopted, which are QD, GQD and one-norm GQD. It has been shown that the dynamics of these quantum correlation measures in the reservoirs with sub-Ohmic densities are similar to the cases of Ohmic ones. Depending on the choose of initial parameter, QD and GQD may be frozen for a while or undergo an almost invariable process after decaying monotonously and before sudden change time for $0<s\le 1$. By contrast, one-norm GQD may also display the frozen phenomenon. In particular, it is interesting to find that one-norm GQD is able to take on the double sudden transition behavior for suitable initial parameters in sub-Ohmic environment. However, we have found that quantum correlation presents complicated dynamical behaviors in super-Ohmic reservoirs with $s>1$ when initial parameter and reservoir temperature are given. The results have demonstrated that depending on s, quantum correlation may exhibit some interesting phenomenon, such as the frozen or “revival” behavior, and stable value phenomenon in infinite time and so on. In the meantime, we have made a detailed comparison on the time evolution of QD, GQD and one-norm GQD and shown the similarities and differences among these correlation.

Appendix

Taking qutrit system as example, we give the following derivation. We first transform to the interaction picture, the Hamiltonian becomes $\tau _z\sum \limits _{k}(g^*_{k_2}b_{k_2}e^{-i\omega _{k_2}t}+g_{k_2}b^+_{k_2}e^{i\omega _{k_2}t})$. Following the idea of [39], we next calculate the time evolution operator $U^2_{I}(t)$ corresponding to $\tau _z\sum \limits _{k}(g^*_{k_2}b_{k_2}e^{-i\omega _{k_2}t}+g_{k_2}b^+_{k_2}e^{i\omega _{k_2}t})$. The Magnus expansion [40] tells us that $U^2_{I}(t)=\exp [\sum ^\infty _{i=1}A_i(t)]$ in which $A_1(t)=-i\int ^t_0\mathrm{d}t_1\tau _z\sum \limits _{k}(g^*_{k_2}b_{k_2}e^{-i\omega _{k_2}t_1}+g_{k_2}b^+_{k_2}e^{i\omega _{k_2}t_1})$, $A_2(t)=-\frac{1}{2}\int ^t_0\mathrm{d}t_1\int ^{t_1}_0\mathrm{d}t_2[\tau _z\sum \limits _{k}(g^*_{k_2}b_{k_2} e^{-i\omega _{k_2}t_1}+g_{k_2}b^+_{k_2}e^{i\omega _{k_2}t_1}),\tau _z\sum \limits _{k}(g^*_{k_2}b_{k_2} e^{-i\omega _{k_2}t_2}+g_{k_2}b^+_{k_2}e^{i\omega _{k_2}t_2})]$. It is straightforward to find $A_1(t)=\frac{\tau _z}{2}\sum \limits _{k}(b^+_{k_2}\alpha _{k_2}(t)-b_{k_2}\alpha ^*_{k_2}(t))$, where $\alpha _{k_2}(t)=\frac{2g_{k}(1-e^{i\omega _{k}t})}{\omega _{k}}$. Further using $[\tau _z\sum \limits _{k}(g^*_{k_2}b_{k_2}e^{-i\omega _{k_2}t_1}+g_{k_2}b^+_{k_2}e^{i\omega _{k_2}t_1}), \tau _z\sum \limits _{k}(g^*_{k_2}b_{k_2}e^{-i\omega _{k_2}t_2}+g_{k_2}b^+_{k_2}e^{i\omega _{k_2}t_2})] =-2i\tau ^2_z\sum \limits _{k}| g_{k}|^2\sin [\omega _{k}(t_1-t_2)]$, we obtain $A_2(t)=\frac{1}{2}\int ^t_0\mathrm{d}t_1\int ^{t_1}_0\mathrm{d}t_22i\tau ^2_z\sum \limits _{k}| g_{k}|^2\sin [\omega _{k}(t_1-t_2)]=-\frac{1}{4}\tau ^2_zt\Delta (t)$. Since this is a c-number, the higher-order terms in the Magnus expansion are all zero. The exact unitary time evolution operator is hence found, i.e., $U_2(t)=e^{-\frac{1}{2}i\omega _0\tau _zt}e^{-i(\sum _{k}\omega _{k_2}b^\dag _{k_2}b_{k_2})t}U^2_I(t)$, where $U^2_I(t)=exp\{\frac{1}{2}\tau _z\sum \limits _{k}[b^+_{k_2}\alpha _{k_2} (t)-b_{k_2}\alpha ^*_{k_2}(t)]-\frac{1}{4}\tau ^2t\Delta (t)\}$. In the same way, we can get $U_1(t)$.