1 Introduction

As a kind of quantum correlations, quantum entanglement plays a central role in quantum information processing (QIP) and has attracted considerable attention [1]. However, recent investigations reveal that the entanglement is not the only type of quantum correlations and there exist quantum tasks that display quantum advantages without entanglement [2–4]. Therefore, recent research has explored nonclassical correlation other than entanglement [5–12]. Quantum discord defined as the difference between quantum mutual information and classical correlation [5] is supposed to characterize all of nonclassical correlations in a bipartite state, including entanglement. It is suggested that the quantum discord, rather than entanglement, is responsible for the efficiency of a quantum computer, which is confirmed both theoretically and experimentally [13, 14]. Therefore, quantum discord could be a new resource for quantum information processing.

However, real quantum systems are never completely isolated from the environment. The unavoidable coupling of the quantum system with the environment will lead to quantum decoherence. So, quantum coherence protecting is crucially important in effective QIP. Decoherence suppression may be accomplished in a number of ways, including quantum error correction [15, 16], decoherence-free subspace [17, 18], and dynamical decoupling [19, 20]. Recently, the application of weak measurement and measurement reversal has been suggested as a practically implementable method to suppress amplitude damping decoherence for a single qubit [21–23]. For the case of two-qubit, Kim et al. experimentally demonstrate the protection of entanglement from amplitude damping decoherence using weak measurement and measurement reversal [24] and this idea has also been extended to protect the entanglement of two-qutrit system [25]. However, their discussion is mainly limited to a special case of zero-temperature environment. In ref [26], the authors have studied how weak measurement can be used for entanglement protection of two qubits interacting with environment at finite temperature. In our previous studies, we find that the qubit–qutrit system possess rich properties of quantum correlations under various decoherent channels [27] and the research dealing with protecting quantum correlations of a qubit–qutrit system is scarce. Therefore, in this paper, concerning with a qubit–qutrit system exposed in the nonzero temperature environment, we study the dynamics and the protection of quantum correlations, including entanglement and quantum discord, in such a situation based on weak measurement and measurement reversal.

This paper is organized as follows. In Sect. 2, we give the definition of quantum correlations, including negativity and quantum discord. In Sects. 3 and 4, the evolution and protection of the quantum correlations of the qubit–qutrit system by weak measurement and measurement reversal are investigated. Finally, we conclude in Sect. 5.

2 Quantum correlations

In order to quantify the quantum correlations of the qubit–qutrit system, we use two types of measures including negativity and geometric measure of quantum discord. It is proved that for an arbitrary mixed state of \(2\otimes 2\) or \(2\otimes 3\) system, its entanglement can well be characterized by its negativity [28]

$$\begin{aligned} N(\rho _{AB})=\sum _i|\mu _i|, \end{aligned}$$
(1)

where \(\mu _i\) are the negative eigenvalues of \(\rho ^{T_A}\), and \(T_A\) denotes the partial transpose with respect to the first system. If \( N(\rho _{AB})>0\), then the bipartite state is entangled.

On the other hand, for an arbitrary bipartite state \(\rho _{AB}\), the total correlations between two subsystems are expressed by quantum mutual information [29]

$$\begin{aligned} \mathcal {L}(\rho _{AB})=S(\rho _{A})+S(\rho _{B})-S(\rho _{AB}), \end{aligned}$$
(2)

where \(S(\rho )=Tr(\rho \log _2\rho )\) is the von Neumann entropy and \(\rho _{A(B)}=Tr_{B(A)}\rho \) is the reduced density matrix by tracing out the system \(B(A)\). The classical correlation for subsystems \(A\) and \(B\) can be defined as

$$\begin{aligned} \mathcal {C}(\rho _{AB})=\max _{\{B_k\}}\mathcal {L}(\rho _{AB}|\{B_k\}), \end{aligned}$$
(3)

where \(\mathcal {L}(\rho _{AB}|\{B_k\})\) is a variant of quantum mutual information based on a given measurement basis \(\{B_k\}\) on the system \(B\) as follows:

$$\begin{aligned} \mathcal {L}(\rho _{AB}|\{B_k\})=S(\rho _A)-\sum _kp_kS(\rho _k), \end{aligned}$$
(4)

where \(\rho _k=\frac{1}{p_k}(I_A\otimes B_k)\rho _{AB}(I_A\otimes B_k)\) is the post-measurement state of \(A\) after obtaining the outcome \(k\) on \(B\) with the probability \(p_k=Tr[(I_A\otimes B_k)\rho _{AB}(I_A\otimes B_k)]\). The quantum correlation described by quantum discord can be defined as [5]

$$\begin{aligned} D(\rho _{AB})=\mathcal {L}(\rho _{AB})-\mathcal {C}(\rho _{AB}). \end{aligned}$$
(5)

However, since the calculation of classical correlation in Eq. (3) involves a potentially complex optimization process, there exists no general analytical expression of quantum discord even for the simplest case of two-qubit states. To avoid this difficulty, using a geometric method, Dakic et al. give a geometric measure of quantum discord (GMQD) in a bipartite state as the distance of the state from the closest zero-discord state [30]

$$\begin{aligned} D_g(\rho _{AB})=\min _{\chi \in \Omega _0}\Vert \rho _{AB}-\chi \Vert ^2, \end{aligned}$$
(6)

where \(\Omega _0\) is the set of all zero-discord states and \(\Vert X\Vert ^2=Tr(X^\dagger X)\) is the usual Hilbert–Schmidt norm. It is possible to obtain an explicit expression of GMQD for an arbitrary bipartite state of \(2\otimes n\) dimensions [31]. Therefore, for a general \(2\otimes 3\) bipartite state,

$$\begin{aligned} \rho _{AB}&= \frac{1}{6}\left( I_6+\sum _{i=1}^3x_i\sigma _i\otimes I_3+\sum _{j=1}^8y_jI_2\otimes \lambda _j\right. \nonumber \\&\left. +\sum _{i=1}^3\sum _{j=1}^8t_{ij}\sigma _i\otimes \lambda _j\right) \!, \end{aligned}$$
(7)

where \(\sigma _{i=1..3}\) and \(\lambda _{j=1..8}\) are the generators of SU(2) and SU(3) group satisfying the relations \(Tr(\sigma _i\sigma _j)=Tr(\lambda _i\lambda _j)=2\delta _{ij}\). Then, the exact formula of GMQD for qubit–qutrit states is given by

$$\begin{aligned} D_g(\rho _{AB})=\frac{1}{6}||\mathbf x ||^2+\frac{1}{4}||T||^2-k_{\max }, \end{aligned}$$
(8)

where the matrix \(T=(t_{ij})_{3\times 3}\) is the correlation matrix, \(||\mathbf x ||^2=Tr(\mathbf x \mathbf x ^\dagger )\) with Bloch vector \(\mathbf x =(x_1,x_2,x_3)^t\), and \(k_{\max }\) is the largest eigenvalues of the matrix \(\frac{\mathbf{xx }^t}{6}+\frac{TT^t}{4}\). The elements of the correlation matrix and Bloch vector can be obtained from the following relations: \(x_i=Tr(\rho _{AB}\sigma _i\otimes I_3)\) and \(t_{ij}=Tr(\rho _{AB}\sigma _i\otimes \lambda _j)\). In this paper, in order to make the maximum of negativity and GMQD equal to 1 for the maximally entangled state, the values of negativity and GMQD have been enlarged 2 times in the following.

3 Physical model and dynamics process

The dynamics of a qubit interacting with a dissipative environment at zero temperature can be described by the following amplitude damping (AD) channel

$$\begin{aligned} \rho (t)=\sum _{i=0}^1E_i\rho (0)E_i^\dagger \end{aligned}$$
(9)

with

$$\begin{aligned} E_0=\left( {\begin{array}{*{20}c} 1&{}\quad 0 \\ 0 &{}\quad \sqrt{1-D} \\ \end{array}} \right) ,\quad E_1=\left( {\begin{array}{*{20}c} 0&{}\quad \sqrt{D} \\ 0 &{}\quad 0 \\ \end{array}} \right) \!, \end{aligned}$$
(10)

where \(D\) represents the transition probability from the excited state \(|1\rangle \) to the ground state \(|0\rangle \). However, the environment temperature cannot be regarded as zero in practice. When it is nonzero, the situation turns out to be more complicated since except for the loss of excitations, the system can gain excitations by interacting with the environment. This process can be characterized by the generalized amplitude damping (GAD). Suppose the probability of losing the excitation \(|1\rangle \) is \(r\), then the probability of gaining the excitation is \(1-r\). Therefore, the action of the GAD noise can be written as

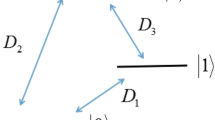
$$\begin{aligned} E_0&= \sqrt{r}\left( {\begin{array}{*{20}c} 1&{}\quad 0 \\ 0 &{}\quad \sqrt{1-D} \\ \end{array}} \right) ,\quad E_1=\sqrt{r}\left( {\begin{array}{*{20}c} 0&{}\quad \sqrt{D} \\ 0 &{}\quad 0 \\ \end{array}} \right) ,\nonumber \\ E_2&= \sqrt{1-r}\left( {\begin{array}{*{20}c} \sqrt{1-D}&{}\quad 0 \\ 0 &{}\quad 1 \\ \end{array}} \right) , E_3=\sqrt{1-r}\left( {\begin{array}{*{20}c} 0&{}\quad 0 \\ \sqrt{D} &{}\quad 0 \\ \end{array}} \right) . \end{aligned}$$
(11)

For qutrits, we consider a qutrit system of V-configuration in this paper. We note the lower level as \(|0\rangle \) and the two upper levels as \(|1\rangle \) and \(|2\rangle \). Then, following the approach discussed above, the GAD channel at finite temperature can be obtained as

$$\begin{aligned} F_0&= \quad \sqrt{r}\left( {\begin{array}{*{20}c} 1&{}\quad 0&{}\quad 0 \\ 0 &{}\quad \sqrt{1-D_1}&{}\quad 0 \\ 0 &{}\quad 0&{}\quad \sqrt{1-D_2} \\ \end{array}} \right) \!,\nonumber \\ F_1&= \sqrt{r}\left( {\begin{array}{*{20}c} 0&{}\quad \sqrt{D_1}&{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array}} \right) ,\nonumber \\ F_2&= \sqrt{r}\left( {\begin{array}{*{20}c} 0&{}\quad 0 &{}\quad \sqrt{D_2} \\ 0 &{}\quad 0&{}\quad 0 \\ 0 &{}\quad 0&{}\quad 0 \\ \end{array}} \right) ,\nonumber \\ F_3&= \sqrt{1-r}\left( {\begin{array}{*{20}c} \sqrt{1-D_1-D_2}&{}\quad 0&{}\quad 0 \\ 0 &{}\quad 0&{}\quad 0 \\ 0 &{}\quad 0&{}\quad 0 \\ \end{array}} \right) ,\nonumber \\ F_4&= \sqrt{1-r}\left( {\begin{array}{*{20}c} 0&{}\quad 0&{}\quad 0 \\ \sqrt{D_1} &{}\quad 0&{}\quad 0 \\ 0 &{}\quad 0&{}\quad 0 \\ \end{array}} \right) ,\nonumber \\ F_5&= \sqrt{1-r}\left( {\begin{array}{*{20}c} 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0 \\ \sqrt{D_2} &{}\quad 0&{}\quad 0 \\ \end{array}} \right) , \end{aligned}$$
(12)

where \(D_1\) and \(D_2\) are the transition probabilities from \(|1\rangle \) and \(|2\rangle \) to \(|0\rangle \), respectively.

Let us consider a qubit–qutrit system interacting independently with the local GAD channels. The evolved state of such a system can be described by

$$\begin{aligned} \rho _{AB}(t)=\sum _{i=0}^3\sum _{j=0}^5F_j^BE_i^A\rho _{AB}(0) E_i^{A\dagger }F_j^{B\dagger }, \end{aligned}$$
(13)

where \(\rho _{AB}(0)\) is the initial state of the qubit–qutrit system; here we consider one-parameter class of qubit–qutrit state described by

$$\begin{aligned} \rho _{AB}(0)&= \frac{\alpha }{2}(|00\rangle \langle 00| +|01\rangle \langle 01|+|00\rangle \langle 12|+|11\rangle \langle 11|\nonumber \\&+|12\rangle \langle 12|+|12\rangle \langle 00|) +\frac{1-2\alpha }{2}(|02\rangle \langle 02|\nonumber \\&+|02\rangle \langle 10|+|10\rangle \langle 02|+|10\rangle \langle 10|), \end{aligned}$$
(14)

with \(0\le \alpha \le 1/2\). After the GAD decoherence, we can calculate the negativity and GMQD by solving the density matrix of the qubit–qutrit system. However, the general analytic expressions of the nonzero elements of the density matrix are too complicated to present, so we will give the numerical results in the discussion below.

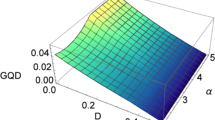
In Fig. 1, the entanglement and GMQD versus \(D\) and \(r\) are plotted when the qubit–qutrit system is initially in the maximally entangled state \(|\psi _{AB}\rangle =1/\sqrt{2}(|02\rangle +|10\rangle )\). One can observe that when the temperature is zero, i.e., \(r=1\), both the entanglement and GMQD decay asymptotically with increasing \(D\). However, as \(r\) increases, the entanglement suffers sudden death, but the GMQD is still nonzero. This indicates that under the influence of the temperature, the qubit–qutrit system becomes fully separable, but the quantum correlations still persist. In addition, a sudden change is found in the dynamics of the GMQD, and the critical point where the change emerges depends on the value of \(r\). In Fig. 2, we give the plot of the dynamics of entanglement and GMQD for different initial states characterized by the parameter \(\alpha \) at finite temperature. It can be seen that the entanglement sudden death always exists and the smaller the initial degree of entanglement, the longer the entanglement remains zero. One interesting observation is that for a fixed value of \(\alpha \), the GMQD and entanglement show the opposite behaviors as \(D\) increases, that is, the GMQD can be generated in the decoherence process but the entanglement always decays to zero with increasing \(D\). Therefore, the GMQD is more robust than entanglement under the decoherence with finite temperature.

Fig. 1
figure 1

Entanglement and GMQD are plotted as a function of \(D\) and \(r\) for the maximally entangled state (\(\alpha =0\)). The parameters are chosen to be \(D_1=D_2=0.5D\)

Full size image
Fig. 2
figure 2

Entanglement and GMQD are plotted as a function of \(D\) and \(\alpha \). The parameters are chosen to be \(D_1=D_2=0.5D\) and \(r=0.8\)

Full size image

4 Protecting of entanglement and GMQD

4.1 Weak measurement

A null-result weak measurement that we considered is the POVM measurement or partial-collapse measurement originally discussed in refs [32, 33]. Whenever there is an excitation in the environment, we discard the result. This post-selection removes the term \(\sqrt{p}|0\rangle _S|1\rangle _E\) from the state map. For the qubit, the weak measurement can be written as a nonunitary quantum operation [24]

$$\begin{aligned} M_{w1}&= \left( {\begin{array}{*{20}c} 1&{}\quad 0 \\ 0 &{}\quad \sqrt{1-p} \\ \end{array}} \right) , \end{aligned}$$
(15)

where \(0\le p\le 1\) is the weak measurement strength for the qubit. Similarly, it is easy to construct the weak measurement for the qutrit [25]

$$\begin{aligned} M_{w2}= \left( {\begin{array}{*{20}c} 1&{}\quad 0&{}0 \\ 0 &{}\quad \sqrt{1-p_1}&{}\quad 0 \\ 0 &{}\quad 0&{}\quad \sqrt{1-p_2} \\ \end{array}} \right) , \end{aligned}$$
(16)

where \(0\le p_{1(2)}\le 1\) are the weak measurement strengths for the qutrit. As the computational state \(|0\rangle \) does not couple to the environment, the qubit–qutrit system after the weak measurement \(M_w=M_{w1}\otimes M_{w2}\) is less vulnerable to decoherence.

4.2 Measurement reversal

After a weak measurement, the measured state could be recovered by a proper quantum measurement reversal operation [33, 34]. The measurement reversal operators for qubit and qutrit quantum systems are [24, 25]

$$\begin{aligned} M_{r1}&= \left( {\begin{array}{*{20}c} \sqrt{1-p_r}&{} 0 \\ 0 &{} 1 \\ \end{array}} \right) ,\nonumber \\ M_{r2}&= \left( {\begin{array}{*{20}c} \sqrt{(1-p_{r1})(1-p_{r2})}&{} 0&{}0 \\ 0 &{} \sqrt{1-p_{r1}} &{}0 \\ 0 &{} 0 &{}\sqrt{1-p_{r2}} \\ \end{array}} \right) , \end{aligned}$$
(17)

where \(0\le p_{r}\le 1\) and \(0\le p_{r_1,r_2}\le 1\) are the strengths of the measurement reversals for the qubit and the qutrit, respectively. For simplicity, we assume that the qubit and the qutrit have the same weak measurement strengths and the measurement reversal strengths, i.e., \(p_1=p_2=p\) and \(p_{r_1}=p_{r_2}=p_r\). In order to gain as much quantum correlations as possible, we will choose the optimal measurement reversal strength which gives the maximum amount of entanglement and GMQD.

4.3 Protecting entanglement and GMQD by weak measurement and measurement reversal

Now we turn to discuss the protection of the quantum correlations of the qubit–qutrit system using weak measurement and measurement reversal. Firstly, before the system undergoes the GAD channel, we perform a weak measurement on the qubit and qutrit, respectively. Then, the qubit and the qutrit go through the decoherent channel, and finally the measurement reversals are carried out on the qubit and the qutrit. In Fig. 3, under the condition of optimal measurement reversal, the dynamics of entanglement and GMQD for the initial maximally entangled state (\(\alpha =0\)) at zero temperature are plotted. Our results show that the protection of the quantum correlations is independent of the weak measurement, only the measurement reversal affects the entanglement and GMQD. Comparing with the dynamics without protection, we can observe that the decays of entanglement and GMQD can be suppressed by the measurement reversal to a great extent. However, for other initial states, such as \(\alpha =0.25\), the optimal values of entanglement and GMQD depend on the weak measurement. In Fig. 4, we give the plot of the dynamics of entanglement and GMQD for different values of weak measurement strengths under the optimal measurement reversal. One can observe that when there is no weak measurement (\(p=0\)), the entanglement still suffers sudden death and the death time is scarcely prolonged. This indicates that the protection of entanglement with only measurement reversal is much less efficient. But as weak measurement strength \(p\) increases, the death time of entanglement becomes longer, and when \(p\) is large enough, the sudden death is circumvented. Meanwhile, with regard to the evolution of GMQD, we find that the enhancement of GMQD by the weak measurement and measurement reversal is more evident and the phenomenon of sudden change can be eliminated in the process of protection. Therefore, only the measurement reversal cooperated with the weak measurement can protect the quantum correlations of the qubit–qutrit system from decoherence. In addition, we also find that the enhancement of entanglement at \(D=0\) is very weak, which is in great contrast with the evolution of GMQD, since as \(p\) increases the value of GMQD at \(D=0\) is strengthened.

Fig. 3
figure 3

Entanglement and GMQD versus amplitude damping parameter \(D\) under the protection protocol at zero temperature. The parameters are chosen to be \(D_1=D_2=0.5D\), \(r=1\), and \(\alpha =0\). The dotted lines are for the unprotected state (\(p=p_1=p_2=0, p_r=p_{r1}=p_{r2}=0\))

Full size image
Fig. 4
figure 4

Entanglement and GMQD versus amplitude damping parameter \(D\) for different strengths of weak measurement under the protection protocol at zero temperature. The parameters are chosen to be \(D_1=D_2=0.5D\), \(r=1\), and \(\alpha =0.25\)

Full size image

Next, we consider the protection of the quantum correlations dynamics at finite temperature. In Fig. 5, for the initial state \(\alpha =0.5\), the entanglement and GMQD versus amplitude damping parameter \(D\) for different strengths of weak measurement at finite temperature are plotted. It is shown that comparing with the unprotected case, the protections of entanglement and GMQD by weak measurement and measurement reversal are efficient only for small values of \(D\). The decays of entanglement and GMQD are enhanced with increasing \(p\) in most regions of \(D\). Therefore, the weak measurement and measurement reversal fail to protect the quantum correlations from decoherence induced by the decoherence channel with finite temperature. Taking into account the difference between the entanglement and GMQD, we find that the GMQD has larger regions of \(D\) where the protection is successful. That is to say, under certain conditions, we can realize the protection of GMQD by weak measurement and measurement reversal, but for the entanglement, the protection is invalid. Figure 6 shows the above conclusion most clearly. One can see that for the initial state \(\alpha =0.25\), the protection of entanglement is completely failed, but the GMQD can still be enhanced with increasing \(p\) under the protection protocol in some regions of \(D\) at finite temperature. Therefore, the protection of GMQD is more efficient than that of entanglement by weak measurement and measurement reversal.

Fig. 5
figure 5

Entanglement and GMQD versus amplitude damping parameter \(D\) for different strengths of weak measurement under the protection protocol at finite temperature. The parameters are chosen to be \(D_1=D_2=0.5D\), \(r=0.1\), and \(\alpha =0.5\)

Full size image
Fig. 6
figure 6

Entanglement and GMQD versus amplitude damping parameter \(D\) for different strengths of weak measurement under the protection protocol at zero temperature. The parameters are chosen to be \(D_1=D_2=0.5D\), \(r=0.1\), and \(\alpha =0.25\)

Full size image

5 Conclusion

In conclusion, employing the concepts of negativity and geometric measure of quantum discord (GMQD), we firstly investigated the dynamics of the quantum correlations of a qubit–qutrit system, each locally interacting with a generalized amplitude damping with finite temperature. It is shown that the GMQD is more robust than entanglement against the decoherence, in the sense that the entanglement sudden death is induced by increasing the temperature of the channel, but the GMQD does not vanish at finite temperature. Secondly, we studied the protection of the quantum correlations by weak measurement and measurement reversal. Our results show that for the initial maximally entangled state, the protection is independent of the weak measurement. But for other initial states, the weak measurement is necessary for more efficient protection of the quantum correlations. Under the condition of optimal measurement reversal strength, the entanglement sudden death can be avoided and the GMQD is significantly improved. However, as the temperature of the channel increases, the protection of the entanglement is failed but the protection of GMQD can still be realized. Therefore, the GMQD performs better in detecting the quantum correlations in the decoherent process at finite temperature.