Correlation dynamics of a qubit system interacting with a qutrit environment embedded in a magnetic field

Abstract

We investigate the correlation dynamics of a non-interacting two-qubit system which is embedded in a qutrit environment with a constant magnetic field. Two archetypal states, mainly a Bell state and a coherent state, are considered as the initial state, and their correlation dynamics are studied in the presence of the mentioned environment. It is shown that the concurrence, a measure of entanglement, and discord can be controlled by tuning the number of degrees of freedom the environment, the coupling strength, and the strength of external magnetic field. Furthermore, we analytically evaluate the discord for spin cat-state. Our results imply that decoherence is inevitable and death of entanglement may happen periodically; however, if certain ranges of the parameters are adhered to, the total entanglement death may be avoided.

1 Introduction

Entanglement is an important resource that has applications in quantum information and computation such as quantum secret sharing [1], quantum teleportation [2], quantum dense coding [3] and quantum computation [4,5,6]. Spin systems and specifically spin chains have been used to study these entanglement-based applications [7, 8]. Quantum discord was introduced by Ollivier and Zurek to quantify the non-classical correlation of bipartite system and it is defined as the difference between two quantum versions of classical mutual information[9,10,11]. On the other hand, correlation is subject to decoherence due to the inevitable interactions with the environment. There are numerous papers on the general characteristics of decoherence [12, 13] and also on the study of correlation dynamics and decoherence of the qubit systems in the qubit environments [14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31]; however, to our knowledge, the case of qutrit environments has not been investigated yet. Recent experiments have also been performed on molecular magnets. These are small clusters of a few atoms embedded into a crystal, which can be described as large spins [32, 33]. Thus, here we generalize these investigations to environments formed by qutrits (spin-one). This will enable us to draw some conclusions about the advantages and the inconveniences of using this kind of environment compared to the qubit environment. The results provide more insights into the effect of the spin environments on the dynamics of the quantum correlation. Recently, the authors in [34,35,36] have made an analysis of the correlation properties of two qubit states under decoherence from a qubit environment. In a similar way in this work, we consider a qubit system embedded in a qutrit environment. The qubits are non-interacting but do interact with the qutrit environment, which itself is embedded in a constant magnetic field. Two archetypal states, mainly Bell state and coherent state, are considered as the initial state, and their correlation dynamics are studied in the mentioned environment. The organization of the rest of this paper is as follows. We introduce the model and derive its time-dependent density matrix in Sect. 2. The dynamics of entanglement and discord are presented in Sects. 3 and 4, respectively. Finally, Sect. 5 is devoted to conclusions and discussion.

2 Hamiltonian and the time dependent density matrix

We consider a model consisting of a two-qubit (spin one-half) system, where the qubits do not interact with each other but do interact with an environment consisting of a chain of qutrits (spin-one), which itself is embedded in a magnetic field. The Hamiltonian of the system, the interaction and the environment can be expressed as follows:

$$ \begin{gathered} H_{s} = J\,S_{A}^{z} \,\,S_{B}^{z} \hfill \\ H_{B} = \sum\limits_{{i = 1}}^{N} {h_{i} } S_{{Ei}}^{x} \hfill \\ H_{I} = S_{A}^{z} \sum\limits_{{i = 1}}^{N} {\varepsilon _{i} } S_{{Ei}}^{z} + S_{B}^{z} \sum\limits_{{i = 1}}^{N} {\lambda _{i} } S_{{Ei}}^{z} \hfill \\ H_{{I + B + S}} = H_{I} + H_{B} + H_{S} = S_{A}^{z} \sum\limits_{{i = 1}}^{N} {\varepsilon _{i} } S_{{Ei}}^{z} + S_{B}^{z} \sum\limits_{{i = 1}}^{N} {\lambda _{i} } S_{{Ei}}^{z} + \sum\limits_{{i = 1}}^{N} {h_{i} } S_{{Ei}}^{x} + J\,S_{A}^{z} \,\,S_{B}^{z} \hfill \\ \end{gathered}$$

(1)

where $S_{A}^{z}$ and $S_{B}^{z}$ are qubit operators along the $Z$ direction, $S_{Ei}^{z}$ and $S_{Ei}^{x}$ are qutrit operators along the $Z$ and $x$ direction, respectively.$\varepsilon_{i}$ and $\lambda_{i}$ are coupling constants between the qubits and the site i of the environment, and h_i’s, (i = 1,…,N) are the constants which denote the tunneling matrix elements of the i-th environmental spin [34]. The strength of interaction between the system qubits is given by $J$.We write the general initial state of the systems as:

$$ \left| {\psi_{s} (0)} \right\rangle = C_{1} \left| {00} \right\rangle + C_{2} \left| {01} \right\rangle + C_{3} \left| {10} \right\rangle + C_{4} \left| {11} \right\rangle $$

(2)

where the complex coefficients $C_{i} (1,2,3,4)$ satisfy the normalization condition $\sum\limits_{i = 1}^{4} {\left| {C_{i} } \right|^{2} } = 1$. Furthermore, the initial state of environment is given by

$$ \left| {\psi_{E} \left( 0 \right)} \right\rangle = \otimes_{i = 1}^{N} (\alpha_{i} \left| 0 \right\rangle_{i} + \beta_{i} \left| 1 \right\rangle_{i} + \gamma_{i} \left| 2 \right\rangle_{i} ) $$

(3)

where $\left| {\alpha_{i} } \right|^{2} + \left| {\beta_{i} } \right|^{2} + \left| {\gamma_{i} } \right|^{2} = 1$ and $\left| 0 \right\rangle_{i}$,$\left| 1 \right\rangle_{i}$,$\left| 2 \right\rangle_{i}$ are the eigenstates of the operator $S_{Ei}^{z}$ with corresponding eigenvalues of 1, 0 and − 1, respectively. Now, we need to calculate the time-dependent density matrix of the system; it is obtained by tracing the degrees of freedom of the environment out

$$ \rho_{s} (t) = tr_{E} [e^{ - iHt} \left| {\psi_{s} (0)} \right\rangle \left\langle {\psi_{s} (0)} \right| \otimes \left| {\psi_{e} (0)} \right\rangle \left\langle {\psi_{e} (0)} \right|e^{iHt} ] $$

(4)

In the standard computational basis $\left| {00} \right\rangle$,$\left| {01} \right\rangle$,$\left| {10} \right\rangle$ and $\left| {11} \right\rangle$ we find

$$ \rho_{S} \left( t \right) = \left[ {\begin{array}{*{20}c} {\left| {C_{1} } \right|^{2} } & {C_{1} C_{2}^{*} M_{12} \,e^{{ - \frac{iJt}{2}}} } & {C_{1} C_{3}^{*} M_{13} \,e^{{ - \frac{iJt}{2}}} } & {C_{1} C_{4}^{*} M_{14} } \\ {C_{1}^{*} C_{2} M_{12}^{*} \,e^{\frac{iJt}{2}} } & {\left| {C_{2} } \right|^{2} } & {C_{2} C_{3}^{*} M_{23} } & {C_{2} C_{4}^{*} M_{24} e^{\frac{iJt}{2}} } \\ {C_{1}^{*} C_{3} M_{13}^{*} e^{\frac{iJt}{2}} } & {C_{2}^{*} C_{3} M_{23}^{*} } & {\left| {C_{3} } \right|^{2} } & {C_{3} C_{4}^{*} M_{34} e^{\frac{iJt}{2}} } \\ {C_{1}^{*} C_{4} M_{14}^{*} } & {C_{2}^{*} C_{4} M_{24}^{*} e^{{ - \frac{iJt}{2}}} } & {C_{3}^{*} C_{4} M_{34}^{*} e^{{ - \frac{iJt}{2}}} } & {\left| {C_{4} } \right|^{2} } \\ \end{array} } \right] $$

(5)

where $M_{\alpha \beta }$ are called the decoherence factors and are given by

$$ M_{\alpha \beta } = \prod\limits_{i = 1}^{N} {F_{\alpha \beta }^{i} } (t) $$

(6)

Here, we have defined

$$ \begin{aligned} F_{\alpha \beta }^{i} (t) & = \frac{1}{{3\Lambda_{\alpha }^{2} \Lambda_{\beta }^{2} }}(A_{\beta } (h_{i}^{2} \cos [t\Lambda_{\alpha } ](A_{\beta } - A_{\alpha } ) + A_{\alpha } (h_{i}^{2} + A_{\alpha } A_{\beta } ) \\ & \quad + i\sqrt 2 h_{i} \sin [t\Lambda_{\alpha } ] + \,(A_{\alpha } - A_{\beta } )\Lambda_{\alpha } ) + \cos [t\Lambda_{\beta } ]((A_{\alpha } - A_{\beta } )A_{\alpha } h_{i}^{2} \\ & \quad + \cos [t\Lambda_{\alpha } ](3h_{i}^{4} + h_{i}^{2} A_{\alpha } A_{\beta } + 2A_{\alpha }^{2} (h_{i}^{2} + A_{\beta }^{2} )) \\ & \quad - i\sqrt 2 \sin [t\Lambda_{\alpha } ](2h_{i}^{2} + A_{\beta } (A_{\alpha } + A_{\beta } ))A_{\alpha } ) + \sin [t\Lambda_{\beta } ](i\sqrt 2 h_{i} (A_{\alpha } - A_{\beta } ) \\ & \quad + i\sqrt 2 h_{i} \cos [t\Lambda_{\alpha } ](2h_{i}^{2} + (A_{\alpha } + A_{\beta } )A_{\alpha } ) + \sin [t\Lambda_{\alpha } ](3h_{i}^{2} + 2A_{\beta } A_{\alpha } )\Lambda_{\alpha } )\Lambda_{\beta } )\, \\ \end{aligned} $$

(7)

where

$$ \begin{gathered} \Lambda_{\alpha (\beta )} = \sqrt {h_{i}^{2} + A_{\alpha (\beta )}^{2} } ,A_{1} = \frac{1}{2}(\varepsilon_{i} + \lambda_{i} ) = g_{i} , \hfill \\ A_{2} = \frac{1}{2}(\varepsilon_{i} - \lambda_{i} ),A_{3} = - \frac{1}{2}(\varepsilon_{i} - \lambda_{i} ), \hfill \\ A_{4} = - \frac{1}{2}(\varepsilon_{i} + \lambda_{i} ) = - g_{i} ,\alpha_{i} = \beta_{i} = \gamma_{i} = \frac{1}{\sqrt 3 } \hfill \\ \end{gathered} $$

(8)

3 Dynamics of entanglement

At first, we consider that the initial state of the system is bell-type state, which is expressed by

$$ \left| {\psi_{s} \left( 0 \right)} \right\rangle = \cos \theta \left| {00} \right\rangle + \sin \theta \left| {11} \right\rangle $$

(9)

which reduces to the Bell state for $\theta = \frac{\pi }{4}$. The time-dependent reduced density matrix of the system is obtained as follows:

$$ \rho_{s} \left( t \right) = \left[ {\begin{array}{*{20}c} {\cos \theta^{2} } & 0 & 0 & {M_{14} \cos \theta \sin \theta } \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ {M_{14}^{*} \cos \theta \sin \theta } & 0 & 0 & {\sin \theta^{2} } \\ \end{array} } \right] $$

(10)

where assuming $\varepsilon = \varepsilon_{i}$,$\lambda = \lambda_{i}$ and $g_{i} = \frac{{\varepsilon_{i} + \lambda_{i} }}{2} = g$, the decoherence factor $M_{14}$ is given by

$$ M_{14} = [\frac{{(g^{4} + g^{2} h^{2} + 3h^{4} + g^{2} (4h^{2} Cos(\sqrt {g^{2} + h^{2} } t) + (2g^{2} + h^{2} )Cos(2\sqrt {g^{2} + h^{2} } t)))}}{{3(g^{2} + h^{2} )^{2} }}]^{N} $$

(11)

In the short time, the decoherence factor $M_{14}$ decays as a Gaussian:

$$ M_{14} \simeq e^{{ - \,\,\frac{{N(\varepsilon + \lambda )^{2} }}{6}t^{2} }} $$

(12)

Now, we use concurrence as the measure of entanglement to study the bipartite entanglement dynamics in the system; it is defined by [37]:

$$ C(\rho ) = \left\{ {0,\sqrt {\lambda_{1} } - \sqrt {\lambda_{2} } - \sqrt {\lambda_{3} } - \sqrt {\lambda_{4} } } \right\} $$

(13)

where $\lambda_{4} \le \lambda_{3} \le \lambda_{2} \le \lambda_{1}$ are eigenvalues of the matrix $R$ defined by

$$ R = \rho (\sigma_{y} \otimes \sigma_{y} )\rho^{*} (\sigma_{y} \otimes \sigma_{y} ) $$

(14)

$\sigma_{y}$ and $\rho^{*}$ denote the Pauli y-matrix and the complex conjugation of $\rho$, respectively. Using (10) in (13), the square root of its eigenvalues are given by

$$ \sqrt {\lambda_{1} } = \left( {1 + M_{14} } \right)\cos \theta \sin \theta ,\,\,\,\sqrt {\lambda_{2} } = \left( {1 - M_{14} } \right)\cos \theta \sin \theta ,\,\,\,\sqrt {\lambda_{3} } = \sqrt {\lambda_{3} } = 0 $$

(15)

Finally, the time-dependent concurrence is obtained by means of (13)

$$ C(\rho ) = \max \{ 0,M_{14} \sin 2\theta \} $$

(16)

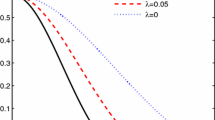
We have presented $C(\rho )$ as a function of time for different values of $h$,$N$ and $g$, while we have kept the other parameters fixed, in Figs.1, 2 and 3, respectively. Inspecting Fig. 1, it is observed that the average concurrence is an increasing function of the field and the periodic regions of entanglement death (PRED) appear for $h < 0.65$. Figure 2 shows that the average entanglement is a decreasing function of the number of qubits, and PRED appears for $N > 400$. Figure 3 also implies that entanglement is a decreasing function of the coupling parameter, and PRED is observed for $g > 0.2$.We note that although decoherence and depletion of entanglement for the Bell state is inevitable in the qutrit environment, however, one may control the dynamics and avoid total death of entanglement if some restrictions on the parameters are observed. More specifically, the external field which may be accessible to the experimenter can help to diminish the decoherence effects.

$$ \left| \psi \right\rangle = \frac{{1 + \left| \alpha \right|^{2} }}{{2\sqrt {1 + \left| \alpha \right|^{4} } }}(\left| \alpha \right\rangle + \left| { - \alpha } \right\rangle ) $$

(17)

Fig. 1

Bell-state concurrence versus time for $h = 0.5$ (dashed line), $h = 0.65$(solid line), $h = 1.5$(dotted line);$N = 100$,$\theta = \frac{\pi }{4}$,$g = \frac{\varepsilon + \lambda }{2} = 0.1$. Entanglement death is observed if $h < 0.65$

Fig.2

Bell-state concurrence versus time for $N = 10$ (dotted line), $N = 100$ (dashed-dotted line),$N = 400$ (Solid line),$N = 800$ (dashed line); $g = \frac{\varepsilon + \lambda }{2} = 0.1$, $\theta = \frac{\pi }{4}$, $h = 1$. Entanglement death is observed if $N > 400$

Fig.3

Bell-state concurrence for $g = 0.05$ (dotted line), $g = 0.2$ (Solid line), $g = 1$ (dashed line);$\theta = \frac{\pi }{4}$, $h = 1$, $N = 100$. Entanglement death is observed if $g > 0.2$

Another interesting case is obtained by setting up the following normalized even cat state,

where a two-qubit spin coherent state, $\left| \alpha \right\rangle$, is given by [38]

$$ \left| \alpha \right\rangle = \frac{1}{{\sqrt {1 + \left| \alpha \right|^{2} } }}\sum\limits_{m = 0}^{2} {\frac{{\alpha^{m} }}{m!}} S_{ + }^{m} \left| {0^{1} 0^{1} } \right\rangle = \frac{1}{{1 + \left| \alpha \right|^{2} }}(\left| {00} \right\rangle + \alpha \left| {01} \right\rangle + \alpha \left| {10} \right\rangle + \alpha^{2} \left| {11} \right\rangle ) $$

(18)

and study its time evolution. The time-dependent density matrix $\rho_{s} (t)$ is given by

$$ \rho_{s} \left( t \right) = \left[ {\begin{array}{*{20}c} {\frac{1}{{1 + \left| \alpha \right|^{4} }}} & 0 & 0 & {M_{14} \frac{{\left| \alpha \right|^{2} }}{{1 + \left| \alpha \right|^{4} }}} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ {M_{14}^{*} \frac{{\left| \alpha \right|^{2} }}{{1 + \left| \alpha \right|^{4} }}} & 0 & 0 & {\frac{{\left| \alpha \right|^{4} }}{{1 + \left| \alpha \right|^{4} }}} \\ \end{array} } \right] $$

(19)

By virtue of (13) and (14), the concurrence is given by

$$ C(\rho_{s} ) = \max \{ 0,\frac{{2\left| {M_{14} } \right|\left| \alpha \right|^{2} }}{{1 + \left| \alpha \right|^{4} }}\} $$

(20)

We have presented $C(\rho )$ as a function of time for different values of $h$, $N$ and $g$, while we have kept the other parameters fixed, in Figs.4, 5 and 6, respectively. Again it is observed that the time average concurrence is an increasing function of the field but a decreasing function of the number of qutrits and the coupling constant. The entanglement death may be avoided again by observing the required restrictions on the parameters involved. Figure 7 displays $C(\rho )$ as a function of time for different values of the parameter $\left| \alpha \right|^{2}$.It is observed that the coherence parameter has an adverse effect on the entanglement; the time average of the latter is a decreasing function of the coherence parameter $\left| \alpha \right|^{2}$.

Fig.4

Cat-state concurrence versus time for $h = 0.3$ (dashed line),$h = 0.65$ (solid line),$h = 1.5$ (dotted line);$g = \frac{\varepsilon + \lambda }{2} = 0.1$,$\left| \alpha \right|^{2} = 2$ and $N = 100$

Fig.5

Cat-state concurrence versus time for $N = 50$ (dotted line), $N = 400$ (Solid line), $N = 800$(dashed line);$g = \frac{\varepsilon + \lambda }{2} = 0.1$, $\left| \alpha \right|^{2} = 2$ and $h = 1$

Fig.6

Cat-state concurrence versus time for $g = 0.05$ (dotted line), $g = 0.2$ (Solid line), $g = 1$ (dashed line);$N = 100$, $\left| \alpha \right|^{2} = 2$ and $h = 1$

Fig.7

Cat-state concurrence versus time for $\left| \alpha \right|^{2} = 1$ (dotted line), $\left| \alpha \right|^{2} = 3$ (Solid line), $\left| \alpha \right|^{2} = 10$(dashed line); $g = \frac{\varepsilon + \lambda }{2} = 0.1$,$N = 100$ and $h = 1$

4 Dynamics of discord

We consider a bipartite system consisting of subsystems $A$ and $B$ whose density matrix is given by $\rho_{AB}$. Quantum discord for two-qubit state $\rho_{AB}$ is defined as the difference between the quantum mutual information,$I(\rho_{AB} )$and the classical correlation $CC(\rho_{AB} \,)$[9,10,11]

$$ D(\rho_{AB} ) = I(\rho_{AB} ) - \,CC(\rho_{AB} \,) $$

(21)

The quantum mutual information is defined as

$$ I(\rho_{AB} ) = S(\rho_{A} ) + S(\rho_{B} ) - S(\rho_{AB} ) $$

(22)

where $S(\rho ) = - Tr(\rho log\rho )$, and $\rho_{A(B)}$ is the reduced state of subsystem $A(B)$ and

classical correlation $C\,C(\rho_{AB} \,)$ is given by

$$ C\,C(\rho_{AB} \,) = \mathop {{\text{Sup}}}\limits_{{\{ \prod_{B}^{k} \} }} [S(\rho_{A} ) - \sum\limits_{k} {P_{k} } S(\rho_{A}^{k} )] $$

(23)

where the projection operator $\prod_{B}^{k}$ describes a Von Neumann measurement for the subsystem $B$. The state of the subsystem $A$ after the measurement $\prod_{B}^{k}$ is given by

$$ \rho_{A}^{k} = \frac{1}{{p_{k} }}\{ (I_{A} \otimes \prod_{B}^{k} )\rho_{AB} (I_{A} \otimes \prod_{B}^{k} )\} $$

(24)

where $\prod_{B}^{k}$ is performed on the system $B$ and

$$ p_{k} = Tr\{ (I_{A} \otimes \prod_{B}^{k} )\rho_{AB} (I_{A} \otimes \prod_{B}^{k} )\} \,\,\,\,\,\,\,\,\,\,\,\,k = 1,2 $$

(25)

Quantum discord of the density matrix given by Eq. (19) is obtained as

$$ \begin{aligned} D(\rho_{AB} ) & = - \frac{{\log_{2} (\frac{1}{{1 + \alpha^{4} }})}}{{1 + \alpha^{4} }} - \frac{{\alpha^{4} \log_{2} (\frac{{\alpha^{4} }}{{1 + \alpha^{4} }})}}{{1 + \alpha^{4} }} \\ & \quad + \frac{1}{2}\left( {1 - \frac{{\sqrt {4\left| {M_{14} } \right|^{2} + ( - 1 + \alpha^{4} )^{2} } }}{{(1 + \alpha^{4} )}}} \right)\log_{2} \left( {\frac{1}{2}\left( {1 - \frac{{\sqrt {4\left| {M_{14} } \right|^{2} + ( - 1 + \alpha^{4} )^{2} } }}{{(1 + \alpha^{4} )}}} \right)} \right) \\ & \quad + \frac{1}{2}\left( {1 + \frac{{\sqrt {4\left| {M_{14} } \right|^{2} + ( - 1 + \alpha^{4} )^{2} } }}{{(1 + \alpha^{4} )}}} \right)\log_{2} \left( {\frac{1}{2}\left( {1 + \frac{{\sqrt {4\left| {M_{14} } \right|^{2} + ( - 1 + \alpha^{4} )^{2} } }}{{(1 + \alpha^{4} )}}} \right)} \right) \\ \end{aligned} $$

(26)

The quantum discord for Bell state may be obtained from (26) for $\alpha = 1$; we find

$$ D(\rho_{AB} ) = (\frac{{1 + \left| {M_{14} } \right|}}{2})\log_{2} (1 + \left| {M_{14} } \right|) + (\frac{{1 - \left| {M_{14} } \right|}}{2})\log_{2} (1 - \left| {M_{14} } \right|) $$

(27)

We noted that for $\alpha = 1$, the coherent state turns into the Bell state. In Fig. 8, the quantum discord for coherent state is plotted as a function of $\alpha$ and $t$. From Fig. 8, we can see that discord maintains its oscillatory behavior for the latter; moreover, discord gains the highest possible value 1, at its peaks. It is observed that the values of discord at its peaks decay with the increasing $\alpha$.

Fig.8

$D$ as a function of $\alpha$ and $t$ for coherent state;$h = 1$, $g = 0.1$, and $N = 100$

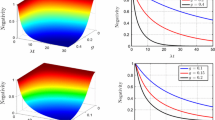
We have displayed discord as a function of time, for different values of $h$, $N$ and $g$, in Figs.9 through 11, respectively. From Fig. 9, we can see that the magnetic field has a favorable effect on the discord, that is, its oscillation amplitude decreases, but its time average increases as the field strength is amplified. Moreover, we can find that the oscillation frequency of the quantum discord apparently increases as increasing $h$.

Fig.9

D versus time for Bell state $h = 0.5$ (dashed line), $h = 0.65$ (solid line), $h = 1.5$(dotted line);$N = 100$, $g = \frac{\varepsilon + \lambda }{2} = 0.1$

Figure 10 reveals that the interaction parameter $g$ has an adverse effect on the discord and its time average decreases as t $g$ is increased. In fact, the decoherence is due to the interaction between the qubits and qutrits, thus enhancement of the interaction diminishes the discord. From Fig. 11, we can find that the number of environmental qutrit system also has an adverse effect on the discord; the latter decreases as the number of the qutrits are increased.

Fig. 10

D versus time for Bell state $g = 0.05$ (dotted line), $g = 0.2$ (Solid line), $g = 1$ (dashed line);$h = 1$,$N = 100$

Fig.11

D versus time for Bell state $N = 10$ (dotted line), $N = 100$ (dashed-dotted line), $N = 400$ (Solid line), $N = 800$ (dashed line);$g = \frac{\varepsilon + \lambda }{2} = 0.1$,$h = 1$

It should also be mentioned that some research has been done in the same field for the qutrit system in the qubit environment [34] and the qubit system and environment [35], but due to the different environmental conditions and different systems, it is not possible to compare results of these researches with results of our work.

5 Discussion and conclusions

We have analyzed correlation dynamics and decoherence of a qubit system by a qutrit environment embedded in a magnetic field. We considered two archetypical initial states, that is, bell and cat state. We have observed that in the two cases, entanglement is a decreasing function of the number of qutrits and the coupling constant, but an increasing function of the magnetic field. The latter observation is very useful, as it provides a means of control of entanglement by adjusting an external parameter which may be accessible to the experimenter. Finally, it was revealed that in the case of cat states, entanglement and discord decreases as the absolute value of the coherence parameter increases.