1 Introduction

Quantum image processing is attracting more and more attention in recent years, from quantum image representation [1–3], quantum image operation [4–7] to quantum image encryption [8–10].

Image scrambling [11, 12] is a basic work of image encryption or information hiding [13]. The image after scrambling removes the correlation of image pixels space, which can make the watermark lose the original information, and then, the watermark information is tucked into the carrier. Thus, even if an attacker extracted carriers from the image, he is almost unable to obtain the original image information in any case. Therefore, scrambling processing for the watermark or information hiding is fairly indispensable in a large sense. The scrambling algorithm mainly includes two categories.

1.1 Change the image pixel position

Its idea is to use the principle of geometric properties to change the pixel geometry so as to disrupt the original image information. At present, by and large, methods based on this idea are: Arnold transform [14], orthogonal Latin square transformation [15], affine transform [16], magic transformation [17, 18], knight tour transform [19] and Fibonacci transform [20–22].

1.2 Change the image pixel value

This idea is to use some certain methods to change the gray value of pixels, thus changing the original color or grayscale image, disturbing the original image information. The principle of this method is mainly to change the gray-level histogram of the original image, so that the illegal user cannot read any information of the original image from the scrambling image histogram. At present, the main algorithms of this transformation are as follows: Gray-code transform, ‘or’ transform, and bit-plane transform.

However, in quantum study area, quantum image scrambling is still few, some researches about this aspect include “The quantum realization of Arnold and Fibonacci image scrambling [22]” and the recently proposed “Quantum Hilbert scrambling [23].” But these methods are all based on the first-type scrambling, i.e., transform the image geometric coordinates for scrambling. Moreover, for quantum image, the circuit cost is very high when the size of quantum image increases. In addition, there is also a limit for the size of quantum image being scrambled in these schemes, which only scrambles the square image, i.e., the “\(n\times n\)” size.

In this paper, we use a novel enhanced quantum representation of digital images (NEQR) and its improved edition, which boldly proposed a novel quantum image Gray-code [24, 25] and bit-plane [26] scrambling scheme. It is fully based on the second-type scrambling, changing the pixel gray value methodically, which has not been researched yet.

Our paper is structured as follows: The next Sect. 2 discusses the backgrounds about the quantum image representation, Gray-code and bit-plane scrambling technique. Section 3 describes the proposed quantum image scrambling scheme, circuit and performance show. Section 4 gives the reconstruct strategies of the design scheme. Finally, an overall conclusion is listed in Sect. 5.

2 Backgrounds

2.1 Quantum image representation

With the rapid development of quantum information, many studies on quantum image representation and algorithm [27–29] had been proposed. Among these researches, quantum image representation is a fundamental task, which subtly arranges the digital image into the quantum computer.

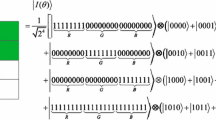
NEQR is an excellent representation for quantum image, which is made on the basis of FRQI (the first successful representation). According to the NEQR model, a quantum grayscale image can be described as in (1):

$$\begin{aligned} |I\rangle =\frac{1}{2^{n}}\sum _{X=0}^{2^{n}-1} {\sum _{Y=0}^{2^{n}-1} {|f(X,Y)\rangle |XY\rangle =} } \frac{1}{2^{n}}\sum _{X=0}^{2^{n}-1} {\sum _{Y=0}^{2^{n}-1} {\mathop \otimes \limits _{i=0}^{q-1} } } |C_{XY}^i \rangle |XY\rangle \end{aligned}$$
(1)

where \(|I\rangle \) stands for a \(2^{n}\times 2^{n}\) image and the gray range of image is \(2^{q}\). Then, binary sequence encodes the gray value \(f(X,Y)\) of corresponding pixel\((X,Y)\), whose implication is,

$$\begin{aligned} f(X,Y)=C_{XY}^0 C_{XY}^1 \cdots C_{XY}^{q-2} C_{XY}^{q-1} ,\quad C_{XY}^k \in [0,1],f(X,Y)\in [0,2^{q}-1] \end{aligned}$$
(2)

Fig. 1 shows a \(2\times 2\) NEQR image example:

Fig. 1
figure 1

A \(2\times 2\) NEQR image representation

Full size image

Taking the general suitability for various digital images into account, the NEQR in our paper is flexibly used or improved. Suppose the size of image is \(M\times N\), the flexible NEQR is described as follows.

$$\begin{aligned} |I\rangle =\frac{1}{2^{n}}\sum _{X=0}^{2^{M}-1} {\sum _{Y=0}^{2^{N}-1} {|f(X,Y)\rangle |XY\rangle =} } \frac{1}{2^{n}}\sum _{X=0}^{2^{M}-1} {\sum _{Y=0}^{2^{N}-1} {\mathop \otimes \limits _{i=0}^{q-1} } } |C_{XY}^i \rangle |XY\rangle , \end{aligned}$$
(3)

here \(n=(M+N)/2\), and then, the proposed scrambling scheme will focus on the quantum grayscale image like this; in other words, quantum image to be scrambled is not restricted to the square image in our schemes.

2.2 Gray-code and bit-plane technique

2.2.1 Gray-code

Gray-code is a signal coding method, which is commonly used in the analog–digital conversion and position–digital conversion. For a arbitrary nonnegative integer \(n\), whose binary code is denoted as \(n=(n_q n_{q-1} \ldots n_1 n_0 )_2 \), the definition is as follows:

$$\begin{aligned} f_q= & {} n_q \end{aligned}$$
(4)
$$\begin{aligned} f_i= & {} n_i \oplus n_{i+1} ,i=0,1,2,\ldots ,q-1 \end{aligned}$$
(5)

\(\oplus \) is addition modulo 2 operation, and thus, this transform is referred to as Gray-code transform. The new transformed binary code \(f(n)=(f_q f_{q-1}\ldots f_1 f_0 )_2 \) is addressed as Gray-code of n. A simple Gray-code transform operation is diagrammed as below (Fig. 2).

Fig. 2
figure 2

Gray-code transform computation

Full size image

More specific, Gray-code transform can be expressed in the following mathematics form (can see Ref. [30]):

$$\begin{aligned} \left[ {\begin{array}{l} f_q \\ f_{q-1} \\ \ldots \\ f_1 \\ f_0 \\ \end{array}} \right] =\left[ {\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} 1 &{} 0 &{} \ldots &{} 0 &{} 0 \\ 1 &{} {}1 &{} \ldots &{} 0 &{} 0 \\ \ldots &{} \ldots &{} \ldots &{} \ldots &{} \ldots \\ 0 &{} 0 &{} \ldots &{} 1 &{} 0 \\ 0 &{} 0 &{} \ldots &{} 1&{} 1 \\ \end{array}} \right] \left[ {\begin{array}{l} n_q \\ n_{q-1} \\ \ldots \\ n_1 \\ n_0 \\ \end{array}} \right] (\hbox {mod 2}) \end{aligned}$$
(6)

2.2.2 Bit-plane

Image bit-plane refers to a series of two-value image planes. To begin with, the pixel values in the image are represented by its corresponding binary values, and then, every single bit of all the pixels will form a two-value image, it is called bit-plane. To be specific, if the image gray value range is [0, 255], the binary length is 8, i.e., the image will be separated into 8 bit-planes. Taking Lena image, for example, Fig. 3 displays the result of bit-planes of Lena.

Fig. 3
figure 3

Bit-planes of Lena

Full size image

From the eight bit-planes, we can easily see that different bit-planes carry different visual information. The outline of image becomes blurred from high bit-plane to low bit-plane, and the lowest bit-plane contains minimal information. In other words, the higher the image bit-plane, the more meaningful information. This bit-plane information rule can greatly facilitate and guide the design of image scrambling algorithms.

3 Quantum Gray-code and bit-plane scrambling

3.1 Used quantum gates and notation

Two quantum gates will be used frequently in our paper: NOT gate and CNOT gate. From the quantum theory, NOT gate is a single quantum bit (qubit) gate, and it modifies the qubit content to its opposition content. Meanwhile, the CNOT gate (controlled-NOT gate) is a two-qubit gate; if the control qubit is one, the target qubit content will be inverted. All of them are often used in quantum circuit and achieve various transformations in quantum image processing. Figure 4 describes the notation of the used quantum gates.

Fig. 4
figure 4

Quantum gates

Full size image

3.2 Scrambling algorithm and circuit

As mentioned earlier, the proposed quantum image scrambling algorithm focuses on the second scrambling concept. Consequently, the scrambling for gray information of pixels in quantum image can be described as (7),

$$\begin{aligned} Scr(|I\rangle )=\frac{1}{2^{n}}\sum _{X=0}^{2^{M}-1} {\sum _{Y=0}^{2^{N}-1} {Scr(|f(X,Y)\rangle )|XY\rangle =} } \frac{1}{2^{n}}\sum _{X=0}^{2^{M}-1} {\sum _{Y=0}^{2^{N}-1} {|g(X,Y)\rangle } } |XY\rangle , \end{aligned}$$
(7)

Here, “Scr” represents the scrambling operation. The \(g(X,Y)\) is the image gray value output after Scr operation.

According to the existed algorithms about Gray-code and the actual application needs, for quantum image, the following three scrambling schemes, including

  1. (1)

    The elementary Gray-code and bit-plane scrambling,

  2. (2)

    The improved fast GB scrambling,

  3. (3)

    GB scrambling integrates with position, are designed in turn.

  1. (1)

    The elementary Gray-code and bit-plane scrambling

Firstly, the image bit-plane is listed in basic order. Considering the bit-plane information rule, the high bit-plane contains most of grayscale information while the low bit-plane contains little; the elementary GB scheme adopts the Gray-code transformation in reverse order, i.e., the lowest bit-plane keep fixed. The function of the elementary GB scrambling is denoted as (8):

$$\begin{aligned} GB(|I\rangle )=\frac{1}{2^{n}}\sum _{X=0}^{2^{M}-1} {\sum _{Y=0}^{2^{N}-1} {GB(|f(X,Y)\rangle )|XY\rangle =} } \frac{1}{2^{n}}\sum _{X=0}^{2^{M}-1} {\sum _{Y=0}^{2^{N}-1} {|g(X,Y)\rangle } } |XY\rangle , \end{aligned}$$
(8)

The GB in (8) stands for the elementary GB scrambling operation. The quantum circuit about this method is shown in Fig. 5.

Fig. 5
figure 5

Circuit of the elementary GB scrambling

Full size image

In the eight qubits which store the grayscale information of quantum image, eight CNOT gates are used according to Gray-code scrambling method, while the qubits representing for position information are not changed by quantum gates. And the image through the above circuit one time is shown in Fig. 6.

Fig. 6
figure 6

Scrambling outcome through elementary GB 1 time

Full size image

Obviously, the scrambled image has been blurred more or less. But, this result cannot still meet strict requirement of image scrambling well. Therefore, according to the Gray-code theory, a further procedure is extremely needed.

As we all know, digital image scrambling transform has its transform cycle, the transformation cycle is the number of times, the scrambled image will return to the original image when scrambling a certain number of times for the original image. This feature can be used to decrypt the scrambled image, and when scrambling an integer multiple times of the cycle for the scrambled image, the initial image will occur again.

Based on relevant researches on Gray-code [30], if the order of Gray-code transformation matrix is \(2^{n}\), then the transformation cycle of Gray-code scrambling is \(2^{n}\). Because the image grayscale is from 0 to 255, the original image is obtained when scrambling 8 or a multiple of 8 times. The following Fig. 7 illustrates the cycle effect of Gray-code scrambling in color space.

Fig. 7
figure 7

Cycle effect of Gray-code scrambling

Full size image

As the above figure shows, the image Lena was disturbed more and more serious with the scrambling times increases. And when after an entire period, i.e., 8, the image will be restored as before without any quality degradation.

  1. (2)

    The improved fast GB scrambling

A good image scrambling method may be capable of scrambling any image under the condition of less scrambling times and transforming the initial image to the “chaos” state rapidly. That is to say, the scrambling algorithm needs to reach a higher efficiency.

In order to improve the scrambling speed and cut down the cost of the used quantum gates, a fast scrambling scheme is designed. This scrambling scheme does not need repeated or iterative scrambling operations, a simple one-time operation in it will produce a very good scrambling effect.

In this scheme, we designed, at first, the bit-plane, which is not arranged in positive sequence; instead, permutation and combination of these bit-planes are chosen properly to achieve the goal of fast scrambling. Because of the bit-plane information rule, this fast scrambling scheme processes the low bit-planes first and applies the results to the high bit-planes, so as to change the initial image dramatically. As Fig. 8 shows, to begin with, the bit-plane 8 and 4, 7 and 3, 6 and 2, 5 and 1 make the CNOT operations, respectively. Then, similarly, the bit-plane 4 and 5, 3 and 6, 2 and 7, 1 and 8 are all performed CNOT operations as well. We call this an improved fast GB scrambling scheme. Thus, the final scrambling will be emerged soon.

On the other hand, it is also important to note that it is not a simple operation that can scramble image or scramble image very well, which can be learned from the bit-plane rule in Fig. 3. If there is only a simple operation, it is a great possibility that the scrambling outcome we obtain is a certain result of the eight bit-planes or the similar case like this. But these bit-planes have something to do with the original image information, particularly the high bit-planes; therefore, the GB scrambling design needs taking the bit-plane rule into account and making appropriately.

Figure 8 describes the quantum operation circuit of the fast scrambling scheme in detail. The performance of the fast GB scrambling is revealed in Fig. 9, which contains a group of different gray-level images. At the same time, the histogram change is also listed.

Fig. 8
figure 8

The bit-plane arrange and its circuit

Full size image

As the Fig. 8 depicts, it just needs eight simple CNOT gates scrambling only 1 time to accomplish the image scrambling task, so the scrambling speed is very fast, which is helpful to the real-time image processing and transmission in network [31, 32].

Fig. 9
figure 9

Performance of the fast GB scrambling and the histogram change

Full size image

The Fig. 9 shows the image histogram changes by a large margin. The woman and man images are transformed to a meaningless scrambling image, and there is almost no clue of the initial image content. Besides, the histogram tends more to the “standard scrambled image”, the histogram of the “standard scrambled image” is flush on the whole and there are no peaks or canyons in it. Hence, it is understood that the fast quantum GB image scrambling is effective.

  1. (3)

    GB scrambling integrates with position information

In the classical image scrambling processing, image scrambling algorithms based on both position space and color space are few. And the computational cost is also too high. But in the quantum image processing, with the benefit of the flexible quantum image representation, and the excellent properties of qubit, scrambling for a quantum image becomes relatively easy. As a consequence, algorithm design for image scrambling with the position information has its enormous potential in quantum image processing field.

This integration scrambling scheme is based on GB scrambling entirely, which is applied in all of the qubit, including the qubits standing for position information and the qubits standing for grayscale information, respectively.

Fig. 10
figure 10

Circuit of GB scrambling with entire position

Full size image

Here, there are only adding \(M+N\) gates acting on the quantum position bits of a \(2^{M}\times 2^{N}\) image. The quantum position bits are in the superposition state, and every qubit cannot make sure in 0 state or in 1 state. In order to realize scrambling at a lower cost, we adopt a simple and convenient operation to the quantum position bits. For one thing, through all the NOT gates for qubits representing for position information, the image pixels will rotate \(180^{\circ }\) in an anticlockwise direction. For another, the qubits standing for gray information still implemented the Gray-code scrambling as before. After these two scrambling processes, which contain position space scrambling and color space scrambling, the degree of the image chaos will rise dramatically. Specific quantum circuit is shown in Fig. 10. The function of the GB scrambling with entire position can be denoted as:

$$\begin{aligned} ECB(|I\rangle )= & {} \frac{1}{2^{n}}\sum _{X=0}^{2^{M}-1} {\sum _{Y=0}^{2^{N}-1} {GB(|f(X,Y)\rangle )NOT(|XY\rangle )} } \nonumber \\= & {} \frac{1}{2^{n}}\sum _{X=0}^{2^{M}-1} {\sum _{Y=0}^{2^{N}-1} {|g(X,Y)\rangle } } NOT(|X\rangle )NOT(|Y\rangle ) \end{aligned}$$
(9)

In (9), the EGB stands for the function implement of GB scrambling with entire position scheme, and the GB still describes the GB scrambling for only qubits storing gray information. Then, the NOT represents the operation by NOT quantum gate. Consequently, from (9), we can easily see that this scheme with whole position information not only scrambles the gray value, but also scrambles the geometrical coordinates simultaneously.

As Fig. 11 shows, the image after scrambling 3 times with the GB scrambling integrated with position information brings the geometrical element into the GB scrambling in color space. Through such global scrambling, the chaos’ degree rises, and in another way, it obviously speeds up the scrambling speed to some extent.

Fig. 11
figure 11

Result of the scheme in Fig. 10

Full size image
Fig. 12
figure 12

Circuit of another GB scrambling with entire position

Full size image

Accordingly, the GB scrambling technique can be entirely used in all the qubits. Thereupon, the pure GB scrambling on the color space and the position space will come up immediately. Circuit about this scheme can be seen in Fig. 12.

At the same time, two image simulation examples using MATLAB explain the effect after scrambling only 1 time, which are cut in from the initial Lena image (can see the first sub-graph effect in Fig. 3), one’ size is \(16\times 64\), the another is \(32\times 64\). It is quite clear that the entire GB scrambling for both the 8 qubits stands for grayscale and the whole coordinate’s information belongs to a reinforced scrambling edition. Only through scrambling 1 time, the initial image achieves a wonderful transformation performance. Compared with GB scrambling only for gray value, the result is rather outstanding. So it brings us the thought of various methods are used comprehensively and properly in practice as they are needed. Only in this flexible way, we can make the image data transmission more secure and difficult penetrated.

The following Fig. 13 illustrates the result of scrambling 1 times using the circuit in Fig. 12. The first image in two groups is the initial image (the image size of group 1 is \(16\times 64 (2^{4}\times 2^{6})\), and the image size of group 2 is \(32\times 64 (2^{5}\times 2^{6})\). As a contrast, the second is the result of GB scrambling only with qubits representing for grayscale information. The third is the result of GB scrambling with whole qubits representing for position information.

Fig. 13
figure 13

Effect of GB scrambling with whole position

Full size image

Certainly, thinking it over further, for the sake of reducing the quantum gate cost more, some partial position information can be considered to take part in the GB scrambling. This type of strategy is also easy to design. Here, the concrete scheme is not enumerated one by one.

4 Reconstruct strategies

Based on the classical image scrambling knowledge, when the receiver receives the encrypted digital image, to restore the scrambled image is a key step for obtaining the original true image, is also the last step. Hence, the reverse work or the reconstruct strategy is also needed to design.

4.1 For the elementary GB scrambling

As discussed earlier, the GB scrambling has an intrinsic scrambled cycle; therefore, the reconstruction work only needs to carry on repeated and same operation as scrambling operation. In general, the operation times of scrambled image can be chosen as the scrambling key. Thus, in the restoration process, the numerical value, the cycle plus key number, is used as the repeated operation times. The Fig. 14 shows the image restoration circuit of the elementary GB scrambling.

Fig. 14
figure 14

Restore circuit for the elementary GB

Full size image

4.2 For the fast GB scrambling

For the one-time fast scrambling method, according to the quantum information knowledge, we need to rotate the quantum circuit to its symmetrical circuit, and it can reconstruct the image quickly as well. So it is also a fast restoration scheme. The symmetrical circuit is revealed in Fig. 15.

Fig. 15
figure 15

Restore circuit for the fast GB

Full size image

4.3 For the GB scrambling with position

For the first integration scrambling scheme, the two steps are necessary for grayscale information and position information, respectively. As the 4.1 reconstruction shows, the same circuit and repeated operation are applied in qubits standing for grayscale information. At the same time, the qubits standing for position information performed the NOT operation one time like scrambling operation. After the two steps, the original image can be restored completely.

For another integration scrambling scheme, it just needs to use the same repeated way as the elementary GB scrambling scheme for grayscale information, and the restore work can be finished. The scrambling one time only needs M+N+8 CNOT gates, and the complexity is rather small compared with the other quantum image scrambling scheme based on position space like the quantum Hilbert image scrambling.

4.4 Complexity and algorithm analysis

From these scrambling schemes based on Gray-code and bit-plane concept, we can discover that the quantum image scrambling has its own particular advantage, it can easily and flexibly scramble image in both position space and color space owing to the excellent quantum image presentation. And moreover, in some cases, the scrambling effect is more effective and robust than the classical one. The former two GB scrambling schemes need only 8 basic quantum gates, and the network complexity of the last GB scrambling with position information is O(M+N+8) at the most. That is to say, the reconstruction work is not only easy to implement but also low cost. Therefore, the proposed scrambling strategies based on the second-type scrambling is fairly efficient.

5 Conclusion

In this paper, the quantum image Gray-code and bit-plane scrambling scheme, based completely on the color space scrambling, is proposed. Three strategies, the elementary GB scrambling, the fast GB scrambling and the GB scrambling with qubits representing for position information, and their circuits are designed and listed. Meanwhile, some examples of scrambling performance are given to illustrate these schemes in more detail. And they all made a good scrambling effect.

The main contributions of this paper include:

  1. 1.

    Propose the quantum grayscale image scrambling edition based on color space for the first time. And the proposed scheme is not strict to the square image scrambling.

  2. 2.

    Give several different quantum image scrambling strategies and their circuits according to Gray-code and bit-plane theory.

  3. 3.

    The scheme’ cost is rather low, and the scrambling speed is very high, compared with other quantum image scrambling like the Quantum Hilbert scrambling.

  4. 4.

    Start and lead the quantum image scrambling research based on color space.

Consequently, the proposed content about the color space scrambling for quantum image is initial, which will drive more new explorations and researches on quantum image scrambling and further deep processing in the future.