Realization of quantum gates with multiple control qubits or multiple target qubits in a cavity

Abstract

We propose a scheme to realize a three-qubit controlled phase gate and a multi-qubit controlled NOT gate of one qubit simultaneously controlling n-target qubits with a four-level quantum system in a cavity. The implementation time for multi-qubit controlled NOT gate is independent of the number of qubit. Three-qubit phase gate is generalized to n-qubit phase gate with multiple control qubits. The number of steps reduces linearly as compared to conventional gate decomposition method. Our scheme can be applied to various types of physical systems such as superconducting qubits coupled to a resonator and trapped atoms in a cavity. Our scheme does not require adjustment of level spacing during the gate implementation. We also show the implementation of Deutsch–Joza algorithm. Finally, we discuss the imperfections due to cavity decay and the possibility of physical implementation of our scheme.

1 Introduction

Quantum computing has the potential ability to carry out certain computational task much faster than classical computing. For example, factorization of a large number via Shor’s algorithm [1] and the search of an item in an unsorted database containing N elements [2]. Two-qubit gates and one-qubit gates are the building blocks for quantum computing networks [3]. Many physical systems have been proposed as candidates for implementation of quantum information processing like atoms in cavity quantum electrodynamics (QED) and nuclear magnetic resonance (NMR). Among them, cavity QED analogs with superconducting qubit systems are getting favorable attention [4]. A two-qubit gate was experimentally realized using superconducting qubit systems coupled through capacitors [5, 6], mutual inductance [7], or cavities [8].

Multi-qubit gates constructed by the conventional gate decomposition method [9], usually makes the procedure complicated for the case of a large number of qubits. Typically, the number of single-qubit gate and two-qubit gates required for the implementation depends on the number of qubits. In this regard, multi-qubit quantum gates play a significant role in quantum information processing system which involves a large number of qubits. Experimentally, a three-qubit controlled NOT gate has been demonstrated with trapped ions [10] and superconducting circuits [11]. The purpose of this work is to realize three-qubit controlled phase gate and multi-qubit controlled NOT gate of one qubit simultaneously controlling $n$ qubits (which we denote as NTCNOT gate) in cavity QED using a four-level system. We have generalized the scheme to realize an n-qubit-phase gate with multiple control qubits. Our scheme does not require adjustment of level spacing during the gate implementation. Interestingly, the implementation time for multi-qubit controlled NOT gate is independent of number of qubits. We first introduce these gates below before their implementation.

1.1 Two kind of multi-qubit quantum gates

In three-qubit quantum controlled phase gates when two control qubits $\left| q_{1}\right\rangle$ and $\left| q_{2}\right\rangle$ are in state $\left| 1\right\rangle$, phase shift $e^{i\eta }$ induces to the state $\left| 1\right\rangle$ of the target qubit $\left| q_{3}\right\rangle$. When control qubits are in state $\left| 0\right\rangle$, nothing happens to the target qubit. This transformation can be written as [12]

$$\begin{aligned} U_{\eta }^{3}\left| q_{1},q_{2},q_{3}\right\rangle =e^{(i\eta \delta _{q_{1},1}\delta _{q_{2},1},\delta _{q_{3},1})}\left| q_{1},q_{2},q_{3}\right\rangle . \end{aligned}$$

(1)

Here, $\delta _{q_{1},1},\ \delta _{q_{2},1},$ and $\delta _{q_{3},1}$ are the standard Kronecker delta functions and $\left| q_{1}\right\rangle ,\left| q_{2}\right\rangle$ and $\left| q_{3}\right\rangle$ stand for basis states $\left| 0\right\rangle$ or $\left| 1\right\rangle$ for qubits $1,\,2$ and $3$. Circuit for three-qubit controlled phase gate is the same as shown in Fig. 1a. Thus three-qubit quantum phase gate introduces a phase $\eta$ only when the input state of all three qubits is $\left| 1\right\rangle .$ In this proposal, we discuss the implementation of a three-qubit quantum phase gate with $\eta =\pi$. It may be mentioned that three-qubit controlled NOT gate (known as a Toffoli gate) can also be achieved using present proposal. Toffoli gate is equivalent to a three-qubit controlled phase gate plus two Hadamard gates on target qubit as shown in Fig. 1b.

Next, we consider NTCNOT gate which consists of control qubit $1$ and $n$ target qubits labeled as $2,\,3,\ldots ,n$ shown in Fig. 2a. We define control qubit in $\left| 0\right\rangle ,\,\left| 1\right\rangle$ basis and each target qubit in $\left| +\right\rangle ,\,\left| -\right\rangle$ basis. Thus, the input state can be written as

$$\begin{aligned} \left| \psi \right\rangle _{i}=\left| 0\right\rangle \overset{n}{ \underset{k=2}{\prod }}\left( \left| +\right\rangle _{k}+\left| -\right\rangle _{k}\right) +\left| 1\right\rangle \overset{n}{\underset{k=2}{ \prod }}\left( \left| +\right\rangle _{k}+\left| -\right\rangle _{k}\right) . \end{aligned}$$

(2)

Fig. 1

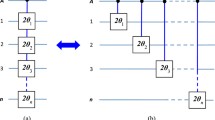
a Three-qubit controlled phase gate. $Z$ represents Pauli rotation $\sigma _{z}$. If control qubits $1$ and $2$ (shown by filled circle) are in state $\left| 1\right\rangle$ then phase of $\pi$ is induced only on state $\left| 1\right\rangle$ at Z. When control qubits are in state $\left| 0\right\rangle$ nothing happens to the target qubit. b Relationship between a three-qubit CNOT gate (known as a Toffoli gate) and a three-qubit controlled phase gate. The circuits on left side and right side of (b) are equivalent to each other. The symbol $\oplus$ on left side of (b) represents NOT gate on target qubit. If control qubits $1$ and $2$ are in state $\left| 1\right\rangle$, then the state at $\oplus$ is flipped such that $\left| 1\right\rangle \,\rightarrow \left| 0\right\rangle$ and $\left| 0\right\rangle \,\rightarrow \left| 1\right\rangle$. However, when control qubits $1$ and $2$ are in state $\left| 0\right\rangle$, then the state at $\oplus$ remains unchanged. For right side of (b), portion enclosed in dashed box represents a three-qubit controlled phase gate. The element $H$ is called a Hadamard gate and leads to the transformation $\left| 0\right\rangle \rightarrow \left| +\right\rangle =(1/\sqrt{2})(\left| 0\right\rangle +\left| 1\right\rangle )$ and $\left| 1\right\rangle \rightarrow \left| -\right\rangle =(1/\sqrt{2})(\left| 0\right\rangle -\left| 1\right\rangle )$

When the NTCNOT gate is applied to the state given by Eq. (1), we obtain

$$\begin{aligned} \left| \psi \right\rangle _{f}=\left| 0\right\rangle \overset{n}{ \underset{k=2}{\prod }}\left( \left| +\right\rangle _{k}+\left| -\right\rangle _{k}\right) +\left| 1\right\rangle \overset{n}{\underset{k=2}{ \prod }}\left( \left| -\right\rangle _{k}+\left| +\right\rangle _{k}\right) . \end{aligned}$$

(3)

It is clear from Eqs. 2 and 3 that when control qubit is in state $\left| 1\right\rangle$, then the state at each target qubit is flipped as $\left| +\right\rangle$ $\rightarrow \left| -\right\rangle$ and $\left| -\right\rangle \,\rightarrow \left| +\right\rangle .$ If control qubit is in state $\left| 0\right\rangle$, nothing happens to each target qubit. It may be mentioned that the NTCNOT gate can be defined in $\left| +\right\rangle ,\, \left| -\right\rangle$ basis. However, two Hadamard gates on control qubit before and after the phase gate with one qubit simultaneously controlling $n$ target qubits would be required as shown in Fig. 2b. The NTCNOT gate can also be defined in $\left| 0\right\rangle ,\, \left| 1\right\rangle$ basis. However, in this case, Hadamard gate on each target qubit before and after the n-target controlled phase gate [i.e., $2(n-1)$ Hadamard gate] would be required as shown in Fig. 2c. In contrast, defining the control qubit in $\left| 0\right\rangle ,\,\left| 1\right\rangle$ basis and each target qubit in $\left| +\right\rangle ,\,\left| -\right\rangle$ basis do not require Hadamard gate (as shown in Sec.  III B) which makes the procedure for the implementation of NTCNOT gate quite simple.

Fig. 2

a Schematic circuit of the NTCNOT gate with qubit $1$ simultaneously, controlling $n$ target qubits. The NTCNOT gate is equivalent to $n$ two-qubit CNOT gates each having a shared control qubit $1$ with different target qubits $2,3,\ldots ,n$. In this case, qubit $1$ is defined in $\left| 0\right\rangle ,\,\left| 1\right\rangle$ basis while the target qubits $2,3,\ldots ,n$ are defined in $\left| +\right\rangle ,\, \left| -\right\rangle$ basis. b Equivalent circuit of NTCNOT gate in $\left| +\right\rangle ,\,\left| -\right\rangle$ basis. The symbol $Z$ represents a phase shift of $\ \pi$ on each target qubit. If control qubit $1$ is in state $\left| -\right\rangle$ then the state $\left| -\right\rangle$ at each $Z$ is phase-shifted as $\left| -\right\rangle \rightarrow -\left| -\right\rangle$ while state $\left| +\right\rangle$ remains unchanged. However, if control qubit $1$ is in state $\left| +\right\rangle ,$ then states $\left| +\right\rangle$ or $\left| -\right\rangle$ at each $Z$ remain unchanged. c Equivalent circuit of NTCNOT gate in $\left| 0\right\rangle ,\,\left| 1\right\rangle$ basis. The symbol $Z$ represents phase shift of $\pi$ on each target qubit. If control qubit $1$ is in state $\left| 1\right\rangle$ then state $\left| 1\right\rangle$ at each $Z$ is phase-shifted as $\left| 1\right\rangle \rightarrow -\left| 1\right\rangle$ while state $\left| 0\right\rangle$ remains unchanged. However, if control qubit $1$ is in state $\left| 0\right\rangle ,$ then states $\left| 0\right\rangle$ or $\left| 1\right\rangle$ at each $Z$ remain unchanged. It may be noted that $2(n-1)$ Hadamard gates are required in this case

1.2 Motivation and advantages

Multi-qubit quantum controlled phase gate as shown in Fig. 1 plays a key role in the realization of quantum error correction [13] and implementation of Grover’s algorithm for eight objects [14, 15]. Quantum gate with multiple target qubits shown in Fig. 2 are of great importance for the realization of entanglement preparation [16], error correction [17], discrete cosine transform [18], and quantum cloning [19]. Some interesting scheme for the realization of multi-qubit quantum gates have been proposed. For example, Chang et al. [20] presented a three-qubit quantum phase gate with a four-level atom in a cascade configuration initially prepared in their ground state interacting with a three-mode optical cavity. Yang et al. [21, 22] presented an n-qubit controlled phase gate with superconducting quantum interference devices (SQUIDs) by coupling them to a superconducting resonator. Recently, some interesting schemes are also proposed for the realization of a multi-qubit phase gate with a fixed phase shift of $\pi$ on each target qubit and multi-qubit phase gate with a random phase shift on each target qubit [23–25].

Our goal here is to realize a three-qubit controlled phase gate shown in Fig. 1a and a NTCNOT gate shown in Fig. 2a with a four-level quantum system in a cavity or coupled to a superconducting resonator. Our proposal has several advantages, for example (1) Decoherence due to spontaneous decay of level $\left| 3\right\rangle$ is suppressed because the excited level $\left| 3\right\rangle$ is unpopulated during the gate operation. (2) The adjustment of level spacing of the qubit system during the gate operations is not needed which may cause decoherence. (3) Operation time for the realization of the NTCNOT gate is independent of the number of qubits. (4) In case of a flux (SQUID) qubit system, each qubit can have much longer storage time. (5) We do not require identical coupling constants for each qubit system with cavity mode. Similarly, detuning of the cavity mode with the transition of the relevant levels in every target qubit system is not identical; therefore our scheme is tolerable to inevitable non-uniformity in device parameters. (6) Finite second-order detuning $\delta =\Delta _{c}-\Delta _{\upmu }$ is not required which improves the gate speed by one order. (7) Three-qubit controlled phase gate shown in Fig. 1 is generalized to n-qubit quantum gate with multiple control qubits. Interestingly, complexity (number of operations) reduces linearly as compared to the conventional gate decomposition method. In addition, our proposal is quite general and can be applied to various kind of four-level physical systems like superconducting devices coupled to a superconducting resonator and trapped atoms in a cavity.

2 System dynamics

We consider here a four-level qubit system which could be either natural atoms or artificial atoms as shown in Fig. 3. It may be mentioned that Fig. 3 applies to (a) a superconducting charged qubit [26], (b) a phase qubit system [27–29], (c) a flux qubit system [26, 30] and (d) a SQUID [31]. The four-level energy diagram shown in Fig. 3b could also be applied to atoms [24].

2.1 System-cavity-pulse resonance Raman interaction

We consider a four-level qubit system $1$ and $2$ coupled to a single-mode cavity field and driven by a classical microwave pulse as shown in Figs. 4a and b. Consider qubit system $1$ for which cavity mode is coupled to $\left| 2\right\rangle _{1}\leftrightarrow \left| 3\right\rangle _{1}$ transition, however, highly decoupled from the transition between any other two levels. In addition, microwave pulse is also applied which is coupled to $\left| 1\right\rangle _{1}\leftrightarrow \left| 3\right\rangle _{1}$ transition however, highly decoupled from the transition between any other two levels as shown in Fig. 4a. The Hamiltonian of the system can be written as

$$\begin{aligned} H&= \hbar \omega _{c}a^{\dag }a\ +\underset{n=1}{\overset{3}{\sum }} E_{n}\left| n\right\rangle _{1}\left\langle n\right| +\hbar g_{1}\left( a^{\dag }\left| 2\right\rangle _{1}\left\langle 3\right| +H.c.\right) \nonumber \\&\quad +\,\hbar \Omega _{13}\left( e^{i\omega _{\upmu }t}\left| 1\right\rangle _{1}\left\langle 3\right| +H.c\right) , \end{aligned}$$

(4)

Fig. 3

Desired four-level qubit systems with four energy levels $\left| 0\right\rangle ,\,\left| 1\right\rangle ,\,\left| 2\right\rangle ,$ and $\left| 3\right\rangle$, respectively. a Represents a charged qubit system: the transition frequencies between the levels satisfy the conditions $\nu _{21}>\nu _{10},\,\nu _{32}$ and $\nu _{32}< \nu _{10}.$ b Represents a phase qubit system: the transition frequencies between the levels satisfy the conditions $\nu _{10}>\nu _{21}>\,\nu _{32}$. c Represents a flux qubit system: the transition frequencies between the levels satisfy the conditions $\ \nu _{21}>\nu _{10},\,\nu _{32}$ and $\nu _{32}>\nu _{10}$. d Represents a SQUIDs qubit system: the transition frequencies between the levels satisfy the conditions $\nu _{32}\,< \nu _{21}<\nu _{20}<\nu _{31}<\nu _{30}$. The levels $\left| 0\right\rangle$ and $\left| 2\right\rangle$ lie in right well of SQUID while level $\left| 1\right\rangle$ lies in left well of SQUID (see Fig. 7), such that their is potential barrier between these two wells

where $a^{\dag } (a)$ is the photon creation (annihilation) operator for the cavity mode with frequency $\omega _{c}$ and $g_{1}$ is the coupling constant between the cavity mode and $\left| 2\right\rangle _{1}\leftrightarrow \left| 3\right\rangle _{1}$ transition of qubit system $1$. The Rabi frequency of pulse is $\Omega _{13}$ having frequency $\omega _{\mu }$. We assume that the cavity mode is off-resonant with $\left| 2\right\rangle _{1}\leftrightarrow \left| 3\right\rangle _{1}$ transition of the qubit system $1$ (i.e., $\Delta _{c}=\omega _{32}-\omega _{c}>>g_{1}$). Here, $\Delta _{c}$ is the detuning between $\left| 2\right\rangle _{1}\leftrightarrow \left| 3\right\rangle _{1}$ transition frequency $\omega _{32}$ of the qubit system $1$ and cavity field frequency $\omega _{c}$. Microwave pulse is off-resonant with $\left| 1\right\rangle _{1}\leftrightarrow \left| 3\right\rangle _{1}$ transition of the qubit system $1$ (i.e., $\Delta _{\mu }=\omega _{13}-\omega _{\mu }>>\Omega _{13}$ ). Here, $\Delta _{\mu }$ is the detuning between $\left| 1\right\rangle _{1}\leftrightarrow \left| 3\right\rangle _{1}$ transition frequency $\omega _{13}$ of the qubit system $1$ and pulse frequency $\omega _{\mu }$. The level $\left| 3\right\rangle _{1}$ can be eliminated adiabatically as discussed in Ref.[32]. Thus, for the case when $\Delta _{\mu }=\Delta _{c}$, the effective Hamiltonian in the interaction picture (assuming $\hbar =1$) can be written as [31]

$$\begin{aligned} H_{I}&= -\left[ \frac{\Omega _{13}^{2}}{\Delta _{c}}\left| 1\right\rangle _{1}\left\langle 1\right| +\frac{g_{1}^{2}}{\Delta _{c}}a^{\dag }a\left| 2\right\rangle _{1}\left\langle 2\right| +\,\, \frac{\Omega _{13}g_{1}}{\Delta _{c}}(a^{\dag }\left| 2\right\rangle _{1}\left\langle 1\right| + {\text{ H.c. }}\right] \end{aligned}$$

(5)

Fig. 4

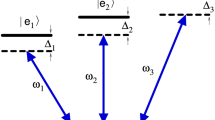
a System-cavity-pulse resonance Raman coupling for qubit system $1$. Here, $\Delta _{c}=\omega _{32}-\omega _{c}$ is the detuning between $\left| 2\right\rangle _{1}\leftrightarrow \left| 3\right\rangle _{1}$ transition frequency $\omega _{32}$ of the qubit system $1$ and frequency of cavity field $\omega _{c}$, while $\Delta _{\mu }=\omega _{13}-\omega _{\mu }$ is the detuning between $\left| 1\right\rangle _{1}\leftrightarrow \left| 3\right\rangle _{1}$ transition frequency $\omega _{13}$ of the qubit system $1$ and frequency of pulse $\omega _{\mu }$. Both detunings are set to be equal (i.e., $\Delta _{\mu }= \Delta _{c}$) to establish resonance Raman coupling between level $\left| 1\right\rangle _{1}$ and $\left| 2\right\rangle _{1}.$ Rabi frequency of pulse applied is $\Omega _{13}$ and $g_{1}$ is the coupling constant between the cavity mode and $\left| 2\right\rangle _{1}\leftrightarrow \left| 3\right\rangle _{1}$ transition of qubit system $1$. b System-cavity-pulse resonance Raman coupling between level $\left| 0\right\rangle _{2}$ and $\left| 2\right\rangle _{2}$ for qubit system $2.$ Rabi frequency of pulse applied is $\Omega _{03}$ and $g_{2}$ is the coupling constant between the cavity mode and $\left| 2\right\rangle _{2}\leftrightarrow \left| 3\right\rangle _{2}$ transition of qubit system $2$. c System-cavity off-resonant interaction for qubit system $k=2,3,\ldots ,n$. Cavity mode is off-resonant with $\left| 2\right\rangle _{k}\leftrightarrow \left| 3\right\rangle _{k}$ transition of qubit system $k$ with detuning $\Delta _{c,k}$ and coupling constant $g_{k}$

The last two terms describe resonance Raman coupling between levels $\left| 1\right\rangle _{1}$ and $\left| 2\right\rangle _{1}.$ For $\Omega _{13}=g_{1},$ initial state $\left| 2\right\rangle _{1}\left| 1\right\rangle _{c}$ and $\left| 1\right\rangle _{1}\left| 0\right\rangle _{c}$ of the qubit system $1,$ under the Hamiltonian given by Eq.(5) can be written as

$$\begin{aligned} \left| 1\right\rangle _{1}\left| 0\right\rangle _{c}&\rightarrow e^{i\theta }[{\text{ cos }}(\theta )\left| 1\right\rangle _{1}\left| 0\right\rangle _{c}-i{\text{ sin }}(\theta )\left| 2\right\rangle _{1}\left| 1\right\rangle _{c}], \end{aligned}$$

(6)

$$\begin{aligned} \left| 2\right\rangle _{1}\left| 1\right\rangle _{c}&\rightarrow e^{i\theta }[{\text{ cos }}(\theta )\left| 2\right\rangle _{1}\left| 1\right\rangle _{c}-i{\text{ sin }}(\theta )\left| 1\right\rangle _{1}\left| 0\right\rangle _{c}]. \end{aligned}$$

(7)

Here, $\theta =g_{1}^{2}t/\Delta _{c}$ and $\left| 0\right\rangle _{c}\, ( \left| 1\right\rangle _{c})$ is the vacuum state (single-photon state) of the cavity field. The state $\left| 0\right\rangle _{1}\left| 0\right\rangle _{c}$ remains unchanged under the Hamiltonian given by Eq.(5). For pulse duration $t_{1}=\pi \Delta _{c}/(2g_{1}^{2})$ (i.e., $\theta = \frac{\pi }{2}$), we obtain the transformation $\left| 1\right\rangle _{1}\left| 0\right\rangle _{c}\rightarrow \left| 2\right\rangle _{1}\left| 1\right\rangle _{c}$ and $\left| 2\right\rangle _{1}\left| 1\right\rangle _{c}\rightarrow \left| 1\right\rangle _{1}\left| 0\right\rangle _{c}$ for qubit system $1$ and cavity field. We denote this transformation as $G_{1}$. In case of qubit system $2$, for notation convenience we denote ground state (first excited state) as level $\left| 1\right\rangle _{2}$ ($\left| 0\right\rangle _{2}$) as shown in Fig. 4b. The cavity mode is coupled to $\left| 2\right\rangle _{2}\leftrightarrow \left| 3\right\rangle _{2}$ transition, while microwave pulse is coupled to $\left| 0\right\rangle _{2}\leftrightarrow \left| 3\right\rangle _{2}$ transition of qubit system $2$ as shown in Fig. 4b. In a similar fashion, for pulse duration $t_{2}=\pi \Delta _{c}/(2g_{2}^{2})$, we obtain the transformation $\left| 0\right\rangle _{2}\left| 0\right\rangle _{c}\rightarrow \left| 2\right\rangle _{2}\left| 1\right\rangle _{c}$ and $\left| 2\right\rangle _{2}\left| 1\right\rangle _{c}\rightarrow \left| 0\right\rangle _{2}\left| 0\right\rangle _{c}$ for qubit system $2$ and the cavity field. We denote this transformation as $G_{2}.$ The states $\left| 1\right\rangle _{2}\left| 0\right\rangle _{c}$ and $\left| 1\right\rangle _{2}\left| 1\right\rangle _{c}$ of qubit system remain unchanged under the transformation $G_{2}$.

2.2 System-cavity off-resonant interaction

Next we, consider qubit system $k$, for which cavity field interacts off-resonantly with $\left| 2\right\rangle _{k}\leftrightarrow \left| 3\right\rangle _{k}$ transition (i.e., $\Delta _{c,k}=\omega _{c}-\omega _{32}>>g_{k})$ while remains decoupled from any transition between the other levels as shown in Fig. 4c. Here, $\Delta _{c,k}$ is the detuning between $\left| 2\right\rangle _{k}\leftrightarrow \left| 3\right\rangle _{k}$ transition frequency $\omega _{32}$ of qubit system $k$ and $\omega _{c}$ is the cavity field frequency while $g_{k}$ is the coupling constant between the resonator mode and $\left| 2\right\rangle _{k}\leftrightarrow \left| 3\right\rangle _{k}$ transition. The effective Hamiltonian for the system in the interaction picture can be written as [33]

$$\begin{aligned} H_{1}=\frac{\hbar g_{k}^{2}}{\Delta _{c,k}}(\left| 3\right\rangle _{k}\left\langle 3\right| -\left| 2\right\rangle _{k}\left\langle 2\right| )a^{\dag }a. \end{aligned}$$

(8)

In the presence of a single photon in the cavity, the evolution of the initial state $\left| 2\right\rangle \left| 1\right\rangle _{c}$ and $\left| 3\right\rangle \left| 1\right\rangle _{c}$ is given by

$$\begin{aligned} \left| 2\right\rangle _{k}\left| 1\right\rangle _{c}&\rightarrow e^{ig_{k}^{2}t/\Delta _{c,k}}\left| 2\right\rangle _{k}\left| 1\right\rangle _{c}, \nonumber \\ \left| 3\right\rangle _{k}\left| 1\right\rangle _{c}&\rightarrow e^{-ig_{k}^{2}t/\Delta _{c,k}}\left| 3\right\rangle _{k}\left| 1\right\rangle _{c}. \end{aligned}$$

(9)

It is clear that the phase shift of $e^{ig_{k}^{2}t/\Delta _{c,k}} ( e^{-ig_{k}^{2}t/\Delta _{c,k}})$ is induced to the state $\left| 2\right\rangle _{k}\left| 1\right\rangle _{c} (\left| 3\right\rangle \left| _{k}1\right\rangle _{c})$ for qubit system $k$. However, states $\left| 2\right\rangle _{k}\left| 0\right\rangle _{c}$ and $\left| 3\right\rangle _{k}\left| 0\right\rangle _{c}$ remain unchanged.

2.3 System-pulse resonant interaction

Let us assume that we apply a microwave pulse which is resonant to $\left| j\right\rangle \rightarrow \left| 2\right\rangle$ transition of each qubit system. Here, $j=1$ for qubit system $1$ and $k$, while $j=0$ for qubit system $2$. Then, the evolution of state is given by [34]

$$\begin{aligned} \left| j\right\rangle&\rightarrow {\text{ cos }}(\Omega _{j2}\tau )\left| j\right\rangle -ie^{-i\varphi }{\text{ sin }}(\Omega _{j2}\tau )\left| 2\right\rangle , \nonumber \\ \left| 2\right\rangle&\rightarrow {\text{ cos }}(\Omega _{j2}\tau )\left| 2\right\rangle -ie^{i\varphi }{\text{ sin }}(\Omega _{j2}\tau )\left| j\right\rangle , \end{aligned}$$

(10)

where $\Omega _{j2}$ is the Rabi frequency between the two levels $\left| j\right\rangle$ and $\left| 2\right\rangle$. Here $\tau$ represents interaction time of qubit system with microwave pulse and $\varphi$ is the associated phase. For pulse duration $\tau =\pi /(2\Omega _{j2})$ and phase $\varphi =\pi /2,$ transformation $\left| 2\right\rangle (\left| j\right\rangle )\rightarrow \left| j\right\rangle (-\left| 2\right\rangle )$ is obtained which is denoted by $R$. For phase $\varphi =-\pi /2,$ we obtain the transformation $\left| 2\right\rangle (\left| j\right\rangle )\rightarrow -\left| j\right\rangle (\left| 2\right\rangle )$ denoted by $R^{\dagger }$. It may be mentioned that the resonant interaction of microwave pulse with qubit system can be carried out in a very short time by increasing the Rabi frequency of the pulse.

3 Implementation of multi-qubit gates

The goal of this section is to demonstrate how a three-qubit quantum phase gate and an NTCNOT gate can be realized based on system dynamics described in Sect. 2.

3.1 Three-qubit controlled phase gate

We consider a qubit system $1,\,2$ and $k$ (with $k=3$) as shown in Fig. 4 for the implementation of a three-qubit controlled phase gate. For each qubit system, two lowest energy levels $\left| 0\right\rangle$ and $\left| 1\right\rangle$ represent logical state of each qubit while other higher energy levels $\left| 2\right\rangle$ and $\left| 3\right\rangle$ are utilized for gate realization. We assume that the cavity is initially prepared in a vacuum state $\left| 0\right\rangle _{c}.$ The three-qubit controlled phase gate can be realized using the following steps:

• Step (i): Apply transformation $G_{1}$ to qubit system $1$ for time $t_{1}$. When qubit $1$ is initially in state $\left| 1\right\rangle _{1}$, a photon is emitted inside cavity. However, the state $\left| 0\right\rangle _{1}\left| 0\right\rangle _{c}$ remains unchanged under the transformation $G_{1}.$

• Step (ii): Apply transformation $R$ to qubit system $1$ and $R^{\dagger }$ to qubit system $2$, simultaneously. In this step, we set $\tau =\pi /(2\Omega _{02})=\pi /(2\Omega _{12})$ by adjusting the intensities of the two microwave pulses.

• Step (iii): After the above operations, level $\left| 2\right\rangle _{1}$ of qubit system $1$ is unpopulated. While the level $\left| 0\right\rangle _{2}$ of qubit system $2$ transforms to level $\left| 2\right\rangle _{2}.$ Apply transformation $G_{2}$ (for time duration $t_{2}$) to qubit system $2$ which absorbs a single photon from the cavity. However, if qubit system $2$ is in state $\left| 1\right\rangle$, the single photon remains there.

• Step (iv): Apply transformation $R^{\dagger }$ (for time duration $\tau$) to qubit system $k=3$. After this operation, when cavity is in a single-photon state, level $\left| 2\right\rangle$ of both qubit system $1$ and $2$ are unpopulated. Under this condition, cavity field interacts off-resonantly to $\left| 2\right\rangle _{3}\rightarrow \left| 3\right\rangle _{3}$ transition of qubit system $3$. It is clear from Eq. (9) that for $t_{3}=(\pi \Delta _{c,3})/g_{3}^{2}$, state $\left| 2\right\rangle _{3}\left| 1\right\rangle _{c}$ of qubit system $3$ changes to $-\left| 2\right\rangle _{3}\left| 1\right\rangle _{c}$. In Fig. 5, $G_{\pi }$ represents this transformation. However, states $\left| 0\right\rangle _{3}\left| 0\right\rangle _{c},\,\left| 0\right\rangle _{3}\left| 1\right\rangle _{c}$ and $\left| 2\right\rangle _{3}\left| 0\right\rangle _{c}$ of qubit system $3$ remain unchanged. Finally, apply transformation $R$ (for time duration $\tau$) to qubit system $3$.

• Step (v): Apply transformation $G_{2}$ (for time duration $t_{2}$) to qubit system $2$.

• Step (vi): Apply transformation $R^{\dagger }$ to qubit system $1$ and $R$ to qubit system $2$, simultaneously, for time duration $\tau$.

• Step (vii): Apply transformation $G_{1}$ to qubit system $1$ for time $t_{1}$. As a result, qubit $1$ is transformed back to state $\left| 1\right\rangle _{1}$ while the cavity field returns to its original vacuum state.

All these operations are schematically presented in Fig. 5. The states of the whole system after these operations are summarized as

$$\begin{aligned}&\begin{array}{c} \left| 100\right\rangle \left| 0\right\rangle _{c} \\ \left| 101\right\rangle \left| 0\right\rangle _{c} \\ \left| 110\right\rangle \left| 0\right\rangle _{c} \\ \left| 111\right\rangle \left| 0\right\rangle _{c}\\ \end{array} \overset{1}{\rightarrow }\begin{array}{c} \left| 200\right\rangle \left| 1\right\rangle _{c} \\ \left| 201\right\rangle \left| 1\right\rangle _{c} \\ \left| 210\right\rangle \left| 1\right\rangle _{c} \\ \left| 211\right\rangle \left| 1\right\rangle _{c} \end{array} \overset{2}{\rightarrow } \begin{array}{c} |120\rangle \left| 1\right\rangle _{c} \\ \left| 121\right\rangle \left| 1\right\rangle _{c} \\ |110\rangle \left| 1\right\rangle _{c} \\ \left| 111\right\rangle \left| 1\right\rangle _{c} \end{array} \overset{3}{\rightarrow } \nonumber \\&\quad \begin{array}{c} |100\rangle \left| 0\right\rangle _{c} \\ \left| 101\right\rangle \left| 0\right\rangle _{c} \\ |110\rangle \left| 1\right\rangle _{c} \\ \left| 111\right\rangle \left| 1\right\rangle _{c} \end{array} \overset{4}{\rightarrow } \begin{array}{c} |100\rangle \left| 0\right\rangle _{c} \\ \left| 101\right\rangle \left| 0\right\rangle _{c} \\ |110\rangle \left| 1\right\rangle _{c} \\ \text {-}\left| 111\right\rangle \left| 1\right\rangle _{c} \end{array} \overset{5}{\rightarrow } \begin{array}{c} |120\rangle \left| 1\right\rangle _{c} \\ \left| 121\right\rangle \left| 1\right\rangle _{c} \\ |110\rangle \left| 1\right\rangle _{c} \\ \text {-}\left| 111\right\rangle \left| 1\right\rangle _{c} \end{array}\nonumber \\&\overset{6}{\rightarrow } \begin{array}{c} |200\rangle \left| 1\right\rangle _{c} \\ \left| 201\right\rangle \left| 1\right\rangle _{c} \\ |210\rangle \left| 1\right\rangle _{c} \\ \text {-}\left| 211\right\rangle \left| 1\right\rangle _{c} \end{array} \overset{7}{\rightarrow } \begin{array}{c} |100\rangle \left| 1\right\rangle _{c} \\ \left| 101\right\rangle \left| 1\right\rangle _{c} \\ |110\rangle \left| 1\right\rangle _{c} \\ \text {-}\left| 111\right\rangle \left| 1\right\rangle _{c}. \end{array} \end{aligned}$$

(11)

Fig. 5

Schematic diagram for the implementation of three-qubit controlled phase gate. Here $G_{1}$ represents the system-cavity-pulse resonance Raman coupling between level $\left| 1\right\rangle _{1}$ and $\left| 2\right\rangle _{1}$ for qubit system $1$ while $G_{2}$ represents system-cavity-pulse resonance Raman coupling between level $\left| 0\right\rangle _{2}$ and $\left| 2\right\rangle _{2}$ for qubit system $2.\,G_{\pi }$ is system-cavity off-resonant interaction where as $R$ and $R^{\dagger }$ represents system-pulse resonant interaction

Here, state $\left| abc\right\rangle$ is the abbreviation for the states $\left| a\right\rangle _{1},\,\left| b\right\rangle _{2}$ and $\left| c\right\rangle _{k}$ for qubit ($1,\,2$, and $3$) with $a,b,c \,\in [0,1,2]$. On the other hand, states $\left| 000\right\rangle \left| 0\right\rangle _{c},\,\left| 001\right\rangle \left| 0\right\rangle _{c},\, \left| 010\right\rangle \left| 0\right\rangle _{c}$ and $\left| 011\right\rangle \left| 0\right\rangle _{c}$ remain unchanged. It is due to the fact that the state $\left| 0\right\rangle _{1}$ of the qubit system $1$ is not effected by the application of transformation $G_{1}$ i.e., no photon is emitted inside cavity when qubit $1$ is in state $\left| 0\right\rangle _{1}.$ Hence, it is clear from Eq. (11) that a three-qubit controlled phase gate can be achieved with three qubits (i.e., control qubit $1,\,2$, and target qubit $3$). Present proposal provides a simple way to realize the Toffoli gate shown in Fig. 1b. It is well known that at least six two-qubit controlled NOT gates and ten single-qubit gates (i.e., two Hadamard, one phase , and seven $\pi /8$ gates) are required to construct a Toffoli gate by conventional gates decomposition methods [35, 36]. The two-qubit CNOT gate is equivalent to two Hadamard gate and a single two-qubit phase gate. If we assume that the realization of single-qubit gate and two-qubit phase gate requires only one step operation, then by using conventional gate decomposition method, at least $28$ steps will be required to realize Toffoli gate. However, present proposal requires only nine steps i.e., seven steps for three-qubit phase gate plus two steps operations for two Hadamard gate which is quite interesting.

Our scheme can easily be generalized to n-qubit controlled phase gate with multiple control qubits. For this purpose, we need to apply transformation (1) $G_{1}$ and $R$ to qubit 1. (2) $R^{\dag }$ and $G_{2}$ to qubit system $2,3,\ldots ,n-1.$ (3) $R^{\dag },\,G_{\pi }$, and $R$ to last qubit. (4) $G_{2}$ and $R$ to qubit system $2,3,\ldots ,n-1$. (5) $R^{\dag }$ and $G_{1}$ to qubit 1. Hence, n-qubit controlled phase gate can be achieved by a sequence of operations which are summarized as

$$\begin{aligned} U_{\eta }^{n}=G_{1}\otimes R^{\dag }\otimes \prod _{n-1}^{i=2}\left[ \overset{i}{R} \otimes \overset{i}{G}_{2}\right]&\otimes (R\otimes G_{\pi } \nonumber \\ \otimes R^{\dag })\otimes \prod _{i=2}^{n-1}\left[ \overset{i}{G}_{2}\otimes \overset{i}{R^{\dag }}\right]&\otimes R\otimes G_{1}, \end{aligned}$$

(12)

where $\prod _{n-1}^{i=2}\overset{i}{G}=\overset{2}{G}\otimes \overset{3}{G} \otimes \ldots \otimes \overset{n-1}{G}$ while $\prod _{i=2}^{n-1}\overset{i}{G}= \overset{n-1}{G}\otimes \ldots \otimes \overset{3}{G}\otimes \overset{2}{G}$. Realization of n-qubit CNOT gate with multiple control qubit can be implemented through $H\otimes U_{\eta }^{n}\otimes H$ transformations.

The total number of steps, required for n-qubit quantum phase gate with multiple control qubits and n-qubit CNOT gate are $4n-5$ and $4n-3$, respectively. According to conventional gate decomposition method, $2n-5$ Toffoli gates are required for n-qubit CNOT gate [35, 36]. As mentioned above, single Toffoli gate required at least $28$ steps of operations. Thus, total number of steps for n-qubit CNOT gate are $(2n-5)\times 28=56n-140$, and for n-qubit controlled phase gate are $56n-142$. In order to make a quantitative comparison of the two approaches, we show the plot of the number of steps for the gate operation as a function of number of qubits n in Fig. 6. It can be seen that the number of steps for gate decomposition method increases rapidly with n as compared to multi-qubit gate. The reduction in the number of steps is $52n-137$. It is clear that , our scheme reduces the number of steps (complexity) linearly as compared to conventional gate decomposition method.

Fig. 6

Plot of the gate implementation steps against the number of qubits

3.2 NTCNOT gate

In order to implement NTCNOT gate, we consider qubit system $1$ (as shown in Fig. 4a) initially prepared in state $(\left| 0\right\rangle _{1}+\left| 1\right\rangle _{1})\,/\sqrt{2}.$ In this case, we consider $n-1$ qubit system of type $k$ as shown in Fig. 4c with $k=2,3,\ldots n$. Each qubit system $k$ is initially prepared in state $\left| 0\right\rangle _{k}$. In the new rotated basis for qubit system $k$, the state of the whole system can be written as

$$\begin{aligned} \left| \psi \right\rangle =\frac{1}{2}(\left| 0\right\rangle _{1}+\left| 1\right\rangle _{1})\otimes \overset{n}{\underset{k=2}{\prod }}(\left| +\right\rangle _{k}+\left| -\right\rangle _{k}), \end{aligned}$$

(13)

where, $\left| \pm \right\rangle _{k}=1/\sqrt{2}(\left| 0\right\rangle _{k}\pm \left| 1\right\rangle _{k}).$ The operations required for realizing NTCNOT gate are described as follow:

• Step (i): Apply transformation $G_{1}$ to qubit system $1$ for time $t_{1}.$ Namely, when qubit $1$ is initially in state $\left| 1\right\rangle _{1}$, a photon is emitted in cavity. However, the state $\left| 0\right\rangle _{1}\left| 0\right\rangle _{c}$ remain unchanged under transformation $G_{1}.$

• Step (ii): Apply transformation $R$ to qubit system $1$ and $R^{\dagger }$ to each qubit system $k$ for time duration $\tau$, simultaneously. As a result transformation $\left| +\right\rangle _{k}(\left| -\right\rangle _{k})\rightarrow \left| a\right\rangle _{k}(\left| b\right\rangle _{k})$ is obtained for each qubit system $k$. Here, $\left| a\right\rangle _{k}=1/\sqrt{2}(\left| 0\right\rangle _{k}+\left| 2\right\rangle _{k})$ and $\left| b\right\rangle _{k}=1/ \sqrt{2}(\left| 0\right\rangle _{k}-\left| 2\right\rangle _{k}).$

• Step (iii): After above operations, when cavity is in single photon state, level $\left| 2\right\rangle _{1}$ and level $\left| 3\right\rangle _{1}$ of qubit system $1$ is unpopulated. Under this condition, cavity field interacts off-resonantly to $\left| 2\right\rangle _{k}\rightarrow \left| 3\right\rangle _{k}$ transition of each qubit system $k$. It is clear from Eq. (9) that for $t_{k}=(\pi \Delta _{c,k})/g_{k}^{2}$, the state $\left| 2\right\rangle _{k}\left| 1\right\rangle _{c}$ of each qubit system $k$ changes to $-\left| 2\right\rangle _{k} \left| 1\right\rangle _{c}$. In the presence of single photon in cavity, the state $\left| a\right\rangle _{k}\left| 1\right\rangle _{c}$ of each qubit system $k$ changes to $\left| b\right\rangle _{k}\left| 1\right\rangle _{c}$ while $\left| b\right\rangle _{k}\left| 1\right\rangle _{c}$ of each qubit system $k$ changes to $\left| a\right\rangle _{k}\left| 1\right\rangle _{c}$. However, states $\left| a\right\rangle _{2}\left| 0\right\rangle _{c}$ and $\left| b\right\rangle _{2}\left| 0\right\rangle _{c}$ remain unchanged.

• Step (iv): Apply transformation $R^{\dagger }$ to qubit system $1$ and $R$ to each qubit system $k$ for time duration $\tau$, simultaneously.

• Step (v): Apply transformation $G_{1}$ to qubit system $1$ for time $t_{1}$. As a result, qubit $1$ is transformed back to state $\left| 1\right\rangle _{1}$ while cavity field returns to its original vacuum state.

After the above operations, one can easily see that controlled NOT gate of one qubit simultaneously controlling $n$ qubits described by Eqs.  (2) and (3) is achieved with $n$ qubit system (i.e., control qubit $1$ and target qubit systems $k=2,3,\ldots n$ ).

In order to get an insight, here we consider an example of three-qubit case. In this case, states of the whole system after the above operations can be summarized as follows:

$$\begin{aligned}&\begin{array}{c} \left| 1++\right\rangle \left| 0\right\rangle _{c} \\ \left| 1+-\right\rangle \left| 0\right\rangle _{c} \\ \left| 1-+\right\rangle \left| 0\right\rangle _{c} \\ \left| 1--\right\rangle \left| 0\right\rangle _{c} \end{array} \overset{1}{\rightarrow } \begin{array}{c} \left| 2++\right\rangle \left| 1\right\rangle _{c} \\ \left| 2+-\right\rangle \left| 1\right\rangle _{c} \\ \left| 2-+\right\rangle \left| 1\right\rangle _{c} \\ \left| 2--\right\rangle \left| 1\right\rangle _{c} \end{array} \overset{2}{\rightarrow } \begin{array}{c} \left| 1aa\right\rangle \left| 1\right\rangle _{c} \\ \left| 1ab\right\rangle \left| 1\right\rangle _{c} \\ \left| 1ba\right\rangle \left| 1\right\rangle _{c} \\ \left| 1bb\right\rangle \left| 1\right\rangle _{c} \end{array} \overset{3}{\rightarrow } \nonumber \\&\begin{array}{c} \left| 1bb\right\rangle \left| 1\right\rangle _{c} \\ \left| 1ba\right\rangle \left| 1\right\rangle _{c} \\ \left| 1ab\right\rangle \left| 1\right\rangle _{c} \\ \left| 1aa\right\rangle \left| 1\right\rangle _{c} \end{array} \overset{4}{\rightarrow } \begin{array}{c} \left| 2--\right\rangle \left| 1\right\rangle _{c} \\ \left| 2-+\right\rangle \left| 1\right\rangle _{c} \\ \left| 2+-\right\rangle \left| 1\right\rangle _{c} \\ \left| 2++\right\rangle \left| 1\right\rangle _{c} \end{array} \overset{5}{\rightarrow } \begin{array}{c} \left| 1--\right\rangle \left| 0\right\rangle _{c} \\ \left| 1-+\right\rangle \left| 0\right\rangle _{c} \\ \left| 1+-\right\rangle \left| 0\right\rangle _{c} \\ \left| 1++\right\rangle \left| 0\right\rangle _{c}. \end{array} \end{aligned}$$

(14)

Hence, it can be concluded from Eq. (14) that three-qubit controlled NOT gate of one qubit simultaneously controlling $2$ qubits with $k=2,3$ is achieved with $3$ qubit system (i.e., control qubit $1$ and two target qubit systems $2$ and $3$). It is clear from the above steps of operations that Hadamard gate is neither required before step 1 nor after step 6. For $k=2$ in Eqs.  (2) and (3), our scheme reduces to two-qubit controlled NOT gate which can be used to implement two-qubit Deutsch–Jozsa algorithm as described below. It may be pointed out that as compared to earlier proposal Ref. [24] which requires $8$ steps of operations to implement NTCNOT gate, present proposal accomplishes the task in just five steps.

3.2.1 Deutsch–Jozsa algorithm

Deutsch–Jozsa algorithm is designed to distinguish between the constant and balanced functions on $2^{n}$ inputs [37]. For constant function, the function $f(x)=constant$ for all $2^{n}$ inputs. For the balanced function, the function $f(x)=0$ for half of all possible inputs, and $f(x)=1$ for other half. A classical algorithm needs $2^{n}/2+1$ queries to determine whether function is constant or balanced since there may be $2^{n}/2$ zero’s before finally a one appears, showing that function is balanced. In contrast, the Deutsch–Jozsa algorithm requires only one query.

Here, we discuss the scheme to implement two-qubit Deutsch-Jozsa algorithm using four-level qubit system shown in Fig. 3 coupled to a cavity or a resonator. The qubit system $1$ shown in Fig. 4a represents query qubit while qubit system $k=2$ shown in Fig. 4c represents auxiliary qubit. We prepare the two-qubit system in the state $\left| \psi \right\rangle =1/\sqrt{2}(\left| 0\right\rangle _{1}+\left| 1\right\rangle _{1})\otimes \left| 1\right\rangle _{2}$ which can be written in rotating basis for qubit system $k=2$ such that

$$\begin{aligned} \left| \psi \right\rangle =\frac{1}{2}(\left| 0\right\rangle _{1}+\left| 1\right\rangle _{1})\otimes (\left| +\right\rangle _{2}-\left| -\right\rangle _{2}). \end{aligned}$$

(15)

The function $f(x)$ is characterized by the unitary mapping transformation $U_{f}$, and $\left| x,y\right\rangle \rightarrow \left| x,y\oplus f(x)\right\rangle$, where $\oplus$ represents addition modulo 2. After unitary transformation $U_{f}$, initial state of the system changes to

$$\begin{aligned} \frac{1}{2}\left[ (-1)^{f(0)}\left| 0\right\rangle _{1}+(-1)^{f(1)}\left| 1\right\rangle _{1}\right] \otimes (\left| +\right\rangle _{2}-\left| -\right\rangle _{2}). \end{aligned}$$

(16)

There are four possible transformations: (1) $U_{f,1}$ corresponding to $f(0)=f(1)=0;$ (2) $U_{f,2}$ corresponding to $f(0)=f(1)=1;$ (3) $U_{f,3}$ corresponding to $f(0)=0$ and $f(1)=1;$ and (4) $U_{f,4}$ corresponding to $f(0)=1$ and $f(1)=0.$ Then Hadamard gate is applied on query qubit. As a result, state of query qubit becomes $\left| f(0)\oplus f(1)\right\rangle$. If $f(x)$ is constant then, the state of query qubit becomes $\left| 0\right\rangle _{1}$. On other hand, if $f(x)$ is balanced, the state of the query qubit becomes $\left| 1\right\rangle _{1}$. Therefore, a measurement on query qubit provides the desired information whether the function $f(x)$ is constant or balanced. The $U_{f,n}$ operations are applied to the state $\left| \psi \right\rangle$ as follow:

• $U_{f,1}$ operation: This is an identity operation. Both qubit system are kept far off with the cavity field and microwave pulse. As a result, system remains in the state $\left| \psi \right\rangle$.

• $U_{f,2}$ operation: We first apply two-qubit controlled NOT gate as described earlier. Next, we apply single-qubit rotations $\left| 0\right\rangle \rightarrow \left| 1\right\rangle$ and $\left| 1\right\rangle \rightarrow -\left| 0\right\rangle$ on qubit system 1. Then we repeat two-qubit controlled NOT operation and perform the single-qubit rotations $\left| 0\right\rangle \rightarrow -\left| 1\right\rangle$ and $\left| 1\right\rangle \rightarrow \left| 0\right\rangle$ on qubit system 1$.$ Finally, we obtain

  $$\begin{aligned} \left| \psi \right\rangle _{2}=\frac{1}{2}\left( -\left| 0\right\rangle _{1}-\left| 1\right\rangle _{1}\right) \otimes \left( \left| +\right\rangle _{2}-\left| -\right\rangle _{2}\right) . \end{aligned}$$

  (17)

• $U_{f,3}$ operation: Next, we apply two-qubit controlled NOT operation, as a result, state of the system evolves to

  $$\begin{aligned} \left| \psi \right\rangle _{3}=\frac{1}{2}\left( \left| 0\right\rangle _{1}-\left| 1\right\rangle _{1}\right) \otimes \left( \left| +\right\rangle _{2}-\left| -\right\rangle _{2}\right) . \end{aligned}$$

  (18)

• $U_{f,4}$ operation: We then apply single-qubit rotations $\left| 0\right\rangle \rightarrow \left| 1\right\rangle$ and $\left| 1\right\rangle \rightarrow -\left| 0\right\rangle$ on qubit system 1. Then we perform controlled NOT operation. Finally, we again apply single-qubit rotations $\left| 0\right\rangle \rightarrow -\left| 1\right\rangle$ and $\left| 1\right\rangle \rightarrow \left| 0\right\rangle$ on qubit system 1. The resultant state becomes

  $$\begin{aligned} \left| \psi \right\rangle _{4}=\frac{1}{2}\left( -\left| 0\right\rangle _{1}+\left| 1\right\rangle _{1}\right) \otimes \left( \left| +\right\rangle _{2}-\left| -\right\rangle _{2}\right) . \end{aligned}$$

  (19)

In this way, we obtain the unitary mapping transformation $U_{f}$. After Hadamard transformation on qubit system $1$, if the state of qubit system $1$ becomes $\left| 0\right\rangle _{1}$, then the function $f(x)$ is constant. On other hand, if the state of qubit system $1$ becomes $\left| 1\right\rangle _{1}$, then the function $f(x)$ is balanced.

4 Possible experimental implementation

In this section, we give a detailed discussion on experimental possibilities of three-qubit controlled phase gate and NTCNOT gate. The total operation time for three-qubit controlled phase gate is given by

$$\begin{aligned} \tau _{3cp}&= 2t_{1}+2t_{2}+t_{3}+4\tau \nonumber \\&= 2\left( \frac{\pi \Delta _{c}}{2g_{1}^{2}}\right) +2\left( \frac{\pi \Delta _{c}}{2g_{2}^{2}} \right) +\left( \frac{\pi \Delta _{c,3}}{g_{3}^{2}}\right) +4\left( \frac{\pi }{2\Omega _{12}}\right) .\ \end{aligned}$$

(20)

Similarly, the total operation time for NTCNOT gate is given by

$$\begin{aligned} \tau _{ntcnot}=2t_{1}+2\tau +t_{k}=2\left( \frac{\pi \Delta _{c}}{2g_{1}^{2}}\right) +2\left( \frac{\pi }{2\Omega _{12}}\right) +\left( \frac{\pi \Delta _{c,k}}{g_{k}^{2}}\right) . \end{aligned}$$

(21)

The operation time $\tau _{cp}$ and $\tau _{ntcnot}$ should be shorter than (1) energy relaxation time $\gamma _{2}^{-1}$ of level $\left| 2\right\rangle$ (it may be mentioned that level $\left| 3\right\rangle$ is unpopulated during the entire operations), and (2) the life time of the cavity mode $\kappa ^{-1}=Q/2\pi \nu _{c}$, where, $Q$ is quality factor of the cavity and $\nu _{c}$ is the resonator frequency. In principle, these requirements can be achieved using the following: (1) reducing operation time by increasing the coupling constant and Rabi frequencies, (2) increasing $\kappa ^{-1}$ by employing high-$Q$ cavity or resonator, and (3) choosing qubit system (e.g., atoms) or designing qubits (e.g., superconducting devices) such that the energy relaxation time $\gamma _{2}^{-1}$ of level $\left| 2\right\rangle$ is sufficiently long.

Here, we consider without loss of generality $g_{1}\thicksim g_{2}\thicksim g_{k}\thicksim g$. On choosing $\Delta _{c}\thicksim \Delta _{c,3}\thicksim \,\Delta _{c,k}\thicksim 10g$, and $\Omega _{12}\thicksim 10g$, the total operation time required for the gates implementation would be $\tau _{3cp}\thicksim 30.2\pi /g\$and$\ \tau _{ntcnot}\thicksim 20\pi /g$. Here, we assume $g/\pi \thicksim 440\,{\text {MHz}}$, which could be achieved for superconducting qubits coupled to a one-dimensional standing-wave coplanar waveguide (CPW) transmission resonator [38]. As a result, we have $\tau _{3cp}\thicksim 0.068\,\upmu s$and$\ \tau _{ntcnot}\thicksim 0.045\,\upmu s$, which is much shorter than $\gamma _{2}^{-1}\thicksim 1\,\upmu s$, and $\kappa ^{-1}\thicksim 5.3\,\upmu s$ for resonator with frequency $\nu _{c}\thicksim 3$ GHz and $Q\thicksim 10^{5}$ [8]. It may be mentioned that superconducting CPW resonator with a quality factor $Q\thicksim 10^{6}$ has been experimentally demonstrated [39].

Fig. 7

An rf SQUID with first four energy levels. Magnetic dipole coupling between two ground levels $\left| 0\right\rangle$ and $\left| 1\right\rangle$ is much smaller than that between any other levels due to potential barrier between two wells. Transition frequencies between the excited levels and ground levels are $\nu _{30}\thicksim 24.4$ GHz, $\nu _{31}\thicksim 21.4$ GHz, $\nu _{12}\thicksim 16.5$ GHz, $\nu _{20}\thicksim 19.5$ GHz, which are much larger than transition frequency $\nu _{32}\thicksim 4.9$ GHz

The schemes proposed here are quite general which can be implemented using different physical systems as pointed out earlier. However, here we consider a specific example of superconducting quantum interference devices (SQUIDs) as a potential qubit system for the implementation of our scheme. For SQUID, the desired level structure can easily be obtained by changing external control parameters e.g., magnetic flux $\phi _{x}$ [31]. For example, consider rf SQUID shown in Fig. 7 with junction capacitance $C=90fF$ , loop inductance $L=100$ pH, junction’s damping resistance $R\thicksim 1G\Omega$, potential shape parameter $\beta _{L}=1.12$, and external flux $\phi _{x}=0.4995\phi _{0}$. Here, $\phi _{0}=h/2e$ is flux quantum. It may be mentioned that SQUIDs with these parameters are available currently [31]. With these choices, decay time of level $\left| 2\right\rangle$ would be $\gamma _{2}^{-1}\thicksim 100\,\upmu s$, the $\left| 2\right\rangle \rightarrow \left| 3\right\rangle$ coupling matrix element is $\phi _{32}\thicksim 7.8\times 10^{-2}$, and $\left| 2\right\rangle \rightarrow \left| 3\right\rangle$ transition frequency is $\nu _{32}\thicksim 4.9\,{\text {GHz}}$. We choose cavity mode frequency $\nu _{c}=\omega _{c}/(2\pi )=3.6GHz,\,Q\thicksim 10^{5}$, and $\kappa ^{-1}\thicksim 4.42\,\upmu s$. The SQUID-cavity coupling constant for $\left| 2\right\rangle \rightarrow \left| 3\right\rangle$ transition is given by $g=(1/L)\sqrt{\omega _{c}/2\,\upmu _{0}\hbar }\phi _{32}\phi _{0}\int \nolimits _{S}{\mathbf {B}}_{c}(r).dS$. Here, $S$ is the surface bounded by the SQUID ring and ${\mathbf {B}}_{c}(r)$ is the magnetic component of cavity mode in the SQUID loop. For standing- wave cavity, ${\mathbf {B}} _{c}(z)=\upmu _{0}\sqrt{2/V}\cos kz$, where $k,\,V$, and $z$ are wave number, cavity volume, and cavity axis, respectively. For $g\thicksim 4.3\times 10^{8}\mathrm{s}^{-1}$ the time required for (1) three-qubit phase gate would be $\tau _{3cp}\thicksim 0.219\,\upmu \mathrm{s}\$and (2) for NTCNOT gate would be $\ \tau _{ntcnot}\thicksim 0.146\,\upmu \mathrm{s}$. These implementation times are much shorter than $\gamma _{2}^{-1}$ and $\kappa ^{-1}$. Moreover, we have an additional advantage in case of flux qubit system that is tunneling between the levels $\left| 1\right\rangle$ and $\left| 0\right\rangle$ is not needed during the gates operation. Therefore, potential barrier between levels $\left| 1\right\rangle$ and $\left| 0\right\rangle$ can be adjusted a priory such that decay from level $\left| 1\right\rangle$ becomes negligibly small [27–29]. As a result, each qubit can have much longer storage time.

Although, in our scheme, both gates can be carried out faster than $\gamma _{2}^{-1}$ and $\kappa ^{-1}$, we should study the imperfection induced due to cavity decay. In ideal case, emission and absorption of a single photon take place with unit probability due to transformation $G_{1}$ and $G_{2}$. As a result occupation probability of levels $\left| 1\right\rangle ,\, \left| 2\right\rangle$ of qubit $1$, and levels $\left| 0\right\rangle ,\,\left| 2\right\rangle$ of qubit $2$ should be exactly one. However, these occupation probabilities are likely to decay exponentially due to cavity decay. Assuming that no photon actually leaks out during implementation, corresponding conditional Hamiltonian can be written as $H_{c}=H_{I}-i\kappa a^{\dag }a$ [15]. Suppose each qubit is initially prepared in generic state $\cos \nu \left| 0\right\rangle +\sin \nu \left| 1\right\rangle$ for three-qubit controlled phase gate, and each target qubit is initially prepared in state $\cos \nu \left| +\right\rangle +\sin \nu \left| -\right\rangle$ for NTCNOT gate. In ideal case, when $\kappa =0$, state of system after steps of operations (as described in Sec. III) becomes $\left| \psi _{id}(\tau )\right\rangle$ which is given by Eqs. 11 and 14. However, when cavity decay is incorporated under the assumption of weak cavity decay, time evolution of the system becomes rather complex which is not presented here. Average fidelity over all possible initial states can be computed using $F_{ave}=\frac{1}{2}\int ^{\pi }_{0} F\sin \nu d\nu$, where $F=|\langle \psi _{id}(\tau )\left| \psi _{decay}(\tau )\right\rangle |^{2}$. Next, we show the plot of average fidelity for three-qubit phase gate (red dots) and NTCNOT gate (black dots) as a function of $\kappa /g$ in Fig. 8. It can be seen that fidelity decreases as cavity decay rate increase. For the choice of $\kappa /g=0.000145\,$ [38] we have $F_{ave}\approx 99\,\%$. It is clear from Fig. 8 that both gates are of high fidelity as long as the cavity decay is small enough. However performance of these gates in the light of further experimental errors like effect of $\gamma _{2}^{-1}$, delay in pulse durations along with cavity decay requires a rather lengthy and complex analysis which should be further investigated.

Fig. 8

Average fidelity of multi-qubit quantum gates as a function of $\kappa /g$. Red (black) dots indicates the fidelity of three qubit controlled phase gate (three-qubit NTCNOT gate) (Color figure online)

Here, we discuss some other issues related to gate operations. During the operation of step (ii) or (iv) or (vi) for three-qubit phase gate and of step (ii) or (iv) for NTCNOT gate, a single photon is populated in the cavity mode while state $\left| 2\right\rangle$ of each qubit system is occupied. The unwanted system-cavity-pulse resonance Raman interaction and system-cavity off-resonant interaction between resonator mode and $\left| 2\right\rangle \rightarrow \left| 3\right\rangle$ transition of qubit system induces an accumulated phase shift to state $\left| 2\right\rangle$ of each qubit system, which can effect the desire gate performance. However, when $\tau <<t_{1},t_{2},t_{k}$ this unwanted phase shift is sufficiently small and can be neglected. Note that for $\Omega _{12}=\Omega _{02}$, we have $\tau =\pi /\quad (2\Omega _{12}),\,t_{1}=\pi \Delta _{c}/(2g_{1}^{2}),\,t_{2}=\pi \Delta _{c}/(2g_{2}^{2})$, and $t_{k}=\pi \Delta _{c,k}/g_{k}^{2}$. Thus condition turns into $\Omega _{12}>>2g_{1}^{2}/\Delta _{c},2g_{2}^{2}/\Delta _{c},g_{k}^{2}/\Delta _{c,k}$ which can be achieved by increasing the Rabi frequency of pulse (i.e, by increasing the intensity of resonant pulse). For $\Delta _{c,k}=10g_{k}$, the occupation probability of level $\left| 3\right\rangle$ for target qubits is approximately $0.04$ which reduces the gate error [31].

5 Conclusion

We have proposed a scheme for realizing a three-qubit controlled phase gate and an NTCNOT gate with three types of interactions. These interactions are system-cavity-pulse resonance Raman coupling, system-cavity off-resonant interaction, and system-pulse resonant interaction. The proposal can be applied to various kind of physical system with four-level configuration. For different systems, frequency regimes of cavity mode could be different, e.g., optical cavities in case of atoms and microwave cavities in case of superconducting qubits.

We have shown that our proposal has following advantages: (1) Decoherence due to spontaneous decay of level $\left| 3\right\rangle$ is suppressed because the excited level $\left| 3\right\rangle$ is unpopulated during the gates operation. (2) The adjustment of level spacing of the qubit system during the gate operations is not needed which may cause decoherence. (3) Finite second-order detuning is not required which improves the gate speed. (4) For the quantum gate with multiple control qubit, the number of steps (complexity) reduces linearly for number $n$ of the qubit, as compared to conventional gate decomposition method. (5) The operation time for the realization of NTCNOT gate is independent of the number of qubits.