1 Introduction

Since the pioneering work by Bennett et al. [1] on teleporting an arbitrary unknown pure state of a qubit from a sender (Alice) to a distant receiver (Bob) with the aid of Einstein–Podolsky–Rosen (EPR) correlation, quantum teleportation (QT) has flourished in both theoretical and experimental aspects and become one of the most important research fields in quantum information science. During the past decade, much progress in QT has been achieved. On the one hand, a great number of theoretical schemes for QT using different quantum entanglement channels (resource entangled states) have been proposed [2–10]. On the other hand, QT has been experimentally demonstrated in various physical systems such as photons [11], optical fields [12], nonclassical wave packets of light [13], nuclear magnetic resonance [14], and ions or atoms [15, 16]. Moreover, QT over 16-km free-space link or between two optical free-space links separated by 97 km has been demonstrated recently [17, 18].

In 1998, Karlsson and Bourennane [19] generalized the idea of Bennett et al. and showed that an arbitrary unknown pure state of a qubit could be teleported to either one of two receivers using a three-qubit entangled Greenberger–Horne–Zeilinger (GHZ) state \(\left( \left| 000\right\rangle +\left| 111\right\rangle \right) /\sqrt{2}.\) However, only one of the two (either one) can fully recover the qubit state conditioned on the measurement outcome of the other. Since then, Hillery et al. [20] first proposed the idea of quantum secret sharing (QSS), i.e., a message is split into several parts such that no subset of parts can read the message, but the entire set does. In their work, it was shown that a qubit of information can be secretly shared by two agents via a three-qubit GHZ state or by more than two agents through a four-qubit GHZ state. Note that both works in [19] and [20] were based on an entangled GHZ state initially shared by the sender, the agents and the receivers. So far, a large number of QSS schemes using various entangled states as quantum channels have been proposed [21–24] since the earlier works in [19, 20]. Moreover, several experimental demonstrations of QSS have also been reported [25–27].

Recently, there is much interest in controlled teleportation (CT), i.e., the teleportation for which a sender sends quantum information to a distant receiver via the control of agents in a network. The CT plays an important role in quantum communication. It has many applications such as networked quantum information processing, cryptographic conferencing, data transfer under the control of multiple supervisors as an application for office networks; remote secure voting, and so on.

In this work, we restrict ourselves to a CT via entanglement. Namely, the CT is implemented by using an entangled state, which is initially shared by the sender, the receiver, and the control agents, prior to their CT operations. Up to today, many schemes for controlled teleportation of a single-qubit or multi-qubit state via entanglement have been proposed [28–41]. In addition, schemes for controlled teleportation of an unknown quantum pure state of a qutrit [42–45] or a qudit [46–53] via entanglement have been also presented. However, we find that the existing entanglement-based CT schemes [28–53] or the CT implementations via entangled-based QSS schemes [19–24] have a drawback, i.e., if one or more agents do not cooperate, the receiver cannot fully reconstruct the original quantum state but can still gain part of the original information (e.g., amplitude information about the qubit state, the qutrit state, or the qudit state to be teleported; for a detailed discussion, see, e.g., Ref. [28]). Also, the existing protocols usually only concern with a simple threshold scheme: As long as the number of cooperating agents exceed some number, then the teleportation goes through. But some more complicated controlling structures among the agents may be of use in practice. A possible scenario is that when several controllers vote to decide whether to allow the transfer of some quantum state, the votes by some privileged voters may have more weight than those of the other voters.

In this paper, we propose a way of performing controlled teleportation of an arbitrary unknown pure state of a qutrit (a quantum system of dimension \(d =3\)) with the control of two groups of agents via entanglement. As shown below, if all agents in the two groups cooperate, the sender can perfectly teleport the qutrit state to a distant receiver. However, even if one agent in each group does not cooperate, the receiver cannot gain any information (including amplitude information or phase information or both) about the qutrit state to be teleported.

In our protocol, the number of agents in the two groups need not be equal. The choice of the agent who does not cooperate (see the condition in the previous paragraph) is independent of the choice in the other group, that is, the protocol does not require a fixed mapping between the members of the two groups.

This paper is organized as follows. In Sect. 2, we present a way to realize the CT of an arbitrary unknown pure state of a qutrit with one agent in each group. In Sect. 3, we consider the CT of the qutrit state with two groups of agents, where each group may contain an arbitrary number of agents. A brief discussion on the security of this proposal and the concluding summary are presented in Sect. 4.

2 Controlled teleportation with one agent in each group via entanglement

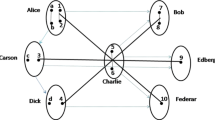
In this section, we present a way for teleporting an arbitrary unknown pure state of a qutrit from the sender Alice to a distant receiver Bob, via the control of two agents 1 and \(1^{\prime }\) each in one group (Fig. 1). Namely, we wish that Bob can fully recover the original state of Alice’s qutrit when the two agents cooperate with him; however, Bob gains no information about Alice’s qutrit state to be teleported if the two agents do not cooperate with him.

Fig. 1
figure 1

Controlled teleportation with one agent in each group. Alice, Bob, agents 1, and \(1^{{\prime }}\) keep the qutrits \(a\), \(b\), 1, and \(1^{{\prime }}\), respectively. Each dashed circle indicates a group while each dot represents a qutrit

Full size image

The message qutrit considered here is labeled as qutrit \(m\) throughout this paper. Generally speaking, in terms of a set of orthonormal basis states {\( \left| 0\right\rangle ,\left| 1\right\rangle ,\, \left| 2\right\rangle \)}, any arbitrary pure state \(\left| \varphi \right\rangle _m\) of qutrit \(m\) can be written as

$$\begin{aligned} \left| \varphi \right\rangle _m=\alpha \left| 0\right\rangle _m+\beta \left| 1\right\rangle _m+\gamma \left| 2\right\rangle _m, \end{aligned}$$
(1)

where \(\alpha ,\,\beta ,\) and \(\gamma \) are coefficients and satisfy the normalization condition \(\left| \alpha \right| ^2+\left| \beta \right| ^2+\left| \gamma \right| ^2=1\).

The procedure for implementing our task is described below:

Firstly, Alice prepares the following entangled state through her local operations

$$\begin{aligned} \left| \varPhi \right\rangle =\sum _{j=0}^2\left| j\right\rangle _a\left| j\right\rangle _1\left( \left| 00\right\rangle _{1^{\prime }b}+\omega ^j\left| 11\right\rangle _{1^{\prime }b}+\omega ^{2j}\left| 22\right\rangle _{1^{\prime }b}\right) , \end{aligned}$$
(2)

where \(\omega =e^{i2\pi /3}\), the subscripts \(a,\) \(b,\) 1, and \(1^{{\prime }}\) represent the qutrits \(a,\) \(b,\) 1, and \(1^{{\prime }},\) respectively. Here and below, normalization factors are omitted for simplicity. Then, Alice sends the qutrits \(1,1^{{\prime }}\), and \(b\) to agent \(1,\) agent \( 1^{{\prime }}\), and Bob, respectively, while keeping the qutrit \(a\) to herself (Fig. 1). The initial state of the whole system is \(\left| \varPsi \right\rangle =\left| \varphi \right\rangle _m\otimes \left| \varPhi \right\rangle \), which can be written as

$$\begin{aligned} \left| \varPsi \right\rangle =\sum _{r,s=0}^2\left| \varphi _{rs}\right\rangle _{ma}\otimes \left| \xi _{rs}\right\rangle _{11^{{\prime }}b}. \end{aligned}$$
(3)

Here, \(\left| \varphi _{rs}\right\rangle _{ma}\) is the basis state of the qutrits \(m\) and \(a,\) which is given by

$$\begin{aligned} \left| \varphi _{rs}\right\rangle _{ma}=\sum \limits _{j=0}^2\omega ^{jr}\left| j\right\rangle _m\left| j\oplus s\right\rangle _a, \end{aligned}$$
(4)

while \(\left| \xi _{rs}\right\rangle _{11^{{\prime }}b}\) is the state of the three qutrits \(1,1^{{\prime }}\), and \(b\), which is given by

$$\begin{aligned} \left| \xi _{rs} \right\rangle _{11^{{\prime }}b}&= \alpha \left| 0\oplus s\right\rangle _1\left( \left| 00\right\rangle _{1^{\prime }b}+\omega ^s\left| 11\right\rangle _{1^{\prime }b}+\omega ^{2s}\left| 22\right\rangle _{1^{{\prime }}b}\right) \nonumber \\&+\,\beta \omega ^{-r}\left| 1\oplus s\right\rangle _1\left[ \left| 00\right\rangle _{1^{\prime }b}+\omega ^{1+s}\left| 11\right\rangle _{1^{\prime }b}+\omega ^{2\left( 1+s\right) }\left| 22\right\rangle _{1^{\prime }b}\right] \nonumber \\&+\,\gamma \omega ^{-2r}\left| 2\oplus s\right\rangle _1\left[ \left| 00\right\rangle _{1^{\prime }b}+\omega ^{2+s}\left| 11\right\rangle _{1^{\prime }b}+\omega ^{2\left( 2+s\right) }\left| 22\right\rangle _{1^{\prime }b}\right] , \end{aligned}$$
(5)

where \(j\oplus s\) means \(j+s\) mod \(3\) (\(j=0,1,2\)).

Secondly, Alice takes a measurement on her two qutrits \(m\) and \(a\) along the basis \(\{\left| \varphi _{rs}\right\rangle _{ma}\}\) and sends the measurement result to Bob through classical communication. From Eq. (3), one can see that if the two qutrits \(m\) and \(a\) are measured to be in the basis state \(\left| \varphi _{rs}\right\rangle _{ma}\) by Alice, then the qutrits \( 1,\) \(1^{{\prime }}\), and \(b\) will be in the state \(\left| \xi _{rs}\right\rangle _{11^{{\prime }}b}\) given in Eq. (5).

Thirdly, agents 1 and \(1^{{\prime }}\) perform a Hadamard transformation on their qutrits, which is described by \(\left| 0\right\rangle \rightarrow \sum _{l=0}^2\left| l\right\rangle ,\) \(\left| 1\right\rangle \rightarrow \sum _{l=0}^2\omega ^l\left| l\right\rangle ,\) and \(\left| 2\right\rangle \rightarrow \sum _{l=0}^2\omega ^{2l}\left| l\right\rangle .\) As a result, we have the following state transformation

$$\begin{aligned} \left| j\oplus s\right\rangle \rightarrow \left| 0\right\rangle +\omega ^{j+s}\left| 1\right\rangle +\omega ^{2(j+s)}\left| 2\right\rangle , \end{aligned}$$
(6)

where \(j,s\in \{0,1,2\}.\) Based on Eq. (6), we can rewrite the above state \( \left| \xi _{rs} \right\rangle _{11^{{\prime }}b}\) as follows

$$\begin{aligned} \left| \xi _{rs} \right\rangle _{11^{{\prime }}b}=\sum _{p,q=0}^2\left| pq\right\rangle _{11^{{\prime }}}\otimes \left| \varphi \right\rangle _b, \end{aligned}$$
(7)

with

$$\begin{aligned} \left| \varphi \right\rangle _b&= \alpha \left[ \left| 0\right\rangle _b+\omega ^{s+q}\left| 1\right\rangle _b+\omega ^{2\left( s+q\right) }\left| 2\right\rangle _b\right] \nonumber \\&\quad +\,\,\omega ^{p-r}\beta \left[ \left| 0\right\rangle _b+\omega ^{1+s+q}\left| 1\right\rangle _b+\omega ^{2\left( 1+s+q\right) }\left| 2\right\rangle _b\right] \nonumber \\&\quad +\,\,\omega ^{2\left( p-r\right) }\gamma \left[ \left| 0\right\rangle _b+\omega ^{2+s+q}\left| 1\right\rangle _b+\omega ^{2\left( 2+s+q\right) }\left| 2\right\rangle _b\right] , \end{aligned}$$
(8)

where \(p,q\in \{0,1,2\}\).

Now, agents 1 and \(1^{\prime }\) take local measurements on their respective qutrits 1 and \(1^{\prime }\) in the \(Z\) basis \(\{\left| 0\right\rangle ,\) \(\left| 1\right\rangle ,\) \(\left| 2\right\rangle \}\) and tell Bob their measurement outcomes through classical communication. It can be seen from Eq. (7) that if the outcomes of the measurements of agents 1 and \(1^{\prime }\) are \(p\) and \(q\), respectively, the qutrit \(b\) will be in the state \(\left| \varphi \right\rangle _b\) as described by Eq. (8).

Lastly, Bob performs a Hadamard transformation on his qutrit \(b\). After that, the state \(\left| \varphi \right\rangle _b\) becomes

$$\begin{aligned} \left| \varphi \right\rangle _b&= \alpha \left( x\left| 0\right\rangle _b+y\left| 1\right\rangle _b+z\left| 2\right\rangle _b\right) \nonumber \\&+\,\,\omega ^{p-r}\beta \left( y\left| 0\right\rangle _b+z\left| 1\right\rangle _b+x\left| 2\right\rangle _b\right) \nonumber \\&+\,\,\omega ^{2\left( p-r\right) }\gamma \left( z\left| 0\right\rangle _b+x\left| 1\right\rangle _b+y\left| 2\right\rangle _b\right) , \end{aligned}$$
(9)

with

$$\begin{aligned} x&= 1+\omega ^{s+q}+\omega ^{2\left( s+q\right) }, \nonumber \\ y&= 1+\omega ^{1+s+q}+\omega ^{2\left( 1+s+q\right) }, \nonumber \\ z&= 1+\omega ^{2+s+q}+\omega ^{2\left( 2+s+q\right) }. \end{aligned}$$
(10)

The value taken by \(s+q\) involved in Eq. (10) satisfies one of the following three cases: (A) \(3\oplus \left( s+q\right) =0\), (B) \(3\oplus \left( s+q\right) =1\), and (C) \(3\oplus \left( s+q\right) =2\). The remaining operations for Bob to recover the original qutrit state (1) depend on these three cases. Fortunately, as discussed previously, Bob knows the values of \( r \) and \(s\) according to the measurement outcomes from Alice as well as the values of \(p\) and \(q\) according to the measurement outcomes from the two agents. Thus, Bob can predict “which of the three cases A, B, and C” the value of \(s+q\) falls into. In the following, we will give a discussion on how Bob recovers the qutrit state (1) for each of the three cases.

  1. (A)

    Case for \(3\oplus \left( s+q\right) =0\)

For \(3\oplus \left( s+q\right) =0,\) we have \(s+q=0\) or \(3.\) In this case, it follows from Eq. (10) that \(x=3\) and \(y=z=0\). Thus, the state (9) can be written as

$$\begin{aligned} \left| \varphi \right\rangle _b=\alpha \left| 0\right\rangle _b+\omega ^{p-r}\beta \left| 2\right\rangle _b+\omega ^{2\left( p-r\right) }\gamma \left| 1\right\rangle _b. \end{aligned}$$
(11)

Define operators \(Z=\sum _{j=0}^2\omega ^j\left| j\right\rangle \left\langle j\right| \) and \(U_0=\sum _{j=0}^2\left| j\oplus j\right\rangle \left\langle j\right| \). One can see that if Bob performs a unitary operation \(Z^{2\left( p-r\right) }U_0\) on the state (11), the state (11) changes to

$$\begin{aligned} \left| \varphi \right\rangle _b=\alpha \left| 0\right\rangle _b+\beta \left| 1\right\rangle _b+\gamma \left| 2\right\rangle _b, \end{aligned}$$
(12)

which implies that the original qutrit state (1) is restored through Bob’s qutrit \(b\).

  1. (B)

    Case for \(3\oplus \left( s+q\right) =1\)

For \(3\oplus \left( s+q\right) =1,\) we get \(s+q=1\) or \(4.\) In this case, it follows from Eq. (10) that \(z=3\) and \(x=y=0\). Hence, the state (9) becomes

$$\begin{aligned} \left| \varphi \right\rangle _b=\alpha \left| 2\right\rangle _b+\omega ^{p-r}\beta \left| 1\right\rangle _b+\omega ^{2\left( p-r\right) }\gamma \left| 0\right\rangle _b. \end{aligned}$$
(13)

Define an operator \(U_1=\sum _{j=0}^2\left| j\oplus j\oplus 2\right\rangle \left\langle j\right| \) (here and below, \(j\oplus j\oplus 2\) means \(j+j+2\) mod \(3,\) and \(j\oplus j\oplus 1\) implies \(j+j+1\) mod \(3\)). It can be seen that if Bob applies a unitary operation \(Z^{2\left( p-r\right) }U_1\) on the state (13), the state (13) changes to the state (12), i.e., the original qutrit state (1).

  1. (C)

    Case for \(3\oplus \left( s+q\right) =2\)

For \(3\oplus \left( s+q\right) =2,\) one has \(s+q=2.\) In this case, we obtain from Eq. (10) that \(y=3\) and \(x=z=0\). As a result, the state (9) reduces to

$$\begin{aligned} \left| \varphi \right\rangle _b=\alpha \left| 1\right\rangle _b+\omega ^{p-r}\beta \left| 0\right\rangle _b+\omega ^{2\left( p-r\right) }\gamma \left| 2\right\rangle _b. \end{aligned}$$
(14)

Define an operator \(U_2=\sum _{j=0}^2\left| j\oplus j\oplus 1\right\rangle \left\langle j\right| \). After Bob applies a unitary operation \(Z^{2\left( p-r\right) }U_2\) on the state (14), the state (14) changes to the state (1).

In the above, we have explicitly shown that for any measurement outcomes of Alice and the two agents, Bob can restore the original qutrit state (1) by performing some suitable unitary operations on his qutrit \(b\).

We now assume that the two agents 1 and \(1^{\prime }\) do not cooperate with Bob. In this case, one can see from Eq. (3) that if the two qutrits \(m\) and \(a\) are measured to be in the basis state \(\left| \varphi _{rs}\right\rangle _{ma}\) by Alice, then the qutrits \(1,\) \(1^{\prime }\) and \( b\) will be in the state \(\left| \xi _{rs}\right\rangle _{11^{{\prime }}b}\) described by Eq. (5). One can verify that for \(s\in \{0,1,2\},\) the states \( \left| 0\oplus s\right\rangle ,\) \(\left| 1\oplus s\right\rangle ,\) and \( \left| 2\oplus s\right\rangle \) involved in Eq. (5) are orthogonal to one another. Thus, it can be easily found from Eq. (5) that after tracing over the qutrits 1 and \(1^{\prime },\) the normalized density operator of qutrit \(b\) belonging to Bob is given by

$$\begin{aligned} \rho _b=\frac{Tr_{11^{\prime }}\left| \xi _{rs}\right\rangle _{11^{\prime }b}\left\langle \xi _{rs}\right| }{_{11^{\prime }b}\left\langle \xi _{rs}\right| \left. \xi _{rs}\right\rangle _{11^{\prime }b}}=I_b, \end{aligned}$$
(15)

where \(I_b=\sum _{j=0}^2\left| j\right\rangle \left\langle j\right| \) is the identity operator for qutrit \(b\). This result (15) shows that if the two agents 1 and \(1^{\prime }\) do not cooperate, Bob cannot gain any information (encoded through amplitude or phase) about Alice’s qutrit message state (1).

3 Controlled teleportation with many agents in each group via entanglement

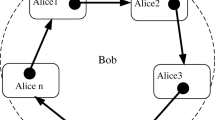
In this section, we consider a more general case that the sender Alice teleports the message state (1) of qutrit \(m\) to a distant receiver Bob, via the control of \(n\) agents (\(1,2,\ldots ,n\)) in one group and \(n^{\prime }\) agents (\(1^{\prime },2^{\prime },\ldots ,n^{\prime }\)) in the other group (Fig. 2). We hope that Bob can fully restore the message state (1) of Alice’s qutrit \(m\) as long as all agents in the two groups cooperate with him; however, Bob gains no information about Alice’s qutrit message state (1) to be teleported if one agent in each group does not collaborate with him.

Fig. 2
figure 2

Controlled teleportation with many agents in each group. Each dashed circle represents a group while each dot denotes a qutrit

Full size image

This task can be implemented using the following prescription:

Firstly, Alice prepares the following entangled state of (\(n+n^{\prime }+2\)) qutrits through her local operations (e.g., using the circuit in Fig. 3)

$$\begin{aligned} \left| \varPhi \right\rangle =\sum _{j=0}^2\left| j\right\rangle _a\left| j\right\rangle ^{\otimes n}\left( \left| 0\right\rangle ^{\otimes n^{\prime }}\left| 0\right\rangle _b+\omega ^j\left| 1\right\rangle ^{\otimes n^{\prime }}\left| 1\right\rangle _b+\omega ^{2j}\left| 2\right\rangle ^{\otimes n^{\prime }}\left| 2\right\rangle _b\right) , \end{aligned}$$
(16)

where subscripts \(a\) and \(b\) represent qutrits \(a\) and \(b;\) \(\left| j\right\rangle ^{\otimes n}=\left| j\right\rangle _1\left| j\right\rangle _2 \ldots \left| j\right\rangle _n\) with subscripts \(1,2,\ldots ,n\) representing qutrits \(1,2,\ldots ,n\); and \(\left| l\right\rangle ^{\otimes n^{\prime }}=\left| l\right\rangle _1\left| l\right\rangle _2 \ldots \left| l\right\rangle _{n^{\prime }}\) (\(l=0,1,2\)) with subscripts \(1,2,\ldots ,n^{\prime }\) labeling qutrits \(1,2,\ldots ,n^{\prime }\), respectively. Then, Alice sends qutrit \(b\) to Bob, qutrits \(1,2,\ldots ,n\) to agents (\(1,2,\ldots ,n\)), and qutrits \( 1,2,\ldots ,n^{\prime }\) to agents (\(1,2,\ldots ,n^{\prime }\)), respectively; while she keeps qutrit \(a\) to herself (see Fig. 2). The initial state of the whole system is \(\left| \varPsi \right\rangle =\left| \varphi \right\rangle _m\otimes \left| \varPhi \right\rangle \), which can be written as

$$\begin{aligned} \left| \psi \right\rangle =\sum _{r,s=0}^2\left| \varphi _{rs}\right\rangle _{ma}\otimes \left| \xi _{rs}\right\rangle _{12 \ldots n1^{^{\prime }}2^{^{\prime }}\ldots n^{^{\prime }}b}, \end{aligned}$$
(17)

where \(\left| \varphi _{rs}\right\rangle _{ma}\) is the basis state of the qutrits \(m\) and \(a,\) given in Eq. (4), while \(\left| \xi _{rs}\right\rangle _{12\ldots n1^{^{\prime }}2^{^{\prime }}\ldots n^{^{\prime }}b}\) is the state of the qutrits \(1,2,\ldots ,n,\) \(1^{\prime },2^{\prime },\ldots ,n^{\prime }\) and \(b\), which is given by

$$\begin{aligned} \left| \xi _{rs}\right\rangle _{12\ldots n1^{\prime }2^{\prime }\ldots n^{\prime }b}&= \alpha \left| 0\oplus s\right\rangle ^{\otimes n}\left( \left| 0\right\rangle ^{\otimes n^{\prime }}\left| 0\right\rangle _b+\omega ^s\left| 1\right\rangle ^{\otimes n^{\prime }}\left| 1\right\rangle _b+\omega ^{2s}\left| 2\right\rangle ^{\otimes n^{\prime }}\left| 2\right\rangle _b\right) \nonumber \\&+\,\beta \omega ^{-r}\left| 1\oplus s\right\rangle ^{\otimes n}\left[ \left| 0\right\rangle ^{\otimes n^{\prime }}\left| 0\right\rangle _b\!+\!\omega ^{1+s}\left| 1\right\rangle ^{\otimes n^{\prime }}\left| 1\right\rangle _b\!+\!\omega ^{2\left( 1+s\right) \otimes n^{\prime }}\left| 2\right\rangle _b\right] \nonumber \\&+\,\gamma \omega ^{-2r}\left| 2\oplus s\right\rangle ^{\otimes n}\left[ \left| 0\right\rangle ^{\otimes n^{\prime }}\left| 0\right\rangle _b\!+\!\omega ^{2+s}\left| 1\right\rangle ^{\otimes n^{\prime }}\left| 1\right\rangle _b\!+\!\omega ^{2\left( 2+s\right) \otimes n^{\prime }}\left| 2\right\rangle _b\right] .\nonumber \\ \end{aligned}$$
(18)

Secondly, Alice takes a measurement on her two qutrits \(m\) and \(a\) along the basis \(\{\left| \varphi _{rs}\right\rangle _{ma}\}\) and sends the measurement result to Bob through classical communication. From Eq. (17), one can see that if the two qutrits \(m\) and \(a\) are measured to be in the basis state \(\left| \varphi _{rs}\right\rangle _{ma}\) by Alice, then the qutrits \( 1,2,\ldots ,n,1^{\prime },2^{\prime },\ldots ,n^{\prime }\), and \(b\) will be in the state \(\left| \xi _{rs}\right\rangle _{12 \ldots n1^{\prime }2^{\prime }\ldots n^{\prime }b}\) given in Eq. (18).

Fig. 3
figure 3

Circuit for preparation of the resource entangled state described in Eq. (16). The operation sequence is from left to right. Each qutrit is initially in the state \(\left| 0\right\rangle \). Each \(H\) gate is a Hadamard gate defined before Eq. (6). Each gate with the symbol circled plus denotes a two-qutrit controlled NOT gate (with control on the filled circle): CNOT\(=\sum _{j=0}^2\left| j\right\rangle _c\left\langle j\right| \otimes X_t^j,\) where \(X=\sum _{j=0}^2\left| j\oplus 1\right\rangle \left\langle j\right| \), the subscripts \(c\) and \(t\) represent the control qutrit and the target qutrit, respectively

Full size image

Thirdly, all agents perform a Hadamard transformation on their qutrits. As a result, we find that the state (18) becomes

$$\begin{aligned} \left| \xi _{rs} \right\rangle _{12\ldots n1^{^{\prime }}2^{^{\prime }}\ldots n^{^{\prime }}b}=\sum _{p_{1,}p_{2},\ldots , p_n,q_{1^{\prime }},q_{2^{\prime }},\ldots ,q_{n^{\prime }=0}}^2\left| p_1p_2\ldots p_nq_{1^{\prime }}q_{2^{\prime }},\ldots , q_{n^{\prime }}\right\rangle \otimes \left| \varphi \right\rangle _b, \end{aligned}$$
(19)

with

$$\begin{aligned} \ \ \ \ \left| \varphi \right\rangle _b&= \alpha \left[ \left| 0\right\rangle _b+\omega ^{s+q^{\prime }}\left| 1\right\rangle _b+\omega ^{2\left( s+q^{\prime }\right) }\left| 2\right\rangle _b\right] \nonumber \\&\ \ \ +\,\omega ^{p^{\prime }-r}\alpha \left[ \left| 0\right\rangle _b+\omega ^{1+s+q^{\prime }}\left| 1\right\rangle _b+\omega ^{2\left( 1+s+q^{\prime }\right) }\left| 2\right\rangle _b\right] \nonumber \\&\ \ \ +\,\omega ^{2\left( p^{\prime }-r\right) }\alpha \left[ \left| 0\right\rangle _b+\omega ^{2+s+q^{\prime }}\left| 1\right\rangle _b+\omega ^{2\left( 2+s+q^{\prime }\right) }\left| 2\right\rangle _b\right] . \end{aligned}$$
(20)

Here, \(p^{\prime }=\sum _{i=1}^np_i\) and \(q^{\prime }=\sum _{i^{\prime }=1^{\prime }}^{n^{\prime }}q_{i^{\prime }}.\)

Now, all agents take a measurement on their qutrits in the \(Z\) basis and send their measurement outcomes to Bob. From Eq. (19), one can see that if the outcomes of the measurements on the qutrits \(1,2,\ldots ,n,1^{\prime },2^{\prime },\ldots ,n^{\prime }\) are \(p_1\), \(p_2, \ldots , p_n\), \( q_{1^\prime }\), \(q_{2^\prime }, \ldots , q_{n^\prime }\), respectively, the qutrit \(b\) will be in the state \(\left| \varphi \right\rangle _b\) described by Eq. (20).

Lastly, Bob performs a Hadamard transformation on his qutrit \(b.\) After that, the state (20) changes to

$$\begin{aligned} \left| \varphi \right\rangle _b&= \alpha \left( x^{\prime }\left| 0\right\rangle _b+y^{\prime }\left| 1\right\rangle _b+z^{\prime }\left| 2\right\rangle _b\right) \nonumber \\&+\,\omega ^{p^{\prime }-r}\beta \left( y^{\prime }\left| 0\right\rangle _b+z^{\prime }\left| 1\right\rangle _b+x^{\prime }\left| 2\right\rangle _b\right) \nonumber \\&+\,\omega ^{2\left( p^{\prime }-r\right) }\beta \left( z^{\prime }\left| 0\right\rangle _b+x^{\prime }\left| 1\right\rangle _b+y^{\prime }\left| 2\right\rangle _b\right) , \end{aligned}$$
(21)

with

$$\begin{aligned} x^{\prime }&= 1+\omega ^{s+q^{\prime }}+\omega ^{2\left( s+q^{\prime }\right) }, \nonumber \\ y^{\prime }&= 1+\omega ^{1+s+q^{\prime }}+\omega ^{2\left( 1+s+q^{\prime }\right) }, \nonumber \\ z^{\prime }&= 1+\omega ^{2+s+q^{\prime }}+\omega ^{2\left( 2+s+q^{\prime }\right) }. \end{aligned}$$
(22)

Note that Eq. (21) has the same form as Eq. (9), and Eq. (22) takes the same form as Eq. (10). In addition, we note that the value taken by \(s+q^{\prime } \) involved in Eq. (22) satisfies one of the following three cases: (A) \( 3\oplus \left( s+q^{\prime }\right) =0\) (i.e., \(s+q^{\prime }=3m_1\)), leading to \(x^{\prime }=3,y^{\prime }=z^{\prime }=0;\) (B) \(3\oplus \left( s+q^{\prime }\right) =1\) (i.e., \(s+q^{\prime }=3m_2+1\)), leading to \( z^{\prime }=3,x^{\prime }=y^{\prime }=0;\) and (C) \(3\oplus \left( s+q^{\prime }\right) =2\) (i.e., \(s+q^{\prime }=3m_3+2\)), resulting in \(y^{\prime }=3,x^{\prime }=z^{\prime }=0\) (where \(m_1,m_2,\) and \(m_3\) are integers). Therefore, for cases A, B, and C here, the state (21) reduces to the states (11), (13), and (14), respectively, with \(p\) there replaced by \( p^{\prime }\) now. Furthermore, according to the discussion given in the previous subsections A, B, and C in Sect. 2, the three reduced states (11), (13), and (14) can be restored to the original qutrit state (1), by Bob performing unitary operations \(Z^{2\left( p^{\prime }-r\right) }U_0,\) \( Z^{2\left( p^{\prime }-r\right) }U_1,\) and \(Z^{2\left( p^{\prime }-r\right) }U_2\) on them, respectively.

The above steps except for the preparation of the resource entangled state in the first step are illustrated in Fig. 4.

Fig. 4
figure 4

Quantum circuit for controlled teleportation with many agents in each group. The element containing \(H\) corresponds to a Hadamard transformation, the large square box with an arrow and the letters BM represents a generalized Bell-state measurement, each small square box with an arrow indicates a measurement in the single-qutrit \(Z\) basis, and \(U\) denotes Bob’s unitary recovery operation on his qutrit \(b\), which equals to \( Z^{2\left( p^{\prime }-r\right) }U_0,\) \(Z^{2\left( p^{\prime }-r\right) }U_1, \) and \(Z^{2\left( p\prime -r\right) }U_2\) for the three cases (A), (B), and (C) discussed in the text, respectively

Full size image

In what follows, we will prove that if one agent in each group does not cooperate, Bob cannot gain any information about the qutrit state (1) to be teleported.

From Eq. (17), one can see that if the two qutrits \(m\) and \(a\) are measured to be in the basis state \(\left| \varphi _{rs}\right\rangle _{ma}\) by Alice, then the qutrits belonging to all agents and Bob will be in the state \( \left| \xi _{rs}\right\rangle _{12\ldots n1^{\prime }2^{\prime }\ldots n^{\prime }b}\) given in Eq. (18). Now suppose that except one agent (say agent \(k\)) in one group and the other agent (say agent \(l^{\prime }\)) in the other group, all the remaining agents cooperate with Bob. Namely, they first perform a Hadamard transformation on their respective qutrits, which leads the state (18) to

$$\begin{aligned} \ \ \left| \xi _{rs} \right\rangle _{12\ldots n1^{\prime }2^{\prime }\ldots n^{\prime }b}\!=\!\sum \left| p_1p_2\ldots p_{k-1}p_{k+1}\ldots p_nq_{1^{\prime }}q_{2^{\prime }}\ldots q_{\left( l-1\right) ^{\prime }}q_{\left( l+1\right) ^{\prime }}\ldots q_{n^{\prime }}\right\rangle \otimes \left| \xi _{rs} \right\rangle _{kl^{\prime }b}, \end{aligned}$$
(23)

with

$$\begin{aligned} \left| \xi _{rs}\right\rangle _{kl^{^{\prime }}b}&= \alpha \left| 0\oplus s\right\rangle _k\left[ \left| 00\right\rangle +\omega ^{s+\widetilde{q} }\left| 11\right\rangle +\omega ^{2\left( s+\widetilde{q}\right) }\left| 22\right\rangle \right] _{l^{^{\prime }}b} \nonumber \\&+\,\beta \omega ^{\widetilde{p}-r}\left| 1\oplus s\right\rangle _k\left[ \left| 00\right\rangle +\omega ^{1+s+\widetilde{q}}\left| 11\right\rangle +\omega ^{2\left( 1+s+\widetilde{q}\right) }\left| 22\right\rangle \right] _{l^{^{\prime }}b} \nonumber \\&+\,\gamma \omega ^{2\left( \widetilde{p}-r\right) }\left| 2\oplus s\right\rangle _k\left[ \left| 00\right\rangle +\omega ^{2+s+\widetilde{q} }\left| 11\right\rangle +\omega ^{2\left( 2+s+\widetilde{q}\right) }\left| 22\right\rangle \right] _{l^{^{\prime }}b},\qquad \end{aligned}$$
(24)

where \(\widetilde{p}=\sum _{i=1,i\ne k}^np_i\), \(\widetilde{q} =\sum _{i^{\prime }=1^{\prime },i^{\prime }\ne l^{\prime }}^{n^{\prime }}q_{i^{\prime }}.\) Next, they take a measurement on their qutrits in the \(Z\) basis. From Eq. (23), one can see that if they measure their qutrits in the state \(\left| p_1p_2 \ldots p_{k-1}p_{k+1}\ldots p_nq_{1^{\prime }}q_{2^{\prime }}\ldots q_{\left( l-1\right) ^{\prime }}q_{\left( l+1\right) ^{\prime }}\ldots q_{n^{\prime }}\right\rangle ,\) the qutrits \(k,l^{\prime },\) and \(b\) belonging to agents \(k\) and \(l^{\prime }\) and Bob are in the state \(\left| \xi _{rs}\right\rangle _{kl^{^{\prime }}b}\) above.

As mentioned previously, the three states \(\left| 0\oplus s\right\rangle ,\) \( \left| 1\oplus s\right\rangle ,\) and \(\left| 2\oplus s\right\rangle \) are orthogonal to one another for \(s\in \{0,1,2\}\). Hence, it can be easily found from Eq. (24) that after tracing over the qutrits \(k\) and \(l^{\prime }, \) the density operator of the qutrit \(b\) belonging to Bob is given by

$$\begin{aligned} \rho _b=\frac{Tr_{kl^{\prime }}\left| \xi _{rs}\right\rangle _{kl^{\prime }b}\left\langle \xi _{rs}\right| }{_{kl^{\prime }b}\left\langle \xi _{rs}\right| \left. \xi _{rs}\right\rangle _{kl^{\prime }b}}=I_b. \end{aligned}$$
(25)

This result (25) demonstrates that Bob can not gain any information (either encoded through amplitude or phase) about the qutrit state (1) to be teleported, when agent \(k\) in one group and agent \(l^{\prime }\) in the other group do not cooperate with him.

4 Discussion and conclusion

Let us discuss the security of this proposal against eavesdropping attack. Like all existing entanglement-based proposals for CT, the security of this proposal is determined by whether the resource state described by Eq. (16) can be safely established among Alice, Bob, and all agents. In other words, the security of this proposal depends on whether Alice could securely transmit the \(n+n^{\prime }+1\) qutrits initially prepared in the state (16) to the \(n+n^{\prime }\) agents and Bob. Since the procedure for testing whether Alice sends a qutrit to each agent is the same as that for testing whether Alice sends a qutrit to Bob, in the following, let us consider how to test if Alice sends a qutrit to Bob safely. The testing procedure is described below.

Alice first prepares many pairs of qubits in Bell states \(\left| \phi ^{\pm }\right\rangle =\left| 00\right\rangle \pm \left| 11\right\rangle \) and \( \left| \psi ^{\pm }\right\rangle =\left| 01\right\rangle \pm \left| 10\right\rangle \). Each pair is randomly chosen to be in one of the four Bell states. She now sends Bob one of the Bell-state qubits in each Bell pair as well as the qutrit in a sequence (note that the qutrit is the qutrit \(b\) involved in the state (16)) while keeping the other half of the Bell-state qubits to herself. Note that in an experimental implementation, each qubit here should be embedded in a qutrit, so that any eavesdropper cannot tell the difference between the qutrit \(b\) from the other qubits simply by looking at the dimensions of the systems. If a third party Eve intercepts some of the Bell-state qubits from Alice, replaces them by fakes, and then sends the false qubits to Bob, or if she entangles those Bell-state qubits with auxiliary systems, then each of the false or disturbed qubits received by Bob does not preserve the original correlation with the corresponding Bell-state qubit at Alice’s hand. Thus, the eavesdropping can be detected in the following way. Alice picks some of her Bell-state qubits randomly and tells Bob which qubits that he received should be selected for the testing. Alice and Bob then take measurements on their selected qubits along a single-qubit Z or X basis that they agree on and then compare their measurement outcomes. Since Alice knows which Bell state was initially prepared for each pair of qubits shared by her and Bob, she knows the desired correlation between their measurement outcomes. If Alice finds that the observed correlation between their measurement outcomes is not what she expected, she knows that there is eavesdropping. If this occurs, Alice informs Bob to discard all qubits and the qutrit that he had received, and then, they restart the whole testing procedure above. On the other hand, if no eavesdropping is revealed, then Alice tells Bob which particle he received is the qutrit \(b\), such that Bob can select it out to be used later in the CT protocol.

In conclusion, we have proposed a way for teleporting an arbitrary unknown pure state of a qutrit to a distant receiver with the control of two groups of multiple agents via entanglement. We first considered the CT with one agent in each group and then expanded the number of agents to \(n\) agents in one group and \(n^{\prime }\) agents in the other group. In our proposal, all agents only need to take single-qutrit measurements and announce their measurement outcomes to the receiver. A sender can successfully teleport the qutrit state to a distant receiver, and the success rate of teleportation is unity, when all agents in the two groups cooperate. However, if one agent in each group does not collaborate, the receiver cannot gain any information (including amplitude information or phase information or both) about the qutrit message state to be teleported. In order for the receiver to see the maximally mixed state of equations (15) and (25), there must be two agents that do not collaborate, one in each group. It should be mentioned that if all of the agents in one group, e.g., the agents knowing \(p_i\, (i=1,2,\ldots ,n),\) decide not to cooperate, Bob can still learn some information about the amplitude. But, in contrast, with just one agent in each group—who does not collaborate, this protocol can prevent any information leakage.

Note that a qubit is a special case of a qutrit when the state lies in a fixed two-dimensional subspace of the qutrit. Hence, the present proposal can be also applied in the implementation of controlled teleportation of an arbitrary unknown pure state of a qubit with many control agents in two groups. This protocol might be extended to controlled teleportation of an arbitrary pure state of a qudit (a \(d\)-dimensional quantum system, where \( d\ge 2\) is arbitrary), for which no information to be teleported can be accessed by the receiver even if two agents (one in each group) do not cooperate.