Comparative study of interpolation methods for low-density sampling

Abstract

Given the high costs of soil sampling, low and extra-low sampling densities are still being used. Low-density soil sampling usually does not allow the computation of experimental variograms reliable enough to fit models and perform interpolation. In the absence of geostatistical tools, deterministic methods such as inverse distance weighting (IDW) are recommended but they are susceptible to the “bull’s eye” effect, which creates non-smooth surfaces. This study aims to develop and assess interpolation methods or approaches to produce soil test maps that are robust and maximize the information value contained in sparse soil sampling data. Eleven interpolation procedures, including traditional methods, a newly proposed methodology, and a kriging-based approach, were evaluated using grid soil samples from four fields located in Central Alberta, Canada. In addition to the original 0.4 ha⋅sample⁻¹ sampling scheme, two sampling design densities of 0.8 and 3.5 ha⋅sample⁻¹ were considered. Among the many outcomes of this study, it was found that the field average never emerged as the basis for the best approach. Also, none of the evaluated interpolation procedures appeared to be the best across all fields, soil properties, and sampling densities. In terms of robustness, the proposed kriging-based approach, in which the nugget effect estimate is set to the value of the semi-variance at the smallest sampling distance, and the sill estimate to the sample variance, and the IDW with the power parameter value of 1.0 provided the best approaches as they rarely yielded errors worse than those obtained with the field average.

In the 2021 Precision Agriculture Dealership Survey (Erickson & Lowenberg-Deboer, 2021), grid and zone sampling are among the most often offered and adopted precision services in the United States. According to the same survey, the use of grids with the common cell size of 1 ha predominates over zone sampling, while many continue to sample using larger grids.

Thus, a scenario in which a field of ≥ 100 ha is soil sampled using grid cells of > 1 ha would not be uncommon. In such a case, the total number of soil samples would be smaller than 100, whereas 100 is recommended as the minimum sample size to obtain adequate experimental variograms for soil properties (Webster & Oliver, 1992). It follows that to produce an interpolated surface, at least some of the available deterministic interpolation methods should be considered. Among them, inverse distance weighting (IDW) is one of the most popular as it has no limitations on the number of samples, is computationally efficient, and easy-to-apply (Kravchenko, 2003).

As IDW is an exact interpolator (i.e., it predicts values identical to observed values at sampling locations), a known issue with maps obtained with this method is the influence of isolated extreme values on their surroundings, which creates an effect called “bull’s eye.” Although many modifications of the original IDW method (Shepard, 1968) have been tested and compared to other interpolation methods (Franke & Nielson, 1980; Robinson & Metternicht, 2006), further evaluation and improvement of interpolation techniques for low-density soil sampling is needed.

One could argue that when measurements are sparse or weakly correlated in space, an interpolation method using co-variables observed at a higher resolution (e.g., satellite imagery, soil sensing techniques) may improve interpolation accuracy (Goovaerts, 1999). This is a valid point, but it assumes that the co-variables are spatially cross-correlated with the target variable (Isaaks & Srivastava, 1989; Webster & Oliver, 2007). If this assumption is proven to be wrong for co-variables for which historical or free-access datasets are available, new information must be collected, which may not be feasible due to additional costs or lack of time.

Clearly, sampling soils with low-density grids imposes difficulties in extracting useful information from the data. Thus, more efficient and accurate sampling strategies for precision agriculture practitioners and the industry are still required. Since the 1990s (Larocque et al., 2007; Laslett & McBratney, 1990; Wadoux et al., 2019), research results have supported that slight modifications made to a grid sampling design (e.g., by collecting extra samples close to grid sampling nodes) can improve the estimation of variogram model parameters and decrease kriging interpolation errors. Nevertheless, the 2021 survey mentioned above suggests that, in large part, soil sampling data may continue to be collected in agricultural fields using the traditional grid sampling design at low or extra-low resolution.

Therefore, methodologies or approaches that maximize the value of datasets with too small a size to use classical geostatistical methods must be developed and explored further. Sobjak et al. (2023) used samples collected at a density of approximately 3 samples⋅ha⁻¹ to build and test an automated process to improve the selection of the parameters that maximize the accuracy for ordinary kriging (OK) and IDW. These authors reported an improvement in the interpolation accuracy when the best interpolation parameters were identified using a newly proposed assessment index (i.e., effective spatial dependence index). Others have focused on evaluating the potential of machine learning algorithms for interpolating soil properties. Hengl et al. (2018) proposed an approach that uses the distance between samples as co-variables in a random forest model to perform spatial interpolation. Pereira et al. (2022b) reported a potential improvement in the interpolation accuracy of soil properties when using a combination of support vector machines and IDW to interpolate samples collected from one field at densities ranging from 1.4 to 5.7 samples⋅ha⁻¹ when compared to OK and IDW. However, there is still a lack of comprehensive comparison of different interpolation methods and the definition of universal approaches for interpolating low-density soil sampling datasets.

The objective of this study was to develop alternative interpolation procedures and to assess them in comparison with other methods to produce soil test maps that are robust and maximize the information value contained in datasets collected with low soil sampling density.

Material and methods

Study area and data

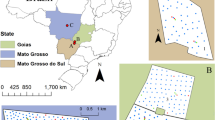
Soil samples were collected from four fields in Central Alberta, Canada (Fig. 1a). The four fields were mainly grown under wheat, barley, and canola crop rotation. A summary of the field characteristics is presented in Table 1.

Fig. 1

Experimental sites: a map of the Canadian province of Alberta with a zoomed-in window showing the distribution of the four experimental sites located within a region known as Central Alberta, and b field boundaries and grid centroids representing the three sampling design densities—different shapes, and colors are used to represent the distribution of the sampling locations for 0.4 (solid black circles), 0.8 (hallow red circles), 3.5 (hallow blue squares) ha⋅sample⁻¹, and validation points (solid green diamonds); the latter are only available for Field 1 (Color figure online)

Table 1 Description of the studied fields

All soil samples from 0 to 0.15 m deep were collected during Fall 2022, using grids of cells of about 0.4 ha. A total of 128 (including 20 independent validation samples), 216, 274, and 144 samples were collected from Fields 1, 2, 3, and 4, respectively (Fig. 1b). The locations for the validation samples from Field 1 were chosen based on the spatial variability of the field data observed in previous years; see the diamond shapes in Fig. 1b for Field 1. These validation samples were collected on the same day and under the same conditions as the grid samples from this field. All samples were sent to the same laboratory for the analysis of their chemical properties. The reported values for pH, plant-available phosphorus (P), and potassium (K) were used to compare the interpolation approaches and methods. P and K values were reported in parts per million (ppm), while the pH followed the scale from 0 (most acidic) to 14 (most basic). These three soil chemical properties were chosen to evaluate the interpolation methods due to their relevance in the soil management practices performed in precision agriculture. Thematic maps from pH are often used to determine areas with lower pH values, which can be amended through site-specific lime application. Similarly, prescription maps can be generated by mapping the spatial distribution of P and K to address and improve the levels of these two macronutrients in regions within the field where their availability is below the ideal values for crop development.

From the original 0.4 ha⋅sample⁻¹ sampling scheme, samples were gradually removed to create sampling design densities of 0.8 and 3.5 ha⋅sample⁻¹, thus, broadening the scope of the comparison. Only regular grid designs were considered because they still predominate over other sampling designs (Erickson & Lowenberg-Deboer, 2021). The three sampling designs for the four fields are presented in Fig. 1b.

Conventional interpolation methods

The three datasets from each of the four fields were submitted to Shepard’s original IDW algorithm (Shepard, 1968). This algorithm requires setting two parameters: the power and the search neighborhood. The power value controls the influence of the closest samples to an interpolated location—the higher the power, the greater the influence of the samples closer to the interpolated point. The search neighborhood is defined by the number of points used for estimating the value at the interpolation location; for example, with a search neighborhood of 4, the interpolated value is determined from the 4 closest sample data. This study used power values of 1 and 2 and a search neighborhood equal to all available neighbors (108, 216, 274, and 144 for Fields 1, 2, 3, and 4, respectively) to evaluate Shepard’s original IDW.

An approach, called “Optimal IDW” hereafter, was also evaluated. This approach uses brute-force search and Leave One-Out Cross-Validation (LOOCV) to assess a wide range of combinations of values for the power and search neighborhood parameters. Power values between 1 and 5, in increments of 0.2, and a search neighborhood from 4 to all available neighbors, in increments of 1, were tested. Based on the Mean Absolute Error (MAE) from this procedure, a combination of both parameters that minimized the MAE was selected. In addition, a separate approach in which the power value is set to 0 and the search neighborhood to 1 was evaluated as “Nearest neighbor.” Both approaches described above are variants of Shepard’s original IDW algorithm (Shepard, 1968).

The local modified Shepard’s IDW interpolator (Franke & Nielson, 1980), another IDW variant, uses estimates from a locally fitted polynomial and a limited neighborhood for the inverse distance weights calculation to address some of the caveats imposed by the original Shepard’s IDW (e.g., the influence of isolated extreme values). This interpolator requires setting two independent parameters that control the neighborhood size for a local quadratic polynomial fitting and inverse distance weights. According to Franke and Nielson (1980), properly setting these two parameters can significantly influence the performance of this method. In implementing the local modified Shepard’s IDW, a brute-force search was employed to select the combination of parameters that minimized the MAE from a LOOCV. Neighborhood sizes varying from 4 to all available neighbors, in increments of 1, were tested for both parameters.

The original OK, called “Fitted variogram model” hereafter, was evaluated as an interpolation option in the geostatistical approach. Thus, using the R library gstat (Pebesma, 2004), experimental variograms were computed for all datasets from all fields, soil properties, and sampling designs. Spherical, exponential, and Gaussian models were fitted to each experimental variogram, and the best model was selected based on the residual sum of squares for a weighted least-squares fitting procedure. Even though Webster and Oliver (1992) recommend 100 as the minimum sample size to obtain adequate experimental variograms for soil properties, “Fitted variogram model” was used to broaden the discussion of results when this minimum number was not reached in this study.

In the following two subsections, two new methods are proposed for interpolating low-density soil sample data, one model-based and the other model-free.

A modification of the kriging-based approach

Due to limited information about variability below the shortest sampling distance and the small number of pairs of observations available to estimate semi-variances at a number of distance lags, fitting a model to an experimental variogram computed from a sparse dataset is challenging and highly uncertain. Accordingly, the proposed approach sets the sill and the nugget effect to values directly derived from the sample data without passing by the nugget-effect and sill estimates obtained from a fitted variogram model.

When data are not correlated, the sample variance is the classical estimator of the population variance. Barnes (1991) already raised the awareness that if the data are evenly distributed in an area with dimensions greater than the range of spatial correlation, the sample variance could be a reasonable first estimate of the sill. Based on a different reason leading to the same outcome, instead of relying on an experimental variogram and variogram model parameter estimates that are uncertain due to a small sample size (Larocque et al., 2007), it is proposed that a sample variance estimated under the assumption of independence should be used as an alternative to a sill estimate obtained from an experimental variogram that does not completely represent the correlation structure of the data.

The challenges mentioned above for the sill concern the estimation of the nugget effect in a similar way, more particularly the absence (lack) of direct (indirect) information in the data about the behavior of the semi-variance function at distances smaller than the shortest sampling distance (between grid nodes if regular). Thus, estimating the nugget effect accurately by fitting a variogram model is at the least very difficult or practically impossible, so it is proposed that the semi-variance estimate at the shortest sampling distance be used as the nugget-effect estimate in that case. This nugget-effect estimator is likely to be biased upwards, and the nugget-effect estimates might even approach the sample variance, used as the sill estimate. This would then be interpreted as there is no spatial correlation in the data, and a flat, pure nugget-effect variogram model would be adopted. The expectation, however, is that the generated interpolated surface would be better than the field average and as good as the field average otherwise. For comparison purposes, interpolated surfaces were also produced with the nugget effect set to 0 (“Set Sill, and Nugget = 0”), which represents the theoretical minimum value for this parameter in a variogram model.

Finally, the alternative estimates of the sill and the nugget effect described above are inserted in the equation of a spherical variogram model, and an estimate of the range of spatial correlation is obtained by fitting the equation to the experimental variogram by least squares. A spherical variogram model is preferred to a member of the Matérn family, such as the exponential and Gaussian variogram models, because the semi-variance reaches the process variance only asymptotically in them. The steps for this modification of the kriging-based approach (“Set Sill and Nugget”) are summarized in Fig. 2.

Fig. 2

Flowchart explaining the proposed modification of the kriging-based approach to obtain interpolated surfaces from soil data collected at low and extra-low sampling densities; OK ordinary kriging

Proposed modification of the original IDW

In this paper, a new model-free method is also proposed: IDW Smoothed. It postulates that a better, more representative interpolated surface can be produced by jointly minimizing the difference between an optimized value and the observed value at each sampling location and a quantity called “distance gradient” (DG), which indicates the rate of change of measurements with distance. Therefore, the following Pareto multi-objective optimization procedure is proposed:

• 1. Define a search domain. The minimum and maximum values from the observed values are calculated for a specific soil test. The precision for the values reported in the lab results is determined and used as an incremental value to define the search domain (e.g., minimum, maximum, and precision of laboratory analysis of 1, 3, and 0.1, respectively, were determined; thus, a search domain is defined by all numbers between 1 and 3, in increments of 0.1)

• 2. Randomly select an array of values from inside the search domain with the same sample size (number of observations) as the input data. The newly selected values are referred to as “trial values.”

• 3. Calculate the Mean Absolute Error (MAE) between the observed and trial values. Using the trial values and the matrix of geographic distances between each sampling location and the n − 1 other sampling locations, calculate the distance gradients:

  $$DG_{k} = \frac{{\mathop \sum \nolimits_{{\begin{array}{*{20}c} {i = 1 } \\ {i \ne k } \\ \end{array} }}^{n} \frac{{\left| {x_{k} - x_{i} } \right|}}{{d\left( {x_{k} , x_{i} } \right)}}}}{n - 1} {\text{for}}\,k = { 1}, \, \ldots ,n$$

  (1)

where n is the number of sampling locations, x_k is the trial value for the sampling location (k) for which the distance gradient is calculated in Eq. (1), x_i denotes the trial value for sampling location i, and d(x_k, x_i) is the geographic distance between sampling locations k and i.

Obtain the mean DG by averaging the n DGs.

• 4. Repeat Steps 2 and 3 for a user-set number of times (trials), with the objective of minimizing the MAE and mean DG. The two objectives are plotted in Fig. 3.

• 5. Obtain the optimal solution (shown with the red triangle in Fig. 3) by selecting the solution closest to the origin of the biplot from the Pareto optimal solutions (i.e., the blue squares in Fig. 3).

• 6. Produce a continuous surface by using the optimized values and their respective spatial coordinates in an IDW with n − 1 neighbors for each sampling location and a small distance power value (e.g., 1).

Fig. 3

Biplot of Mean Distance Gradient (DG) versus Mean Absolute Error (MAE) for 3,500 trials (black dots), with the Pareto-optimal solutions (blue squares) and the optimal solution (red triangle) (Color figure online)

A customized script written in Python 3 programming language was developed to implement the multi-objective optimization process for the proposed methodology. The Optuna library (Akiba et al., 2019), Nondominated Sorting Genetic Algorithm II (Deb et al., 2002), and a total of 3500 trials were used to obtain the Pareto front and select the optimal solution for each soil property. In the definition of the search domain, increments were 0.1 for pH and 1 ppm for the K and P tests. To compare this method with the original IDW (Shepard, 1968), values of 1 and 2 were used for the power parameter (Step 6).

A summary of the 10 interpolation approaches and methods described above and the interpolation procedures used in each are provided in Table 2. In addition, for each sampling density, the field average was used as a benchmark.

Table 2 Summary table of all the different methods and approaches evaluated in this study and their respective reference name used for figures and tables

Data analysis

For a given sampling density and soil property (pH, K, P), the data were standardized to a zero mean and a unit variance before performing the interpolation, except for IDW Smoothed, where the data span is part of the optimization. The standardized data were back-transformed for the report of results.

The Mean Squared Error (MSE) and the G criterion (Eq. 2) proposed by Agterberg (1984) were used to assess the performance of the interpolation procedures. The G criterion, which involves the MSE, compares the residuals for a specific approach with the residuals obtained if the field average was used:

$$G= \left(1-\frac{MSE}{{MSE}_{Average}}\right)\times 100$$

(2)

where MSE is the mean of squared errors for the evaluated method, while MSE_Average denotes the mean of squared error if the field average was used instead for the interpolation. Positive G values indicate an advantage of using the evaluated interpolation method over the field average. Negative G values imply that the field average and the associated flat surface provide a more accurate interpolated surface. A zero G value means equivalency.

Independent validation samples were only available for Field 1, which allowed for validation at all three sampling densities. For Fields 2, 3, and 4, the samples discarded to produce the 0.8 and 3.5 ha⋅sample⁻¹ sampling grids were used to validate the results for these two densities only (Fig. 1). Cross-validation could have been used but was considered to be out of the scope of the study, and biased results could be obtained by cross-validation in the case of low-density sampling designs (Wadoux et al., 2021).

A pairwise Levene’s test was employed to evaluate the standard errors calculated through the validation samples. When the above-mentioned statistical test rejected the null hypothesis (homogeneity of variances) at a significance level of 0.05 for a pair of interpolation procedures, their interpolation accuracy was considered significantly different since there was heterogeneity in the variance of their standard errors. Data processing, interpolation, and statistical analysis were performed using customized scripts written in the R language (R Core Team, 2022).

Results and discussion

The descriptive statistics for the different grid sampling designs and validation samples are reported in Table 3. For Field 1, the mean and median values of the K and P variables are slightly smaller for the validation set than for the grid samples, whereas the contrary is observed for pH. For Fields 2, 3, and 4, where the samples removed from the 0.4 ha⋅sample⁻¹ grid sampling design were used for validation, the descriptive statistics for grid and validation samples are very similar. From the highest sampling density down to 0.8 and 3.5 ha⋅sample⁻¹, the number of samples is reduced by about 50 and 90%, respectively. However, the means and medians calculated from the grid samples in a given field for a given soil property present only slight changes across the different sampling densities. This indicates that representative samples from the underlying surface were collected regardless of the sampling density.

Table 3 Descriptive statistics for plant available Potassium (K), plant available Phosphorus (P), and pH for all the fields, sampling densities, and validation samples (a hyphen indicates that values are not available)

The experimental variogram from the highest sampling density available (0.4 ha⋅sample⁻¹) and a weighted least-squares fitting procedure were used to obtain variogram model parameters estimates for each field and soil property (Table 4). The obtained values were considered the best available estimates of the spatial structure of the underlying surface from which the samples were collected. Note that for this sampling density, the number of samples available was higher than 100 (Table 3), as Webster and Oliver (1992) recommended.

Table 4 Variogram model parameter estimates from a standard variogram fitting procedure for the four fields at the highest sampling density collection (Table 3) after data was standardized to a zero mean and a unit variance

An analysis of Table 4 presents differences and similarities in the spatial variability of soil properties within and across fields. For example, for Field 1, an exponential model was selected for K. In contrast, a spherical model was selected for P and pH, indicating a difference in the behavior of the spatial correlation in the data. For this same field, all soil properties presented a strong spatial structure (classification modified from Cambardella et al., 1994), whereas, for Field 2, a strong spatial structure is only observed for pH and weak for K and P. In general, the different spatial structure classes in Table 4 highlight the differences in the spatial variability across the fields and soil properties, an important data characteristic when evaluating different interpolation methods.

Box plots showing the distribution of interpolation errors for the 11 procedures evaluated for Field 1 (3 variables × 3 sampling densities) are presented in Fig. 4. In each panel, box plots are sorted by increasing values of MSE from top to bottom. The letters a and b beside the reported MSE values correspond to the results of Levene’s test; two MSE values that are not followed by the same letter differ significantly at α = 0.05. The largest number of significant differences among MSE values are for variable P at the sampling densities of 0.4 and 0.8 ha⋅sample⁻¹ (Fig. 4b and e). The G values (on the left in box plots) reveal advantages and disadvantages relative to the field average. For example, in Fig. 4g, G values indicate that “IDW Smoothed P:1 and P:2”, “Set Sill and Nugget,” and “IDW P:1” generated surfaces with MSEs similar to or better than “Average.” In contrast, interpolating data using “IDW P:2”, “Set Sill, and Nugget = 0”, “Optimal IDW,” “Nearest Neighbor,” and “IDW Modified Shepard” results in less accurate surfaces than when the field average is used. No box plot is presented for “Fitted variogram model” in Fig. 4g and i, because the model fitting algorithm failed to converge.

Fig. 4

Box plots of interpolation errors for Field 1 at grid sampling densities of 0.4 ha⋅sample⁻¹ (a–c), 0.8 ha⋅sample⁻¹ (d–f), and 3.5 ha⋅sample⁻¹ (g–i). Results are presented for a total of 11 interpolation procedures, each identified by a capital letter and a color; for details, see Table 2. “Fitted variogram model” was removed from the analysis and does not appear in a few panels because the variogram model fitting algorithm failed to converge for that specific sampling density and soil property. Letters a and b indicate the differences in MSE among interpolation procedures that are declared statistically significant (α = 0.05) with Levene’s test

Only “IDW P:1” and “Set Sill and Nugget” show positive G values in all 9 panels of Fig. 4, meaning absolute superiority over “Average” in Field 1. With the field average set aside, some interpolation procedures proved to be more or less reliable than others. For example, based on MSE values, “Optimal IDW” and “Nearest Neighbor” surfaces were found to be the most accurate (Fig. 4b) or the least accurate (Fig. 4a), although Levene’s test detected no statistically significant differences in Fig. 4a. Overall, with a lower sampling density, the advantage of using the evaluated interpolators over the field average is reduced. Also, as expected (Larocque et al., 2007; Webster & Oliver, 1992), fitting a variogram model becomes more difficult or even practically impossible at the lowest sampling density of 3.5 ha⋅sample⁻¹; the variogram model fitting algorithm then failed to converge for two of the three soil properties sampled from Field 1 (number of samples: 12; Table 3).

Concerning the alternative interpolation methods proposed in this paper, “Set Sill and Nugget” shows signs of lesser performance than “Set Sill, and Nugget = 0” based on the G values from Fig. 4h and i. That might indicate some advantage to setting the nugget-effect value to 0. However, the G value of “Set Sill, and Nugget = 0” is negative in Fig. 4g (K, lowest sampling density), whereas the corresponding G value for “Set Sill and Nugget” is positive. Leading to the assumption that for Field 1, “Set Sill and Nugget” performed as expected, producing either better results than the field average (i.e., positive G values) or as good as the field average (i.e., G = 0; Fig. 4i), while the same does not apply for “Set Sill, and Nugget = 0”. Thus, even though “Sill and Nugget” might not be the highest-performing interpolator in all situations, it might be a reliable interpolation procedure for datasets from low and extra-low sampling densities since it did not produce results worse than average. As for “IDW Smoothed P:1” and “IDW Smoothed P:2”, slightly negative G values are observed only for pH at the 3.5 ha⋅sample⁻¹ sampling density (Fig. 4i).

The interpolated surfaces for P—the only variable that presented some statistical significance among the different interpolation procedures and for which the variogram fitting converged for all sampling densities—are presented in Figs. 5, 6, 7. These maps exemplify the effect of the 10 different interpolation procedures in the spatial variability of P for all three sampling densities. Clearly, some procedures generate rougher surfaces, with abrupt changes between neighboring values (e.g., Nearest Neighbor—Figs. 5g, 6g, and 7g), while others generate smoother surfaces, presenting little to no spatial variability (e.g., IDW Smoothed P:1—Fig. 5d).

Fig. 5

Interpolated maps from Field 1 representing the spatial variability for phosphorous (P) using the 0.4 ha⋅sample⁻¹ sampling density and 10 different interpolation procedures (maps for the “Average” procedure were not included as it does not show spatial variability). All the maps share the same legend—depicted between the two rows of maps

Fig. 6

Interpolated maps from Field 1 representing the spatial variability for phosphorous (P) using the 0.8 ha⋅sample⁻¹ sampling density and 10 different interpolation procedures (maps for the “Average” procedure were not included as it does not show spatial variability). All the maps share the same legend—depicted between the two rows of maps

Fig. 7

Interpolated maps from Field 1 representing the spatial variability for phosphorous (P) using the 3.5 ha⋅sample⁻¹ sampling density and 10 different interpolation procedures (maps for the “Average” procedure were not included as it does not show spatial variability). All the maps share the same legend—depicted between the two rows of maps

From a soil management perspective, challenges can be encountered in both extreme scenarios mentioned above. For example, the “Nearest Neighbor” interpolated surface would generate variable rate maps with neighboring regions with abrupt changes in the amount of P fertilizer. These sudden changes in the prescribed fertilizer rate, combined with the rate adjustment lag existing in most variable rate applicators (Fulton et al., 2005), would reduce the quality and accuracy of the application. On the other hand, extremely smooth surfaces (e.g., “IDW Smoothed P:1”; Fig. 5d) could lead to the recommendation of a uniform rate application of P, even though there is a clear spatial variability of this nutrient in Field 1 (Fig. 5a). Applying the same rate of P throughout Field 1 would result in a surplus and deficiency of this macronutrient in the field, negatively affecting the crop yield and potentially contaminating surface and groundwater (Liu et al., 2021). Although the levels of plant-available P in Field 1 are classified as medium to very-high for western Canadian soils (Alberta Ministry of Agriculture and Irrigation, n.d.), the above-described scenarios highlight the impact of interpolation procedures on soil management practices.

A visual comparison of Figs. 5, 6, 7 shows similarities among “Set Sill, and Nugget = 0”, “IDW Modified Shepard,” and “Optimal IDW” maps, and that smoother maps are obtained from “IDW Smoothed P:1 and P:2” in comparison to the original IDW. Also, compared to “Set Sill, and Nugget = 0” and “Fitted variogram model,” “Set Sill and Nugget” tends to generate smoother surfaces, an effect of the higher nugget-effect estimates obtained from the latter procedure, a well-known behavior in geostatistics (Chilès & Delfiner, 2012).

Box plots for Field 2 are presented in Fig. 8. Due to the similarity/dissimilarity in spatial structure of the three soil properties in this field (weak for K and P, and strong for pH; Table 4), the behavior of the G criterion is not only influenced by sampling density, but also by the spatial correlation present in the data. At the 0.8 ha⋅sample⁻¹ sampling density (i.e., the higher evaluated density in Field 2), the G values are higher for pH (Fig. 8c) than for K and P (Fig. 8a and b). At the lower density in Field 2 (3.5 ha⋅sample⁻¹), the G values of pH show a clear worsening in performance of the interpolation procedures relative to the field average for this soil property (see Fig. 8c vs. f), while the G values of K and P rather tend to show a statu quo (see Fig. 8a and b vs. d and e).

Fig. 8

Box plots of interpolation errors for Field 2 at grid sampling densities of 0.8 ha⋅sample⁻¹ (a–c) and 3.5 ha⋅sample⁻¹ (d–f). Results are presented for a total of 11 interpolation procedures, each identified by a capital letter and a color; for details, see Table 2. “Fitted variogram model” was removed from the analysis and does not appear in most panels because the variogram model fitting algorithm frequently failed to converge. Letters a, b, c, d, and e indicate the differences in MSE among interpolation procedures that are declared statistically significant (α = 0.05) with Levene’s test

The above result is consistent with findings reported in the literature. For example, Kravchenko (2003) compared kriging and IDW by simulating surfaces with various spatial structures and sampling densities, and found that for surfaces with stronger spatial structures, a reduction in sampling density produces a drop of the G values, whereas for weaker spatial structures, only slight changes are observed. This does not imply that the selection of a reliable interpolator can be neglected for soil properties with weak spatial structure. Indeed, the results for P in Fig. 8e indicate that depending on the choice of the interpolation procedure, the G value can be as low as –264%, the exception to the statu quo rule mentioned above. Also, the data are not ‘known’ before sampling, nor is their spatial correlation.

Besides “IDW Smoothed P:1”, all the other interpolation procedures are less accurate than the field average in Fig. 8e. In particular, the G value for the modified kriging-based procedure “Set Sill and Nugget” is slightly negative (− 13.6%), while “Set Sill, and Nugget = 0” is one of the worst when compared to “Average” (G = − 106.0%). It is noteworthy that for a soil property with a stronger spatial structure, or equivalently a smaller nugget effect (e.g., pH in Field 2; see Table 4), setting the nugget effect value to zero yields a more accurate surface than “Set Sill and Nugget.” In contrast, for properties with a larger nugget effect (e.g., P and K in Field 2; see Table 4), setting this model parameter (or its estimate) to zero produced less accurate interpolated surfaces than when the semi-variance estimate at the shortest sampling distance was used. For example, for P sampled at the density of 3.5 ha⋅sample⁻¹ in Field 2, the interpolated surface of “Set Sill and Nugget” is significantly more accurate than that of “Set Sill and Nugget = 0” based on Levene’s test (Fig. 8e), even though both their G values are negative. The interpolation procedure “IDW Smoothed P:1” is the only one that produced surfaces more accurate than those of “Average” for all three soil properties in Field 2 at the extra-low sampling density of 3.5 ha⋅sample⁻¹, but not so much at the 0.8 ha⋅sample⁻¹ density (Fig. 8b).

Soil properties K and P show medium spatial structure in Field 3, while the spatial structure for pH appears strong (Table 4). Field 3 is the largest in size of the four study sites, thus yielding the largest number of observations at the sampling densities of 0.8 and 3.5 ha⋅sample⁻¹. Since a medium to strong spatial structure and a larger number of sample data reduce the uncertainty in variogram analysis, including the estimation of model parameters (Larocque et al., 2007), the variogram model fitting algorithm converged without exception for Field 3 (Fig. 9).

Fig. 9

Box plots of interpolation errors for Field 3 at grid sampling densities of 0.8 ha⋅sample⁻¹ (a–c) and 3.5 ha⋅sample⁻¹ (d–f). Results are presented for a total of 11 interpolation procedures, each identified by a capital letter and a color; for details, see Table 2. Letters a, b, c, d, and e indicate the differences in MSE among interpolation procedures that are declared statistically significant (α = 0.05) with Levene’s test

Fields 1 and 2 results indicated limited advantages reflected by positive G values for some interpolation procedures over “Average,” with little evidence for statistical significance. For Field 3, many of the MSEs computed from the interpolation errors show a significant improvement in interpolation accuracy over the field average. Except for P sampled at the extra-low density in Field 3 (Fig. 8e), all the panels in Fig. 8 identify a group of procedures yielding interpolated surfaces declared significantly more accurate than “Average” by Levene’s test. “Fitted variogram model” and “Set Sill and Nugget” are the only two interpolation procedures that consistently appear in these groups.

Following the interpretation rules developed and applied for Fields 1 and 2, the results obtained for Field 3 can be presented and discussed as follows. The G value of “Set Sill, and Nugget = 0” is greater than that of “Set Sill and Nugget” for pH at both sampling densities in Field 3, which was expected as the estimated nugget effect was close to zero (Table 4). Since the estimated nugget effect for K and P were higher than for pH in Field 3 but did not reach 0.5 for a maximum value of 1.0 (Table 4), it is ‘as expected’ that “Set Sill and Nugget” performed better than “Set Sill, and Nugget = 0” for one of these two soil properties (K), but not the other (P) at the low sampling density (Fig. 8b). Levene's test for P detected no significant difference between “Set Sill and Nugget” and “Set Sill, and Nugget = 0” at both sampling densities in Field 3. Concerning the interpolation procedures “IDW Smoothed P:1” and “IDW Smoothed P:2”, their G values were mostly positive, except for K at 0.8 ha⋅sample⁻¹ (Fig. 8a); in the comparisons with “Average,” “IDW Smoothed P:2” consistently presents an advantage over “IDW Smoothed P:1” in Field 3, with no significant difference between the two.

Several of the results obtained for Field 4 (Fig. 10), located approximately 100 km east of the other three fields (Fig. 1a), resemble some of those obtained for Field 1 (Fig. 4). For example, there is no significant difference among most of the interpolation procedures that are compared at their respective sampling densities. Notably, “IDW Smoothed P:1 and “P:2” consistently yielded positive G values for all the soil properties and densities. The variogram model fitting algorithm failed to converge for K and pH at the extra-low sampling density (Fig. 10d and f). For the same soil properties and sampling density, a flat variogram was obtained with “Set Sill and Nugget.” For obvious reasons, “Set Sill and Nugget” presents a clear advantage over “Set Sill, and Nugget = 0” in these two cases.

Fig. 10

Box plots of interpolation errors for Field 4 at grid sampling densities of 0.8 ha⋅sample⁻¹ (a–c) and 3.5 ha⋅sample⁻¹ (d–f). Results are presented for a total of 11 interpolation procedures, each identified by a capital letter and a color; for details, see Table 2. Fitted variogram model” was removed from the analysis and does not appear in a few panels because the variogram model fitting algorithm failed to converge for that specific sampling density and soil property. Letters a and b indicate the differences in MSE among interpolation procedures that are declared statistically significant (α = 0.05) with Levene’s test

Based on the results presented, none of the interpolation procedures consistently emerged as the best for all fields, soil properties, and sampling densities, suggesting that the optimal interpolator will change depending on the spatial structure present in the data and sampling density. This conclusion is consistent with the findings reported in the literature (Kravchenko, 2003; Kravchenko & Bullock, 1999; Robinson & Metternicht, 2006). It is noteworthy that for all fields, the field average never emerged as being the basis for the best approach.

Concluding the investigation at this point would leave the research question, “What is a robust and reliable interpolation procedure that maximizes the value of low-density soil sampling data?” unanswered. The keywords here are “reliable” and “robust,” and not “best,” as the presented results suggest that without having prior knowledge about the spatial structure of the data and the collection of validation samples, it would be difficult, if not impossible, to know which interpolation procedure would result in the most accurate surface.

Considering that a reliable and robust interpolator for low and extra-low sampling density is based on a procedure that will hardly yield surfaces less accurate than the field average and possibly represent the most accurate surface. The G values reported in the box plots (Figs. 4, 8, 9, 10) were classified in three groups—G < 0 (surface less accurate than field average), 0 ≤ G < Highest G (surface is as accurate as the field average but not the highest G value), and Highest G (interpolation approach with the most accurate surface), and the frequency of each category was assessed for the procedures. The results are presented in Fig. 11.

Fig. 11

Robustness and reliability analysis for the 11 interpolation procedures at the three different sampling densities. G values from Figs. 4 and 8, 9, 10 were grouped in the categories listed in the legend. “No Convergence” applies to the kriging approach “B—Fitted variogram model” when the model fitting algorithm failed to converge, and “Flat Variogram” applies to the modified kriging approach “J—Set Sill and Nugget” when estimated nugget-effect is the equal or higher than sample variance (Color figure online)

Focusing the analysis on the two lower sampling densities in Fig. 11 and evaluating the different procedures by their robustness and reliability, following the definition provided earlier, the most robust procedure at 0.8 ha⋅sample⁻¹ would be “Set Sill and Nugget.” For the extra-low sampling design, determining which procedure is the most robust proves to be challenging, as negative G values or “No convergence or Flat Variogram” are observed in all procedures with no exceptions.

One might argue that the “Fitted variogram model” could be considered the most robust procedure for the 3.5 ha⋅sample⁻¹ sampling density, as it did not yield any negative G values. If, in cases where the fitting algorithm failed to converge, the field average would be used instead, this would be a plausible affirmation. However, 7 out of 12 maps would lack spatial information. Moreover, over or underestimation of the variogram model parameters during the fitting procedure could produce highly inaccurate surfaces—a scenario not covered by the dataset used in this paper but supported by the findings from Webster and Oliver (1992) and Larocque et al. (2007) which suggest that a variogram originating from a low number of samples can present a wide confidence interval, leading to high uncertainty in the estimation of the model parameters.

The “Set Sill and Nugget” results are not too different from the “Fitted variogram model,” for 5 out of 12 maps, a flat variogram would be used to obtain the kriging estimates, producing the same result as for the field average (assuming global neighborhood—all available neighbors—was used). In contrast to the “Fitted variogram model,” “Set Sill and Nugget” once generated the most accurate surface for the 3.5 ha⋅sample⁻¹ but also presented a negative G value—a specific case where most of the procedures also presented G < 0 (Fig. 8e). Notably, both model-based approaches presented difficulties in consistently estimating model parameters that would generate an interpolated surface with a representation of the field spatial variability. Two other potential candidates for a robust interpolation procedure for this extra-low-density design were “IDW P:1” and “IDW Smoothed P:1”. Since “IDW P:1” was among the most robust methods for the 0.8 ha⋅sample⁻¹ sampling density, this method could be selected as the most robust. However, by using IDW, the issues with non-smooth surfaces due to the “bull’s eye” effect would remain, affecting the quality of prescription maps created based on the IDW surface.

Further analysis of the results presents that when the “Set Sill and Nugget” results in “pure nugget effect” (Figs. 4g, i, 8d, f, and 10d), “IDW P:1” and “IDW Smoothed P:1” presented positive G values, with an exception for the latter which presented slightly negative G value for pH from Field 1 sampled at 3.5 ha⋅sample⁻¹ (Fig. 4g). Thus, “Set Sill and Nugget” could be used when some spatial structure is still available in the data, but when a flat variogram is estimated, either “IDW P:1” or “IDW Smoothed P:1” could be employed to generate an interpolated surface that would at least provide a general trend of that soil property in the field. To make the newly proposed interpolation procedures readily available to precision agriculture practitioners, they could be implemented in existing open-source tools such as the Smart-Map (Pereira et al., 2022a) plugin for QGIS and AgDataBox-Map web platform (Michelon et al., 2019).

Even though the results indicate a potential for the use of the combination of “Set Sill and Nugget” with “IDW P:1” or “IDW Smoothed P:1,” the analysis was still limited to soils available in Central Alberta. Also, since the samples used for validation were not consistent for all sampling densities (except for Field 1), a formal statistical analysis of the effect of sampling density in each interpolation procedure was not performed, as it could generate biased results.

Therefore, future research should further explore the above-suggested combination of procedures and compare these to some of the already available machine learning-based spatial interpolation methodologies (Hengl et al., 2018; Pereira et al., 2022b). In addition, the robustness of the different interpolation methods could be evaluated from a perspective of the risks (economic and environmental) related to the soil management decisions that the practitioners would adopt based on the resulting interpolated surfaces. Based on the results from the comprehensive analysis presented in this paper, the focus should not be on identifying the best overall method but on the one that would be the most robust (e.g., lower economic and environmental risks) in a wide range of scenarios. Also, for more representative results and identification of a “universal” solution for interpolation, soil samples from more fields, different sampling designs, and parts of the world should be included in future analysis.

Conclusions

A total of eleven interpolation procedures were undertaken—including a newly proposed methodology, two proposed approaches, and the use of field average—but none emerged as the best interpolator across all different fields, soil properties, and sampling densities. In terms of robustness, the proposed modification to the kriging approach, IDW, and IDW Smoothed with a power parameter of 1 appear among the most robust approaches, as they rarely yielded errors worse than when using the field average. In addition, when the kriging-based approach estimated a flat, “pure nugget effect,” variogram interpolated surfaces using IDW and IDW Smoothed often presented an advantage over using the field average, which indicates that a combination of these procedures could lead to interpolated surfaces that would maximize the value of low-density sampling designs.

A few other important outcomes were identified while performing this extensive comparison of interpolation methods and approaches. Among all fields, soil properties, and sampling density, at least one interpolation method always yielded a surface more accurate than the field average (not necessarily producing a statistically significant difference). Moreover, the best interpolation procedure is tied to the sampling density and spatial structure present in the data. Finally, forcing the nugget to be zero when there is poor information about the behavior of the variogram at short distances is a high-risk decision, as it can lead to a low accuracy result if the spatial correlation of the underlying surface is weak—information that cannot be determined based on low and extra low-density data.

Therefore, PA practitioners should avoid using interpolation tools that tend to force the nugget to be zero unless the variogram estimates calculated from the data provide enough direct (indirect) information about the absence of a nugget effect. Also, to identify a “universal” interpolation approach for low-density sampling designs, a focus should be given to methods that hardly produce results worse than average and not necessarily the best results. Before making any soil management decisions based on thematic maps, practitioners should carefully evaluate different interpolation procedures through validation samples (when available) or cross-validation to avoid causing economic or environmental impacts.