Introduction

Precision farming (PF) or precision agriculture aims to improve farming through the management of variation within the field (Auernhammer 2001; Earl et al. 2000; Buresh et al. 2005; Robert 2002; Zhang et al. 2002). Therefore, understanding and monitoring variation to apply the inputs non-uniformly is crucial in this process (Sadler et al. 1998; Blackmore 2003; Zhang 2007). This information will then lead to informed decisions to spend the agricultural inputs in the right place and right time and help the economy of farming and ultimately preserving the environment. Over time and space, soil variation is normally affected by farming activities and several other factors like soil physical and chemical interactions (Goovaerts 1997; Lin et al. 2005; Wong and Asseng 2006; Kariuki et al. 2006). Therefore, a constant monitoring of the soil spatial variability is important than the goals of precision farming.

Soil samples collected by manual soil sampling or soil sensors are major solutions for obtaining accurate soil variability information. Manual soil sampling for investigating the structure of soil is common, but using these samples for monitoring the short-term variability in chemical properties of soil could be daunting. Soil sensors mounted on tractors could be a viable alternative that can generate loads of information that could be useful for monitoring soil chemical variability. These sensors, however, are still under development and to some extent, are too costly, and their calibration in different environments is intricate (Kim et al. 2007; Terzis et al. 2010). Another major problem of these sensors is their ineffective use over the already planted fields. Therefore, manual soil sampling for short term is feasibly provided; we know the number and approximate location in which we can get a representative sample from the field. In this situation, finding cost-effective and accurate manual sampling methods for macronutrients have a lot of benefits, especially for larger fields. Compared with a traditional statistical survey, more samples are required to get more accurate data (Zhu and Stein 2006; Webster and Oliver 2007; Allan Reese 2009). Another challenge is the absence of an exclusive sampling design for different areas. Sampling design consists of two major elements; number and scheme. The scheme can be random, systematic, stratified or any possible integration, or bulk. Cochran (2007) defined sampling design as a description of the sample collection plan that specifies the number, type, and location (spatial or temporal) of sampling units to be selected for measurement. There are a variety of sampling techniques and methods devised for soil sampling. Statistical design mandates that for an inference based on a sample (or a realization of the population) to be unbiased and accurate, the scheme should be random (Gruijter et al. 2006).

Design-based samplings, including random and systematic samplings are powerful sampling methods. Most researchers focus on the design-based systematic sampling scheme and its comparison with other sampling schemes. Wang and Qi (1998) found out that given a certain sampling density, systematic sampling had better estimation performance than either a stratified or a random sampling design. Furthermore, Entz and Chang (1991) evaluated 16 soil sampling schemes to determine their impacts on directional sample variogram and kriging. Kerry et al. (2010) also found out that variograms estimated from sample data collected from stratified and grid designs provided the same data on the spatial variability of the soil bulk density. Stratification of the target population into groups (called strata) using prior or other information is one of the most desirable sampling designs that can be more accurate and cost effective. The stratification can be performed with equal or unequal stratum. In the former, the field can be divided into grids of the equal area (Franco-Marina et al. 2003) while in the latter, other previous information about the variable of interest or information from highly correlated variables can be used to stratify the area. Stratified sampling design can be the optimum sampling technique from agricultural (Simbahan and Dobermann 2006) to ecological research (Oggier et al. 1998).

Stratification can also be carried out using existing soil maps (Brus and De Gruijter 1997) or landscape used classifications (Sastre et al. 2001). One method uses the geostatistical techniques to model spatial variation and defines the boundaries of strata based on the spatial structure and kriging (Zhang et al. 2012; Safari et al. 2013). In this method, patterns of variation used to classify the kriging map can be distinguished as homogeneous (Elliot et al. 2000). For instance, Simbahan and Dobermann (2006) used the continuous secondary variables and one categorical (soil series) variable to propose a stratification for optimizing soil sampling and mapping, in cases with no previous direct measurement of variable of interest. The quality of stratified sampling is strongly dependent on the quality in the data, whether the data comes from the previous surveys or from other highly correlated variables (Thompson 1992).

The aim of this research was to evaluate the performance of the different number of samples and different designs through sampling on a map created from real data. The performance was analyzed through (i) the ability to provide a mean close to population mean with fewer standard deviations and (ii) reproducing the spatial variability of the base map for each of macronutrients in the soil.

Materials and methods

Study area

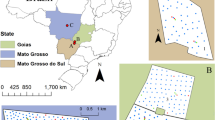
This study was conducted in a paddy plantation located in Sawah Sempadan, block C. It is a compartment of the Tanjung Karang irrigation project in Selangor, Malaysia. Block C (3° 28′ 15″ N, 101° 13′ 15″ E) which consists of 118 plots covering 145 ha has been allocated to precision farming studies (Fig. 1).

Fig. 1
figure 1

The location of study area in block C Sawah Sempadan

Full size image

Original data

The original survey was conducted using a semi-systematic grid with 236 samples for the entire block C area. The grid has two intervals of 200 and 60 m (Aimrun et al. 2009). All samples were taken manually from the depth of 0–20 cm of soil. The sample support was 1 m2 for each sample. The positions of sampling points have been logged using a Differential Global Positioning System (DGPS) instrument, and the obtained coordinates were later converted from WGS1984 coordinate system to the Selangor Cassini-Soldner coordinate system. Variables of interest were percentage of total nitrogen (N), phosphorus (P) in milligrams per kilogram or parts per million (ppm), and amount of potassium (K) in milliequivalents per gram (meq/100 g) of soil.

Preparing the base maps

An interpolated map for N, P, and K was created to act as the base maps. Normal exploratory data analysis was done on the data based on the methodology by Kerry and Oliver (2007a, b). All three datasets were also examined for the existence of trend in the data. The method to recognize the trend in the data had two steps; first, a visual examination of scatter plot of the data to see if the values in the dataset showed a gradual increase in any direction, and second, looking over the standard error map created by each kriging operation (Yang et al. 2011). If the error in all predictions was much more than 25 %, then there was a need to consider the trend in the data analysis. The method of ordinary kriging was used to create a surface for N, P, and K data. The created maps of the data were classified using the geometric intervals (Johnston et al. 2001) of predicted data distribution. All map classifications are done using the same cutoff for each macronutrient.

Preparing sample coordinates

Four major schemes were used to create samples required during the analysis: random, systematic, stratified random, and stratified systematic. Random and systematic samples were created for both block C and also for each stratified polygons. For each scheme, seven trials with 100, 150, 200, 250, 300, 500, and 1000 samples were created. The coordinates of these schemes were used to extract the sample values on the base maps.

Random and systematic samples

The boundary of block C was used to create different sampling schemes for random and systematic methods. Predetermined number of samples was used to fill the area with either random coordinates or systematic coordinates. For random schemes, pseudo-random generator produces a sequence of unrelated numbers, which are coordinated within the boundary of the polygons (Hassig et al. 2004). Since the samples were selected randomly, major statistical assumptions were preserved. However, other problems like clusters and large unsampled areas may occur. To tackle the problem of statistical assumptions in the systematic scheme, the location of the starting point was selected at random (Hassig et al. 2004). The grid spacing (L) in the two-dimensional area was calculated using the following equation (Zhang 2007):

$$ L=\sqrt{A/0.866n} $$
(1)

where, A is the area in square meter and n is the number of samples. Therefore, for 100, 150, 200, 250, 300, 500, and 1000, the intervals were 129.60, 105.82, 91.64, 81.97, 74.82, 57.96, and 40.98 m (A = 1454743.513 m2), respectively. A total of 37 schemes was created for random and systematic sampling on N, P, and K base maps using the above procedures.

Stratified samples

In this study, the cost of sampling was considered to be equal for all schemes in stratified sampling. Therefore, for all strata, the method of Neyman’s allocation (Gilbert 1987; Hassig et al. 2004) could be used to allocate the number of samples. A total predetermined number of samples was allocated into different polygons based on the population standard deviation (σ h of the stratum h) using the expression:

$$ {n}_h=n\frac{N_h{\sigma}_h}{{\displaystyle {\sum}_{h=1}^L{N}_h{\sigma}_h}},n={\displaystyle \sum_{h=1}^L{n}_h},N={\displaystyle \sum_{k=1}^L{N}_K} $$
(2)

where n h is the number of samples allocated to stratum h, L is the number of strata, N h is the total number of units (sample-able) in stratum h, n is the total number of units sampled in all strata, and N is the total number of units within the population. Standard deviation for each stratum (polygon) of base maps was calculated using the raster that was created from kriging (Table 1). The standard deviation for the whole block was also calculated using the raster maps (the value of raster pixels).

Table 1 Standard deviation for different strata of N, P, and K
Full size table

As shown in Table 2, the number of samples is different in each stratum for N, P, and K. Since the shapes of the strata (polygons) were not uniform, the formula was not able to allocate an integer number of samples. Therefore, for stratified N(251), stratified P(101), and stratified K(101, 201, 1001), one sample was added to the total number of samples so that the number of samples became an integer. Consequently, when allocating samples for random and systematic schemes for all block C area, one sample was added to the corresponding schemes to maintain the same amount of samples across all 74 schemes.

Table 2 Number of samples allocated to each stratum for stratified N, P, and K maps
Full size table

For stratified random sampling, the number of samples was determined for each stratum, and pseudo-random generator was used to allocate the sample coordinates randomly inside that strata. For stratified systematic schemes, the calculated number of samples was used to define the triangular grid space (formula 2) then the samples were allocated using the random start point and grid spacing.

Statistical analysis of samples

For each sample mean, the standard deviation as well as other measures was calculated. In random sampling, the sample mean (\( \overline{x} \)) is an unbiased estimator of population mean or global mean, μ, (\( E\left(\overline{x}\right)=\mu \)), and since the sample was the only available information, it was impossible to adjust the sample mean with the population units (N):

$$ \overline{x}=\frac{1}{n}{\displaystyle \sum_{i=1}^n{x}_i} $$
(3)

The variance of sample is:

$$ {s}^2=\frac{1}{n-1}{\displaystyle \sum_{i=1}^n{\left({x}_i-\overline{x}\right)}^2} $$
(4)

In stratified sampling, the population with N units is partitioned into L regions or strata. There are N h units. n h samples can be taken by random sampling inside each strata. Given each strata has its own mean \( {\overline{x}}_h \) and variance, s 2 h , the formula for calculating the mean of stratification is;

$$ {\mu}_{st}={\overline{x}}_{st}=\frac{1}{N}{\displaystyle \sum_{h=1}^L{N}_h{\overline{x}}_h} $$
(5)

An unbiased estimator of variance is:

$$ \operatorname{var}\left({\overline{x}}_{st}\right)={\displaystyle \sum_{h=1}^L{\left(\frac{N_h}{N}\right)}^2\left(\frac{N_h-{n}_h}{N_h}\right)\frac{s_h^2}{n_h}} $$
(6)

Map algebra

A representative sample presumably should create the same patterns of variability on the map as the population does. Therefore, it is important to compare the patterns of variability between the base maps and all 74 maps created by the samples. Like the base maps, for each sample scheme, a continuous map was created. The data were used to create the variogram models of the region using the fitted models. Kriging was then used to create the maps of spatial variability for each scheme. The maps were then classified into three classes using the same cutoff values used for the base maps (Table 4). The result was 74 maps of different patterns for N, P, and K sampling schemes. The next step was to compare the sample maps with the base maps to see the ability of each sample to reproduce the same spatial patterns as base maps. To do this, all the 74 maps were “intersected” with their respected base maps of N, P, and K. The result was a map that resembled the base map of N, P, and K but with major or minor difference. For each class, the area that coincided with the same class in the base maps was derived from the intersections.

Results and discussions

The analysis started with examining the original datasets for N, P, and K, and then creating maps of spatial variability for each of the three datasets using the method of geostatistical kriging.

Base map analysis results

The investigation into the existence of outliers revealed that they were mostly erroneous data and therefore, removing them would not harm the analysis. Table 3 shows the number of data that remained after the removal of outliers and were used to create the base maps. The dataset for P was very much different to deal with because even with the removal of outliers from the dataset, it showed non-normal behavior; consequently, a logarithm transformation was used for the rest of analysis for P dataset. The datasets were also analyzed for the existence of deterministic trend, which is a disturbance over the kriging procedure. The result showed that there was a quadratic trend for K and linear trend for P (Table 3). For all the three datasets, the method of ordinary kriging with specifications for trend was used to create the surface as only this method could create surfaces with less kriging standard errors. Even with the data that has the trend (P and K), incorporating trend in the kriging system (universal kriging) instead of removing the trend first and then performing the kriging (ordinary kriging), yielded surfaces with high level of standard error, which means the universal kriging was not able to reproduce the spatial patterns of base maps.

Table 3 Number, methods, and the requirement for trend removal and transformation
Full size table

Figure 2 shows the base maps created from the data. The three classes are labeled to show the different ranges of concentrations for N, P, and K in classes 0 (low), 1 (medium), and 2 (high) (Johnston et al. 2001). The actual units from the population were 1,454,743, which is the area of the whole block (Fig. 2). Based on the recommendation of the managers, only three classes are being used in the precision farming studies in the region, and therefore this study follows these three classes.

Fig. 2
figure 2

Bases maps created from 2011 data with their class numbers

Full size image

Since the entire population was available, mean (μ) and standard deviation (σ) of these units are shown in Table 4. Limits 1 and 2 are the cutoff values used to classify the base maps. These values are chosen based on the geometrical interval classification of the population distribution. The same values are used to classify the sample maps.

Table 4 Statistics and classification limits for the populations
Full size table

The distribution of classes was different for N, P, and K (Table 5). For N, there was a mixed balance of concentration for the whole area while for P, most of the area was covered by medium to low amount (classes 0 and 1) and for K, medium to high (classes 1 and 2).

Table 5 Percent coverage of each class for N, P, and K base maps
Full size table

Analysis of samples

Nitrogen

Figure 3 shows the mean and standard deviation (SD) of samples as well as the population. All schemes except the random scheme could reproduce the mean from the population even with the smallest number of samples. Both stratified random and stratified systematic schemes predicted means closer to the population mean.

Fig. 3
figure 3

Mean and standard deviation (SD) for N sampling schemes

Full size image

The trend could reach the population mean which was close to sample number (200–250). After that, however, the random scheme fluctuated considerably while the systematic scheme did not respond to the sample size of the sample scheme of 1000 where it could get closer to the population mean. It is, conversely, noticeable that the number of samples did not follow any specific trend for any of the schemes. In general, random schemes tended to fluctuate around the population mean while systematic samples maintained a trend even if it was a negative one.

Standard deviation of the schemes is also shown in Fig. 3. Both stratified schemes reduced the standard deviation while random and systematic samples created the same standard deviation around the population standard deviation.

This result showed that increasing the number of samples does not guarantee a better prediction for the global mean. In terms of variability, random and systematic schemes were capable of reproducing the variability (SD) in the population while both stratified schemes could predict the mean steadier with lower variability. This conveys that the stratified sampling actually reduces the standard deviation dramatically; however, this might not be the goal of this analysis. Here, unlike the sampling projects, the whole population (values from the base maps is available and therefore the goal is to provide the closes mean and standard deviation.

Phosphorus

Figure 4 shows the mean and standard deviation of samples for P. There was a trend of increasing accuracy of means from the minimum sample to the highest. Random and stratified random samples showed fluctuations around population mean while systematic and stratified systematic respond to the increase of sample size. Random sample could create a mean closer than the population mean line with the sample number around 250 and stratified random sample around 500. Both systematic samples did not perform well for P, and they reach the desired accuracy with the highest number of samples. Stratified random with 200 samples created very low mean (10 ppm), and it was omitted from the graph on Fig. 4 to give a better view of other schemes. This shows one of the pitfalls of random sampling even when they are applied to stratified scheme. The situation for standard deviation was similar to that of N, except random schemes, which showed more fluctuations around the population standard deviation. In general, for ascertaining the true mean for a population for P, more samples were needed as most of the schemes reached the population mean of the maximum sample (1000 samples).

Fig. 4
figure 4

Mean and standard deviation (SD) for P sampling schemes

Full size image

Potassium

Figure 5 shows mean and standard deviation of the K samples. Random and systematic schemes showed very high fluctuations, and stratified samples demonstrated more consistent pattern for the prediction of mean. The most accurate scheme was the stratified systematic as it could accurately estimate the mean even with the 100 samples. Random sample also had difficulty in following standard deviation of population with samples below 300. In general, random and systematic schemes do not show any trend towards increasing accuracy since they constantly underestimate or overestimate the mean while the stratified sample, especially stratified systematic, could estimate the mean more accurately using all sample sizes.

Fig. 5
figure 5

Mean and standard deviation (SD) for K sampling schemes

Full size image

Summary of sample’s statistics

Two main conclusions include (i) the unreliability of the random sampling to predict the mean concentration of macronutrients over a field and (ii) the power of stratified sampling to predict the average concentration in a sampling project with inaccurate standard deviation of population. In statistical jargon, a sample is only a realization of what is happening, and the best is to provide repeated sampling to increase the accuracy of the prediction. For agricultural fields, this might be quite costly; therefore, the best way would be to design the sampling project so that it can produce the best result.

Table 6 shows the results of modeling using sample schemes for each macronutrient as fixed effects and sample sizes as random effects. The estimation was done based on optimization of the residual maximum likelihood function of linear fixed effect models. This aim here is to show how different sampling designs (or treatments) are in deriving the mean (μ) of the population for each macronutrient. For N, the lowest standard error belonged to the stratified random. Both stratified schemes had higher t values than the random or systematic samples. For P, the estimates are very close except for the stratified random that showed higher standard error and lower t value. This shows that in terms of reproducing the mean of the populations, there is not much difference between the sampling designs for the chosen sampling schemes. The situation for K is the same as N where lower standard error and higher t values belong to stratified samples.

Table 6 Linear fixed effect estimates (using REML) and standard error of mean
Full size table

In the precision farming context, the patterns of variation are more important from the global measures like mean and standard deviation of the population. Therefore, the measures of local mean or spatial patterns in the form of percent overlap with the original variable are presented next.

Overlay analysis

Nitrogen

Figure 6 shows the arithmetic mean and weighted mean of the percentage overlay for all classes. Since the area of all three classes was not in the same range, a weighted mean was considered so that the contribution of each class to the overall percentage overlay became proportional. The weights for classes 0, 1, and 2 were 0.3801, 0.4481, and 0.1717, respectively. Clearly, systematic sampling was superior to all schemes for all sample sizes. The accuracy starts from 85 % for the stratified random to above 98 % for the systematic sampling. The performance of map overlay for the stratified systematic was also superior to the random sampling. In general, for all sampling schemes, the increase over the percentage of the common area was steady from the least sample to the most.

Fig. 6
figure 6

Percentage of common area for all classes’ average and weighted average for N

Full size image

Figure 7 shows the common areas for each class for all 28 schemes and the base map. The sample positions were also overlaid on each map to show their degree of representativeness. For random and systematic samples, simply one standard deviation was considered, and Neyman’s allocation was not applicable because there was only one stratum. Therefore, the number of samples was the same everywhere. For stratified sample, the number of samples was different in each polygon (most recognizable for stratified systematic). The samples on the base map were those of the original survey.

Fig. 7
figure 7

Common areas for each scheme with the base map and their samples (Ran random, SR stratified random, SS stratified systematic, Syst systematic)

Full size image

White areas on each map in Fig. 7 are the areas of conflict between the base map and the sample map when they were intersected. Uncommon areas are very much obvious in the low sampling schemes. However, they are more obvious for random sample maps than the others because the samples do not cover the area as frequently as systematic samples which in contrast, show consistency and even with the small number of samples common areas are much higher.

Phosphorus

Since class areas were extremely different for the three classes, the result for each class was ambiguous. Class 1 covers almost 76 % of the block while class two covers only 1 %. Moreover, for some of the schemes, there is not any area for class 1 or 2 in the sample maps. For example, most of the systematic maps, classes 0 and 2 occupy no area in the map. The percentage for other schemes, however, remained very high for class 0 from 40 % to around 100 % for stratified random with 200 samples and above 90 % for class 1. For class 2, most of the schemes showed 0 % occupation for class 2 and a few schemes like random 150, 500, and 1000 and systematic 500 and 1000 displayed a small portion of their maps in class 2.

Figure 8 shows the overall result for all schemes. Again, the problem for the area represented by class 2 tremendously affected the overall accuracy of the common areas for all classes. The overall accuracy was leveled up to 100 % for systematic and random schemes.

Fig. 8
figure 8

Percentage of common area for all three classes’ average and weighted average for P

Full size image

Figure 9 shows the average and weighted average for all classes without considering class 2. Here, the random and systematic schemes demonstrated almost equal trend up to sample number 300 beyond which random sample shows the good result for 500 samples and systematic sample with 1000 is superior to random sample. Overall as shown for N, systematic sample tends to keep a steady rise with the increase with the number of samples while random samples tend to fluctuate between sampling numbers.

Fig. 9
figure 9

Trend of sampling schemes percentage overlay without stratified random for P

Full size image

Figure 10 shows the maps produced by samples from the base map for P. The scheme for stratified random with 200 samples neglects most of the base map patterns, and therefore, its pattern is different from others.

Fig. 10
figure 10

Common areas for each scheme with the base map and their samples

Full size image

Potassium

Both systematic and stratified systematic schemes showed a more consistent upward trend than the two random schemes. For class 0 which was the smallest class (14 % in base map), systematic scheme showed a rather flat line around percent accuracy of 97.5. Only at sample size of 300 was the accuracy higher (up to 99 %). The result was different for classes 1 and 2 in that there were many fluctuations in all maps. Both systematic schemes, however, performed slightly above the random schemes. Systematic scheme performed strongly in classes 1 and 2 as the best accuracy with the minimum sample size (100) belonged to be the systematic sampling scheme.

Figure 11 shows the plot of average and weighted average overlay accuracy for all the schemes. Both plots showed that systematic sampling was superior to all the others as it was more accurate with the minimum number of samples. Stratified systematic scheme also performed like the systematic sample to the sample above 200 (Fig. 12).

Fig. 11
figure 11

Trends of percentage of common area of sampling schemes with the base map for K

Full size image
Fig. 12
figure 12

Common areas for each scheme with the base map and samples

Full size image

Overall accuracy

Figure 13 shows the mean of overall accuracies for N, P, and K where each point is the average accuracy. Like most of the plots for the above sections, systematic sampling performs the best for most of the schemes, and more importantly, it showed the highest accuracy for the least number of samples (100) and for the most number of samples (1000). Second to systematic sampling was the random sampling that performed best for all of the schemes. For all schemes, the overlay accuracy starts from 73 that belonged to stratified random sampling (200) to 93 %, which belonged to systematic sampling (1000). One of the challenges of random sampling is the problem of clustering and unrepresentativeness of the samples from the area. The samples do not cover the area evenly, a problem that is addressed very well by the systematic scheme. Both stratified random and systematic samples followed the pattern of the random or systematic schemes. Stratified systematic performed well above the stratified random and more importantly showed a consistent pattern of increasing accuracy.

Fig. 13
figure 13

Overall accuracy for N, P, and K

Full size image

In the study area, fertilizer spreading operation was carried out three times after sowing the seeds using machinery in 1 day. Therefore, given the patterns of the fertilizer spread which is systematic over the field, this can be inferred that even with the mobile fertilizers like N, the pattern of variability can mostly be ascertained by the systematic sampling scheme.

Conclusion

In this study, we compared the result of sampling simulation based on real samples from a rice field. We conducted sampling on the base maps of N, P, and K that were created from real data. In total, 74 schemes with over 140,000 samples were derived from the original survey. Maps of the spatial variability of these elements were created. These original maps were considered as base maps, and their statistics were calculated. The sampling schemes included random, systematic, stratified random, and stratified systematic. Each of the samples was analyzed statistically, and the result was compared with the population for each element. A map of each sample was also created using the geostatistical kriging and their common areas with the base maps were calculated. The result was analyzed both statistically and in terms of ability of samples to produce the same spatial pattern as the base maps for N, P, and K. In terms of the mean and standard deviation of each sampling scheme, the result was mixed with a clear separation between the performance of random, systematic and stratified schemes. For nitrogen, stratified systematic performed the best for samples over 200. For phosphorus, all employed schemes could not estimate the population means correctly, and they became close to population mean only with samples over 300. For potassium, stratified systematic scheme could also estimate the population means from the minimum number of samples (100). The performance of stratified systematic sampling however is suspicious as it could not reproduce the standard deviation of populations for all the schemes. In terms of mapping, between all the sampling schemes, systematic sampling performed the best and most importantly; it provided better accuracy than other sampling schemes for the minimum number of samples. Random sampling is another candidate for the choice of sampling scheme. However, its performance, especially instability in the plots of samples requires more investigation.

Since the patterns of variation are highly different in agricultural fields, the most important property of a sample scheme is representativeness. From this point of view, we demonstrated that systematic sampling is still the best choice as there is no need to provide many samples. However, its performance for phosphorus should be investigated further.