Investigating the influence of assigning a higher priority to scheduling work and school activities in the activity-based models on the simulated travel/activity patterns

Abstract

Two dynamic, gap-based activity scheduling models are tested by applying a short-run microsimulation approach to replicate workers’ travel/activity patterns over a 1-week time period. In the first model, a two-level work episode scheduling model is applied to schedule weekly work episodes (Dianat et al. in Transp Res Rec 2664:59–68, 2017. https://doi.org/10.3141/2664-07). This includes joint choices of working or not on each day and work episode duration and start time in case of choosing to work. Assigning higher priority to scheduling work episodes, and assuming night sleep to be pre-determined, provides a weekly “skeleton schedule”. Non-work/school (NWS) episodes are then generated and scheduled in the available gaps as a joint choice of activity type and destination followed by a continuous time expenditure choice. The second model applies the same mathematical framework as the NWS model for scheduling all activity types including work/school, considering only night sleep as the pre-determined skeleton schedule. This exercise allows us to study the impact of assigning a higher priority to scheduling work/school activities on complete out-of-home travel/activity pattern prediction, compared to the alternative hypothesis, which is scheduling all the activities simultaneously. Comparing the simulation outcomes of the two models with the observed dataset reveals that organizing NWS episodes around the schedule skeleton not only is behaviorally more representative but also increases the accuracy of the predicted NWS episodes’ patterns. Moreover, applying the work scheduling model results in a more accurate prediction of the weekly work schedule compared to the second model.

Introduction

Activity-based models (ABMs) emerged to overcome deficiencies in traditional trip-based models. The concept behind ABMs is that travel is a derived demand, motivated by individuals’ needs to participate in spatially distributed activities. Most ABMs in the literature fix individuals’ routine activities and schedule non-work/school (NWS) episodes around them. Work is a primary activity in a worker’s schedule with a regular nature, attributes of which are normally defined by an external agent (employer) within a longer planning horizon (e.g. at least before the commencement of the week) compared to NWS activities. For work episodes that do not have a regular nature the argument of commitment to an external agent remains valid, still indicating a level of pre-planning. Moreover, work locations are normally fixed for most workers in the short-run and are generally not contingent on the daily schedule. Work episodes also impose spatio-temporal constraints on other activities and limit individuals’ potential action space, as they consume a significant portion of the daily time budget. Therefore, it is reasonable to assume that all work episodes have priority over other activities in scheduling.

For example, CEMDAP (Bhat et al. 2004) is an ABM which first models individuals’ work/school participation. Participation in other activities is then modeled within a fixed priority order applying econometric models. ALBATROSS (Arentze and Timmermans 2004; Rasouli et al. 2018) is a rule-based ABM which fixes all work and school activities in the schedule, as they include formal commitments, and applies a set of complex rules to schedule flexible activities and plan their attributes in a sequential manner. TASHA (Miller and Roorda 2003) generates the number of daily episodes of each activity type and the start time and duration of each episode based on empirical joint frequency distributions. Activity episodes are scheduled using priority rules with work episodes having the highest priority. PCATS (Kitamura and Fuji 1998) fixes routine activities and generates other activity types continuously until the schedule’s feasible time–space prisms (gaps) are filled. Activity type, mode, and destination are planned sequentially in PCATS applying nested logit models. Finally, duration of the episode is chosen based on the observed distributions. ADAPTS (Auld and Mohammadian 2012; Auld 2011; Langerudi et al. 2017) determines work and school episodes first and then generates discretionary activities using a competing hazard model. Planning horizons and degree of episodes’ attributes’ flexibility determine their scheduling order. Episode start time and duration are chosen from observed distributions. CT-RAMP first schedules mandatory activities (Paul et al. 2015) and then assigns NWS activities in the open segments of the day in a predefined order (Vyas et al. 2015). Next, choices of within-segment activity sequencing, destination and tour formation are made jointly (Paleti et al. 2017). MATSIM’s (Medina 2016) extended version fixes mandatory activities as the weekly schedule skeleton. Then, a utility-maximization approach finds the number of the non-mandatory activities, with their relative sequence and attributes, while the trip algorithm finds the travel time and mode.

Arguments exist in the literature, however, against giving scheduling priority to work. In a few ABMs work is not considered as a qualitatively different activity relative to NWS activities and is modeled simultaneously with the rest of the activities. CUSTOM (Habib 2015) and C-TAP (Märki et al. 2014) both schedule all activity types simultaneously without assigning scheduling priority to work. CUSTOM applies a discrete–continuous Random Utility Maximization (RUM) choice model to jointly generate episode types with their chosen destination and duration. C-TAP applies heuristics to schedule episodes, considering future opportunities and history of activities at each decision point, within an open planning horizon.

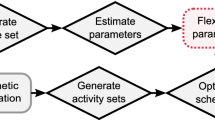
Fixing routine activities as the schedule skeleton is a fundamental assumption in developing the structure of an ABM. The impact of this assumption relative to the “all-activities” approach, however, on predicted travel/activity patterns is not tested in the literature. It is essential to conduct a hypothesis test to determine which alternative hypothesis best fits observed behavior (Miller 2005). For this purpose, this study applies two microsimulation models of travel and activity scheduling in a fully econometric framework to replicate workers’ path through time and space over a 1-week time period. The two models differ in the way they schedule work activities. The activity/travel patterns in the first ABM result from a combined work episode scheduling model (Dianat et al. 2017) and a NWS episode scheduling model. In this model, weekly work episodes are first scheduled, generating a skeleton schedule. This skeleton schedule contains gaps of available time within which NWS activities can potentially be scheduled. In the second model, work is scheduled simultaneously with all other activities, applying the same mathematical framework as the NWS episode scheduling model. The predictions of the two simulation models are then compared with the observed dataset. In the rest of the paper, the first model is referred to as the “combined model” and the second model as the ‘all-activities” model.

In the following sections, an overview of the method and data are presented followed by the discussion of the simulation outcomes. Finally, a brief conclusion and discussion of future work are presented.

Method

Combined model

The combined model consists of three levels. The first two levels apply a work episode scheduling model (Dianat et al. 2017) to generate the skeleton schedule. In the first level, an individual’s weekly preplanned work schedule is generated, consisting of work episodes planned prior to the start of the week. The available time budget on each day is an individual’s specific time awake, which is a model input. Starting from Monday, the choice of working or not that day is first simulated using a nested logit model. If working is chosen, the work episode’s duration and start time are determined. Duration is simulated in 5 min time intervals applying a RUM-based continuous duration choice model discussed later in the paper and the continuous start time is simulated, applying the inverse of a cumulative survival function, assuming a Weibull distribution for the baseline hazard, as further discussed in (Dianat et al. 2017). The scheduled preplanned work episode on each day is the input for the subsequent days’ schedule generation. The same simulation procedure is repeated for each day in the week.

The generated weekly preplanned work schedule is the input to the second stage in the model, which generates any unplanned work episodes. These are added to the skeleton schedule along with the planned work episodes. The available time each day is calculated by subtracting the simulated preplanned work episode duration from the individual’s awake time. Starting from Monday, unplanned work episodes are scheduled for the entire week with the same procedure discussed for preplanned work episodes.

The outcomes of these first two levels of the combined model determine gaps in the schedule where an individual can potentially participate in NWS episodes. An individual’s wake up time is also an input to the model. NWS episode scheduling starts from the first gap on Monday with the binary decision of whether to stay home for the duration of the entire gap or to undertake an out-of-home NWS activity episode during this gap, prior to the next skeleton activity, which defines the end time point for this gap. Two cases exist, depending on whether: (a) the next skeleton activity is a work/school episode, or (b) night sleep (i.e. no more out-of-home skeleton activities exist in the schedule for the day currently being scheduled). These two cases are modelled separately since quite different utility functions are found to exist for the two cases. A binary logit model used to choose between staying home or engaging in an out-of-home NWS activity episode during gap g:

$$pr\left( {engage\; in\; a\;NWS\; episode\; in\; gap\; g} \right) = \frac{1}{{1 + \exp \left( {\mu_{{s_{g} }} V_{{s_{g} }} } \right)}}$$

(1)

$$V_{{s_{g} }} = \mathop \sum \limits_{p} \left( {\beta_{p} x_{p} } \right)_{{S_{g} }}$$

(2)

where $V_{{s_{g} }}$ is the difference in the utility of staying home relative to engaging in an out-of-home NWS activity in gap g for case “s”, where s = a is when the next skeleton activity is work/school and s = b is when the next skeleton activity is night sleep. $V_{{s_{g} }}$ is sum of the explanatory variables such as situational variables (e.g. time of the day, day of the week) and socio-demographic variables the sequence of which is shown by index $p \cdot {{\upmu }}_{{s_{g} }}$ is activity type choice scale parameter which is set to 1. For those individuals with a gap duration equal to the travel time to the subsequent fixed activity, going to the next skeleton component is deterministic.

If participation in an NWS episode is chosen, the time expenditure at home before departing is first simulated to determine the first trip’s start time. Next, is the choice of the episode’s type and destination, using a nested logit model with activity type choice in the upper level. In each sequence $k$ of scheduling, activity type choice probability is calculated using Eq. 3, where $V_{{a_{k} }}$ is the utility function for activity type “a” in the feasible activity type choice set $A_{k}$. As defined in Eq. 4, activity type utility $(V_{{a_{k} }} )$ is defined as summation of the explanatory variables such as situational variables and socio-demographic variables the sequence of which is shown by index $m$ and normalized expectations of destination choice $(I_{{l_{k} }} )$, except for the activity types with a known location (home/work/school). The latter component of the utility function captures the influence of the utility gained from the feasible destinations individual can travel within the time budget on the choice of activity type. $\mu_{{a_{k} }}$ and $\mu_{{l_{k} }}$ are activity type and destination choice scale parameters, respectively.

$$pr\left( {a_{k} } \right) = \frac{{\exp \left( {\mu_{{a_{k} }} V_{{a_{k} }} } \right)}}{{\mathop \sum \nolimits_{{A_{k} }} \exp \left( {\mu_{ak^{\prime}} V_{ak^{\prime}} } \right)}}$$

(3)

$$V_{{a_{k} }} = \mathop \sum \limits_{m} \left( {\beta_{m} x_{m} } \right)_{{a_{k} }} + \frac{{I_{{l_{k} }} }}{{\mu_{{l_{k} }} }}$$

(4)

Given Eq. 4, the first step in simulating episode type and destination is determining the feasible destination choice set to calculate the normalized destination choice expectations added to the activity type utility function. The feasible destination choice set is formed by utilizing Hagerstränd’s time–space prism concept (Hagerstraand 2005) to capture the effect of time–space constraints on destination choice. The prism’s origin vertex is the current location of the person; however, as at the point of decision-making the individual’s next activity is not yet scheduled, the prism’s terminal vertex is assumed to be the posterior fixed activity. The feasibility of each alternative destination in the universal choice set to be chosen for an episode is checked based on the ratio of the time budget to the round travel time from the origin of the trip to a given location ($tt_{ol}$) and from this location to the next fixed activity in the schedule ($tt_{lS}$), see Eq. 5. M is the lower bound of the ratio for a location to be feasible, which is more than one to assure there would be enough time for execution of the activity. M is chosen in a trial and error process during the model’s estimation and testing.

$$\frac{Time \;budget}{{tt_{ol} + tt_{lS} }} \ge {\text{ M}}$$

(5)

As the size of the feasible choice set might still be large, for computational purposes, the destination choice component of the framework is estimated based on a maximum of 10 randomly chosen alternatives including the chosen location from the feasible set, while in application of the model, the entire feasible set is used. The location utility is:

$$V_{{l_{{k \in L_{k} }} }} = \mathop \sum \limits_{c} \beta_{c} x_{c}$$

(6)

where $l$ refers to the destination alternative, $x$ and β are vectors of destination attributes and their corresponding parameters, and $L_{k}$ is the choice set. In calculating the destination choice logsum term, theoretically, all feasible destinations should be considered, not just the restricted choice set used in estimation. To adjust for this, the maximum expectation is calculated as follows (Habib 2015):

$$I_{{l_{k} }} = { \ln }\left( {\frac{size \;of\; the\; feasible \;set}{number\; of\;randomly \;chosen \;locations = 10} \times \mathop \sum \limits_{{L_{k} }} { \exp }\left( {\mu_{{l_{k} }} v_{{l_{k} }} } \right)} \right)$$

(7)

After an episode type is chosen, its destination is simulated using Eq. 8.

$$pr\left( {l_{k} } \right) = \frac{{{ \exp }\left( {\mu_{{l_{k} }} v_{{l_{k} }} } \right)}}{{\mathop \sum \nolimits_{{L_{k} }} \mu_{{l_{k} }} v_{{l_{k} }} }}$$

(8)

Scale factors of activity type and destination choice are included to capture the correlation between alternatives of the two choices in each scheduling sequence, defined as in Eqs. 9 and 10 to satisfy the assumed hierarchical nest structure in each sequence (Habib 2015), where x’s are sets of explanatory variables and $\lambda$ are their corresponding parameters.

$$\mu_{{a_{k} }} = 1$$

(9)

$$\mu_{{l_{k} }} = \mu_{{a_{k} }} + { \exp }\left( {\mathop \sum \limits_{q = 1}^{Q} \lambda_{q} x_{q} } \right)$$

(10)

Lastly, the episode’s duration is simulated using a RUM continuous choice model. The model finds each episode duration relative to a composite activity, which includes all the unplanned activities in the schedule. The composite activity represents the effect of time pressure from unplanned episodes on the current episode’s time expenditure and implies time reservation for the unplanned activities. Thus, it implies an explicit future look-ahead in the schedule and captures the trade-offs between activities over the course of one gap. In this approach the probability of assigning $t_{k}$ unit of time to the chosen episode in sequence $k$ is (Habib 2011):

$$pr\left( {t_{k} } \right) = \left( {\frac{{\left( {1 - \alpha_{k} } \right)}}{{t_{k} }} + \frac{{\left( {1 - \alpha_{c} } \right)}}{{t_{c} }}} \right)\mu_{{t_{k} }} \exp \left( { - \mu_{k} \left( {v_{c} - v_{k} } \right)} \right)\left( {1 + \exp \left( { - \mu_{{t_{k} }} \left( {v_{c} - v_{k} } \right)} \right)} \right)^{ - 2}$$

(11)

$$v_{c} = \left( {\alpha_{c} - 1} \right)\ln \left( {T - t_{k} } \right)$$

(12)

$$v_{k} = \left( {\alpha_{k} - 1} \right)\ln \left( {t_{k} } \right) + \gamma_{k} w_{k}$$

(13)

$t_{c}$ is the time remaining for the composite activity under time budget T. $v_{c}$ and $v_{k}$ are utility functions of time expenditure at the composite activity and the chosen episode, respectively. $\gamma_{k} w_{k}$ in Eq. 13 is the baseline utility function which is the marginal utility gained by spending zero time at the chosen episode. $w_{k}$ is a set of explanatory variables and $\gamma_{k}$ are coefficients. $\alpha_{k,c}$ is the satiation parameter which captures the diminishing marginal utility in an episode by increasing the time assigned to it (Bhat 2008). $\alpha_{k}$ should be less than 1 and is parameterized as shown in Eq. 14 (Habib 2015). x is the set of explanatory variables and ${{\uprho }}$ are the corresponding coefficients.

$$\alpha_{k} = 1 - { \exp }\left( {\mathop \sum \limits_{t = 1}^{T} \uprho_{t} x_{t} } \right)$$

(14)

$$\alpha_{c} = \, 0$$

(15)

$\mu_{{t_{k} }}$ is the scale parameter for time expenditure in sequence k which is the inverse of the choice variance and is set to be positive:

$$\mu_{{t_{k} }} = { \exp }\left( {\mathop \sum \limits_{r = 1}^{R} \delta_{r} x_{r} } \right)$$

(16)

where $\delta$x are a set of explanatory variables with their parameters.

After execution of each episode, the remaining time budget within the current gap for the next scheduling sequence is calculated by subtracting the sum of the duration of the current episode and travel time to get there from the previous sequence’s time budget. If there is sufficient time left, choice between participating in another NWS episode or returning home is determined. Returning home is only feasible if the available time budget is larger than the round travel time to home and from home to the next skeleton activity. Home and work/school locations are exogenous to the model.

For gaps that start at an out-of-home activity location, the choice set includes participating in an NWS episode or returning home. In each case the model framework discussed above is applied. The start time of the first trip, in this case, is the end time of the posterior fixed activity, assuming that the person starts the next trip as soon as the fixed activity is finished.

Finally, the likelihood for the entire week scheduling choices is:

$$L = \mathop \prod \limits_{n = 1}^{N} \mathop \prod \limits_{g = 1}^{G} \mathop \prod \limits_{k = 1}^{K} pr\left( {a_{kgn} } \right)^{{\delta_{{a_{kgn} }} }} \times pr\left( {l_{kgn} } \right)^{{\delta_{{l_{kgn} }} }} \times pr\left( {t_{kgn} } \right) \times pr\left( {s_{g} } \right)^{{\delta_{{s_{gn} }} }}$$

(17)

Here k, g, and n indicate scheduling sequence, gap sequence, and the individual, respectively; $\delta_{{s_{gn} }}$ is 1 if individual n chooses alternative s at the beginning of the gap g and 0 otherwise; $\delta_{{a_{k} gn}}$ is 1 if individual n chooses activity type “a” in sequence k of gap g and 0 otherwise; $\delta_{{l_{k} gn}}$ is 1 if individual n chooses location “$l$” in sequence k of gap g and 0 otherwise.

The likelihood function of the model is closed-form and is estimated using the BFGS gradient search algorithm in the GAUSS software (2014).

All-Activities model

Knowing night sleep’s start time and duration, the all-activities model is applied to generate the sequences of episode participation. In this model, work/school episodes are not treated differently from NWS episodes, and so the first two levels of the simulation procedure applying the combined model are not needed. As the only skeleton component in this part of the study is night sleep, there are seven initial gaps (days of the week) for all the workers with a duration equal to the time period they are awake, and all initial gaps originate from home. Work/school locations are exogenous to the model, while work durations are endogenously chosen. The all-activities model simulation starts on Monday with the choice of staying home for the entire day or participating in an out-of-home episode. If participation in an out-of-home episode is chosen, the same framework as the NWS scheduling model is applied. The terminal vertex of the prism for forming the destination feasible set is always home. Therefore, in this model workers have larger time budgets compared to the NWS model which results in larger feasible choice sets. For consecutive scheduling sequences, there are choices of participating in another activity or returning home. After scheduling each episode, the remaining time budget is compared with the travel time to get home, which is the location of the next skeleton component (night sleep). If there is enough time left to participate in another NWS episode, simulation continues; otherwise, the individual would return home. The same simulation procedure is repeated for the rest of the days of the week and all the workers in the dataset to simulate the entire week’s travel/activity pattern.

The simulation framework of alternative travel/activity pattern prediction models are represented in Fig. 1.

Fig. 1

Combined and all-activities scheduling simulation models

Empirical model

The dataset used to estimate the models is the CHASE dataset collected in Toronto in 2002–2003. The dataset includes one full week activity/travel diary of 416 individuals from 262 households (Doherty and Miller 2000). Activity types in CHASE are aggregated into 11 classes in this study as follows:

• (1) Work/school related activities

• (2) Work/school

• (3) Social/entertainment/recreational activities

• (4) Household(HH) obligations and basic needs

• (5) Services/medical (e.g. banking)

• (6) Return home

  Shopping activities:

• (7) Convenience store/drug store shopping/minor grocery

• (8) Major grocery

• (9) Housewares/other shopping types

• (10) Clothing/personal items

• (11) Work at home

Estimation results of the NWS scheduling model and all-activities model are shown in Table 1. Estimation results of the work scheduling model are presented in Table 2. These results are discussed in detail in (Dianat 2018; Dianat et al. 2017). Because of the small sample size, variables with t-statistics smaller than a 95% confidence interval threshold are retained where they are of correct sign and policy relevance. Some of the variables such as gender which are not policy sensitive are still kept in the model, as otherwise their effect will be captured within the rest of the variables’ coefficients and will introduce error into the model application.

Table 1 Estimation results of the nws model with M = 1.5 and all-activities models with M = 3

Table 2 Estimation results of the pre-planned and unplanned work scheduling models

Hypothesis testing

The developed models are applied to reproduce workers’ weekly travel/activity patterns using Monte Carlo simulation method. 10 replications of each of the two activity-based simulation models are run (Roorda et al. 2008). Simulation outcomes, including episodes’ frequency, travelled distances, start time and duration, are compared with those observed in CHASE. The results are discussed in the following sections.

Work episode scheduling model

Figure 2 presents the simulation outcomes for the preplanned and unplanned work scheduling models as the first level of the combined model. Both models generate work episodes with high accuracy. The simulated frequency of preplanned work episodes is more accurate than unplanned episodes, as they are the first level of the model, while errors in generating preplanned work schedules enter the unplanned work scheduling model (Fig. 1I). Both models over-predict durations between 5 and 8 h, while under-predicting durations of 9 h or more (Fig. 1II). The wide range of the observed durations, starting in different times of day, is the reason for the observed error in the outcomes of the duration model. Simulated work episode start times are later than the observed ones because the models are generating all the work episodes during the day and not just the morning episodes, thus, they are fit to the average start time during the day (Fig. 1III). The mean absolute error in predicting the work start time during the morning peak (6–9 am) is 8% for the preplanned work episodes and 6.7% for unplanned work episodes. Figure 3 shows the start time and duration of the schedule gaps, as a result of scheduling work episodes, versus those observed. Based on the simulation outcomes, gaps starting at 5 and 6 pm are under-predicted, while later gaps are over-predicted. Moreover, shorter gaps are generated with less accuracy compared to longer ones. One source of these errors is the later assigned start time to the work episodes comparing with the observed data.

Fig. 2

Work Scheduling Model Simulation Outcomes

Fig. 3

Schedule gaps’ attributes: a duration, b start time

Simulation outcomes of the combined model versus the all-activities model

Episode frequency

Due to the nested structure of the activity type and destination choice models, the accuracy of the episode type generation model depends on the size of the feasible destination choice set. The value of the normalized expectations of destination choice, added to the utility function of the activity types with an unknown destination, is a function of the size of the feasible choice set. As the normalized expectation is a large positive value, it leads to under-prediction of the episodes with a known location (i.e. return home and work/school episodes).

In the NWS episode scheduling model, a destination is feasible if the feasibility ratio M is more than 1.5, which is consistent with the value used for the model estimation. In the all-activities model, which has longer gaps than the combined model, feasible destination choice sets are formed with both M = 1.5 and M = 3 to test the impact of the size of the feasible set on the activity pattern prediction.

Figure4I shows the ratio of episode type frequency to the total number of episodes for each model. The combined model over-predicts the weekly total number of the NWS episodes by 12.8%, while the M = 3 and M = 1.5 all-activities model over-predict by 34.6% and 53%, respectively, indicating that the combined model generates NWS episodes with a higher accuracy compared with the all-activities model with both M values.

Fig. 4

Simulation outcomes of the episode generation model: (I) ratio of the frequency of each episode type to the total number of trips, (II) distribution of the work episodes during the week: a work scheduling model, b M = 3 all-activities scheduling

The work scheduling model and the M = 3 all-activities model under-predict weekly work episodes (total of preplanned and unplanned episodes) by 4% and 11.3%, respectively, while the M = 1.5 all-activities model has a significant lower accuracy by under-predicting work episodes by 23.9%. Besides the total number of work episodes, the distribution of work episodes over the week is more accurate in the work model of the combined model (Fig. 4II). The accuracy of the episode’s frequency in the all-activities’ model improves significantly by reducing the size of the destination choice set. Returning home episodes are under-predicted in the combined and all-activities model with M = 3 by 4% and 6% respectively, while the M = 1.5 all-activities model over-predicts these episodes by 3%, due to the significant over-prediction of the NWS episodes in this case. These results emphasize the necessity of developing a more systematic destination choice set in a nested structure model, as size of the choice set plays a significant role in the accuracy of the activity generation model.

Distances travelled

Episode destinations are chosen at the traffic zone level from the feasible destination choice set. As the models do not include a mode choice component, simulated versus observed trip distances, rather than travel times, are compared. It is notable that in the estimation process observed modal travel times are used; however, in the application of the models auto travel time is applied for all the trips. NWS trip length histograms are shown in Fig.5I for each category of NWS episodes. The models display similar trends of under-predicting trip frequencies under 5 km and over-predicting longer distances. The time–space constraints in the combined model improve its performance relative to the all-activities model when shorter distances are actually chosen, while the all-activities model performs better when destinations further than 20 km are actually chosen. However, as a relatively low percentage of longer-distance trips are observed, we can conclude that the combined model generally is the better-performing model. Reducing the feasible set size in the all-activities model does not make a significant improvement in destination predictions, as the more negative coefficients of the impedance factors in the M = 1.5 all-activities model compensates for its larger time budgets.

Fig. 5

Destination choice model’s simulation outcomes: distribution of distances travelled: a work/school related, HH-obligations and medical/services, b social/recreational/entertainment, c shopping

Episode duration and start time

Episode durations are simulated in 5-min time intervals. The subsequent episode’s trip start time is calculated by summing up the current episode’s trip start time with its associated duration and travel time to reach its chosen destination. Travel time is an input to the model from road network skims generated by an EMME network model for the Toronto region (Miller et al. 2015). Examples of episodes’ simulated duration and start time are shown in Figs. 4 and 5, respectively. Due to a wide range of duration for each episode type in the dataset, shorter durations are over-predicted for work/school related, social/recreational/entertainment, shopping, WAH and stay-at-home episodes in the simulation models. As the models run until an individual’s time-budget ends, shorter simulated episodes lead to longer available time budgets; leading to the total number of the episodes being over-predicted.

Simulated shopping episodes start slightly earlier than those observed. In the combined model, this is caused by the later assigned start time to the work episodes in the first step of the simulation, which means longer before-work gaps and shorter after-work gaps. Moreover, simulating trips using auto travel time, which is mostly shorter than the actual travel times experienced with transit and active modes, results in earlier episode start times in both models. Shorter assigned duration to the episodes is another reason for having earlier start times. The calculated mean absolute error in the predicted start time of different episode types over the day shows that the all-activities model shows a slightly better fit in modeling shopping and WAH episodes’ start time. However, for the other NWS episode types the combined model has a better fit to the dataset.

As shown in Figs. 6 and 7 simulated work episodes in the all-activities model start later than observed and are over-predicted for durations between 5 and 8 h, which is consistent with the results of the work scheduling model. The M = 3 all-activities model has a more accurate work start time prediction during the morning peak with a mean absolute error of 6% compared to the work scheduling model with a mean absolute error of 15%. The all-activities model work episode predicted start time mean absolute error is 2.29%, compared to 4.4% for the work scheduling model which indicates that both models have a good fit over a day. However, as a result of a more accurate work episode frequency prediction, the work scheduling model shows a better fit to the observed work pattern compared to the all-activities model, as demonstrated in Fig 8. Predicted patterns for the preplanned work episodes with 8% of under-prediction during the week is more accurate than unplanned ones with 13.9% of under-prediction.

Fig. 6

Episodes’ start time: a social/recreational/entertainment, b major grocery, c clothing/personal items, d return home, e work

Fig. 7

Episodes’ duration: a social/recreational/entertainment, b major grocery, c clothing/personal items, d return home, e work

Fig. 8

Weekly pattern of the work episodes: a work scheduling model, b all-activities model with M = 3, c preplanned work episodes, d unplanned work episodes

Conclusion

In summary, two ABMs were applied to replicate complete workers’ out-of-home travel/activity patterns in the CHASE dataset. Monte Carlo simulation is applied to generate the travel/activity decisions of the individuals in a short-run dynamic microsimulation model. In the first model, work/school episodes are scheduled prior to the NWS episodes within a separate model, while in the second model all activity types are modeled within the same framework without any priority assumption. The purpose was to investigate the influence of the common practice of fixing work/school episodes as the schedule skeleton on predicted travel/activity patterns. The simulation outcomes indicate that assigning a higher priority to work episodes’ scheduling not only is behaviorally plausible but also improves the accuracy of the travel/activity pattern prediction. The predicted NWS episodes’ schedule as well as the work episodes’ pattern in the combined model are significantly more accurate than the all-activities models. Generally scheduling NWS episodes is more complicated compared with work/school episodes. This complexity arises from the randomness inherent in the NWS episodes’ attributes and insufficient explanatory variables to define them as well as data limitation. When scheduling NWS and work/school episodes simultaneously, errors in scheduling NWS episodes propagates into the work scheduling and decreases the accuracy of work/school predictions. The conducted hypothesis test in this study confirms the validity of this argument.

Both models over-predict the frequency of NWS episodes, while under-predicting the frequency of work/school episodes and the ratio of the return home to NWS episodes. The models assign shorter durations to NWS and stay-at-home episodes compared to those observed. In such a complex scheduling model, performance of the models’ components is obviously inter-related. As the models run until an individual’s time-budget ends, it is important to improve the accuracy of the duration model. Shorter simulated episodes’ duration leads to over-prediction of the total number of episodes. Considering the nested structure of the activity type and destination choice models, activities with known destination are under-predicted. A more systematic destination choice set formation instead of arbitrarily increasing the feasibility ratio (M) would improve the accuracy of the activity type and destination choice models by reducing the size of the feasible set. Because of the sequential nature of the model, shorter time expenditures for NWS episodes introduce error into the subsequent episodes’ start time. The current models predict later start time for work episodes and earlier start times for shopping episodes.

The study is not without limitations. First, adding a mode choice component to the models would improve the models’ overall performance by improving the accuracy of episodes’ predicted destinations and start times. Adding a mode choice component to the model is considered as a future work, as identifying a modelling approach which is computationally tractable, theoretically defensible and empirically validated (Dianat 2018) is another significant research challenge. Another component of the model that needs further investigation is the destination choice model, especially the choice set formation. As the simulation results revealed, in a nested structure of activity type and destination choices, the size of the choice set influences the predicted frequency of the episode types. A more systematically formed destination choice set would reduce the size of the choice set by excluding destinations that are not considered by individuals. The size of the feasible choice set can also be reduced considering the availability of locations for a specific episode purpose in each spatial unit. This is possible upon availability of a rich disaggregate and accurate dataset of the points of interest. Moreover, instead of finding the final destination choice set for model estimation by a purely random choice of destinations, more behavioural approaches such as importance sampling can be applied. Third, as a future research joint activity episodes might also be considered as part of the schedule skeleton as they are a “contract” between their participants.