Introduction

The activity-based approach has proven to be the most behavioral approach to travel demand modeling and urban transportation policy analysis (Joh 2004; Roorda 2005; Habib 2007). Over the last two decades, the activity-based approach of modeling travel demand has matured to such an extent that it produced several operational models in different parts of the world (Roorda et al. 2008). However, a unified modeling framework that can represent an activity-based travel demand model (as is available for the traditional trip-based four-stage model) is yet to be developed. Different researchers use different conceptual and analytical procedures for activity-based travel demand modeling. Many issues related to the modeling framework, such as the concept of activity utility, application of so-called rules, modeling time frame (daily vs. weekly), and time discretization are still under debate in the research community (Habib 2009). The only significant consensus that has been apparently reached so far is the reorganization of two general components for an activity-based travel demand model: the activity generation component and the activity scheduling-rescheduling component (Habib and Miller 2009).

In terms of the empirical method used within the activity generation and scheduling components of any activity-based travel demand model, three distinct categories are easily identifiable: (1) the econometric approach, (2) the rule-based approach and (3) a hybrid mix of econometrics and rules (Habib and Miller 2006). However, application of econometrics in activity-based models varies from the unified discrete choice approach with its inherent assumption of global optimization behavior (Bowman et al. 1998) to the conglomeration of a series of econometric models (Bhat et al. 2004). On the other hand, application of behavioral rules varies from applying the simulation-based approach with data mining techniques (Arentze and Timmemans 2000) to researcher-defined simplified rules which connect different components of the sub-models within a general activity-based framework (Roorda 2005). Travel demand modelers are now inclined to adopt a hybrid approach of behavioral rules and econometrics rather than depending on only either one alone (Auld and Mohammadian 2009). A tendency is clear in the literature that previously scrutinized applications of the utility-based econometric approach (Garling et al. 1994) are now considered to be unavoidable (Miller 2005c). There is now significant interest among researchers in capturing the dynamic process of activity generation and scheduling within the utility-based modeling framework of an activity-based approach. Habib and Miller (2008) have presented utility-based models of activity generation considering the day-to-day and within-day dynamics of activity agenda formation. However, to date no such unified econometric model is available for the activity scheduling. Conceptually, activity scheduling process is very different from the activity generation process. Such differences as definition of time in terms of time allocation versus time consumption/expenditure, temporal resolution requirements of planning horizon versus actual implementation etc. clearly distinguish the modeling of activity generation than the modeling of activity scheduling. As such, it is imperative that a modeling technique should be developed which can capture the process of activity/travel pattern formation in a unified and comprehensive way. The most demanding issues in this regard are related to the development of a utility-based framework for the activity scheduling process (Miller 2005a, b, c). In an effort to address this issue, a random utility maximization-based econometric model for the activity scheduling processFootnote 1 is presented in this paper.

The proposed modeling framework exploits the random utility maximization (RUM)-based approach to modeling activity scheduling by considering the dynamics of the time budget constraint over the course of a day. The proposed framework does not consider different activity patters as alternatives to choose from; rather, it models the pattern formation process. The outcome of the model will be the activity patterns resulting from dynamic activity scheduling processes along a longitudinal time scale. The unique feature of the proposed model is that it does not need to discretize the time (activity start-time, end time, and duration) to fit into an econometric modeling scope. It uses an entirely RUM-based discrete continuous modeling specification that can capture time expenditure dynamics explicitly. For empirical investigation, the proposed framework is applied for a weekend activity scheduling using 2002–2003 Computerized Household Activity Scheduling Elicitor (CHASE) survey data collected in Toronto, Canada.

The paper is organized as follows: “Activity scheduling model” section presents the literature review on activity scheduling models. “Random utility maximization based activity scheduling model” section presents the conceptual framework of the proposed dynamic activity scheduling model. “Econometric model formulation” section presents the econometric formulations of the proposed RUM-based dynamic scheduling model. “Application in weekend activity scheduling model” section discusses the importance of weekend activity scheduling models as well as the data preparation for empirical estimation of the model. “Empirical model” section discusses the estimated parameters of the empirical model. “Demonstration of model application” section discusses the application of the model in predicting scheduling patterns. Finally, “Conclusions and direction for future research” section concludes the paper by summarizing important findings and identifying directions for future research.

Activity scheduling model

The activity scheduling process is inherently complex in nature. The complexity of the activity scheduling process creates problems in terms of modeling the process to simulate activity-travel behavior. Problems with respect to modeling the activity scheduling process can be divided into three general categories: (1) the problems of detailing the process of schedule formation over time; (2) the problems associated with collecting data that aptly reflects the complexity of the scheduling process and (3) developing an appropriate mathematical modeling technique without making strong assumptions (Doherty 1998, 2005). Detailing the activity scheduling process has been investigated by various studies to develop conceptual models for activity scheduling (Litwin and Miller 2004; Miller 2005c; and Auld and Mohammadian 2009 are a few recent examples). Considerable advances have been achieved in the design and implementation of behavioral data collection related to the activity scheduling process (Doherty et al. 2004; Lee and McNally 2006; Ruiz and Timmermans 2006). However, the third and the most challenging problem of developing unified modeling technique is still evolving. The primary challenge in this regard is the need to develop a unified framework for activity scheduling which supports the inherent dynamics of the activity scheduling process under time budget constraints. While arguments in favor of modeling the activity scheduling process rather than modeling the choice of alternative scheduling patterns are well established (Garling et al. 1994), most of the empirical models either directly or indirectly focus on replicating observed scheduling patterns. This trend is mainly due to the simplifications of the complex behavioral process of activity scheduling, which is often unavoidable. TASHA (Roorda et al. 2008), ALBATROS (Arentze and Timmemans 2000), CEMDEP (Bhat et al. 2004)—a few of the most cited operational models in the literature that are all involved in simplifications of behavior in different ways in different levels. While simplification of behavioral process is unavoidable, research efforts to avoid higher simplication by following model formulation according to the behavioral processes is important.

Among all operational activity-based models, the CEMPDEP is the only one that relies primarily on an econometric modeling approach to replicate the scheduling process. However, the scheduling process component in CEMDEP incorporates a number of individual, primarily univariate model components, which consider a fixed (modeler-defined) sequence of process/planning attributes. While the econometric approach is highly efficient in capturing behavioral ingredients within the component models by integrating different variables, it is also important to ensure that the basic dimensions of the dynamic scheduling process are handled comprehensively. Researchers criticizing such ad hoc approaches often propose more complicated conceptual frameworks without necessarily tackling the fundamental issues related to scheduling dynamics in a unified econometric modeling framework (Auld and Mohammadian 2009). Habib and Miller (2008, 2009) argue in favor of adopting distinct definitions of time and activity utility in order to model the behavioral processes in a manner that overcomes these challenges. The main arguments are that time is a continuous entity and that it plays separate roles in activity generation and activity scheduling processes. Time acts as a resource to be allocated among a number of alternative activities in the activity generation process and as a commodity to be consumed in the activity scheduling process. In order to capture the dynamics of the activity scheduling process, it is necessary that the time budget be taken into consideration directly in the modeling framework. At the same time, in order to overcome modeler-induced biases, time should be considered as a continuous entity within the econometric modeling structure.

Habib and Miller (2008, 2009) have presented a unified econometric modeling framework for the activity generation process. The framework considers time as a continuous entity with an embedded time budget limitation. However, to our knowledge, similar efforts aimed at modeling the activity scheduling process have been few. Developing such a modeling framework for the activity scheduling process is more challenging than that for the generation process. The activity scheduling process is complex and not temporally linear (in that temporally later activities can influence the time, place and other characteristics of earlier activities). As an initial simplification, in this paper we treat the process as unfolding sequentially in time. In such a sequential and dynamic process, time budget changes with the successive completion of activities. Moreover, developing a unified econometric modeling framework for the scheduling process requires that the sequential process of execution and the dynamic changes in time budget should be embedded into the econometric modeling framework. One strategy for conceptualizing such a dynamic process is to consider it as a sequential, time-dependent activity type choice and corresponding time expenditure process. In such a framework, endogeneity and self-selection between activity type choice and corresponding time expenditure should be taken into consideration. Considering the dynamics of time budget changes along a longitudinal time scale should also be explicitly ingrained in the model. For such a complicated behavioral process with several interconnected elements (activity type choice, time expenditure, time budget dynamics, continuous time scale, etc.) a random utility maximization (RUM)-based modeling framework may be the most appropriate approach. Furthermore, a RUM-based approach can also effectively facilitate integration of the travel demand model within an integrated land use and transportation modeling framework (Miller 2005c). Developing a RUM-based model for discrete activity type choice is not difficult. However, the development of a similar model for continuous time expenditure which considers dynamic time budget effects while addressing endogeneity/self-selection between activity type choice and time expenditure choice is a more formidable challenge. The next section describes this unified model in greater detail.

Random utility maximization based activity scheduling model

Let us consider that an individual, i, at a particular point in the day is to choose an activity to perform and corresponding time expenditure or duration, t j . We can assume that a rational individual will maximize her utility in choosing the activity type to schedule and the total time expenditure on it. In expending time for the chosen activity, however, the individual faces a time budget limitation. This time budget limitation is not constant throughout the day. The day begins with a 24-h time budget limitation which is gradually reduced with the number of activities performed over the course of the day in different locations. The remaining time budget at any point of scheduling an activity is the left over time after all previously performed activities have been completed. While executing an activity, i.e., defining the duration of a specific activity, the individual trades off between time expenditure to the chosen activity and travel time required to reach the activity location versus total time left over for all other activities to be completed in the balance of the day. As we do not know for certain the causes and factors that influence the individual’s tradeoffs in choosing alternative activity types and time expenditures out of a limited time budget, it is reasonable to consider the assumption that the utility associated with activity type and time expenditure includes random elements. Hence, the utility maximizing approach to model activity type choice and time expenditure choice is really a Random Utility Maximizing (RUM) approach. Addressing the facts that the time budget decreases as the day progresses and that the scheduling of any particular activity type is affected by what activities the individual already completed in a given day means that the method captures some (though not all) of the behavioral dynamics of the activity scheduling process. In the context of such a situation the choice of a given activity type at any point in time influences expenditures of the limited amount of time from the left over time budget, and vice versa.

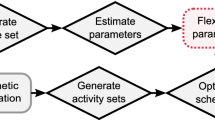
Figure 1 presents the schematic diagram of such a prototype example of the activity scheduling choice process. This is an example of a single day (a 24-h time span) modeling framework. However, in the case of a multi-day scheduling process the end of day activity of the previous day is regarded as the first activity of the following day. In this paper we are presenting a single-day activity scheduling model, where the scheduling process begins at midnight (t = 0) and continues until the end of the day. For a 24-h modeling timeframe such temporal referencing is unavoidable, even though it creates left and right censoring issues for the first and last activities. However, beginning at the reference time (t = 0) different people might perform different numbers and types of activities before the end of the day and thereby may have different types of activity patterns. The most important point is that this approach does not consider different activity patterns as alternatives. We are modeling the scheduling process, so that the activity pattern emerges out of the dynamic scheduling process.

Fig. 1
figure 1

Dynamic discrete-continuous approach to model activity pattern formation

Full size image

Econometric model formulation

From a modeling point of view the challenge is to develop a mathematical model able to facilitate the implementation of the theoretical framework explained above but parsimonious enough to suit model parameter estimation and practical implementation of the model. In this regard, it is important that the dynamics of activity scheduling and correlation between activity type choice, location and corresponding time expenditure are sufficiently captured in the RUM-based model formulation. Such a relationship between activity type, location and time expenditure choice can be influenced by both observed and unobserved factors. While the influence or self-selection effects of observed factors can be captured using the same variable in both activity type choice and time expenditure component, it is also necessary to address the correlation among the random or unobserved elements influencing the choices. The following sub-sections develop a modeling framework that can address these issues.

Formulation of utility function

Suppressing the subscript, i, in the mathematical expressions for the sake of simplicity, let us assume that the utility function of the individual person, i, for the j alternative activity type choice is:

$$ U_{j} = V_{j} + \varepsilon_{j} = \beta_{j} x_{j} + \varepsilon_{j} ; \quad j = 1,2,3, \ldots \ldots A $$
(1)

where V j is the systematic utility of activity type choice, which is a function of a set of explanatory variables, (x j ), and corresponding parameters of weighting factors, (β j ). The random variable, ε j , is the unobservable random error component of activity type choice utility. Similarly, let us assume that the total direct utility function of the same individual for time expenditure, (t k ), can be expressed as:

$$ U(t_{k} ) = \sum\limits_{k = 1}^{2} {{\frac{1}{{\alpha_{k} }}}\,\exp (\psi_{k} z_{k} + \,\varepsilon_{k}^{\prime} )\,\,(t_{k}^{{\alpha_{k} }} - 1)} $$
(2)

Here k = 1 indicates the chosen activity and k = 2 indicates the remainder of the amount of time (the composite activity) under the available time budget. The component, exp(ψ k z k  + \( \varepsilon^{\prime}_{k} \)), is the baseline utility function that indicates marginal utility at the point of zero time expenditure to the corresponding activity type. In the baseline utility function, z k indicates a vector of explanatory variables; Ψ k indicates a vector of coefficient corresponding to z k ; and \( \varepsilon^{\prime}_{k} \) is the unobserved random error component of the random utility function. Among other components of the utility function, α k is the satiation parameter. The satiation parameters, α k , capture the decreasing rate of satiation with increasing expenditure of time to the corresponding activity types (Bhat 2008). The composite activity encapsulates all of the rest of the day’s activities against which the current chosen activity time expenditure tradeoff takes place. This is synonymous to the well-known Hicksian composite good concept in consumption economics (Hicks 1946). The concept of composite activity is very important for both activity planning (generation) and activity scheduling process modeling. In case of activity planning process modeling, the composite activity accommodates the scope of unplanned activities within a planning horizon (Habib 2007). In case of activity scheduling, at any particular scheduling step, the composite activity refers to the planned but yet to be scheduled activities altogether. In this case, the composite activity captures the time pressure effect within the activity scheduling process, which is derived from planning of the activity participation before the scheduling process begins.

The function of the total utility of time expenditure for the chosen activity and corresponding composite activity as specified in Eq. 2 is the well-known translated Constant Elastic of Substitution (CES) direct utility function (Bhat 2005, 2008; Pollak and Wales 1992). This utility function specifies the direct utility derived from the time expenditure (t k ) to a specific activity and the composite activity. It is clear that for different alternative activity types the time expenditure tradeoff between the specific activity and the corresponding composite activity may be different. If the total time budget remaining is given by T, then the time expenditure decision becomes an optimization problem under time budget constraints:

$$ t_{j} + t_{c} = T $$
(3)

Here the subscript, j, indicates the time allocated to the current chosen activity (activity episode duration) while c indicates the time left over for the composite activity under the available time budget constraints. In order to integrate the time budget constraints within the utility function of time expenditure, we can use the Lagrangian function:

$$ \begin{gathered} l = \sum\limits_{k = 1}^{2} {{\frac{1}{{\alpha_{k} }}}\exp (\psi_{k} z_{k} + \,\varepsilon^{\prime}_{k} )} \,\,(t_{k}^{{\alpha_{k} }} - 1) - \lambda \left[ {\sum\limits_{k = 1}^{2} {t_{k} - T} } \right] \hfill \end{gathered} $$
(4)

Here k = 1, 2 refer to j and c

In the above Lagrangian function, λ is the Lagrangian multiplier. According to the first-order Kuhn–Tucker optimality condition (Kuhn and Tucker 1951), the generalized expression can be written as:

$$ \exp (\psi_{k} z_{k} + \,\varepsilon^{\prime}_{k} )\,t_{k}^{{\alpha_{k} - 1}} - \lambda = 0, \quad {\text{if}}\;t_{k} > 0,\,\,k = 1,2 $$
(5)
$$ \exp (\psi_{k} z_{k} + \,\varepsilon^{\prime}_{k} )\,t_{k}^{{\alpha_{k} - 1}} - \lambda < 0, \quad {\text{if}}\,\,t_{k} = 0\,,\,\,k = 1,2 $$
(6)

Considering the composite activity as the reference activity (k = c) for time expenditure and given the circumstance that composite activity time expenditure is a non-zero value, we can specify λ as a function of the composite activity function:

$$ \lambda = \exp (\psi_{c} z_{c} + \,\varepsilon^{\prime}_{c} )\,\,t_{c}^{{\alpha_{k} - 1}} $$
(7)

Substituting λ in the Kuhn–Tucker optimality conditions we can specify that for a case of t j  > 0:

$$ \begin{gathered} \exp (\psi_{j} z_{j} + \,\varepsilon^{\prime}_{j} )\,\,t_{j}^{{\alpha_{j} - 1}} - \exp (\psi_{c} z_{c} + \,\varepsilon^{\prime}_{c} )\,\,t_{c}^{{\alpha_{j} - 1}} = 0\, \hfill \\ \exp (\psi_{j} z_{j} + \,\varepsilon^{\prime}_{j} )\,\,t_{j}^{{\alpha_{j} - 1}} = \exp (\psi_{c} z_{c} + \,\varepsilon^{\prime}_{c} )\,\,t_{c}^{{\alpha_{j} - 1}} \hfill \\ \end{gathered} $$

Taking the logarithm of both sides:

$$ \begin{aligned} (\psi_{j} z_{j} + \varepsilon^{\prime}_{j} ) + (\alpha_{j} - 1)\ln \left( {t_{j} } \right) &= (\psi_{c} z_{c} + \varepsilon^{\prime}_{c} ) + (\alpha_{c} - 1)\ln \left( {t_{c} } \right) \hfill \\ \left[ {\psi_{j} z_{j} + (\alpha_{j} - 1)\ln \left( {t_{j} } \right)} \right] + \varepsilon^{\prime}_{j} &= \left[ {\psi_{c} z_{c} + (\alpha_{c} - 1)\ln \left( {t_{c} } \right)} \right] + \varepsilon^{\prime}_{c} \hfill \\ V^{\prime}_{j} + \varepsilon^{\prime}_{j} &= V^{\prime}_{c} + \varepsilon^{\prime}_{c} \hfill \\ \end{aligned} $$
(8)

The above condition of equality applies to an expenditure of t j amount of time on the given activity. Similarly, for the case where t < t j

$$ V^{\prime}_{j} + \varepsilon^{\prime}_{j} < V^{\prime}_{c} + \varepsilon^{\prime}_{c} $$

Here,

$$ V^{\prime}_{k} = \left[ {\psi_{k} z_{k} + (\alpha_{k} - 1)\ln \left( {t_{k} } \right)} \right], \quad k = j,\,\,c $$

Now to derive the probability function of spending a specific amount of time, (t 2), we can further modify Eq. 8

$$ \begin{array}{*{20}c} {\varepsilon^{\prime}_{j} - \varepsilon^{\prime}_{c} = V^{\prime}_{c} - V^{\prime}_{j} } & {{\text{for}}\,\,t_{j} > 0} \\ {\varepsilon^{\prime}_{j} - \varepsilon^{\prime}_{c} < V^{\prime}_{c} - V^{\prime}_{j} } & {{\text{for}}\,\,t_{j} = 0} \\ \end{array} $$
(9)

Assumption of error term distributions and deriving probability distribution functions

According to RUM theory, an alternative activity, j, will be chosen if the utility of that alternative activity is the maximum of all considered alternatives.

$$ \begin{gathered} U_{j} > \begin{array}{*{20}c} {\max } \\ {n = 1,2,3 \ldots \ldots A,n \ne j} \\ \end{array} U_{n} \hfill \\ V_{j} > \left\{ {\begin{array}{*{20}c} {\max } \\ {n = 1,2,3 \ldots \ldots A,n \ne j} \\ \end{array} U_{n} } \right\} - \varepsilon_{j} \hfill \\ \end{gathered} $$

So,

$$ \begin{aligned} \Pr \left(U{}_{j} > \begin{array}{*{20}c} {\max } \\ {n = 1,2,3 \ldots \ldots A,n \ne j} \\ \end{array} U_{n} \right) = & \Pr \left( {V_{j} > \left\{ {\begin{array}{*{20}c} {\max } \\ {n = 1,2,3 \ldots \ldots M,n \ne j} \\ \end{array} U_{n} } \right\} - \varepsilon_{j} } \right) \\ = & \Pr \left( {V_{j} > (V_{n} + \varepsilon_{n} ) - \varepsilon_{j} } \right) \\ = & \Pr \left( {V_{n} < V_{j} + (\varepsilon_{j} - \varepsilon_{n} )} \right) \\ \end{aligned} $$
(10)

In the above formulations the systematic utility of a chosen alternative is a function of the difference between two random error terms: the error term of the chosen alternative, ε j , and the error term of the second best alternative, ε n . Let us assume that the random variable, ε j , has the Independently and Identically Distributed (IID) Type I Extreme-Value (Gumbel) distribution with a mean value of 0 and a scale parameter of 1. According to the properties of IID Type I Extreme-Value distribution, the maximum over an IID Extreme-Value random variable is also extreme-value distributed, and the difference of two IID Extreme-Value random terms is logistically distributed (Johnson et al. 1995; Pendyala and Bhat 2004). Hence, the implied cumulative distribution of the random error term of the chosen alternative, F(ε A ), can be written as (Ben-Akiva and Lerman 1985; Lee 1983; Train 2003):

$$ \begin{gathered} \Pr \left( {(\varepsilon_{n} - \varepsilon_{j} ) < (V_{j} - V_{n} )} \right) = {\frac{{\exp (V_{j} )}}{{\exp (V_{j} ) + \sum\nolimits_{n \ne j} {\exp (V_{n} )} }}} \hfill \\ \Pr (\varepsilon_{n} < (V_{j} - V_{n} + \varepsilon_{j} )) = {\frac{{\exp (\beta_{j} x_{j} )}}{{\exp (\beta_{j} x_{j} ) + \sum\nolimits_{n \ne j} {\exp (\beta_{n} x_{n} } )}}} \hfill \\ \end{gathered} $$
(11)

For the time expenditure model of chosen activity, as shown in Eq. 9, let us assume the similar distribution assumption for the random error component, \( \varepsilon^{\prime}_{j} \), to be an IID Type I Extreme-Value (Gumbel) distribution with a mean value of 0 and a scale parameter of σ. Since the time expenditure follows the discrete activity type choice, the time expenditure is concerned with two alternative options (the chosen activity and the composite activity). According to RUM theory, (considering the time budget constraints and the Kuhn-Tucker optimality condition), the time expenditure, t j , to the chosen activity depends on the condition shown in Eq. 9. As mentioned above, the difference between two IID Extreme-Value random terms is logistically distributed. Moreover, the Probability Distribution Function (PDF) and Cumulative Distribution Function (CDF) of \( \varepsilon^{\prime}_{j} \) are given by (Johnson et al. 1995):

$$ \begin{aligned} \Pr \left( {(\varepsilon^{\prime}_{j} - \varepsilon^{\prime}_{c} ) = (V^{\prime}_{c} - V^{\prime}_{j} )} \right) = & \,{\frac{1}{\sigma }}\,\exp \left( {{\frac{{ - (V^{\prime}_{c} - V^{\prime}_{j} )}}{\sigma }}} \right)\left[ {1 + \exp \left( {{\frac{{ - (V^{\prime}_{c} - V^{\prime}_{j} )}}{\sigma }}} \right)} \right]^{ - 2} \\ \Pr \left( {(\varepsilon^{\prime}_{j} - \varepsilon^{\prime}_{c} ) < (V^{\prime}_{c} - V^{\prime}_{j} ) + } \right) = & \left[ {1 + \exp \left( {{\frac{{ - (V^{\prime}_{c} - V^{\prime}_{j} )}}{\sigma }}} \right)} \right]^{ - 1} \\ \Pr \left( {\varepsilon^{\prime}_{j} < (V^{\prime}_{c} - V^{\prime}_{j} + \varepsilon^{\prime}_{c} )} \right) = & \left[ {1 + \exp \left( {{\frac{{ - (V^{\prime}_{c} - V^{\prime}_{j} )}}{\sigma }}} \right)} \right]^{ - 1} \\ \end{aligned} $$
(12)

To ensure model identification, the specification of \( V^{\prime}_{ji} \) and \( V^{\prime}_{ci} \) can be further specified as (Bhat 2008):

$$ \begin{aligned} V^{\prime}_{j} &= \left[ {\psi_{j} z_{j} + (\alpha_{j} - 1)\ln \left( {t_{j} } \right)} \right]\, \hfill \\ {\text{and}} \hfill \\ V^{\prime}_{c}& = (\alpha_{c} - 1)\ln (t_{c} ) \hfill \\ \end{aligned} $$
(13)

Here \( V^{\prime}_{ci} \) indicates the composite activity for the corresponding chosen activity type under remaining time budget constraints. Now, according to the change of variables theorem (Kottegoda and Rosson 2008), the PDF can be determined as follows:

$$ \begin{aligned} \Pr \left( {t = t_{j} } \right) = & \left( {{\frac{{\delta \left( {(V^{\prime}_{c} - V^{\prime}_{j} )} \right)}}{{\delta t_{j} }}}} \right){\frac{1}{\sigma }}\exp \left( {{\frac{{ - (V^{\prime}_{c} - V^{\prime}_{j} )}}{\sigma }}} \right)\left[ {1 + \exp \left( {{\frac{{ - (V^{\prime}_{c} - V^{\prime}_{j} )}}{\sigma }}} \right)} \right]^{ - 2} \\ =\, & \left( {{\frac{{1 - \alpha_{j} }}{{t_{j} }}} + {\frac{{1 - \alpha_{c} }}{{t_{c} }}}} \right){\frac{1}{\sigma }}\exp \left( {{\frac{{ - (V^{\prime}_{c} - V^{\prime}_{j} )}}{\sigma }}} \right)\left[ {1 + \exp \left( {{\frac{{ - (V^{\prime}_{c} - V^{\prime}_{j} )}}{\sigma }}} \right)} \right]^{ - 2} \\ & {\rm where}, \\ & \left( {{\frac{{\delta \left( {(V^{\prime}_{c} - V^{\prime}_{j} )} \right)}}{{\delta t_{j} }}}} \right) = {\frac{\delta }{{\delta t_{j} }}}\left( {(\alpha_{c} - 1)\ln (T - t_{j} ) - \psi z - (\alpha_{j} - 1)\ln \left( {t_{j} } \right)} \right) \\ \, & =\,{\frac{{(1 - \alpha_{j} )}}{{t_{j} }}} + \,{\frac{{(1 - \alpha_{c} )}}{{t_{c} }}} \\ \end{aligned} $$
(14)

Joint probability of activity type choice and time expenditure

Joint estimation of RUM-based activity type choice and time expenditure requires the assumption that the random error terms of the models have an unrestricted correlation. In our case the random error terms, ε j and \( \varepsilon^{\prime}_{j} \), have the same type of distribution but with different scale parameter. In the case of RUM activity type choice, we cannot differentiate the scale parameter from estimated coefficient parameter values. Hence, the scale parameter is assumed to be normalized to a value of 1. For the RUM-based time expenditure model, alternatively, in considering the fundamental difference between the unit time expenditure rate in the chosen activity and in the composite activity we can estimate the scale parameter, σ. One means of specifying the unrestricted correlation between these two random variables is to transform both random variables into an equivalent standard normal variable and specify the joint distribution as an equivalent bivariate normal distribution (Lee 1983). In our case, both of the random error components have completely specified implied marginal distributions. Hence, the marginal distributions can be transformed into corresponding standard normal distributions. In transforming these marginal distributions into equivalent standard normal variables, it can be shown that (Lee 1983):

$$ \begin{gathered} \varepsilon_{j}^{*} = J_{1} (\varepsilon_{j} ) = \Upphi^{ - 1} [(\varepsilon_{n} - \varepsilon_{j} ) < (V_{j} - V_{n} )] \hfill \\ \varepsilon_{k}^{*} = J_{2} (\varepsilon^{\prime}_{j} ) = \Upphi^{ - 1} [(\varepsilon^{\prime}_{j} - \varepsilon^{\prime}_{c} ) < (V^{\prime}_{c} - V^{\prime}_{j} )] \hfill \\ \end{gathered} $$
(15)

Here, Φ−1 indicates an inverse of the cumulative standard normal variable. The transformed variables, J 1 (ε j ) and J 2(\( \varepsilon^{\prime}_{j} \)), are transformed into standard normal variables of the corresponding random variables, ε j and \( \varepsilon^{\prime}_{j} \), respectively. The joint decision process of activity type choice and time expenditure now can be described by considering that the transformed standard normal variables are bivariate normal (BVN) distributed with correlation ρ jt : BVN[J 1 (ε j ), J 2(\( \varepsilon^{\prime}_{j} \)), ρ jt ]. Hence, the joint probability of observing that any individual (ignoring the individual identifier, i) choosing an alternative mode, j, and corresponding time expenditure, t j can be expressed as follows (Habib et al. 2008):

$$ \begin{aligned} \Pr (Time &= t_{j} \cap Activity\,Type = j) = \Pr (Time = t_{j} \cap \varepsilon \le J_{1} (\varepsilon_{j} )) \hfill \\ &= \left( {{\frac{{1 - \alpha_{j} }}{{t_{j} }}} + {\frac{{1 - \alpha_{c} }}{{t_{c} }}}} \right){\frac{1}{\sigma }}\exp \left( {{\frac{{ - (V^{\prime}_{c} - V^{\prime}_{j} )}}{\sigma }}} \right)\left[ {1 + \exp \left( {{\frac{{ - (V^{\prime}_{c} - V^{\prime}_{j} )}}{\sigma }}} \right)} \right]^{ - 2} \Upphi \left( {{\frac{{J_{1} (\varepsilon_{j} ) - \rho_{jt} J_{2} (\varepsilon_{j}^{\prime} )]}}{{\sqrt {1 - \rho_{jt}^{2} } }}}} \right) \hfill \\ \end{aligned} $$
(16)

Based on the above formulation, the likelihood function, L i , of an individual observation, i, can be written as:

$$ \begin{gathered} L_{i} = \prod\limits_{j = 1}^{n} {\left( \begin{gathered} \left( {{\frac{{1 - \alpha_{ji} }}{{t_{ji} }}} + {\frac{{1 - \alpha_{ci} }}{{t_{ci} }}}} \right){\frac{1}{\sigma }}\exp \left( {{\frac{{ - (V^{\prime}_{ci} - V^{\prime}_{ji} )}}{\sigma }}} \right)\left[ {1 + \exp \left( {{\frac{{ - (V^{\prime}_{ci} - V^{\prime}_{ji} )}}{\sigma }}} \right)} \right]^{ - 2} \hfill \\ \Upphi \left( {{\frac{{J_{1} (\varepsilon_{ji} ) - \rho_{jt} J_{2} (\varepsilon^{\prime}_{ji} )]}}{{\sqrt {1 - \rho_{jt}^{2} } }}}} \right) \hfill \\ \end{gathered} \right)^{{D_{ji} }} } \hfill \\ \hfill \\ \end{gathered} $$
(17)

D ij is a binary indicator variable for the chosen activity type

Here D ji is a binary indicator variable for the chosen alternative activity. Now if we consider the sequence of activity selection and corresponding time expenditure, i.e., the activity scheduling process for 24-h time period, the joint likelihood function of the complete schedule of an individual, i, becomes:

$$ L_{Ti} = \prod\limits_{Z = 1}^{S} {\left[ {\prod\limits_{j = 1}^{A} {\left( \begin{gathered} \left( {{\frac{{1 - \alpha_{ji} }}{{t_{ji} }}} + {\frac{{1 - \alpha_{ci} }}{{t_{ci} }}}} \right){\frac{1}{\sigma }}\,\exp \left( {{\frac{{ - (V^{\prime}_{ci} - V^{\prime}_{ji} )}}{\sigma }}} \right)\left[ {1 +\,\exp \left( {{\frac{{ - (V^{\prime}_{ci} - V^{\prime}_{ji} )}}{\sigma }}} \right)} \right]^{ - 2} \hfill \\ \Upphi \left( {{\frac{{J_{1} (\varepsilon_{ji} ) - \rho_{jt} J_{2} (\varepsilon^{\prime}_{ji} )]}}{{\sqrt {1 - \rho_{jt}^{2} } }}}} \right) \hfill \\ \end{gathered} \right)^{{D_{ji} }} } } \right]_{Z} } $$
(18)

Joint probability of activity type choice, location choice and time expenditure

The joint model presented in “Joint probability of activity type choice and time expenditure” section does not include activity location choice. However, integrating activity location choice is very straight forward in this case. If we assume that individual derived a joint utility (U jl ) in choosing an activity type to schedule and choosing its location, then Eq. 1 can be re-written as:

$$ \begin{gathered} U_{jl} = V_{j} + V_{l} + \varepsilon_{j} + \varepsilon_{l} = \beta_{j} x_{j} + \beta_{l} x_{l} + \varepsilon_{j} \, + \varepsilon_{l} ; \hfill \\ {\text{Activity type subscript }}j = 1,2,3, \ldots \ldots \ldots A\,\,\,\,\,\, \hfill \\ {\text{Activity location subscript }}\,l = 1,2,3, \ldots \ldots \ldots L \hfill \\ \end{gathered} $$
(19)

Here the additional V l is the systematic utility of activity location choice, which is a function of location attributes (x l ) and corresponding weighting factors (β l ). The additional random error term, ε l is the unobserved random error component of activity location choice utility. A indicates the total number of alternative activity types in activity type choice set and L indicates the total number of alternative locations for a particular activity type. If we assume that the joint additive random error component (ε jl  = ε j  + ε l ) is Generalized Extreme Value (GEV) distributed, the joint probability of choosing a specific activity and corresponding location can take a nested logit structure. Now, depending on the variations of error correlations between activity type choice utility functions and activity location choice utility functions, the joint activity type and location choice probability function can be either

$$ \begin{aligned} \Pr \left( {{\text{Activity}} = j \,\,{\text{\& Location }} = l} \right) =\, & {\frac{{\exp (V_{j} + \lambda I)}}{{\exp (V_{j} + \lambda I) + \sum\nolimits_{n \ne j} {\exp (V_{n} + \lambda I)} }}} \times {\frac{{\exp (V_{l} /\lambda )}}{{\exp (V_{l} /\lambda ) + \sum\nolimits_{m \ne l} {\exp (V_{m} /\lambda )} }}} \\ {\text{the inclusive value, }}I = & \ln \left( {\exp (V_{l} /\lambda ) + \sum\nolimits_{m \ne l} {\exp (V_{m} /\lambda )} } \right) \\ \end{aligned} $$
(20)

Or

$$ \begin{aligned} \Pr \left( {{\text{Activity}} = j{\text{ \& Location }} = l} \right) = \ ,& {\frac{{\exp (V_{l} + \lambda I)}}{{\exp (V_{l} + \lambda I) + \sum\nolimits_{m \ne l} {\exp (V_{m} + \lambda I)} }}} \times {\frac{{\exp (V_{j} /\lambda )}}{{\exp (V_{j} /\lambda ) + \sum\nolimits_{n \ne j} {\exp (V_{n} /\lambda )} }}} \\ {\text{the inclusive value, }}I = & \ln \left( {\exp (V_{j} /\lambda ) + \sum\nolimits_{n \ne j} {\exp (V_{n} /\lambda )} } \right) \\ \end{aligned} $$
(21)

Here the term λ refers to the ration of scale parameters of two error terms. In any case, under Random Utility Maximization (RUM) the necessary condition of choosing a specific activity type and corresponding location is

$$ \begin{gathered} U_{jl} > \begin{array}{*{20}c} {\max } \\ {mn = 1,2,3 \ldots \ldots AL,nm \ne jl} \\ \end{array} U_{nm} \hfill \\ V_{j} > \left\{ {\begin{array}{*{20}c} {\max } \\ {nm = 1,2,3 \ldots \ldots AL,nm \ne jl} \\ \end{array} U_{nm} } \right\} - (\varepsilon_{j} + \varepsilon_{l} ) \hfill \\ V_{j} > \left\{ {\begin{array}{*{20}c} {\max } \\ {nm = 1,2,3 \ldots \ldots AL,nm \ne jl} \\ \end{array} U_{nm} } \right\} - (\varepsilon_{jl} ) \hfill \\ \end{gathered} $$
(22)

Under RUM condition, choosing a specific activity type and corresponding location is a joint discrete choice problem. In fact, Eq. 22 represents a series (total A times L) of binary activity type and location pair choice situations. In each of these cases the distribution of joint systematic utility of activity type and location choice depends on the distribution of total random error (ε jl  = ε j  + ε l ). In either type of nesting structure presented in Eqs. 20 and 21, the pairs of activity type choice and location choice options can be assumed as Type I Extreme Value distributed. As explained by Falaris (1987) and Habib et al. (2009a, b), such a joint probability can be transformed into an equivalent normally distributed variable. Now, if we consider activity location choice jointly with activity type choice, the transformed variable and can be used in place of \( \varepsilon_{j}^{*} \) in Eq. 15. Rewriting the Eq. 17 we find:

$$ \begin{aligned} J_{1} (\varepsilon_{jl} ) &= \Upphi^{ - 1} [(\varepsilon_{nm} - \varepsilon_{jl} ) < (V_{jl} - V_{nm} )] = \Upphi^{ - 1} \left( {\Pr \left( {{\text{Activity}} = j{\text{ \&\, Location }} = l} \right)} \right) \hfill \\ J_{2} (\varepsilon^{\prime}_{j} ) &= \Upphi^{ - 1} [(\varepsilon^{\prime}_{j} - \varepsilon^{\prime}_{c} ) < (V^{\prime}_{c} - V^{\prime}_{j} )] \hfill \\ \end{aligned} $$
(23)

Subsequently, the joint activity type, location and time expenditure choice makes the likelihood function of the complete schedule of an individual i:

$$ L_{Ti} = \prod\limits_{Z = 1}^{S} {\left[ {\prod\limits_{j = 1}^{A} {\left( \begin{gathered} \left( {{\frac{{1 - \alpha_{ji} }}{{t_{ji} }}} + {\frac{{1 - \alpha_{ci} }}{{t_{ci} }}}} \right){\frac{1}{\sigma }}\exp \left( {{\frac{{ - (V^{\prime}_{ci} - V^{\prime}_{ji} )}}{\sigma }}} \right)\left[ {1 + \exp \left( {{\frac{{ - (V^{\prime}_{ci} - V^{\prime}_{ji} )}}{\sigma }}} \right)} \right]^{ - 2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\Upphi \left( {{\frac{{J_{1} (\varepsilon_{jli} ) - \rho_{jit} J_{2} (\varepsilon_{ji}^{\prime} )]}}{{\sqrt {1 - \rho_{jit}^{2} } }}}} \right) \hfill \\ \end{gathered} \right)^{{D_{ji} }} } } \right]_{Z} } $$
(24)

This is the similar likelihood function as of Eq. 18 except, the J 1 (ε ji ) of Eq. 18 is replaced by J 1 (ε jli ). This is also a closed form likelihood function and can be estimated by classical MLE algorithm (for similar joint formulation, please see Falaris 1987 and Habib et al. 2009a, b). However, due to data limitation, the empirical application of the proposed modeling framework presented in this paper concentrates only on activity type and time expenditure choice.

In Eqs. 18 and 24, S is the total number of activities performed in the 24-h time period. Now, if we have a sample of observation with sample size, N, the joint likelihood function for the sample, L, becomes:

$$ L = \prod\limits_{i = 1}^{N} {L_{Ti} } $$
(25)

This expression is a sample likelihood function of a dynamic RUM discrete–continuous model. It is of a closed form and can be estimated using classical Maximum Likelihood Estimation (MLE) algorithms. However, it is also possible to consider random coefficient and preference heterogeneity by introducing error correlation at both levels (discrete and continuous). In this paper, the parameter estimates are obtained by maximizing the log-likelihood function using code written in GAUSS which applies the BFGS optimization algorithm (Aptech 2009). The goodness-of-fit measure of the mode is estimated using an adjusted Rho-square value:

$$ {\text{Adjusted Rho-square}}\, = 1 - {\frac{{{\text{Log \,likelihood \,of \,full\, model }} - {\text{ Number\, of\, parameters}}}}{{{\text{Log\, likelihood \,of \,the \,constant}} - {\text{Only\, model}}}}} $$
(26)

Here the constant-only mode indicates the model with only two parameters: the generic baseline utility function constant and the generic constant for the satiation parameter. The number of parameters in the Adjusted Rho-square equation indicates the total number of parameters in the full model more than the constant-only model.

In the joint probability distribution, the probability of choosing the discrete alternative is modified by the probability of not spending time to it. This modification is weighted by the correlation coefficient of two decisions. As per Eqs. 18 and 24, a positive value of correlation coefficient refers to a negative correlation between unobserved factors affecting activity type choice and choice of spending no time to it, and vice versa. For empirical application in the activity scheduling model, a negative correlation indicates that the probability of longer time expenditure increases the probability of choosing the corresponding activity. In case of empirical estimation of the models, it is necessary to impose restriction on correlation coefficients to ensure model identification. In case of scheduling model without location choice, considering same correlation coefficient for all activity types avoid arbitrary fixing of correlation coefficient for a specific activity type and avoids complexities in model estimation. Similarly, in case of activity scheduling with location choice, considering same correlation for all locations eliminates complexity in estimation. However, in all cases it should be clear that the values of correlation coefficients indicate the correlations between unobserved random elements influencing activity type and time expenditure choice or among unobserved random elements influencing activity type, location and time expenditure choice. A higher value of this correlation coefficient is an indication of poorly specified deterministic specifications of the utility functions of both model components. However, statistical insignificance of the correlation coefficient will nullify the argument of the joint estimation of mode and departure time model.

Application in weekend activity scheduling model

All operational activity-based models developed are for a typical weekday. However, with the increasing complexity of daily life, weekend trips are also becoming pertinent with respect to the transportation system optimization and demand management points of view. Traffic congestion on weekends is becoming increasingly common in many North American cities. It is for this reason that Levinson and Kumar (1995) strongly argue in favour of research on weekend activity scheduling behavior in addition to weekday analyses. There are some published papers that deal with weekend activity behavior. Among these, Bhat and Misra (1999) have focused on only discretionary type activities in their efforts to identify time expenditure differences between weekday and weekend scheduling behaviors. Fukuda et al. (2003) investigated time expenditure behavior to weekend discretionary activities in order to estimate the value of weekend time. Bhat and Copperman (2007) investigated children’s weekend physical activity participation behaviors. All investigations of weekend activity behavior published in the literature, however, have been with respect to specific types of activities or specific population groups. No research study has yet investigated weekend activity scheduling/participation behavior comprehensively.

In this paper we apply our econometric modeling framework in order to conduct a more comprehensive investigation of weekend activity scheduling behavior. We consider a 24-h modeling timeframe to investigate participation rates and time expenditures in all activities under consideration. Activities are classified into nine general categories, which also include work/school activities. Critics may argue against considering work/school activities in a weekend scheduling model, but the observed data show that many people participate in work/school activities on the weekend. However, in order to acknowledge the fact that weekends are more flexible and relaxed than weekdays, we do not segregate activities into any fixed commitments (e.g., work activity is considered as a skeleton activity in weekday schedules, etc.). The decision not to consider any hard-wired rules in the model is also intended to test the capacity of the model in capturing any behavioral patterns that may exist. However, incorporation of any such fixed commitments or rules within such an econometric modeling framework is also possible.

Data for empirical investigation

CHASE survey data from the first wave of the Toronto Travel-Activity Panel survey (TAPS) are used in this paper for empirical modeling of weekend activity scheduling (Roorda and Miller 2004). The CHASE survey was conducted in Toronto in 2002–2003 among 426 individuals in 271 households. A detailed description of the methods and a general data summary are available in Doherty et al. (2004) and Doherty and Miller (2000). This multi-day self-reporting survey lists the processes of activity planning and scheduling over a period of 7 days. In this paper, we separate the weekend activity schedules of the respondents only. After cleaning the dataset for missing information, a total of 423 individuals from 264 households were selected for the sample to estimate the empirical model. The sample consists of almost a 1:1 male–female ratio, and the average age of the individuals in the sample is 43 years. The average household size in the sample is 3, and the average number of children per household in the sample is 0.6. The average duration of having lived in that city by the people in the sample is 18 years and the average personal income is around 47,000 Canadian Dollars.

To simulate the activity scheduling process of this sample population, the choice set of the activity-agenda is defined by nine individual activity types.

Activity Type 1::

Basic Need type activities, such as sleep, wash/dress/pack/snack, lunch/dinner/breakfast and other basic need type activities.

Activity Type 2::

Work/School type activities including telework, volunteer work, training etc.

Activity Type 3::

Household Obligations type activities, such as cleaning, maintenance, attending children, attending pets and other household obligations.

Activity Type 4::

Drop-off/Pick-up type activities dropping/picking people, meals, snacks, video rentals, dry cleaning, mails, etc.

Activity Type 5::

Shopping activities including grocery shopping, personal shopping etc.

Activity Type 6::

Service type activities, such as medical/hospital, personal beautification, banking, banking, religious service, servicing automobile, etc.

Activity Type 7::

Recreational/Entertainment type activities.

Activity Type 8::

Social activities including visiting, hosting, bars/clubs, sports, planned social events, long time telephone conversation, etc.

Activity Type 9::

Other activities that do not fall in the above mentioned categories.

If we define the scheduling of an activity type at any point in time as a scheduling cycle, then the observed weekend schedules are composed of a minimum of 3 cycles and a maximum of 30 cycles. The modal number of scheduling cycles is 10. Intuitively, activity type 1: Basic Need (sleep in the most case) is the first activity in maximum cases; however, some people were also involved in Work/School, Household Obligations, Service, Recreational, Social and Other activities at the beginning of the day (starting at t = 0). As the day progresses, participation in Basic Need activities decreases while the participation rate in all other types of activities increases. This trend reverses during the later part of the day and at the end of the day participation in Basic Need activities increases again. In terms of time expenditure, initial activities are of a longer duration than the activities performed in the later part of the day. Activities involving longer travel times are primarily performed during mid-day.

For estimation of the empirical model, 24-h schedules of each individual are arranged along a longitudinal time scale. Considering midnight to be the beginning of the day, the schedules are arranged into a sequence of activity type and corresponding time expenditure. Having more than one activity per day, each individual’s 24-h schedule is similar to a panel data of activity type choice and corresponding time expenditure choice.

The variables considered in the empirical model can be classified into three general categories: socio-economic, activity-specific, and dynamic. Socio-economic variables includes person- and household-specific variables, e.g., age, gender, household size, number of children in the household, number of automobiles in the household, yearly income, employment status, number of years having lived in the same city. Activity-specific variables include activity-specific dummy constants and activity location attributes (the time required to travel from one activity place to another in this case). In the case of dynamic variables, the start-time of the scheduling cycle and the number of activities already performed are considered. In addition to the dynamic variables, the time budget decreases with an increasing number of performed activities.

Empirical model

The modeling begins with activity type choice at the beginning of the day, and the corresponding time expenditures are monitored. At the end of the first activity, the same process of type selection and corresponding time expenditure follows until the end of the day. The process of choosing an activity and consequent time expenditure may be referred as scheduling steps or scheduling cycle. At every scheduling step in the continuous time expenditure model component, we consider the trade-off in time expenditure to the specific chosen activity type, with respect to the leftover time for the composite activity.

In the econometric specification of the utility maximizing time expenditure mode, the satiation parameter, α k , must be less than 1(Bhat 2008). To ensure such a restriction, we consider the following specifications: α k  = 1 − exp(−τy). Here, y indicates a vector of variables and τ is the corresponding parameter vector. Without any loss of generality, we also normalized the variance parameter (σ) of the continuous time expenditure model component to 1.

The estimated model parameters are presented in Table 1. Several types of variables are considered in the model estimation process. These include socio-economic, residential location, transportation system performance, and activity specific attributes. The complicated structure of the model and the intention of joint estimation of a dynamic 24-h activity scheduling process posed a significant challenge in parameter estimation for the given sample of data. However, surprisingly, it was found that the estimation process is fairly efficient and a large number of parameters can be estimated using even a small sample. It proves that the econometric modeling structure fits well with the observed dynamic scheduling formation process. However, to be valid in interpreting the estimated parameters, we must consider the statistical significance of the parameter estimates. Considering that the data set is rather small in relation to the large number of parameters to be estimated, the estimated coefficients are considered statistically significant if the corresponding two-tailed ‘t’ statistics satisfy the 90% confidence interval, (t = 1.64). Some variables with statistically insignificant parameters are also retained in the models because they provide considerable insight into the behavioral process. Retention of some of the insignificant variables is also due to the expectation that, if a larger data set were available, these parameters might show statistical significance.

Table 1 Estimated parameters of weekend activity scheduling model
Full size table

A series of specifications were tested and, after removing insignificant parameters in different combinations of variable specifications, the final specification (presented in Table 1) was reached. In terms of variables, similar variables entered into the systematic part of the activity type choice utility function and the baseline utility function of the continuous time expenditure model component. In addition to the accommodation of self-selection effects in activity type selection for scheduling and corresponding time expenditure, an unrestricted correlation between unobserved factors influencing activity type choice and time expenditure is accommodated. The goodness-of-fit of the estimated model is calculated using the adjusted Rho-square value of 0.1, which is reasonable for such a complicated model structure. Given that a single value of goodness-of-fit cannot reflect the actual performance of the model, the empirical model is validated using the same data set. The validation results are discussed in the model application section.

Parametric specifications are presented for the utility function of the activity type choice model component and time expenditure model component. The time expenditure model component is represented by a baseline time expenditure utility function component and a satiation parameter function. It should be mentioned that this empirical model does not include activity location choice component. The time expenditure at each scheduling cycle refers to only the activity episode duration. Travel time to reach the scheduled activity location from the previous activity location, which is an output of activity location choice component, is considered as an exogenous input here. However, integration of an activity location choice component with activity type and time expenditure model will generate the travel time variable endogenously.

Utility of activity type choice

For the activity type choice model component, alternative specific constants indicate that only Household Obligation activity type has positive utility compared to all other activity types. However, we should be careful in our interpretation of the constant term. The alternative specific constants work as error baskets that capture the effects not explained by the variables considered in the model. Hence, a larger constant term indicates the lack of sufficient variables to explain the choice preference process. The constant term thus acts as a balancing factor against the effects of the available variables considered in the model. In this case, only Household Obligation activity has a constant term. For this type of activity, intra-household interaction and household task allocation are important. In this empirical model we modeled at the individual level while considering household-level variables that may indirectly capture these effects. However, there are still aspects of the household-level variables that remained unexplained.

Dynamic scheduling effect is captured by using the start-time of the scheduling cycle as a variable in the activity type choice model component. Considering the within-day dynamics of activity scheduling, it is expected that the time of the day should have a significant effect on choosing a specific activity type. In this model the start-time is expressed as a continuous variable that measures the hour from the beginning of the day. A positive coefficient of this variable indicates that the variable is influencing lower preference at the beginning of the day and higher preference at the end of the day. In our case, it is clear that Drop-off/Pick-up, Shopping and Service activities are more preferred to be started earlier in the day than is Recreation activity type. However, preferences to Basic Need, Work/School, Household Obligation, Shopping, Social and Other activities are insensitive to start-time. In addition to the start-time variable, consideration of the number of activities already performed as a variable serves to capture the within-day rhythm of weekend activity scheduling. This variable captures the effects of smaller numbers of longer-duration activities already done versus larger numbers of shorter-duration activities already done on next activity type scheduling. It seems that a higher number of shorter-duration activities performed increase the probability of scheduling Drop-off/Pick-up, Shopping, Service and Social activities. While, a lower number of longer-duration activities performed increase the probability of scheduling Basic Need activity. However Work/School, Household Obligation, Recreational and Others activity scheduling are insensitive to this variable.

The variable indicating travel time to the activity location captures an interesting weekend activity scheduling behavior. Travel time has either a negative effect or no effect for all activity types. It is clear that increasing the travel time requirement reduces the utility of participating in Basic Need, Work/School, Household Obligation, Recreation, and Other activity types. Travel time does not show any effect on the utility of choosing Drop-off/Pick-up, Service, Shopping and Social activities on the weekend. In this case travel time required for Basic Need activity includes both return home travel time and travel time required to go any out-of-home place for Basic Need activity. Regarding the travel time for returning home, it refers to the behavior that people tend to schedule the last activity closer to home so that return home travel time is smaller.

Household size captures the inter-household interaction effects on weekend scheduling. A larger household size reduces the utility of scheduling Work/School, Household Obligation, Shopping, Recreation, Social and Others activity types over Basic Need, Drop-off/Pick-up, and Service activities. The logarithm of age in years captures the personal choice of activity scheduling on the weekend. This variable has negative signs for Work/School, Household Obligation, Shopping, Recreation, Social and Other activity types with respect to zero coefficient for Basic Need, Drop-off/Pick up and Service activity types. This indicates that older people tend to schedule Basic Need, Drop-off/Pick up and Service activity types in weekends than younger people. Within the Work/School, Household Obligation, Shopping, Recreation, Social and Other activity type older people prefer Recreational activity most in the weekends.

Regarding job attributes, yearly income level and full-time job status are considered as variables in the model. It is clear that a higher income level increases the utility of participating in Social activity on the weekend. This means higher-income people are more likely to schedule Social activities than are lower-income people in weekends. On the other hand, a higher-income level reduces the utility of participating in Household Obligation, Service, and Other activity types on the weekend. Furthermore, this indicates that lower-income people are more likely to schedule Household Obligations, Service, and Other activities on the weekend than are higher-income people. However, income level does not show any significant impact on the utility of scheduling Basic Need, Drop-off/Pick-up, and Shopping activities on the weekend. In terms of full-time versus non-full-time job status, it seems that people who do not have full time jobs are more likely to participate in Recreational and Social activities than Shopping activity on the weekend than are people with full-time jobs. A higher number of children in the household increases the utility of Household Obligation and Drop-off/Pick-up activities, but reduces the utility of Shopping activity on the weekend. It is fairly obvious that a higher number of children in the household increases the need for Household Obligation and Drop-off/Pick-up activities in the weekends.

Baseline utility of time expenditure

Baseline utility function indicates the baseline preference of spending time in the various activities under consideration compared to the composite activity under time budget constraint. The baseline utility function of individual activities as specified in Eq. 2 is an exponential function of two additive components: the deterministic component and the random component. The deterministic component is parameterized as a function of a number of variables. The estimated parameters presented in Table 1 are explained below.

Interestingly, no activity type has a statistically significant constant baseline utility for weekend activity scheduling except the Basic Need, Social and Other activity types. The presence of the positive baseline utility constant in this case refers to preference of time expenditure at any point in time to the given activity with respect to composite activity for the remainder of the day. If the constant is less than zero, this indicates that people give more preference to rest of the day composite activity while scheduling the specific activity type of concern on the weekend. In this empirical model positive constant value of Basic Need, Shopping, Social and Other activity types clearly captures the minimum duration requirement for these activity types in weekends. Other hand, the positive constants captures the fact that some portion of duration of these activity types is not explainable by the available explanatory variables used in the baseline utility function specification. However, the effects of this baseline behavior are modified by different variables accommodated in the baseline utility function.

Similar to activity type choice utility function, the start-time of the activity scheduling cycle is expressed as a continuous variable in hours from the beginning of the day. It is clear that this variable has a positive effect for Household Obligation, Drop-off/Pick-up, Shopping, Services and Recreational activity types on time expenditure trade-off with respect to composite activity. This indicates that people spend more time on these activities in the later part of the day. However, this variable has a negative coefficient for Work/School activity on time expenditure trade-off with respect to composite activity. This indicates that people spend more time on Work/School activity in the earlier part of the day. Interestingly, start-time has no effect on time expenditure in Basic Need and Social activities. This suggests that the durations of Basic Need and Social activities are not influenced by start-time in weekends.

The number of the scheduling cycle is represented by the number of activities already performed and is considered a variable in the baseline utility of the time expenditure function. It is clear that a higher number of activity cycle increases the utility of time expenditures on Basic Need and Social activities. It refers that longer-duration Basic Need activities are normally scheduled at the later part of the day. However, the combined effect of this variable with start-time indicates that if an individual participates in a smaller number of activities with longer durations the baseline utility of spending time on Basic need is low. However, if the individual participates in a large number of activities with shorter durations, it is likely that the person will spend a longer duration on Basic Need type activities.

Travel time does not have any significant effect on the baseline utility of spending time in Basic Need, Work/School and Recreational activities. In the case of Work/School and Recreational activities, increasing travel time reduces their probability of being scheduled. However, once these activities have been scheduled, the time expenditure is not influenced by how long to the individual must travel to the activity location, especially on the weekend. In the case of Household Obligation activity, longer travel time reduces the utility of being scheduled and if someone does schedule an activity of this type a longer travel time requirement influences the decision to spend shorter duration of time. While in case of Other activity type a longer travel time reduces the utility of being scheduled, but if someone does schedule an activity of this type, a longer travel time requirement influences the decision to choose a longer-duration activity. On the other hand, the utility of scheduling Drop-off/Pick-up, Shopping, Service, or Social activities on the weekend is not affected by travel time requirements. However, if someone schedules an activity of these types on the weekend a longer travel time induces spending a longer duration on that activity. A possible explanation of the longer duration induced by a longer travel time requirement is the psychological compensation or justification for travel time expenditure. Different effects of travel time requirement on activity scheduling and time expenditure decisions of different activity types indicates the existence of duration flexibility of different activity types in comparison to travel time to reach the activity location. It should be mentioned that the travel time variable is considered as an exogenous input in both activity type choice and time expenditure model components of this empirical exercise. If we estimate activity type, duration and location choice jointly, this variable will be generated endogenously. However, in either case, implementation of the model for forecasting will require an iterative approach of first assuming travel times and then use the model to forecast it for the next iteration to start with until getting a convergence. Habib et al (2009a, b) presents an algorithm of this type.

In case of household and personal attributes: a larger household size ensures the positive utility of spending time on Work/School, Household Obligation and Recreational activities. Intuitively larger household size incurs higher level of expenditure and influence people to work longer. Similarly, larger household size indicates higher number of household obligation type activity requirements as well as more Recreational demand. Older people seem to derive a lower utility from longer duration activities of Drop-off/Pick-up, Social and Other activity types, but they derive higher utility from longer duration activities of Work/School and Recreational activities in weekends. In case of Basic Need, Household Obligation, Shopping and Service activities, age is not an influential factor of deriving utility from activity duration in weekends. A higher income level increases the utility of spending time on Work/School and Household Obligation activity on the weekend. A higher number of household automobiles reduce utility of spending longer duration on Household Obligation activities than any other activity types on the weekend. People living in the residential neighborhood for a long time are less interested in spending time on Household Obligation and Recreational activities compared to Other activity type. Finally, a larger number of children at home increases the utility of scheduling a higher number of Household Obligation type activities, but reduces time expenditures on individual activity episodes on the weekend.

Satiation parameter and correlation coefficient

The satiation parameters are expressed as functions of the constant and the start-time of the activity. Such parameterization of the satiation parameter captures the inherent weekend time expenditure patterns according to the time of day scheduling information. The satiation parameter defines the final time expenditure on a specific activity in addition to the baseline utility value. As per the definition, the satiation parameter must be less than 1. A positive value of this parameter indicates the tendency to spend a longer duration of time. A negative value of this parameter refers to the tendency to spend a shorter duration of time. On the contrary, zero value of the satiation parameter indicates no satiation effect. Absence of satiation effect indicates more or less constant time expenditure tendency. In this application of a weekend scheduling model, it is clear that Basic Need and Work/School do not show any satiation effect in weekends. The constant values of Household Obligation, Drop-off/Pick-up, Shopping, Recreational, Social and Other activity types are negative, but the constant value of the Composite activity is positive. The Composite activity represents the time available for rest of the day activities at any scheduling cycle. Positive constant value of Composite activity satiation factor compared to the negative or zero values of other specific activity types indicates the presence of time pressure to shorten the scheduled specific activity duration to save time for rest of the day unscheduled (planned, but yet to be scheduled) activities. The model clearly captures the effect of activity planning within the activity scheduling process. It is conceivable that people often plan activity participations ahead of scheduling. The presence of such plan creates time pressure in the scheduling process. Incorporation of the composite activity to address the time budget limitations at each scheduling cycle makes it possible to capture such time pressure effects resulting from activity planning within the proposed dynamics scheduling model framework.

In addition to the constant term, activity start time as a continuous variable is considered as an influential variable to affect the satiation parameters of the specific activities. However, it is seen that only Recreational and Social activity types seems to have influence of start time on satiation parameters. It is clear that the start-time parameters are positive for Recreational and Social activity. This reveals a basic weekend time expenditure behavior—that individuals tend to spend a shorter duration of time at the beginning of the day and a longer duration of time at the end of the day for Recreational and Social activities. In order to capture the within day dynamics of the time pressure effect in term of saving time for rest of the day unscheduled (planned but yet to be scheduled) activities, the satiation parameter of the Composite activity is expressed a function of time of the day. In order to capture the non-linear effect of time of the day, in this case we found that hourly dummy variables represent the time of the day better. It is clear that all of the time of the day dummy variables have negative coefficients compared to the positive constant term. The negative values are higher at the beginning of the day and gradually reduce with the time of the day, subsequently reach to zero after 5 PM. This indicates that at the beginning of the day people are more relaxed about planned but yet to be scheduled activities, but with increasing time of the day the time pressure increases. In this empirical application, we are only concerned about activity scheduling process. However, these empirical evidences suggest that integrating activity generation (planning) and scheduling model will result in more behavioral and comprehensive activity-based travel demand model. Such an integrated model will allow us incorporation of activity planning attributes in terms of activity priority, flexibility, etc. within the activity scheduling model.

In terms of correlations between unobserved factors influencing activity type choice and time expenditure, significant correlations for all activity types exist. The estimated correlation coefficients has a negative sign, which indicates that the unobserved random factors influencing activity type choice and not allocating time are positively correlated. However, one should be careful in interpretation of this parameter, as it may change its sign as well as magnitude with changes in model specification. Basically, this parameter does not have any behavioral interpretation, but the magnitude and statistical significance reflect the necessity of joint estimation of activity type choice and time expenditure. However, the high statistical significance of this parameter justifies the joint estimation of the activity type and departure time choice model.

Demonstration of model application

In order to demonstrate the performance of the empirical model, the estimated model is validated using the same data set. It is clear that the model captures the variation of weekend activity participation and time expenditure behavior perfectly. The model clearly demonstrates its capacity to replicate the trend of activity choice and the corresponding time expenditure with the time of day. It is difficult to present all validation graphs/tables in a single paper, so we present only the validation results of the 10th scheduling cycle, which is the modal number of observed weekend scheduling cycles. However, in Fig. 2 we present the observed versus model-predicted activity type choice for the 9th, 10th and 11th scheduling cycle. It is clear that the model captures the trend of activity type choice. It terms of notable deviation from observed data, the model slightly under-predicts Recreational type activity, while it slightly over-predicts Household Obligation activity. Model performance in predicting time expenditure on some activities of the 10th scheduling cycle is presented in Fig. 3. It is clear that the model captures the time expenditure trend for all activities. The apparent deviations in model prediction from the observed values of some specific activity types are primarily due to the relatively small number of observations recorded. However, given that the model captures the trends and rhythm of weekend activity scheduling behavior, it can be used in the analyses of various scenarios for weekend transportation policy investigation.

Fig. 2
figure 2

Model validation results of activity type choice

Full size image
Fig. 3
figure 3

Model validation results of activity time expenditure (cycle 10)

Full size image

One thing becomes clear from the validation results—that the model performance improves with the increasing number of scheduling cycles modeled. This is because of the left censoring effects at the beginning of the day. For a 24-h scheduling model, we have to consider a start time of the day (12 midnight is considered in this case) that may not be the same for every person. This indicates the importance of adopting a multi-day scheduling model or at least of integrating the scheduling model with an activity generation model (considering an activity choice set varying with time of day). However, the expectation is that if the model were to be estimated with a large data set the results would be much more definitive.

In case of using the model for forecasting travel demand one has to apply the activity type choice and time expenditure model repeatedly in a sequential manner beginning from the beginning of the day. However, we need specific criteria to stop scheduling process, otherwise one can continue the scheduling cycle for infinite times and budget may not be exhausted. The solution to this potential forecasting problem is integrating activity location choice model with the scheduling model. We can fairly assume that we can ignore scheduling process after someone returns home at the end of the day.

Conclusions and direction for future research

This paper has presented a dynamic RUM-based activity scheduling model. The proposed model uses a RUM-based approach to model the behavioral process of activity scheduling so that activity patterns emerge as outcomes of the scheduling process. In order to demonstrate the power of the proposed econometric model, we have chosen weekend activity scheduling for empirical application. Normally, weekends are more flexible than weekdays and hence the application of this model for weekend scheduling may demonstrate the capacity to better capture the dynamic behavioral process. However, the model can also be applied for weekdays, even when considering different fixed commitments that are to be presented in the future extension of this current research. For empirical application of the weekend activity scheduling model, CHASE data collected in Toronto, Canada, has been used. First of all, the model proves its capacity to capture the behavioral process of activity scheduling by allowing a high number of statistically significant parameters with a relatively small sample data set.

The model accommodates dynamic variables such as time of day and number of scheduling cycles in order to capture the within-day dynamics of activity scheduling. In addition to the dynamic variables, the activity-specific variables explain the basic nature of weekend scheduling and time expenditure behavior with regard to different activities. The socio-economic variables capture systematic variations in behavioral processes (scheduling and time expenditure) across the population for weekend activity scheduling. The estimated model parameters are reasonable in terms of sign and relative values that explain interesting weekend activity scheduling behavior. In order to investigate the predicting capacity of the model, the model is validated using the same data set. The validation results prove that the model captures the trend of activity scheduling on weekend. Although in this empirical exercise we did not consider any hard scheduling rules (e.g., fixed commitments), the model captures variations in activity type choice and corresponding time expenditure based on the time of day. For example, participation in and time expenditure on Recreational and Social activities are well predicted by the model. The probability of some people’s scheduling of Work/School activities is also well predicted by the model. The model also effectively anticipates weekend time expenditure trends on Household Obligation, Shopping, Service, Recreational, and Social activities. Thus, the model validation results clearly prove the capacity of the model for various scenario analyses for transportation policy investigations.

Finally, many variables related to activity location and inter-household interactions are incorporated as exogenous variables in this paper. It is important to estimate activity location choice model jointly with the activity type and time expenditure choice model since, in many ways; it influences activity type choice and corresponding time expenditure. The empirical application presented in this paper clearly captures the presence of time pressure in activity scheduling. Logically, the time pressure in activity scheduling comes from activity planning (planning to do certain number and type of activities). The empirical model presented in these paper only deals with activity scheduling process and uses the scheduled activity information for empirical estimation. So, one obvious next step of research would be developing combined activity planning and scheduling model. Future application of this modeling framework for weekday or complete weekday-weekend scheduling behavior should also be explored. Similarly, inter-household interactions and travel mode choice (if a trip is necessary in order to arrive at the location of the activity) are also important. All of these issues pose methodological as well as data related challenges and hence are taken into account in recommendations for further research.