Introduction

Route choice modeling is probably one of the most complex and challenging problems in traffic assignment. It investigates the process of route selection by an individual, making a trip between predefined origin and destination (OD) pairs. The heterogeneity in travelers’ behavioral characteristics, in conjunction with the complex effect of route attributes, further increases the inherent complexity of route choice modeling. Although several approaches have been proposed to tackle this problem, one of the remaining challenges in route choice modeling is the consistency of the modeling approach with the underlying behavioral process of drivers’ decision making.

In general, most of the proposed route choice models focus on route related attributes of choice alternatives. This implies that in these “route-based” formulations, the route is perceived as an entity, and only attributes concerning the whole trajectory are used to characterize each choice alternative. From a behavioral perspective, this formulation suggests that the consideration set is formed based on route-level characteristics of trajectories and the final choice is made by selecting an entire route out of a considered set of alternatives. C-Logit (Cascetta et al. 1996) and Path-Size Logit (PSL) (Ben-Akiva and Bierlaire 1999) are among the most widely used route-based models. In these models, the similarity issue between alternatives has been addressed by adding a correction term to the deterministic part of the utility function, which alters the utility of pathsFootnote 1 based on their similarities. However, the applied correction factors in these models account only for similarities between the considered set of paths. To overcome this limitation, Frejinger et al. (2009) have proposed the Extended-Path-Size Logit (EPSL) model, which accounts for correlations between sampled and non-sampled alternatives.

An alternate approach offers a “link-based” formulation to deal with the correlation issue among alternatives. This approach, firstly proposed by Vovsha and Bekhor (1998) and later applied by Lai and Bierlaire (2015), adopts a cross-nested logit structure in which each link of the network constitutes a nest and each route belongs to several nests. Another application of the sequential link choice method has been applied by Fosgerau et al. (2013) in the context of a recursive logit model, which can be consistently estimated without the need of path sampling. The link-based formulation suggests that drivers have a link-by-link perception of the network and their choices are based on link-level attributes. Since a real network consists of a large number of links, the estimation of these models could be very computationally expensive.

A third approach is the “anchor-based” formulation which gives an exclusive importance to the effect of some prominent features of the road network, so-called landmarks or anchor points. This approach basically argues that anchor points are decisive points based on which drivers choose their paths. It has been pointed out by several researchers that individual’s perception of the road network follows a hierarchical representation (Hirtle and Jonides 1985; Holding 1994), and anchor points play a crucial role in the behavioral nature of route choice decisions (Manley et al. 2015b; Habib et al. 2013; Kazagli and Bierlaire 2015). The space hierarchy and the role of anchor points have also been found to be significant in similar decision making contexts such as location choice modeling (Elgar et al. 2009, 2015).

The importance of anchor points is emphasized in riverside cities. In these cities, the two sides, separated by the river, are usually connected through several bridges and tunnels. These infrastructures are usually prone to become traffic bottlenecks and to face recurrent traffic congestion (Woo et al. 2015; Habib et al. 2013; Sun et al. 2014). The high travel time variability of these small segments of the route, which is usually due to the large fluctuation of travel demand, turns them into influential points in the process of route selection. Accordingly, the choice of anchor points has a major effect on route selection, and routes crossing same anchor points share unobserved components such as safety, scenery, driving comfort, etc., emerging from the similarities of the road network and geographical characteristics.

In this work we argue that the three abovementioned formulations, in isolation, are not behaviorally accurate enough to represent the underlying nature of route choice behavior; rather a hybrid approach is needed. Route-based formulations suggest that route selection is mostly based on route-level attributes (Manley et al. 2015a), and ignore the influence of anchor points. Link-based formulations neglect the higher importance of anchor points by allocating the same level of importance to every link. Moreover, the anchor-based model proposed by Habib et al. (2013) incorporates a full probabilistic choice set generation, which is behaviorally inaccurate, and theoretically impractical and unmanageable in large route choice datasets and real world networks (Prato 2009).

We propose a generic “anchor-based nested” structure to promote the behavioral aspect of route choice models by incorporating the effect of route level attributes as well as anchor points on drivers’ choices. First, we adopt a classic Nested Logit (NL) structure within a discrete choice framework, in which upper nests correspond to anchor points and lower nests include route alternatives. Second, a nested Logit Kernel (LK) model is estimated to capture the reciprocal effect of route level attributes and anchor points on route selection. In the former model, the nested structure captures the shared unobserved components of the utility function among routes crossing the same bridge, while in the latter, the adopted factor analytic approach accounts for the interdependencies and latent similarities.

Similarly to anchor-based models, these approaches allocate a distinctive importance to the selection of anchor points as crucial segments of the route. Moreover, they can handle very large datasets and real world networks; considering multiple route alternatives within each bridge is easily manageable; and route-level attributes are also considered to be decisive and influential in the final route selection.

To explore the performance of the proposed formulations, GPS traces of taxi trips between the islands of Montreal and Laval have been used. The unique aspect of these trips is that drivers have to choose among a maximum of nine bridges separating the two regions. The access to these bridges face recurrent congestion, and despite their small share in the whole route, they have a significant impact on the total travel time and hence on drivers’ route choice decisions. In our application, bridges are considered as anchor points for trips between Montreal and Laval, and their effects on route choice decisions have been evaluated in conjunction with route level attributes. A very large real-world road network, with more than 40,000 nodes and 19,000 links, is used for choice set generation as well as model estimation. Estimates are then compared to three alternate models, representing route-based and anchor-based formulations; namely PSL, EPSL, and Independent Availability Logit (IAL) models.

Taxi drivers are considered to have a more precise knowledge of the road network and its traffic conditions, due to their higher driving experience. In order to capture the effect of anchor-points, we have focused on the behavior of taxi drivers as well-informed individuals who are more familiar with travel time variations and congestion periods over bridges connecting Montreal to Laval.

This work contributes to the existing state-of-the-art through the following aspects: (1) the presented formulations capture the effect of anchor points in conjunction with route level attributes in route choice modeling, (2) they improve the behavioral aspect of anchor-based formulations by capturing shared unobserved components among route alternatives crossing the same anchor point, and (3) the MH algorithm has been employed, for the first time, on a large real world route network to generate alternative choice sets.

This paper is organized as follows. First we review earlier approaches to route choice modeling and in that context further clarify the contributions of this study. The case study and data are presented next. We then discuss in detail the proposed econometric formulations and the estimated comparative models, as well as their respective utility function specifications and choice set generation algorithms. We then discuss the results, validation process, and comparison between models. In the end, we highlight the most significant findings of this study, underscore its limitations, and suggest further research directions.

State-of-the-art

There is a large body of literature in microeconomics, behavioral science, psychology, and behavioral geography that focuses on improving the understanding of the underlying process of decision making. Accordingly, several modeling frameworks have been proposed to simulate drivers’ route choice behavior. Prospect theory (Kahneman and Tversky 1979; Gao et al. 2010) and cumulative prospect theory (Tversky and Kahneman 1992; Xu et al. 2011; Connors and Sumalee 2009) have been applied by researchers to take into account the limited rationality of drivers in making decisions, by incorporating psychological and behavioral aspects. In some other studies, the uncertainty and imprecision of drivers in making route choice decisions have been taken into account using Fuzzy Logic (Henn 2003; Murat and Uludag 2008; Quattrone and Vitetta 2011; Luisa De Maio and Vitetta 2015). Artificial neural networks have also been used to take into account the non-linearity of the decision making process by imitating the human conscious structure (Dougherty 1995; Kim et al. 2005). Recently, a Random Regret Minimization (RRM) approach has been adopted by Prato (2014) in route choice modeling context. This approach argues that choice makers tend to choose the alternative which minimizes the regret of not having chosen other alternatives.

Among the proposed approaches, Random Utility Maximization (RUM) models have received considerable attention. In this approach, individuals’ preferences are represented by a value called “utility”, which captures the effect of different factors on the actual choice, and decision makers tend to maximize their perceived utilities. Since the decision maker may not have a perfect knowledge about these factors, an error component has been introduced to take into account the stochasticity and imprecision caused by uncertainty and behavioral randomness (Ben-Akiva and Bierlaire 2003). This paper is built upon the random utility maximization framework.

In the context of route choice, the perceived utility can be attributed to factors such as travel time, distance, congestion, safety, scenery, route complexity, number of traffic signals, trip purpose, fuel consumption, toll, road type, anchor points, etc. Behavioral and mental factors such as the inertia of taking the same route, memory, spatial abilities, driving experience, and the learning process may also play a role and add to the complexity of the modeling process (Prato 2009).

It has been suggested that individuals have a hierarchical planning strategy following the hierarchical representation of space and its connectivity (Manley et al. 2015b; Wiener and Mallot 2003), which yields an anchor-based navigation in which individuals orient themselves based on distinguished features of the route (Foo et al. 2005). Anchor points are defined as being important focal points and cognitively salient cues with prominent features, with applications in cognitive tasks, comprising way-finding, distance assessment, and direction estimation. Major route infrastructures, such as bridges, highways, eminent road interchanges, intersections and roundabouts, can be considered as anchor points in route choice modeling.

Several studies have argued that anchor points influence route choice decisions (Lynch 1960; Prato et al. 2012; Kaplan and Prato 2012; Golledge et al. 1985; Couclelis et al. 1987; Habib et al. 2013; Prato and Bekhor 2007). Manley et al. (2015a) studied minicab drivers in London, using GIS and statistical analysis, and concluded that their route choice behavior is poorly described by shortest-path algorithms and is improved when the role of anchor points is considered. To emphasize the significant role of anchor points, they have also proposed a conceptual subjective anchor-based route choice modeling schema. Similarly, Kazagli and Bierlaire (2015) argue that drivers describe their routes using a short sequence of Mental Representation Items (MRIs) such as anchor points or pieces of infrastructures instead of using a link-sequence representation. Moreover, a recent study by Manley et al. (2015b) confirms that the mental representation of the spatial hierarchy influences route choices. They propose a coarse to granular hierarchical representation of space, represented from top to bottom by Regions, Nodes, and Roads, where Regions represent clusters of nodes sharing a common characteristic; Nodes represent certain road junctions, landmarks, and anchor points; and Roads form the basis of the hierarchy, defining the route between consecutive Nodes. In this hierarchical schema, route choice is made through the selection of a sequence of regions, nodes across subsequent regions, and eventually, roads between successive nodes.

Despite the undeniable importance of anchor points on drivers’ route choice decisions, relatively little attention has been given to anchor-based route choice models. An interesting approach has been investigated by Habib et al. (2013) in which the authors applied an Independent Availability Logit (IAL) model, originally proposed by Swait and Ben-Akiva (1987), in a route choice context to emphasize the role of bridge choice in route choice decisions; the case study was the Greater Montreal Area. The IAL model follows the probabilistic two-stage choice model proposed by Manski (1977) in which the selection probability of an alternative depends on the selection probability of all subsets of the universal choice set containing that particular alternative. The IAL model jointly estimates the final choice and choice sets among all the possible combinations.

The study by Habib et al. (2013) was based on data collected from the OD survey of Montreal, in which the authors had only access to declared chosen bridges. They have considered a shortest path algorithm, based on segments’ speed limits, to generate one path per bridge for each OD pair, comprising the choice set of route alternatives. A noticeable limitation, pointed out by Prato (2009), of the fully probabilistic choice set generation approach adopted by the IAL approach, is its immense calculation burden when the size of the choice set increases. Considering m as the total number of possible alternatives, the total number of possible non-empty choice sets \((2^{m} - 1)\) increases exponentially with m, which makes it impractical to apply this model in route choice problems, where the considered choice set is large. In Habib et al. (2013), the inability of the IAL model in handling large choice sets might be an additional reason to their data limitation issue for considering only one alternative per bridge. In behavioral terms, the consideration of a single shortest path per bridge scales down the route choice problem to a bridge choice problem. Moreover, it is behaviorally unrealistic to assume that decision makers would consider every possible subset of the consideration choice set, before making a choice. Also, it is worth mentioning that the problem of shared segments between alternatives is not addressed in this recent application of the IAL model.

Context and dataset

Nowadays, the prevalent use of GPS technology provides researchers with an abundance of high-resolution geospatial data, which allows obtaining continuous and detailed (link-by-link) information on drivers’ travel paths, accompanied by possible additional information such as travel direction and speed. A relatively new source of GPS data is recorded by taxi companies around the world, mainly for operational purposes.

This study is based on GPS traces of taxi drivers, collected by a taxi company, in the context of the metropolitan region of Greater Montreal, depicted in Fig. 1a. The data was collected by a taxi company that constitutes around 25% of the Montreal Island taxi fleet, and its operation is restricted to trips starting or ending in the central part the island. Data has been stored in a PostgreSQL database, and the PostGIS spatial extension has been added to support geographical datatypes and queries. A direction-based nearest link point-to-curve map matching algorithm has been adopted to associate each GPS record to the road network. In point-to-curve map matching algorithms, every GPS point is matched onto the closest link in the network. The major shortcoming of these algorithms is that they do not produce reliable results in high road density networks and specially at intersections due to directional problems (White et al. 2000; Zhou and Golledge 2006). To overcome this issue, we associated each GPS record to its nearest link on the network with respect to its azimuth, so that it ensures that GPS points are not incorrectly matched to closer links with incorrect directions. A distance-based shortest-path algorithm has then been applied between consecutive GPS records to deduce the entire path for each trip.

Fig. 1
figure 1

Context of the studied region. a The metropolitan region of Greater Montreal; b locations of bridges connecting Montreal to Laval

Full size image

Montreal is an island city, separated from its suburbs by two rivers. This means that drivers entering or exiting Montreal need to cross one of the sixteen bridges connecting Montreal to its suburbs. These bridges face recurrent congestion and act as bottlenecks. For trips heading to or exiting Montreal, bridge choice can have a significant importance on route choice decisions (Habib et al. 2013). Considering bridges as anchor points, the geographical context of Montreal allows us to study the effect of anchor points in conjunction with route level attributes in route choice decisions.

In this study we focus on trips taking place between the Islands of Montreal and Laval, the largest suburb of Montreal located on the north of the city. These two islands are directly connected through seven bridges; B1–B7. Since bridges B8 and B9 might also provide convenient alternatives for trips between the East of Montreal and Laval, they have been included in this study. Figure 1b depicts the location of these nine bridges and Table 1 summarizes some of the pertaining properties of these bridges.

Table 1 Description of bridges connecting Montreal to Laval
Full size table

Montreal and Laval cover a total surface of 632.3 km2 containing a population of roughly 2.3 million inhabitants (Communauté métropolitaine de montréal 2012). Their road networks comprise more than 40,000 nodes and 19,000 links. The network data has been extracted from OpenStreetMap project in the format of geographical layers (shapefiles).

GPS records for the month of October 2014 have been extracted for this study. The dataset includes two tables: (a) GPS table containing information for every recorded point such as ID, time, geographical position, speed, and etc.; (b) the Events table, including information regarding the state of the taxi such as when the passenger has boarded and got off the taxi, etc. These two tables are related through a unique trip identifier (Ride ID). Table 2 shows the schema of the dataset.

Table 2 Internal structure of the database
Full size table

Our dataset consists of 4409 GPS records comprising 543 journeys with an average length of around 11 km and a standard deviation of 9 km. The average recorded travel time is around 15 min with a standard deviation of 12 min. The dataset comprises weekdays, as well as weekends and trips made in peak hours as well as off-peak trips. Eighty percent of the dataset (434 records) was randomly selected for calibration purposes, while the remainder 20% (109 records) was used for result validation.

Methodology

The principal aim of this research is to provide a behavioral framework, which explicitly takes into account the effect of anchor points as well as route-level attributes in route selection. To highlight the importance of anchor points in conjunction with route-level attributes, we adopt the following nested structures. First, we adopt a classic Nested Logit model in which the effect of anchor points is addressed in upper nests while route level decisions are represented in lower nests. Then, we adopt a nested Logit Kernel model, which accounts for the interdependencies of route alternatives crossing the same anchor point through the specification of its error structure.

In behavioral terms, our application of these nested structures suggests that individual taxi drivers, travelling between Montreal and Laval, consider bridges as crucial elements, along with other route level attributes, which affect their route choices. This section delineates the formulations of the abovementioned econometric models, presents the comparative route-based and anchor-based models, and describes their respective utility functions and choice set generation algorithms.

Econometric model formulation

Nested Logit

The Nested Logit (NL) formulation was proposed by Ben-Akiva (1973) and proved to be consistent with the stochastic utility maximization theory by McFadden (1978). It is an extension of the Multinomial Logit (MNL) model, and captures some of the unobserved similarities among alternatives by dividing the choice set into several nests. These nests are considered to be collectively exhaustive and mutually exclusive in covering the considered alternatives. Every nest contains a subset of alternatives sharing a particular characteristic, independent from other subsets of alternatives in other nests. In other words, the probability of choosing an alternative from a nest is considered to be independent from alternatives in other nests, which is known as the Independence of Irrelevant Alternatives (IIA) property. Therefore, the probability of choosing an alternative can be expressed as the product of the conditional probability of choosing that alternative given a particular nest and the choice probability of that respective nest (Guevara and Ben-Akiva 2013; Ben-Akiva 1973). It is worth mentioning that in our case, the nine considered bridges between Montreal and Laval are located relatively far apart from each other, and it is not far-fetched to assume that the IIA property holds within each nest of the model.

NL is a member of the Generalized Extreme Value (GEV) models (McFadden 1978), also known as Multivariate Extreme Value (MEV) models (Guevara and Ben-Akiva 2013). Within this framework, the probability of choosing alternative i by individual n within the true choice set C n is given by

$$P\left( {i |C_{n} } \right) = \frac{{e^{{V_{in} }} G_{i} \left( {e^{{V_{1n} }} , \ldots ,e^{{V_{{J_{n} }} }} } \right)}}{{G\left( {e^{{V_{1n} }} , \ldots ,e^{{V_{{J_{n} }} }} } \right)}}$$
(1)
$$G_{i} \left( {e^{{V_{1n} }} , \ldots ,e^{{V_{{J_{n} }} }} } \right) = \frac{\partial G}{{\partial e^{{V_{in} }} }}\left( {e^{{V_{1n} }} , \ldots , e^{{V_{{J_{n} }} }} } \right)$$
(2)

where G is a non-negative differentiable MEV generating function, \(G_{i}\) is its partial derivative with respect to \(e^{{V_{in} }}\), \(V_{in}\) specifies the systematic part of the utility function, and \(J_{n}\) is the number of alternatives in C n . The probability of choosing alternative i from the true choice set can be written as:

$$P\left( {i |C_{n} } \right) = \frac{{e^{{V_{in} + \ln G_{i} \left( {e^{{V_{1n} }} , \ldots ,e^{{V_{{J_{n} }} }} } \right)}} }}{{\mathop \sum \nolimits_{j = 1}^{{J_{n} }} e^{{V_{jn} + \ln G_{j} \left( {e^{{V_{1n} }} , \ldots ,e^{{V_{{J_{n} }} }} } \right)}} }}$$
(3)

where the partial derivative of the MEV generating function for Nested Logit G i , for the true choice set C, is:

$$G_{i} \left( C \right) = G_{i} \left( {e^{{V_{1} }} , \ldots , e^{{V_{J} }} } \right) = \mu e^{{V_{i} \left( {\mu_{m} - 1} \right)}} \left( {\mathop \sum \limits_{i = 1}^{{J_{m} }} e^{{\mu_{m} V_{i} }} } \right)^{{\frac{\mu }{{\mu_{m} }} - 1}}$$
(4)

in which \(\mu\) and \(\mu_{m}\) are scale parameters for the model and its nests, respectively, where \(\mu /\mu_{m} \le 1\), and m is the nest including alternative i. Since it is not feasible to enumerate the true choice set, a subset D has to be sampled, which must include the chosen alternative \(i\). To consistently estimate this model on a subset of alternatives, the correction approach proposed by McFadden (1978) can be adopted, in which an alternative specific correction term is added to the utility function.

$$P\left( {i |D} \right) = \frac{{e^{{V_{in} + \ln G_{i} \left( C \right) + \ln \pi \left( {D |i} \right)}} }}{{\mathop \sum \nolimits_{j = 1}^{J} e^{{V_{jn} + \ln G_{j} \left( C \right) + \ln \pi \left( {D |j} \right)}} }}$$
(5)

\(\ln \pi (D|i)\) is the sampling correction factor, and \(\pi \left( {D |i} \right)\) is the conditional probability of choosing subset D given the alternative i has been chosen. The approach developed by McFadden (1978) has been adopted by Bierlaire et al. (2008) to demonstrate that the maximization of the quasi-log-likelihood function of Eq. (5) yields consistent parameter estimates. It is worth mentioning that in our case, since a finite set of anchor points (bridges B1–B9, connecting the two regions) is considered for the upper nest level, the application of this correction factor is found to be superfluous and unneeded.

Although this function leads to the conditional probability of choosing alternative i given the subset D, its application is not valid with sampling of alternatives because \(\ln G_{j} \left( C \right)\) is still dependent on the true choice set (Guevara and Ben-Akiva 2013). In order to compensate for the loss of information due to sampling in each nest, an expansion factor w should be considered to approximate the generating function based on the considered sample \(D^{'}\). Moreover, to take into account the physical overlap between routes crossing the same anchor point, the Extended Path-Size factor (see Eq. (17)) has been added to the deterministic part of the utility function, so that:

$$P\left( {i|D,D^{\prime},w} \right) = \frac{{e^{{V_{i} + \ln EPS_{i} + \ln \hat{G}_{i} \left( {D^{\prime},w} \right) + \ln \pi (D|i)}} }}{{\mathop \sum \nolimits_{j = 1}^{J} e^{{V_{j} + \ln EPS_{j} + \ln \hat{G}_{j} \left( {D^{\prime},w} \right) + \ln \pi (D|j)}} }}$$
(6)

The closed form quasi-log-likelihood function has the following structure:

$$QL_{{MEV, D,D^{\prime},w}} = \mathop \sum \limits_{n = 1}^{N} \ln P\left( {i|D,D^{\prime},w} \right) = \mathop \sum \limits_{n = 1}^{N} \ln \frac{{e^{{V_{i} + \ln EPS_{i} + \ln \hat{G}_{i} \left( {D^{\prime},w} \right) + \ln \pi (D|i)}} }}{{\mathop \sum \nolimits_{j = 1}^{J} e^{{V_{j} + \ln EPS_{j} + \ln \hat{G}_{j} \left( {D^{\prime},w} \right) + \ln \pi (D|j)}} }}$$
(7)

Guevara and Ben-Akiva (2013) demonstrated that in order to achieve unbiasedness and consistency, the expansion factor should have the following structure:

$$w_{j} = \frac{{k_{j} }}{{E\left[ {k_{j} } \right]}}$$
(8)

in which \(k_{i}\) is the number of times alternative i has been sampled, and \(E\left[ {k_{j} } \right]\) denotes its expected value or its sampling probability. In this study, we adopt the formulation proposed by Lai and Bierlaire (2015) to approximate Eq. (5) over the choice set \(D^{\prime}\):

$$w_{j} = \frac{{k_{j} }}{{k_{s} }}\frac{{b_{\left( s \right)} }}{{b_{\left( j \right)} }}$$
(9)

where s denotes the path that has been sampled the most, k s is the number of times alternative s has been sampled (\(k_{s} \ge k_{i} \forall i \in D^{\prime}\)), and b (s) and b (j) are the theoretical frequencies of the most sampled path and path j, respectively.

Logit kernel (LK)

Logit Kernel, which is a combination of Probit and Logit models, was first proposed by Bolduc and Ben-Akiva (1991). The random component of its utility function is composed of a Probit-like term, which captures the interdependencies among alternatives, and an i.i.d. Gumbel distributed random component. The interdependencies between alternatives can be explicitly specified using a factor analytic approach, proposed by McFadden (1984). This approach accommodates different error structures and reduces the estimation complexity of the model (Bekhor et al. 2002; Bierlaire and Frejinger 2005). The utility function for individual n is defined as below:

$$U_{n} = X_{n} \beta + F_{n} T\zeta_{n} + \nu_{n}$$
(10)

where U n  − (J n  × 1) is the utility vector, and J n is the number of alternative in the choice set C n ; \(X_{n}\) − (\(J_{n} \times K)\) is the matrix of explanatory variables; \(\beta\) − (\(K \times 1)\) is the vector of unknown parameters; \(F_{n}\) − (\(J_{n} \times M)\) is the factor loading matrix; \(T\) − (\(M \times M)\) is a diagonal matrix of the standard deviation of each factor; \(\zeta_{n}\) − (\(M \times 1)\) is the vector of i.i.d. random variables with zero mean and unit variance; and \(\nu_{n}\) − (\(J_{n} \times 1)\) is the vector of i.i.d. Gumbel distributed random term with zero location, a scale equal to \(\mu\), and a variance equal to \((\pi^{2} /6\mu^{2} )\).

The LK model can replicate any error structure and approximate any random utility model (Walker et al. 2004; McFadden and Train 2000; Ben-Akiva et al. 2001). In a Nested Logit analog of the LK model, also known as the nested LK model, \(F_{n}\) is defined to be the alternative-nest incident matrix and is obtained by defining a dummy variable for each nest that equals 1 if an alternative belongs to that particular nest, and 0 otherwise. Moreover, \(\zeta_{n}\) is usually assumed to be normally distributed \(N\left( {0, 1} \right)\), and \(T\) captures the amount of correlation between alternatives belonging to the same nest (Train 2009; Walker et al. 2004). In this study, the correlation related to the physical overlap between routes crossing the same bridge is expressed through the Extended Path-Size factor (see Eq. (17)), which is added to the utility function \(\left( {\ln EPS} \right)\). If the factors \(\zeta_{n}\) are known, the probability of choice \(i\) given \(\zeta_{n}\) is estimated using the MNL formulation:

$$\Lambda \left( {i |\zeta_{n} } \right) = \frac{{e^{{\mu (X_{in} \beta + lnEPS_{in} + F_{in} T\zeta_{n} )}} }}{{\mathop \sum \nolimits_{j = 1}^{{J_{n} }} e^{{\mu (X_{jn} \beta + lnEPS_{jn} + F_{jn} T\zeta_{n} )}} }}$$
(11)

Since \(\zeta_{n}\) is unknown, the unconditional probability takes the following form:

$$P\left( i \right) = \mathop \smallint \limits_{\zeta }\Lambda \left( {i |\zeta_{n} } \right)\mathop \prod \limits_{m = 1}^{M} \phi (\zeta_{m} )d\zeta$$
(12)

where \(\phi \left( {\zeta_{m} } \right)\) is the standard univariate normal density function, and \(\mathop \prod \limits_{m = 1}^{M} \phi (\zeta_{m} )\) represents the joint density function of \(\zeta\). Since the probability function does not have a closed form, it is approximated through simulation:

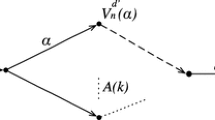
$$\hat{P}\left( i \right) = \frac{1}{D}\mathop \sum \limits_{d = 1}^{D}\Lambda \left( {i |\zeta_{n}^{d} } \right)$$
(13)

where \(D\) is the number of simulation draws and \(\zeta^{d}\) denotes draw d from the distribution of \(\zeta\). In this study, the factor analytic specification takes into account the effect of anchor points on route choice decisions and corresponds to bridges connecting Montreal to Laval. These factors capture the unobserved similarities among routes crossing the same anchor points. Accordingly, the \(F_{n}\) matrix is defined to be the route-bridge incident matrix with a dummy variable for each bridge, equal to 1 if a route crosses that particular bridge, and 0 otherwise.

Comparative models specification

The two presented anchor-based nested formulations are compared with three other models representing route-based and anchor-based formulations, namely the PSL, EPSL and IAL models. A concise introduction to these models follows.

Path-size Logit

First, a PSL model is estimated as an instance of route-based models (Prato 2009; Ben-Akiva and Bierlaire 1999). This model uses a correction factor in the deterministic part of the utility function to account for the correlation among sampled paths; however, it ignores the correlation with non-sampled paths:

$$P_{PSL} \left( {i|C_{n} } \right) = \frac{{e^{{\mu \left( {V_{in} + \ln PS_{in} } \right)}} }}{{\mathop \sum \nolimits_{{j \in C_{n} }} e^{{\mu \left( {V_{jn} + \ln PS_{jn} } \right)}} }}$$
(14)

where \(P_{PSL} \left( {i |C_{n} } \right)\) is the conditional probability of user \(n\) choosing alternative \(i\) from the universal choice set \(C_{n}\), \(\mu\) is a scale factor, and \(V\) is the deterministic part of the utility function. The Path-Size factor \(lnPS\) is added in a logarithmic scale to the deterministic part and is calculated as below:

$$PS_{in} = \mathop \sum \limits_{{a \in \varGamma_{i} }} \frac{{L_{a} }}{{L_{i} }}\frac{1}{{\mathop \sum \nolimits_{{j \in \varphi_{n} }} \delta_{aj} }}$$
(15)

where \(L_{a}\) and \(L_{i}\) represent the length of link \(a\) and path \(i\), \(\Gamma _{i}\) is the set of road segments in path \(i\), \(\varphi_{n}\) denotes the considered choice set, and \(\delta_{aj}\) is the link-path incident binary variable which is 1 if link \(a\) is on path \(i\), and 0 otherwise. In other words, \(\mathop \sum \nolimits_{{j \in \varphi_{n} }} \delta_{aj}\) indicates the total number of alternatives in the choice set sharing link \(a\), for observation in \(\varphi_{n}\).

Extended-path-size Logit

Second, an EPSL model (Frejinger et al. 2009) has been estimated which is also an instance of route-based models, in which the PS factor has been extended to take into account the correlation of each alternative with all the possible paths in the true choice set. However, the structure of the conditional probability stays the same:

$$P_{EPSL} \left( {i|C_{n} } \right) = \frac{{e^{{\mu \left( {V_{in} + \ln EPS_{in} } \right) + \ln \left( {\frac{{k_{in} }}{q\left( i \right)}} \right)}} }}{{\mathop \sum \nolimits_{{j \in C_{n} }} e^{{\mu \left( {V_{jn} + \ln EPS_{jn} } \right) + \ln \left( {\frac{{k_{jn} }}{q\left( j \right)}} \right)}} }}$$
(16)

and the EPS factor is defined by

$$EPS_{in} = \mathop \sum \limits_{{a \in \varGamma_{i} }} \frac{{L_{a} }}{{L_{i} }}\frac{1}{{\mathop \sum \nolimits_{{j \in \varphi_{n} }} \delta_{aj} \omega_{jn} }}$$
(17)

where \(\omega_{jn}\) is an extension factor with a value equal to 1 if \(\delta_{aj} = 1 {\text{or}} \, q\left( j \right)\, R_{n} \ge 1\), and \(1/\left( {q\left( j \right)R_{n} } \right)\) otherwise; where \(R_{n}\) denotes the total number of paths drawn with replacement from the universal choice set, \(q\left( j \right)\) is the sampling probability of path \(j\), and k jn is the empirical frequency or the actual number of times path j is drawn.

Independent availability Logit

Third, an IAL model (Swait and Ben-Akiva 1987) has been estimated to illustrate the performance of anchor-based models. In this formulation the choice set is latent and the probability of considering any combinations of alternative as the final choice set is calculated. The conditional probability of alternative i being chosen is calculated as

$$P_{i}^{IAL} = \mathop \sum \limits_{D \subseteq \varGamma } P_{D} P_{i|D} = \mathop \sum \limits_{D \subseteq \varGamma } \frac{{\mathop \prod \nolimits_{i \in D} A_{i} \mathop \prod \nolimits_{i \in C - D} \left( {1 - A_{i} } \right)}}{{1 - \mathop \prod \nolimits_{i \in C} \left( {1 - A_{i} } \right)}}\left( {\frac{{\exp \left( {\mu V_{i} } \right)}}{{\mathop \sum \nolimits_{j \in D} \exp \left( {\mu V_{j} } \right)}}} \right)$$
(18)

where P D is the probability of drawing the choice set D from a set of all possible non-empty choice sets \(\Gamma\) of the universal choice set C; P i|D denotes the probability of choosing alternative i from the choice set D; and \(A_{i} = \left( {1 + \exp \left( { - \alpha x} \right)} \right)^{ - 1}\), where x denotes attributes and α refers to parameters to be estimated. In order to achieve the proposed formulation for \(P_{D}\), it is assumed that the IIA property holds for alternatives in the considered choice set.

Utility function specification

Four attributes are used to specify the systematic part of the utility function:

  • Mtl_Len specifies the portion of trip length made on the island of Montreal,

  • Lvl_Len denotes the portion of trip length made on the island of Laval,

  • Hgw_Len stands for the portion of trip length made on highways, and

  • Seg_Len indicates the average length of road segments.Footnote 2

The minimum, maximum, average and median values of these attributes over the whole dataset are reported in Table 3.

Table 3 Statistics on attributes included in the systematic part of the utility function
Full size table

In estimating NL, LK, PSL, and EPSL models, the utility function for observation \(i\) is defined to be:

$$V_{i} = \beta_{Mtl\_Len} \times {\text{Mtl}}\_{\text{Len}}_{i} + \beta_{Lvl\_Len} \times {\text{Lvl}}\_{\text{Len}}_{i} + \beta_{Hgw\_Len} \times {\text{Hgw}}\_{\text{Len}}_{i} + \beta_{Seg\_Len} \times {\text{Seg}}\_{\text{Len}}_{i}$$
(19)

For the IAL model, the length of the trip made on the island of Montreal, which practically specifies the distance from the origin to the bridge, is used in the first part of the model to determine the selection probability of each choice sets:

$$A_{i} = \left( {1 + \exp \left( { - \beta_{Mtl\_Len} \times {\text{Mtl}}\_{\text{Len}}_{i} } \right)} \right)^{ - 1}$$
(20)

The other three variables are used to define the systematic part of the utility function:

$$V_{i}^{IAL} = \beta_{Lvl\_Len} \times {\text{Lvl}}\_{\text{Len}}_{i} + \beta_{Hgw\_Len} \times {\text{Hgw}}\_{\text{Len}}_{i} + \beta_{Seg\_Len} \times {\text{Seg}}\_{\text{Len}}_{i}$$
(21)

Choice set generation

The consideration set should include attractive alternatives. Since random sampling of alternatives in large universal choice sets is not efficient in terms of providing information, an importance sampling method would be more convenient and favorable (Hess and Daly 2010). Several deterministic and probabilistic path generation methods which are mostly based on repeated shortest path algorithms have been proposed in the literature to form the consideration set. Among them are link labelling (Ben-Akiva et al. 1984), link elimination (Azevedo et al. 1993), and link penalty (de la Barra et al. 1993) methods. A thorough review of these methods is presented in (Prato 2009) and (Frejinger and Bierlaire 2010). The major downside of using these methods is that they do not provide researchers with sampling probabilities of the generated alternatives. Model estimates based on these path generation methods are biased, unless the sampling probability of every alternative in the universal set is equal, which is not the case in route choice modeling.

Several alternative approaches have been proposed. Cascetta et al. (2002) adopted a two stage process, where in the first step, a complete set of alternatives is generated for all the observations by maximizing a coverage factor between the generated set and the set of routes perceived as available. Then, in the second step, a binomial Logit model is adopted to estimate the probability of including a given route in the users’ consideration set. Frejinger et al. (2009) applied a biased random walk to sample a subset of paths and derived a sampling correction to obtain unbiased parameter estimates. More recently, Flötteröd and Bierlaire (2013) used a Metropolis–Hastings (MH) algorithm to generate sample sets based on an arbitrary distribution providing the sampling probability of each alternative. This algorithm requires a road network and a definition of path weight as an input. It uses an underlying Markov Chain process to sample alternatives and calculates its sampling probability without the need of normalizing it over the full choice set.

For the NL model estimated in this study, the MH algorithm has been adopted to generate nine alternatives per nest. In order to apply this algorithm on the large road network of Montreal and Laval, 100 separate input files have been prepared to provide the possibility of parallel calculation. Files have been imported into a cluster of 26 computers (2 processors Intel(R) Xeon(R) X5675 @ 3.07 GHz) which took about 104 h (4 days and 8 h) to generate the output files. For the LK, PSL, and EPSL models, the MH algorithm has been adopted to draw 19 choice alternatives from the universal choice set. Similarly to the NL model, 100 separate input files have been prepared to provide the possibility of parallel calculation, which resulted in a calculation time of 46 h (1 day and 22 h).

For the IAL model, a shortest path algorithm, using segments’ speed limits as travel cost, has been adopted. The same algorithm was used in the original application by Habib et al. (2013) and provides the possibility of comparison between the outputs. In the IAL formulation, the feasible choice set built in the choice generation step is considered to be the equivalent of the universal choice set C. Since the algorithm calculates the choice probability of every non-empty subset of the universal choice, the number of considered alternatives should be restricted for computational purposes. The chosen alternative and eight shortest-distance paths, crossing the eight alternative bridges, comprise the nine feasible alternatives for each observation. Although Habib et al. (2013) showed that the IAL performs well in anchor choice prediction, it is very computationally expensive for applications involving large choice sets, such as route choice modeling applications.

In this study, different sizes of choice sets have been generated for practicality reasons. Considering larger choice sets would have increased the computational time dramatically; however, similarly to Elgar et al. (2009) the estimation gain would have probably been minor. In all the above mentioned applications, the chosen alternative has been added to the choice set, where it was not generated by the adopted choice set generation algorithm (McFadden 1978; Elgar et al. 2009; Arifin 2012; Prato et al. 2012; Frejinger et al. 2009; Habib et al. 2013; Dhakar and Srinivasan 2014; Hess et al. 2015).

Results and discussion

This section presents, compares and discusses the estimation and prediction abilities of the aforementioned models. The BIOGEME software package (Bierlaire and Fetiarison 2009; Bierlaire 2003) has been used for all model estimations.

Estimation

Eighty percent of the observations, that is 434 trips, were randomly selected for estimation purposes. A heat-map of origin and destination points, presented in Fig. 2, illustrates higher density regions, located mostly around metro stations, airport, downtown Montreal, and commercial centers, which have an expectedly higher taxi demand. A heat-map of chosen routes between OD pairs is illustrated in Fig. 3. Around 40% of the whole network size, considered for choice set generation, has been covered by drivers’ route choices.

Fig. 2
figure 2

Heat-map of origin and destination points for trips between Montreal and Laval

Full size image
Fig. 3
figure 3

Heat-map of chosen routes between OD pairs for trips between Montreal and Laval

Full size image

A detailed description of models’ estimates is provided in Table 4. Presented models are fully identified according to the smallest singular value approach implemented in BIOGEME (Bierlaire 2015). The scale parameter in PSL, EPS and LK models were estimated while they have been fixed to 1 in IAL and NL models for identification purposes. Scale factors for nests in the NL model have been estimated and μ ≤ μ m holds for every nest. Since the composition of the choice set differs from a model to another, not much can be inferred from the comparison of their scale factors. However, an out-of-sample validation method has been used to properly compare the models’ performances, which will be presented and discussed in the subsequent section.

Table 4 Model estimates for taxi trips between Montreal and Laval
Full size table

Intuitively, taxi drivers are apt to minimize their travel distance by choosing a shorter route, and their travel time by riding on segments with higher speed limits. This behavior is confirmed by the obtained results from all the estimated models. Coefficients β Mtl_Len and β Lvl_Len are negative while β Hgw_Len has a positive sign, meaning that taxi drivers are more willing to take shorter alternatives and are more inclined to ride on highways. These findings are in agreement with results reported by Duan and Wei (2014) who claimed that most taxi drivers tend to minimize their travel time. The effect of the average length of the segment is expectedly positive for PSL, EPSL, LK, and NL models, implying that taxi drivers tend to avoid intersections and prefer to take routes with a longer average segment length. However, this estimate has a negative sign for the IAL model, which might be attributed to the fact that alternatives are assumed to be completely independent from each other and their correlations have been neglected. The positive signs of β PS and β EPS are a negative correction of the utility for overlapping routes, giving a higher chance to less similar alternatives to be chosen. Similar findings are reported by (Dhakar and Srinivasan 2014; Prato and Bekhor 2006, 2007; Bierlaire and Frejinger 2008).

Note that the anchor-based nested models, namely LK and NL models, result in significantly higher Rho-square values compared to the route-based and anchor-based models. This emphasizes the importance of bringing the concept of anchor points in route choice modeling, so that it becomes more consistent with the actual behavior of drivers. The σ estimates are highly significant (except for bridge 6) for the LK model, implying that the factor analytic structure captures a significant correlation structure between routes crossing the same bridges. It is also noted that this effect is statistically different from the effect captured by the EPS factor. This is consistent with findings in Bekhor et al. (2002) and Bierlaire and Frejinger (2005), where the authors presented a LK route choice model considering subpath components. The better fit of the LK model with an EPS attribute over the PSL and EPSL models is in line with findings reported by Ramming (2001) and Bierlaire and Frejinger (2005). It is worth mentioning that the travel time-based shortest path algorithm, used in the choice set generation step of the IAL model, does not provide the researcher with the sampling probability of paths in order to correct the sampling effect. The better fit of all other models can be partially attributed to the application of MH algorithm, which provides the possibility of considering the sampling correction factor.

The estimation time has also been reported in Table 4. All model estimations were conducted on a machine with a core i7-4720HQ CPU running at 2.6 GHz and a Random Access Memory (RAM) of 16.0 GB. Concerning PSL and EPSL models, the computational time was found to be less than 1 s which is probably due to their simple multinomial logit structure. The small number of considered alternatives per observation may be a further reason for the simplicity of their calculation. However, there is a large difference in computational costs between these models and the IAL model. Although the number of feasible alternatives for the IAL model is limited to 9, the high computational cost might be related to the fact that every possible non-empty subset (29 − 1 = 511 subsets) must be considered for every observation. Implementing a NL structure reduces the calculation time substantially, compared to the IAL model, by providing a more realistic structure to represent drivers’ route choice behavior. It is behaviorally not realistic and computationally not feasible to assume that drivers consider 511 non-empty subsets in order to make a choice from a set of 9 nine alternatives. However, the increase in computational time compared to the PSL and EPSL models might be explained by the more complex structure of NL compared to MNL, and the greater number of alternatives considered for the NL model (82 alternatives per observation compared to 20 alternatives for PSL and EPSL models). Expectedly, the largest estimation time is recorded for the LK model. The normally distributed portion of the disturbance requiring large number of draws in model estimation, leads to a computationally demanding model (Ben-Akiva et al. 2001; Walker et al. 2004).

Validation

In order to further compare these models, their ability to predict should also be evaluated in the final stage. An out of sample validation has been performed to evaluate the prediction capability of the estimated models. Twenty percent of the observations (109 trips), which have not been used for model estimation, have been randomly sampled for this purpose. The validation has been performed based on models’ abilities to correctly predict:

  1. 1.

    The chosen bridge,

  2. 2.

    The chosen route, and

  3. 3.

    The total overlapping percentage with chosen alternatives (coverage rate).

The aforementioned three indicators have been calculated and results are illustrated in Fig. 4. Part A of Fig. 4 compares models’ performances in terms of correctly predicting the taken route. It clearly shows that LK and NL perform better than the three other models with a prediction rate of 72.5 and 73.4% compared to 51.4, 53.2 and 55% for the PSL, EPSL and IAL models, respectively. The ability to correctly predict the chosen bridge is compared in part B of Fig. 4. Similarly, LK and NL outperform PSL and IAL with prediction rates of 91.8 and 92.7% compared to 89 and 55%, respectively. The performance of EPSL is roughly similar to the anchor-based nested formulations with a small difference of around 1.0%, which may be attributed to simulation errors. In order to understand how closely each model has predicted the chosen route, we have calculated the length percentage that has been correctly predicted by each model. This coverage rate is compared in part C of Fig. 4, and clearly demonstrates the superiority of anchor-based nested formulations.

Fig. 4
figure 4

Comparison of models’ prediction abilities

Full size image

Since IAL model is an anchor-based model, it was expected to perform better in bridge choice prediction with respect to studied route-based models. The poor performance of this model, in this study, in terms of both estimation and prediction might be attributed to the fact that a fixed utility function has been used to compare the four models. Using more explanatory variables describing bridge characteristics in Eq. (18) might have improved both the model’s fit over data and its prediction abilities.

Based on the abovementioned results, we conclude that the proposed anchor-based nested approaches outperform route-based as well as anchor based models. This conclusion is in line with findings reported by (Manley et al. 2015a; Kazagli and Bierlaire 2015; Habib et al. 2013; Manley et al. 2015b; Prato and Bekhor 2007) who claimed that anchor points have an important effect on individuals’ route selection behavior. However, the important aspect of this study, which is the estimation of the comprehensive effect of both route-level attributes and anchor points, clearly demonstrates that considering the role of bridges as anchor points in conjunction with route-level attributes, for trips between Montreal and Laval, enhances both the estimation and prediction abilities of the model.

Conclusions

In this paper we have explored the application of a nested structure to improve the behavioral aspect of route choice modeling by incorporating the effect of space hierarchy in drivers’ decision making process. We have argued that current approaches have either neglected the effect of anchor points by considering only route level attributes (route-based formulations), or have adopted a full probabilistic approach for choice set generation, which is behaviorally inaccurate, and theoretically impractical to implement in real world networks (anchor-based formulations).

The anchor-based nested approaches, proposed in this paper, attempt to improve the behavioral aspect of route choice modeling by incorporating the effects of anchor points and route level attributes at the same time. As previous studies have shown (Habib et al. 2013; Sun et al. 2014; Woo et al. 2015), in riverside cities such as Montreal, route choice decisions are highly influenced by their respective bridge choices. Moreover, routes crossing a same bridge share unobserved components such as safety, scenery, driving comfort, etc., which is mainly because they share the same network and geographical characteristics. In this study, we capture this reciprocal effect through a nested structure.

GPS data provided by a taxi company in Montreal has been used to study trips made between the island cities of Montreal and Laval. For these trips, drivers have to choose between a maximum of nine bridges, providing plausible route alternatives between these cities. These bridges face recurrent congestion and play an important role in drivers’ route decisions due to their high travel time variability. To address the role of bridges as anchor points, a discrete choice utility maximization framework has been adopted. First, a NL formulation has been proposed, in which upper nests represent bridges and lower nests consist of route alternatives crossing respective bridges. Second, a nested LK with a factor analytic structure is specified. The EPS factor has been added to the deterministic part of the utility functions of these models to account for physical overlap among routes crossing the same bridge. The unobserved similarities among these routes are captured through the nested structure and the factor analytic structure in NL and LK models, respectively.

To evaluate the performance of the proposed anchor-nested formulations, they are compared to the recent route- and anchor-based models, namely PSL, EPSL and IAL models. For the sake of simplicity in estimation and comparison, four most important variables have been selected to define a common utility function between models. Findings revealed that the nested structures provided better model fits and underscored the importance of considering the comprehensive effect of anchor points and route level attributes in route choice decisions. Results have expectedly illustrated that taxi drivers are more likely to drive on highways and tend to decrease their travelled distance. It has also been found that they prefer to avoid intersections and tend to drive on routes with a higher average segment length. The predictive ability of these models has also been compared by an out-of-sample validation approach. Three indicators have been used for this purpose, namely the number of correctly predicted routes, the number of correctly predicted bridges, and the overlap percentage between the predicted and chosen alternatives. The overall results suggest that LK and NL outperform the other three models in the validation step.

In short, incorporating the effects of anchor points in a nested structure has the following advantages over the previously studied anchor based model: (1) the nested structure improves the behavioral aspect of decision making process. In the conventional anchor based model (IAL), a probability is assigned to every subset of the universal choice set, and the conditional probability of an alternative being chosen implies that the decision maker has considered every possible combinations of alternatives as his final choice set, which is behaviorally unrealistic, (2) LK and NL models are easily manageable and practical, even by considering a large number of alternatives (McFadden 1978). IAL incorporates a full probabilistic choice set generation approach which is inapplicable in route choice modeling (Prato 2009). For instance, considering a small dataset of 10 alternatives, a selection probability has to be calculated for every 1023 non-empty subsets of alternatives which is very time-consuming and impractical, and (3) the nested structure allows the consideration of multiple anchor points and their effects on route choice decisions. It is worth mentioning that the inclusion of multiple landmarks and anchor-points, and the consideration of several forms of heterogeneity, such as decision makers’ taste variations, are much more manageable and can be accommodated more easily in LK than in the NL mode. This is due to the flexible structure of the error term, which can approximate almost any desirable error structure (Walker et al. 2004).

This study contributes to the existing literature in two ways. First, it improves the behavioral, theoretical, and practical aspects of anchor-based route choice models by capturing the effects of both anchor points and route level attributes within a nested choice model framework, and clearly underscores the importance of considering the effects of anchor points in conjunction with route-level attributes. Second, a large real-world road network, consisting of over 40,000 nodes and 19,000 links, has been studied and a MH algorithm has been adopted to generate a set of considered alternatives. To the best of the authors’ knowledge, the largest network previously tested on this algorithm was composed of about 8000 nodes and 17,000 links (Flötteröd and Bierlaire 2013). The major advantage of MH sampling algorithm over conventional methods (e.g. link labelling, link elimination, etc.) is that it provides researchers with path sampling probabilities, so that model estimates based on these sets are not biased. It is noted that in route-based models and most of the link-based formulations, the consideration set is commonly generated using shortest-path algorithms with some pre-defined impedance function, which do not provide path sampling probabilities, and hence do not account for the correlation between sampled and non-sampled paths, resulting in biased estimates.

It is worth mentioning that since this paper is based on a dataset covering a fraction of taxi fleets operating in Montreal, results may not be directly transferable to other car drivers in Montreal or any other similar regions in the world. Additional datasets from different contexts and population segments are needed to provide more insights on this subject. However, it reveals the undeniable effect of anchor points on the decision of the whole path, and provides valuable insights regarding drivers’ route selection behavior.

As the core of traffic assignment methods, a more realistic route choice model improves the travel demand assessment on the road network. An application instance of the proposed models would be their utilities in predicting drivers’ behavior under hypothetical situations, and the way drivers react to different policies and changes. For example, the effect of a temporary lane closure on one of the bridges can be assessed on other bridges and route segments.

For future works, it would be interesting to investigate the spatial and temporal transferability of the proposed structure for different datasets on similar case studies. Also, more interesting structures such as multilevel nested models can be estimated to explore the effects of multiple anchor points on route choice decisions. In this work, we have neglected the effect of shared segments between routes crossing different bridges (alternatives in different nests), to accommodate the IIA property of the NL model. The inclusion of a correction factor accounting for this shared similarity might improve estimation results.

Route choice is also influenced by travel time and congestion. A shortcoming of this study is that travel time related attributes have been neglected in this study due to data availability issues. In order to improve models’ estimation and prediction abilities, it is recommended to consider travel time related attributes on bridges and route segments. Furthermore, including physical characteristics of bridges can also be interesting and can provide useful insights on their effects on the attractiveness of an alternative. It is expected that the inclusion of these factors will enhance models’ estimation and prediction abilities. Another appealing aspect to investigate would be the incorporation of some socio-demographic and behavioral factors which were not available in our dataset. Also, incorporating the role of dynamic information, knowledge, and level of experience would add an interesting aspect to this modeling process. A recent study by Vitetta (2016) explores a new realm of route choice models called Quantum Utility Model (QUM), which captures the effect of intermediate (during the trip) decisions, where decision makers are uncertain about their final choices. A comparison study between the proposed approach in this study and the study by Vitetta (2016) might also be interesting as a future expansion of this work. Another interesting area to explore would be the extension of the Recursive Logit (RL) model proposed by Fosgerau et al. (2013) by incorporating the effects of anchor points.